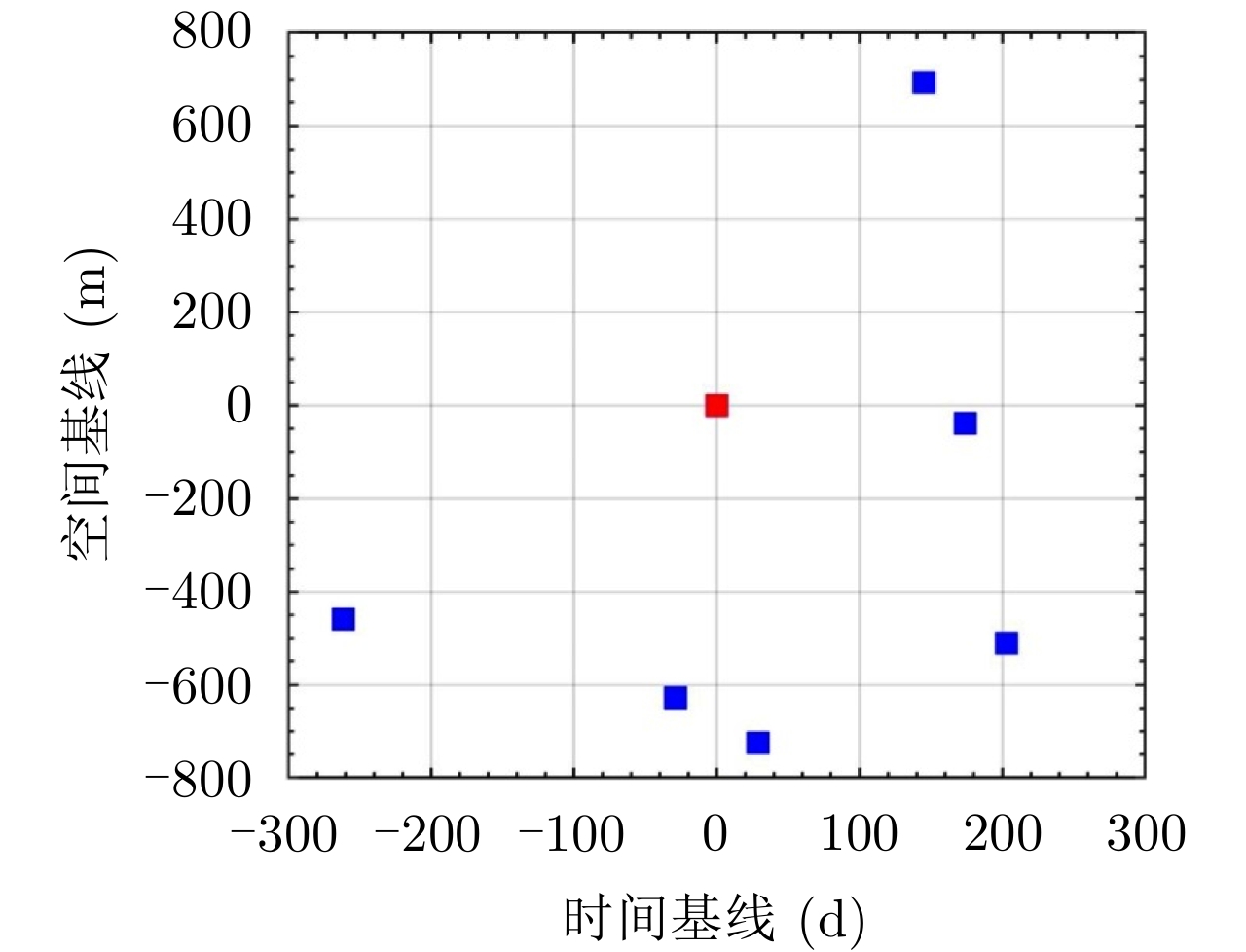
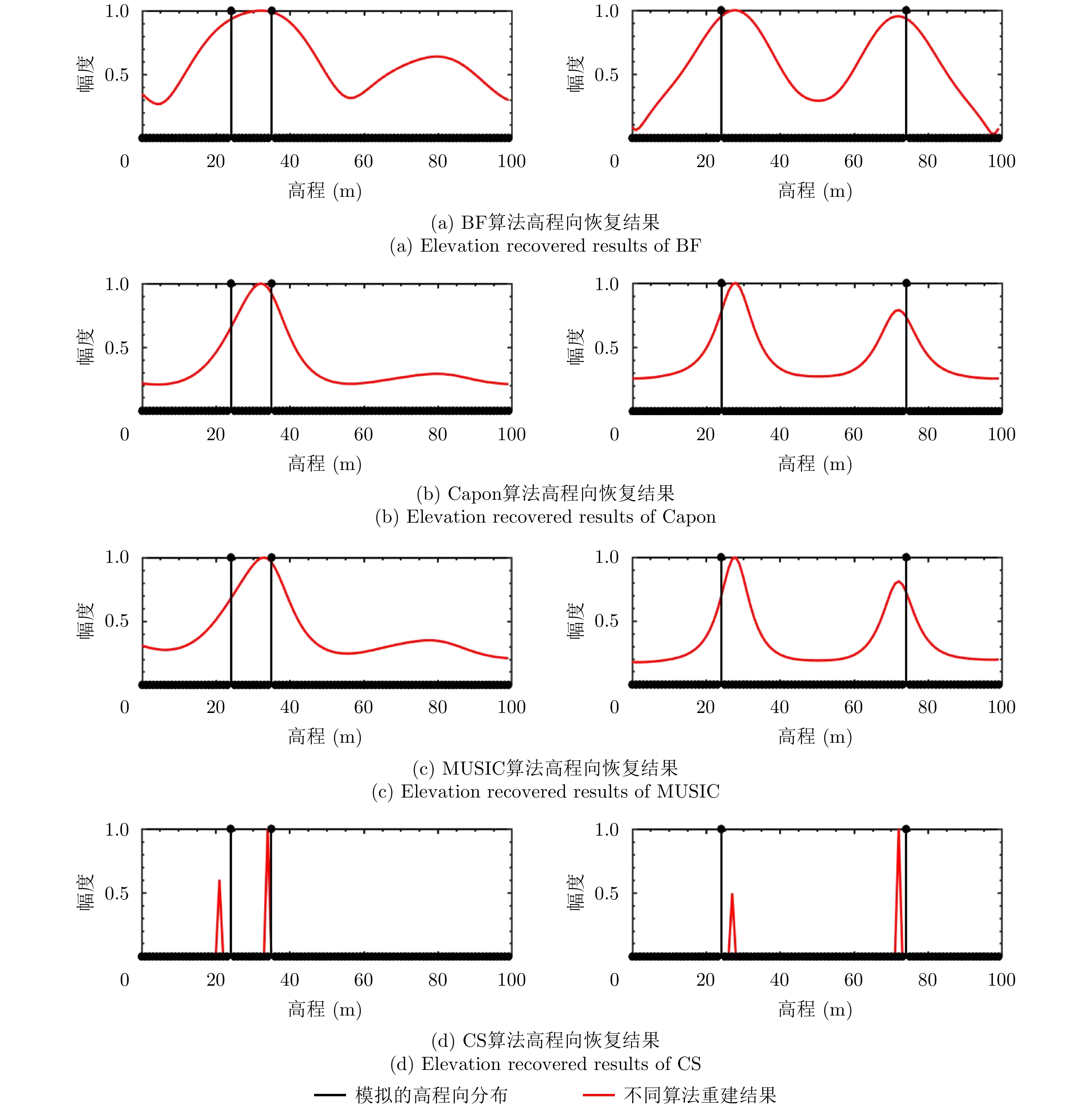
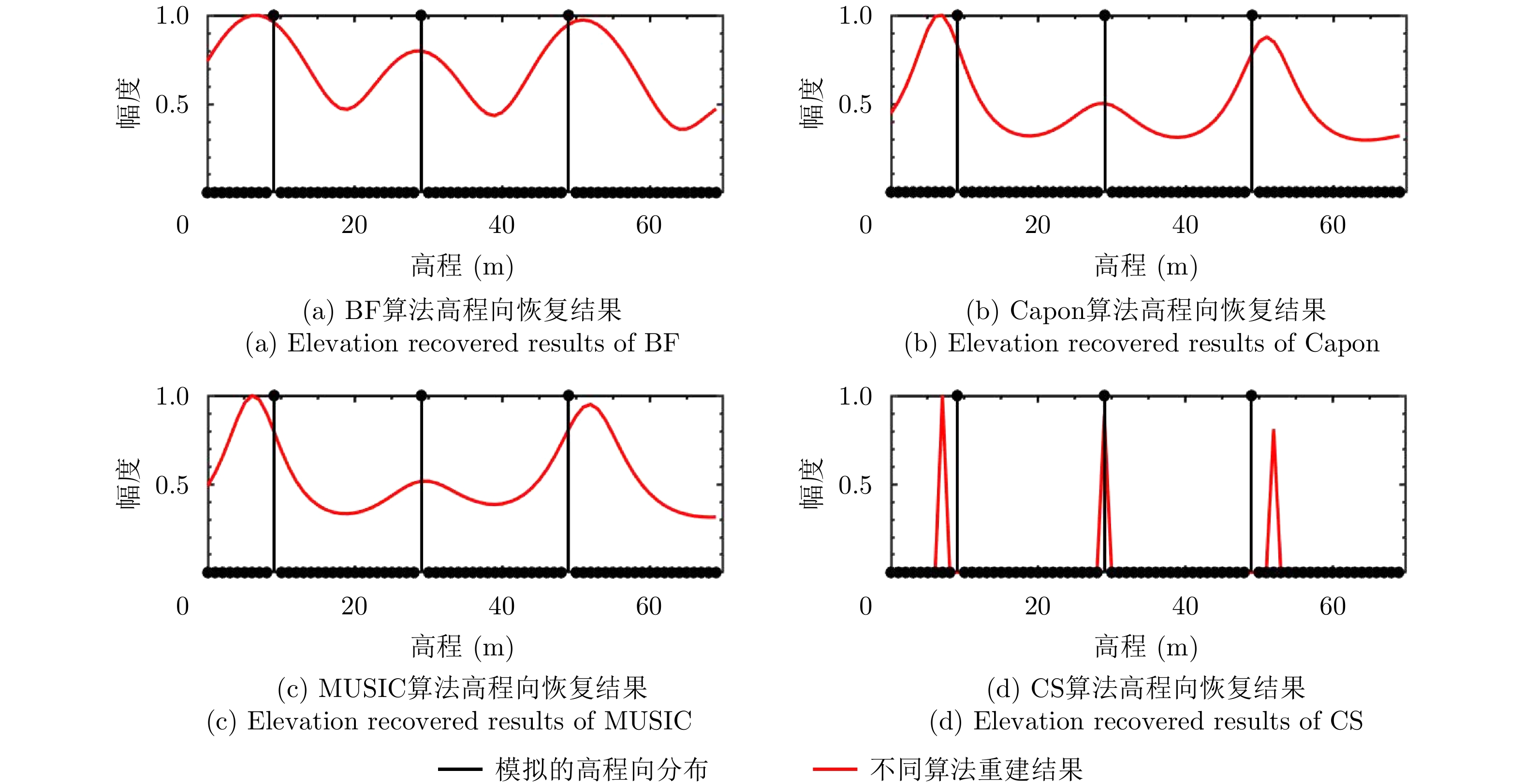
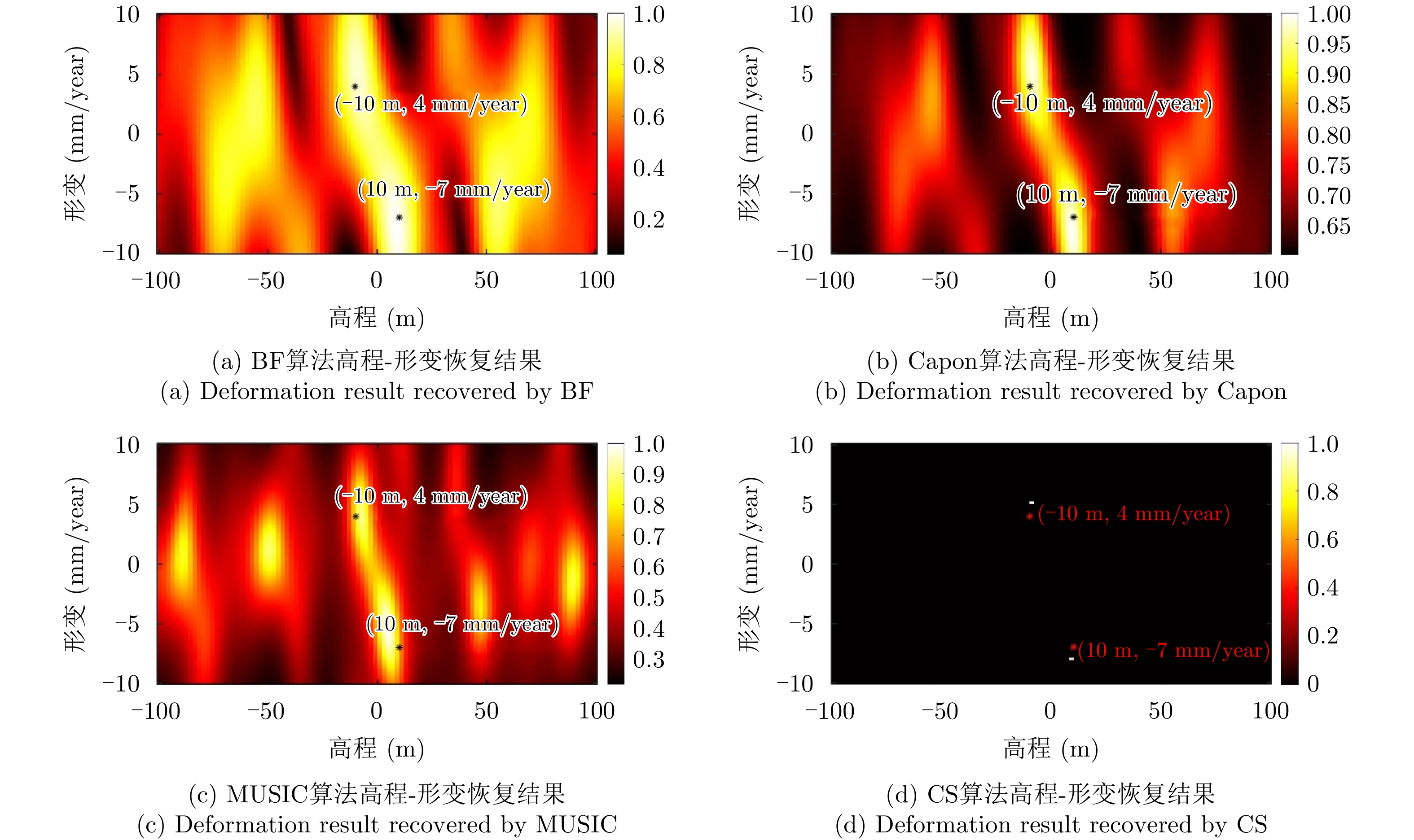
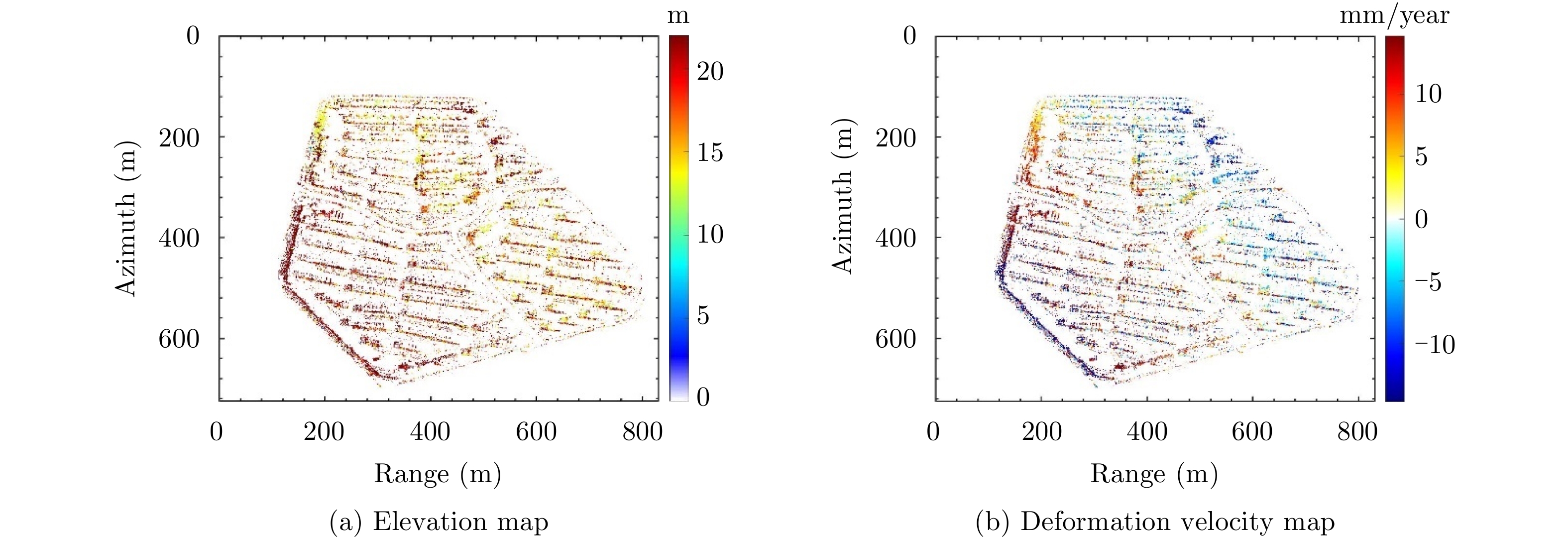
| [1] |
CURLANDER J C and MCDONOUGH R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. New York: Wiley, 1991.
|
| [2] |
BUDILLON A, JOHNSY A C, and SCHIRINZI G. Contextual information based SAR tomography of urban areas[C]. 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, Italy, 2019: 1–4. doi: 10.1109/JURSE.2019.8809076. |
| [3] |
REIGBER A, MOREIRA A, and PAPATHANASSIOU K P. First demonstration of airborne SAR tomography using multibaseline L-band data[C]. IEEE 1999 International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 1999: 44–46. doi: 10.1109/IGARSS.1999.773395. |
| [4] |
REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873 |
| [5] |
FORNARO G and SERAFINO F. Imaging of single and double scatterers in urban areas via SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3497–3505. doi: 10.1109/TGRS.2006.881748 |
| [6] |
REALE D, FORNARO G, PAUCIULLO A, et al. Tomographic imaging and monitoring of buildings with very high resolution SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 661–665. doi: 10.1109/LGRS.2010.2098845 |
| [7] |
SHAHZAD M and ZHU Xiaoxiang. Reconstruction of building façades using spaceborne multiview TomoSAR point clouds[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium - IGARSS, Melbourne, Australia, 2013: 624–627. doi: 10.1109/IGARSS.2013.6721234. |
| [8] |
WANG Xiao, XU Feng, and JIN Yaqiu. The iterative reweighted alternating direction method of multipliers for separating structural layovers in SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1883–1887. doi: 10.1109/LGRS.2017.2694825 |
| [9] |
WANG Yuanyuan and ZHU Xiaoxiang. Robust nonlinear blind SAR tomography in urban areas[C]. 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2018: 1–6.
|
| [10] |
QIN Fei, LIANG Xingdong, ZHANG Fubo, et al. Building target extraction methods in array SAR tomography based on machine learning[J]. Journal of Signal Processing, 2019, 35(2): 176–186. doi: 10.16798/j.issn.1003-0530.2019.02.003 |
| [11] |
LOMBARDINI F. Differential tomography: A new framework for SAR interferometry[C]. IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, French, 2003: 1206–1208. doi: 10.1109/IGARSS.2003.1294059. |
| [12] |
FORNARO G, PAUCIULLO A, and SERAFINO F. Multipass SAR processing for urbanized areas imaging and deformation monitoring at small and large scales[C]. 2007 Urban Remote Sensing Joint Event, Paris, 2007: 1–7. doi: 10.1109/URS.2007.371879. |
| [13] |
FORNARO G, REALE D, and SERAFINO F. 4D SAR focusing: A tool for improved imaging and monitoring of urban areas[C]. IGARSS 2008 - 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, USA, 2008: V-475–V-478. doi: 10.1109/IGARSS.2008.4780132. |
| [14] |
ZHU Xiaoxiang, ADAM N, and BAMLER R. Space-borne high resolution tomographic interferometry[C]. 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009: IV-869–IV-872. doi: 10.1109/IGARSS.2009.5417515. |
| [15] |
FORNARO G, SERAFINO F, and REALE D. 4-D SAR imaging: The case study of Rome[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 236–240. doi: 10.1109/LGRS.2009.2032133 |
| [16] |
ZHU Xiaoxiang and BAMLER R. Let’s do the time warp: Multicomponent nonlinear motion estimation in differential SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 735–739. doi: 10.1109/LGRS.2010.2103298 |
| [17] |
SIDDIQUE M A, HAJNSEK I, AERSOSPACE G, et al. Investigating the combined use of differential SAR tomography and PSI for spatio-temporal inversion[C]. 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Swiss, 2015: 1–4. doi: 10.1109/JURSE.2015.7120504. |
| [18] |
WANG Zhigui and LIU Mei. Seasonal deformation and accelerated motion of infrastructure monitoring using a generalized differential SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(4): 626–630. doi: 10.1109/LGRS.2019.2917324 |
| [19] |
CANDÈS E J. Compressive sampling[C]. The International Congress of Mathematicians, Madrid, Spain, 2006: 1433–1452.
|
| [20] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 |
| [21] |
CANDÈS E J, ROMBERG J K, and TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. doi: 10.1002/cpa.20124 |
| [22] |
ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L1-Norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117 |
| [23] |
ZHU Xiaoxiang and BAMLER R. Super-resolution of sparse reconstruction for tomographic SAR imaging-demonstration with real data[C]. EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, Nuremberg, USA, 2012: 215–218.
|
| [24] |
WEISS M, FORNARO G, and REALE D. Multi scatterer detection within tomographic SAR using a compressive sensing approach[C]. 2015 3rd International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, 2015: 11–15. doi: 10.1109/CoSeRa.2015.7330254. |
| [25] |
LI Xinwu, PENG Xing, and LIANG Lei. Sparse reconstruction-based SAR tomography and it’s application[C]. 2017 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 2017: 1–5. doi: 10.1109/IST.2017.8261514. |
| [26] |
ZHU Xiaoxiang and BAMLER R. Super-resolution for 4-D SAR tomography via compressive sensing[C]. 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2010: 1–4.
|
| [27] |
ZHU Xiaoxiang and BAMLER R. Compressive sensing for high resolution differential SAR tomography - the SL1MMER algorithm[C]. 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, USA, 2010: 17–20. doi: 10.1109/IGARSS.2010.5654021. |
| [28] |
LENG Ying, LI Fei, SHAO Yunfeng, et al. Elevation and deformation estimation based on TomoSAR[C]. EUSAR 2014; 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1–4.
|
| [29] |
姚天宇. 长征四号丙运载火箭成功发射高分三号卫星[J]. 中国航天, 2016(8): 8.
YAO Tianyu. The Long March 4C carrier rocket successfully launched the GaoFen-3 satellite[J]. Aerospace China, 2016(8): 8.
|
| [30] |
ZHANG Qingjun. System design and key technologies of the GF-3 satellite[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 269–277. doi: 10.11947/j.AGCS.2017.20170049 |
| [31] |
李胜阳, 许志辉, 陈子琪, 等. 高分3号卫星影像在黄河洪水监测中的应用[J]. 水利信息化, 2017(5): 22–26, 72.
LI Shengyang, XU Zhihui, CHEN Ziqi, et al. Application of GF-3 satellite remote sensing image on Yellow River flood monitoring[J]. Water Resources Informatization, 2017(5): 22–26, 72.
|
| [32] |
MA Jianwei, SUN Yayong, CHEN Deqing, et al. Applications of GF-3 satellite in flood and landslide disasters emergency monitoring[J]. Spacecraft Engineering, 2017, 26(6): 161–166. doi: 10.3969/j.issn.1673-8748.2017.06.026 |
| [33] |
余博, 李如仁, 陈振炜, 等. 基于高分三号数据的干涉测量研究[J]. 测绘工程, 2019, 28(4): 19–23, 28.
YU Bo, LI Ruren, CHEN Zhenwei, et al. Experimental research on interferometry based on GF-3 SAR data[J]. Engineering of Surveying and Mapping, 2019, 28(4): 19–23, 28.
|
| [34] |
HUANG Zhen, ZHAO Shuangming, and CHANG Qing. Interferometric test using domestic GF-3 satellite[J]. Journal of Geomatics, 2021, 46(4): 7–11. doi: 10.14188/j.2095-6045.2019083 |
| [35] |
FORNARO G, SERAFINO F, and SOLDOVIERI F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507–517. doi: 10.1109/TGRS.2003.809934 |
| [36] |
ZHU X. High-resolution spaceborne radar tomography[D]. Technische Universität München, 2008.
|
| [37] |
FORNARO G, REALE D, and SERAFINO F. Four-dimensional SAR imaging for height estimation and monitoring of single and double scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224–237. doi: 10.1109/TGRS.2008.2000837 |
| [38] |
PATI Y C, REZAIIFAR R, and KRISHNAPRASAD P S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]. 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1993: 40–44. doi: 10.1109/ACSSC.1993.342465. |
| [39] |
BI Hui and BI Guoan. Performance analysis of iterative soft thresholding algorithm for L1 regularization based sparse SAR imaging[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–6. doi: 10.1109/RADAR.2019.8835551. |
| [40] |
毕辉. 基于稀疏信号处理的SAR/TomoSAR成像方法研究[D]. [博士论文], 中国科学院大学, 2017: 33–41.
BI Hui. Research on the imaging method of SAR/TomoSAR based on sparse signal processing[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2007: 33–41.
|
| [41] |
STOICA P and MOSES R. Spectral Analysis of Signals[M]. Upper Sadle River, New Jersey: Pearson Prentice Hall, 2005.
|
| [42] |
CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278 |
| [43] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 |
| [44] |
STOICA P and NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound: Further results and comparisons[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(12): 2140–2150. doi: 10.1109/29.61541 |




 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work

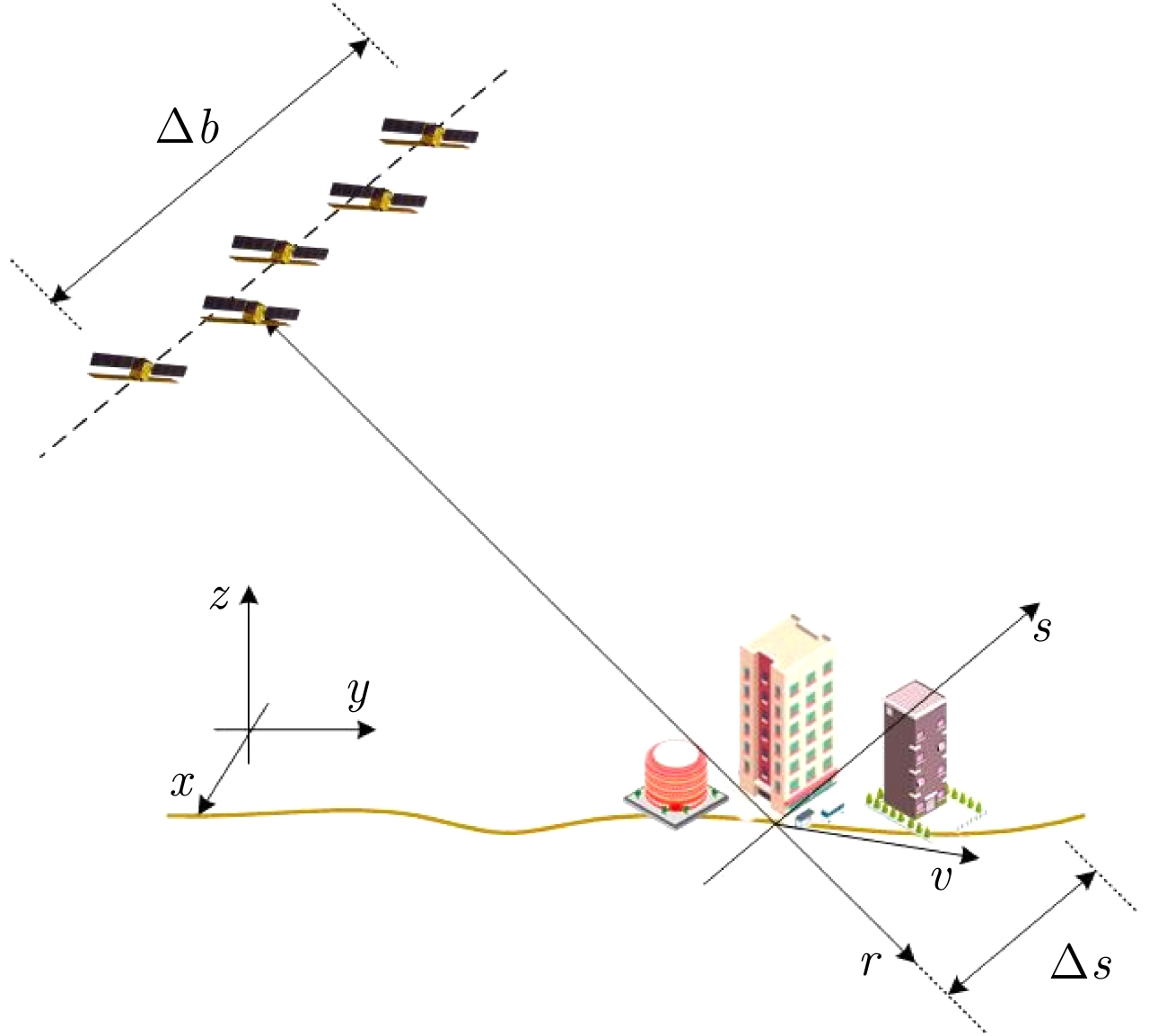



 DownLoad:
DownLoad: