Submit Manuscript
Peer Review
Editor Work
| Citation: | MA Yuxin, HAI Yu, LI Zhongyu, et al. 3D high-resolution imaging algorithm with sparse trajectory for millimeter-wave radar[J]. Journal of Radars, 2023, 12(5): 1000–1013. doi: 10.12000/JR23001
|
3D High-resolution Imaging Algorithm with Sparse Trajectory for Millimeter-wave Radar
doi: 10.12000/JR23001
More Information-
Abstract
In recent years, millimeter-wave radar has been widely used in safety detection, nondestructive detection of parts, and medical diagnosis because of its strong penetration ability, small size, and high detection accuracy. However, due to the limitation of hardware transmission bandwidth, achieving ultra-high two-dimensional resolution using millimeter-wave radar is challenging. Two-dimensional high-resolution imaging of altitude and azimuth can be realized using radar platform scanning to form a two-dimensional aperture. However, during the scanning process, the millimeter-wave radar produces sparse tracks in the height dimension, resulting in a sparse sampling of the altitude echo, thus reducing the imaging quality. In this paper, a high-resolution three-dimensional imaging algorithm for millimeter-wave radar based on Hankel transformation matrix filling is proposed to solve this problem. The matrix filling algorithm restores the sparse sampling echo, which guarantees the imaging accuracy of the millimeter-wave radar in the scanning plane. First, the low-rank prior characteristics of the millimeter-wave radar's elevation-range section were analyzed. To solve the problem of missing whole rows and columns of data during sparse trajectory sampling, the echo data matrix was reconstructed using the Hankel transform, and the sparse low-rank prior characteristics of the constructed matrix were analyzed. Furthermore, a matrix filling algorithm based on truncated Schatten-p norm combining low-rank and sparse priors was proposed to fill and reconstruct the echoes to ensure the three-dimensional resolution of the sparse trajectory millimeter-wave radar. Finally, using simulation and several sets of measured data, the proposed method was proved to achieve high-resolution three-dimensional imaging even when only 20%–30% of the height echo was used. -
-
References
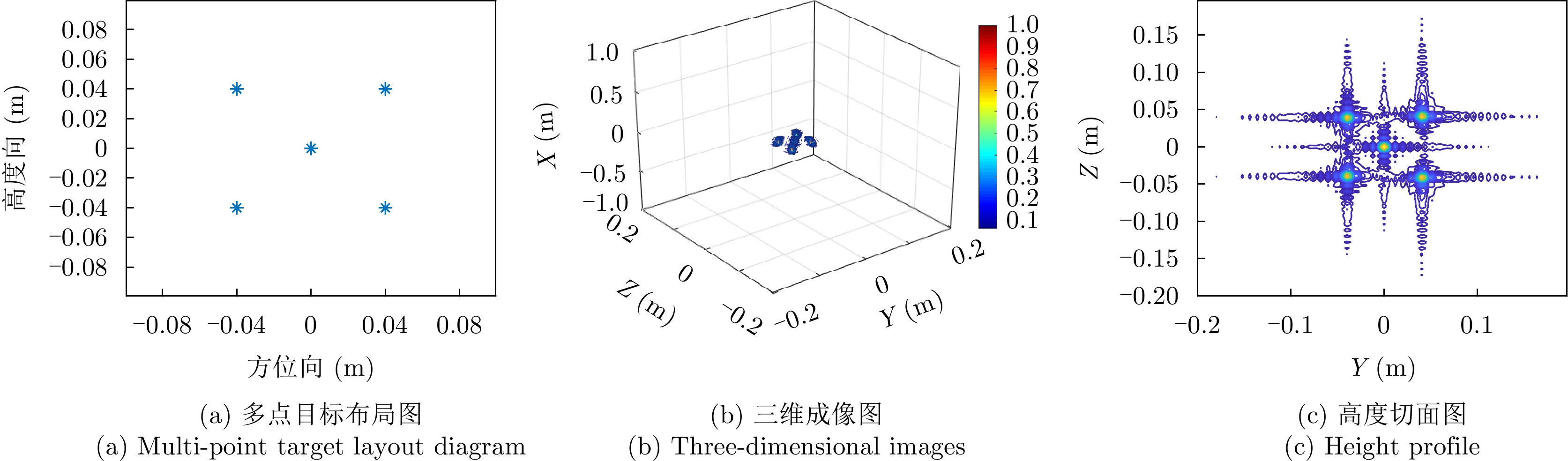
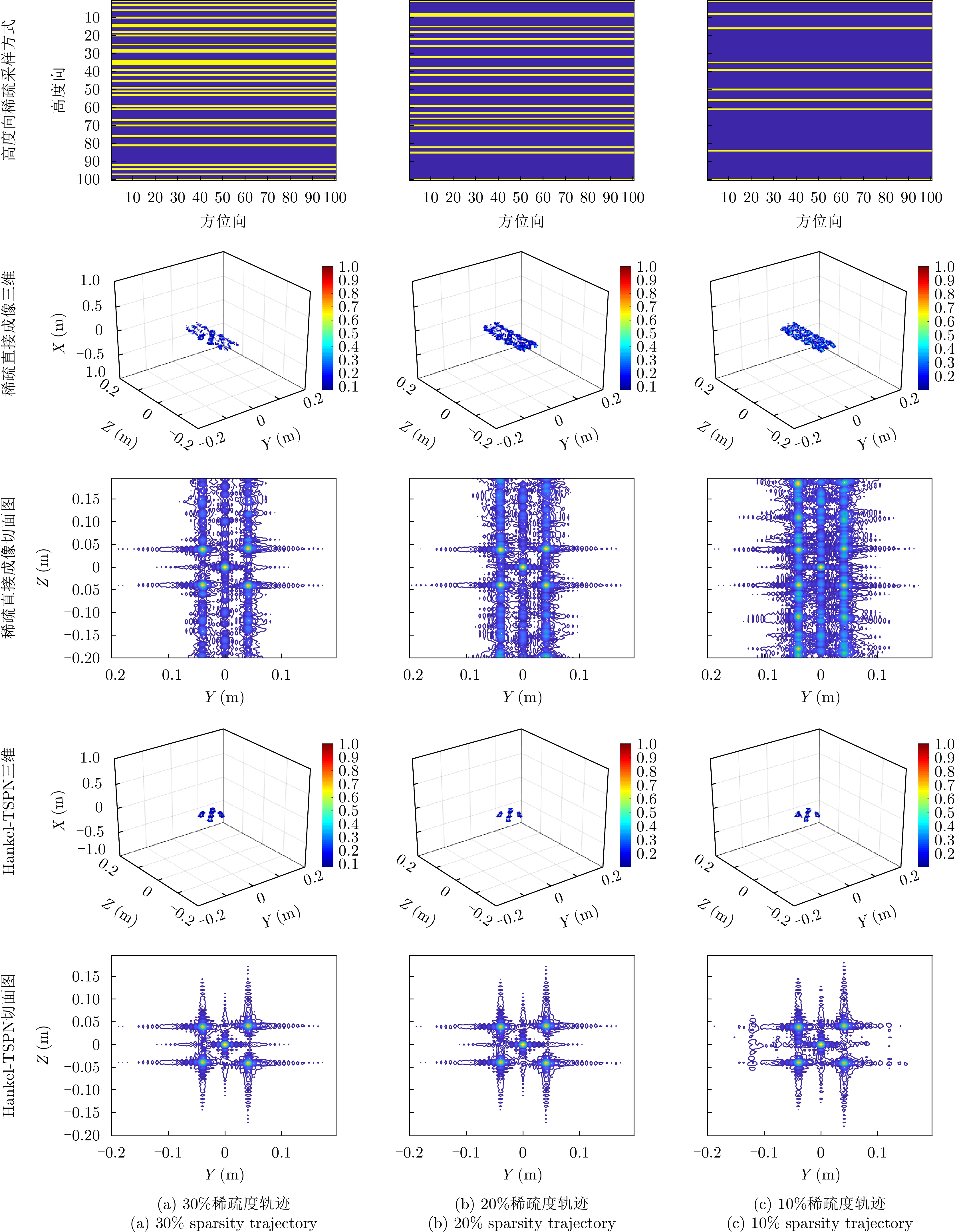
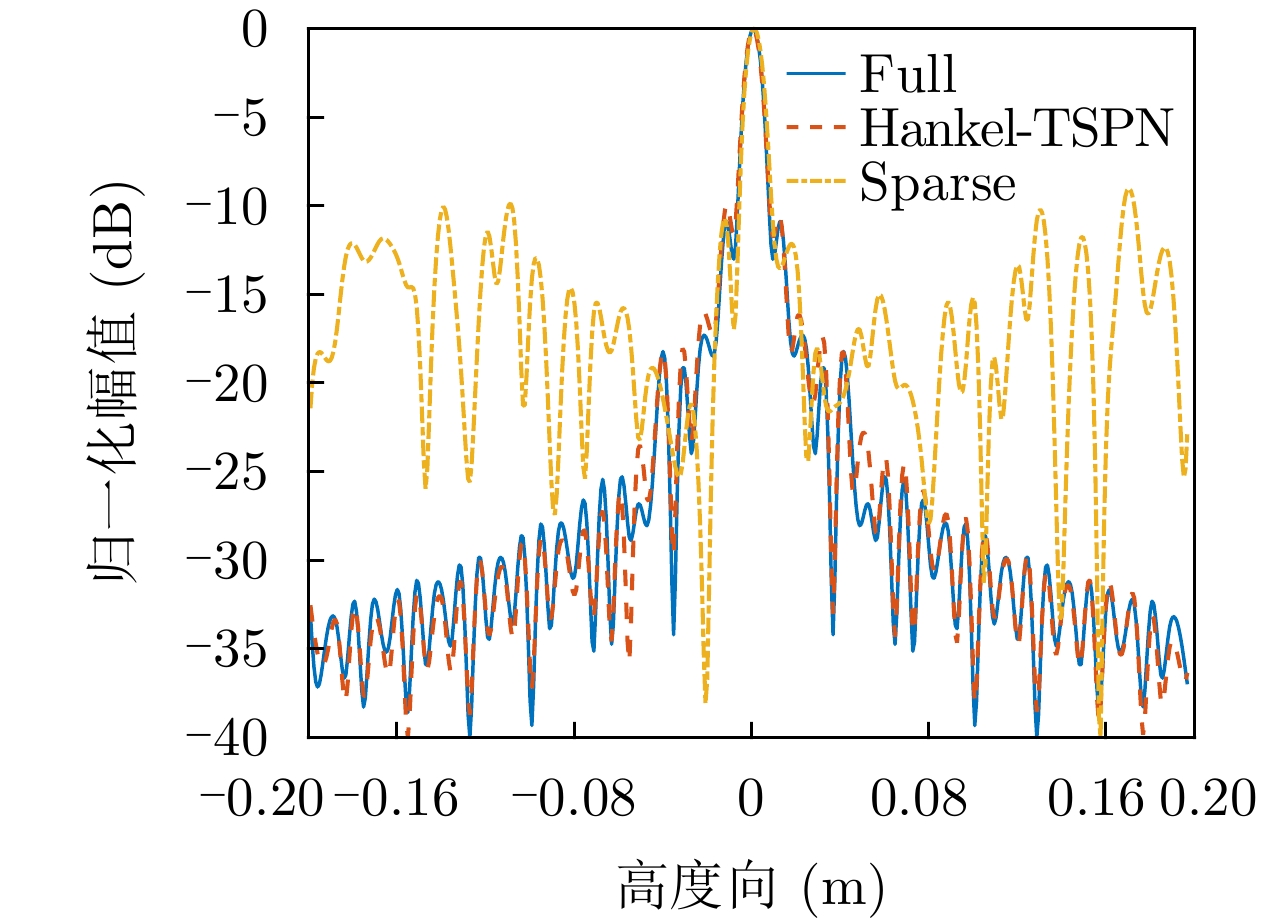
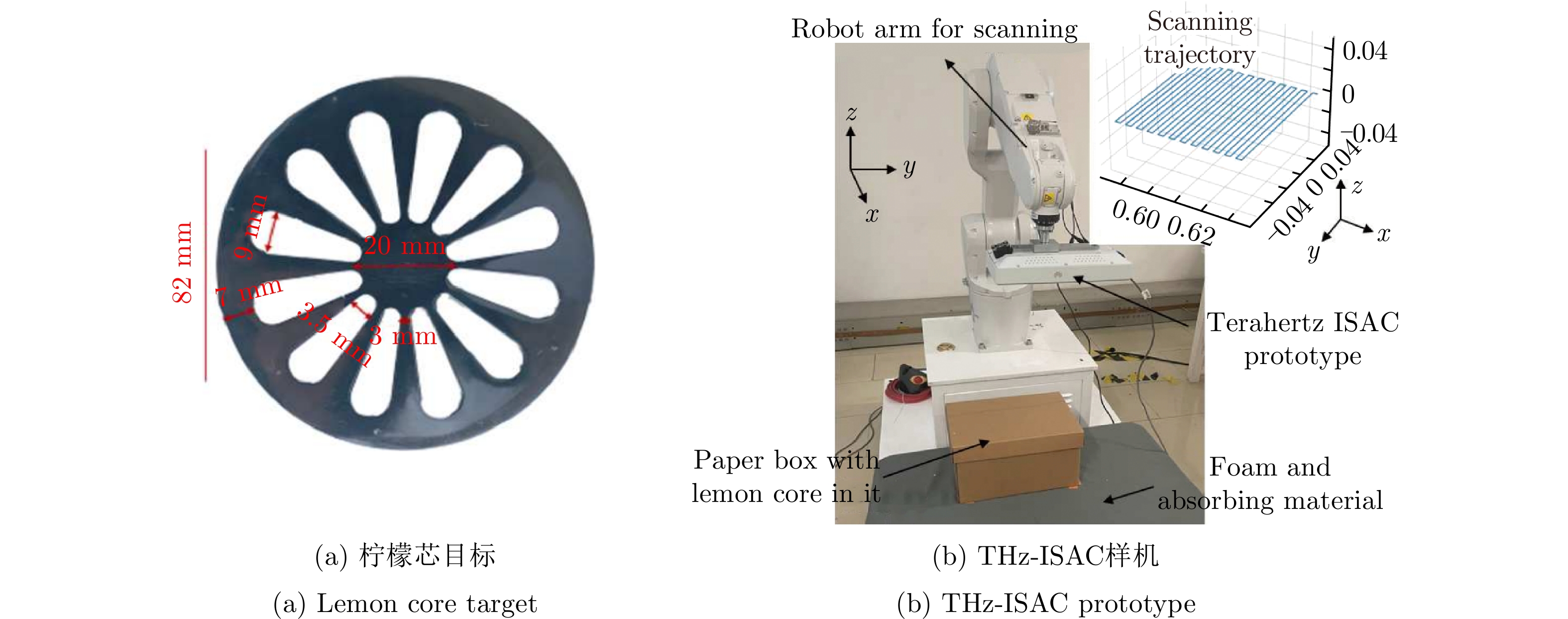
[1] 石星. 毫米波雷达的应用和发展[J]. 电讯技术, 2006, 46(1): 1–9. doi: 10.3969/j.issn.1001-893X.2006.01.001SHI Xing. Application and development of millimetre-wave radars[J]. Telecommunication Engineering, 2006, 46(1): 1–9. doi: 10.3969/j.issn.1001-893X.2006.01.001[2] 黄昌霸. 车载毫米波雷达目标检测技术研究[D]. [硕士论文], 电子科技大学, 2020.HUANG Changba. Research of on-vehicle millimeter wave radar target detection technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2020.[3] ZHANG Weite, HEREDIA-JUESAS J, DIDDI M, et al. Experimental imaging results of a UAV-mounted downward-looking mm-wave radar[C]. 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, USA, 2019: 1639–1640.[4] 乞耀龙. 近景微波三维成像模型与方法研究[D]. [博士论文], 中国科学院大学, 2012.QI Yaolong. Study on the model and method of close-up microwave three-dimensional imaging[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2012.[5] ESSEN H, LORENZ F, HANTSCHER S, et al. Millimeterwave radar for runway debris detection[C]. 2011 Tyrrhenian International Workshop on Digital Communications - Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 2011: 65–68.[6] ROHMAN B P A, RUDRAPPA M T, SHARGORODSKYY M, et al. Moving human respiration sign detection using mm-wave radar via motion path reconstruction[C]. 2021 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications, Bandung, Indonesia, 2021: 196–200.[7] VERMA P, SHAKYA V S, SHARMA D, et al. MM-wave radar application for autonomous vehicles[C]. 2020 2nd International Conference on Advances in Computing, Communication Control and Networking, Greater Noida, India, 2020: 556–559.[8] 皮亦鸣, 杨建宇, 付毓生, 等. 合成孔径雷达成像原理[M]. 成都: 电子科技大学出版社, 2007: 49–50.PI Yiming, YANG Jianyu, FU Yusheng, et al. Synthetic Aperture Radar Imaging Technology[M]. Chengdu: University of Electronic Science and Technology of China Press, 2007: 49–50.[9] 陈文江, 陈麒安, 陈宏铭, 等. 5G毫米波天线阵列模组技术挑战与未来发展趋势[J]. 中国集成电路, 2021, 30(11): 40–45. doi: 10.3969/j.issn.1681-5289.2021.11.008CHEN Wenjiang, CHEN Qi’an, CHEN Hongming, et al. Technical challenges and development trend of 5G mm wave antenna array module[J]. China Integrated Circuit, 2021, 30(11): 40–45. doi: 10.3969/j.issn.1681-5289.2021.11.008[10] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582[11] ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L1 -norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117[12] OLIVERI G, ROCCA P, and MASSA A. A Bayesian-compressive-sampling-based inversion for imaging sparse scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3993–4006. doi: 10.1109/TGRS.2011.2128329[13] CANDÈS E J and RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717–772. doi: 10.1007/s10208-009-9045-5[14] CANDES E J and PLAN Y. Matrix completion with noise[J]. Proceedings of the IEEE, 2010, 98(6): 925–936. doi: 10.1109/JPROC.2009.2035722[15] BI Dongjie, LI Xifeng, XIE Xuan, et al. Compressive sensing operator design and optimization for wideband 3-D millimeter-wave imaging[J]. IEEE Transactions on Microwave Theory and Techniques, 2022, 70(1): 542–555. doi: 10.1109/TMTT.2021.3100499[16] WANG Mou, WEI Shunjun, SHI Jun, et al. CSR-Net: A novel complex-valued network for fast and precise 3-D microwave sparse reconstruction[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4476–4492. doi: 10.1109/JSTARS.2020.3014696[17] HU Yue, LIU Xiaohan, and JACOB M. A generalized structured low-rank matrix completion algorithm for MR image recovery[J]. IEEE Transactions on Medical Imaging, 2019, 38(8): 1841–1851. doi: 10.1109/TMI.2018.2886290[18] KHALIFA M O, ABDELHAFIZ A H, and ZERGUINE A. Sparse channel estimation using adaptive filtering and compressed sampling[C]. 2013 International Conference on Computing, Electrical and Electronic Engineering (ICCEEE), Khartoum, Sudan, 2013: 144–147.[19] WENG Zhiyuan and WANG Xin. Low-rank matrix completion for array signal processing[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 2012: 2697–2700.[20] ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Matrix completion for downward-looking 3-D SAR imaging with a random sparse linear array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1994–2006. doi: 10.1109/TGRS.2017.2771826[21] MA Yuxin, HAI Yu, YANG Jianyu, et al. A near-field 3-D SAR imaging method with non-uniform sparse linear array based on matrix completion[C]. IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 2022: 1664–1667.[22] ZENG Xuan, MA Yuxin, LI Zhongyu, et al. A near-field fast time-frequency joint 3-D imaging algorithm based on aperture linearization[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021: 5163–5166,[23] YING Jiaxi, CAI Jianfeng, GUO Di, et al. Vandermonde factorization of hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5520–5533. doi: 10.1109/TSP.2018.2869122[24] AHMED N, NATARAJAN T, and RAO K R. Discrete cosine transform[J]. IEEE Transactions on Computers, 1974, C-23(1): 90–93. doi: 10.1109/T-C.1974.223784[25] 胡循勇, 杨晓梅, 李昊怡, 等. 融合低秩和稀疏先验的结构性缺失图像修复[J]. 北京航空航天大学学报, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663HU Xunyong, YANG Xiaomei, LI Haoyi, et al. Structural missing image inpainting based on low rank and sparse prior[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663[26] BOYD S, PARIKH N, CHU E, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[M]. Hanover: Now Foundations and Trends, 2011: 13–23. doi: 10.1561/2200000016.[27] MERHAV N and KRESCH R. Approximate convolution using DCT coefficient multipliers[J]. IEEE Transactions on Circuits and Systems for Video Technology, 1998, 8(4): 378–385. doi: 10.1109/76.709404[28] LI Oupeng, HE Jia, ZENG Kun, et al. Integrated sensing and communication in 6G a prototype of high resolution THz sensing on portable device[C]. 2021 Joint European Conference on Networks and Communications & 6G Summit, Porto, Portugal, 2021: 544–549.[29] 韦顺军. 线阵三维合成孔径雷达稀疏成像技术研究[D]. [博士论文], 电子科技大学, 2013.WEI Shunjun. Research on linear array three-dimensional synthetic aperture radar sparse imaging technology[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2013.[30] WEI Shunjun, ZHOU Zichen, WANG Mou, et al. 3DRIED: A high-resolution 3-D millimeter-wave radar dataset dedicated to imaging and evaluation[J]. Remote Sensing, 2021, 13(17): 3366. doi: 10.3390/rs13173366 -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. Geometric configuration of sparse trajectory millimeter wave radar
- Figure 2. Diagram of sampling layout
- Figure 3. Diagram of Hankel structural transformation
- Figure 4. Flow diagram of imaging method
- Figure 6. Different methods of height-distance section matrix restoration
- Figure 5. Multi-point target layout and imaging diagram
- Figure 7. Imaging results of point targets with different sparsity trajectories
- Figure 8. Height profile comparison of center points under 20% sparse trajectory
- Figure 9. System and target diagram[28]
- Figure 10. Location diagram of sparse trajectory with a sparsity of 20%
- Figure 11. Images of lemon core
- Figure 12. Location diagram of sparse trajectory with different sparsity
- Figure 13. Imaging results of different targets with different sparse trajectories