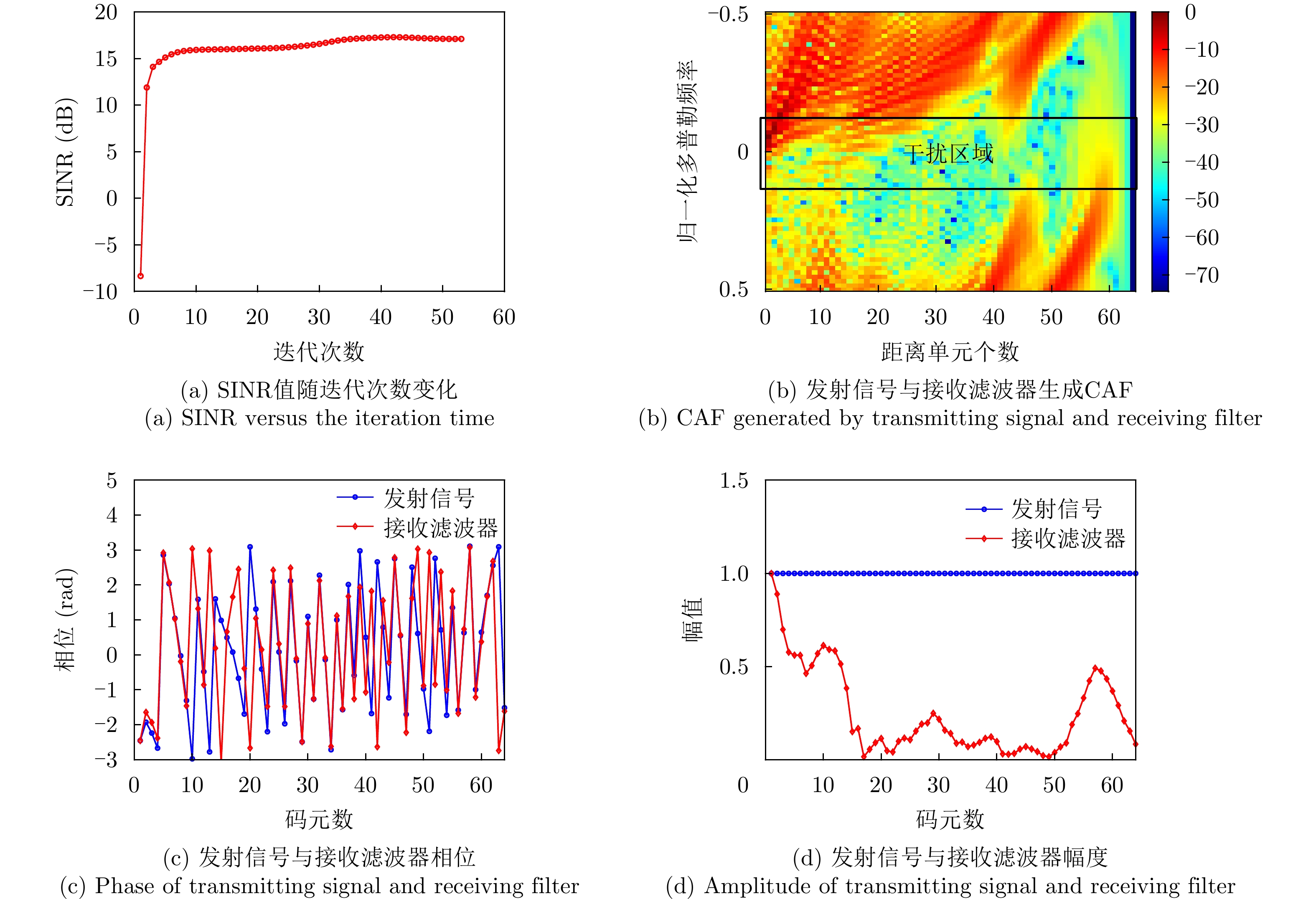
| [1] |
STOICA P, HE Hao, and LI Jian. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1730–1740. doi: 10.1109/TSP.2011.2179652 |
| [2] |
STOICA P, LI Jian, and XUE Ming. Transmit codes and receive filters for radar[J]. IEEE Signal Processing Magazine, 2008, 25(6): 94–109. doi: 10.1109/MSP.2008.929231 |
| [3] |
YU Ruofeng, YANG Wei, FU Yaowen, et al. A review on cognitive waveform optimization for different radar missions[J]. Acta Electronica Sinica, 2022, 50(3): 726–752. doi: 10.12263/DZXB.20211068 |
| [4] |
LEVANON N and MOZESON E. Radar Signals[M]. New York: John Wiley & Sons, 2004: 7–9.
|
| [5] |
CUI Guolong, FU Yue, YU Xianxiang, et al. Local ambiguity function shaping via uni-modular sequence design[J]. IEEE Signal Processing Letters, 2017, 24(7): 977–981. doi: 10.1109/lsp.2017.2700396 |
| [6] |
HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/msp.2006.1593335 |
| [7] |
ARLERY F, KASSAB R, TAN U, et al. Efficient gradient method for locally optimizing the periodic/aperiodic ambiguity function[C]. IEEE Radar Conference (RadarConf), Philadelphia, USA, 2016: 1–6
|
| [8] |
ARLERY F, KASSAB R, TAN U, et al. Efficient optimization of the ambiguity functions of multi-static radar waveforms[C]. 17th International Radar Symposium (IRS), Krakow, Poland, 2016: 1–6.
|
| [9] |
WANG Fulai, FENG Sijia, YIN Jiapeng, et al. Unimodular sequence and receiving filter design for local ambiguity function shaping[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5113012. doi: 10.1109/tgrs.2022.3171253 |
| [10] |
AUBRY A, DE MAIO A, JIANG Bo, et al. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5603–5619. doi: 10.1109/TSP.2013.2273885 |
| [11] |
QIU Xiangfeng, JIANG Weidong, ZHANG Xinyu, et al. Quartic riemannian trust region algorithm for cognitive radar ambiguity function shaping[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4022005. doi: 10.1109/LGRS.2022.3151679 |
| [12] |
WU Linlong, BABU P, and PALOMAR D P. Cognitive radar-based sequence design via sinr maximization[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 779–793. doi: 10.1109/tsp.2016.2621723 |
| [13] |
HE Hao, STOICA P, and LI Jian. On synthesizing cross ambiguity functions[C]. IEEE Internationl Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 3536–3539
|
| [14] |
CHEN Zihao, LIANG Junli, WANG Tao, et al. Generalized MBI algorithm for designing sequence set and mismatched filter bank with ambiguity function constraints[J]. IEEE Transactions on Signal Processing, 2022, 70: 2918–2933. doi: 10.1109/TSP.2022.3181346 |
| [15] |
HE Hao, LI Jian, and STOICA P. Waveform Design for Active Sensing Systems: A Computational Approach[M]. Cambridge: Cambridge University Press, 2012: 106–121.
|
| [16] |
SOLTANALIAN M, TANG Bo, LI Jian, et al. Joint design of the receive filter and transmit sequence for active sensing[J]. IEEE Signal Processing Letters, 2013, 20(5): 423–426. doi: 10.1109/lsp.2013.2250279 |
| [17] |
ESMAEILI-NAJAFABADI H, LEUNG H, and MOO P W. Unimodular waveform design with desired ambiguity function for cognitive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(3): 2489–2496. doi: 10.1109/taes.2019.2942411 |
| [18] |
付月, 崔国龙, 余显祥. 信号相关杂波背景下稳健的恒模序列与接收滤波器设计方法[J]. 雷达学报, 2017, 6(3): 292–299. doi: 10.12000/JR16158FU Yue, CUI Guolong, and YU Xianxiang. Robust design of constant modulus sequence and receiver filter in the presence of signal-dependent clutter[J]. Journal of Radars, 2017, 6(3): 292–299. doi: 10.12000/JR16158 |
| [19] |
LIU Tianjun, FAN Pingzhi, ZHOU Zhengchun, et al. Unimodular sequence design with good local auto- and cross-ambiguity function for MSPSR system[C], IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 2019: 1–5.
|
| [20] |
WU Linlong, BABU P, and PALOMAR D P. Transmit waveform/receive filter design for MIMO radar with multiple waveform constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(6): 1526–1540. doi: 10.1109/tsp.2017.2787115 |
| [21] |
QIU Xiangfeng, JIANG Weidong, ZHANG Xinyu, et al. Joint optimization design method for cognitive MIMO radar transmit waveform and receive filter[J]. Systems Engineering and Electronics, 2023, 45(2): 386–393. doi: 10.12305/j.issn.1001-506X.2023.02.08 |
| [22] |
AUBRY A, DEMAIO A, FARINA A, et al. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 93–117. doi: 10.1109/TAES.2013.6404093 |
| [23] |
SOLTANALIAN M and STOICA P. Designing unimodular codes via quadratic optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(5): 1221–1234. doi: 10.1109/tsp.2013.2296883 |
| [24] |
GHARANJIK A, SOLTANALIAN M, SHANKAR M R B, et al. Grab-n-Pull: A max-min fractional quadratic programming framework with applications in signal and information processing[J]. Signal Processing, 2019, 160: 1–12. doi: 10.1016/j.sigpro.2019.02.006 |
| [25] |
TROPP J A, DHILLON I S, HEATH R W, et al. Designing structured tight frames via an alternating projection method[J]. IEEE Transactions on Information Theory, 2005, 51(1): 188–209. doi: 10.1109/tit.2004.839492 |
| [26] |
张贤达. 矩阵分析与应用[M]. 2版. 北京: 清华大学出版社, 2013: 447–450.
ZHANG Xianda. Matrix Analysis and Applications[M]. 2nd ed, Beijing: Tsinghua University Press, 2013: 447–450.
|




 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work

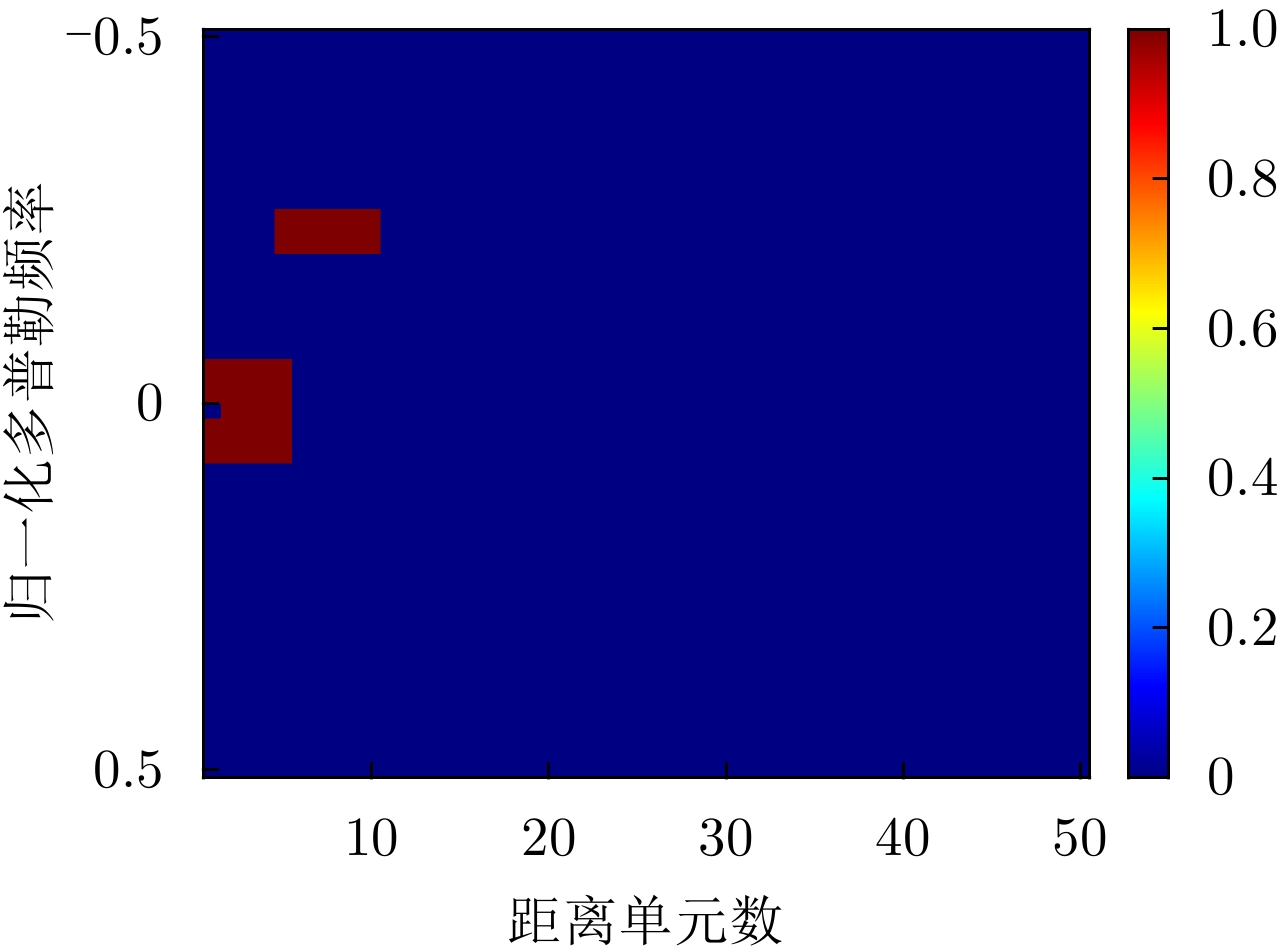



 DownLoad:
DownLoad: