一种低截获背景下的集中式MIMO雷达快速功率分配算法

李正杰; 谢军伟; 张浩为; 温泉; 刘斌

doi:10.12000/JR22203

一种低截获背景下的集中式MIMO雷达快速功率分配算法

DOI: 10.12000/JR22203

1.
空军工程大学防空反导学院西安 710051
2.
国防科技大学信息通信学院西安 710106
3.
国防大学联合作战学院北京 100091

基金项目: 国家自然科学基金(62001506)

详细信息

作者简介:
李正杰，博士生，主要研究方向为MIMO雷达资源分配

谢军伟，博士，教授，主要研究方向为新体制雷达、主动抗干扰

张浩为，博士，讲师，主要研究方向为新体制雷达资源管理

温　泉，硕士，主要研究方向为教育训练学

刘　斌，博士，讲师，主要研究方向为电磁频谱管理

通讯作者:
张浩为 zhw_xhzf@163.com

责任主编：时晨光 Corresponding Editor: SHI Chenguang
中图分类号: TN972
计量
- 文章访问数: 657
- HTML全文浏览量: 395
- PDF下载量: 179
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-10
- 修回日期: 2022-10-28
- 网络出版日期: 2022-11-07
- 刊出日期: 2023-06-28

A Fast Power Allocation Algorithm in a Collocated MIMO Radar under Low Interception Backgrounds

1.
Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China
2.
School of Information and Communication, National University of Defense Technology, Xi’an 710106, China
3.
Joint Operations College, National Defense University, Beijing 100091, China

Funds: The National Natural Science Foundation of China (62001506)

More Information

Corresponding author: ZHANG Haowei, zhw_xhzf@163.com

摘要

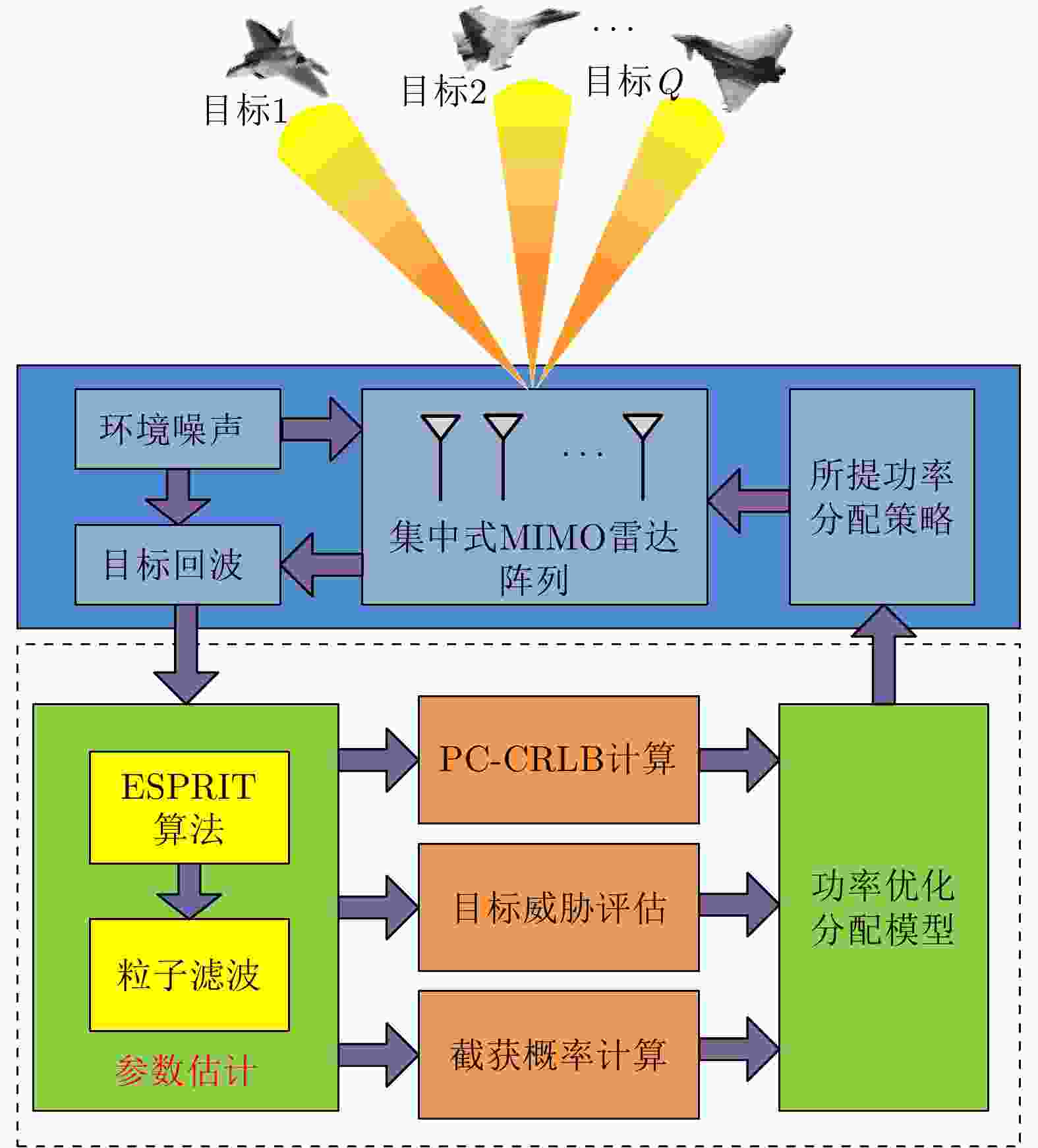
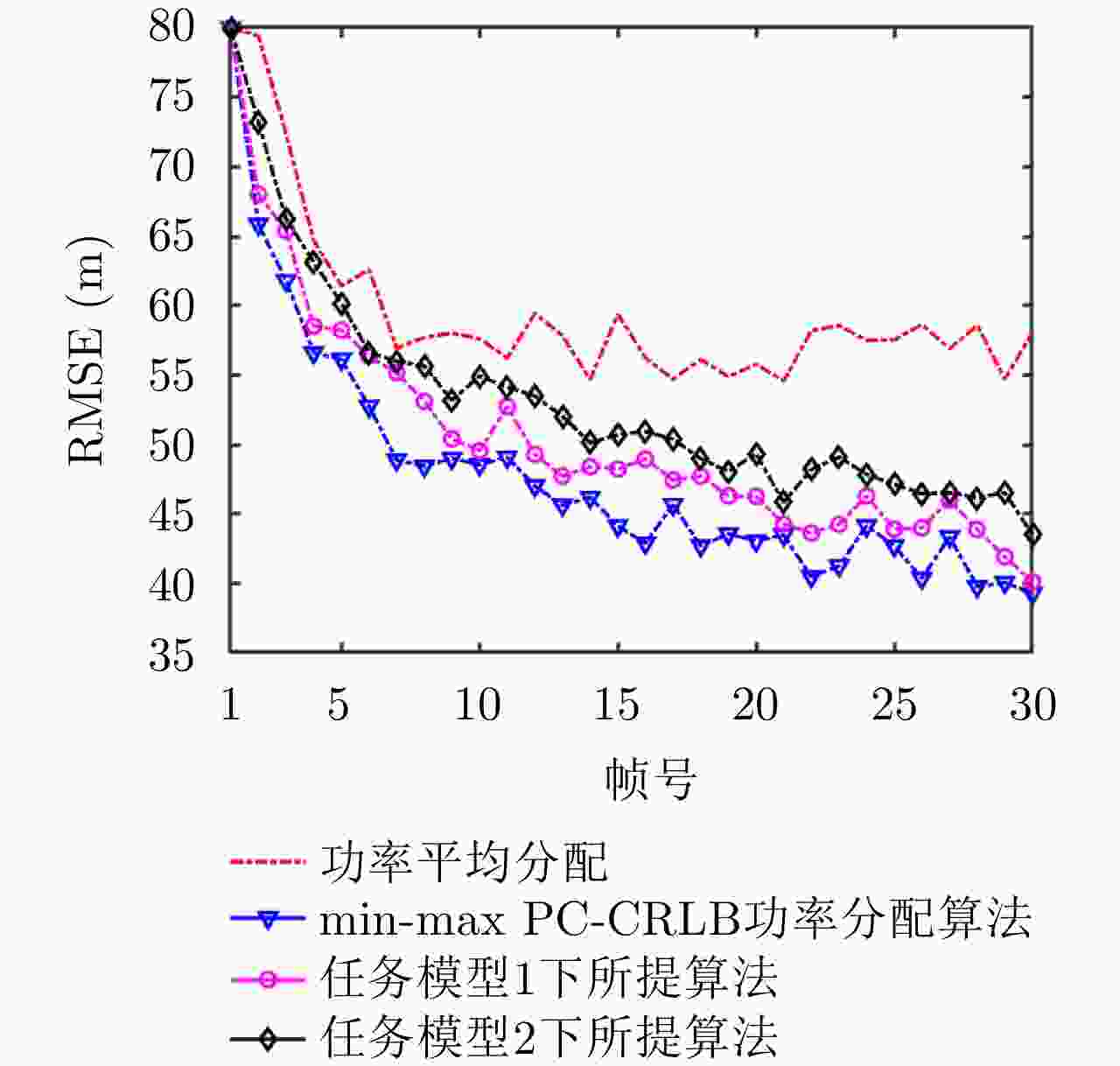
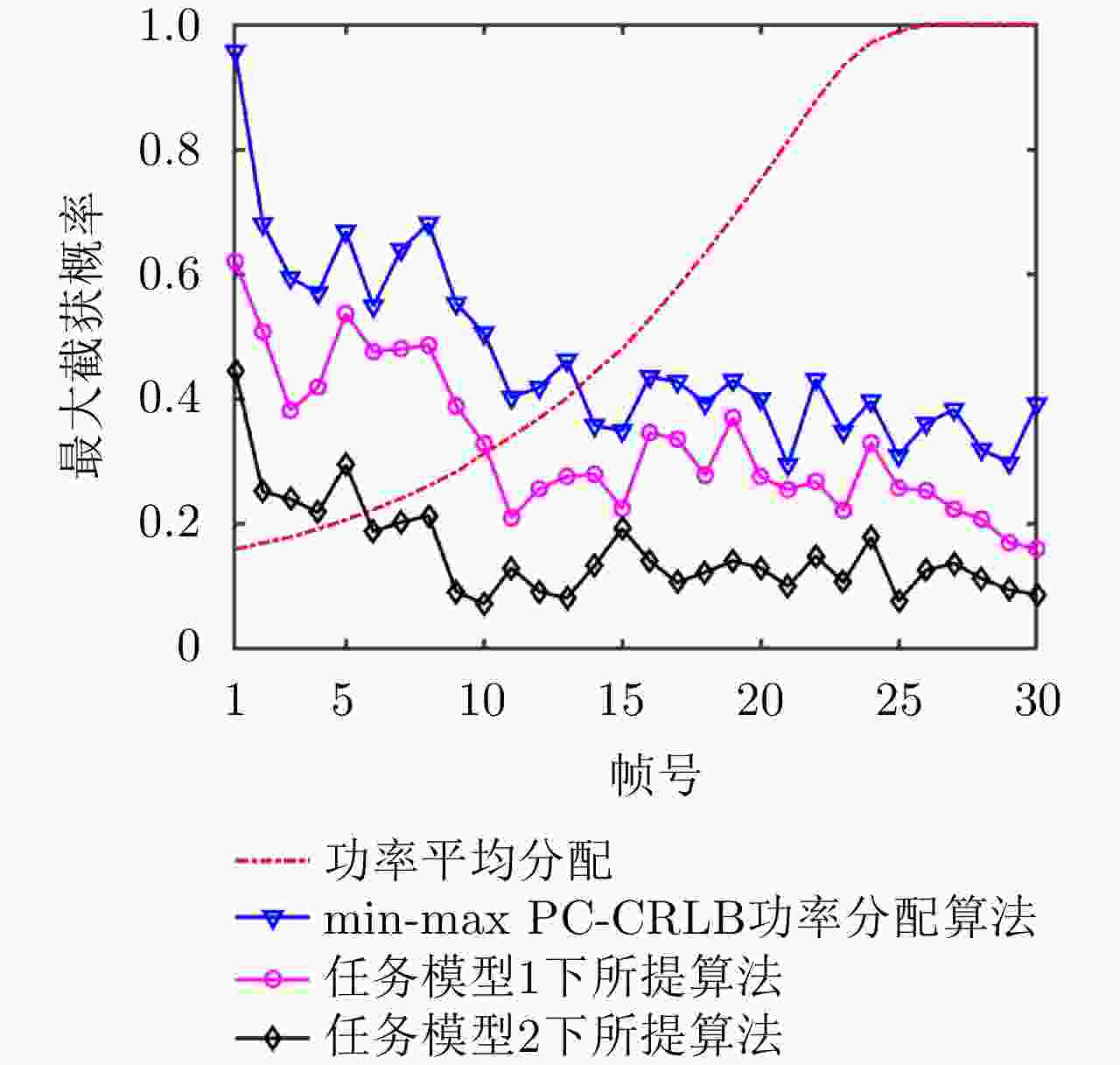
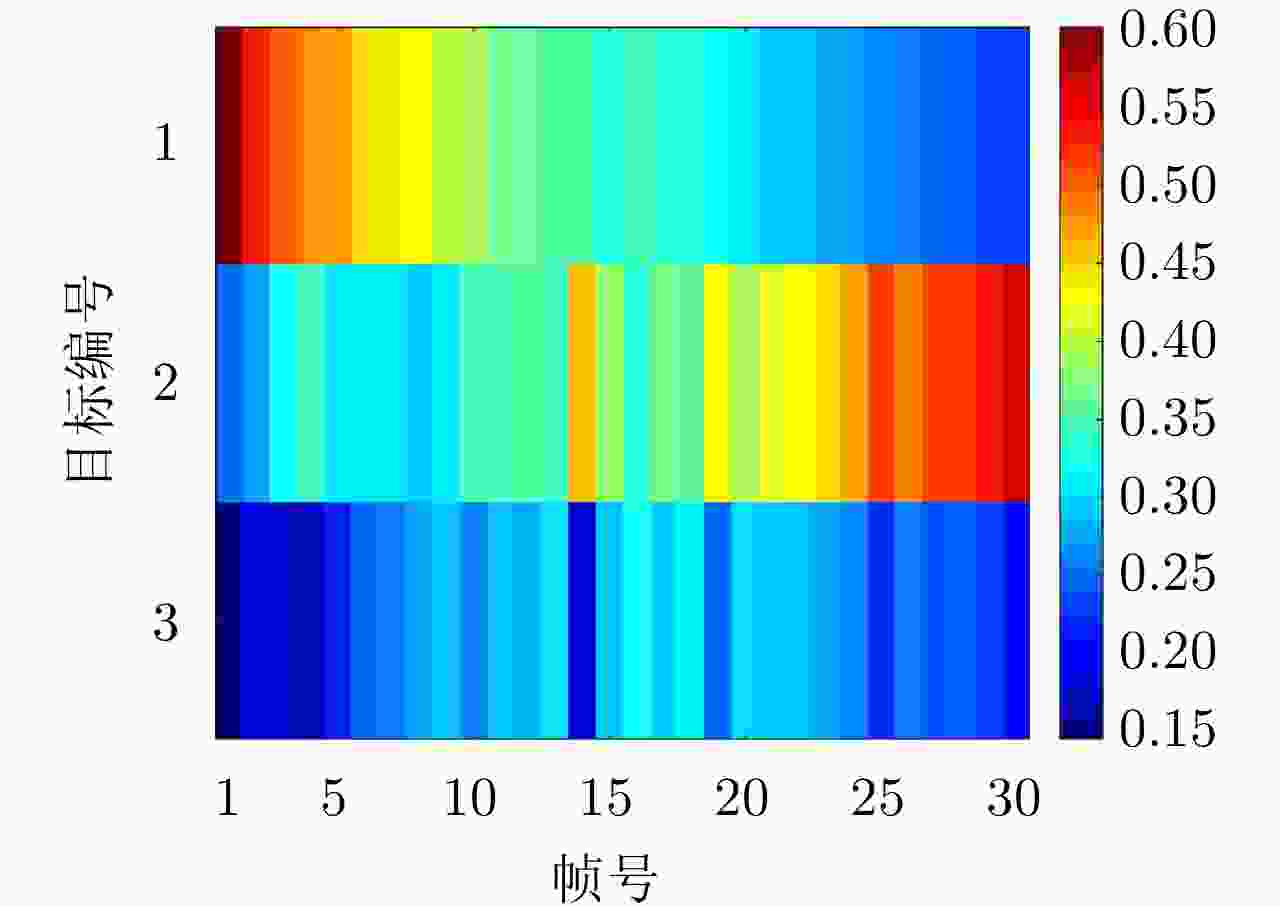
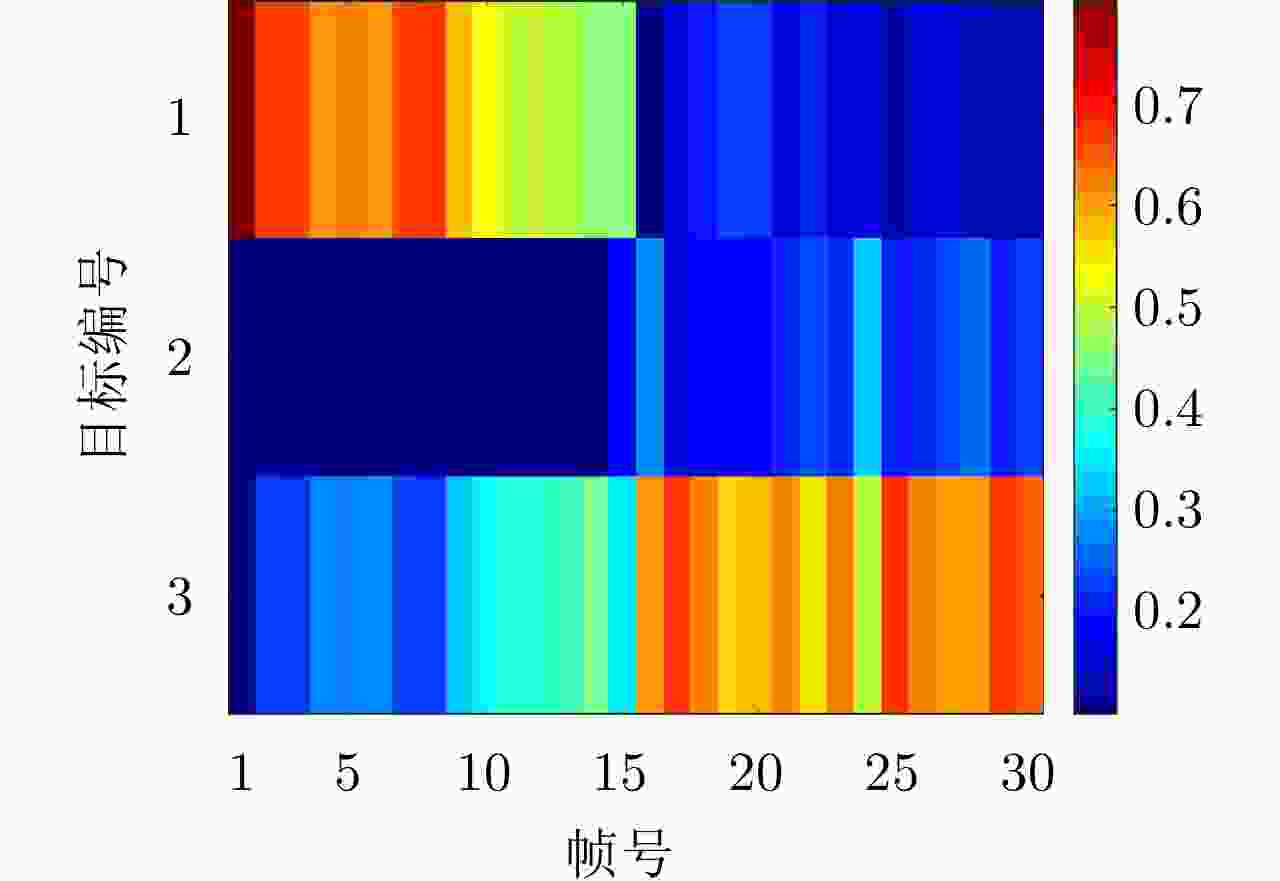
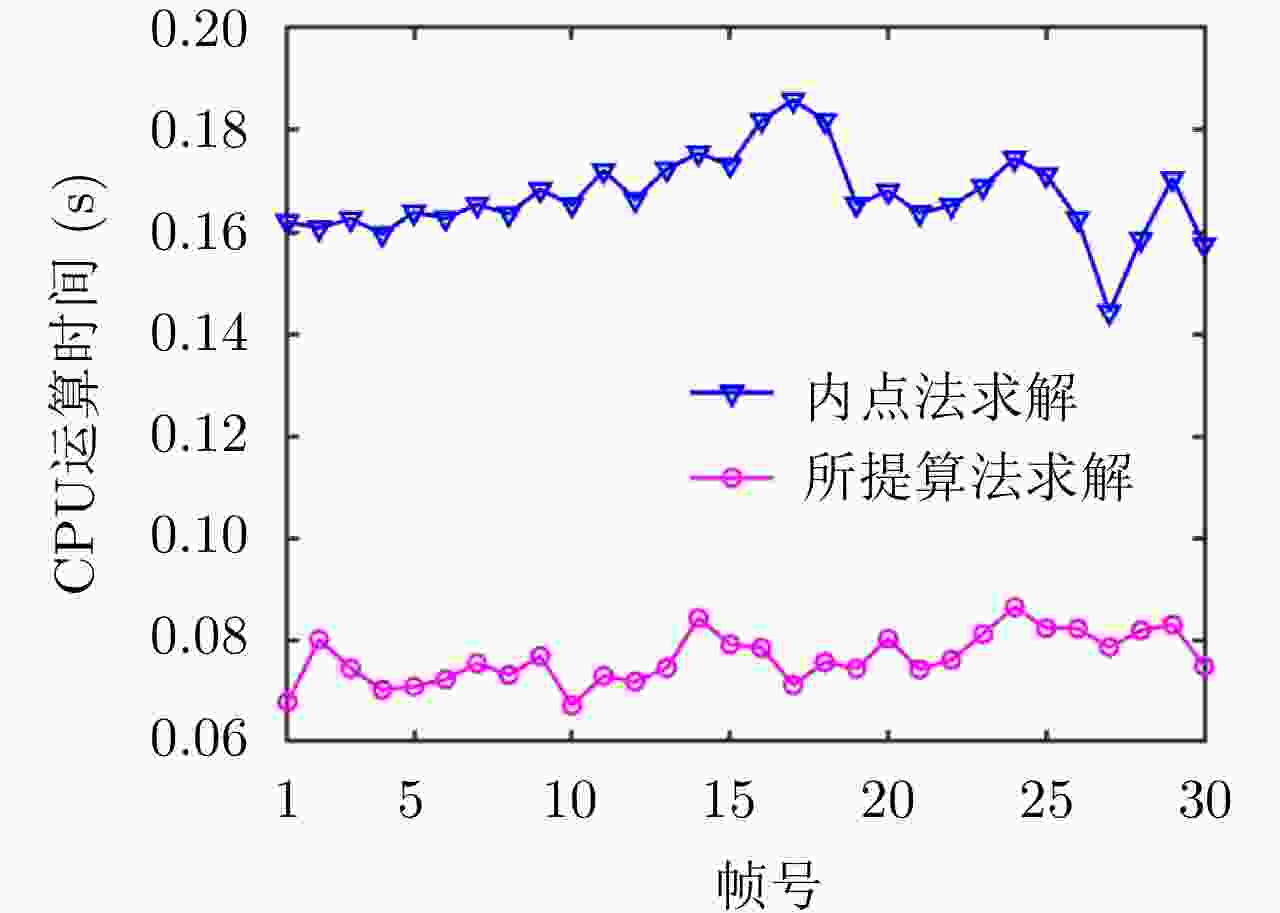
摘要: 针对集中式MIMO雷达同时跟踪多批机动目标场景，该文提出一种低截获背景下的快速功率分配算法。首先，将目标机动过程建模为自适应当前统计(ACS)模型，并采用粒子滤波对各目标状态进行估计。其次，对条件克拉默-拉奥下界(PC-CRLB)进行推导，并基于目标运动特性和电磁特性构建目标综合威胁度评估模型。随后，将目标跟踪误差评估指数和雷达未被截获概率的加权和作为优化目标，建立了关于发射功率的优化模型，利用目标函数单调递减性质，提出了一种基于序列松弛的求解算法进行模型求解。最后，通过仿真验证所提算法的有效性和时效性。结果表明，所提算法能够有效提高目标跟踪精度和雷达系统低截获性能，相比采用内点法求解运算速度提高近50%。
- 集中式MIMO雷达 /
- 功率分配 /
- 机动跟踪 /
- 低截获性能 /
- 条件克拉默-拉奥下界(PC-CRLB)
Abstract: This study proposes a fast power allocation algorithm under a low interception background for a collocated MIMO radar that simultaneously tracks multiple maneuvering targets. First, the target maneuver process is modeled as an Adaptive Current Statistical (ACS) model, and a particle filter is used to estimate the state of each target. Second, the Predicted Conditional Cramer-Rao Lower Bound (PC-CRLB) is derived, and the target comprehensive threat assessment model is constructed based on the target motion and electromagnetic characteristics. Subsequently, an optimization model with respect to transmitting power is established by developing the weighted sum of the target tracking error evaluation index and the unintercepted probability of radar as the optimization objective. Thereafter, to solve the model using the monotonically decreasing property of the objective function, a solving algorithm based on sequence relaxation is proposed. Finally, a simulation is conducted to verify the effectiveness and timeliness of the proposed algorithm. The results indicate that the proposed algorithm can effectively improve the target tracking accuracy and low interception performance of the radar system. Further, its run speed is increased by nearly 50% compared with that of the interior point method.
- Collocated MIMO radar /
- Power allocation /
- Maneuvering tracking /
- Low interception performance /
- Predicted Conditional Cramer-Rao Lower Bound (PC-CRLB)

HTML全文

1. 引言

穿墙雷达是一种利用低频电磁波穿透特性探测建筑物结构和墙后目标的技术，可不受障碍物遮挡影响，对墙后遮蔽空间信息进行穿透感知^[1−3]。目前穿墙雷达的工作体制主要包括多发多收(Multiple-Input Multiple-Output, MIMO)雷达和合成孔径雷达(Synthetic Aperture Radar, SAR)。MIMO穿墙雷达常用于室内目标的定位与跟踪，具有较高时效性；穿墙SAR具有观测范围广、分辨率高等优势，常用于建筑物结构布局重构和室内静目标成像^[4]。穿墙SAR通常利用超宽带信号提供距离向高分辨率，利用水平方位的合成孔径提供方位向高分辨率^[5]。三维穿墙SAR成像能直观反映出目标高度维信息，在灾害救援、城市反恐等领域具有重要应用，近年来受到广泛关注^[6−9]。目前，穿墙雷达主要使用车载或手持平台，在城市复杂高层楼宇场景中，传统车载穿墙雷达通常在地面上运行，无法胜任不可达高楼层场景，例如高层火灾救援、高楼反恐作战等；手持固定平台MIMO穿墙雷达观测范围受限问题更为突出，无法对大规模场景进行探测与成像。相比之下，将无人机的灵活性与穿墙雷达的穿透能力相结合的无人机载穿墙雷达(如图1所示)，可无视高度限制，对高层建筑进行穿透探测与成像，从而有效解决传统穿墙雷达探测高度受限问题，但目前还鲜有利用无人机载穿墙雷达在城市建筑开展穿透探测的研究报道。

图 1 无人机载穿墙雷达高层建筑探测场景示意图

Figure 1. Schematic diagram of detection scenario for UAV-TWR in high-rise buildings

下载: 全尺寸图片幻灯片

在传统直视场景三维层析SAR中，无人机通过水平方向飞行实现方位向合成孔径，不同高度多航过飞行实现高度向合成孔径。目前已有的无人机载三维层析SAR通常采用多基线飞行方式(Multi Baseline SAR, MB-SAR)^[10]，即以多个密集的水平航过扫描相同区域进行成像。这种飞行模式下，为避免高度向空域欠采样导致的栅瓣效应(或高程模糊)，相邻基线间距需要小于半波长，由于电池容量限制，无人机飞行续航时间有限，无法满足城市楼宇大范围穿墙成像的需求^[11]。而使用大间距基线扫描以满足更大探测区域时，成像质量会因栅瓣效应而严重恶化^[12]。针对上述问题，可使用压缩感知技术替代传统的高度向脉冲压缩，在一定程度上缓解高度向栅瓣严重的问题，但面临稀疏恢复计算量大的难题^[13]。针对MIMO雷达中稀疏阵列产生的栅瓣问题，通常的解决办法是使用阵列设计与优化方法，通过非均匀化阵元间距起到栅瓣抑制的效果^[14]。Feng等人^[15]通过复合算法迭代优化阵元位置，实现稀疏MIMO阵列低栅瓣高分辨率成像。因此，机载穿墙SAR可借鉴MIMO雷达天线阵列的设计思路，对无人机进行任意形态航迹规划，使其轨迹非均匀化，抑制高度向周期性栅瓣能量，从而达到最优的三维成像效果，克服成像质量与成像效率无法兼顾的问题^[16]。

对于视距场景无人机全局航迹规划问题而言，通常采取的方法是根据飞行距离^[17]、成像质量^[18]等设置代价函数，将航迹规划问题转化为代价函数最小的优化问题进行求解^[19]。而在具体的求解方法上，大致可分为两类：传统优化算法和智能优化算法^[20]。

传统优化算法包括凸松弛、整数规划等，通常需要对问题进行近似或分割，以转化为凸优化问题进行求解。传统优化算法优点在于可解释性强，但存在局部最优和初始点敏感等问题。Lahmeri等人^[21]使用混合整数非线性规划算法，并加以逐次凸近似算法进行优化问题求解，进行实时任务规划，在兼顾SAR成像质量条件下最大化无人机载雷达对地面的覆盖率，但该方法仍使用MB-SAR飞行方式，仅改变基线间距，依然存在飞行效率较低的问题。Drozdowicz等人^[18]系统阐述了无人机载SAR三维成像的场景与原理，并基于Nelder-Mead优化算法，提出了一种降低三维SAR成像旁瓣能量的航迹规划方法，然而其算法核心是在“Z”字型轨迹上进行扭曲与优化，成像质量提升有限，受随机初始值影响较大，也未进行实测数据验证，在本文中记为“Z-SAR”。

智能优化算法主要包括粒子群算法(Particle Swarm Optimization, PSO)、遗传算法(Genetic Algorithm, GA)和模拟退火算法(Simulated Annealing, SA)等，这类启发式智能算法通常是归纳自然界及动物活动规律所得，对非线性、非凸问题的适应性和鲁棒性更好，在搜索复杂问题最优解中有着广泛的应用，但也存在收敛速度慢、超参数选择困难等问题^[22,23]。Brown等人^[17]提出了一种基于多目标PSO算法的航迹规划方法，实现了最大化搜索区域和最小化燃料消耗之间的权衡，然而该研究的应用局限于海上监视场景，无法在城市楼宇穿墙成像场景中应用。王楚涵等人^[24]结合使用PSO和GA，提出了一种机载分布式MIMO雷达的航迹规划算法，兼顾雷达监视区域大小和性能，该研究主要实现多无人机的平面布站，无人机抵达指定位置后便不再移动，不适用于单无人机的穿墙三维SAR场景。

上述航迹规划的飞行模式较为单一，基本局限为平面直线轨迹，尚无针对无人机载穿墙雷达场景航迹规划方法研究。因此，本文针对无人机探测效率与成像质量之间的矛盾，创新性地将航迹规划应用于无人机载穿墙SAR成像领域，提出基于遗传算法的无人机载穿墙三维SAR航迹规划方法，实现无人机飞行效率与穿墙SAR成像质量的平衡。根据不同飞行模式设立相应基因型，经过遗传算法不断迭代，得到不同飞行模式下最优的航迹，并通过仿真与实测数据对所提方法进行验证。仿真与实验数据表明：在相同飞行距离的情况下，本航迹规划方法SAR成像质量明显优于传统多基线航迹穿墙SAR成像质量，其中斜线飞行模式可兼顾最佳的探测效率和最优的成像质量。

2. 空域欠采样栅瓣问题分析

当雷达空间阵列间距大于半波长时，空间欠采样将导致栅瓣效应，影响成像效果。假设如所示平面场景，为栅瓣推导简便起见，设置两个竖直排布间距为d的雷达，目标与雷达的水平距离为D，目标与雷达的竖直距离分别为 ${x_1}$ 和 ${x_2}$ ，栅瓣与目标竖直距离为 $\Delta x$ ， $\Delta {R_1}$ 表示“雷达1-目标”间距和“雷达1-栅瓣”间距的差值， $\Delta {R_2}$ 同理，如图2中粉色实线所示。

图 2 栅瓣场景示意图

Figure 2. Schematic diagram of grating scene

下载: 全尺寸图片幻灯片

对于上述场景，SAR成像过程是两个雷达各自成像结果的相干叠加，故而栅瓣所处位置应满足两个雷达在该点的辐角相等，即满足式(1)：

${{\mathrm{e}}^{ - \textstyle\frac{{4{\mathrm{j}}\pi \Delta {R_1}}}{\lambda }}} = {{\mathrm{e}}^{ - \textstyle\frac{{4{\mathrm{j}}\pi \Delta {R_2}}}{\lambda }}}$

(1)

设置参数 $\alpha$ 和 $\beta$ 使其满足式(2)：

$\left.\begin{aligned} & \alpha = \frac{{2\pi (\Delta {R_1} + \Delta {R_2})}}{\lambda } \\ & \beta = \frac{{2\pi (\Delta {R_1} - \Delta {R_2})}}{\lambda } \end{aligned}\right\}$

(2)

将式(1)根据欧拉公式展开，按三角函数和差化积公式合并，并以式(2)化简，可得式(3)：

$\sin \beta \cdot [{\mathrm{j}}\cos \alpha - \sin \alpha ] = 0$

(3)

其中，中括号部分恒不为0，因此当且仅当式(4)成立时，式(3)成立。

$\sin \beta = 0$

(4)

代入参数，可得式(5)：

$\begin{split} \Delta {R_1} - \Delta {R_2} = \,& \sqrt {{D^2} + x_1^2} - \sqrt {{D^2} + x_2^2} \\ & +\sqrt {{{(D - \Delta D)}^2} + {{(\Delta x - {x_2})}^2}} \\ & - \sqrt {{{(D - \Delta D)}^2} + {{(\Delta x - {x_1})}^2}} \end{split}$

(5)

当满足 $D \gg {x_1},{x_2},\Delta D$ 时，式(5)可化简为

$\Delta {R_1} - \Delta {R_2} = \Delta x \cdot \frac{d}{D}$

(6)

将式(6)代入式(4)中，化简得到栅瓣在竖直方向的位置：

$\Delta x = k\frac{{\lambda D}}{{2d}}\;\;(k = \pm 1, \pm 2,\cdots)$

(7)

由式(7)可知，等间距空间采样时，若间距大于半波长，则会导致成像结果出现周期性的栅瓣，且雷达间距d越大，栅瓣间距就越小，栅瓣效应就越严重。因此，从阵列设计的角度而言，非等间距的随机采样能够在兼顾效率的同时抑制栅瓣的形成。在这种随机采样的模式下，雷达回波无法在非目标位置同相叠加，从而达到抑制栅瓣的目的。对于机载雷达而言，应该选取某种随机的飞行轨迹，以此同时满足高飞行效率和高成像质量。

3. 基于遗传算法的无人机载穿墙SAR航迹规划

3.1 航迹规划代价函数

无人机载穿墙雷达的飞行方式会显著影响目标区域的成像质量，需要在有限的飞行距离下对三维成像的质量进行定量评估，最终结合雷达成像质量与飞行距离构造代价函数。峰值栅瓣比(Peak-to-Grating Lobe Ratio, PGLR)定义为最大栅瓣幅值与主瓣幅值的比值^[25]，通常用dB表示，常用于反映成像结果的栅瓣强弱，方便起见在本文中记为 ${R_{\rm{pgl}}}$ 。其数学形式如式(8)所示：

${R_{\rm{pgl}}} = 20\lg \left(\frac{{\max ({P_{{\mathrm{gl}}}})}}{{\max ({P_{\rm{ml}}})}}\right)$

(8)

其中， ${P_{{\mathrm{gl}}}}$ 代表栅瓣的点集，而 ${P_{\rm{ml}}}$ 代表主瓣的点集，因此 ${R_{\rm{pgl}}}$ 越小说明成像质量越高。SAR图像的三维分辨率虽然也常用于评估成像质量，但主要受方位向和高度向的孔径大小影响，而不同飞行方式下的方位和高度向范围大致相同，即不同飞行轨迹的分辨率近似一致，因此不将分辨率作为评判标准，重点考虑栅瓣对成像质量的影响。

遗传算法对代价函数高度依赖，因此合理地构造飞行距离和成像质量的联合代价函数至关重要。为符合无人机实际情况，代价函数中飞行距离部分设计为分段函数形式，如式(9)所示：

$\left\{ \begin{aligned} & C(L) = {w_1}L,{\text{ }}\qquad\qquad\qquad\qquad\;\; L < {L_{\max }} \\ & C(L) = {w_1}{L_{\max }} + {w_2}(L - {L_{\max }}),{\text{ }}L \ge {L_{\max }} \end{aligned} \right.$

(9)

其中，C为飞行距离的代价函数，L为无人机飞行距离， ${L_{\max }}$ 为期望的最大飞行距离，设置为80 m；权重值 ${w_1},{w_2}$ 满足 ${w_1} \ll {w_2}$ 。故总代价函数J包含两部分，分别为飞行距离和雷达成像结果 ${R_{\rm{pgl}}}$ ，可表示为

$J(L,{R_{\rm{pgl}}}) = C(L) + {w_3} \cdot {R_{\rm{pgl}}}$

(10)

其中， ${w_3}$ 为评估 ${R_{\rm{pgl}}}$ 的超参数权重，具体取值上应满足 ${w_3} > {w_1}$ ，即图像质量对总代价函数的影响占比最大。无人机飞行距离和机载穿墙雷达的成像结果并非相互独立， ${R_{\rm{pgl}}}$ 是依赖于无人机载雷达飞行轨迹L的隐式函数，因此无人机载穿墙SAR航迹规划问题可描述为最优化问题：

$\mathop {\min }\limits_L J(L,{R_{\rm{pgl}}})$

(11)

由飞行轨迹获取得到图像 ${R_{\rm{pgl}}}$ ，并通过最小化联合总代价函数 $J(L,{R_{\rm{pgl}}}) = C(L) + {w_3} \cdot {R_{\rm{pgl}}}$ ，来获取当前评估准则下的最优飞行路径。

3.2 基于遗传算法的机载穿墙雷达航迹优化

针对上述无人机载穿墙雷达航迹规划问题，局部最优化算法和全局启发式搜索算法均可进行求解，但是局部最优化算法需要严格的数学理论推导，求解较为困难，同时容易陷入目标函数局部极值点，无法找到全局最优解。全局启发式优化算法理论较为简单，具备目标函数的全局搜索能力，本文以遗传算法为例，开展基于遗传算法的无人机载SAR航迹规划方法研究。遗传算法起源于自然界中种群的遗传与进化，是一种启发式的搜索算法，具有不易过早陷入局部极值的优点，在许多非凸优化问题的求解中有广泛应用。针对无人机载穿墙雷达的航迹规划问题，本节提出了3种可行的飞行模式，并结合遗传算法，对建立的目标函数进行优化，以获取在特定飞行模式下的最优飞行航迹，对穿墙雷达目标进行成像。

3.2.1 无人机载穿墙雷达飞行模式基因编码

(1) 非等间距水平多基线飞行模式

对于传统机载多基线雷达而言，为了具有良好的栅瓣抑制效果，其相邻基线间距通常相等且小于雷达半波长。当均匀间距大于半波长时，会产生栅瓣，严重影响三维层析SAR的成像效果。针对上述问题，本节提出一种基于遗传算法优化的非等间距水平多基线SAR (Unequally-spaced Multi Baseline SAR, UMB-SAR)飞行模式，通过改变水平基线高度向位置实现栅瓣抑制。虽然这种飞行方式在水平方位向仍有较大的航迹冗余，但无人机飞行方式简单，易于操控实现。

假设场景的高度向范围为0～5 m，将每个整体的航迹视为一个独立的个体，则个体的基因型可以表示为长度为500的01向量G，即左侧绿色框所示的向量。其中，深绿色位置值为1，浅绿色位置值为0，500个位置均匀对应5 m的高度向范围，每个位置对应0.01 m的高度。将无人机经过的高度位置设为1，没有经过的位置设为0。因此，当基因型G中第i个位置为深色时，代表该处取值为1，即高度 $0.01i$ m处有一条水平的航过。

图 3 UMB-SAR基因型

Figure 3. UMB-SAR genotype

下载: 全尺寸图片幻灯片

为了保证飞行轨迹具有足够高的效率，应确保基线最短间距大于半波长，即对于基因型的下标而言，任意两个“1”的下标差应大于固定值c，如式(12)所示：

$\forall i,j \in [1,500]{\text{ where }}{{{G}}_i} = {G_j} = 1{\text{ then }}\left| {i - j} \right| > c$

(12)

(2) 水平-竖直交叉飞行模式

UMB-SAR仅改变了水平方位向飞行的基线间距，其本质上仍是水平多航过飞行，没有考虑竖直方向上的飞行。故在UMB-SAR的基础上加入竖直飞行，提出交叉飞行SAR (Cross Flight SAR, CF-SAR)模式，通过竖直方向的航过，以二维网格的形式进一步抑制高度向栅瓣。

CF-SAR的基因型与UMB-SAR类似，同样设置为01向量形式。设高度向长度为5 m，方位向长度为10 m，为保证同等长度的基因对应同样的物理长度，故将基因型长度由500扩展为长度为1500的01向量G，其中前一部分1～500仍表征水平方向飞行，后一部分501～1500则表征竖直方向的飞行，如图4所示。其中绿色框图部分代表水平飞行的基因型，红色框图代表竖直飞行的基因型。当基因型G中第i个位置为深色时，若i小于等于500，即图中深绿色，表示高度向 $0.01i$ m处有一条水平的基线；若i大于500，即图中深红色，则表示 $0.01(i - 500)$ m处有一条竖直的基线。

图 4 CF-SAR基因型

Figure 4. CF-SAR genotype

下载: 全尺寸图片幻灯片

同样地，为保证航过最短间距大于半波长，有类似式(12)的限制条件，如式(13)所示，其中c₁和c₂为固定值：

$\left. \begin{aligned} & \forall i,j \in [1,500]{\text{ where }}{G_i} = {G_j} = 1{\text{ then }}\left| {i - j} \right| > {c_1} \\ & \forall i,j \in [501,1500]{\text{ where }}{G_i} = {G_j} = 1{\text{ then}}\left| {i - j} \right| > {c_2} \end{aligned}\right\}$

(13)

(3) 三维斜线飞行模式

直线飞行模式虽然轨迹简单易于操控，但仍存在航迹冗余，若将成像模式调整为三维斜线飞行SAR (Oblique Flight SAR, OF-SAR)模式，相同飞行距离条件下，能达到更优的成像质量。

若总航过数目为n，则其基因型是行数为 $n + 1$ 、列数为3的二维矩阵。基因矩阵每一行数据对应 $n + 1$ 个路径点的三维XYZ坐标，其航迹为这 $n + 1$ 个点依次连接而成，如所示。为避免相邻两点之间的基线太短，本研究对单个基线的长度添加限制，必须大于最短距离 ${l_{\min }}$ ，如式(14)所示：

图 5 OF-SAR基因型

Figure 5. OF-SAR genotype

下载: 全尺寸图片幻灯片

$\forall i,\left| {{P_{i + 1}} - {P_i}} \right| > {l_{\min }}$

(14)

其中，i为途径点下标，P为途径点的三维向量， $|A|$ 代表向量A的模。另外，为避免航迹中出现角度过大的转向而耗费时间，在航迹途径点中加入了角度限制，即相邻两条基线夹角应大于 $\theta$ ，如式(15)所示：

$\begin{split} & \forall i,{\text{ where }}i = 1,2,\cdots,s - 1\\ & {\mathrm{arccos}}\left( {\frac{{({P_{i + 1}} - {P_i}) \cdot ({P_{i + 2}} - {P_{i + 1}})}}{{\left| {{P_{i + 1}} - {P_i}} \right| \cdot \left| {{P_{i + 2}} - {P_{i + 1}}} \right|}}} \right) > \theta \end{split}$

(15)

3.2.2 选择与杂交

在选择与杂交前，需要对这一代所有个体计算代价函数，并对代价函数进行降序排列。若每一代有M个个体，那么一定只能有K个个体能够参与繁殖，其中满足 $K < M$ 。这是因为必须引入优胜劣汰的过程，整体的基因型才会得到进化。而其中筛选比例 $K/M$ 的选择将对遗传算法的收敛性产生较大的影响，当 $K/M$ 太大时，选择性便会下降，优化速度与收敛速度也会随之下降；而当 $K/M$ 太小时，容易导致种群基因型过于单一，提前收敛而陷入局部最优值，因此需要根据情况选择合理的筛选比例。在具体数值上，选取为M为100，K为10。

在具体从M个个体中选择K个个体时，本研究采用代价加权的随机选择方式，即每个个体都有概率被选择留下子代，而其代价函数越小，被选择的概率越高，如式(16)所示：

${P_i} = \frac{{{{\mathrm{e}}^{ - \lambda {J_i}}}}}{{\displaystyle\sum\limits_{k = 1}^M {{{\mathrm{e}}^{ - \lambda {J_k}}}} }}$

(16)

其中， ${P_i}$ 表示个体i被选择的概率， ${J_i}$ 是个体i的代价函数，λ为调节参数，取值为0.3，用于控制代价对选择概率的影响程度。与直接选择概率最高的前K个个体相比，该方式更符合自然界中的选择过程，能更大限度地避免基因型固化。

选择之后是杂交步骤，用于生成子代。杂交函数是遗传算法能否学习到遗传特性、能否快速收敛的关键步骤。一般地，杂交函数的输入是从K个已选择亲代中随机抽取两个个体，杂交函数将其基因型重组后，输出一个或多个新个体，当新个体不满足式(14)或式(15)时，需要重新生成。

(1) UMB-SAR

采用一种“随机位点交叉互换”的方法，即先在500个下标中随机选取一个下标r作为交换位点，设亲代基因型为 ${G_{\mathrm{a}}}$ 和 ${G_{\mathrm{b}}}$ ，子代基因型为G，则G可由式(17)表示：

$\left.\begin{aligned} & G[1:r] = {G_{\mathrm{a}}}[1:r] \\ & G[(r + 1):500] = {G_{\mathrm{b}}}[(r + 1):500] \end{aligned}\right\}$

(17)

式(17)表示子代的基因型G在位点r处以前和亲代 ${G_{\mathrm{a}}}$ 的对应位点相同，在位点r处以后和亲代 ${G_{\mathrm{b}}}$ 的对应位点相同。

(2) CF-SAR

CF-SAR的杂交方法与上述杂交方法相似，需要在1～500和501～1500中分别随机选取两个下标 ${r_1},{r_2}$ 作为交换位点，设亲代基因型为 ${G_{\mathrm{a}}}$ 和 ${G_{\mathrm{b}}}$ ，子代基因型为G，则G可由式(18)表示：

$\left. \begin{aligned} & G[1:{r_1}] = {G_{\mathrm{a}}}[1:{r_1}] \\ & G[({r_1} + 1):500] = {G_{\mathrm{b}}}[({r_1} + 1):500] \\ & G[501:{r_2}] = {G_{\mathrm{a}}}[501:{r_2}] \\ & G[({r_2} + 1):1500] = {G_{\mathrm{b}}}[({r_2} + 1):1500] \end{aligned}\right\}$

(18)

(3) OF-SAR

此模式下的杂交函数也是在 $1{\text{～}}(s + 1)$ 范围内随机选取下标。设亲代基因型为 ${G_{\mathrm{a}}}$ 和 ${G_{\mathrm{b}}}$ ，子代基因型为G，则G可由式(19)表示：

$\left.\begin{aligned} & G[1:3,1:r] = {G_{\mathrm{a}}}[1:3,1:r] \\ & G[1:3,(r + 1):(s + 1)] = {G_{\mathrm{b}}}[1 : 3,(r + 1) : (s + 1)] \end{aligned}\right\}$

(19)

3.2.3 基因突变

若只依靠杂交函数，那么种群中将不会产生新位点上的基因，这将导致算法结果高度依赖于种群的初始随机生成，因此还需要在杂交函数之后引入基因突变，在具体数值上设置突变概率为0.2。

(1) UMB-SAR与CF-SAR

这两种飞行模式的基因型均为01向量，故基因突变的方式相似：每次突变随机选取其中一个“1”，将其置为“0”，在随机选择附近下标一个原本为“0”的点，将其置为“1”。突变结束后需要判断是否满足限制条件，若不满足同样需要重新生成。

(2) OF-SAR

此模式下基因型为数值类型，与之前两种不同，故OF-SAR的基因突变为：在 $s + 1$ 个坐标点中随机选取一个三维坐标，并在满足式(15)和式(16)约束的条件下，在 $\pm 10\%$ 范围内改变其三维坐标的数值。

4. 实验结果及分析

本节将通过仿真数据，对比分析所提无人机载穿墙雷达航迹规划算法对成像质量的改善效果，并通过华诺星空CEM 200线性调频连续波机载穿墙雷达进行外场挂飞实验，不同飞行轨迹的穿墙雷达实测数据处理结果进一步验证了本文所提算法的有效性。

4.1 数值仿真与分析

为验证穿墙场景下所提方法的有效性，电磁波需要穿过较为复杂的墙体介质，使用解析公式获取穿墙场景的雷达回波存在一定困难，本研究使用开源时域有限差分数值仿真软件gprMax生成雷达回波数据^[26]，对上述所提UMB-SAR, CF-SAR和OF-SAR飞行模式航迹优化结果进行验证。在生成仿真雷达回波数据时，直接使用gprMax发射大脉宽调频连续波信号将导致仿真时间过长，故设置雷达天线发射信号为无载波的冲激脉冲波形，所得回波近似为系统冲激响应。仿真场景可视为一个线性时不变系统，将冲激响应与线性调频信号卷积，从而得到对应于输入线性调频信号的仿真穿墙场景回波信号。对该回波进行脉冲压缩，并经过距离插值、后向投影(Back Projection, BP)、相干累加等过程，最终得到三维后向投影成像结果。

上述遗传算法迭代过程中，设置单点目标坐标为(5.0 m, 5.0 m, 2.0 m)，并对其 ${R_{\rm{pgl}}}$ 进行迭代优化。为衡量多点目标场景的算法效果，仿真场景在前期航迹优化处理基础上添加点目标1与点目标3，具体仿真参数如表1所示。

表 1 穿墙场景数值仿真参数

Table 1. Simulation parameter settings

参数	数值
雷达载频	2.95 GHz
雷达带宽	440 MHz
场景方位向范围	0～10 m
场景高度向范围	0～5 m
场景距离向范围	0～10 m
墙体厚度	0.2 m
墙体相对介电常数	4.0
点目标1坐标	(8.0 m, 7.0 m, 2.7 m)
点目标2坐标	(5.0 m, 5.0 m, 2.0 m)
点目标3坐标	(2.0 m, 6.0 m, 3.7 m)
超参数权重 $({w_1},{w_2},{w_3})$	(0.02, 0.43, 0.55)

下载: 导出CSV

| 显示表格

穿墙仿真的三维场景如所示，其中方位向范围为0～10 m，距离向范围为0～10 m，高度向范围为0～5 m。墙体位于距离向4 m处，无人机在墙体左侧空间内飞行，点目标位于墙体右侧，即图中小球所示。因墙体的反射回波能量显著强于目标散射回波，利用gprMax进行穿墙仿真后，通过墙体回波和目标回波在距离向的差异，将墙体回波从雷达数据中移除，以便后续三维SAR成像结果的比较。式(9)与式(10)中的超参数权重 $({w_1},{w_2},{w_3})$ 分别设置为0.02, 0.43和0.55。 ${w_2}$ 是飞行距离超出期望最大飞行距离时的权重，本研究为了避免超出最大飞行距离的情况，将 ${w_2}$ 设置得较大。倘若对最大飞行距离没有严格的限制，可以适度调小 ${w_2}$ 取值。 ${w_3}$ 与 ${w_1}$ 的比例应当选用合适的取值，经仿真测试，若 ${w_3}/{w_1}$ 太小(小于10)，遗传算法会过于重视飞行距离而忽视成像质量，导致最终成像质量较差；若 ${w_3}/{w_1}$ 太大(大于50)，则基本等同于对单变量 ${R_{\rm{pgl}}}$ 的优化，不能起到兼顾成像质量的同时缩减飞行距离的作用。

图 6 三维穿墙仿真场景

Figure 6. Through-the-wall 3D simulation scene

下载: 全尺寸图片幻灯片

4.1.1 MB-SAR

为比较算法优劣，设置8条间距为0.625 m的MB-SAR成像结果作为对照，航迹如图7(a)所示，其中虚线代表无人机水平方位向的飞行航过，实心点代表每条飞行航过的起始与结束位置。由于墙后3个目标点的方位、距离与高度均不相同，无法采用一幅截面表示，故将3幅截面投影合一，以距离-高度向投影图和方位-高度向投影图反映成像质量。图7(b)与图7(c)中可观察到明显的高度向周期性栅瓣。

图 7 MB-SAR航迹与成像结果

Figure 7. MB-SAR trajectory and imaging results

下载: 全尺寸图片幻灯片

4.1.2 UMB-SAR

UMB-SAR飞行模式下，以不同数值作为随机数种子，经过10次遗传算法迭代过程得到如图8(a)所示代价函数下降图线，不同迭代过程用不同的颜色表示。因初始种群基因型随机生成，初始代价函数在−1.8～−2.3随机分布。随着迭代次数增加，代价函数逐渐降低，当代价函数连续10次降低不超过1E−6时停止迭代，最终迭代约50次后收敛。在最优的情况(#9)中，代价函数从−2.12降低至−3.15。遗传算法迭代得到的最优航迹有8条长度为10 m的水平方位向航过，飞行距离为80 m。其水平航过间距各不相同，呈近似随机排布。

图 8 UMB-SAR航迹优化与成像结果

Figure 8. UMB-SAR trajectory optimization and imaging results

下载: 全尺寸图片幻灯片

对比图7与图8可知，MB-SAR成像结果存在严重栅瓣效应，难以确定点目标高度位置。UMB-SAR高度向栅瓣能量更为分散，无周期性栅瓣强点，优于MB-SAR的对应结果，但栅瓣效应仍较为显著。

4.1.3 Z-SAR

为对比已有飞行模式与所提模式的优劣，对Drozdowicz等人^[18]的Z-SAR进行遗传算法优化，因其基因型与UMB-SAR相似，故不过多赘述。算法迭代结果如图9(a)所示，种群初始代价函数大致位于−2至−3区间内，其中#6为最优情况，对应代价函数从−2.23降至−3.68，相较于UMB-SAR的最佳飞行结果提升16.8%。对应的航迹如图9(b)所示，共有8条锯齿状航过，总飞行距离为80.16 m。

图 9 Z-SAR航迹优化与成像结果

Figure 9. Z-SAR trajectory optimization and imaging results

下载: 全尺寸图片幻灯片

与UMB-SAR相比，Z-SAR整体栅瓣能量进一步降低，距离-高度图中栅瓣覆盖范围明显缩小，表明以斜线代替直线航迹将提升栅瓣抑制效果。

4.1.4 CF-SAR

在CF-SAR模式下，遗传算法迭代结果如图10(a)所示，种群初始代价函数基本位于−2.7至−3.0区间内，在第40次迭代左右收敛，其中#5为最优情况，对应代价函数从−2.88降至−4.21，相较于UMB-SAR的最佳飞行结果提升33.7%。对应的航迹如图10(b)所示，共有12条航过，包含4条长度为10 m的水平方位向航过和8条长度为5 m的竖直航过，总飞行距离为80 m，与最大飞行距离相同。

图 10 CF-SAR航迹优化与成像结果

Figure 10. CF-SAR trajectory optimization and imaging results

下载: 全尺寸图片幻灯片

CF-SAR中栅瓣情况较UMB-SAR进一步分散，整体栅瓣能量进一步降低，但图10(b)中高度向仍存在少量周期性栅瓣。

4.1.5 OF-SAR

在OF-SAR模式下，遗传算法迭代结果如图11(a)所示，在第50次迭代左右收敛，最低代价函数为−5.25，相较于UMB-SAR的最佳飞行结果提升约66.7%。该结果对应的航迹如图11(b)所示，总飞行距离为56.5 m，小于前述所有模式。

图 11 OF-SAR航迹优化与成像结果

Figure 11. OF-SAR trajectory optimization and imaging results

下载: 全尺寸图片幻灯片

OF-SAR中栅瓣情况前两种飞行模式有明显提升，在飞行距离最短的情况下，有着相对最佳的成像质量，说明了所提方法在机载穿墙雷达成像中有较好的效果。

4.1.6 对比与分析

为对比传统MB-SAR算法、Z-SAR与本文所提UMB-SAR, CF-SAR和OF-SAR算法，选取经遗传算法优化的点目标 ${R_{\rm{pgl}}}$ 衡量飞行模式的优劣，代价函数(遗传算法运行结果)与 ${R_{\rm{pgl}}}$ 如表2所示。

表 2 算法仿真结果对比

Table 2. Comparison of algorithm simulation results

飞行模式	代价函数	${R_{\rm{pgl}}}$ (dB)
MB-SAR	\	−0.51
UMB-SAR	−3.15	−8.64
Z-SAR	−3.68	−9.73
CF-SAR	−4.21	−10.56
OF-SAR	−5.25	−11.60

下载: 导出CSV

| 显示表格

中 ${R_{\rm{pgl}}}$ 是不同算法成像结果的峰值栅瓣比，其数值越小说明成像效果越好。根据对比结果可知，在相同飞行距离限制条件下，本文所提UMB-SAR方法优于传统MB-SAR飞行，而本文所提CF-SAR与OF-SAR方法则优于Z-SAR算法，从理论层面验证了所提方法的有效性。

MB-SAR因其在欠采样场景下航过间距相等，栅瓣效应最为明显；UMB-SAR在其基础上改变航过间距，故栅瓣效应有所抑制；Z-SAR可视为UMB-SAR的改进，航过由水平直线转变为锯齿状斜线，引入更多采样位置的非均匀性，故成像质量优于UMB-SAR；CF-SAR在UMB-SAR的基础上添加竖直方向的航过，进一步降低高度向栅瓣；OF-SAR使用三维斜线飞行，采样位置非均匀性最大，在飞行距离最短的情况下有着最佳成像效果。

4.2 实测数据

为进一步验证所提算法轨迹优化后的无人机载穿墙雷达成像性能，本研究开展了无人机载穿墙雷达的外场实验验证。所用的无人机为大疆M350型号四旋翼无人机(图12)，该型号无人机可利用网络实时动态(Real-Time Kinematic, RTK)差分定位技术提供高精度的无人机位置信息，可为后续BP成像提供定位数据。将预先优化好的航迹存储到大疆飞控端，再通过飞控系统将航迹文件将上传到无人机，通过预设航迹，无人机能够按照指定的航迹、速度与机头朝向进行规划飞行。

图 12 CEM200型号无人机载穿墙雷达

Figure 12. UAV-TWR CEM200

下载: 全尺寸图片幻灯片

本文实验使用华诺星空CEM200型号无人机载穿墙雷达进行数据采集，实测数据参数如表3所示。为了保证天线结构的小型化，雷达射频信号频率为2.95～3.35 GHz，使用调频连续波信号，提供足够的平均发射功率，脉冲重复频率为1923 Hz，能够保证较大的多普勒带宽，中频信号的采样率为10 MHz。无人机的飞行速度可通过大疆的航迹规划软件进行设置，本文所有的实验均采用2 m/s的飞行速度(在控制点会降速，以保证无人机航迹切换的稳定性)。

表 3 实测数据参数

Table 3. Actual measured data parameters

实验参数	数值
雷达载频	2.95 GHz
脉冲重复频率	1923 Hz
雷达带宽	440 MHz
采样率	10 MHz
飞行速度	2 m/s

下载: 导出CSV

| 显示表格

为验证算法结果在城市非视距场景的适用性，本研究在穿墙模式下开展了实验，飞行轨迹由提前上传的轨迹进行控制。其场景如图13(a)所示，角反射器坐标大约位于(5 m, 7 m, 2 m)处；图13(b)中的建筑物外墙高度约10 m，建筑物的宽度约8 m，建筑物外墙采用多孔红心砖墙修建，墙体厚度约为24 cm。无人机在距离墙面约4 m距离沿预设的4种轨迹进行自动巡航飞行，飞行轨迹通过图中的白色曲线线条进行示意。

图 13 穿墙场景测试图

Figure 13. Measurement of through-the-wall scene

下载: 全尺寸图片幻灯片

4.2.1 无人机飞行轨迹与分析

通过RTK记录的4种飞行模式航迹如所示，与理想轨迹基本一致，但因为受无人机飞行控制、近地表气流影响，不可避免地与理想轨迹有一定偏差，为对比评估轨迹偏差对成像质量的影响，本文将实测轨迹作为仿真输入，进行仿真SAR成像，获取不同飞行模式下的 ${R_{\rm{pgl}}}$ ，仿真参数与4.1节设置相同。实际轨迹与理想轨迹的对比结果如图15所示。

图 14 实测穿墙场景下不同模式的无人机飞行航迹

Figure 14. Actual measurement of UAV flight trajectory in different modes in through-the-wall scenarios

下载: 全尺寸图片幻灯片

图 15 理想与实测航迹

${R_{\rm{pgl}}}$ 仿真对比

Figure 15. Comparison of

${R_{\rm{pgl}}}$ between ideal and real trajectory in simulation

下载: 全尺寸图片幻灯片

由上述结果可知，除MB-SAR模式外，其余模式下实际轨迹均会导致成像质量略有下降，但下降幅度较小，总体趋势仍符合前述结论，无人机轨迹误差对成像质量的影响在合理范围内，可近似忽略。

4.2.2 成像结果与分析

因墙体回波和目标回波存在距离向上的差异，可使用时域选通将墙体回波去除，再通过三维成像获得目标位置。经过BP成像处理，MB-SAR, UMB-SAR, CF-SAR和OF-SAR成像结果的距离-高度向截面和方位高度截面图分别如图16所示，其中目标点由红色虚线圈出。

图 16 穿墙场景下4种模式的成像情况(“Ⅰ”表示距离-高度向截面，“Ⅱ”表示方位-高度向截面)

Figure 16. Imaging situation of four modes in through-the-wall scenario (“Ⅰ” represents the range-height section, “Ⅱ” represents the azimuth-height section)

下载: 全尺寸图片幻灯片

由图16(a)和图16(b)可知，穿墙场景MB-SAR成像结果存在显著的周期性栅瓣，与仿真结果一致。图16(c)和图16(d)中UMB-SAR的成像结果栅瓣有一定改善，但仍存在较强栅瓣点。图16(e)和中CF-SAR的栅瓣情况进一步降低，但目标点存在栅瓣聚集的现象，方位向仍存在较强栅瓣。和中OF-SAR的效果最佳，整体栅瓣较为分散，且能量较低，与仿真结果吻合，再一次验证算法与实验结果的准确性。4种算法的 ${R_{\rm{pgl}}}$ 结果如表4所示。

表 4 算法实测结果对比(dB)

Table 4. Comparison of algorithm measured results (dB)

算法	${R_{\rm{pgl}}}$
MB-SAR	−1.91
UMB-SAR	−4.14
CF-SAR	−7.71
OF-SAR	−9.52

下载: 导出CSV

| 显示表格

5. 结语

针对无人机载穿墙雷达在高层建筑遮蔽空间穿透探测场景中，高度向欠采样导致成像结果包含大量栅瓣能量的问题，本文提出了一种基于遗传算法的无人机载穿墙雷达三维SAR成像的航迹规划方法。通过权衡无人机飞行距离和穿墙三维SAR的成像质量，构建了无人机航迹规划的代价函数，该最优化问题可从数学关系上描述无人机飞行轨迹与雷达成像质量的内在联系，具有较好的通用性。构建了3类无人机飞行模式，使用具有全局搜索能力的遗传算法，建立对应飞行轨迹的基因表达形式、种群的选择与杂交过程以及个体的变异特性。仿真和实测结果表明，本方法能够在较短飞行距离的情况下显著抑制栅瓣能量。在仿真数据中，本文所提3种飞行方式相较于传统等间距多基线飞行有显著的提升；在穿墙场景实验中，所提飞行方式实测成像结果与仿真结果均能相互印证，验证了算法的有效性。

本文构建了统一的无人机载穿墙层析SAR航迹优化代价函数，但是由于三维空域采样的复杂性，若直接对该问题进行直接求解，在计算量上存在显著的困难。本研究所提方法基于不同飞行模式分别开展航迹规划，没有建立统一的航迹规划求解框架，后续将针对这一问题深入研究，实现无需规定飞行模式，即可实现探测区域内最优航迹自动规划。

图 1 集中式MIMO雷达同时多波束工作模式

Figure 1. Simultaneous multi-beam working mode of the collocated MIMO radar

下载: 全尺寸图片幻灯片

图 2 认知跟踪系统示意图

Figure 2. Schematic diagram of cognitive tracking system

下载: 全尺寸图片幻灯片

图 3 集中式MIMO雷达阵列模型

Figure 3. Collocated MIMO radar array model

下载: 全尺寸图片幻灯片

图 4 雷达与目标的空间位置关系

Figure 4. Spatial position relationship between radar and target

下载: 全尺寸图片幻灯片

图 5 各机动目标的加速度变化情况

Figure 5. Acceleration variation of each maneuvering target

下载: 全尺寸图片幻灯片

图 6 目标RCS起伏模型

Figure 6. Target RCS fluctuation model

下载: 全尺寸图片幻灯片

图 7 目标威胁权重模型

Figure 7. Task threat weight model

下载: 全尺寸图片幻灯片

图 8 ${\ell _2}$ 模型中的任务重要性权值

Figure 8. Task importance weight in model ${\ell _2}$

下载: 全尺寸图片幻灯片

图 9 ${\ell _1}$ 模型下的目标跟踪轨迹

Figure 9. Target tracking trajectory in model ${\ell _1}$

下载: 全尺寸图片幻灯片

图 10 ${\ell _2}$ 模型下的目标跟踪轨迹

Figure 10. Target tracking trajectory in model ${\ell _2}$

下载: 全尺寸图片幻灯片

图 11 各算法关于最差情况的PC-CRLB性能对比

Figure 11. PC-CRLB performance comparison of each algorithm on the worst case

下载: 全尺寸图片幻灯片

图 12 各算法关于最差情况的RMSE性能对比

Figure 12. RMSE performance comparison of each algorithm on the worst case

下载: 全尺寸图片幻灯片

图 13 各算法关于最大截获概率的性能对比

Figure 13. Performance comparison of each algorithm for maximum intercept probability

下载: 全尺寸图片幻灯片

图 14 ${\ell _1}$ 模型中的雷达功率分配结果

Figure 14. Results of radar power allocation in model ${\ell _1}$

下载: 全尺寸图片幻灯片

图 15 ${\ell _2}$ 模型中的雷达功率分配结果

Figure 15. Results of radar power allocation in model ${\ell _2}$

下载: 全尺寸图片幻灯片

图 16 各目标相对雷达的径向距离

Figure 16. Radial distance of each target relative to radar

下载: 全尺寸图片幻灯片

图 17 算法平均计算时间

Figure 17. Average calculation time of algorithm

下载: 全尺寸图片幻灯片

表 1 功率快速求解算法

Table 1. Fast power solving algorithm

步骤1　应用式(30)计算 ${D_k}$ ；
步骤2　定义 ${{\boldsymbol{Q}}_0}$ 为集合 ${\boldsymbol{Q}} = \{ 1,2,\cdots,Q\}$ 中所有满足不等式　 ${D_k} > {{\rm{fun}}_q}(\arg \min ({\bf{1} }_Q^{\text{T} }{ {\boldsymbol{P} }_k}))$ 元素的集合。若 ${{\boldsymbol{Q}}_0} \ne \varnothing$ ，则进入　步骤3；否则，令 ${P_{k,q,{\text{opt} } } } = {\bar P_{\min } }$ , ${ {\boldsymbol{Q} }_0} = { {\boldsymbol{Q} }_0} \cup \{ q\}$ , 　 ${\boldsymbol{Q}} = {\boldsymbol{Q}}\backslash \{ q\}$ ，并返回步骤1；
步骤3　令对目标q进行功率分配结果的最优解为　 ${P_{k,q,{\text{opt} } } } = {\rm{fun}}_q^{ - 1}({D_k})$ ；
步骤4　令最优解对应函数值为 ${D_{k,{\text{opt}}}} = {D_k}$ 。

下载: 导出CSV

表 2 仿真参数设置

Table 2. Simulation parameter setting

参数	取值	参数	取值
${p_{{\text{fa}}}}$	10^–8	${G_{\text{t}}}$	30 dB
${G_{\text{I}}}$	6 dB	${G_{{\text{IP}}}}$	3 dB
${\beta _{k,q}}$	1 MHz	${T_{k,q}}$	1 ms
$\lambda$	0.3 m	$\eta$	45 m
${T_{\rm{s}}}$	1 s	${P_{{\text{total}}}}$	5 kW
${\bar P_{{\text{max}}}}$	4 kW	${\bar P_{\min }}$	0.5 kW

下载: 导出CSV

表 3 初始时刻目标运动参数

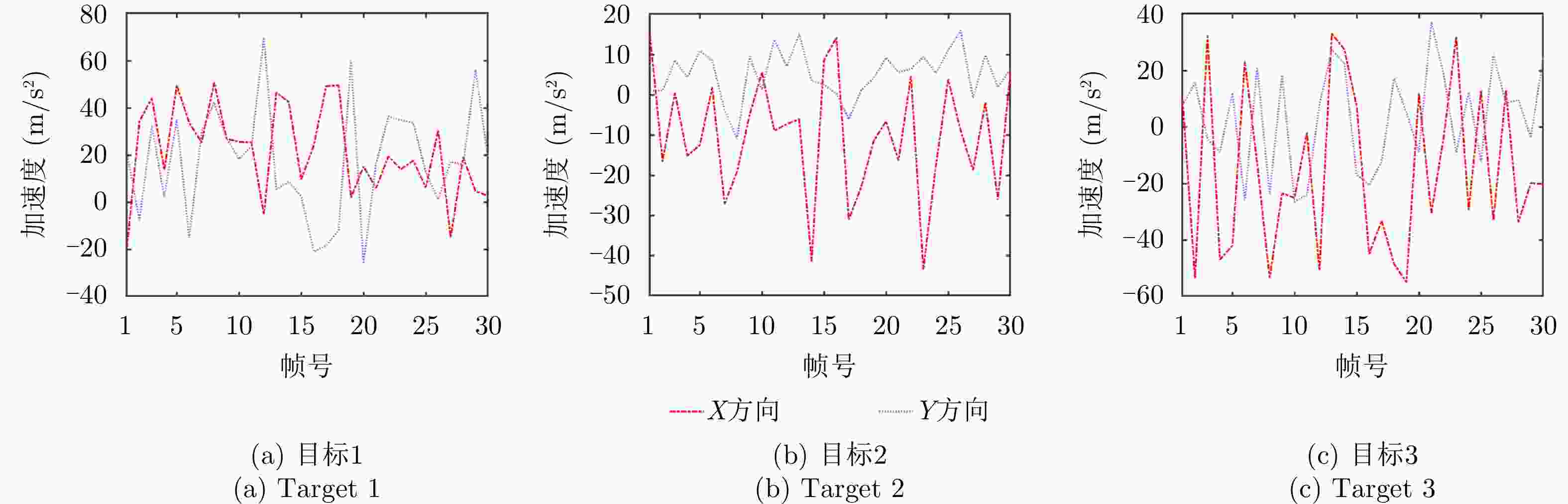
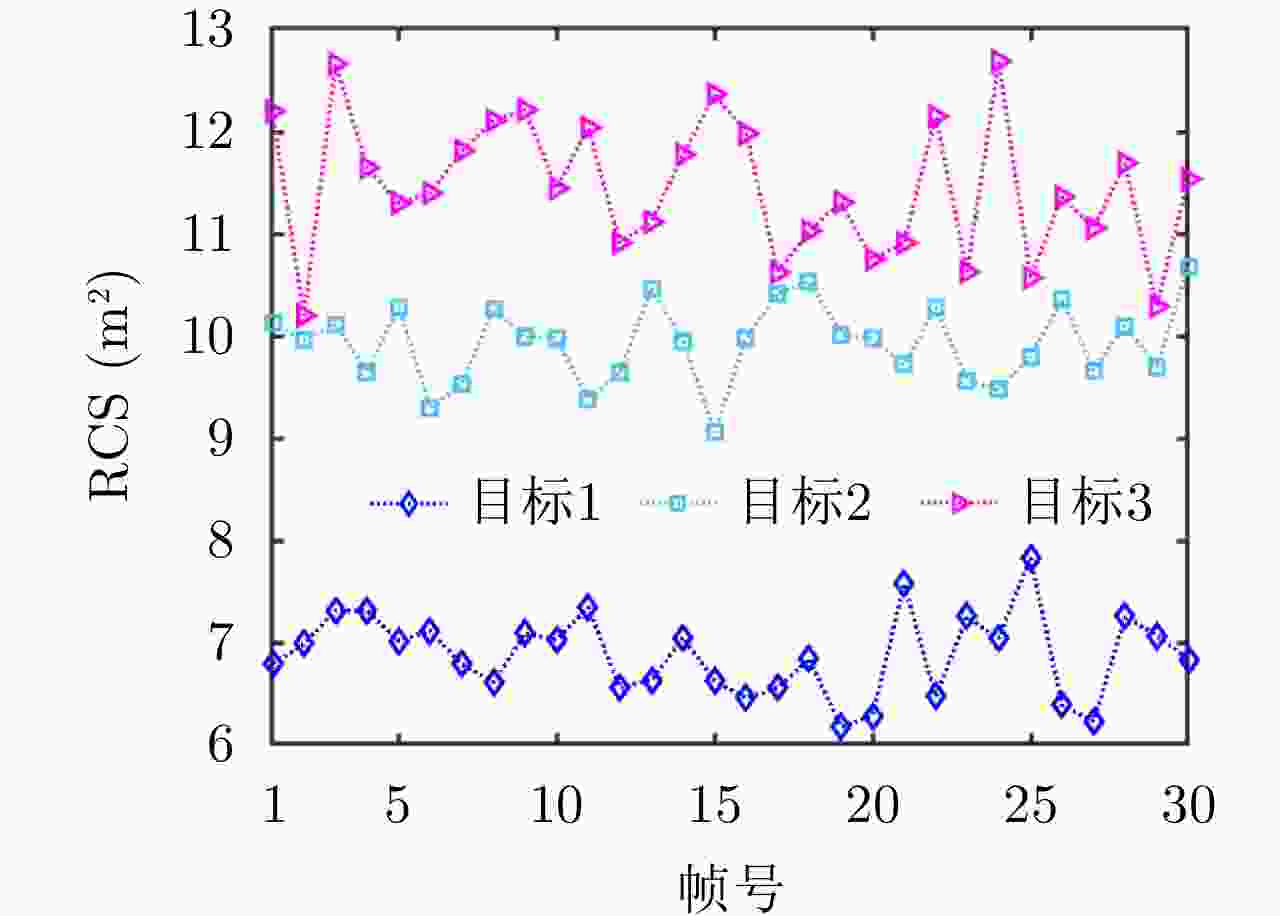
Table 3. Initial target motion parameters

目标编号	位置(km)	速度(m/s)	加速度(m/s²)	最大加速度(m/s²)
1	(9.6, 84.1)	(–494.2, –1346.1)	(–19.4, 20.7)	80
2	(89.7, 24.4)	(533.2, 468.5)	(14.6, 0.9)	50
3	(66.9, 72.4)	(–257.1, 695.1)	(9.6, 7.7)	60

下载: 导出CSV

参考文献(41)

[1]	何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128 HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128
[2]	范文, 蔚保国, 陈镜, 等. 基于波形优化和天线位置选择的MIMO雷达波束扫描算法研究[J]. 雷达学报, 2022, 11(4): 530–542. doi: 10.12000/JR22135 FAN Wen, YU Baoguo, CHEN Jing, et al. Joint waveform optimization and antenna position selection for MIMO radar beam scanning[J]. Journal of Radars, 2022, 11(4): 530–542. doi: 10.12000/JR22135
[3]	严俊坤, 陈林, 刘宏伟, 等. 基于机会约束的MIMO雷达多波束稳健功率分配算法[J]. 电子学报, 2019, 47(6): 1230–1235. doi: 10.3969/j.issn.0372-2112.2019.06.007 YAN Junkun, CHEN Lin, LIU Hongwei, et al. Chance constrained based robust multibeam power allocation algorithm for MIMO radar[J]. Acta Electronica Sinica, 2019, 47(6): 1230–1235. doi: 10.3969/j.issn.0372-2112.2019.06.007
[4]	LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812
[5]	韩金旺, 张子敬, 刘军, 等. 基于贝叶斯的高斯杂波背景下MIMO雷达自适应检测算法[J]. 雷达学报, 2019, 8(4): 501–509. doi: 10.12000/JR18090 HAN Jinwang, ZHANG Zijing, LIU Jun, et al. Adaptive Bayesian detection for MIMO radar in Gaussian clutter[J]. Journal of Radars, 2019, 8(4): 501–509. doi: 10.12000/JR18090
[6]	HAYKIN S, ZIA A, XUE Yanbo, et al. Control theoretic approach to tracking radar: First step towards cognition[J]. Digital Signal Processing, 2011, 21(5): 576–585. doi: 10.1016/j.dsp.2011.01.004
[7]	YAN Junkun, JIAO Hao, PU Wenqiang, et al. Radar sensor network resource allocation for fused target tracking: A brief review[J]. Information Fusion, 2022, 86/87: 104–115. doi: 10.1016/j.inffus.2022.06.009
[8]	YAN Junkun, LIU Hongwei, JIU Bo, et al. Simultaneous multibeam resource allocation scheme for multiple target tracking[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3110–3122. doi: 10.1109/TSP.2015.2417504
[9]	ZHANG Haowei, ZONG Binfeng, and XIE Junwei. Power and bandwidth allocation for multi-target tracking in collocated MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(9): 9795–9806. doi: 10.1109/TVT.2020.3002899
[10]	XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 729–743. doi: 10.1109/TSP.2017.2777394
[11]	LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Joint beam selection and resource allocation for cognitive multiple targets tracking in MIMO radar with collocated antennas[J]. IET Radar, Sonar & Navigation, 2020, 14(12): 2000–2009. doi: 10.1049/iet-rsn.2020.0332
[12]	YAN Junkun, LIU Hongwei, and BAO Zheng. Power allocation scheme for target tracking in clutter with multiple radar system[J]. Signal Processing, 2018, 144: 453–458. doi: 10.1016/j.sigpro.2017.11.006
[13]	ZHANG Haowei, LIU Weijian, XIE Junwei, et al. Joint subarray selection and power allocation for cognitive target tracking in large-scale MIMO radar networks[J]. IEEE Systems Journal, 2020, 14(2): 2569–2580. doi: 10.1109/JSYST.2019.2960401
[14]	YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587
[15]	YAN Junkun, ZHANG Peng, DAI Jinhui, et al. Target capacity based simultaneous multibeam power allocation scheme for multiple target tracking application[J]. Signal Processing, 2021, 178: 107794. doi: 10.1016/j.sigpro.2020.107794
[16]	LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Joint beam selection and power allocation in cognitive collocated MIMO radar for potential guidance application under oppressive jamming[J]. Digital Signal Processing, 2022, 127: 103579. doi: 10.1016/j.dsp.2022.103579
[17]	时晨光, 丁琳涛, 汪飞, 等. 面向射频隐身的组网雷达多目标跟踪下射频辐射资源优化分配算法[J]. 电子与信息学报, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636 SHI Chenguang, DING Lintao, WANG Fei, et al. Radio frequency stealth-based optimal radio frequency resource allocation algorithm for multiple-target tracking in radar network[J]. Journal of Electronics &Information Technology, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636
[18]	LU Xiujuan, XU Zhenchang, REN Haiwei, et al. LPI-based resource allocation strategy for target tracking in the moving airborne radar network[C]. 2022 IEEE Radar Conference (RadarConf22), New York City, USA, 2022: 1–6.
[19]	YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519
[20]	LI Xi, CHENG Ting, SU Yang, et al. Joint time-space resource allocation and waveform selection for the collocated MIMO radar in multiple targets tracking[J]. Signal Processing, 2020, 176: 107650. doi: 10.1016/j.sigpro.2020.107650
[21]	HAN Qinghua, PAN Minghai, LONG Weijun, et al. Joint adaptive sampling interval and power allocation for maneuvering target tracking in a multiple opportunistic array radar system[J]. Sensors, 2020, 20(4): 981. doi: 10.3390/s20040981
[22]	SHI Chenguang, DING Lintao, WANG Fei, et al. Joint target assignment and resource optimization framework for multitarget tracking in phased array radar network[J]. IEEE Systems Journal, 2021, 15(3): 4379–4390. doi: 10.1109/JSYST.2020.3025867
[23]	SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869
[24]	张浩为, 谢军伟, 葛佳昂, 等. 自适应CS模型的强跟踪平方根容积卡尔曼滤波算法[J]. 系统工程与电子技术, 2019, 41(6): 1186–1194. doi: 10.3969/j.issn.1001-506X.2019.06.03 ZHANG Haowei, XIE Junwei, GE Jiaang, et al. Strong tracking square-root cubature Kalman filter over adaptive current statistical model[J]. Systems Engineering and Electronics, 2019, 41(6): 1186–1194. doi: 10.3969/j.issn.1001-506X.2019.06.03
[25]	ZHOU Hongren and KUMAR K S P. A ‘current’ statistical model and adaptive algorithm for estimating maneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 1984, 7(5): 596–602. doi: 10.2514/3.19900
[26]	KHALOOZADEH H and KARSAZ A. Modified input estimation technique for tracking manoeuvring targets[J]. IET Radar, Sonar & Navigation, 2009, 3(1): 30–41. doi: 10.1049/iet-rsn:20080028
[27]	YANG Yongjian, FAN X, WANG Shengda, et al. A new parameters adaptively adjusting method of current statistical model[C]. 2015 IEEE International Conference on Information and Automation, Lijiang, China, 2015: 1738–1742.
[28]	ZHANG Haowei, XIE Junwei, GE Jiaang, et al. Adaptive strong tracking square-root cubature Kalman filter for maneuvering aircraft tracking[J]. IEEE Access, 2018, 6: 10052–10061. doi: 10.1109/ACCESS.2018.2808170
[29]	梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1828–1835. doi: 10.11999/JEIT141295 LIANG Hao, CUI Chen, DAI Lin, et al. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics &Information Technology, 2015, 37(8): 1828–1835. doi: 10.11999/JEIT141295
[30]	BELL K L, BAKER C J, SMITH G E, et al. Cognitive radar framework for target detection and tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1427–1439. doi: 10.1109/JSTSP.2015.2465304
[31]	ZHENG Yujiao, OZDEMIR O, NIU Ruixin, et al. New conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(10): 5549–5556. doi: 10.1109/TSP.2012.2205686
[32]	ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227
[33]	王祥丽, 易伟, 孔令讲. 基于多目标跟踪的相控阵雷达波束和驻留时间联合分配方法[J]. 雷达学报, 2017, 6(6): 602–610. doi: 10.12000/JR17045 WANG Xiangli, YI Wei, and KONG Lingjiang. Joint beam selection and dwell time allocation for multi-target tracking in phased array radar system[J]. Journal of Radars, 2017, 6(6): 602–610. doi: 10.12000/JR17045
[34]	史小斌, 顾红, 苏卫民, 等. 地面侦察雷达目标威胁度评估方法研究[J]. 兵工学报, 2015, 36(6): 1128–1135. doi: 10.3969/j.issn.1000-1093.2015.06.024 SHI Xiaobin, GU Hong, SU Weimin, et al. Study of target threat assessment for ground surveillance radar[J]. Acta Armamentarii, 2015, 36(6): 1128–1135. doi: 10.3969/j.issn.1000-1093.2015.06.024
[35]	刘秀祥, 雷振亚, 谢拥军, 等. 空中隐身目标威胁等级的仿真研究[J]. 计算机仿真, 2011, 28(7): 46–49. doi: 10.3969/j.issn.1006-9348.2011.07.013 LIU Xiuxiang, LEI Zhenya, XIE Yongjun, et al. Simulation research of air stealth targets threat grade[J]. Computer Simulation, 2011, 28(7): 46–49. doi: 10.3969/j.issn.1006-9348.2011.07.013
[36]	蒋春启, 郑娜娥, 左宗, 等. 突出重点目标跟踪的分布式MIMO雷达阵元选取[J]. 系统工程与电子技术, 2021, 43(10): 2860–2868. doi: 10.12305/j.issn.1001-506X.2021.10.20 JIANG Chunqi, ZHENG Na’e, ZUO Zong, et al. Antenna selection of distributed MIMO radar on target tracking with key target highlighted[J]. Systems Engineering and Electronics, 2021, 43(10): 2860–2868. doi: 10.12305/j.issn.1001-506X.2021.10.20
[37]	ZHANG Weiwei, SHI Chenguang, SALOUS S, et al. Convex optimization-based power allocation strategies for target localization in distributed hybrid non-coherent active-passive radar networks[J]. IEEE Transactions on Signal Processing, 2022, 70: 2476–2488. doi: 10.1109/TSP.2022.3173756
[38]	BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004: 67–78.
[39]	GOLUB G H and VAN LOAN C F. Matrix Computations[M]. 3rd ed. Baltimore: The Johns Hopkins University Press, 1996: 509–520.
[40]	LUSS H and SMITH D R. Resource allocation among competing activities: A lexicographic minimax approach[J]. Operations Research Letters, 1986, 5(5): 227–231. doi: 10.1016/0167-6377(86)90012-X
[41]	BAZARAA M S and SHETTY C M. Nonlinear Programming: Theory and Algorithms[M]. New York: Wiley, 1979: 538–557.

施引文献

资源附件(0)

访问统计

图(17) / 表(3)

计量

文章访问数: 657
HTML全文浏览量: 395
PDF下载量: 179
被引次数: 0

1. 引言
2. 空域欠采样栅瓣问题分析
3. 基于遗传算法的无人机载穿墙SAR航迹规划
3.1 航迹规划代价函数
3.2 基于遗传算法的机载穿墙雷达航迹优化
4. 实验结果及分析
4.1 数值仿真与分析
4.2 实测数据
5. 结语

一种低截获背景下的集中式MIMO雷达快速功率分配算法

DOI: 10.12000/JR22203

通讯作者:
张浩为 zhw_xhzf@163.com

计量

A Fast Power Allocation Algorithm in a Collocated MIMO Radar under Low Interception Backgrounds

Corresponding author: ZHANG Haowei, zhw_xhzf@163.com

1. 引言

2. 空域欠采样栅瓣问题分析

3. 基于遗传算法的无人机载穿墙SAR航迹规划

3.1 航迹规划代价函数

3.2 基于遗传算法的机载穿墙雷达航迹优化

3.2.1 无人机载穿墙雷达飞行模式基因编码

3.2.2 选择与杂交

3.2.3 基因突变

4. 实验结果及分析

4.1 数值仿真与分析

4.1.1 MB-SAR

4.1.2 UMB-SAR

4.1.3 Z-SAR

4.1.4 CF-SAR

4.1.5 OF-SAR

4.1.6 对比与分析

4.2 实测数据

4.2.1 无人机飞行轨迹与分析

4.2.2 成像结果与分析

5. 结语

计量

目录

1. 引言

2. 空域欠采样栅瓣问题分析

3. 基于遗传算法的无人机载穿墙SAR航迹规划

3.1 航迹规划代价函数

3.2 基于遗传算法的机载穿墙雷达航迹优化

4. 实验结果及分析

4.1 数值仿真与分析

4.2 实测数据

5. 结语

期刊介绍

联系我们

一种低截获背景下的集中式MIMO雷达快速功率分配算法

DOI: 10.12000/JR22203

通讯作者: 张浩为 zhw_xhzf@163.com

计量

出版历程

A Fast Power Allocation Algorithm in a Collocated MIMO Radar under Low Interception Backgrounds

Corresponding author: ZHANG Haowei, zhw_xhzf@163.com

1. 引言

2. 空域欠采样栅瓣问题分析

3. 基于遗传算法的无人机载穿墙SAR航迹规划

3.1 航迹规划代价函数

3.2 基于遗传算法的机载穿墙雷达航迹优化

3.2.1 无人机载穿墙雷达飞行模式基因编码

3.2.2 选择与杂交

3.2.3 基因突变

4. 实验结果及分析

4.1 数值仿真与分析

4.1.1 MB-SAR

4.1.2 UMB-SAR

4.1.3 Z-SAR

4.1.4 CF-SAR

4.1.5 OF-SAR

4.1.6 对比与分析

4.2 实测数据

4.2.1 无人机飞行轨迹与分析

4.2.2 成像结果与分析

5. 结语

计量

出版历程

目录

1. 引言

2. 空域欠采样栅瓣问题分析

3. 基于遗传算法的无人机载穿墙SAR航迹规划

3.1 航迹规划代价函数

3.2 基于遗传算法的机载穿墙雷达航迹优化

4. 实验结果及分析

4.1 数值仿真与分析

4.2 实测数据

5. 结语

期刊介绍

联系我们

通讯作者:
张浩为 zhw_xhzf@163.com