Flight Path Optimization Method for Dynamic Area Coverage Based on Multi-aircraft Radars
-
摘要: 传统面向区域覆盖的多机航迹优化方法大多针对静态环境建立优化模型,在复杂动态环境下面临着模型失配的挑战。因此,该文提出了一种多机雷达协同区域动态覆盖航迹优化方法。首先,该方法引入衰减因子来表征机载雷达对动态环境的实际覆盖效果,将动态覆盖背景下的区域覆盖率作为优化函数,并结合待优化多维航迹控制参数约束,构建了多机雷达协同区域动态覆盖航迹优化的数学模型。然后,采用随机优化法对协同区域动态覆盖航迹优化问题进行了求解。最后,仿真实验表明,相对于采用预设航迹的多机雷达搜索模式,所提航迹优化方法能够显著提高动态区域的动态覆盖性能,且相较于面向静态环境的传统航迹优化模型,动态覆盖性能平均提升约6%。Abstract: Most traditional multi-aircraft flight path optimization methods are oriented toward area coverage, use static optimization models, and face the challenge of model mismatch under complex dynamic environments. Therefore, this study proposes a flight path optimization method for dynamic area coverage based on multi-aircraft radars. First, we introduce an attenuation factor to this method to characterize the actual coverage effect of airborne radar on a dynamic environment, and we take the area coverage rate under the dynamic area coverage background as the optimization function. After integrating the constraints of multi-dimensional flight path control parameters to be optimized, we built a mathematical model for dynamic area coverage flight path optimization based on multi-aircraft radars. Then, the stochastic optimization method is used to solve the flight path optimization problem of dynamic area coverage. Finally, the simulation results show that the proposed flight path optimization method can significantly improve the dynamic coverage performance in dynamic areas compared with the search mode using preset flight paths based on multi-aircraft radars. Compared with the traditional flight path optimization method oriented to static environments, the dynamic coverage performance of our proposed method is improved by approximately 6% on average.
-
1. 引言
无人机区域覆盖航迹规划定义为:在满足某种(某些)性能指标最优的前提下,避开障碍物和威胁源,规划出一条能够遍历待覆盖区域的最优飞行路线[1]。近年来,复杂多变的搜索环境以及日渐成熟的反侦察技术为无人机区域覆盖所采用的探测硬件和执行模式带来了新的挑战。传统的静态区域覆盖模型和独立的单无人机运行模型已不能满足现代动态搜索环境的任务要求,机载雷达探测技术和多机协同技术在区域覆盖领域的应用也越来越普遍,因此必须要建立面向复杂搜索环境的多机雷达协同区域动态覆盖模型以适应当下全新的区域覆盖任务。
目前,国内外关于多机雷达协同控制的工作主要针对机载平台的发射参数[2-5],对于多无人机航迹优化问题的研究还相对较少。面向目标跟踪,李春霄等人[6]推导出了以雷达发射功率与无人机航向角为优化变量的决策函数,给出了一种联合在线航迹优化和雷达功率分配方法;时晨光等人[7]针对机载组网雷达的单目标跟踪问题,设计了雷达辐射参数与航迹规划联合优化算法,有效提升了机载组网雷达的目标跟踪精度。面向区域突防,Besada-Portas等人[8]提出的基于进化算法的无人机航迹规划方法,能够很好地适应于包含雷达和导弹等威胁要素的复杂突防场景。面向区域覆盖,Berger等人[9]基于平台和传感器之间的能力差异,为各无人机分配扫描任务,实现了有效的扫描轨迹规划,该方法适用于广泛的现实任务场景;王自亮等人[10]实现了凹多边形区域向凸多边形区域的转化,在此基础上提出了一种协助无人机自主完成给定区域覆盖搜索的有效算法;张小孟等人[11]针对现有无人机区域覆盖侦察航迹规划中对任务区域分解算法复杂、任务规划效率低的问题,设计出一种基于区域分解、Z字形扫描方式和
η 形转弯方法的多无人机覆盖航迹规划的改进方法。然而在区域覆盖任务背景下,已有研究均针对静态搜索场景设计优化模型。在实际机载雷达空域覆盖任务中,待覆盖区域随时间呈高动态特性,要求雷达对该区域进行重复搜索。换句话说,已搜索区域会因环境变化而出现已获信息衰减的情况,需被多机雷达重复搜索确认。在移动传感器网络信息测量背景下,Sugimoto等人[12]就测量信息可靠性随时间的变化构建了信息衰减模型。Li等人[13]针对谣言传播信息有效性的衰减设计了信息衰减因子。结合现有研究基础,本文在传统区域覆盖任务的基础上引入了衰减因子来表征机载雷达对动态环境的实际覆盖效果,结合待优化多维航迹控制参数约束,设计了以动态区域覆盖率为优化函数的区域动态覆盖数学优化模型,并通过随机优化法对航迹控制参数进行求解,以规划出机组中各机体在动态环境中的较优航迹。最后,本文对该航迹优化模型进行了数值仿真,验证了算法有效性。
2. 模型构建
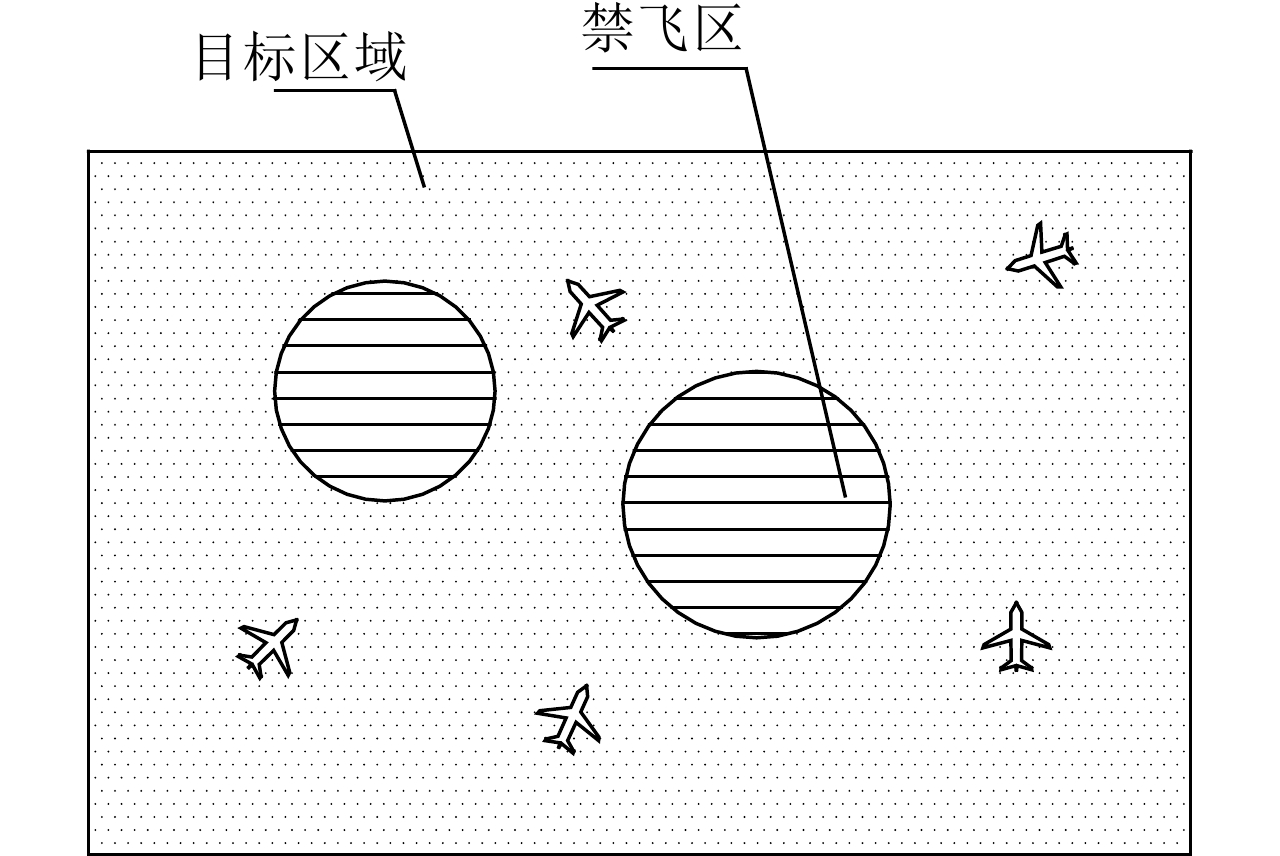
本文将航迹规划问题简化在二维平面内讨论,即认为所有无人机在地面平面内飞行。M架同构且各携带一部机载雷达的无人机对目标区域A执行区域动态覆盖任务,如图1所示,A为一个矩形区域去除若干圆形禁飞区所剩余的区域。为了方便后续的论述,为机组中各无人机赋予1至M的编号。
2.1 区域动态覆盖评估指标构建
区域动态覆盖模型是基于机载雷达的扫描探测特性构建的。现规定编号为j(
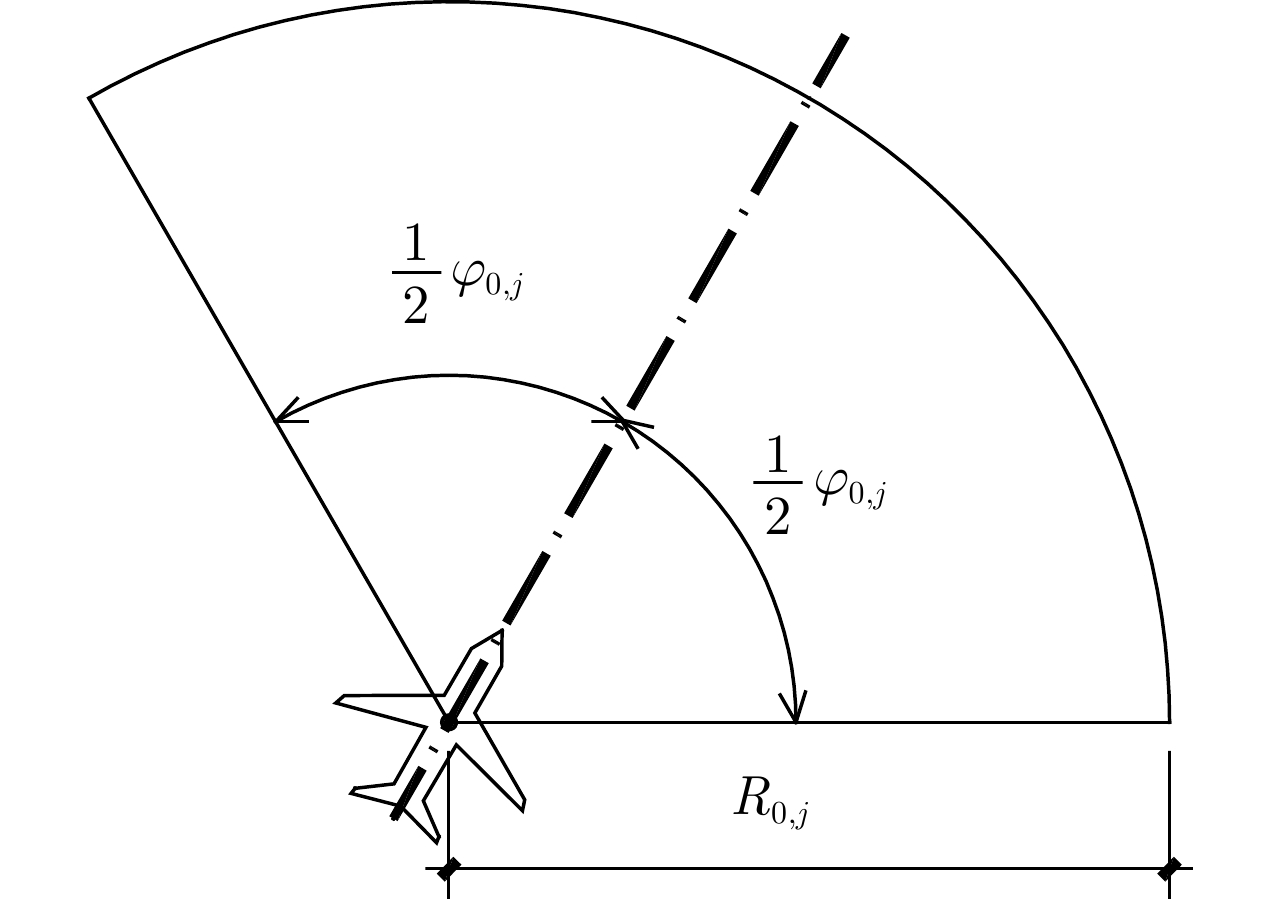
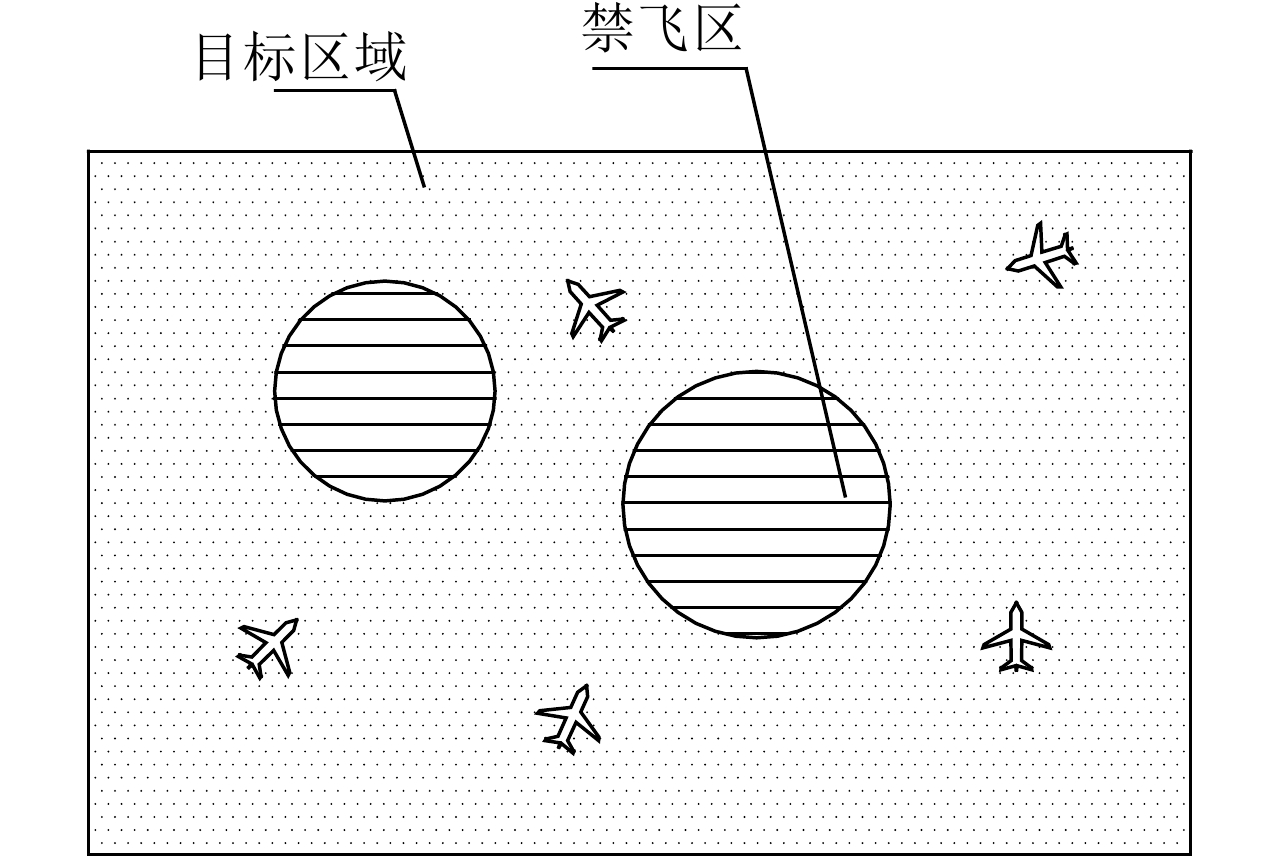
j=1,2,⋯,M )的无人机携带的机载雷达在方位维上的辐射范围为[−12φ0,j,12φ0,j] (以无人机当前机头朝向的机轴为零轴),φ0,j∈[0,2π) 。受雷达功率孔径积的限制,机载平台的探测区域面积往往是受限的[14]。具体地说,该区域为一个以机载雷达(可视为质点)为圆心,圆心角为φ0,j 的扇形区域,其半径由雷达最远探测距离决定,设为R0,j ,其对称轴由无人机当前的机头朝向确定,如图2所示,称该区域为机载雷达的地面最大可探测区域。由于本文的区域动态覆盖问题涉及计算量较大的几何计算,若对一条完整的无人机航迹进行求解,则会出现算力需求超限及组合爆炸的问题。因此,本文仅在间隔一固定时长
td 的离散时刻群ntd (∀n∈N∗ )优化控制无人机群航迹控制参数,以获取多个离散时刻的粗略航迹。为了更简单地表述问题,任意离散时刻ntd 简称为时刻n,也可在非特指情况下简称为时刻。机组中各无人机机载雷达在每个时刻对地面最大可探测区域完成一次完整搜索,称每次搜索完毕后形成的区域为扫描区域。传统的静态搜索环境中,扫描区域的覆盖效果可用多个离散时刻的覆盖区域面积之并集来描述。但在动态搜索环境中,任意时刻已生成的扫描区域的覆盖信息量会随时间的推移和环境的动态变化而发生衰减,因此引入衰减因子来辅助描述扫描区域在动态区域覆盖任务中的覆盖效果。衰减因子在区域覆盖问题中应具有的普适特性为:在生成时刻,扫描区域中的覆盖信息量为最大值,对应衰减因子在该时刻应为最大值1;随着时刻的推移,覆盖信息量不断衰减,对应衰减因子应严格递减,且递减模式应能被1个参数控制;当时刻推移到某一临界值时,扫描区域中不存在任何覆盖信息,对应衰减因子在此时刻应达到最小值0,若在此之后不对该扫描区域进行重新搜索,衰减因子值应保持为0,表明扫描区域中的覆盖信息没有得到更新。基于上述特性,对衰减因子进行构建。衰减因子
α 的唯一自变量是某时刻与该扫描区域生成时刻的差值绝对值(以下简称时刻差值),其表达式为αi(n) = {ln(−γ|n−i|+γnα+1)ln(γnα+1),|n−i|≤nα0,|n−i|>nα,n≥i,i∈N∗ (1) 其中,
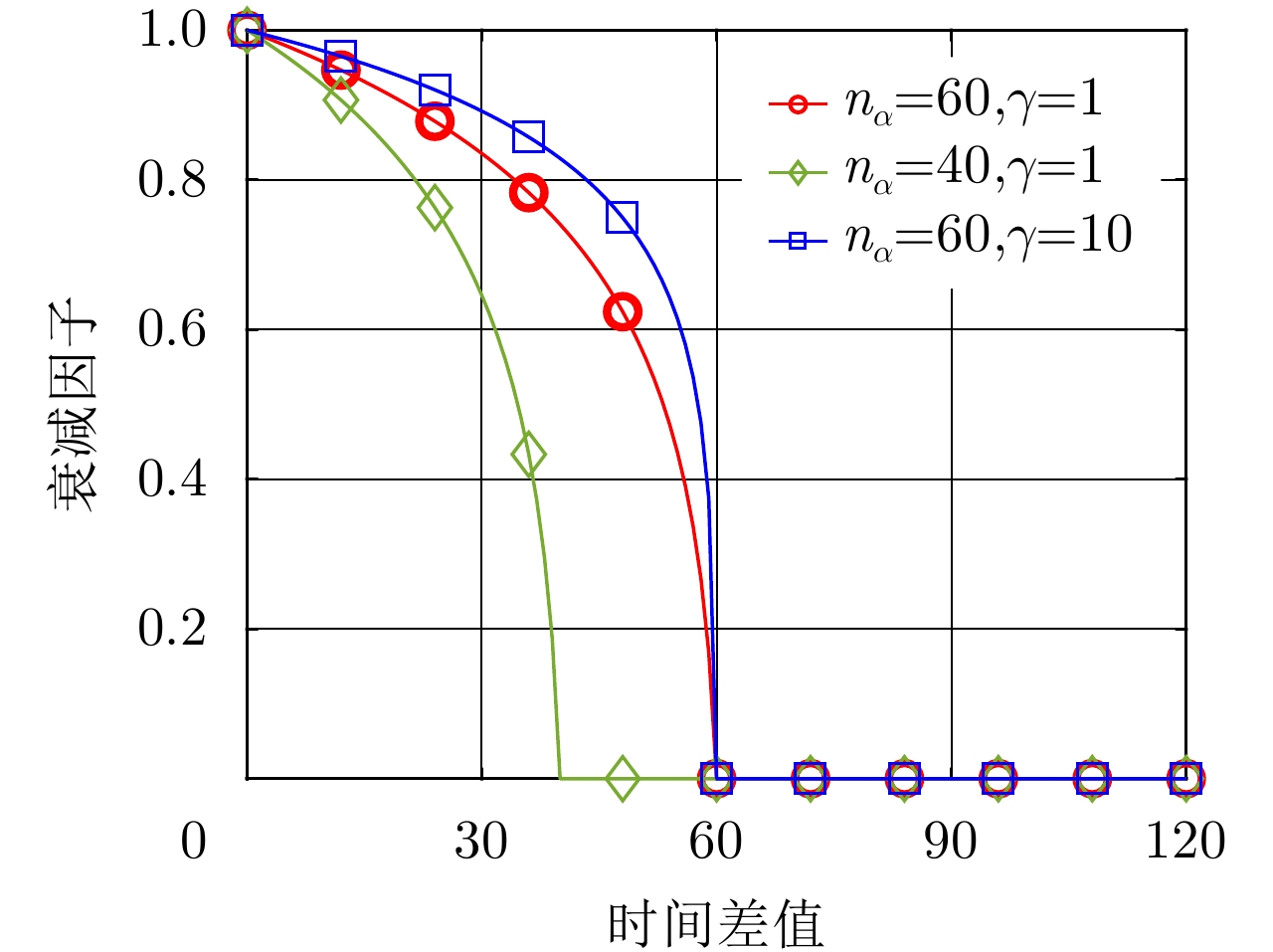
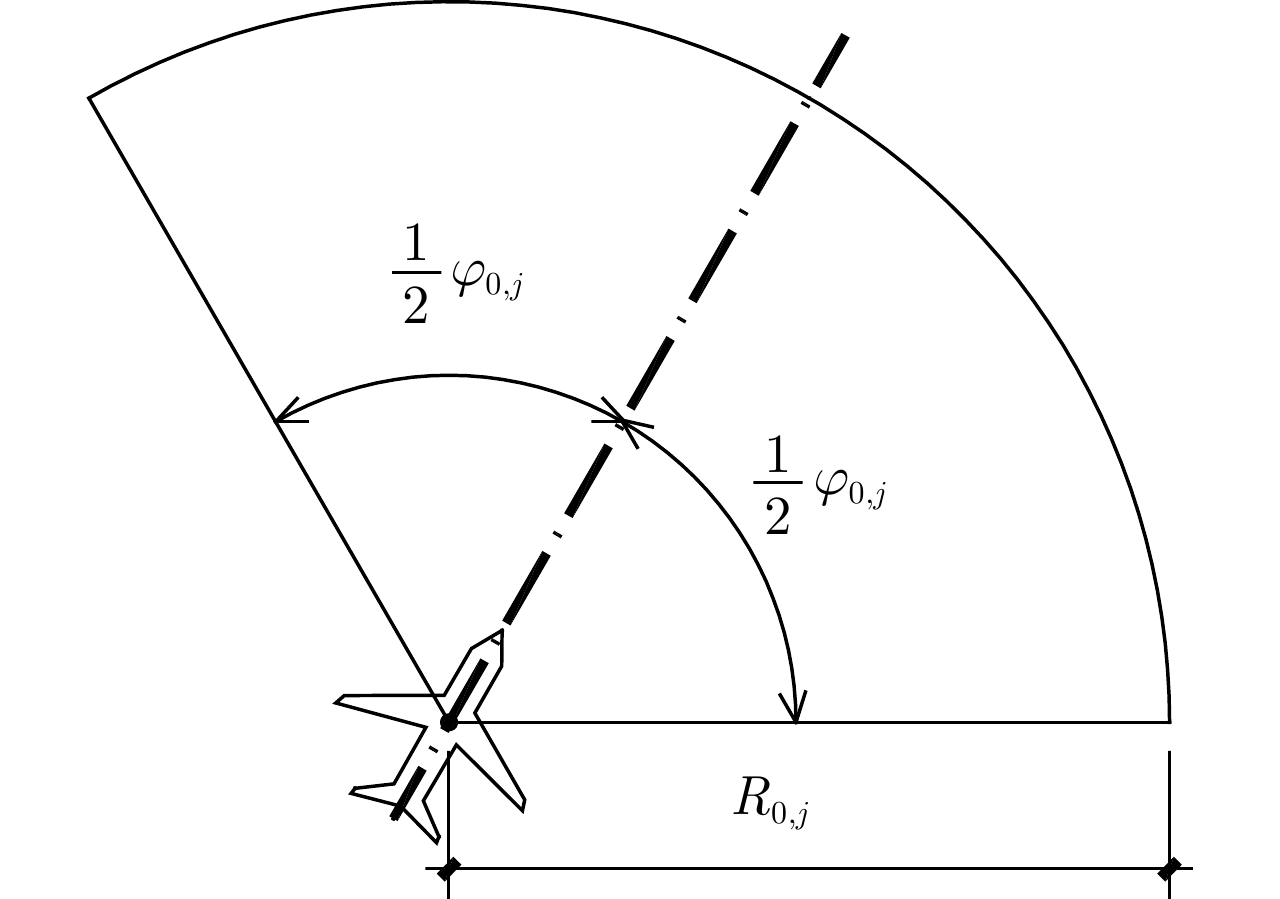
αi(n) 表示在时刻i生成的某扫描区域在后续时刻n的衰减因子值,nα 称为截止时差,γ 称为速度因子。图3为不同nα 和γ 对应的衰减因子随时刻差值变化的各曲线图。由图3可知,nα 决定了衰减因子归零的总时长,γ 决定了同nα 下衰减因子的衰减模式。在时刻差值为0时,α 为最大值1,表明扫描区域的覆盖效果还未出现衰减;在时刻差值达到截止时差nα 前,α 严格递减,表明覆盖效果随之出现衰减;在时刻差值达到nα 时,α 达到最小值0,并在此之后保持为0,表明扫描区域不再具有任何覆盖效果。结合构建的衰减因子,定义机组中所有无人机的机载雷达在时刻i生成的扫描区域,在后续时刻n的实际总覆盖效果
si(n) 为si(n)=αi(n)sfi(n),n≥i (2) 其中,
sfi(n) 表示机组中所有无人机的机载雷达在时刻i生成的扫描区域,在后续时刻n的组合有效面积,其值等于这些扫描区域组成的并集区域,去除与所有生成时刻大于i的扫描区域的交集区域后,剩余区域与目标区域A的交集区域的面积。基于式(2),可继续给出有效覆盖率
f(n) 的表达式。假设当前时刻为n,机组中所有无人机均完成了该时刻的对地搜索操作,则此时的有效覆盖率的表达式为f(n)=n∑i=1si(n)sA (3) 其中,
sA 表示目标区域A的面积,f(n) 表示该优化进程下的有效覆盖率。有效覆盖率能够反映区域动态覆盖任务在某当前时刻的全局覆盖进度,在本问题中,设定该评估指标作为航迹优化模型的优化函数。2.2 航迹控制参数梳理
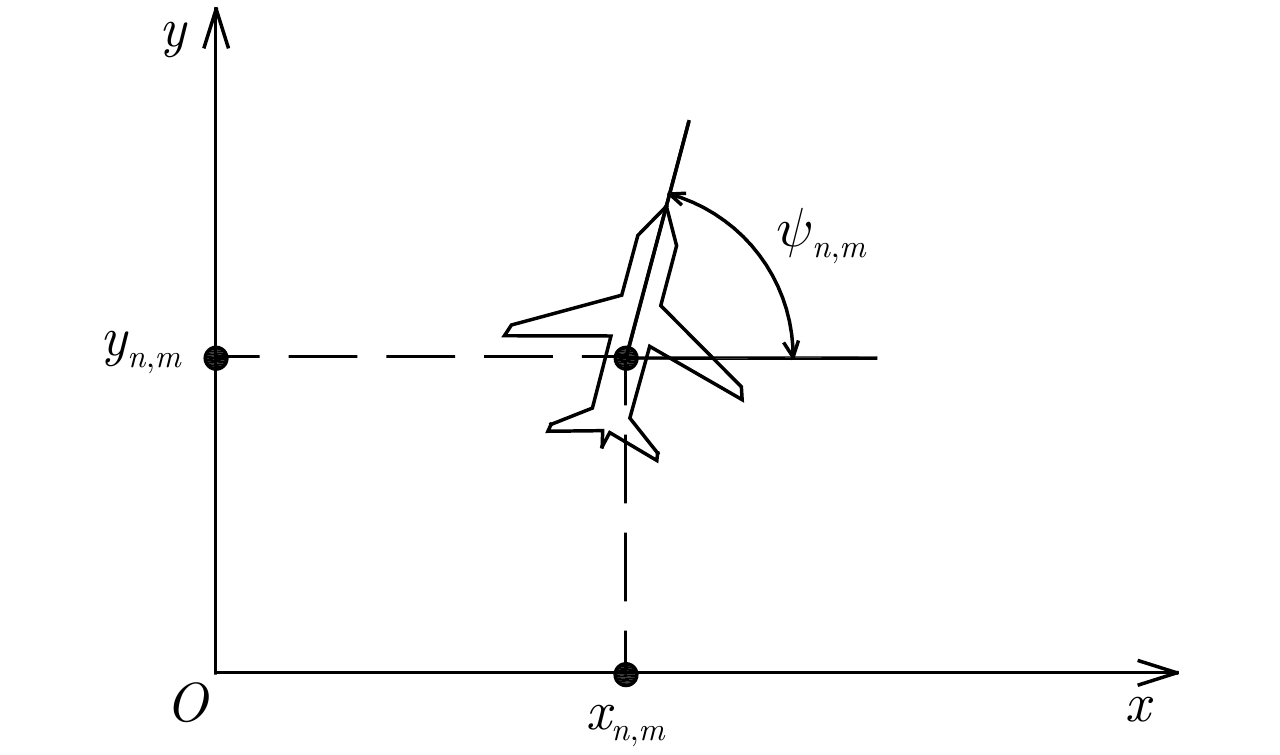
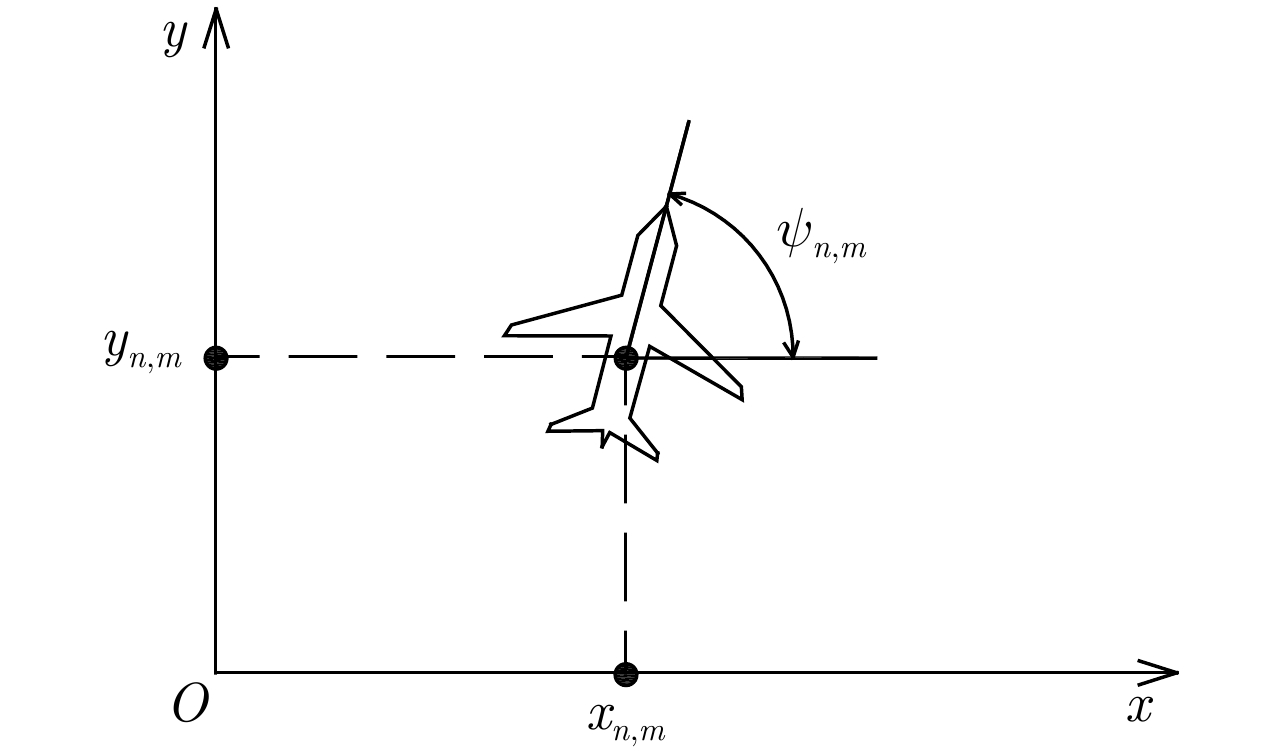
文中无人机的状态由以下航迹控制参数确定:机载雷达在地面坐标系中的平面坐标以及无人机当前的偏航角[15](以地面坐标系的x轴为地轴)。对于某时刻n的编号为m(
m=1,2,⋯,M )的无人机,上述平面坐标用横坐标xn,m 和纵坐标yn,m 表示,偏航角用ψn,m 表示(ψn,m∈[0,2π) ),它们的大小如图4所示确定。无人机在一个
td 内的可飞行距离和偏航角可变化差值均存在上限,这一上限用本文的航迹控制参数可以描述为0≤√(xn,m−xn−1,m)2+(yn,m−yn−1,m)2≤Lmax (4) \begin{split} & 0 \le \left| {{\psi _{n,m}} - {\psi _{n - 1,m}}} \right| \le \Delta {\psi _{\max }},\forall n \in {N^ * },\\ & \forall m \in \left\{ {1,2, \cdots ,M} \right\} \end{split} (5) 式(4)中,
{L_{\max }} 表示一个{t_d} 内无人机最大可飞行的直线距离,式(5)中,\Delta {\psi _{\max }} 表示一个{t_d} 内无人机偏航角的最大可变化差值。除此之外,对于无人机可飞行的区域也存在限制,若用{w_{n,m}} 表示编号为m的无人机在时刻n时,机载雷达在地面坐标系中的坐标点,则该限制条件可以描述为{w_{n,m}} \in A,\forall n \in N,\forall m \in \left\{ {1,2, \cdots ,M} \right\} (6) 式(6)可以理解为机载雷达的坐标点必须落在目标区域A内,即无人机全程必须在A中飞行。式(4)—式(6)中,
{x_{0,m}} ,{y_{0,m}} ,{\psi _{0,m}} 及{w_{0,m}} 表示编号为m的无人机在零时刻的参数。3. 数学模型及求解算法
本文构建的航迹优化模型的优化目标为:令每个时刻n对应的有效覆盖率
f\left( n \right) 最大化。 将式(3)、式(4)、式(5)、式(6)代入,可得到该优化模型的数学表达形式:\mathop {\max }\limits_{{x_{n,m}},{y_{n,m}},{\psi _{n,m}}} f\left( n \right),n = 1,2, \cdots ,N (7) \begin{split} & {\rm{s.t}}.{\text{ }}0 \le \sqrt {{{\left( {{x_{n,m}} - {x_{n - 1,m}}} \right)}^2} + {{\left( {{y_{n,m}} - {y_{n - 1,m}}} \right)}^2}} \\ & \qquad \le {L_{\max }},\forall n \in {N^ * }, \forall m \in \left\{ {1,2, \cdots ,M} \right\} \\ & \quad\;\; 0 \le \left| {{\psi _{n,m}} - {\psi _{n - 1,m}}} \right| \le \Delta {\psi _{\max }},\forall n \in {N^ * },\\ & \qquad\; \forall m \in \left\{ {1,2, \cdots ,M} \right\} \\ & \quad\;\; {w_{n,m}} \in A,\forall n \in N^*,\forall m \in \left\{ {1,2, \cdots ,M} \right\} \end{split} (8) 在进行模型求解时,本文采用分步求解的优化模式。由式(8)可见,当前时刻的航迹控制参数会影响下一时刻解的可行域,因此当前时刻解的最优化可能会导致后续时刻的所有可行解严重不符合预期(无人机飞入目标区域边界或禁飞区附近,导致有效覆盖率可取值相较正常情况出现一定衰落)。为了尽量避免这种情况,本文适当降低了模型对最优解的需求程度,转而搜索当前时刻的较优解以提高后续时刻的可行解保持较优性的能力,这一目标契合了随机优化法搜索较优解较快的特性[16];同时,随机优化法简单直观,并且较为契合本文模型分步求解的优化模式,合理控制迭代次数和生成解的分布情况,便能够大大提高求解效率。综上考虑,本文最终选择随机优化法作为航迹优化模型的求解算法,并给出基于此算法的优化模型的大致运行流程(以某当前时刻n机组全无人机完整优化流程为例),如表1所示。
表 1 优化模型运行流程示意表Table 1. Running process of the optimization model步骤 流程内容 ① 计算基于时刻n的各时刻{\alpha _i}\left( n \right),i = 1,2, \cdots ,n ② 设置待优化无人机编号m = 1 ③ 基于待优化无人机时刻 n - 1 的解,生成可行解数量为{q_{\max }}的解空间{ {\boldsymbol{C} }_n} = \left\{ {{\boldsymbol{c}}'_1,{\boldsymbol{c}}'_2, \cdots ,{\boldsymbol{c}}_{ {q_{\max } } }'} \right\} ④ 求解待优化无人机时刻n的解{{\boldsymbol{c}}_n} \in {{\boldsymbol{C}}_n},使{{\boldsymbol{c}}_n}对应的有效覆盖率为{{\boldsymbol{C}}_n}中最大 ⑤ 令m = m + 1,若m \le M则返回步骤③ ⑥ 令n = n + 1,优化程序进入下一时刻 4. 仿真实验及结果分析
4.1 仿真参数设计
设定目标区域A中矩形区域的长宽均为1000 m,禁飞区数量为2。两禁飞区的圆心位置和半径大小随机生成,二者不存在任何重叠且完全包含在矩形区域内。设定影响各机载雷达最远探测距离的所有变量分别一致,对应的
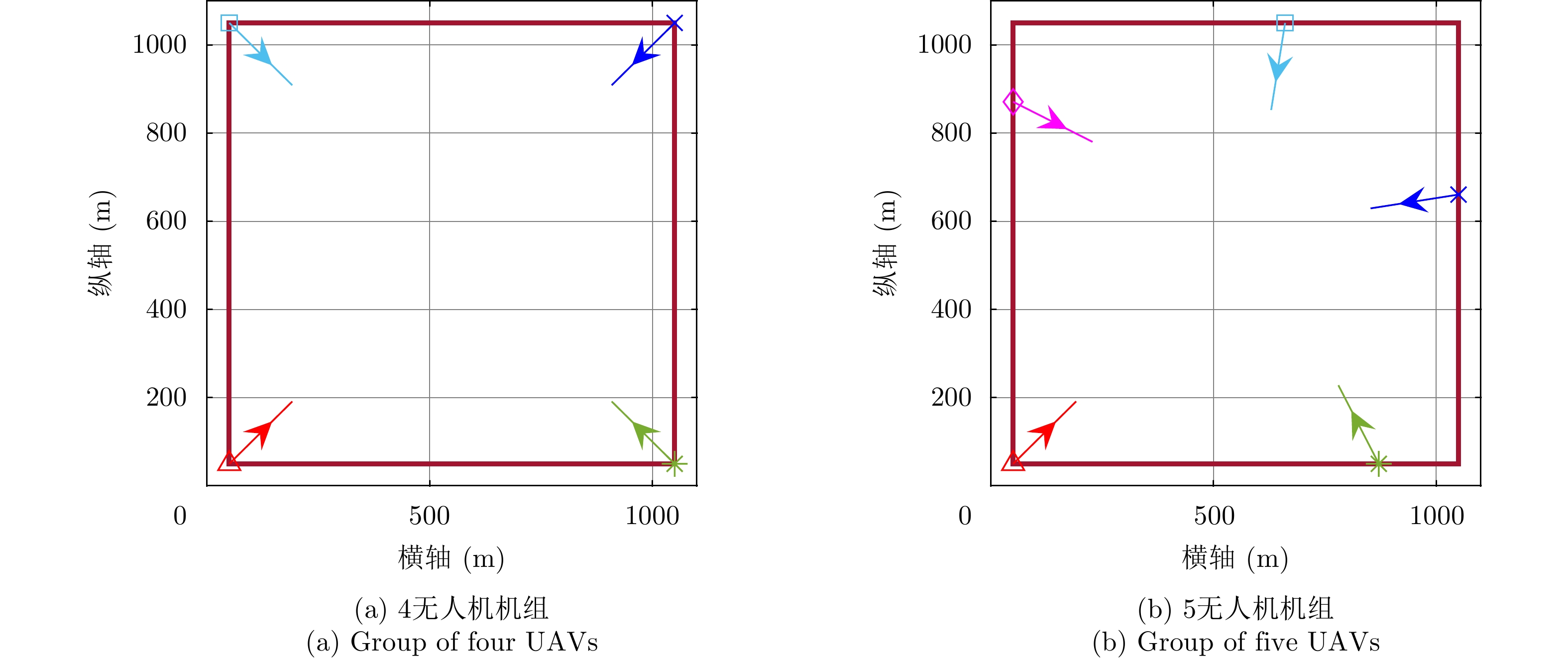
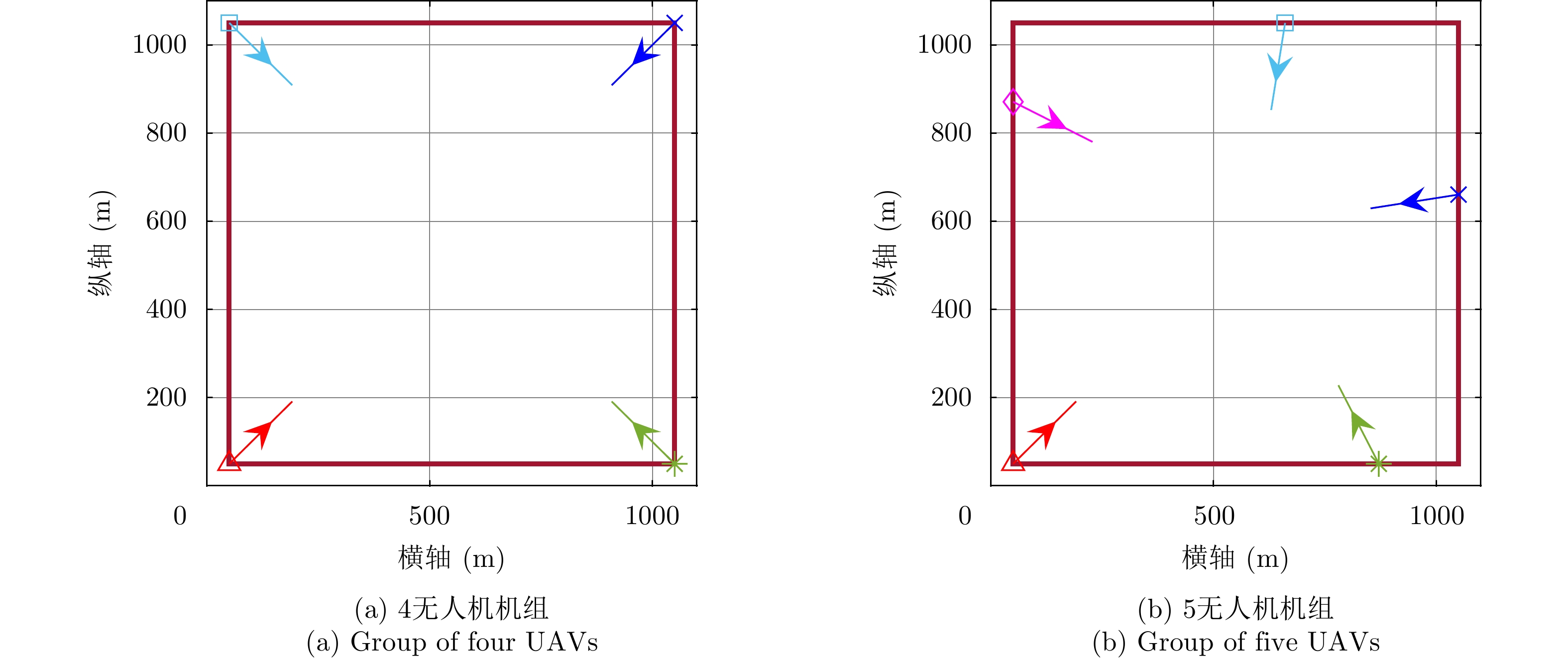
{\varphi _{0,j}} 相等,以统一任意无人机机载雷达在任意位置任意时刻的地面最大可探测区域的{\varphi _{0,j}} 和{R_{0,j}} 分别为一固定值{\varphi _0} 和{R_0} 。仿真参数设定值如表2所示。表 2 仿真参数设定表Table 2. Simulation parameter settings参数 设定值 {R_0} 90 m {\varphi _0} \dfrac{2}{3}\pi {t_d} 1 s {L_{\max }} 200 m \Delta {\psi _{\max }} \dfrac{1}{4}\pi {n_\alpha } 60 s \gamma 10 {q_{\max }} 100 为了验证所提方法的有效性,我们将针对不同无人机数量M的机组进行仿真实验。零时刻机组中各无人机的航迹控制参数按如下准则确定:编号为1的无人机机载雷达坐标点为目标区域的外框矩形西南方向上(左下角)的顶点,其余无人机机载雷达分散在外框矩形的四边和顶点上,且两编号上紧邻的无人机机载雷达,以外框矩形的几何中心点为顶点所形成的夹角大小为
{{2\pi } \mathord{\left/ {\vphantom {{2\pi } M}} \right. } M} ,并确保所有无人机的机头均指向外框矩形的几何中心点。图5为无人机数量分别为4和5的两机组零时刻各无人机航迹控制参数示意图,图5中深红色四边为目标区域中的矩形外框,不同颜色和样式的标识符号点代表不同无人机机载雷达在零时刻的坐标点,不同颜色的带箭头线表明了不同无人机在零时刻的机头指向。4.2 实验结果及分析
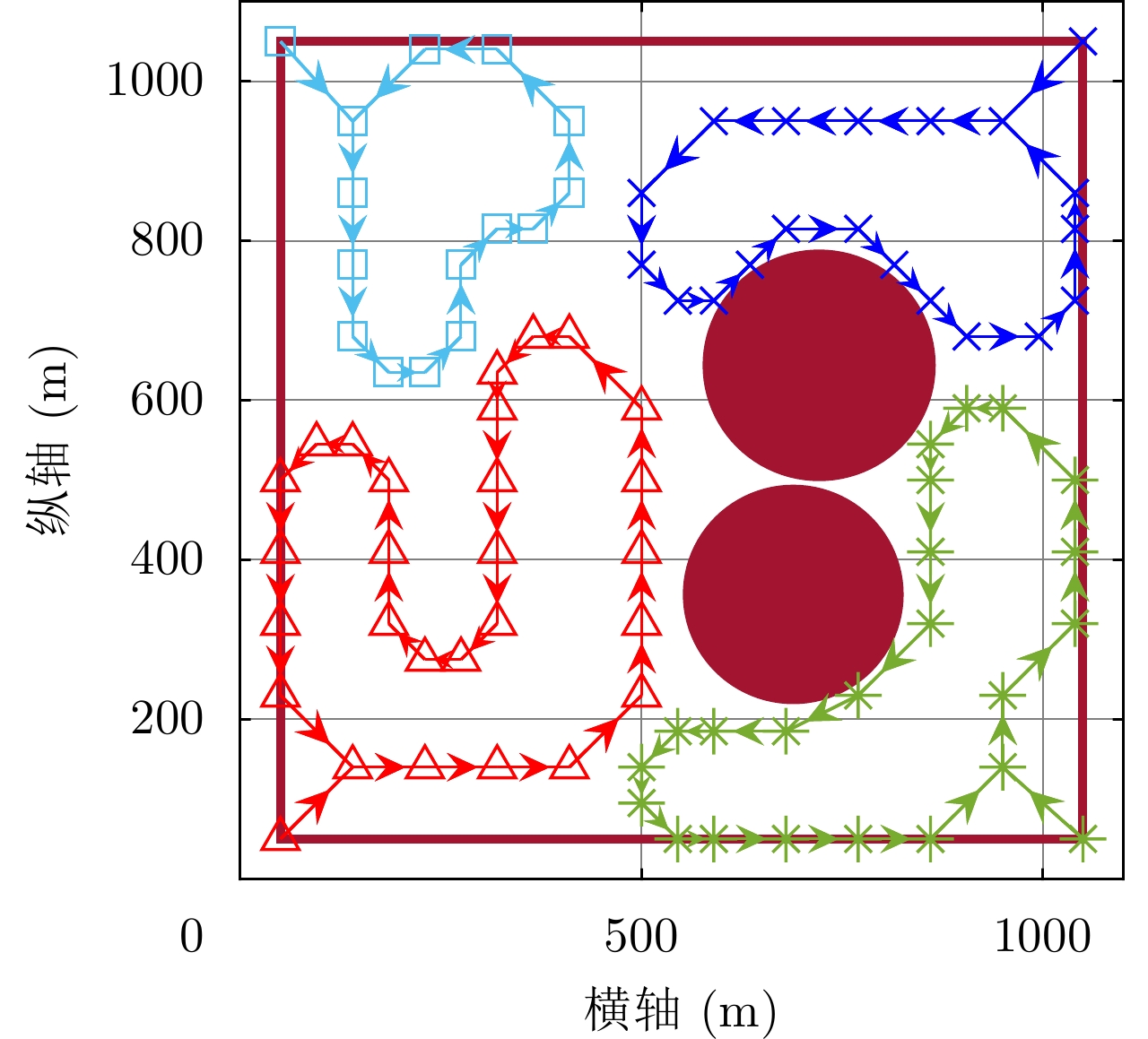
现令无人机数量分别为3, 4, 5, 6, 7的机组各自在本文模型的航迹优化下执行区域动态覆盖任务80 s。图6为上述各机组在前30 s的大致航迹图。图6中深红色圆形为禁飞区,标识符号所标识的点为无人机在各时刻的坐标点(机载雷达在地面坐标系中的坐标点),带箭头线段表示无人机在各时刻间的飞行路径,同时根据线段箭头的方向能够大致反映出无人机在各时刻的偏航角。不同的标识符号及不同的线段和标识符号颜色对应机组中不同编号的无人机。由各机组的优化后航迹可以看出,无人机在特定时期会回到任务执行早期生成的扫描区域附近进行重新扫描,契合了搜索环境的动态特性,一定程度上体现了区域动态覆盖任务的搜索要求。
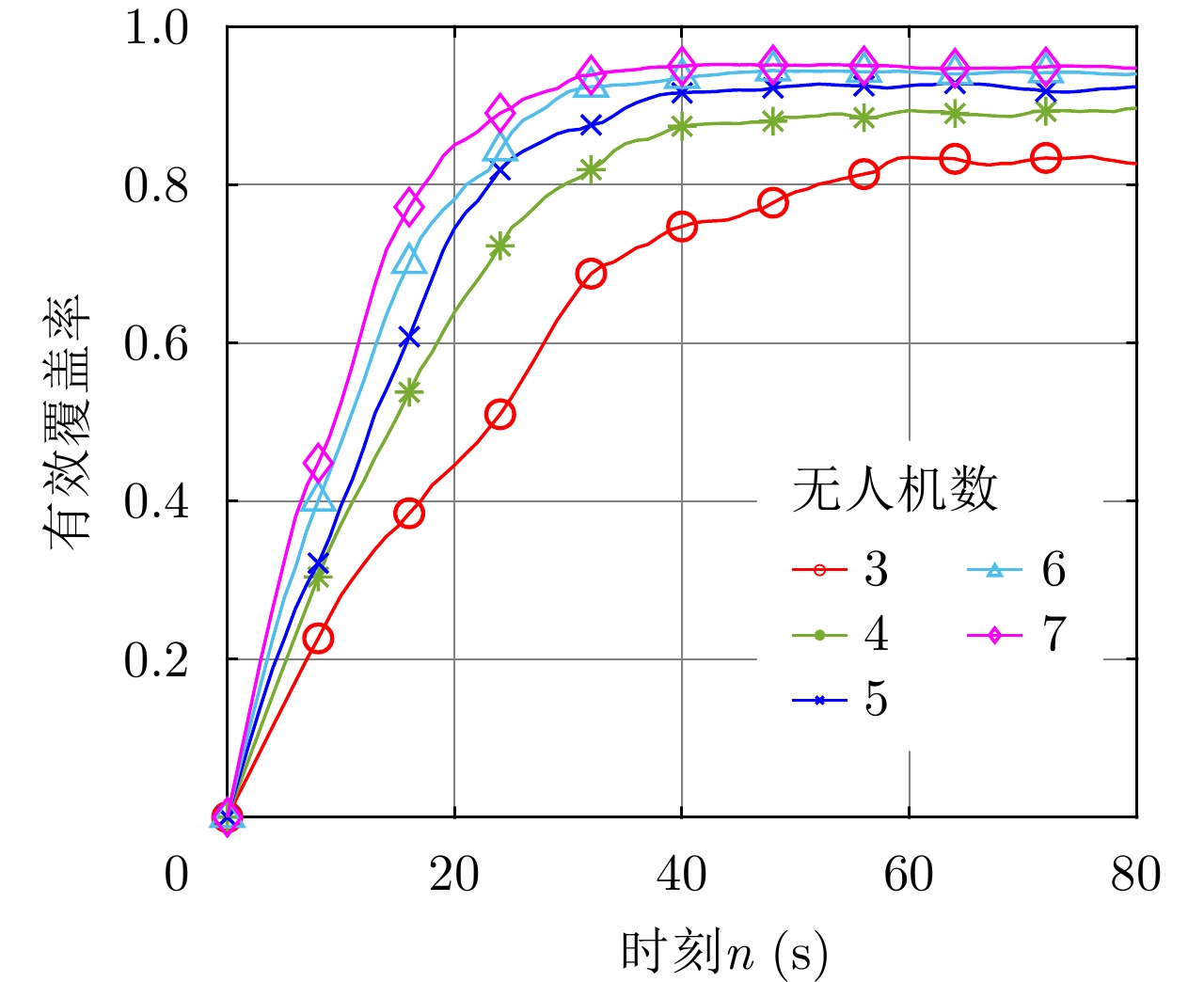
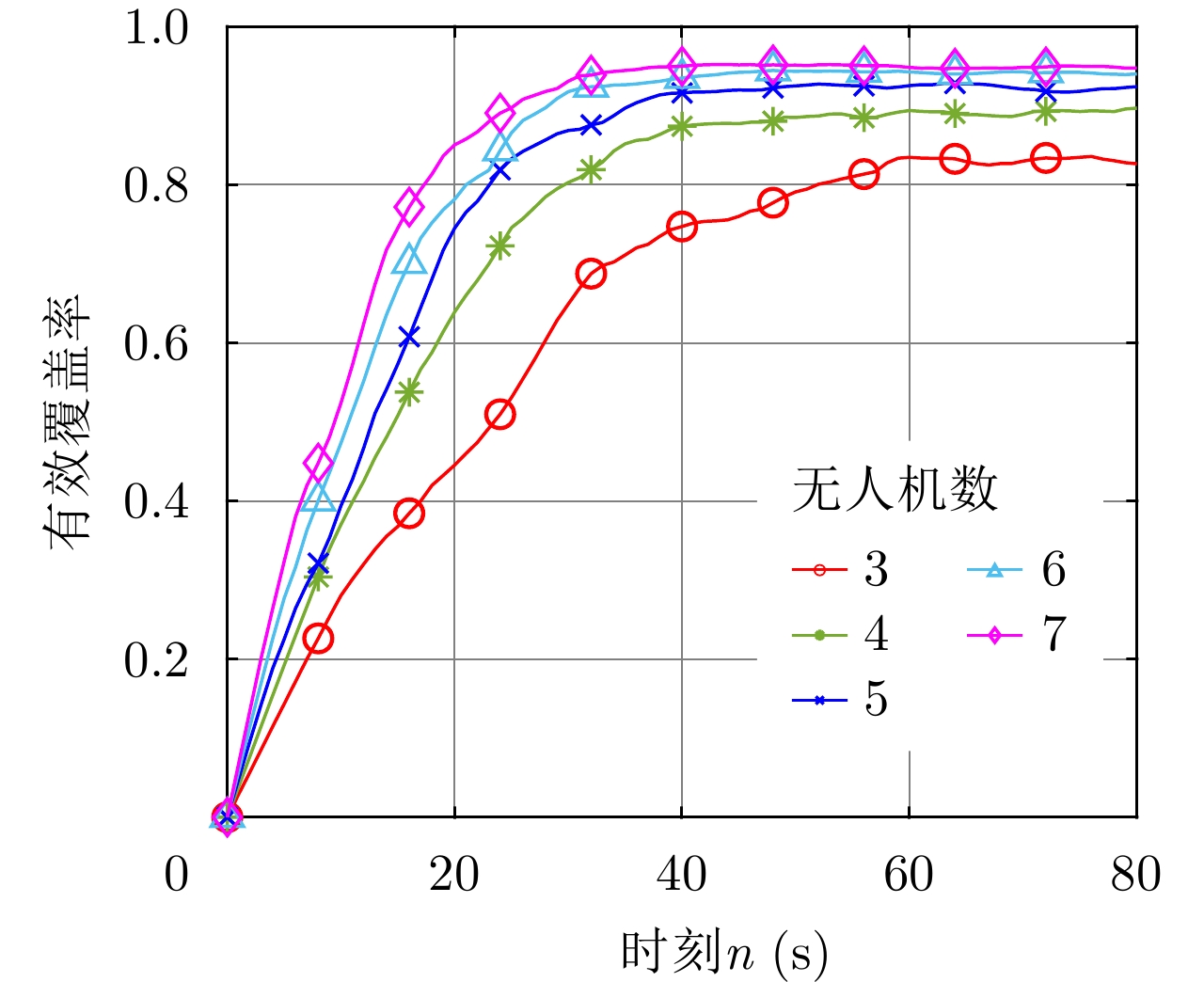
图7为上述5个机组的有效覆盖率
f\left( n \right) 随时刻n变化的曲线图。观察图7中各机组对应的曲线可知,任意机组的有效覆盖率曲线在任务执行早期均呈上升趋势,且随着n的增大,曲线也更加平缓,直至进入任务执行后期,曲线以某一有效覆盖率值为中心上下小幅度波动,称该中心值为机组的近似最大有效覆盖率,该波动状态为机组的近似稳定状态。上述这一曲线特性本质上是目标区域的边界限制造成的:在任务执行的开始阶段,目标区域内已生成的扫描区域的数量很小,则待生成的扫描区域能够占有的未覆盖区域的面积很大,因此任务执行早期的有效覆盖率增长较快,曲线也较陡峭;随着时刻的递增,目标区域内已生成的扫描区域的数量增大,待生成的扫描区域难免会与其他扫描区域出现影响较大的面积重叠,有效覆盖率的增速就相应下降,曲线也越平缓;当时刻达到一定的值时,目标区域可容纳的扫描区域数量已十分接近上限,有效覆盖率随之达到近似最大有效覆盖率,虽然无人机机载雷达在之后会继续对已生成的扫描区域进行重新扫描使其对应衰减因子大小提高,但这一过程中,其余较多扫描区域的对应衰减因子大小会出现下降,因此有效覆盖率只能维持在接近最大值的近似稳定状态,即曲线出现上下小幅度波动。同时,将图7中所有曲线进行对比分析可知,任意时刻下无人机数量较大的机组拥有比其余机组更高的有效覆盖率;另外,无人机数量越大,机组任务执行早期的有效覆盖率增速就越大,但是增速下降得也越快,进入近似稳定状态的时间越早。上述这一机组曲线间的特性差异是由无人机数量和目标区域的边界限制共同造成的:无人机数量越大,机组在一个时刻生成的扫描区域总数就越大,在任务执行早期的有效覆盖率增速就越大,能够在同一段运行时间内获得更大的有效覆盖率;但由于目标区域可容纳的扫描区域的数量存在上限,无人机数量越多的机组会更早遇到影响较大的扫描区域间重叠,且会更早填满目标区域,因此有效覆盖率增速的下降速度较大,机组会较早地进入近似稳定状态;另外,无人机数量较大的机组能够在近似稳定状态获得更高的扫描区域重新扫描的效率,因此该阶段有效覆盖率具有相比于其余机组较高的波动值。
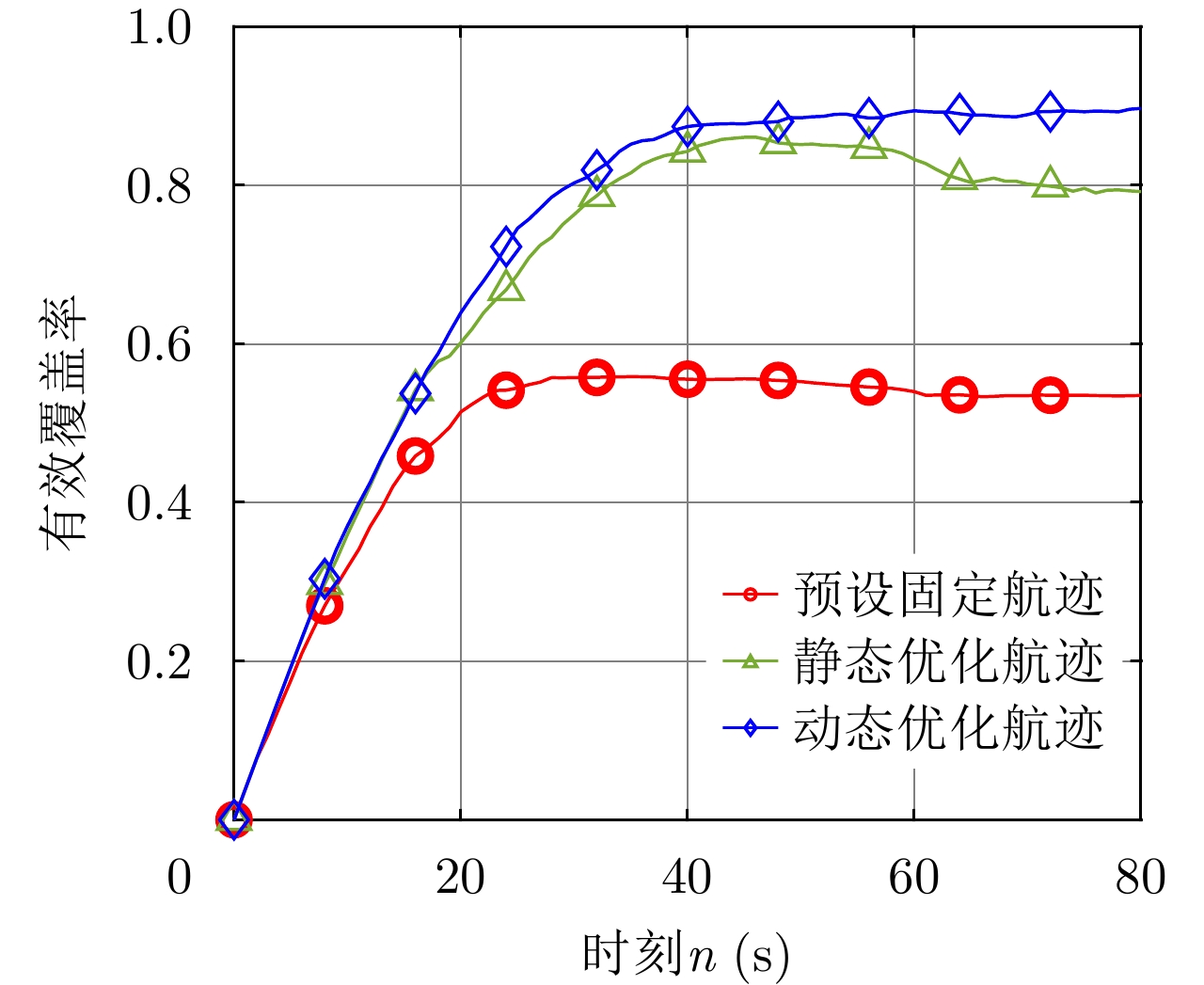
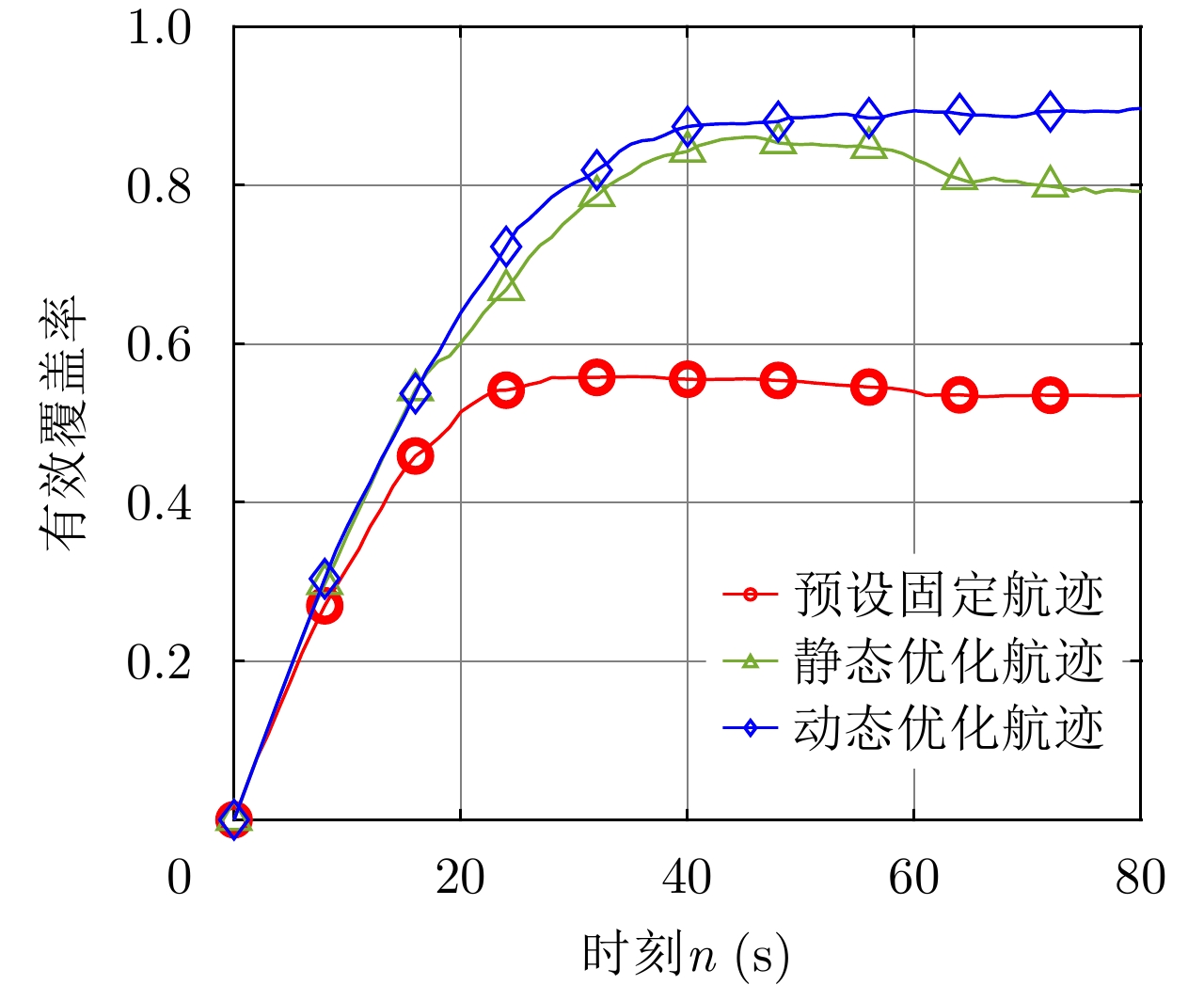
为了对比显示本文算法的有效性,现以4无人机机组作为研究对象,将预设航迹的搜索方法、面向静态搜索环境的传统优化方法与本文的航迹优化方法进行三者间的对比。基于文献[17]的区域划分原理和单无人机的搜索航迹特性所预设的固定航迹如图8所示,各无人机在零时刻的航迹控制参数与上文采用本文所提航迹优化搜索方法的4无人机机组一致,它们的飞行区域被尽可能独立开来,单个无人机在各时刻的平面位置互相间隔一定距离以确保机载雷达生成的各扫描区域间的重叠面积尽可能小,且各无人机在其头尾相接的某段航迹上循环运行。传统静态航迹优化模型采用本文的求解算法进行求解,零时刻各无人机的航迹控制参数的确定方式与4.1节介绍的一致。令机组采用上述二航迹规划方法分别执行任务80 s,计算在各时刻各自的有效覆盖率
f\left( n \right) ,并将其随时刻n变化的曲线与上文的4无人机机组的曲线进行对比分析。图9为机组采用面向静态搜索环境的传统优化方法所得出的前30 s大致航迹图,可见机组也具有对已扫描区域重新扫描的趋势,但具体的搜索航迹特征与图6(b)所示航迹特征之间存在一定差异。由图10可见,采用面向静态搜索环境的传统优化方法的机组,其有效覆盖率在任务执行后期会出现一定幅度的衰落,而采用本文的航迹优化方法的机组能够综合考虑各扫描区域在动态区域中的实际覆盖效果,始终以区域动态覆盖效果最大化为目标,对扫描区域的重新搜索具有较强的目的性,因此不会出现任务执行后期有效覆盖率衰落的问题。相较于传统静态航迹优化模型,本文所提航迹优化模型在动态覆盖性能层面上,平均提升约6%。另外,采用本文航迹优化搜索方法的机组,不论是在任务执行效率(有效覆盖率增速)还是在最终执行效果(近似最大有效覆盖率)层面上,都比采用预设航迹搜索模式的机组有较大的性能优势,这是由于本文的航迹优化搜索方法能够较好地把控扫描区域间的重叠以及对已扫描区域进行重新扫描的时机,是预设航迹搜索模式难以实现的。综上考虑,可以认为本文设计的航迹优化方法具有较好的面向动态搜索环境的适应性,解决了传统航迹优化模型在动态环境背景下的模型失配问题。5. 结语
本文在定义区域动态覆盖评估指标和航迹控制参数约束条件的基础上,设计了多机雷达协同区域动态覆盖航迹优化方法。本文引入了搜索信息衰减因子,实现了对动态待覆盖区域覆盖效果的量化描述;采用分步求解的优化模式,选择面向较优解快速搜索的随机优化法对模型进行求解,提高了航迹优化方法的运行效率。仿真结果表明,该航迹优化方法给出的机组航迹,满足了复杂动态环境的区域覆盖需求,解决了传统航迹优化模型在动态环境背景下的失配问题,且相较于预设航迹的搜索模式,该航迹优化方法在任务执行效率和最终覆盖效果等性能层面上均有较大的提升。在后续研究中,将会在本文所提航迹优化方法的基础上,设计适用于三维任务空间和精细航迹规划的方法,并优化求解算法的运行效率。
-
表 1 优化模型运行流程示意表
Table 1. Running process of the optimization model
步骤 流程内容 ① 计算基于时刻n的各时刻{\alpha _i}\left( n \right),i = 1,2, \cdots ,n ② 设置待优化无人机编号m = 1 ③ 基于待优化无人机时刻 n - 1 的解,生成可行解数量为{q_{\max }}的解空间{ {\boldsymbol{C} }_n} = \left\{ {{\boldsymbol{c}}'_1,{\boldsymbol{c}}'_2, \cdots ,{\boldsymbol{c}}_{ {q_{\max } } }'} \right\} ④ 求解待优化无人机时刻n的解{{\boldsymbol{c}}_n} \in {{\boldsymbol{C}}_n},使{{\boldsymbol{c}}_n}对应的有效覆盖率为{{\boldsymbol{C}}_n}中最大 ⑤ 令m = m + 1,若m \le M则返回步骤③ ⑥ 令n = n + 1,优化程序进入下一时刻 表 2 仿真参数设定表
Table 2. Simulation parameter settings
参数 设定值 {R_0} 90 m {\varphi _0} \dfrac{2}{3}\pi {t_d} 1 s {L_{\max }} 200 m \Delta {\psi _{\max }} \dfrac{1}{4}\pi {n_\alpha } 60 s \gamma 10 {q_{\max }} 100 -
[1] AGARWAL A, LIM M H, ER M J, et al. ACO for a new TSP in region coverage[C]. 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, Canada, 2005: 1717–1722. [2] YAN Junkun, JIAO Hao, PU Wenqiang, et al. Radar sensor network resource allocation for fused target tracking: A brief review[J]. Information Fusion, 2022, 86/87: 104–115. doi: 10.1016/j.inffus.2022.06.009 [3] YAN Junkun, PU Wenqiang, ZHOU Shenghua, et al. Optimal resource allocation for asynchronous multiple targets tracking in heterogeneous radar networks[J]. IEEE Transactions on Signal Processing, 2020, 68: 4055–4068. doi: 10.1109/TSP.2020.3007313 [4] YAN Junkun, PU Wenqiang, ZHOU Shenghua, et al. Collaborative detection and power allocation framework for target tracking in multiple radar system[J]. Information Fusion, 2020, 55: 173–183. doi: 10.1016/j.inffus.2019.08.010 [5] YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587 [6] 李春霄, 王冠绪, 殷辉, 等. 面向目标跟踪任务的蜂群无人机雷达协同航迹规划方法[J]. 战术导弹技术, 2021(6): 30–37. doi: 10.16358/j.issn.1009-1300.2021.1.561LI Chunxiao, WANG Guanxu, YIN Hui, et al. Target tracking task-oriented cooperative path planning method for swarm UAV radar[J]. Tactical Missile Technology, 2021(6): 30–37. doi: 10.16358/j.issn.1009-1300.2021.1.561 [7] 时晨光, 王奕杰, 代向荣, 等. 面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法[J]. 雷达学报, 2022, 11(5): 778–793. doi: 10.12000/JR22005SHI Chenguang, WANG Yijie, DAI Xiangrong, et al. Joint transmit resources and trajectory planning for target tracking in airborne radar networks[J]. Journal of Radars, 2022, 11(5): 778–793. doi: 10.12000/JR22005 [8] BESADA-PORTAS E, DE LA TORRE L, DE LA CRUZ J M, et al. Evolutionary trajectory planner for multiple UAVs in realistic scenarios[J]. IEEE Transactions on Robotics, 2010, 26(4): 619–634. doi: 10.1109/TRO.2010.2048610 [9] BERGER C, WZOREK M, KVARNSTRÖM J, et al. Area coverage with heterogeneous UAVs using scan patterns[C]. 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 2016: 342–349. [10] 王自亮, 罗德林, 吴顺祥. 凹多边形区域覆盖无人机航迹规划方法[J]. 航空兵器, 2019, 26(1): 95–100. doi: 10.12132/ISSN.1673-5048.2018.0068WANG Ziliang, LUO Delin, and WU Shunxiang. A UAV path planning method for concave polygonal area coverage[J]. Aero Weaponry, 2019, 26(1): 95–100. doi: 10.12132/ISSN.1673-5048.2018.0068 [11] 张小孟, 胡永江, 李文广, 等. 一种改进的多无人机覆盖航迹规划方法[J]. 兵器装备工程学报, 2020, 41(10): 215–221. doi: 10.11809/bqzbgcxb2020.10.040ZHANG Xiaomeng, HU Yongjiang, LI Wenguang, et al. Improved method for coverage track planning of multi-UAV[J]. Journal of Ordnance Equipment Engineering, 2020, 41(10): 215–221. doi: 10.11809/bqzbgcxb2020.10.040 [12] SUGIMOTO K, HATANAKA T, FUJITA M, et al. Experimental study on persistent coverage control with information decay[C]. The 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 2015: 164–169. [13] LI Weimin, WEI Dingmei, ZHOU Xiaokang, et al. F-SWIR: Rumor Fick-spreading model considering fusion information decay in social networks[J]. Concurrency and Computation: Practice and Experience, 2022, 34(22): e7166. doi: 10.1002/CPE.7166 [14] 陈伯孝, 杨林, 魏青. 雷达原理与系统[M]. 西安: 西安电子科技大学出版社, 2021: 22–24.CHEN Boxiao, YANG Lin, and WEI Qing. Radar Principle and System[M]. Xi’an: Xidian University Press, 2021: 22–24. [15] 张弘, 魏榕祥. 通用飞机抗坠撞设计指南[M]. 北京: 航空工业出版社, 2009: 13–14.ZHANG Hong and ZHANG Rongxiang. General Aircraft Crashworthiness Design Guide[M]. Beijing: Aviation Industry Press, 2009: 13–14. [16] FOUSKAKIS D and DRAPER D. Stochastic optimization: A review[J]. International Statistical Review, 2002, 70(3): 315–349. doi: 10.1111/j.1751-5823.2002.tb00174.x [17] 彭辉, 沈林成, 霍霄华. 多UAV协同区域覆盖搜索研究[J]. 系统仿真学报, 2007, 19(11): 2472–2476. doi: 10.16182/j.cnki.joss.2007.11.022PENG Hui, SHEN Lincheng, and HUO Xiaohua. Research on multiple UAV cooperative area coverage searching[J]. Journal of System Simulation, 2007, 19(11): 2472–2476. doi: 10.16182/j.cnki.joss.2007.11.022 期刊类型引用(4)
1. 杨诗兴,张国鑫,梁雲飞,易伟,孔令讲. 动平台分布式雷达系统动目标低比特数据检测算法. 雷达学报. 2024(03): 584-600 .  本站查看
本站查看2. 袁振涛,王成,涂岗刚. 雷达组网协同作战的标准化问题研究. 现代雷达. 2024(09): 18-21 .  百度学术
百度学术3. 袁野,杨剑,刘辛雨,易伟,孔令讲. 基于任务效用最大化的多雷达协同任务规划算法. 雷达学报. 2023(03): 550-562 .  本站查看
本站查看4. 易伟,袁野,刘光宏,葛建军,孔令讲,杨建宇. 多雷达协同探测技术研究进展:认知跟踪与资源调度算法. 雷达学报. 2023(03): 471-499 .  本站查看
本站查看其他类型引用(2)
-



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公



 下载:
下载:
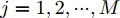
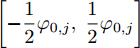
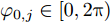
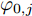
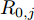

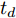

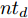

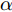

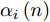
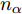
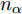


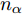
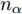

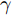
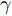
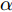
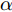
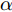

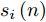
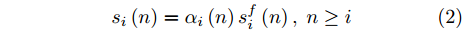
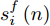
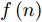
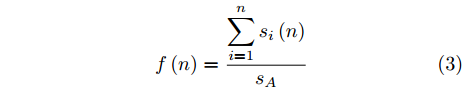
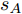
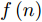

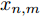
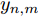
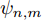


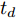
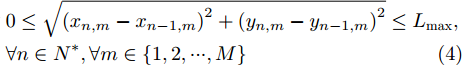
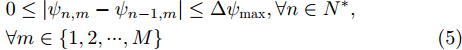

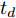
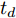
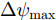
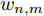
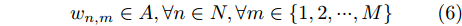
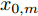

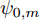
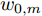
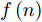
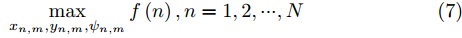
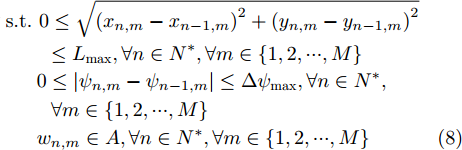
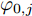
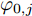
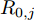











 下载:
下载:



 百度学术
百度学术