全息凝视雷达系统技术与发展应用综述

郭瑞; 张月; 田彪; 肖钰; 胡俊; 徐世友; 陈曾平

doi:10.12000/JR22153

全息凝视雷达系统技术与发展应用综述

DOI: 10.12000/JR22153

中山大学·深圳电子与通信工程学院深圳 518107

基金项目: 国家自然科学基金(U2133216)，深圳市科技计划资助(GXWD20201231165807008, 20200828174754001, KQTD20190929172704911)，深圳市基础研究资助项目(JCYJ20180307151430655)，广东省科技技术项目(2019ZT08X751)

详细信息

作者简介:
郭　瑞，博士，助理教授，主要研究方向为数字阵列雷达技术、阵列信号处理技术等

张　月，博士，副教授，主要研究方向为全息雷达技术、宽带数字化技术等

肖　钰，博士，副教授，主要研究方向为雷达天线、毫米波相控阵技术等

胡　俊，博士，助理教授，主要研究方向为先进探测系统、智能信号处理技术等

徐世友，博士，教授，博士生导师，主要研究方向为宽带雷达成像、自动目标识别、信息融合、多功能数字阵列雷达等

陈曾平，教授，博士生导师，主要研究方向为空间态势感知、软件化雷达探测、宽带成像识别等

通讯作者:
陈曾平 chenzengp@mail.sysu.edu.cn

责任主编：杨建宇 Corresponding Editor: YANG Jianyu
中图分类号: TN958
计量
- 文章访问数: 3502
- HTML全文浏览量: 1335
- PDF下载量: 647
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-18
- 修回日期: 2022-10-20
- 网络出版日期: 2022-11-02
- 刊出日期: 2023-04-28

Review of the Technology, Development and Applications of Holographic Staring Radar

School of Electronics and Communication Engineering, Shenzhen Campus of Sun Yat-sen University, Shenzhen 518107, China

Funds: The National Natural Science Foundation of China (U2133216), Shenzhen Science and Technology Program (GXWD20201231165807008, 20200828174754001, KQTD20190929172704911), Shenzhen Fundamental Research Program (JCYJ20180307151430655), Guangdong Provinical Science and Technology Program (2019ZT08X751)

More Information

Corresponding author: CHEN Zengping, chenzengp@mail.sysu.edu.cn

摘要

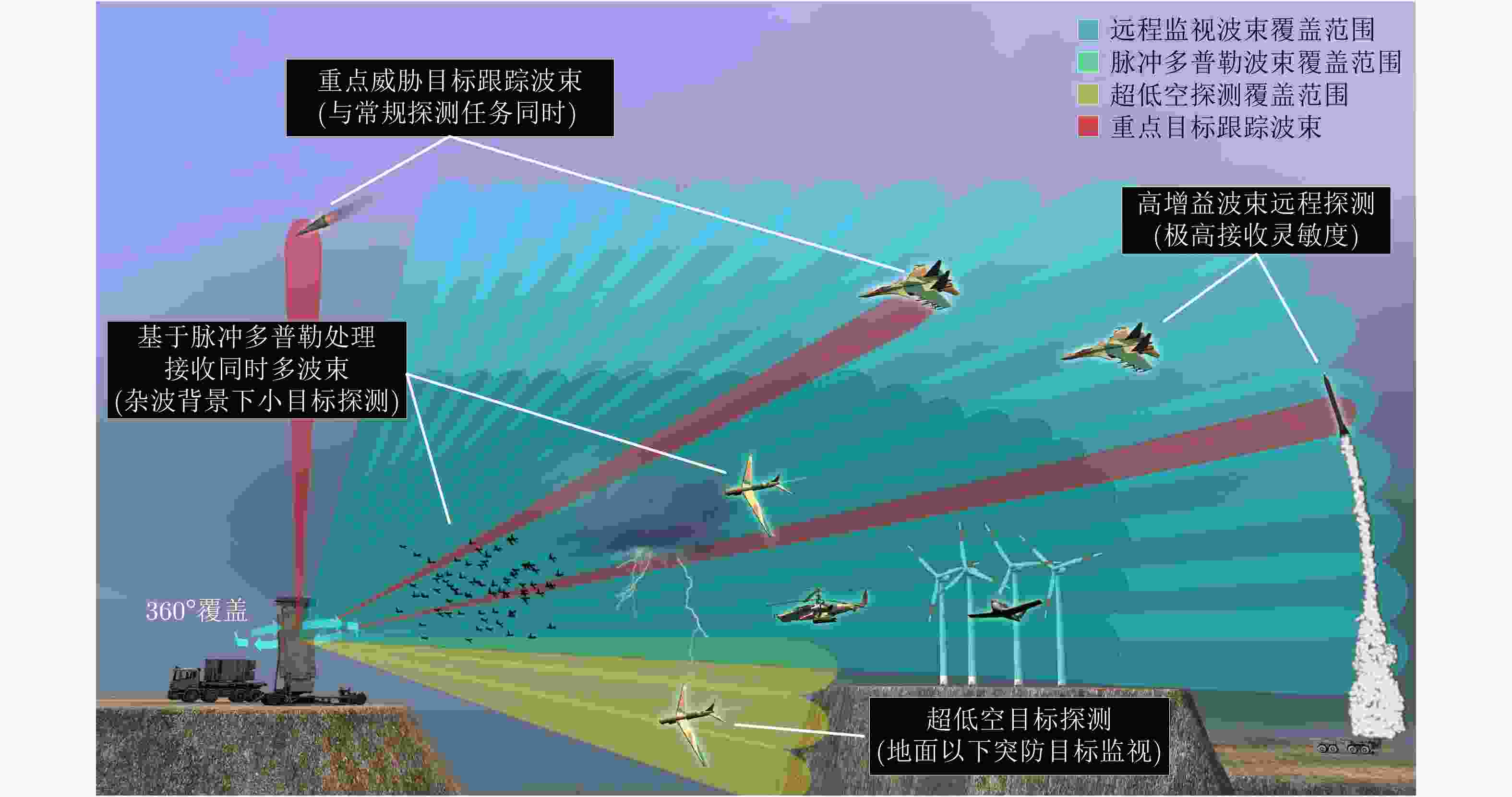
摘要: 全息凝视雷达是一种同时覆盖全空域、同时多功能的阵列雷达，该文首先明确全息凝视雷达定义，并概述全息凝视雷达特点、性能优势以及处理难点；然后，较为全面地介绍了全息凝视雷达的发展历程，归纳了当前的主要应用方向，并对中山大学在全息凝视雷达系统研究方面的进展情况进行了介绍，给出了实际场景下目标探测结果，展示了全息凝视雷达在低空目标监视等方面的应用潜力；接着较为全面地介绍了全息凝视雷达相关关键技术的研究进展，包括系统设计、收发波束控制、目标积累检测以及参数估计等方面；最后总结了全息凝视雷达的发展趋势。
- 数字阵列雷达 /
- 全息凝视雷达 /
- 全时空探测 /
- 同时多功能 /
- 多普勒分辨率
Abstract: Holographic staring radar is an array radar that continuously looks everywhere and performs multiple functions simultaneously instead of sequentially. First, this paper clarifies the definition of holographic staring radar and summarizes the features, performance advantages, and accompanying risks of holographic staring radar. Then, the research history and main application directions of holographic staring radar are reviewed. Next, the holographic staring radar series of Sun Yat-sen University in China is introduced. The target detection results of this holographic staring radar are given, showing the application potential of a holographic staring radar system in low-altitude target monitoring. Next, the research progress of related key technologies is examined, including system design, beam control, target detection, and parameter estimation. Finally, the development trends of holographic staring radar are discussed.
- Digital array radar /
- Holographic staring radar /
- Detect everywhere continuously /
- Multifunctional simultaneously /
- Doppler resolution

HTML全文

图 1 全息凝视雷达体制概念示意图

Figure 1. Schematic diagram of holographic staring radar

下载: 全尺寸图片幻灯片

图 2 OLPI雷达^[12]

Figure 2. OLPI radar^[12]

下载: 全尺寸图片幻灯片

图 3 Aveillant公司全息雷达系统^[24-30]

Figure 3. Holographic staring radars of Aveillant^[24-30]

下载: 全尺寸图片幻灯片

图 4 QinetiQ公司全息雷达系统^[41-43]

Figure 4. Holographic staring radars of QinetiQ^[41-43]

下载: 全尺寸图片幻灯片

图 5 OMEGA360全息凝视雷达^[44-46]

Figure 5. OMEGA360 holographic staring radar^[44-46]

下载: 全尺寸图片幻灯片

图 6 L波段全息凝视雷达

Figure 6. L band holographic staring radar

下载: 全尺寸图片幻灯片

图 7 S波段全息凝视雷达

Figure 7. S band holographic staring radar

下载: 全尺寸图片幻灯片

图 8 全息凝视雷达机场鸟情感知试验

Figure 8. Birds detection trials in airport

下载: 全尺寸图片幻灯片

图 9 集群目标速度分辨结果

Figure 9. Group target detection results

下载: 全尺寸图片幻灯片

图 10 针对边防应用的外场探测试验

Figure 10. Target detection trials for frontier defense applications

下载: 全尺寸图片幻灯片

图 11 海面目标探测试验

Figure 11. Sea surface target detection trials

下载: 全尺寸图片幻灯片

图 12 多波束凝视成像示意图^[75]

Figure 12. Schematic diagram of staring digital multiple beams SAR^[75]

下载: 全尺寸图片幻灯片

图 13 澳大利亚HILOW超视距雷达试验发射阵列^[81]

Figure 13. Photograph of the OTHR transmitter array used in the HILOW experiment^[81]

下载: 全尺寸图片幻灯片

图 14 自动驾驶雷达波束示意图^[1]

Figure 14. The illumination beam and multiple receive beams of a vehicular radar system^[1]

下载: 全尺寸图片幻灯片

图 15 亨索尔特公司Twinvis被动雷达^[1]

Figure 15. The Hensoldt Twinvis passive radar system^[1]

下载: 全尺寸图片幻灯片

图 16 全息凝视雷达信号处理流程

Figure 16. The signal processing diagram of holographic staring radars

下载: 全尺寸图片幻灯片

图 17 波束展宽前后的波束图^[89]

Figure 17. Beam before and after broadening^[89]

下载: 全尺寸图片幻灯片

图 18 混合积累原理示意图^[143]

Figure 18. Diagram of the principle of hybrid integration^[143]

下载: 全尺寸图片幻灯片

图 19 复杂阵地低空目标俯仰角估计模型^[157]

Figure 19. Multipath signal model for locating low-altitude small target in complex terrain environment^[157]

下载: 全尺寸图片幻灯片

图 20 雷达多工作模式示意图^[166]

Figure 20. Schematic diagram of multifunctional radar^[166]

下载: 全尺寸图片幻灯片

图 21 分布式全息雷达协同探测

Figure 21. Schematic diagram of distributed holographic staring radar

下载: 全尺寸图片幻灯片

表 1 相控阵雷达、全息凝视雷达和MIMO雷达对比

Table 1. The comparison of phased array radar, holographic staring radar and MIMO radar

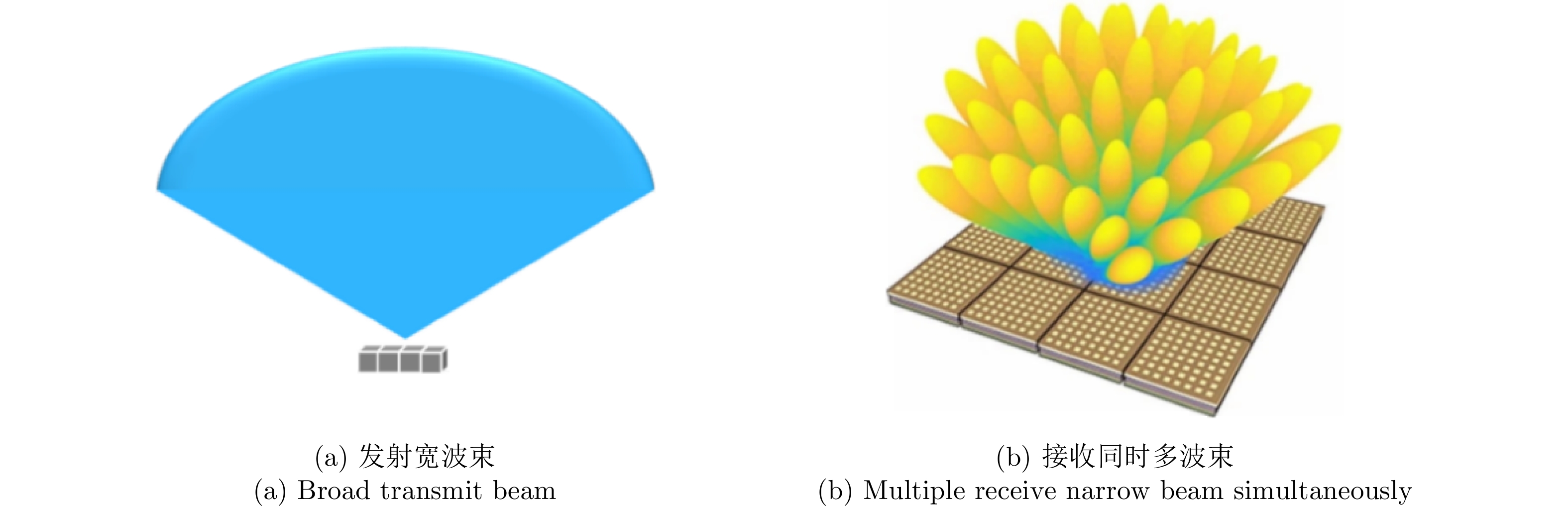
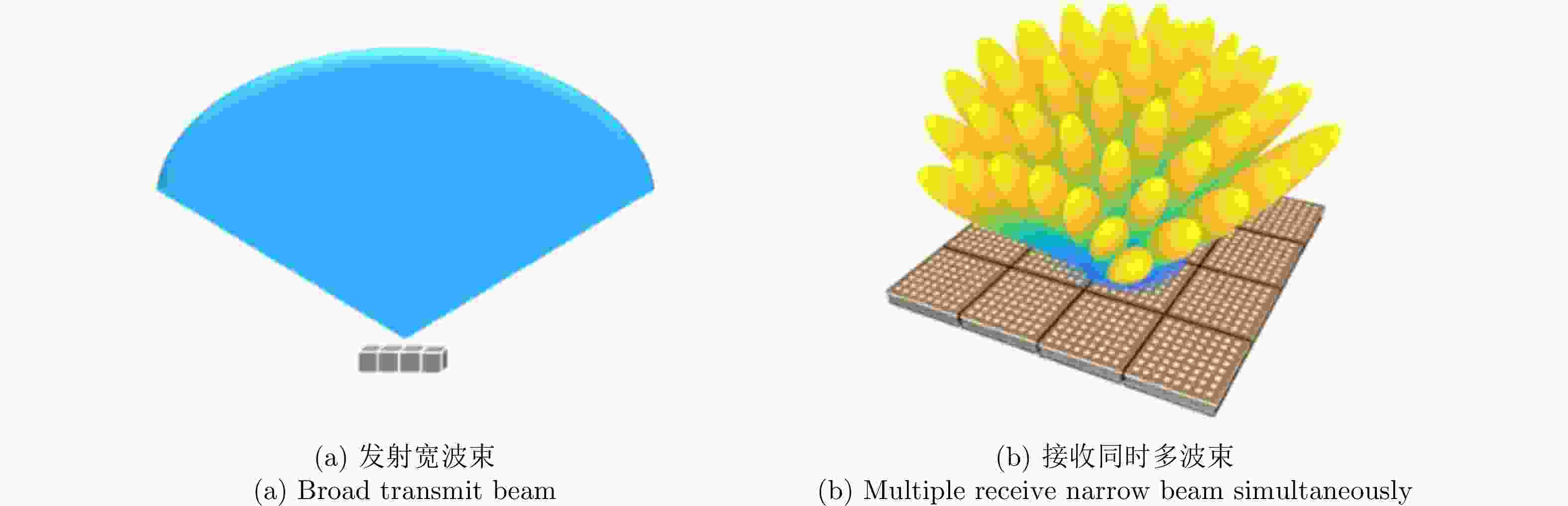
对比项	相控阵雷达	全息凝视雷达	MIMO雷达
工作模式示意图^[7]
发射波束特点	单个集中波束发射	发射宽波束	多个发射天线发射分集波形
接收波束特点	单个集中波束接收	同时多波束接收	同时多波束接收
相同发射总功率、积累时间输出信噪比^[6,7]	SNR_PA	SNR_PA/e (e为波束展宽倍数)	SNR_PA/N (N为发射阵元数)
角度分辨率^[6]	由接收天线孔径决定	由接收天线孔径决定	由发射阵列与接收阵列卷积得到虚拟阵列孔径决定
优势	相同孔径发射增益大	多目标跟踪能力强、同时多功能、多普勒分辨率高、射频隐身性高等	多目标跟踪能力强、虚拟孔径扩展测角精度高、多普勒分辨率高、射频隐身性高等
劣势	相同孔径观测范围小	相同孔径发射增益低、计算量大、不适合单目标跟踪	相同孔径发射增益低、计算量大、脉冲综合距离副瓣高、不适合单目标跟踪

下载: 导出CSV

表 2 Aveillant公司全息雷达系统参数^[24-30]

Table 2. Basic technical parameters of Aveillant's holographic radar^[24-30]

参数名称	原理样机	Gamekeeper 16U	Theia 64A	QUAD (128)
频率	L波段	L波段	L波段	L波段
带宽	~2 MHz	~2 MHz	~2 MHz	~2 MHz
发射功率	~1 kW	~1 kW	~10 kW	\
接收通道数	8×8	4×16	32×8	\
方位覆盖范围	90°	90°	90°	360°
俯仰覆盖范围	90°	30°	90°	90°
PRF	\	~7.5 kHz	~3.8 kHz	\
更新率	\	~0.25 s	~0.5 s	~1 s
探测距离	5 n mile (@RCS 1 m²)	5 km (@RCS 0.01 m²)	20 n mile (@RCS 0.01 m²)	40 n mile (@RCS 0.01 m²)
探测距离精度	\	\	<50 m	\
探测方位精度			<250 m
速度分辨率			<0.5 m/s

下载: 导出CSV

表 3 中山大学全息雷达系统参数

Table 3. Basic parameters of the holographic staring radar developed by SYSU

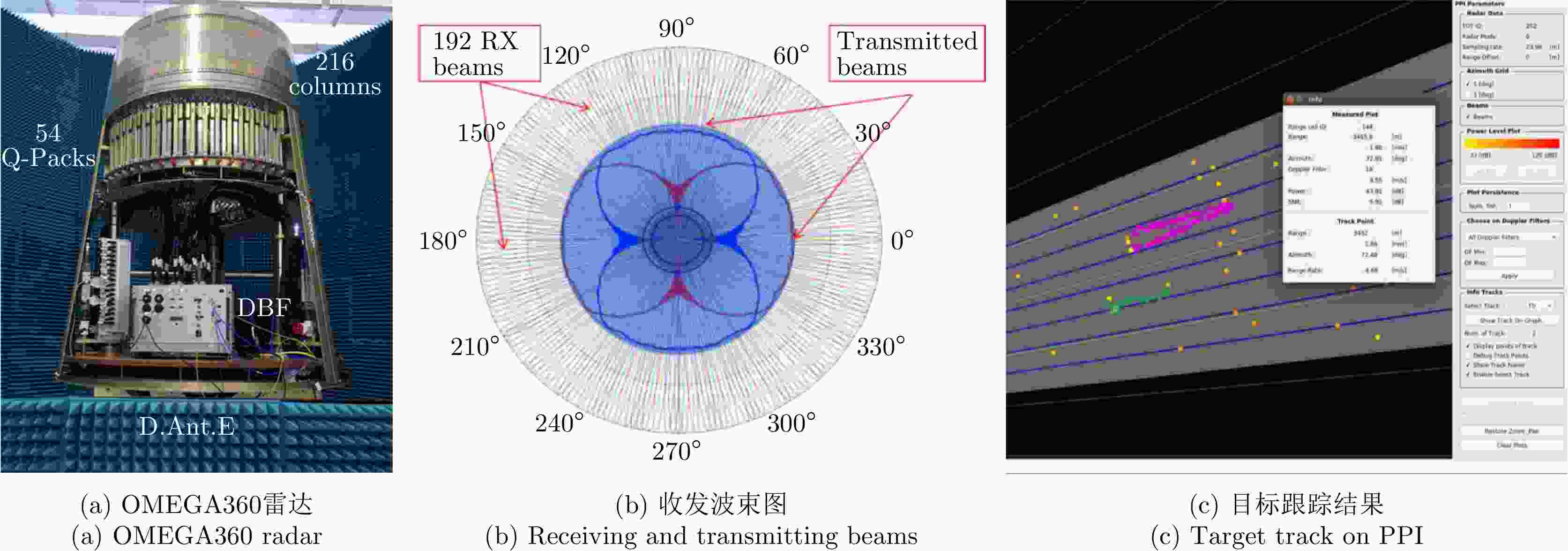
参数名称	L波段全息凝视雷达	S波段全息凝视雷达
频率	L波段	S波段
带宽	2～16 MHz	2～10 MHz
发射功率	～500 W	～400 W
接收通道数	8×8	4×16
方位覆盖范围	90°	90°
俯仰覆盖范围	22.5°, 30.0°, 45.0°, 60.0° (可设定)	30°
PRF	~5 kHz	~7.5 kHz
更新率	～1 s	～1 s
探测距离	10 km (@RCS 0.01 m²)	8 km (@RCS 0.01 m²)
探测距离精度	<10 m	<15 m
方位角分辨精度	<1.5°	<0.75°
速度分辨率	<0.1 m/s	<0.05 m/s

下载: 导出CSV

参考文献(166)

[1]	OSWALD G and BAKER C. Holographic Staring Radar[M]. London, United Kingdom: Institution of Engineering and Technology, 2021: 7–35.
[2]	汤小为, 汤俊, 彭应宁, 等. 一种新体制雷达——“泛探”雷达的关键技术研究[C]. 第十届全国雷达学术年会论文集, 北京, 2008: 43–46. TANG Xiaowei, TANG Jun, PENG Yingning, et al. Research on some key techniques of a new radar syestem ubiquitous radar[C]. The 10th Annual Radar Conference of China, Beijing, China, 2008: 43–46.
[3]	RADAR SYSTEMS PANEL. IEEE standard for radar definitions[R]. IEEE Std 686, 2017.
[4]	王盛利. 多波束凝视雷达[M]. 北京: 国防工业出版社, 2017: 1–10. WANG Shengli. Multibeam Staring Radar[M]. Beijing: National Defense Industry Press, 2017: 1–10.
[5]	赵永波, 刘宏伟. MIMO雷达技术综述[J]. 数据采集与处理, 2018, 33(3): 389–399. doi: 10.16337/j.1004-9037.2018.03.001 ZHAO Yongbo and LIU Hongwei. Overview on MIMO radar[J]. Journal of Data Acquisition and Processing, 2018, 33(3): 389–399. doi: 10.16337/j.1004-9037.2018.03.001
[6]	何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128 HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128
[7]	RABIDEAU D J and PARKER P. Ubiquitous MIMO multifunction digital array radar[C]. The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, USA, 2003: 1057–1064.
[8]	DOREY J, BLANCHARD Y, and CHRISTOPHE F. The RIAS project, a new approach to air surveillance radar[J]. Radiant, Journal of the Dutch Meteor Society, 1984: 113–118.
[9]	LUCE A S, MOLINA H, MULLER D, et al. Experimental results on RIAS digital beamforming radar[C]. 92 International Conference on Radar, Brighton, UK, 1992: 74–77.
[10]	COLIN J M. Phased array radars in France: Present and future[C]. International Symposium on Phased Array Systems and Technology, Boston, USA, 1996: 458–462.
[11]	WIRTH W D. Long term coherent integration for a floodlight radar[C]. International Radar Conference, Alexandria, USA, 1995: 698–703.
[12]	WIRTH W D. Radar Techniques Using Array Antennas[M]. London: Institution of Engineering and Technology, 2013: 419–446.
[13]	WIRTH W D. Omnidirectional low probability of intercept radar[C]. International Conference on Radar, Paris, France, 1989: 25–30.
[14]	保铮, 张庆文. 一种新型的米波雷达—综合脉冲与孔径雷达[J]. 现代雷达, 1995, 17(1): 1–13. doi: 10.16592/j.cnki.1004-7859.1995.01.001 BAO Zheng and ZHANG Qingwen. A new style metric wave radar — Synthetic impulse and aperture radar[J]. Modern Radar, 1995, 17(1): 1–13. doi: 10.16592/j.cnki.1004-7859.1995.01.001
[15]	陈伯孝, 张守宏. 稀布阵综合脉冲孔径雷达时域与频域脉冲综合方法[J]. 现代雷达, 1997, 19(6): 12–17. doi: 10.16592/j.cnki.1004-7859.1997.06.003 CHEN Boxiao and ZHANG Shouhong. Synthetic pulse processing in frequency-domain and time-domain for sparse-array synthetic impulse and aperture radar[J]. Modern Radar, 1997, 19(6): 12–17. doi: 10.16592/j.cnki.1004-7859.1997.06.003
[16]	陈伯孝, 张守宏, 赵永波. 稀布阵综合脉冲孔径雷达旁瓣对消性能分析[J]. 现代雷达, 1998, 20(5): 55–61. doi: 10.16592/j.cnki.1004-7859.1998.05.010 CHEN Boxiao, ZHANG Shouhong, and ZHAO Yongbo. The performance analysis of interference cancellation for sparse-array synthetic impulse and aperture radar[J]. Modern Radar, 1998, 20(5): 55–61. doi: 10.16592/j.cnki.1004-7859.1998.05.010
[17]	党晓方. 微波综合脉冲孔径雷达若干关键技术研究[D]. [博士论文], 西安电子科技大学, 2014: 1–8. DANG Xiaofang. Study on some key issues of microwave array synthetic impulse and aperture radar[D]. [Ph. D. dissertation], Xidian University, 2014: 1–8.
[18]	吴剑旗, 阮信畅. 稀布阵综合脉冲孔径雷达主要性能分析[J]. 现代电子, 1994(3): 1–6. WU Jianqi and RUAN Xinchang. Main performance analysis of sparse array synthetic pulse aperture radar[J]. Modern Electronics, 1994(3): 1–6.
[19]	SKOLNIK M. Improvements for air-surveillance radar[C]. 1999 IEEE Radar Conference. Radar into the Next Millennium, Waltham, USA, 1999: 18–21.
[20]	SKOLNIK M. Systems aspects of digital beam forming ubiquitous radar[R]. NRL Report: NRLhlW 5007-02-8625, June 28, 2002.
[21]	SKOLNIK M. Attributes of the ubiquitous phased array radar[C]. IEEE International Symposium on Phased Array Systems and Technology, 2003, Boston, USA, 2003: 101–106.
[22]	ALTER J J, WHITE R M, KRETSCHMER F F, et al. Ubiquitous radar: An implementation concept[C]. 2004 IEEE Radar Conference, Philadelphia, USA, 2004: 65–70.
[23]	JAHANGIR M and QUILTER T. The practicality and benefit of a 3-D wide-area persistent surveillance micro-Doppler radar[C]. 2015 16th International Radar Symposium (IRS), Dresden, Germany, 2015: 272–277.
[24]	JAHANGIR M. Target centric wide-area 3-D surveillance using a non-scanning multibeam receiver array[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 652–657.
[25]	JAHANGIR M and BAKER C. Robust detection of micro-UAS drones with L-band 3-D holographic radar[C]. 2016 Sensor Signal Processing for Defence, Edinburgh, UK, 2016: 1–5.
[26]	JAHANGIR M and BAKER C. Persistence surveillance of difficult to detect micro-drones with L-band 3-D holographic radar™[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–5.
[27]	JAHANGIR M and BAKER C J. Extended dwell Doppler characteristics of birds and micro-UAS at l-band[C]. 2017 18th International Radar Symposium, Prague, Czech Republic, 2017: 1–10.
[28]	JAHANGIR M, BAKER C J, and OSWALD G A. Doppler characteristics of micro-drones with L-Band multibeam staring radar[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 1052–1057.
[29]	JAHANGIR M and BAKER C J. L-band staring radar performance against micro-drones[C]. 2018 19th International Radar Symposium, Bonn, Germany, 2018: 1–10.
[30]	BENNETT C, JAHANGIR M, FIORANELLI F, et al. Use of symmetrical peak extraction in drone micro-doppler classification for staring radar[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6.
[31]	JAHANGIR M, AHMAD B I, and BAKER C J. Robust drone classification using two-stage decision trees and results from SESAR SAFIR trials[C]. 2020 IEEE International Radar Conference, Washington, USA, 2020: 636–641.
[32]	JAHANGIR M, AHMAD B I, and BAKER C J. The application of performance metrics to staring radar for drone surveillance[C]. 2020 17th European Radar Conference, Utrecht, Netherlands, 2021: 382–385.
[33]	JAHANGIR M, ATKINSON G M, ANTONIOU M, et al. Measurements of birds and drones with L-band staring radar[C]. 2021 21st International Radar Symposium, Berlin, Germany, 2021: 1–10.
[34]	GHAZALLI N, BALLERI A, JAHANGIR M, et al. Passive detection using a staring radar illuminator of opportunity[C]. 2019 International Radar Conference, Toulon, France, 2019: 1–5.
[35]	JAHANGIR M and BAKER C J. CLASS U-space drone test flight results for non-cooperative surveillance using an L-band 3-D staring radar[C]. 2019 20th International Radar Symposium, Ulm, Germany, 2019: 1–11.
[36]	DALE H, BAKER C, ANTONIOU M, et al. An initial investigation into using convolutional neural networks for classification of drones[C]. 2020 IEEE International Radar Conference, Washington, USA, 2020: 618–623.
[37]	DALE H, BAKER C, ANTONIOU M, et al. A comparison of convolutional neural networks for low SNR radar classification of drones[C]. 2021 IEEE Radar Conference, Atlanta, USA, 2021: 1–5.
[38]	GRIFFIN B, BALLERI A, BAKER C, et al. Optimal receiver placement in staring cooperative radar networks for detection of drones[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6.
[39]	GRIFFIN B, BALLERI A, BAKER C, et al. Prototyping a dual-channel receiver for use in a staring cooperative radar network for the detection of drones[C]. 2021 21st International Radar Symposium, Berlin, Germany, 2021: 1–7.
[40]	JAHANGIR M, BAKER C J, ANTONIOU M, et al. Advanced cognitive networked radar surveillance[C]. 2021 IEEE Radar Conference, Atlanta, USA, 2021: 1–6.
[41]	HARMAN S. A comparison of staring radars with scanning radars for UAV detection: Introducing the Alarm™ staring radar[C]. 2015 European Radar Conference, Paris, France, 2015: 185–188.
[42]	HARMAN S A and HUME A L. Applications of staring surveillance radars[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 270–273.
[43]	HARMAN S. Analysis of the radar return of micro-UAVs in flight[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 1159–1164.
[44]	MASSARDO M and STALLONE R. Experimental validation of a frustum of cone antenna applied to Omega 360 ubiquitous 2D radar[C]. 2017 IEEE International Workshop on Metrology for AeroSpace, Padua, Italy, 2017: 36–39.
[45]	FRANCO S and QUATTROCIOCCHI S. Experimental validation of a frustum of cone antenna radiation patterns[C]. 2017 IEEE International Workshop on Metrology for AeroSpace, Padua, Italy, 2017: 32–35.
[46]	STALLONE R, MASSARDO M, MONTANARI G, et al. Omega360 an innovative radar for detection and tracking of small drones[C]. 2019 International Radar Conference, Toulon, France, 2019: 1–5.
[47]	陈曾平, 张月, 鲍庆龙. 数字阵列雷达及其关键技术进展[J]. 国防科技大学学报, 2010, 32(6): 1–7. doi: 10.3969/j.issn.1001-2486.2010.06.001 CHEN Zengping, ZHANG Yue, and BAO Qinglong. Advance in digital array radar and its key technologies[J]. Journal of National University of Defense Technology, 2010, 32(6): 1–7. doi: 10.3969/j.issn.1001-2486.2010.06.001
[48]	张月, 邹江威, 陈曾平. 泛探雷达长时间相参积累目标检测方法研究[J]. 国防科技大学学报, 2010, 32(6): 15–20. doi: 10.3969/j.issn.1001-2486.2010.06.003 ZHANG Yue, ZOU Jiangwei, and CHEN Zengping. Long-time coherent integration targets detection method for ubiquitous radar[J]. Journal of National University of Defense Technology, 2010, 32(6): 15–20. doi: 10.3969/j.issn.1001-2486.2010.06.003
[49]	鲍庆龙, 张月, 吴桐, 等. 泛探雷达时-空级联目标检测与DOA估计算法[J]. 国防科技大学学报, 2010, 32(6): 21–25. doi: 10.3969/j.issn.1001-2486.2010.06.004 BAO Qinglong, ZHANG Yue, WU Tong, et al. Joint time-space target detection and DOA estimation algorithm on ubiquitous radar[J]. Journal of National University of Defense Technology, 2010, 32(6): 21–25. doi: 10.3969/j.issn.1001-2486.2010.06.004
[50]	郭瑞. 主被动一体化数字阵列雷达波达方向估计技术研究[D]. [博士论文], 国防科技大学, 2017: 1–13. GUO Rui. Research on direction of arrival estimation for integrated active-passive digital array radar[D]. [Ph. D. dissertation], National University of Defense Technology, 2017: 1–13.
[51]	赵英潇. 全息雷达长时间积累目标检测关键技术研究[D]. [博士论文], 国防科技大学, 2019. ZHAO Yingxiao. Long time integration and target detection technologies applied in holographic radar[D]. [Ph. D. dissertation], National University of Defense Technology, 2019.
[52]	田瑞琦. 泛探雷达微弱目标检测关键技术研究[D]. [博士论文], 国防科技大学, 2018: 1–112. TIAN Ruiqi. Research on key technology of ubiquitous radar weak target detection[D]. [Ph. D. dissertation], National University of Defense Technology, 2018: 1–112.
[53]	ZHANG Yue, GUO Yongqiang, and CHEN Zengping. Range-Doppler domain signal processing for medium PRF ubiquitous radar[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–4.
[54]	CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: Phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2–21. doi: 10.1109/TAES.2006.1603402
[55]	CHEN Xiaolong, ZHANG Hai, SONG Jie, et al. Micro-motion classification of flying bird and rotor drones via data augmentation and modified multi-scale CNN[J]. Remote Sensing, 2022, 14(5): 1107. doi: 10.3390/rs14051107
[56]	陈小龙, 关键, 于晓涵, 等. 基于短时稀疏时频分布的雷达目标微动特征提取及检测方法[J]. 电子与信息学报, 2017, 39(5): 1017–1023. doi: 10.11999/JEIT161040 CHEN Xiaolong, GUAN Jian, YU Xiaohan, et al. Radar micro-doppler signature extraction and detection via short-time sparse time-frequency distribution[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1017–1023. doi: 10.11999/JEIT161040
[57]	陈小龙, 南钊, 张海, 等. 飞鸟与旋翼无人机雷达微多普勒测量实验研究[J]. 电波科学学报, 2021, 36(5): 704–714. doi: 10.12265/j.cjors.2020192 CHEN Xiaolong, NAN Zhao, ZHANG Hai, et al. Experimental research on radar micro-Doppler of flying bird and rotor UAV[J]. Chinese Journal of Radio Science, 2021, 36(5): 704–714. doi: 10.12265/j.cjors.2020192
[58]	陈小龙, 陈唯实, 饶云华, 等. 飞鸟与无人机目标雷达探测与识别技术进展与展望[J]. 雷达学报, 2020, 9(5): 803–827. doi: 10.12000/JR20068 CHEN Xiaolong, CHEN Weishi, RAO Yunhua, et al. Progress and prospects of radar target detection and recognition technology for flying birds and unmanned aerial vehicles[J]. Journal of Radars, 2020, 9(5): 803–827. doi: 10.12000/JR20068
[59]	WU Qi, CHEN Jie, LU Yue, et al. A complete automatic target recognition system of low altitude, small RCS and slow speed (LSS) targets based on multi-dimensional feature fusion[J]. Sensors, 2019, 19(22): 5048. doi: 10.3390/s19225048
[60]	WU Qi, CHEN Jie, WU Hongming, et al. Experimental study on micro-doppler effect and micro-motion characteristics of aerial targets based on holographic staring radar[C]. 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 2019: 1186–1190.
[61]	DAI Ting, XU Shiyou, TIAN Biao, et al. Extraction of micro-doppler feature using LMD algorithm combined supplement feature for UAVs and birds classification[J]. Remote Sensing, 2022, 14(9): 2196. doi: 10.3390/rs14092196
[62]	ELTA Systems Lt. Persistent ground & coastal surveillance radar family[OL]. https://www.iai.co.il/p/elm-2112.
[63]	ELTA Systems Lt. Persistent foliage penetration radar[OL]. https://www.iai.co.il/p/elm-2112fp.
[64]	ELTA Systems Lt. Persistent perimeter detection radar[OL]. https://www.iai.co.il/p/elm-2114.
[65]	DE QUEVEDO Á D, URZAIZ F I, MENOYO J G, et al. Drone detection and RCS measurements with ubiquitous radar[C]. 2018 International Conference on Radar, Brisbane, Australia, 2018: 1–6.
[66]	DE QUEVEDO Á D, URZAIZ F I, MENOYO J G, et al. X-band ubiquitous radar system: First experimental results[C]. 2017 IEEE SENSORS, Glasgow, UK, 2017: 1–3.
[67]	DE QUEVEDO Á D, URZAIZ F I, MENOYO J G, et al. Remotely piloted aircraft detection with persistent radar[C]. 2018 15th European Radar Conference, Madrid, Spain, 2018: 317–320.
[68]	DE QUEVEDO Á D, URZAIZ F I, MENOYO J G, et al. Drone detection with X-band ubiquitous radar[C]. 2018 19th International Radar Symposium (IRS), Bonn, Germany, 2018: 1–10.
[69]	URZAIZ F I, DE QUEVEDO Á D, AYUSO A M, et al. Design, implementation and first experimental results of an X-band ubiquitous radar system[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 1150–1155.
[70]	Elbit Systems. Multi Beam Radar MBR 16-V1 real-time detection and tracking of moving ground and naval targets[OL]. https://elbitsystems.com/product/mbr-2/
[71]	Propatria Inc. Ground & Air Surveillance Radar[OL]. https://propatria-inc.com/products/radars/mbr-3d.
[72]	SUESS M, GRAFMUELLER B, and ZAHN R. A novel high resolution, wide swath SAR system[C]. IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 2001: 1013–1015.
[73]	WANG Wei, WANG Robert, DENG Yunkai, et al. Improved digital beam-forming approach with scaling function for range multi-channel synthetic aperture radar system[J]. IET Radar, Sonar & Navigation, 2016, 10(2): 379–385. doi: 10.1049/iet-rsn.2015.0276
[74]	KRIEGER G and MOREIRA A. Spaceborne bi- and multistatic SAR: Potential and challenges[J]. IEE Proceedings - Radar, Sonar and Navigation, 2006, 153(3): 184–198. doi: 10.1049/ip-rsn:20045111
[75]	江涛, 陈翼, 王盛利. 凝视数字多波束合成孔径雷达系统性能分析[J]. 系统工程与电子技术, 2013, 35(4): 745–752. doi: 10.3969/j.issn.1001-506X.2013.04.12 JIANG Tao, CHEN Yi, and WANG Shengli. System performance analysis of staring digital multiple beam synthetic aperture radar[J]. Systems Engineering and Electronics, 2013, 35(4): 745–752. doi: 10.3969/j.issn.1001-506X.2013.04.12
[76]	RINCON R F, VEGA M A, BUENFIL M, et al. NASA’s L-band digital beamforming synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3622–3628. doi: 10.1109/TGRS.2011.2157971
[77]	REIGBER A, NOTTENSTEINER A, LIMBACH M, et al. DBFSAR: An airborne very high-resolution digital beamforming SAR system[C]. 2017 European Radar Conference, Nuremberg, Germany, 2017: 175–178.
[78]	REIGBER A, SCHREIBER E, TRAPPSCHUH K, et al. The high-resolution digital-beamforming airborne SAR system DBFSAR[J]. Remote Sensing, 2020, 12(11): 1710. doi: 10.3390/rs12111710
[79]	ZHOU Yashi, WANG Wei, CHEN Zhen, et al. Digital beamforming synthetic aperture radar (DBSAR): Experiments and performance analysis in support of 16-channel airborne X-band SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(8): 6784–6798. doi: 10.1109/tgrs.2020.3027691
[80]	WANG Hui, DAI Shoulun, and ZHENG Shichao. Airborne Ka-band digital beamforming SAR system and flight test[C]. 2017 International Workshop on Remote Sensing with Intelligent Processing, Shanghai, China, 2017: 1–4.
[81]	FRAZER G J, ABRAMOVICH Y I, JOHNSON B A, et al. Recent results in MIMO over-the-horizon radar[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–6.
[82]	万显荣, 易建新, 占伟杰, 等. 基于多照射源的被动雷达研究进展与发展趋势[J]. 雷达学报, 2020, 9(6): 939–958. doi: 10.12000/JR20143 WAN Xianrong, YI Jianxin, ZHAN Weijie, et al. Research progress and development trend of the multi-illuminator-based passive radar[J]. Journal of Radars, 2020, 9(6): 939–958. doi: 10.12000/JR20143
[83]	MOFRAD R F, SADEGHZADEH R A, and ALIDOOST S. Comparison of antenna beam broadening methods for phased array radar applications[C]. 2011 Loughborough Antennas & Propagation Conference, Loughborough, UK, 2011: 1–4.
[84]	MARCANO D and DURAN F. Synthesis of antenna arrays using genetic algorithms[J]. IEEE Antennas and Propagation Magazine, 2000, 42(3): 12–20. doi: 10.1109/74.848944
[85]	KHZMALYAN A D and KONDRAT'YEV A S. Phase-only synthesis of antenna array amplitude pattern[J]. International Journal of Electronics, 1996, 81(5): 585–589. doi: 10.1080/002072196136490
[86]	ALP Y K, ALTIPARMAK F, GOK G, et al. Two different approaches for wide beam synthesis: Second order cone programming and swarm intelligence[C]. 20th European Signal Processing Conference, Bucharest, Romania, 2012: 1329–1333.
[87]	SAYIDMARIE K, SULTAN Q H. Synthesis of wide beam array patterns using quadratic-phase excitations[J]. International Journal of Electromagnetics and Applications, 2013, 3(6): 127–135. doi: 10.5923/j.ijea.20130306.01
[88]	SAYIDMARIE K H and SULTAN Q H. Synthesis of wide beam array patterns using random phase weights[C]. 2013 International Conference on Electrical Communication, Computer, Power, and Control Engineering, Mosul, Iraq, 2013: 52–57.
[89]	BROWN G C, KERCE J C, and MITCHELL M A. Extreme beam broadening using phase only pattern synthesis[C]. Fourth IEEE Workshop on Sensor Array and Multichannel Processing, 2006, Waltham, USA, 2006: 36–39.
[90]	ERÇIL E. An alternative method for phase only array pattern synthesis[C]. 2012 IEEE International Symposium on Antennas and Propagation, Chicago, USA, 2012: 1–2.
[91]	KINSEY R. Phased array beam spoiling technique[C]. IEEE Antennas and Propagation Society International Symposium, Montreal, Canada, 1997: 698–701.
[92]	LEIFER M C. Revisiting a method of beam shaping using phase weights[C]. 2016 IEEE International Symposium on Phased Array Systems and Technology, Waltham, USA, 2016: 1–3.
[93]	LEIFER M C. An airborne radar phased array with low sidelobes and a spoiled beam[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 72–76.
[94]	BUCKLEY K. Spatial/Spectral filtering with linearly constrained minimum variance beamformers[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(3): 249–266. doi: 10.1109/tassp.1987.1165142
[95]	GRIFFITHS L and JIM C. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(1): 27–34. doi: 10.1109/TAP.1982.1142739
[96]	XU Jingwei, LIAO Guisheng, and ZHU Shengqi. Robust LCMV beamforming based on phase response constraint[J]. Electronics Letters, 2012, 48(20): 1304–1306. doi: 10.1049/el.2012.2619
[97]	COX H, ZESKIND R, and OWEN M. Robust adaptive beamforming[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(10): 1365–1376. doi: 10.1109/TASSP.1987.1165054
[98]	FELDMAN D D and GRIFFITHS L J. A projection approach for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing, 1994, 42(4): 867–876. doi: 10.1109/78.285650
[99]	LEE C C and LEE J H. Eigenspace-based adaptive array beamforming with robust capabilities[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(12): 1711–1716. doi: 10.1109/8.650188
[100]	LORENZ R G and BOYD S P. Robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2005, 53(5): 1684–1696. doi: 10.1109/TSP.2005.845436
[101]	VOROBYOV S A, GERSHMAN A B, and LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313–324. doi: 10.1109/TSP.2002.806865
[102]	LI Jian, STOICA P, and WANG Zhisong. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702–1715. doi: 10.1109/TSP.2003.812831
[103]	LIE J P, SER W, and SEE C M S. Adaptive uncertainty based iterative robust capon beamformer using steering vector mismatch estimation[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4483–4488. doi: 10.1109/TSP.2011.2157500
[104]	LIE J P, LI Xiaohui, SER W, et al. Adaptive uncertainty based iterative robust capon beamformer[C]. 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, USA, 2010: 2526–2529.
[105]	NAI S E, SER W, YU Zhuliang, et al. Iterative robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1601–1611. doi: 10.1109/TSP.2010.2096222
[106]	CHEN Yilun, WIESEL A, ELDAR Y C, et al. Shrinkage algorithms for MMSE covariance estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5016–5029. doi: 10.1109/TSP.2010.2053029
[107]	DONG Mei, ZHENG Qiaozhen, and SU Hongtao. Automatic robust adaptive beamforming via ridge regression using l1-norm approximation[C]. 2013 International Conference on Radar, Adelaide, Australia, 2013: 385–387.
[108]	GONG C, HUANG L, XU D, et al. Knowledge-aided robust adaptive beamforming with small snapshots[J]. Electronics Letters, 2013, 49(20): 1258–1259. doi: 10.1049/el.2013.2198
[109]	GU Yujie and LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3881–3885. doi: 10.1109/TSP.2012.2194289
[110]	MALLIPEDDI R, LIE J, RAZUL S G, et al. Robust adaptive beamforming based on covariance matrix reconstruction for look direction mismatch[J]. Progress in Electromagnetics Research Letters, 2011, 25: 37–46. doi: 10.2528/PIERL11040104
[111]	D'ADDIO E, FARINA A, and STUDER F A. Performance compparison of optimum and conventional MTI and Doppler processors[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, AES-20(6): 707–715. doi: 10.1109/taes.1984.310453
[112]	陈小龙, 黄勇, 关键, 等. MIMO雷达微弱目标长时积累技术综述[J]. 信号处理, 2020, 36(12): 1947–1964. doi: 10.16798/j.issn.1003-0530.2020.12.001 CHEN Xiaolong, HUANG Yong, GUAN Jian, et al. Review of long-time integration techniques for weak targets using MIMO radar[J]. Journal of Signal Processing, 2020, 36(12): 1947–1964. doi: 10.16798/j.issn.1003-0530.2020.12.001
[113]	ZHENG Jibin, SU Tao, ZHU Wentao, et al. Radar high-speed target detection based on the scaled inverse fourier transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 1108–1119. doi: 10.1109/JSTARS.2014.2368174
[114]	KONG Lingjiang, LI Xiaolong, CUI Guolong, et al. Coherent integration algorithm for a maneuvering target with high-order range migration[J]. IEEE Transactions on Signal Processing, 2015, 63(17): 4474–4486. doi: 10.1109/TSP.2015.2437844
[115]	HUANG Penghui, LIAO Guisheng, YANG Zhiwei, et al. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 4013–4026. doi: 10.1109/TSP.2016.2558161
[116]	ZHANG Jiancheng, SU Tao, ZHENG Jibin, et al. Novel fast coherent detection algorithm for radar maneuvering target with jerk motion[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(5): 1792–1803. doi: 10.1109/JSTARS.2017.2651156
[117]	CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al. Maneuvering target detection via radon-fractional fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939–953. doi: 10.1109/TSP.2013.2297682
[118]	LI Xiaolong, CUI Guolong, YI Wei, et al. Coherent integration for maneuvering target detection based on radon-Lv’s distribution[J]. IEEE Signal Processing Letters, 2015, 22(9): 1467–1471. doi: 10.1109/LSP.2015.2390777
[119]	LI Xiaolong, KONG Lingjiang, CUI Guolong, et al. ISAR imaging of maneuvering target with complex motions based on ACCF-LVD[J]. Digital Signal Processing, 2015, 46: 191–200. doi: 10.1016/j.dsp.2015.06.015
[120]	LI Xiaolong, SUN Zhi, YI Wei, et al. Detection of maneuvering target with complex motions based on ACCF and FRFT[C]. 2017 IEEE Radar Conference, Seattle, USA, 2017: 17–20.
[121]	LI Xiaolong, CUI Guolong, YI Wei, et al. A fast non-searching method for maneuvering target detection based on ACCF[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 11–14.
[122]	WANG Genyuan, XIA Xianggen, ROOT B T, et al. Maneuvering target detection in over-the-horizon radar by using adaptive chirplet transform and subspace clutter rejection[C]. 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 2003: 49–52.
[123]	NAMIAS V. The fractional order fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3): 241–265. doi: 10.1093/imamat/25.3.241
[124]	陈小龙, 刘宁波, 黄勇, 等. 雷达目标检测分数域理论及应用[M]. 北京: 科学出版社, 2022: 56–80. CHEN Xiaolong, LIU Ningbo, HUANG Yong, et al. Fractional Domain Theory and Application of Fractional Domain for Radar Target Detection[M]. Beijing: Science Press, 2022: 56–80.
[125]	LV Xiaolei, BI Guoan, WAN Chunru, et al. Lv’s distribution: Principle, implementation, properties, and performance[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3576–3591. doi: 10.1109/TSP.2011.2155651
[126]	LUO Shan, BI Guoan, LV Xiaolei, et al. Performance analysis on Lv distribution and its applications[J]. Digital Signal Processing, 2013, 23(3): 797–807. doi: 10.1016/j.dsp.2012.11.011
[127]	XU Jia, YU Ji, PENG Yingning, et al. Radon-fourier transform for radar target detection, I: Generalized Doppler filter bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1186–1202. doi: 10.1109/TAES.2011.5751251
[128]	XU Jia, YU Ji, PENG Yingning, et al. Radon-fourier transform for radar target detection (II): Blind speed sidelobe suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2473–2489. doi: 10.1109/TAES.2011.6034645
[129]	YU Ji, XU Jia, PENG Yingning, et al. Radon-fourier transform for radar target detection (III): Optimality and fast implementations[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 991–1004. doi: 10.1109/TAES.2012.6178044
[130]	XU Jia, XIA Xianggen, PENG Shibao, et al. Radar maneuvering target motion estimation based on generalized radon-fourier transform[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6190–6201. doi: 10.1109/TSP.2012.2217137
[131]	陈小龙, 刘宁波, 王国庆, 等. 基于Radon-分数阶傅里叶变换的雷达动目标检测方法[J]. 电子学报, 2014, 42(6): 1074–1080. doi: 10.3969/j.issn.0372-2112.2014.06.006 CHEN Xiaolong, LIU Ningbo, WANG Guoqing, et al. Radar detection method for moving target based on radon-fourier fractional fourier transform[J]. Acta Electronica Sinica, 2014, 42(6): 1074–1080. doi: 10.3969/j.issn.0372-2112.2014.06.006
[132]	CARLSON B D, EVANS E D, and WILSON S L. Search radar detection and track with the Hough transform. I. System concept[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102–108. doi: 10.1109/7.250410
[133]	CARLSON B D, EVANS E D, and WILSON S L. Search radar detection and track with the Hough transform. II. Detection statistics[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 109–115. doi: 10.1109/7.250411
[134]	CARLSON B D, EVANS E D, and WILSON S L. Search radar detection and track with the Hough transform. III. Detection performance with binary integration[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 116–125. doi: 10.1109/7.250412
[135]	CARRETERO-MOYA J, GISMERO-MENOYO J, ASENSIO-LOPEZ A, et al. Small-target detection in sea clutter based on the Radon Transform[C]. 2008 International Conference on Radar, Adelaide, Australia, 2008: 610–615.
[136]	COPELAND A C, RAVICHANDRAN G, and TRIVEDI M M. Localized radon transform-based detection of ship wakes in SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(1): 35–45. doi: 10.1109/36.368224
[137]	BARNIV Y and KELLA O. Dynamic programming solution for detecting dim moving targets part II: Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(6): 776–788. doi: 10.1109/TAES.1987.310914
[138]	TONISSEN S M and EVANS R J. Peformance of dynamic programming techniques for Track-Before-Detect[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4): 1440–1451. doi: 10.1109/7.543865
[139]	SALMOND D J and BIRCH H. A particle filter for track-before-detect[C]. 2001 American Control Conference, Arlington, USA, 2001: 3755–3760.
[140]	HOSEINNEZHAD R, VO B N, and VO B T. Visual tracking in background subtracted image sequences via multi-bernoulli filtering[J]. IEEE Transactions on Signal Processing, 2013, 61(2): 392–397. doi: 10.1109/TSP.2012.2222389
[141]	童慧思, 张颢, 孟华东, 等. PHD滤波器在多目标检测前跟踪中的应用[J]. 电子学报, 2011, 39(9): 2046–2051. TONG Huisi, ZHANG Hao, MENG Huadong, et al. Probability hypothesis density filter multitarget track-before-detect application[J]. Acta Electronica Sinica, 2011, 39(9): 2046–2051.
[142]	XU Jia, ZHOU Xu, QIAN Lichang, et al. Hybrid integration for highly maneuvering radar target detection based on generalized radon-fourier transform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2554–2561. doi: 10.1109/TAES.2016.150076
[143]	DING Zegang, YOU Pengjie, QIAN Lichang, et al. A subspace hybrid integration method for high-speed and maneuvering target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(1): 630–644. doi: 10.1109/TAES.2019.2919478
[144]	HOWARD D D, SHERMAN S M, THOMSON D N, et al. Experimental results of the complex indicated angle techique for multipath correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 779–787. doi: 10.1109/TAES.1974.307884
[145]	WHITE W D. Double null technique for low angle tracking[J]. Microwave Journal, 1976, 19: 35–38, 60.
[146]	吴剑旗, 杨雪亚. 一种基于空域滤波的米波雷达测高新方法[J]. 现代雷达, 2015, 37(3): 1–4. doi: 10.3969/j.issn.1004-7859.2015.03.001 WU Jianqi and YANG Xueya. Novel height finding technique based on spatial filtering in meter-wave radar[J]. Modern Radar, 2015, 37(3): 1–4. doi: 10.3969/j.issn.1004-7859.2015.03.001
[147]	SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830
[148]	BOHME J. Estimation of source parameters by maximum likelihood and nonlinear regression[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, San Diego, USA, 1984: 271–274.
[149]	STOICA P, OTTERSTEN B, VIBERG M, et al. Maximum likelihood array processing for stochastic coherent sources[J]. IEEE Transactions on Signal Processing, 1996, 44(1): 96–105. doi: 10.1109/78.482015
[150]	赵光辉, 陈伯孝, 董玫. 基于交替投影的DOA估计方法及其在米波雷达中的应用[J]. 电子与信息学报, 2008, 30(1): 224–227. doi: 10.3724/SP.J.1146.2006.00835 ZHAO Guanghui, CHEN Baixiao, and DONG Mei. A new DOA estimator based on alternating projection and its application in VHF radar[J]. Journal of Electronics &Information Technology, 2008, 30(1): 224–227. doi: 10.3724/SP.J.1146.2006.00835
[151]	LO T and LITVA J. Use of a highly deterministic multipath signal model in low-angle tracking[J]. IEE Proceedings F - Radar and Signal Processing, 1991, 138(2): 163–171. doi: 10.1049/ip-f-2.1991.0022
[152]	LO T and LITVA J. Low-angle tracking using a multifrequency sampled aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(5): 797–805. doi: 10.1109/7.97325
[153]	LI Cunxu, CHEN Baixiao, ZHENG Yisong, et al. Altitude measurement of low elevation target in complex terrain based on orthogonal matching pursuit[J]. IET Radar, Sonar & Navigation, 2017, 11(5): 745–751. doi: 10.1049/iet-rsn.2016.0468
[154]	LI Cunxu, CHEN Baixiao, YANG Minglei, et al. Altitude measurement of low-elevation target for VHF radar based on weighted sparse bayesian learning[J]. IET Signal Processing, 2018, 12(4): 403–409. doi: 10.1049/iet-spr.2016.0738
[155]	ZHU Wei and CHEN Baixiao. Altitude measurement based on terrain matching in VHF array radar[J]. Circuits, Systems, and Signal Processing, 2013, 32(2): 647–662. doi: 10.1007/s00034-012-9472-4
[156]	LIU Yuan, JIU Bo, XIA Xianggen, et al. Height measurement of low-angle target using MIMO radar under multipath interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(2): 808–818. doi: 10.1109/TAES.2017.2767919
[157]	GUO Rui, PENG Xiangyu, TIAN Biao, et al. Low elevation target altitude measurement for ubiquitous radar based on known transmitted waveform and sparse representation[J]. IET Radar, Sonar & Navigation, 2022, 16(2): 346–355. doi: 10.1049/rsn2.12187
[158]	GUO Rui, ZHANG Yue, TIAN Biao, et al. Height measurement of micro-UAVs with L-band staring radar[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 2021: 7967–7970.
[159]	时晨光, 董璟, 周建江, 等. 飞行器射频隐身技术研究综述[J]. 系统工程与电子技术, 2021, 43(6): 1452–1467. doi: 10.12305/j.issn.1001-506X.2021.06.02 SHI Chenguang, DONG Jing, ZHOU Jianjiang, et al. Overview of aircraft radio frequency stealth technology[J]. Systems Engineering and Electronics, 2021, 43(6): 1452–1467. doi: 10.12305/j.issn.1001-506X.2021.06.02
[160]	王谦喆, 何召阳, 宋博文, 等. 射频隐身技术研究综述[J]. 电子与信息学报, 2018, 40(6): 1505–1514. doi: 10.11999/JEIT170945 WANG Qianzhe, HE Zhaoyang, SONG Bowen, et al. Overview on RF stealth technology research[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1505–1514. doi: 10.11999/JEIT170945
[161]	余显斌, 吕治东, 李涟漪, 等. 太赫兹感知通信一体化波形设计与信号处理[J]. 通信学报, 2022, 43(2): 76–88. doi: 10.11959/j.issn.1000-436x.2022015 YU Xianbin, LYU Zhidong, LI Lianyi, et al. Waveform design and signal processing for terahertz integrated sensing and communication[J]. Journal on Communications, 2022, 43(2): 76–88. doi: 10.11959/j.issn.1000-436x.2022015
[162]	马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146 MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146
[163]	许京伟, 朱圣棋, 廖桂生, 等. 频率分集阵雷达技术探讨[J]. 雷达学报, 2018, 7(2): 167–182. doi: 10.12000/JR18023 XU Jingwei, ZHU Shengqi, LIAO Guisheng, et al. An overview of frequency diverse array radar technology[J]. Journal of Radars, 2018, 7(2): 167–182. doi: 10.12000/JR18023
[164]	RABIDEAU D J. MIMO radar waveforms and cancellation ratio[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1167–1178. doi: 10.1109/TAES.2012.6178055
[165]	SUN Hongbo, BRIGUI F, and LESTURGIE M. Analysis and comparison of MIMO radar waveforms[C]. 2014 International Radar Conference, Lille, France, 2014: 1–6.
[166]	Lockheed Martin. TPY-4 next generation multi-mission radar[OL]. https://www.lockheedmartin.com/en-us/products/ground-based-air-surveillance-radars/tpy-4.html.