作者中心
专家审稿
责编办公
编辑办公
-
摘要: 基于随机有限集的扩展目标跟踪方法通常根据量测的空间信息进行量测划分，在杂波密集环境下有可能将杂波量测划入目标单元，从而造成跟踪性能的下降。为此，该文将目标和杂波的幅度信息引入高斯逆威沙特概率假设密度(GIW-PHD)滤波器，通过计算量测子集的幅度似然寻找最优的量测划分方法。此外，计算量测单元的中心时，采用幅度加权的方法计算量测单元的质量中心，以取代目前广泛使用的几何中心，从而进一步降低杂波对滤波器的干扰。在信杂比分别为13 dB和6 dB的条件下，通过对Rayleigh杂波中Swerling 1型起伏目标的跟踪结果证明了所提方法相比高斯逆威沙特概率假设密度滤波器具有更优的势估计和状态估计性能。
-
关键词:
- 扩展目标跟踪 /
- 随机有限集 /
- 幅度信息 /
- 高斯逆威沙特概率假设密度滤波器
Abstract: The random finite set-based extended target tracking methods generally partition measurements by spatial information. It is possible to place clutter measurements into target cells in a dense clutter environment resulting in degradation of tracking performance. To solve this issue, in this paper, the amplitude information of the target and clutter was introduced into the Gaussian Inverse Wishart Probability Hypothesis Density (GIW-PHD) filter, and thus, the optimal partition was found by calculating the amplitude likelihood of the measurement cells. Additionally, when calculating the centroid of a measurement cell, amplitude was used as a weighting factor to find the mass center instead of the widely used geometric center. This further reduced clutter interference. The tracking results of Swerling 1 fluctuating targets in a Rayleigh clutter when the signal-to-clutter ratios were 13 dB and 6 dB showed that the performance of the proposed algorithm in cardinality estimation and state estimation was better than that of the GIW-PHD filter. -
图 2 扩展目标真实航迹(SCR=13 dB)
Figure 2. Real trajectories of the extended targets (SCR=13 dB)
图 3 GIW-PHD单次航迹估计结果(SCR=13 dB)
Figure 3. Track estimation of the GIW-PHD in a run (SCR=13 dB)
图 4 AI-GIW-PHD单次航迹估计结果(SCR=13 dB)
Figure 4. Track estimation of the AI-GIW-PHD in a run (SCR=13 dB)
图 5 GIW-PHD单次扩展状态估计结果(SCR=13 dB)
Figure 5. Extended state estimation of the GIW-PHD in a run (SCR=13 dB)
图 6 AI-GIW-PHD单次扩展状态估计结果(SCR=13 dB)
Figure 6. Extended state estimation of the AI-GIW-PHD in a run (SCR=13 dB)
-
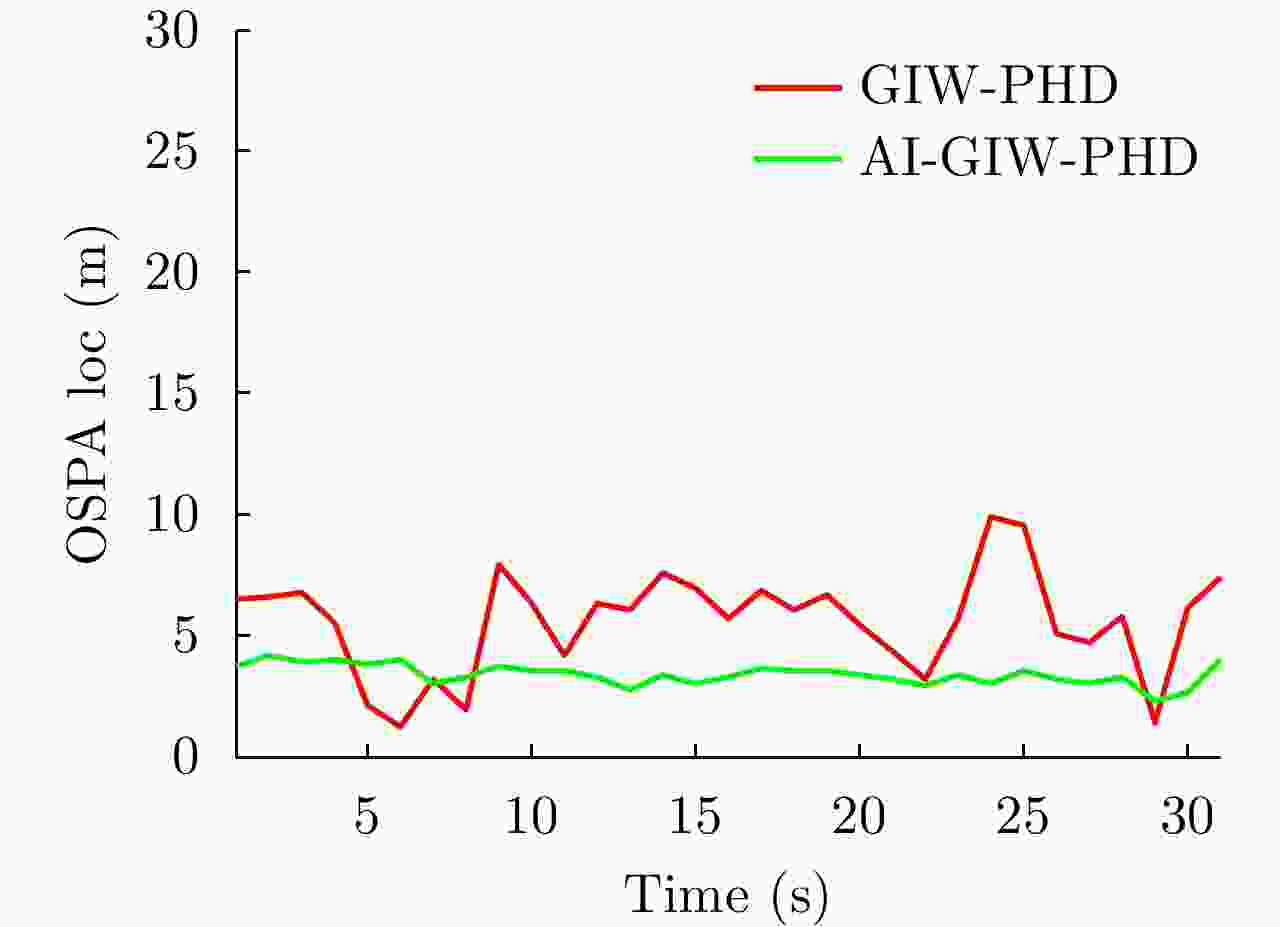
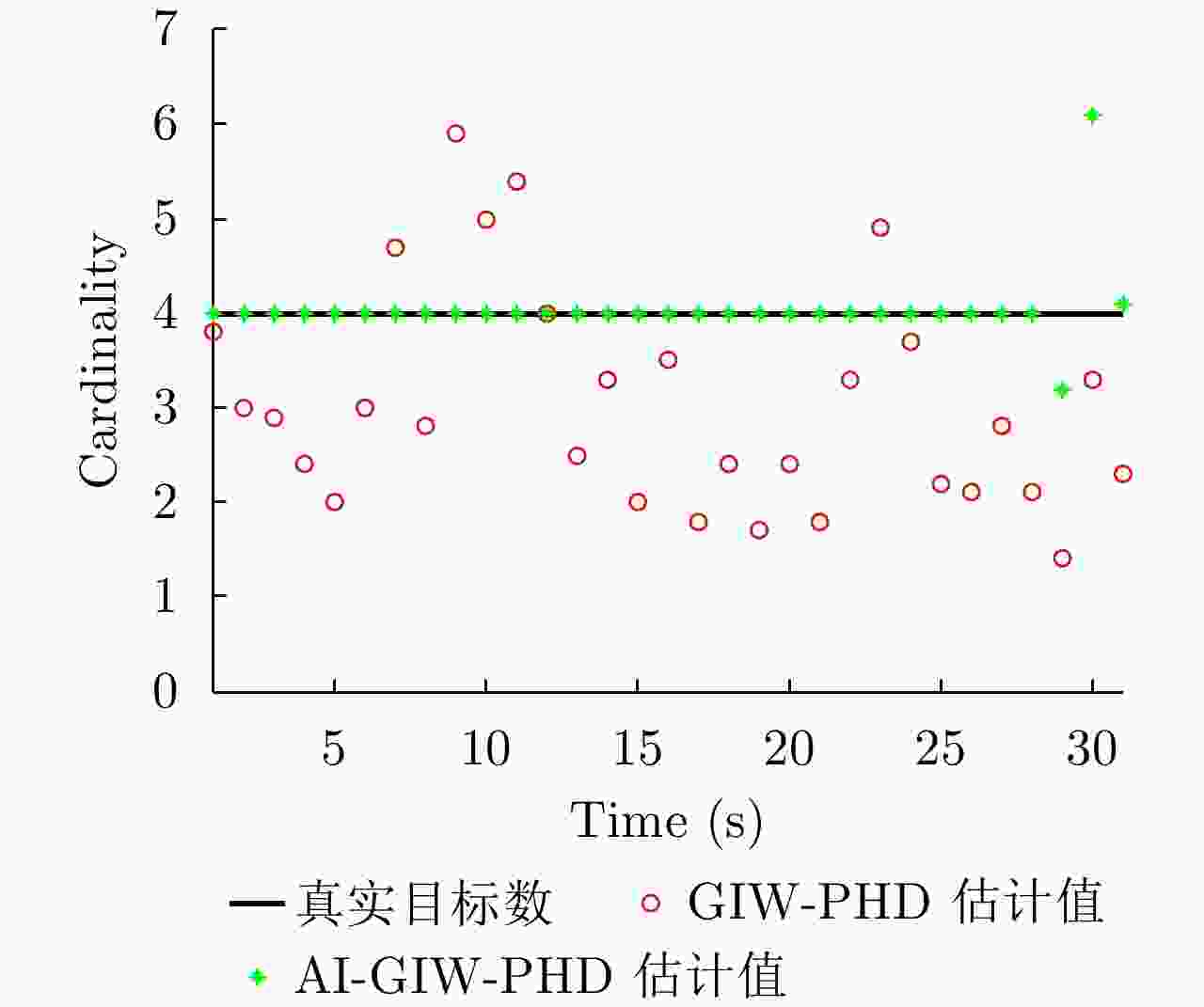
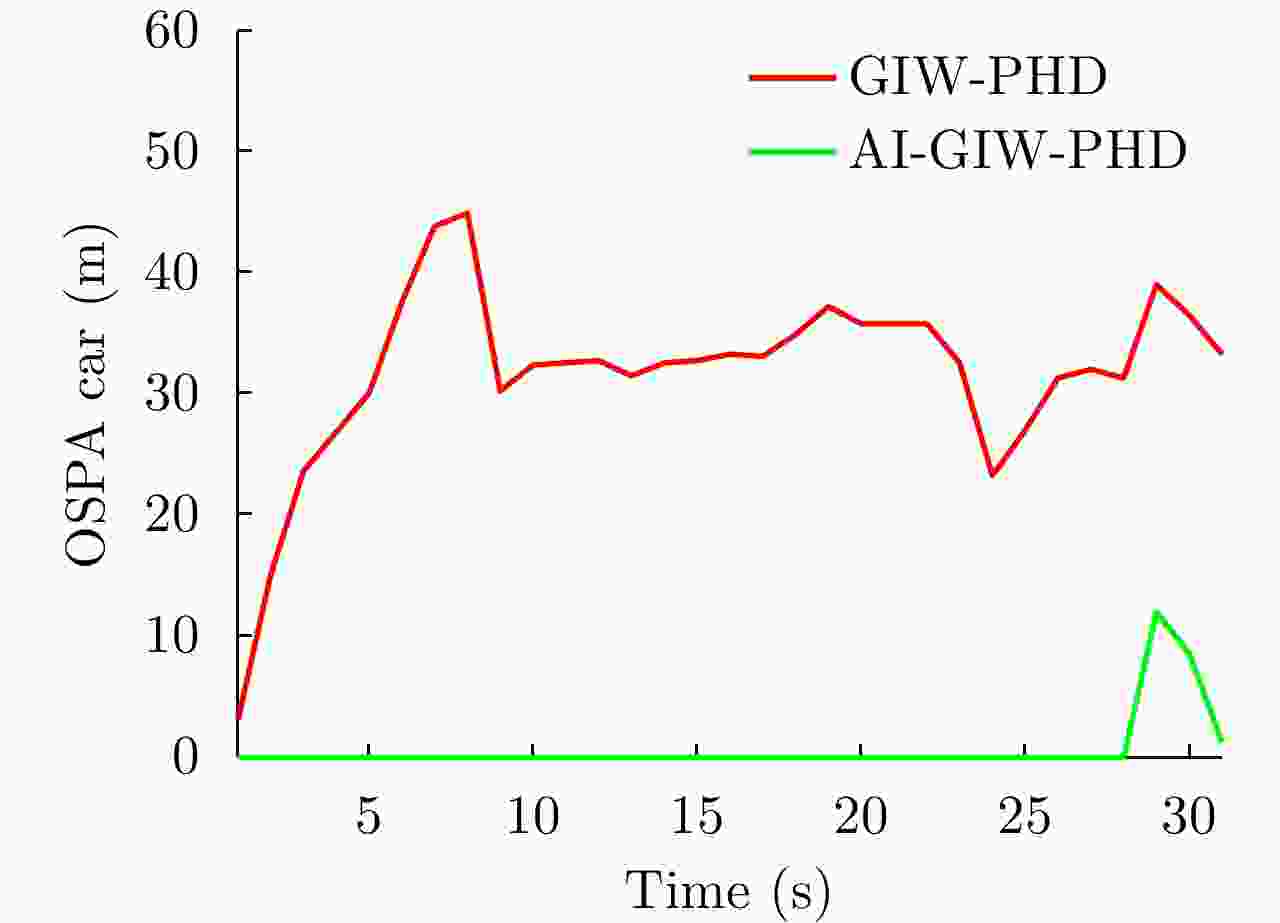
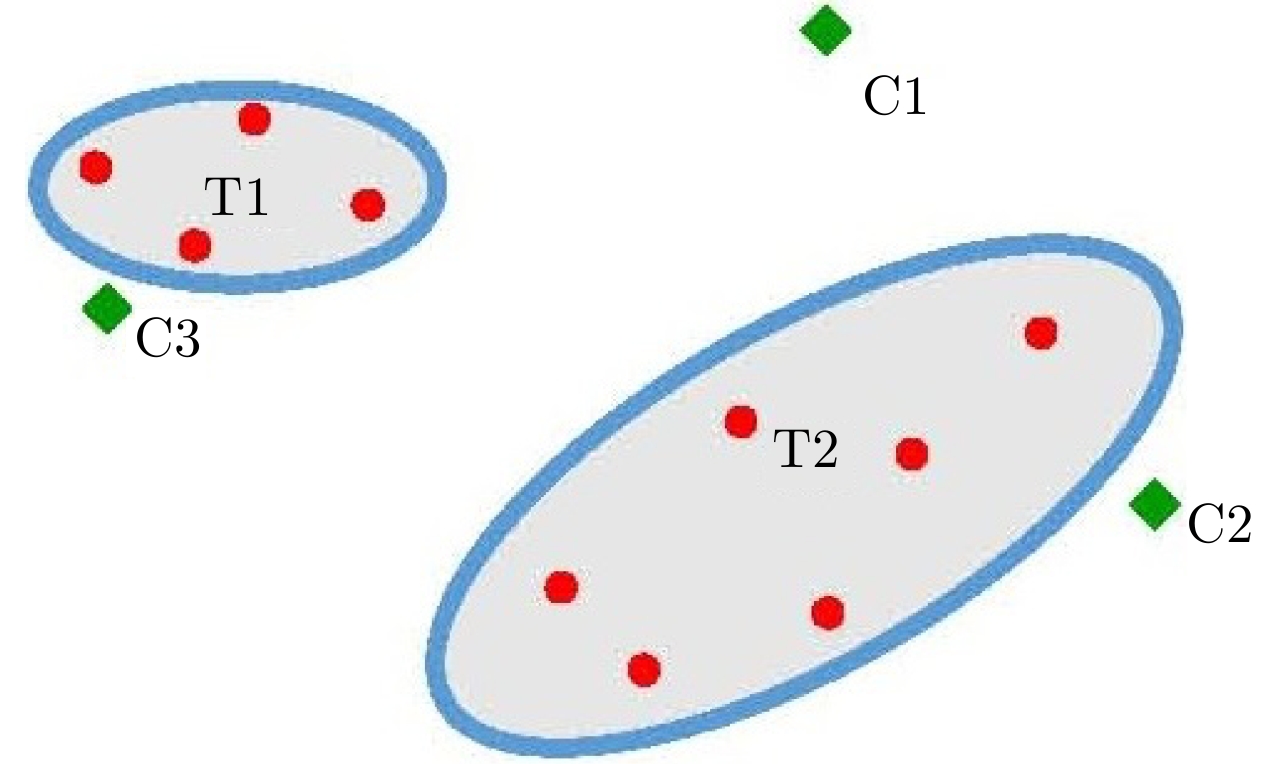
[1] VO B N, VO B T, and PHUNG D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6554–6567. doi: 10.1109/TSP.2014.2364014 [2] 尉强, 刘忠. 多普勒盲区下基于GM-PHD的雷达多目标跟踪算法[J]. 雷达学报, 2017, 6(1): 34–42. doi: 10.12000/JR16125WEI Qiang and LIU Zhong. A radar multi-target tracking algorithm based on Gaussian mixture PHD filter under Doppler blind zone[J]. Journal of Radars, 2017, 6(1): 34–42. doi: 10.12000/JR16125 [3] GILHOLM K and SALMOND D. Spatial distribution model for tracking extended objects[J]. IEE Proceedings - Radar, Sonar and Navigation, 2005, 152(5): 364–371. doi: 10.1049/ip-rsn:20045114 [4] BOERS Y, DRIESSEN H, TORSTENSSON J, et al. Track-before-detect algorithm for tracking extended targets[J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(4): 345–351. doi: 10.1049/ip-rsn:20050123 [5] MAHLER R. PHD filters for nonstandard targets, I: Extended targets[C]. The 2009 12th International Conference on Information Fusion, Seattle, USA, 2009: 915–921. [6] GRANSTRÖM K, LUNDQUIST C, and ORGUNER U. A Gaussian mixture PHD filter for extended target tracking[C]. The 2010 13th International Conference on Information Fusion, Edinburgh, UK, 2010: 1–8. [7] GRANSTRÖM K, LUNDQUIST C, and ORGUNER U. Extended target tracking using a Gaussian-Mixture PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268–3286. doi: 10.1109/TAES.2012.6324703 [8] ORGUNER U, LUNDQUIST C, and GRANSTRÖM K. Extended target tracking with a cardinalized probability hypothesis density filter[C]. The 14th International Conference on Information Fusion, Chicago, USA, 2011: 1–8. [9] ORGUNER U, LUNDQUIST C, and GRANSTRÖM K. Extended target tracking with a cardinalized probability hypothesis density filter[OL]. http://www.control.isy.liu.se/research/reports/2011/2999.pdf. 2011. [10] KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042–1059. doi: 10.1109/TAES.2008.4655362 [11] GRANSTRÖM K and ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657–5671. doi: 10.1109/TSP.2012.2212888 [12] LAN Jian and LI X R. Tracking of extended object or target group using random matrix—part I: New model and approach[C]. The 2012 15th International Conference on Information Fusion, Singapore, 2012: 2177–2184. [13] LAN Jian and LI X R. Tracking of extended object or target group using random matrix—part II: Irregular object[C]. The 2012 15th International Conference on Information Fusion, Singapore, 2012: 2185–2192. [14] GRANSTRÖM K and ORGUNER U. On spawning and combination of extended/group targets modeled with random matrices[J]. IEEE Transactions on Signal Processing, 2013, 61(3): 678–692. doi: 10.1109/TSP.2012.2230171 [15] ZHANG Yongquan and JI Hongbing. A novel fast partitioning algorithm for extended target tracking using a Gaussian mixture PHD filter[J]. Signal Processing, 2013, 93(11): 2975–2985. doi: 10.1016/j.sigpro.2013.04.006 [16] ZHANG Yongquan and JI Hongbing. Robust Bayesian partition for extended target Gaussian inverse Wishart PHD filter[J]. IET Signal Processing, 2014, 8(4): 330–338. doi: 10.1049/iet-spr.2013.0150 [17] 杨金龙, 刘风梅, 王冬, 等. 基于近邻传播聚类的多扩展目标量测集划分算法[J]. 雷达学报, 2015, 4(4): 452–459. doi: 10.12000/JR15003YANG Jinlong, LIU Fengmei, WANG Dong, et al. Affinity propagation based measurement partition algorithm for multiple extended target tracking[J]. Journal of Radars, 2015, 4(4): 452–459. doi: 10.12000/JR15003 [18] LERRO D and BAR-SHALOM Y. Interacting multiple model tracking with target amplitude feature[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(2): 494–509. doi: 10.1109/7.210086 [19] CLARK D, RISTIC B, VO B N, et al. Bayesian multi-object filtering with amplitude feature likelihood for unknown object SNR[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 26–37. doi: 10.1109/TSP.2009.2030640 [20] SCHUHMACHER D, VO B T, and VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447–3457. doi: 10.1109/TSP.2008.920469 -
下载:
图(12)
计量
- 文章访问数: 2847
- HTML全文浏览量: 1202
- PDF下载量: 153
- 被引次数: 0
