作者中心
专家审稿
责编办公
编辑办公
Solution to Layover Problemin Airborne Multi-baseline SAR Based on Spectrum Estimation with Fourth-order Cumulant
-
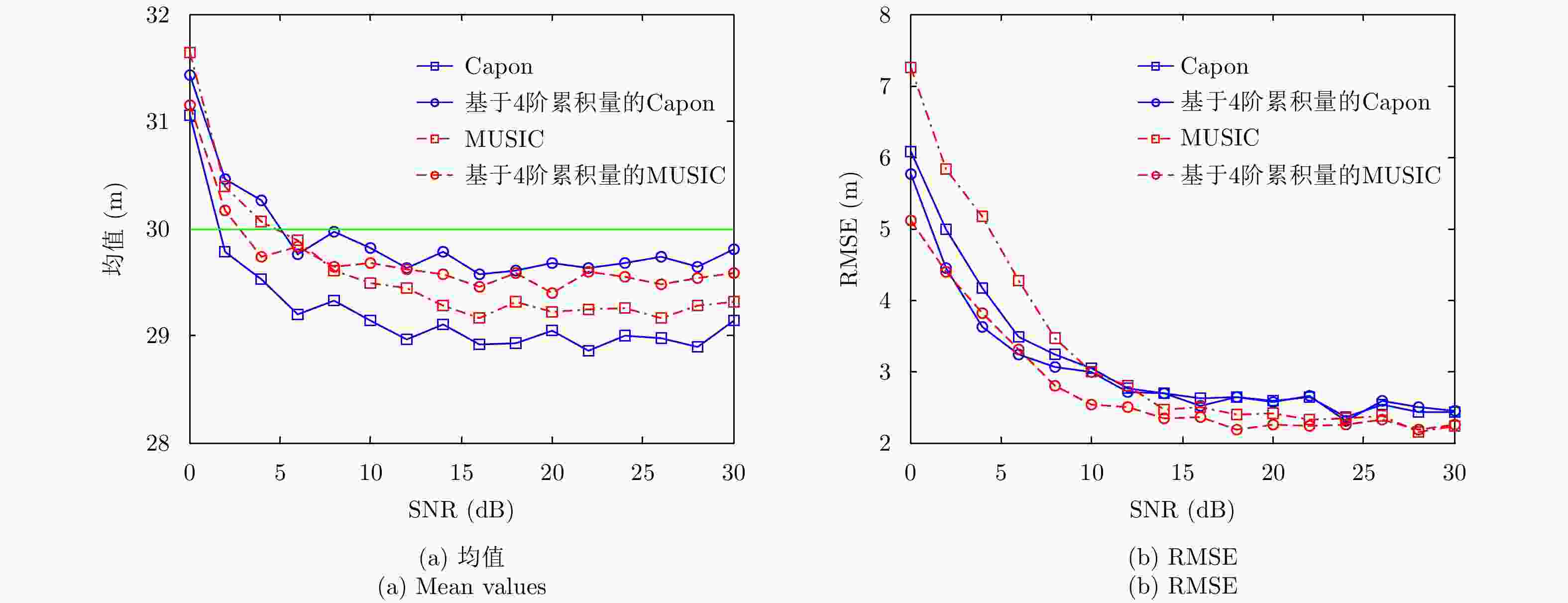
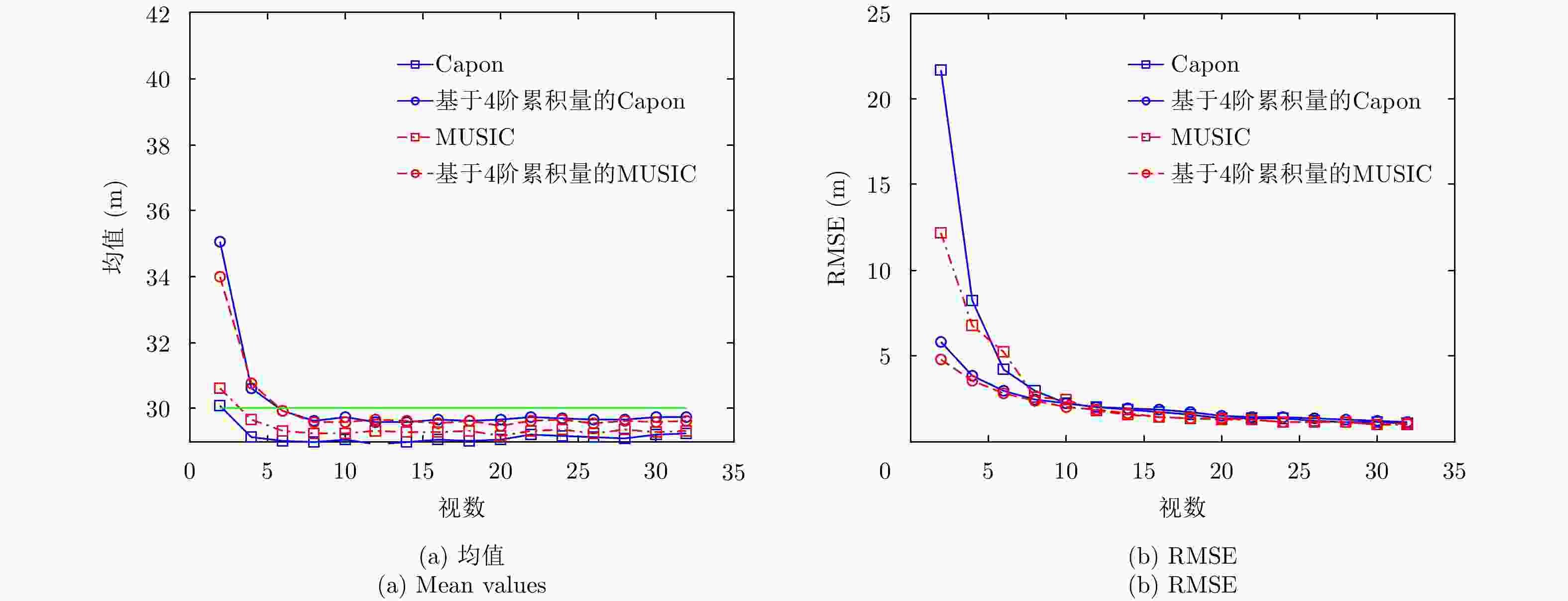
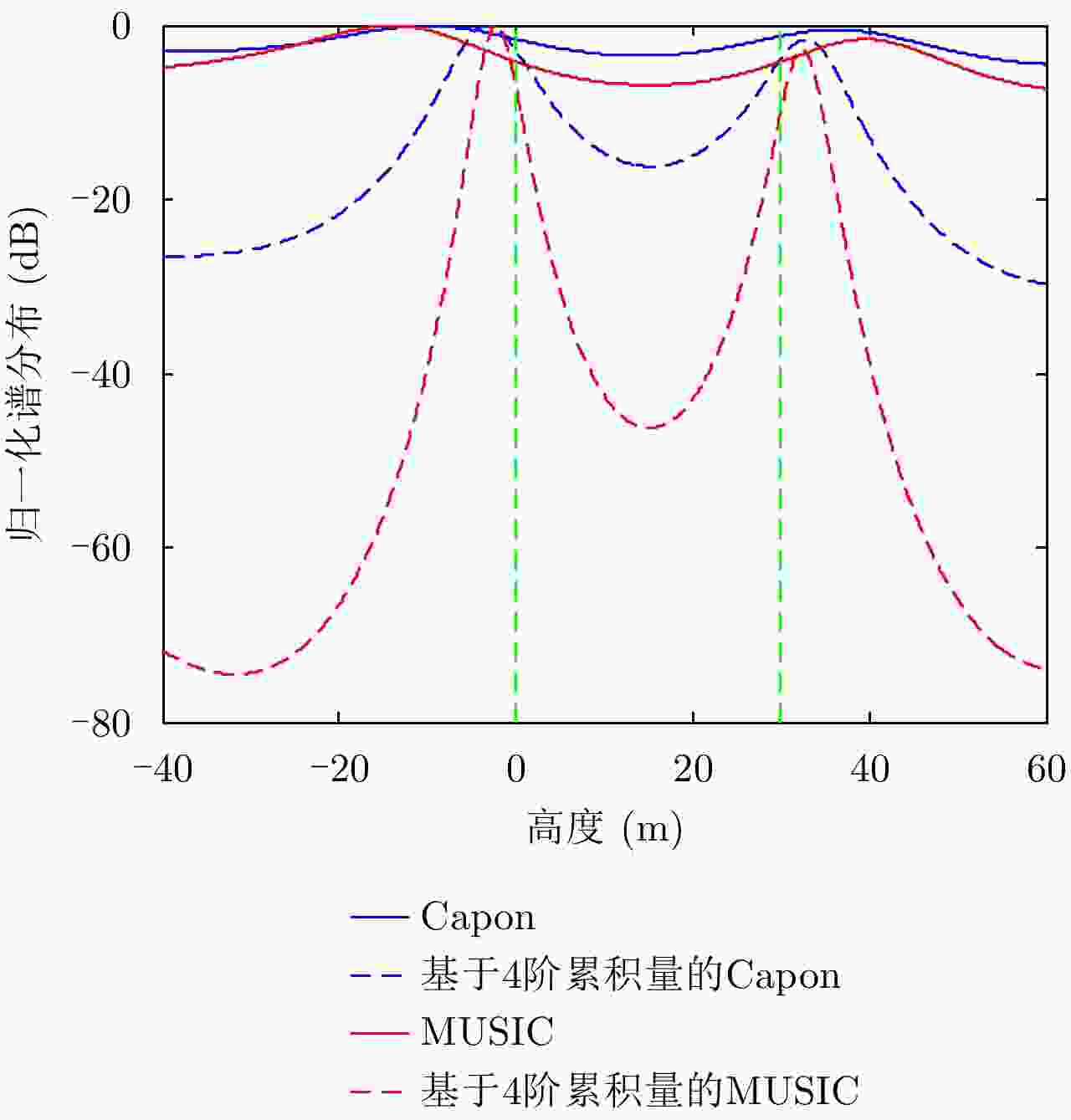
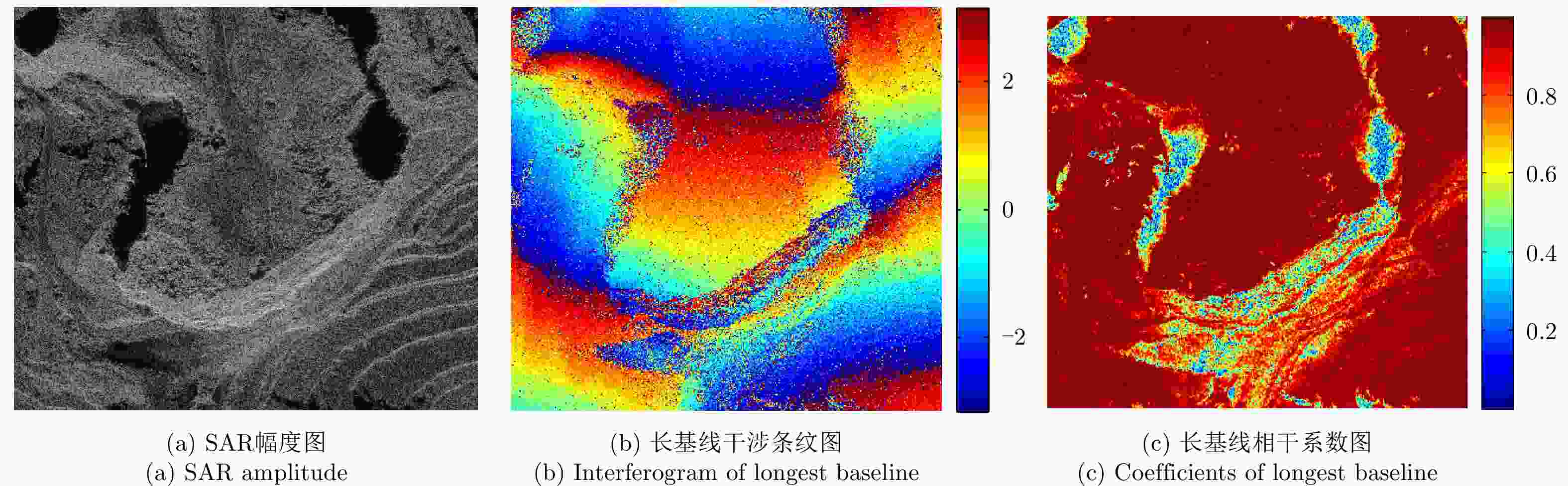
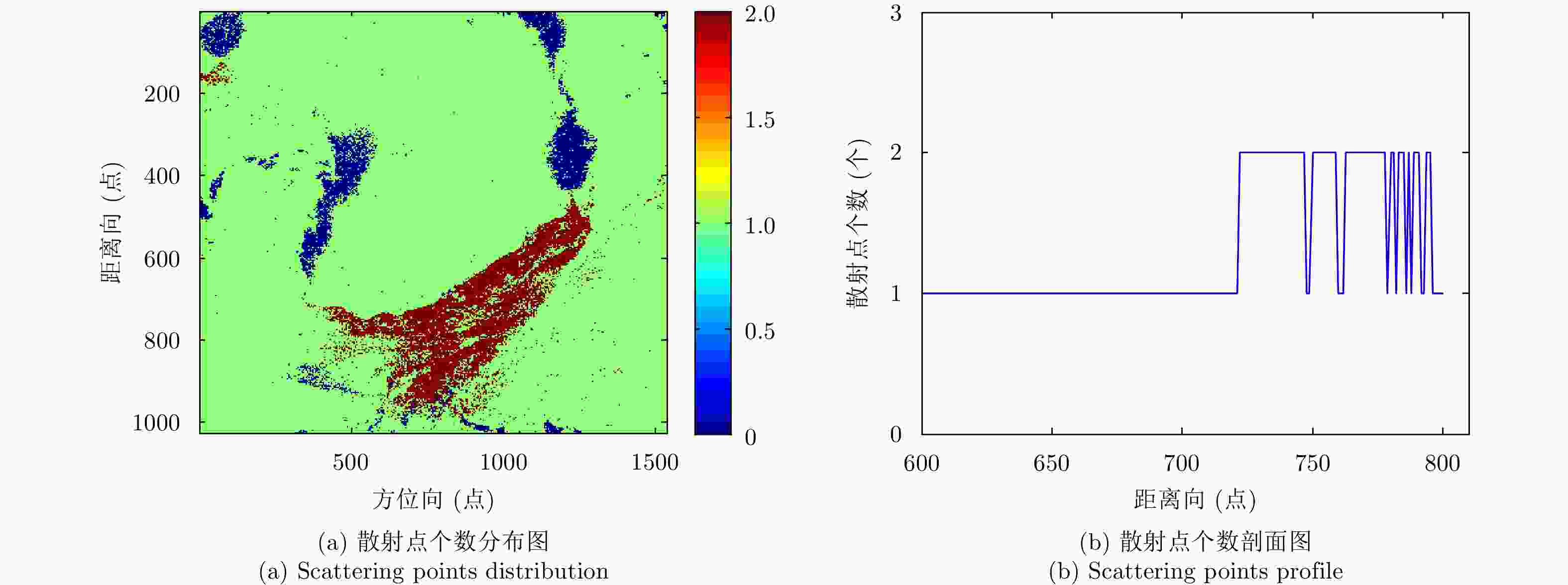
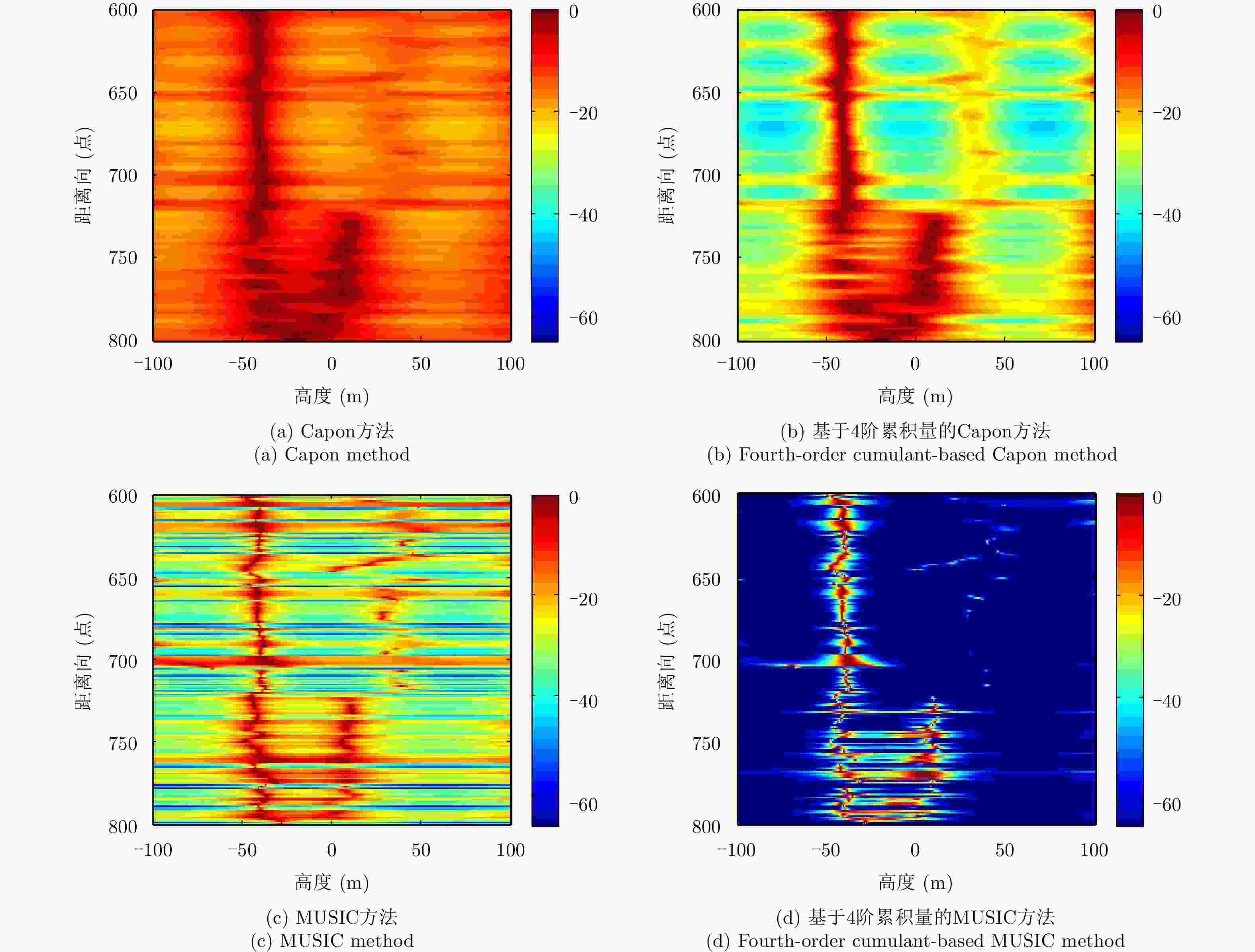
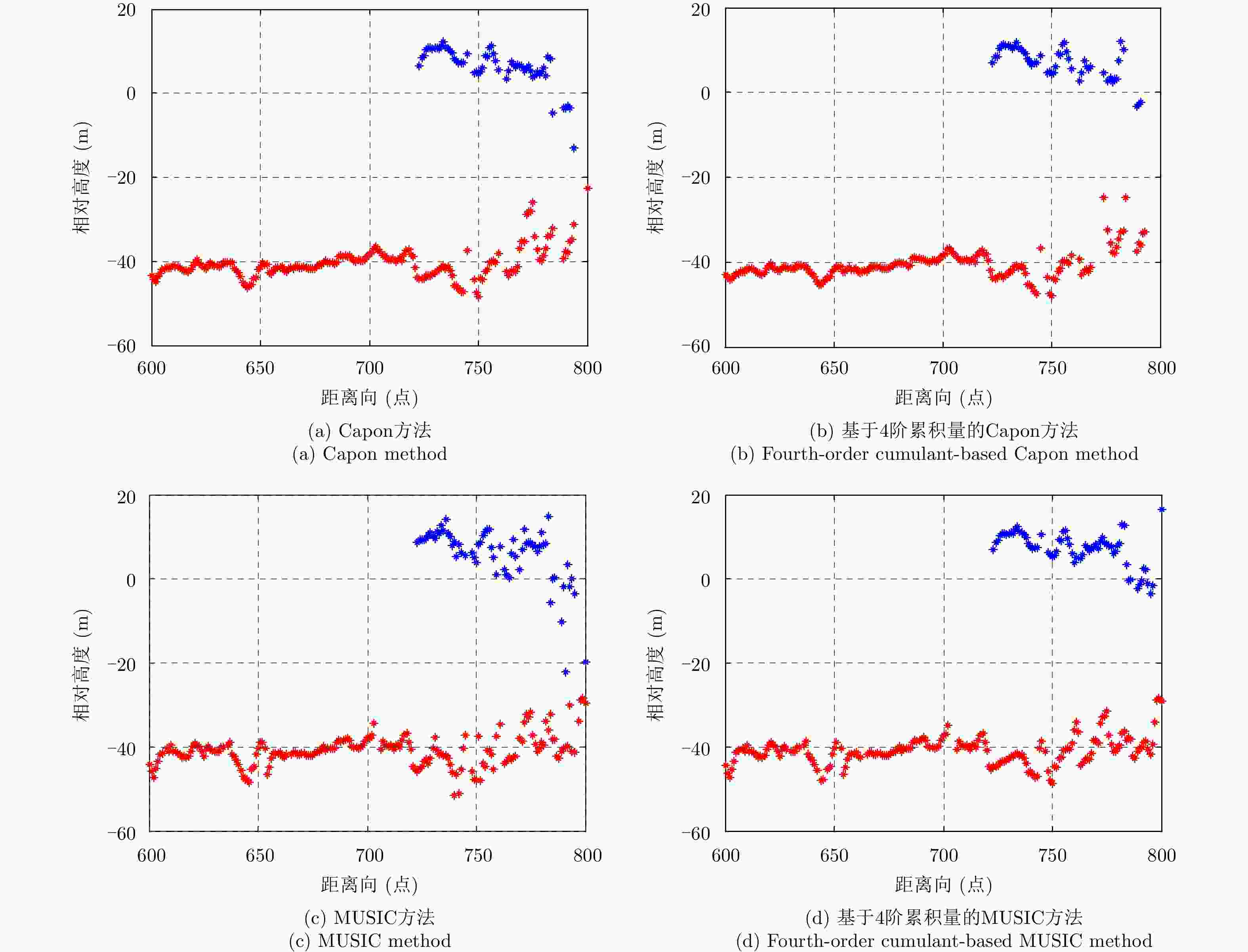
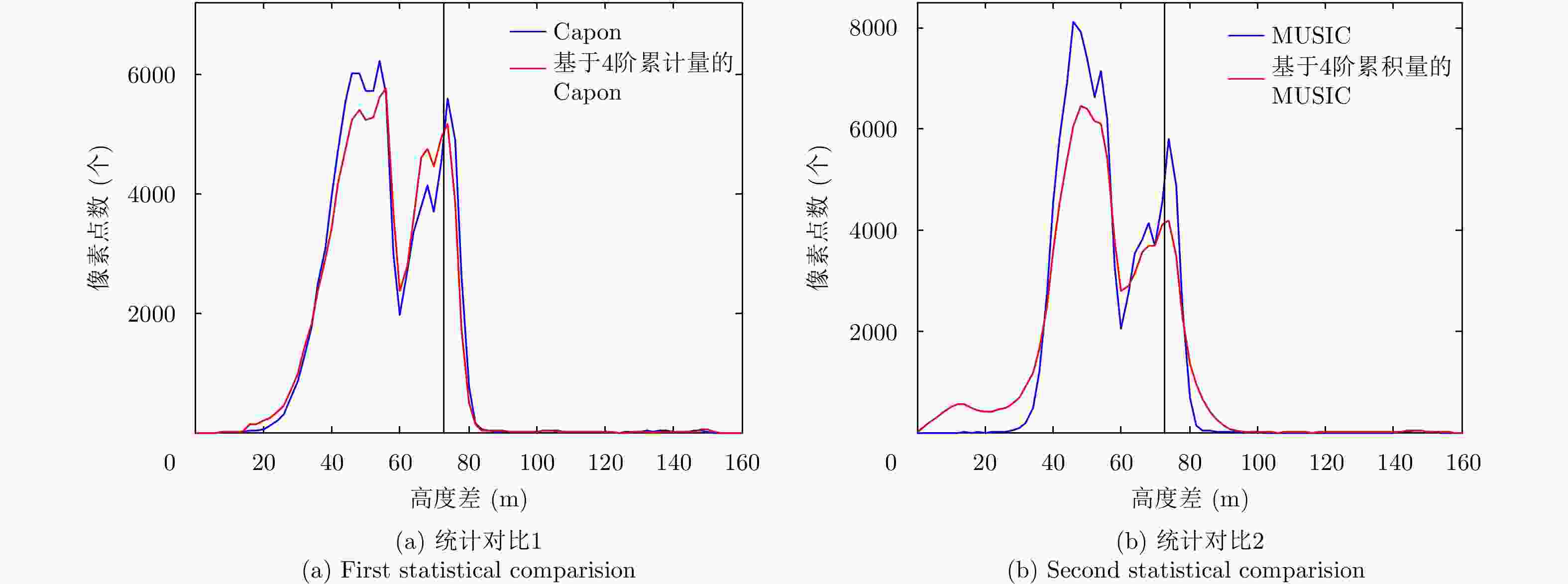
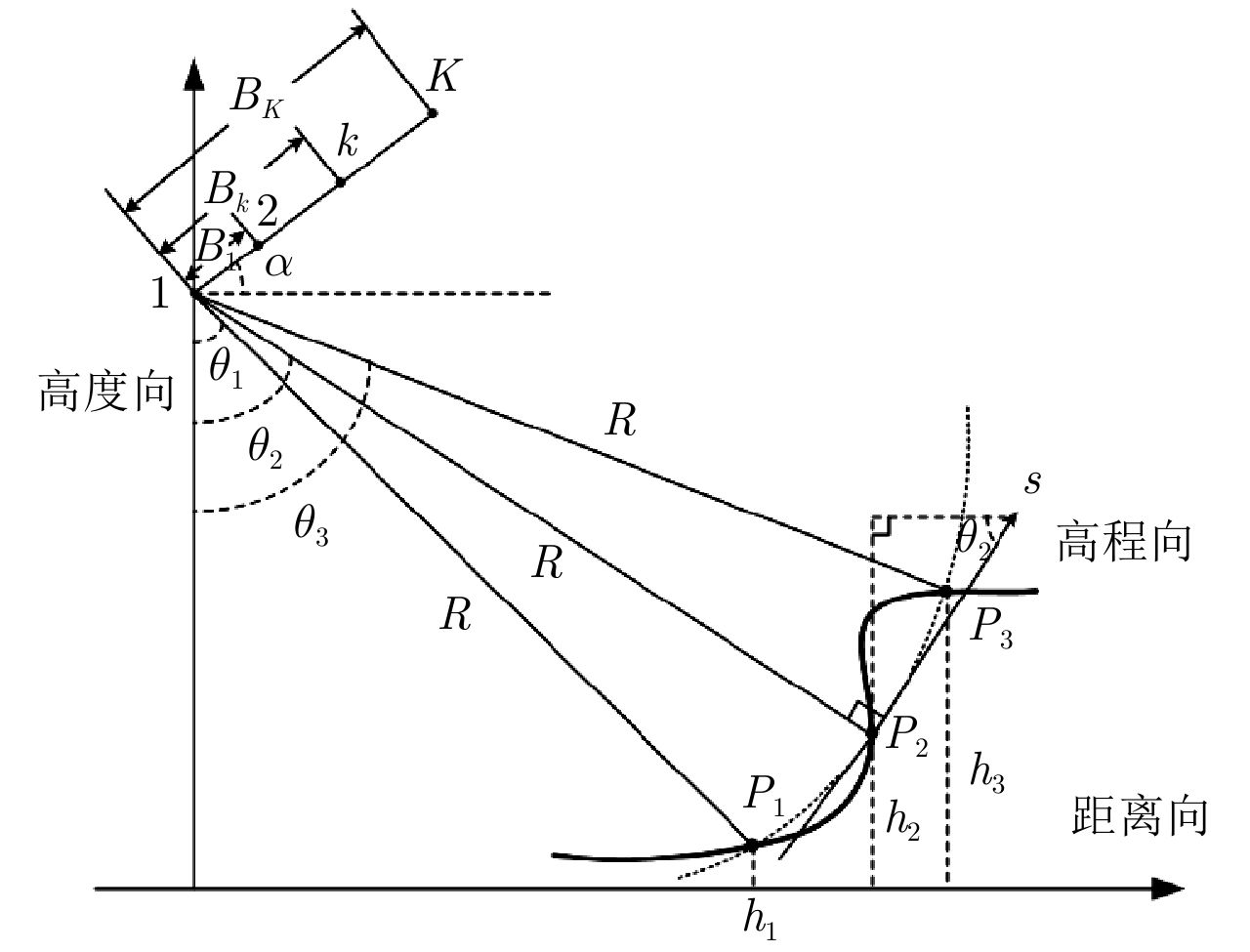
摘要: 叠掩问题是SAR成像处理的一个技术难点，在机载多基线SAR系统中，传统的谱估计解叠掩方法受到非均匀基线和基线数目少的限制，使得其在解叠掩过程中的散射点高度向测量误差大、分辨性能差。针对以上问题，该文将4阶累积量统计特性用于传统的谱估计解叠掩方法中，利用4阶累积量的盲高斯性和非均匀阵列的虚拟阵列扩展性能，结合传统的Capon, MUSIC谱估计方法，能在有效去除高斯噪声的同时，提高叠掩处各散射点的高度向测量精度及分辨率。仿真和实测数据实验证明了该文方法的有效性。Abstract: Layover is a difficult problem in SAR imaging technology. Airborne multi-baseline SAR systems are constrained by non-uniform baselines that are also few in number, which means the measured scattering point height is characterized by unacceptable error and poor resolution when using traditional spectrum estimation methods. To solve these problems, in this paper, we combine fourth-order cumulant statistical properties with traditional spectrum estimation methods. With its blind Gaussian noise characteristic, non-uniform virtual array extension of the fourth-order cumulant, and traditional Capon and MUSIC spectrum estimation approaches, the proposed method can effectively remove the Gaussian noise, while also improving the measurement accuracy and resolution of the scattering point heights. The simulation and real-data experimental results validate the effectiveness of our proposal.
-
Key words:
- Non-uniform baseline /
- Tomography /
- Fourth-order cumulant /
- Spectrum estimation /
- Layover
-
图 10 叠掩处散射点高度差统计
Figure 10. Height difference statistics of scattering points in layover
表 1 系统仿真参数
Table 1. System parameters of simulation data
传感器 MEMPHIS 载频(GHz) 35 下视角 $\theta $(°) 60 基线长度(m) 0, 0.055, 0.165, 0.275 斜距(m) 1545 SNR(dB) 20 基线倾角 $\alpha $(°) 60 
下载: 导出CSV
-
[1] Magnard C, Frioud M, Small D, et al. Analysis of a maximum likelihood phase estimation method for airborne multibaseline SAR interferometry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1072–1085. DOI: 10.1109/JSTARS.2015.2487685 [2] Schmitt M and Zhu X X. Demonstration of single-pass millimeterwave SAR tomography for forest volumes[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(2): 202–206. DOI: 10.1109/LGRS.2015.2506150 [3] 徐西桂, 庞蕾, 张学东, 等. 多基线层析SAR技术的研究现状分析[J]. 测绘通报, 2018(1): 14–21. DOI: 10.13474/j.cnki.11-2246.2018.0003Xu Xi-gui, Pang Lei, Zhang Xue-dong, et al. The research status analysis on multi-baseline tomographic SAR[J]. Bulletin of Surveying and Mapping, 2018(1): 14–21. DOI: 10.13474/j.cnki.11-2246.2018.0003 [4] Gini F, Lombardini F, and Montanari M. Layover solution in multibaseline SAR interferometry[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1344–1356. DOI: 10.1109/TAES.2002.1145755 [5] Lombardini F, Cai F, and Pasculli D. Spaceborne 3-D SAR tomography for analyzing garbled urban scenarios: Single-look superresolution advances and experiments[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 960–968. DOI: 10.1109/JSTARS.2012.2211339 [6] Fornaro G, Lombardini F, Pauciullo A, et al.. Advanced interferometric and 3-/4-/5-D tomographic processing of SAR data[C]. Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 1432–1435. [7] Zhu X X and Bamler R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. DOI: 10.1109/TGRS.2010.2050487 [8] Huang Y, Ferro-Famil A, and Reigber A. Under-foliage object imaging using SAR tomography and polarimetric spectral estimators[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(6): 2213–2225. DOI: 10.1109/TGRS.2011.2171494 [9] 张福博, 刘梅. 基于频域最小二乘APES的非均匀多基线SAR层析成像算法[J]. 电子与信息学报, 2012, 34(7): 1568–1573. DOI: 10.3724/SP.J.1146.2011.01184Zhang Fu-bo and Liu Mei. Uneven multi-baseline SAR tomography base on frequency domain least squares amplitude and phase estimation (APES)[J]. Journal of Electronics&Information Technology, 2012, 34(7): 1568–1573. DOI: 10.3724/SP.J.1146.2011.01184 [10] Schmitt M and Stilla U. Maximum-likelihood-based approach for single-pass synthetic aperture radar tomography over urban areas[J]. IET Radar,Sonar&Navigation, 2014, 8(9): 1145–1153. DOI: 10.1049/iet-rsn.2013.0378 [11] Baselice F, Budillon A, Ferraioli G, et al. Layover solution in SAR imaging: A statistical approach[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 577–581. DOI: 10.1109/LGRS.2009.2021489 [12] Budillon A, Evangelista A, and Schirinzi G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488–499. DOI: 10.1109/TGRS.2010.2054099 [13] Zhu X X and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. DOI: 10.1109/TGRS.2011.2160183 [14] Wang X, Xu F, and Jin Y Q. The iterative reweighted alternating direction method of multipliers for separating structural layovers in SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1883–1887. DOI: 10.1109/LGRS.2017.2694825 [15] 李烈辰, 李道京. 基于压缩感知的连续场景稀疏阵列SAR三维成像[J]. 电子与信息学报, 2014, 36(9): 2166–2172. DOI: 10.3724/SP.J.1146.2013.01645Li Lie-chen and Li Dao-jing. Sparse array SAR 3D imaging for continuous scene based on compressed sensing[J]. Journal of Electronics&Information Technology, 2014, 36(9): 2166–2172. DOI: 10.3724/SP.J.1146.2013.01645 [16] 王爱春, 向茂生. 基于块压缩感知的SAR层析成像方法[J]. 雷达学报, 2016, 5(1): 57–64. DOI: 10.12000/JR16006Wang Ai-chun and Xiang Mao-sheng. SAR tomography based on block compressive sensing[J]. Journal of Radars, 2016, 5(1): 57–64. DOI: 10.12000/JR16006 [17] 赵克祥, 毕辉, 张冰尘. 基于快速阈值迭代的SAR层析成像处理方法[J]. 系统工程与电子技术, 2017, 39(5): 1019–1023. DOI: 10.3969/j.issn.1001-506X.2017.05.11Zhao Ke-xiang, Bi Hui, and Zhang Bing-chen. SAR tomography method based on fast iterative shrinkage-thresholding[J]. Systems Engineering and Electronics, 2017, 39(5): 1019–1023. DOI: 10.3969/j.issn.1001-506X.2017.05.11 [18] Bu Y C, Liang X D, Wang Y, et al. A unified algorithm for channel imbalance and antenna phase center position calibration of a single-pass multi-baseline TomoSAR system[J]. Remote Sensing, 2018, 10(3): 456. DOI: 10.3390/rs10030456 [19] 张小飞, 陈华伟, 仇小锋, 等. 阵列信号处理及MATLAB实现[M]. 北京: 电子工业出版社, 2015: 22–27.Zhang Xiao-fei, Chen Hua-wei, Qiu Xiao-feng, et al.. Array Signal Processing and Matlab Implementation[M]. Beijing: Publishing House of Electronics Industry, 2015: 22–27. [20] Dogan M C and Mendel J M. Applications of cumulants to array processing. I. Aperture extension and array calibration[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1200–1216. DOI: 10.1109/78.382404 [21] Schmitt M and Stilla U. Compressive sensing based layover separation in airborne single-pass multi-baseline InSAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 313–317. DOI: 10.1109/LGRS.2012.2204230 [22] 韩树楠, 李东生, 雍爱霞, 等. 四阶累积量稀疏表示的DOA估计方法[J]. 信号处理, 2015, 31(3): 314–318. DOI: 10.3969/j.issn.1003-0530.2015.03.009Han Shu-nan, Li Dong-sheng, Yong Ai-xia, et al. DOA estimation method by sparse representation of fourth-order cumulants[J]. Journal of Signal Processing, 2015, 31(3): 314–318. DOI: 10.3969/j.issn.1003-0530.2015.03.009 [23] 陈建, 王树勋. 基于高阶累积量虚拟阵列扩展的DOA估计[J]. 电子与信息学报, 2007, 29(5): 1041–1044Chen Jian and Wang Shu-xun. DOA estimation of virtual array extension based on fourth-order cumulant[J]. Journal of Electronics&Information Technology, 2007, 29(5): 1041–1044 [24] Zhang X F, Lv W, Shi Y, et al.. A novel DOA estimation algorithm based on Eigen space[C]. Proceedings of 2007 IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 2007: 551–554. [25] Bamler R, Eineder M, Adam N, et al. Interferometric potential of high resolution spaceborne SAR[J]. Photogrammetrie-Fernerkundung-Geoinformation, 2009, 2009(5): 407–419. DOI: 10.1127/1432-8364/2009/0029 -
图(10) / 表(1)
计量
- 文章访问数: 2804
- HTML全文浏览量: 536
- PDF下载量: 166
- 被引次数: 0
