一种基于误差反向传播优化的多通道SAR相位误差估计方法

崔磊; 仇晓兰; 郭嘉逸; 温雪娇; 杨俊莹; 付琨

doi:10.12000/JR20096

一种基于误差反向传播优化的多通道SAR相位误差估计方法

DOI: 10.12000/JR20096

崔磊^1, ,,
仇晓兰^{1, 2, 3, ,},
郭嘉逸^{2, 3},
温雪娇¹,
杨俊莹^{2, 3},
付琨^{2, 3}

1.
中国科学院电子学研究所苏州研究院苏州 215123
2.
中国科学院空天信息创新研究院北京 100190
3.
微波成像技术国家级重点实验室北京 100190

基金项目: 国家自然科学基金(61991420, 61991421)

详细信息

作者简介:
崔　磊(1989–)，男，甘肃天水人，2016年在北京理工大学信息与电子学院获得硕士学位，中国科学院电子学研究所苏州研究院助理研究员。主要研究领域为SAR数据预处理。E-mail: cuilei1167@163.com

仇晓兰(1982–)，女，中国科学院空天信息创新研究院研究员，博士生导师，主要研究领域为SAR成像处理、SAR图像理解，IEEE高级会员、IEEE地球科学与遥感快报副主编、雷达学报青年编委。E-mail: xlqiu@mail.ie.ac.cn

通讯作者:
崔磊 cuilei1167@163.com

仇晓兰 xlqiu@mail.ie.ac.cn

责任主编：陈杰 Corresponding Editor: CHEN Jie
中图分类号: TN957.52
计量
- 文章访问数: 1772
- HTML全文浏览量: 530
- PDF下载量: 135
- 被引次数: 6
出版历程
- 收稿日期: 2020-07-07
- 修回日期: 2020-09-04
- 网络出版日期: 2020-10-28

Multi-channel Phase Error Estimation Method Based on an Error Backpropagation Algorithm for a Multichannel SAR

CUI Lei^{1
, ,},
QIU Xiaolan^{1, 2, 3
, ,},
GUO Jiayi^{2, 3},
WEN Xuejiao¹,
YANG Junying^{2, 3},
FU Kun^{2, 3}

1.
Institute of Electronics, Chinese Academy of Sciences, Suzhou Research Center, Suzhou 215123, China
2.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
3.
National Key Lab of Microwave Imaging Technology, Beijing 100190, China

Funds: The National Natural Science Foundation of China (61991420, 61991421)

More Information

Corresponding author: CUI lei, cuilei1167@163.com; QIU Xiaolan, xlqiu@mail.ie.ac.cn

摘要

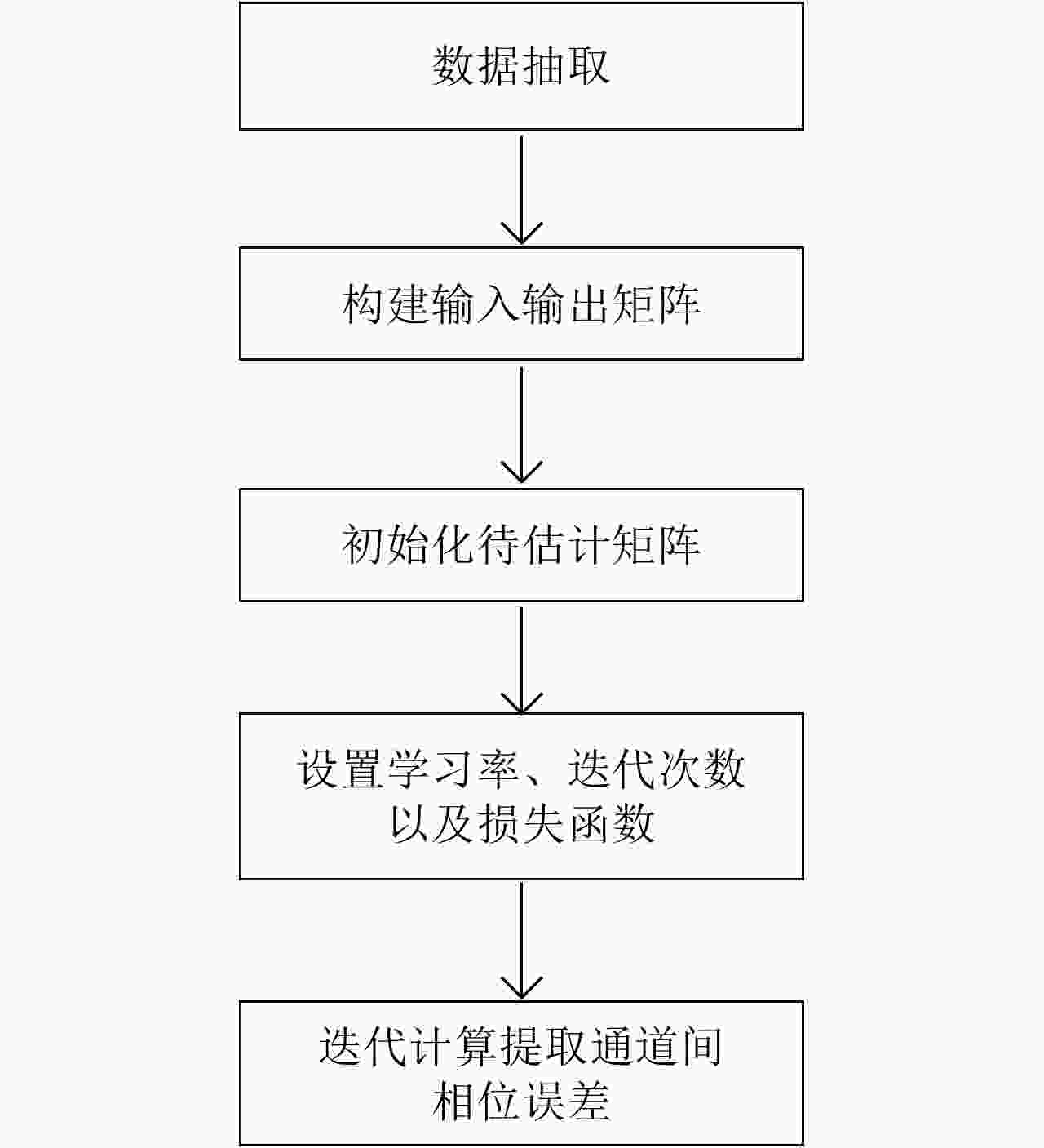
摘要: 方位向多通道合成孔径雷达(SAR)可实现高分辨率宽测绘带成像，准确估计通道间相位误差是保障成像质量的关键。该文提出了基于误差反向传播训练优化的通道相位误差估计方法，该方法根据多通道SAR回波生成的物理过程，构建含有通道间相位误差待估计参数的观测矩阵，通过初始化的通道误差和初始化的目标散射系数参数生成初始化的SAR回波，并计算该回波与多通道SAR实测回波之间的误差，通过深度学习中常用的误差反向传播的方法，不断训练优化上述参数，最终获得通道间相位误差的估计值，同时也得到了对稀疏目标散射系数的估计。该方法基于误差反向传播方法，并将该方法与通道误差的形成原理相结合，在稀疏假设下同时完成了相位估计和成像，为多通道SAR误差估计提供了一种全新的思路。多通道SAR仿真数据验证了该文算法的有效性。
- 合成孔径雷达 /
- 高分辨率宽测绘带 /
- 误差反向传播 /
- 多通道SAR /
- 相位误差估计
Abstract: An azimuth multi-channel Synthetic Aperture Radar (SAR) can be used to obtain high-resolution wide-swath SAR images. Accurate estimation of the phase error between channels is the key to ensuring image quality. In this study, we present a channel phase error estimation method based on the error backpropagation algorithm. During the physical process of a multi-channel SAR echo generation, this method constructs an observation matrix with the parameters to be estimated including the phase error between channels. The initial SAR echo is generated using the initial channel error matrix and initial target scattering coefficient matrix, and the error between the echo and measured multi-channel SAR echo is calculated. Using the backpropagation algorithm commonly used in deep learning, the abovementioned parameters are continuously trained and optimized. Finally, the estimation of the phase error between channels is obtained along with the target scattering coefficient. This method combines the error backpropagation method with the principle of multi-channel SAR channel error. Phase estimation and imaging are realized based on the sparsity assumption, which provides a new approach for estimating an error in a multi-channel SAR. The effectiveness of the presented method is validated using multi-channel SAR simulation data.
- Synthetic Aperture Radar (SAR) /
- High-resolution wide-swath /
- Error backpropagation algorithm /
- Multi-channel SAR /
- Phase error estimation

HTML全文

1. 引言

由于脉冲雷达发射的大功率信号在城市环境下容易干扰电台等其他通讯设备，可以借助通信信号来探测目标。近年来出现的多载波调制(Multi-Carrier Modulation, MCM)技术^[1]引起了人们的关注，由此发展而来的正交频分复用(Orthogonal Frequency Division Multiplex, OFDM)^[2]技术采用多路正交子载波进行信号调制，具有频率分集和波形分集的潜力，在通信、雷达一体化的发展背景下有着重要的研究价值。

相位编码OFDM信号具有多普勒高分辨力，用于雷达动目标检测时可以更精确地估计目标速度。不同的相位编码信号具有不同的自相关特性。霍夫曼编码可以降低信号自相关函数的整体旁瓣水平，但其包络峰均比(Peak-to-Mean Envelope Power Ratio, PMEPR)明显增大^[3]。研究表明，barker码序列具有较好的综合性能^[4]，本文将以13位barker码作为相位编码序列。

最近10年，国内外在OFDM信号特性与波形设计上取得了较好的研究成果^[5–7]，因此OFDM雷达的信号处理问题受到了研究者的关注。张卫等人^[8]利用Keystone变换在信号子载波域、快时间域和慢时间域进行联合解耦合处理，解决了目标的跨距离-多普勒单元走动问题，进而可估计出匀速运动下的多目标参数信息，但计算量较大；Lellouch等人^[9]利用回波与发射信号的载频相位信息得到了点目标距离及径向速度估计，但要求目标在一个距离门内运动，即不发生越距离单元走动现象。除此以外，还需进一步研究OFDM雷达回波处理中面临的一些特殊问题，如速度补偿和多普勒解模糊。

在信号处理领域，最大似然估计是一种渐进有效估计量，但是对于多测量的非线性模型而言其计算量较大，不利于实际应用。为了提高计算效率，本文借鉴文献[10]中MIMO雷达信号处理的思路，结合OFDM信号多载波正交结构的特点，对信号进行通道分离，形成多通道信号。通过相关处理得到不同子载波上的距离像；利用Keystone变换进行速度补偿并解多普勒模糊，对同一载波的相同距离单元进行脉冲多普勒处理，得到每个子载波对应的多普勒频谱；进一步在子载波域作相参积累，得到距离-多普勒2维谱。通过谱峰搜索和CLEAN技术^[11]的运用，从中提取出峰值位置对应的时延和多普勒参数。将其作为初值，结合观测数据的似然函数，利用牛顿迭代法获得更精确的参数估计，本文称之为近似最大似然估计。近似最大似然估计量可构成复合假设检验的重要环节，提升检测器的目标检测性能。论文组织结构如下：第2节给出了相位编码OFDM信号的回波模型；第3节给出了目标距离和速度参数的最大似然估计模型；为了提高目标运动参数估计的运算效率，第4节提出一种基于通道分离的近似最大似然估计算法；第5节利用仿真实验验证了算法的性能；第6节是总结。

2. 相位编码OFDM信号模型

设雷达发射相位编码OFDM信号为：

${s_{\rm T}\, }(t) = {{\rm{e}}^{{\,\rm{j2{{π}} }}{f_{\!\rm c}}t}}\sum\limits_{n = 0}^{N - 1} {u(t - n{T_{\rm r}}} ){\rm{rect}}\left( \frac{{t - n{T_{\rm r}}}}{{{T_{\rm r}}}}\right)$

(1)

其中， ${\rm{rect}}(t) = \left\{ \begin{array}{l}1,\;\; 0 \le t \le 1\\0,\;\; {\rm{else}}\end{array} \right.$ 表示窗函数， ${f\!_{\rm c}}$ 为雷达信号的工作频率，N是脉冲个数， ${T_{\rm r}}$ 是脉冲重复周期， $u(t)$ 为相位编码OFDM信号的复包络：

$u(t) = \sum\limits_{k = 0}^{K - 1} {\sum\limits_{m = 0}^{M - 1} {{a_{k,m}}} } {{\rm{e}}^{{\,\rm{j2{{π}} }}k\Delta ft}} \;{\rm{rect}}\left(\frac{{t - m{t_{\rm c}}}}{{{t_{\rm c}}}}\right)$

(2)

其中，K是载波个数，第k个子载波上的相位编码序列 ${a_{k,m}}$ 由M个码元组成， ${t_{\rm c}}$ 为码元宽度，B是信号总带宽，为了满足子载波间的正交性，子载波间隔 $\Delta f = B/K = 1/{t_{\rm c}}$ 。

对目标散射的回波进行下变频处理，可获得相应的OFDM基带信号：

${s_{\rm r}}(t) = {A_0}{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}{f\!_{\rm c}}t}}{s_{\rm T}\,}(t - \tau )$

(3)

其中， ${A_0}$ 为目标散射强度， $\tau = \displaystyle\frac{{2(R - vt)}}{c} =$ ${\tau _0} \!-\! \displaystyle\frac{{2vt}}{c}$ 是匀速运动目标对应于t 时刻的时延。 ${\tau _0}{\rm{ = }}\displaystyle\frac{{2R}}{c}$ 表示 $t = 0$ 时刻的目标距离时延， $v$ 是目标的径向速度。若满足条件 $\displaystyle\frac{{2vt}}{c} \ll {t_{\rm c}}$ ，则式(3)可以简化为：

$\begin{align} {s_{\rm r}}(t) \approx & \sum\limits_{n = 0}^{N - 1} \sum\limits_{k = 0}^{K - 1} \sum\limits_{m = 0}^{M - 1} {{A_0}{a_{k,m}}{\rm{rect}}\left(\frac{{t - n{T_{\rm r}} - {\tau _0}}}{{{T_{\rm r}}}}\right)}\\ & \cdot {\rm{rect}}\left( \frac{{t - n{T_{\rm r}} - {\tau _0} - m{t_{\rm c}}}}{{{t_{\rm c}}}}\right){{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({f_{\rm c}} + k\Delta f){\tau _0}}} \\ &\cdot {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta ft}}\,{{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f_{\rm d}} + {f_{{\rm d}k}})t}}\,{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}k\Delta fn{T_{\rm r}}}} \end{align}$

(4)

其中，子载波间的多普勒频差 ${f_{{\rm d}k}} = \displaystyle\frac{{2vk}}{c}\Delta f$ 。记全时间 $t = n{T_{\rm r}} + \tilde t$ ，其中快时间 $\tilde t \in [0,{T_{\rm r}})$ ，则式(4)表示为：

$\begin{align} {s_{\rm r}}(\tilde t,n) =& \sum\limits_{k = 0}^{K - 1} \sum\limits_{m = 0}^{M - 1} {A_0}{a_{k,m}} {\rm{rect}}\left(\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}}}}\right)\\ & \cdot{\rm{rect}}\left( \frac{{\tilde t - {\tau _0} - m{t_{\rm c}}}}{{{t_{\rm c}}}}\right){{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({f_{\rm c}} + k\Delta f){\tau _0}}}\\ & \cdot {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta f\tilde t} \;{{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f_{\rm d}} + {f_{{\rm d}k}}) (\tilde t + n{T_{\rm r}})}} \end{align}$

(5)

其中，第2个指数项表示不同子载波的回波信号具有不同的频率偏移；由第3个指数项可以看出，子载波分别与慢时间和快时间相耦合。

在加性高斯白噪声背景下，观测信号可以表示为：

$y(\tilde t,n) = {s_{\rm r}}(\tilde t,n) + w(\tilde t,n)$

(6)

其中， ${\rm{E}}\left( {w(\tilde t,n)} \right) = 0$ , ${\rm{Var}}\left( {w(\tilde t,n)} \right) = {\sigma ^2}$ 。

3. 最大似然估计

针对式(6)在快时间域采样，采样时刻为 $\tilde t = m{t_{\rm c}} + p{T_{\rm s}}$ ，其中， ${T_{\rm s}} = \displaystyle\frac{1}{{K\Delta f}}$ , $p \in [0,K - 1]$ , $m \in [0,M - 1]$ 。由于 ${f_{{\rm d}k}}\tilde t \ll 1$ ，式(5)进一步化简

$\begin{align} {s_{\rm r}}(p,m,n) =& \sum\limits_{k = 0}^{K - 1} {A_0}{a_{k,m}}{\rm{rect}}\left(\frac{{m{t_{\rm c}} + p{T_{\rm s}} - {\tau _0}}}{{{T_{\rm r}}}}\right)\\ & \cdot {\rm{rect}}\left(\frac{{p{T_{\rm s}} - {\tau _0}}}{{{t_{\rm c}}}}\right){{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({f_{\rm c}} + k\Delta f){\tau _0}}} \\ & \cdot {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f\!_{\rm d}} + k\Delta f) (m{t_{\rm c}} + p{T_{\rm s}})}} {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f\!_{\rm d}} + {f\!_{{\rm d}k}})n{T_{\rm r}}}} \end{align}$

(7)

令 $A = {A_0}{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}{f_{\rm c}}{\tau _0}}}$ ，则采样信号为：

${{Y}} = A{{S}} + {{W}}$

(8)

其中， ${{S}} = {[{{{s}}_0},·\!·\!·\!,{{{s}}_{N - 1}}]^{\rm T} }$ , ${{Y}} = {[{{{y}}_0},·\!·\!·\!,{{{y}}_{N - 1}}]^{\rm T}}$ ${{{y}}_n} = {\left[y({\tilde t_0},n),·\!·\!·\!,\,y({\tilde t_{MK - 1}},n)\right]^{\rm T}\ }$ ${{{s}}_n} = \displaystyle\sum\limits_{k = 0}^{K - 1} {a_{k,m}}$ ${{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} (}}{f_{\rm d}} + {f_{{\rm d}k}})n{T_{\rm r}}}}$ 　　 $\cdot{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}k\Delta f{\tau _0}}}\left[{{\rm{e}}^{{\rm{j}}2{\rm{{{π}} }}({f_{\rm d}} + k\Delta f){{\tilde t}_0}}}\right.,·\!·\!·\!,$ $\left.{{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f_{\rm d}} + k\Delta f){{\tilde t}_{MK - 1}}}}\right]^{\rm T}$

记待估参数向量 ${u} = {[A,v,R]^{\rm T}}$ ，噪声的协方差矩阵R=σ²I，则观测数据Y对应的似然函数为：

$p({{Y}}\left| {{u}} \right.) = \prod\limits_{n = 0}^{N - 1} {\frac{1}{{{{\rm{{{π}} }}^{MK}}}}} {\left| {{R}} \right|^{ - 1}} {{\rm{e}}^{{\rm{ - }}{{({{{y}}_n} - A{{{s}}_n})}^{\rm H}}{{{R}}^{ - 1}}({{{y}}_n} - A{{{s}}_n})}}$

(9)

式(8)是关于A的条件线性模型，其最大似然估计为：

$\hat A = \sum\limits_{n = 0}^{N - 1} {{{s}}_n^{\rm H}{{{R}}^{ - 1}}{{{y}}_n}} {\Biggr/} \sum\limits_{n = 0}^{N - 1} {{{s}}_n^{\rm H}{{{R}}^{ - 1}}{{{s}}_n}}$

(10)

将其代入式(9)，则距离和速度参数的最大似然估计为：

$\begin{align} [\hat R,\hat v] =& \mathop {\arg \min }\limits_{[R,v]} \sum\limits_{n = 0}^{N - 1} {{{\left({{{y}}_n} - \hat A{{{s}}_n}\right)}^{\rm H}}} {{{R}}^{ - 1}}\left({{{y}}_n} - \hat A{{{s}}_n}\right)\\ =& \mathop {\arg \max }\limits_{[R,v]} {{{{\left| {\sum\limits_{n = 0}^{N - 1} {{{s}}_n^{\rm H}{{{R}}^{ - 1}}{{{y}}_n}} } \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {\sum\limits_{n = 0}^{N - 1} {{{s}}_n^H{{{R}}^{ - 1}}{{{y}}_n}} } \right|}^2}} {\sum\limits_{n = 0}^{N - 1} {{{s}}_n^{\rm H}{{{R}}^{ - 1}}{{{s}}_n}} }}} \right. } {\sum\limits_{n = 0}^{N - 1} {{{s}}_n^{\rm H}{{{R}}^{ - 1}}{{{s}}_n}} }}\\ = &\! {({\sigma ^2}KN)^{ - 1}}\! \mathop {\arg \max }\limits_{[R,v]} \Biggr| \!{\sum\limits_{n = 0}^{N - 1} {\sum\limits_{p = 0}^{K - 1} {\sum\limits_{m = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1}\! {y(p,m,n)} } } } } \\ & \cdot a_{k,m}^*{{\rm{e}}^{{\,\rm{j}}2{{π}}k\Delta f{\tau _0}}} {{\rm{e}}^{{\rm{ - j}}2{{π}}({f_{\rm d}} + k\Delta f) (m{t_{\rm c}} + p{T_{\rm s}})}} \\ & \cdot {{\rm{e}}^{{\rm{ - j}}2{{π}}({f_{\rm d}} + {f_{{\rm d}k}})n{T_{\rm r}}}} \Biggr|^{2} \end{align}$

(11)

针对该模型，通过由粗到精的网格搜索可以得到参数的估计值。记速度搜索范围为 $[ - {v_{\max }},{v_{\max }}]$ ，距离搜索范围为 $[0,{R_{\max }}]$ ，则搜索次数对应为 $U = {\rm{ceil}}\left( {2{v_{\max }}/\Delta v} \right)+ 1$ 和 $V = {\rm{ceil}}\left( {{R_{\max }}/\Delta R} \right)+ 1$ 。其中， ${\rm{ceil}}(x)$ 表示不小于x 的最小整数， $\Delta v$ 和 $\Delta R$ 表示搜索步长。算法计算复杂度为 $O\left( {UVKN{{\log }_2}(KN)} \right)$ 。

令 $\displaystyle\sum\nolimits_{k = 0}^{K - 1} {|{a_{k,m}}} {|^2} = 1$ ，由文献[12]可知，待估参数的Cramer-Rao下限为：

$\begin{align} {\rm{CRLB}}(v) =& {{{c^{\,2}}{\sigma ^2}N} \mathord{\left/ {\vphantom {{{c^2}{\sigma ^2}N} {\left( {32{{({{{π} }}{f_{\rm c}}{T_{\rm r}}{A_0})}^2}} \right.}}} \right.} {\left( {32{{({{{π} }}{f_{\rm c}}{T_{\rm r}}{A_0})}^2}} \right.}}\cdot \Bigr[{N^2}(N \!-\! 1)\\ & \left.\left.(2N \!-\! 1)/6 \!-\! {N^2}{{(N \!-\! 1)}^2}/4\right] \right)\quad\quad\quad\quad\ \end{align}$

(12)

${\rm{CRLB}}(R) = 3{c^2}{\sigma ^2}\Bigr/\left( {8{{({\rm{{{π}} }}\Delta f{A_0})}^2} N\left({K^2} - 1\right)} \right)$

(13)

4. 基于通道分离的近似最大似然估计

直接利用式(11)求最大似然估计时计算量较大，在此考虑提高运算效率的参数估计方法。式(11)中相位项 ${{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}{f_{{\rm d}k}}n{T_{\rm r}}}}$ 和 ${{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta f(m{t_{\rm c}} + p{T_{\rm s}})}}$ 的子载波k分别与慢时间和快时间相耦合。针对不同的子载波，多脉冲联合处理时目标将在距离单元和多普勒单元上走动。鉴于此，文献[8]利用Keystone变换在信号子载波域、快时间域和慢时间域进行联合解耦合处理，解决了目标的跨距离多普勒单元走动问题，计算量约为 $3{K^3}N{\log _2}(KN)$ 。事实上，式(11)中的相位项 ${{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta fp{T_{\rm s}}}}$ 体现了不同子载波的回波信号具有不同的频率偏移，因此可以将多载波正交结构的OFDM雷达信号进行分离，通过多通道接收的方式增大距离分辨单元，避免目标的跨距离单元走动和3维Keystone变换。当 $\left| {{f_{\rm d}} + {f_{{\rm d}k}}} \right| < {{\Delta f}}/{2}$ 时，对式(5)进行通道分离，即用参考信号 ${{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta f\tilde t}}$ 与回波混频并经过低通滤波处理，得到各子载波通道上的信号

$\begin{align} x(\tilde t,n,k) =& \sum\limits_{m = 0}^{M - 1} {A_0}{a_{k,m}}{\rm{rect}}\left(\frac{{\tilde t - {\tau _0}}}{{{T_r}}}\right)\\ & \cdot {\rm{rect}}\left( \frac{{\tilde t - {\tau _0} - m{t_c}}}{{{t_{\rm c}}}}\right) {{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({f_{\rm c}} + k\Delta f){\tau _0}}}\\ & \cdot {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}{f_{\rm d}}\tilde t}} {{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}({f_{\rm d}} + {f_{{\rm d}k}})n{T_{\rm r}}}} \end{align}$

(14)

其中，快时间域的采样时刻 $\tilde t = m{t_{\rm c}} + p{T_{\rm s}}$ 。

用相位编码信号作为参考对式(14)作相关处理，得到第i个距离单元上的信号

$\begin{align} {z_k}(\tilde t,n,i) = & {\sum\limits_{m,l = 0}^{M - 1} {{A_0}{a_{k,m}}} a_{k,l}^*{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}} - \left| {{\tau _0} - i{t_{\rm c}}} \right|}}} \right)}\\ & \cdot {{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{\tilde t - \left| {{\tau _0} - \left( {i + l - m} \right){t_{\rm c}}} \right|}}} \right)}\\ {} & { \cdot {{\rm{e}}^{{\rm{ - j}}2{{π}} ({f_{\rm c}} + k\Delta f){\tau _0}}}{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}\tilde t}}{{\rm{e}}^{{\,\rm{j}}2{{π}} ({f_{\rm d}} + {f_{{\rm d}k}})n{T_{\rm r}}}}} \end{align}$

(15)

此时，信号的距离分辨单元 $\Delta R =c/(2\Delta f)$ 相对较大，目标不易产生跨距离单元走动。当最大多普勒频差小于多普勒分辨单元，即 $(({2v})/{c})(K - 1)\Delta f <$ ${1}/(N{T_{\rm r}})$ 时，子载波和慢时间之间的耦合可以忽略，本文称之为低速运动，否则，称之为高速运动。此时，可利用Keystone变换消除子载波k与慢时间n之间的耦合，即 $({f_{\rm d}} + {f_{{\rm d}k}})n = {f_{\rm d}}h$ ，实现多普勒维对齐。解耦合后的信号

$\begin{align} {{g_k}(\tilde t,h,i) = }&{{z_k}\left(\tilde t,\frac{{{f_{\rm c}}}}{{{f_{\rm c}} + k\Delta f}}h,i\right)}\\ \approx &{\sum\limits_{m,l = 0}^{M - 1} {{A_0}{a_{k,m}}} a_{k,l}^*{\,\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}} - \left| {{\tau _0} - i{t_{\rm c}}} \right|}}} \right)}\\ {}&{ \cdot {\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{\tilde t - \left| {{\tau _0} - \left( {i + l - m} \right){t_{\rm c}}} \right|}}} \right)}\\ {}&{ \cdot {{\rm{e}}^{{\rm{ - j}}2{{π}} ({f_{\rm c}} + k\Delta f){\tau _0}}}{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}\tilde t}}{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}h{T_{\rm r}}}}} \end{align}$

(16)

经Keystone变换后的信号在慢时间域可能出现多普勒速度模糊现象( ${f_{\rm d}} = {\tilde f_{\rm d}} + r/{T_{\rm r}}$ ，其中 $\left| {{{\tilde f}_{\rm d}}} \right| < 1/(2{T_{\rm r}})$ ，折叠因子 $r \in \{ - 8, - 7, ·\!·\!·\! ,7,8\}$ )，则式(16)改为：

$\begin{align} {{g_k}\left( {\tilde t,h,i} \right) \approx }&{\sum\limits_{m,l = 0}^{M - 1} {{A_0}{a_{k,m}}} a_{k,l}^*{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}} - \left| {{\tau _0} - i{t_{\rm c}}} \right|}}} \right)}\\ {}&{ \cdot {\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{\tilde t - \left| {{\tau _0} - \left( {i + l - m} \right){t_{\rm c}}} \right|}}} \right)}\\ {}&{ \cdot {{\rm{e}}^{{\rm{ - j}}2{{π}} ({f_{\rm c}} + k\Delta f){\tau _0}}}{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}\tilde t}}{{\rm{e}}^{{\rm{j}}2{{π}} {{\tilde f}_{\rm d}}h{T_{\rm r}}}}}\\ {}& \cdot {{\rm{e}}^{{\,\rm{j}}2{{π}} r \displaystyle\scriptsize\frac{{{f_{\rm c}}}}{{{f_{\rm c}} + k\Delta f}}h}} \end{align}$

(17)

经过折叠因子补偿后的信号

${f_k}(\tilde t,h,i) = {g_k}(\tilde t,h,i) {{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}r \displaystyle\scriptsize\frac{{{f_{\rm c}}}}{{{f_{\rm c}} + k\Delta f}}h}}$

(18)

对式(18)进行脉冲多普勒处理，即关于慢时间作相参积累，可得第k个子载波上的多普勒频谱

$\begin{align} {{F_k}(\tilde t,u,i) = }&{\sum\limits_{m,l = 0}^{M - 1} {{A_0}{a_{k,m}}} a_{k,l}^*{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}} - \left| {{\tau _0} - i{t_{\rm c}}} \right|}}} \right)}\\ &{ \cdot {\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{\tilde t - \left| {{\tau _0} - \left( {i + l - m} \right){t_{\rm c}}} \right|}}} \right)}\\ & \cdot {\frac{{{\rm{sin}}({{π}} s)}}{{{\rm{sin}}({{π}} s/N)}}{{\rm{e}}^{{\,\rm{j}}{{π}} \displaystyle\scriptsize\frac{{N - 1}}{N}s}}{{\rm{e}}^{{\rm{ - j}}2{{π}} ({f_{\rm c}} + k\Delta f){\tau _0}}}}\\ & \cdot{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}\tilde t}} \end{align}$

(19)

其中， $s = u - {\tilde f_{\rm d}}N{T_{\rm r}}$ , $u \in [0,N - 1]$ 。

进一步，关于k作相参积累可得距离-多普勒谱：

$\begin{align} {F(\tilde t,u,i) = }&{\sum\limits_{m,l = 0}^{M - 1} {{A_0}{a_{k,m}}} a_{k,l}^*{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{{T_{\rm r}} - \left| {{\tau _0} - i{t_{\rm c}}} \right|}}} \right)}\\ {}& \cdot {{\rm{rect}}\left( {\frac{{\tilde t - {\tau _0}}}{{\tilde t - \left| {{\tau _0} - \left( {i + l - m} \right){t_{\rm c}}} \right|}}} \right)}\\ &\cdot {\frac{{{\rm{sin}}({{π}} s)}}{{{\rm{sin}}({{π}} s/N)}}\frac{{{\rm{sin}}({{π}} p)}}{{{\rm{sin}}({{π}} p/K)}}}\\ &{ \cdot {{\rm{e}}^{{\,\rm{j}}{{π}} \displaystyle\scriptsize\frac{{N - 1}}{N}s}}{{\rm{e}}^{{\,\rm{j}}{{π}} \displaystyle\scriptsize\frac{{K - 1}}{K}p}}{{\rm{e}}^{{\rm{ - j}}2{{π}} {f_{\rm c}}{\tau _0}}}{{\rm{e}}^{{\,\rm{j}}2{{π}} {f_{\rm d}}\tilde t}}} \end{align}$

(20)

其中， $p = q + K\Delta f{\tau _0}$ , $q \in [0,K - 1]$ 。

上述基于通道分离和Keystone相结合的方法是对式(11)模型的简化处理。为了进一步提高算法的估计精度，将得到的参数值作为初值，根据式(11)进行牛顿迭代，得到近似最大似然估计量。算法计算量约为 $KN{\log _2}(KN) \!+\! N{\log _2}N \!+\! 2K{\log _2}K \!+\! {K^2}N$ 。

上述模型均是以单目标为例进行讨论的。在多目标情况，可以利用CFAR检测器在距离-多普勒谱域进行谱峰搜索，根据最大峰值对应的参数估计值重构相应的子信号

$b(\tilde t,n) = \sum\limits_{k = 0}^{K - 1} {{{\rm{e}}^{{\,\rm{j}}2{\rm{{{π}} }}k\Delta f{{\hat \tau }_0}}}{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({{\hat f}_{\rm d}} + k\Delta f)\tilde t}}{{\rm{e}}^{{\rm{ - j}}2{\rm{{{π}} }}({{\hat f}_{\rm d}} + {{\hat f}_{{\rm d}k}})n{T_{\rm r}}}}}$

(21)

利用CLEAN技术从原信号中减去重构的子信号，然后对剩余信号继续上述的操作，直到CFAR检测不出峰值为止。算法处理流程如图1所示。

图 1 算法处理流程图

Figure 1. Algorithm processing flow chart

下载: 全尺寸图片幻灯片

5. 仿真实验

仿真参数设置如表1所示。根据表中数据并结合前文的分析可知，目标产生速度模糊的阈值是 ${v_{\rm una}}{\rm{ = }}15\;{\rm{m/s}}$ ，出现跨距离单元走动的速度临界值是 ${v_{\rm t}} \approx {\rm{4}}{\rm{.68}}\,{\rm{m/s}}$ ，速度分辨率 $\Delta {v_{\rm r}}=0.06\,{\rm{m/s}}$ ，且满足 $({{2v{T_{\rm r}}}})/{c} \ll {t_{\rm c}}$ 。由于 $\left| {{f_{\rm d}} + {f_{{\rm d}k}}} \right| \ll {{\Delta f}}/{2}$ ，多普勒频偏导致的子载频间串扰可忽略不计。在高斯白噪声背景下，2个目标距离为 ${R_1} = 10.0\;{\rm{km}}$ , ${R_2} = 1.8\ {\rm{km}}$ , ${R_{\rm{3}}} \!\!=\!\! 17.0\;{\rm{km}}$ ，径向速度 ${v_1} \!\!=\!\! 20\;{\rm{m/s}}$ , ${v_2} \!=\! {\rm{24}}\;{\rm{m/s}}$ , ${v_{\rm{3}}} \!=$ 34 m/s，对应的目标散射强度分别为 ${A_{01}} = 5$ , ${A_{02}} = 2$ , ${A_{0{\rm{3}}}} = {\rm{1}}$ 。虚警率 ${P_{\rm fa}} \!=\! {10^{ - 3}}$ ，蒙特卡洛仿真100次。

表 1 仿真参数

Table 1. Simulation parameters

参数	数值
工作频率 ${f_{\rm c}}$ (GHz)	5
带宽B (MHz)	64
脉冲重复周期 ${T_{\rm r}}$ (ms)	2
脉冲数N	250
载波数K	64

下载: 导出CSV

| 显示表格

信号经过通道分离和相关处理后，在子载波-多普勒平面的投影如图2所示。由图2可以看出，目标的多普勒频移随子载波的变化而变化，因此不能直接进行子载波域的相参积累。

图 2 原始子载波-多普勒平面投影

Figure 2. The contour of the original subcarrier-Doppler plane

下载: 全尺寸图片幻灯片

经过Keystone变换和CLEAN处理后，相应子载波-多普勒平面的投影如图3所示。可见，多普勒频移与子载波之间的耦合得到校正。

图 3 校正后的子载波-多普勒平面投影

Figure 3. The contour of the corrected subcarrier-Doppler plane

下载: 全尺寸图片幻灯片

对Keystone变换的数据在子载波域进行相参积累，获得信号的距离-多普勒2维谱如图4所示。其中图4(a)是聚焦于第1个目标的结果，图4(b)是剔除前两个目标后聚焦于第3个目标的结果。结果表明，本文所述的补偿方法能在快时间域、慢时间域以及子载波域将目标的回波能量积累起来，有利于目标检测和后续的参数估计。

图 4 回波信号的距离-多普勒2维谱

Figure 4. Echo signal range-Doppler two-dimensional spectrum

下载: 全尺寸图片幻灯片

下面考察近似最大似然估计量的性能。当 $v = 20\;{\rm{m/s}}$ , ${\rm{SN}}{{\rm{R}}_i}$ 在0～20 dB之间变化时，分别利用文献[8]所述的联合Keystone变换法、通道分离与Keystone变换组合法以及本文所提的近似最大似然估计法进行速度估计，估计量的均方根误差(RMSE)曲线如图5(a)所示。图5(b)给出了各种算法对应的计算量随脉冲数的变化情况。

图 5 各算法的参数估计精度及计算量

Figure 5. Parameter estimation accuracy and calculation amount of each algorithm

下载: 全尺寸图片幻灯片

由图5(a)可知，文献[8](点划线)与基于通道分离和Keystone相结合的方法(实线)的速度估计的RMSE曲线变化趋势类似。在相同的估计精度下，与上述两种方法相比，本文基于通道分离的近似最大似然估计法(点线)的输入信噪比 ${\rm{SN}}{{\rm{R}}_i}$ 改善约4 dB。同时，本文算法得到的RMSE非常接近Cramer-Rao下限。由图5(b)可知，在相同脉冲数下，本文算法的计算量较文献[8]的算法大幅降低。由于使用了牛顿迭代法，与基于通道分离和Keystone相结合的方法相比，计算量有所增加，但仍然远小于文献[8]中算法的计算量。因此，本文提出的基于通道分离的近似最大似然估计算法在估计精度和计算复杂度上具有综合优势。

6. 总结

本文将OFDM通信信号应用在雷达动目标探测中，在通信、雷达一体化的发展背景下有着重要的应用前景。本文参考多载频MIMO雷达通道分离得到目标高分辨距离信息的方法，将OFDM信号的多载波正交结构与脉冲多普勒处理相结合，并借助Keystone变换解决了多普勒偏移问题。为了得到更好的估计精度，利用牛顿迭代法对似然函数进行优化，得到了基于通道分离的近似最大似然估计方法。仿真结果验证了算法的综合性能。今后还可针对机动目标相干化处理以及参数估计问题展开研究，扩展OFDM雷达的应用范围。

图 1 方位多通道SAR系统对地观测成像构型示意图

Figure 1. Ground observation imaging configuration of azimuth multi-channel SAR system

下载: 全尺寸图片幻灯片

图 2 基于反向传播优化的多通道SAR相位误差估计算法流程图

Figure 2. Flow chart of channel phase error estimation method based on backpropagation algorithm for multichannel SAR

下载: 全尺寸图片幻灯片

图 3 场景目标示意图

Figure 3. Scene target diagram

下载: 全尺寸图片幻灯片

图 4 回波抽取示意图

Figure 4. Schematic diagram of echo data extraction

下载: 全尺寸图片幻灯片

图 5 无噪声估计结果

Figure 5. Noiseless estimation results

下载: 全尺寸图片幻灯片

图 6 估计结果(SNR=0 dB)

Figure 6. Estimation results (SNR=0 dB)

下载: 全尺寸图片幻灯片

图 7 估计结果(SNR=–5 dB)

Figure 7. Estimation results (SNR=–5 dB)

下载: 全尺寸图片幻灯片

表 1 仿真实验系统参数

Table 1. Parameters of simulation experiment system

参数	取值
通道数	4
雷达载频(GHz)	5.35
信号带宽(MHz)	210.00
脉冲重复频率(Hz)	335.10
方位向波束宽度(°)	5.14
雷达高度(m)	4950.00
雷达距场景中心的距离(m)	7000.00
雷达方位向等效速度(m/s)	123.00
场景方位向宽度(m)	20.00
场景地距向宽度(m)	20.00
距离采样个数	4096
方位回波个数	3166

下载: 导出CSV

表 2 通道间相位误差估计结果(°)

Table 2. Estimation results of channel phase error (°)

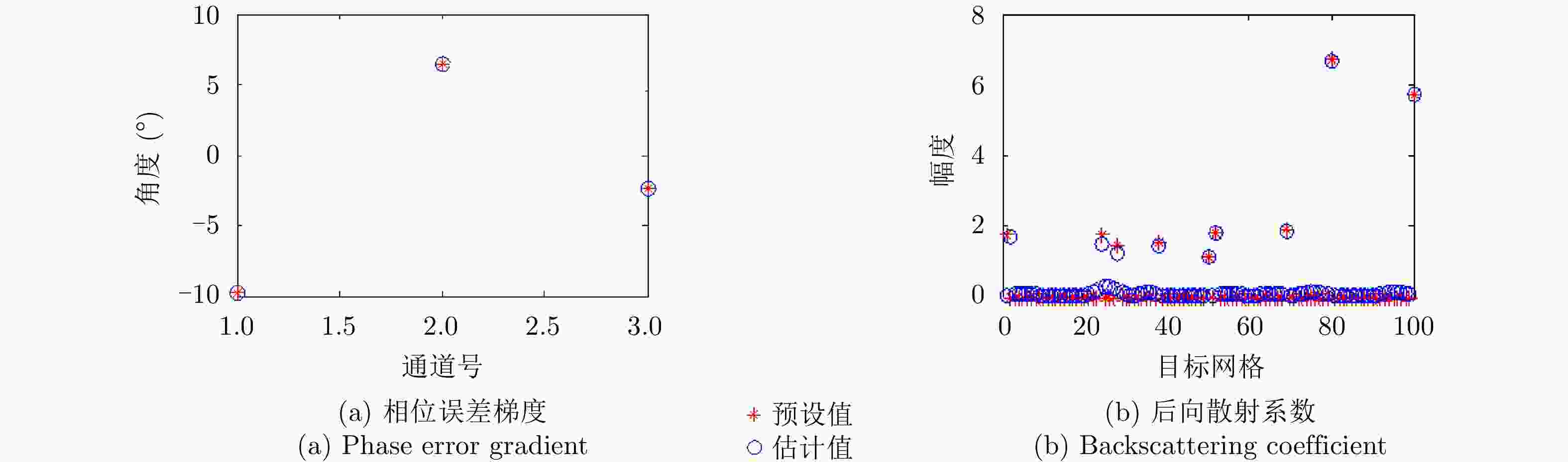
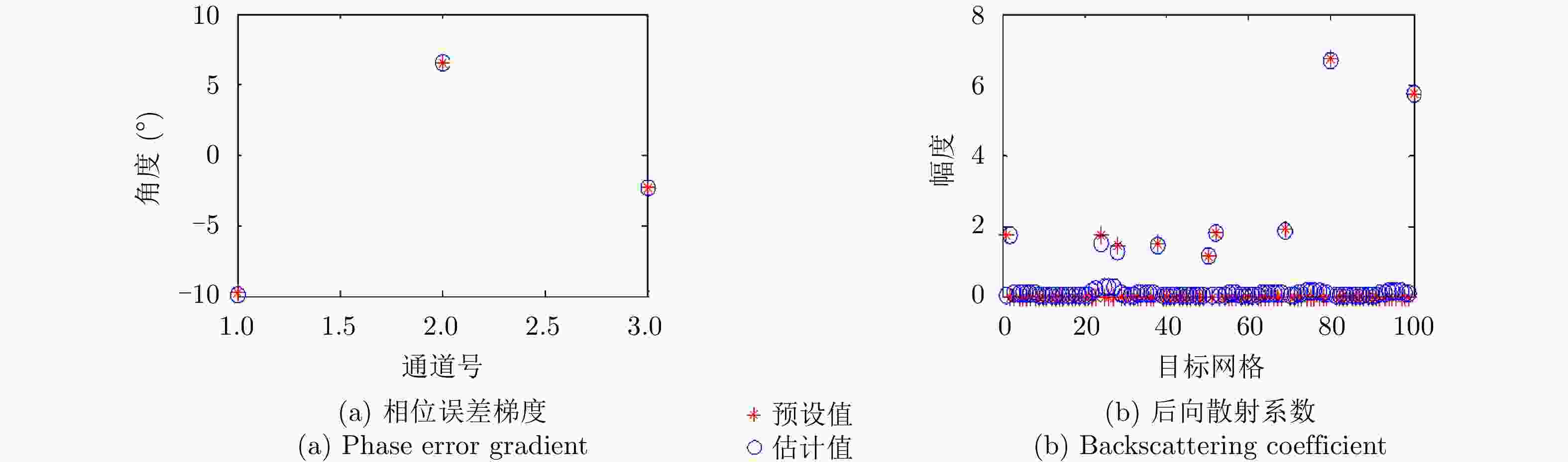
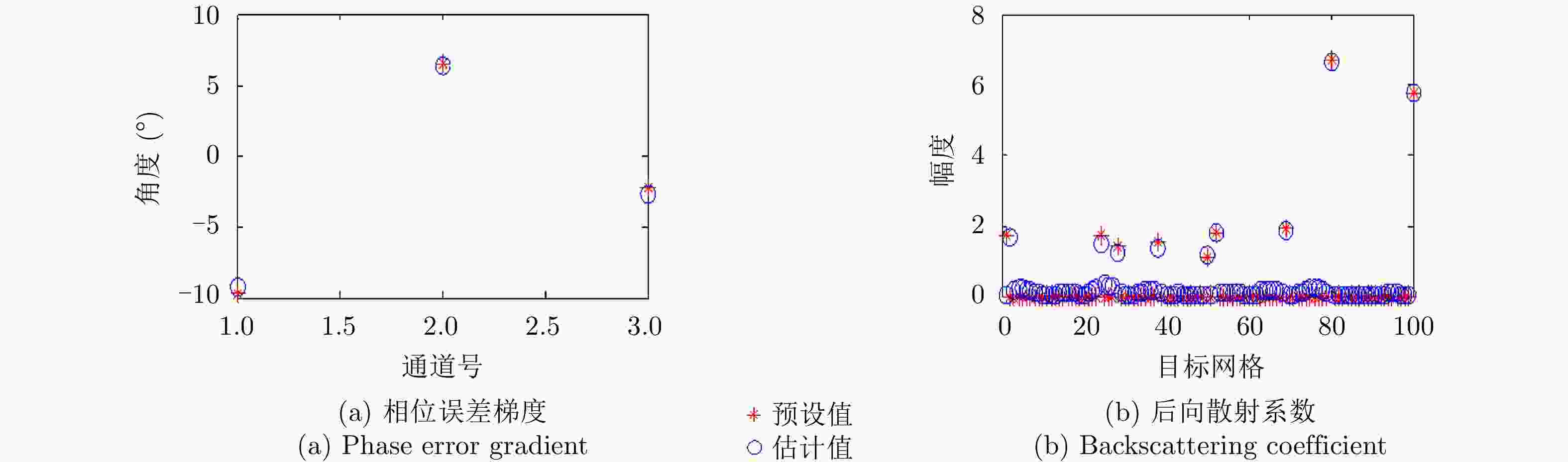
相位误差	通道1/2相位误差	通道2/3相位误差	通道3/4相位误差
实际相位偏差	–9.82	6.44	–2.34
无噪估计	–9.81	6.44	–2.34
SNR=0 dB估计	–9.87	6.46	–2.33
SNR=–5 dB估计	–9.35	6.30	–2.76

下载: 导出CSV

参考文献(19)

[1]	FREEMAN A, JOHNSON W T K, HUNEYCUTT B, et al. The “Myth” of the minimum SAR antenna area constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 320–324. doi: 10.1109/36.823926
[2]	MOREIRA J, SCHWABISCH M, FORNARO G, et al. X-SAR interferometry: First results[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 950–956. doi: 10.1109/36.406681
[3]	JIN Tingting, QIU Xiaolan, HU Donghui, et al. Unambiguous imaging of static scenes and moving targets with the first Chinese Dual-Channel spaceborne SAR sensor[J]. Sensors, 2017, 17(8): 1709. doi: 10.3390/s17081709
[4]	刘艳阳, 李真芳, 杨桃丽, 等. 一种单星方位多通道高分辨率宽测绘带SAR系统通道相位偏差时域估计新方法[J]. 电子与信息学报, 2012, 34(12): 2913–2919. doi: 10.3724/SP.J.1146.2012.00562 LIU Yanyang, LI Zhenfang, YANG Taoli, et al. A novel channel phase bias estimation method for spaceborne along-track multi-channel HRWS SAR in time-domain[J]. Journal of Electronics &Information Technology, 2012, 34(12): 2913–2919. doi: 10.3724/SP.J.1146.2012.00562
[5]	LI Zhenfang, BAO Zheng, WANG Hongyang, et al. Performance improvement for constellation SAR using signal processing techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 436–452. doi: 10.1109/TAES.2006.1642562
[6]	张磊, 全英汇, 邢孟道, 等. 一种子空间投影的高分辨宽测绘带SAR成像通道均衡方法[J]. 电子与信息学报, 2010, 32(1): 1–6. doi: doi:10.3724/SP.J.1146.2008.01821 ZHANG Lei, QUN Yinghui, XING Mengdao, et al. An SSP based channel calibration for high-resolution and wide-swath sar imagery[J]. Journal of Electronics &Information Technology, 2010, 32(1): 1–6. doi: doi:10.3724/SP.J.1146.2008.01821
[7]	杨桃丽, 李真, 刘艳阳, 等. 两种星载高分辨宽测绘带SAR系统通道相位误差估计方法[J]. 电子学报, 2013, 41(5): 931–935. doi: 10.3969/j.issn.0372-2112.2013.05.016 YANG Taoli, LI Zhen, LIU Yanyang, et al. Two channel phase error estimation methods for spaceborne HRWS SAR system[J]. Acta Electronica Sinica, 2013, 41(5): 931–935. doi: 10.3969/j.issn.0372-2112.2013.05.016
[8]	LIU Yanyang, LI Zhenfang, YANG Taoli, et al. An adaptively weighted least square estimation method of channel mismatches in phase for multichannel SAR systems in azimuth[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 439–443. doi: 10.1109/LGRS.2013.2264771
[9]	JIN Tingting, QIU Xiaolan, and HU Donghui. Estimation accuracy and Cramér–Rao Lower bounds for errors in multichannel HRWS SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1772–1776. doi: 10.1109/LGRS.2016.2608386
[10]	ZHANG L, XING M D, QIU C W, et al. Adaptive two-step calibration for high resolution and wide-swath SAR imaging[J]. IET Radar, Sonar & Navigation, 2010, 4(4): 548–559.
[11]	GEBERT N and KRIEGER G. Azimuth phase center adaptation on transmit for high-resolution wide-swath SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 782–786. doi: 10.1109/LGRS.2009.2025245
[12]	王志斌, 刘艳阳, 李真芳, 等. 基于多普勒谱优化的HRWS SAR系统通道相位偏差估计算法[J]. 电子与信息学报, 2016, 38(12): 3026–3033. doi: 10.11999/JEIT161038 WANG Zhibin, LIU Yanyang, LI Zhenfang, et al. Phase bias estimation algorithm for HRWS SAR system in azimuth based on Doppler spectrum optimization[J]. Journal of Electronics &Information Technology, 2016, 38(12): 3026–3033. doi: 10.11999/JEIT161038
[13]	束宇翔. 分布式卫星多相位中心SAR-GMTI技术研究[D]. [博士论文], 西安电子科技大学, 2014. SHU Yuxiang. Research on techniques of SAR-GMTI for distributed satellite SAR systems with multiple phase centers[D]. [Ph. D. dissertation], Xidian University, 2014.
[14]	JANOTH J, JOCHUM M, PETRAT L, et al. High resolution wide swath–the next generation X-band mission[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 3535–3537.
[15]	HAWKES M, NEHORAI A, STOICA P. Performance breakdown of subspace-based methods: Prediction and cure[C]. 2001 IEEE International Conference on Acoustics, Speech, and Signal. Salt Lake City, USA, 2001.
[16]	SHANG Mingyang, QIU Xiaolan, HAN Bing, et al. Channel imbalances and along-track baseline estimation for the GF-3 azimuth multichannel mode[J]. Remote Sensing, 2019, 11(11): 1297. doi: 10.3390/rs11111297
[17]	ZHANG Linjian, GAO Yesheng, and LIU Xingzhao. Robust channel phase error calibration algorithm for multichannel high-resolution and wide-swath SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 649–653. doi: 10.1109/LGRS.2017.2668390
[18]	YANG Taoli, LI Zhenfang, LIU Yanyang, et al. Channel error estimation methods for multi-channel HRWS SAR systems[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 2013.
[19]	DE ALMEIDA F Q, YOUNIS M, KRIEGER G, et al. An analytical error model for Spaceborne SAR multichannel azimuth reconstruction[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(6): 853–857. doi: 10.1109/LGRS.2018.2811786

施引文献

期刊类型引用(3)

1.	付琨，仇晓兰，韩冰，孙显. 多体制遥感卫星成像数据高精度处理新方法. 遥感学报. 2023(07): 1511-1522 . 百度学术
2.	付琨，孙显，仇晓兰，刁文辉，闫志远，黄丽佳，于泓峰. 遥感大数据条件下多星一体化处理与分析. 遥感学报. 2021(03): 691-707 . 百度学术
3.	仇晓兰，焦泽坤，彭凌霄，陈健堃，郭嘉逸，周良将，陈龙永，丁赤飚，徐丰，董秋雷，吕守业. SARMV3D-1.0:SAR微波视觉三维成像数据集. 雷达学报. 2021(04): 485-498 . 本站查看

其他类型引用(3)

资源附件(0)

访问统计

图(7) / 表(2)

计量

文章访问数: 1772
HTML全文浏览量: 530
PDF下载量: 135
被引次数: 6

1. 引言
2. 相位编码OFDM信号模型
3. 最大似然估计
4. 基于通道分离的近似最大似然估计
5. 仿真实验
6. 总结

一种基于误差反向传播优化的多通道SAR相位误差估计方法

DOI: 10.12000/JR20096

通讯作者:
崔磊 cuilei1167@163.com

仇晓兰 xlqiu@mail.ie.ac.cn

计量

Multi-channel Phase Error Estimation Method Based on an Error Backpropagation Algorithm for a Multichannel SAR

Corresponding author: CUI lei, cuilei1167@163.com; QIU Xiaolan, xlqiu@mail.ie.ac.cn

1. 引言

2. 相位编码OFDM信号模型

3. 最大似然估计

4. 基于通道分离的近似最大似然估计

5. 仿真实验

6. 总结

期刊类型引用(3)

其他类型引用(3)

计量

目录

1. 引言

2. 相位编码OFDM信号模型

3. 最大似然估计

4. 基于通道分离的近似最大似然估计

5. 仿真实验

6. 总结

期刊介绍

联系我们

一种基于误差反向传播优化的多通道SAR相位误差估计方法

DOI: 10.12000/JR20096

通讯作者: 崔磊 cuilei1167@163.com 仇晓兰 xlqiu@mail.ie.ac.cn

计量

出版历程

Multi-channel Phase Error Estimation Method Based on an Error Backpropagation Algorithm for a Multichannel SAR

Corresponding author: CUI lei, cuilei1167@163.com; QIU Xiaolan, xlqiu@mail.ie.ac.cn

1. 引言

2. 相位编码OFDM信号模型

3. 最大似然估计

4. 基于通道分离的近似最大似然估计

5. 仿真实验

6. 总结

期刊类型引用(3)

其他类型引用(3)

计量

出版历程

目录

1. 引言

2. 相位编码OFDM信号模型

3. 最大似然估计

4. 基于通道分离的近似最大似然估计

5. 仿真实验

6. 总结

期刊介绍

联系我们

通讯作者:
崔磊 cuilei1167@163.com

仇晓兰 xlqiu@mail.ie.ac.cn