1.   引言

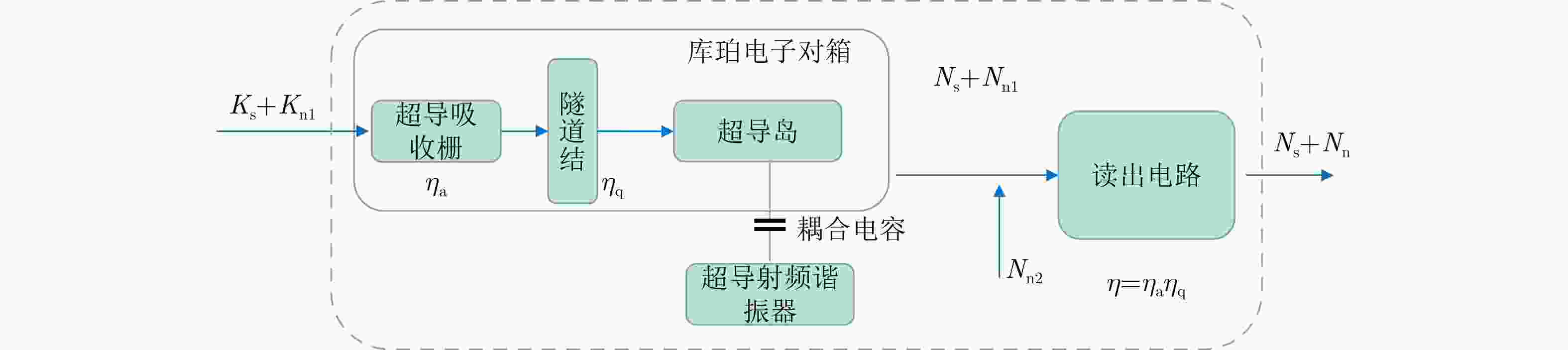
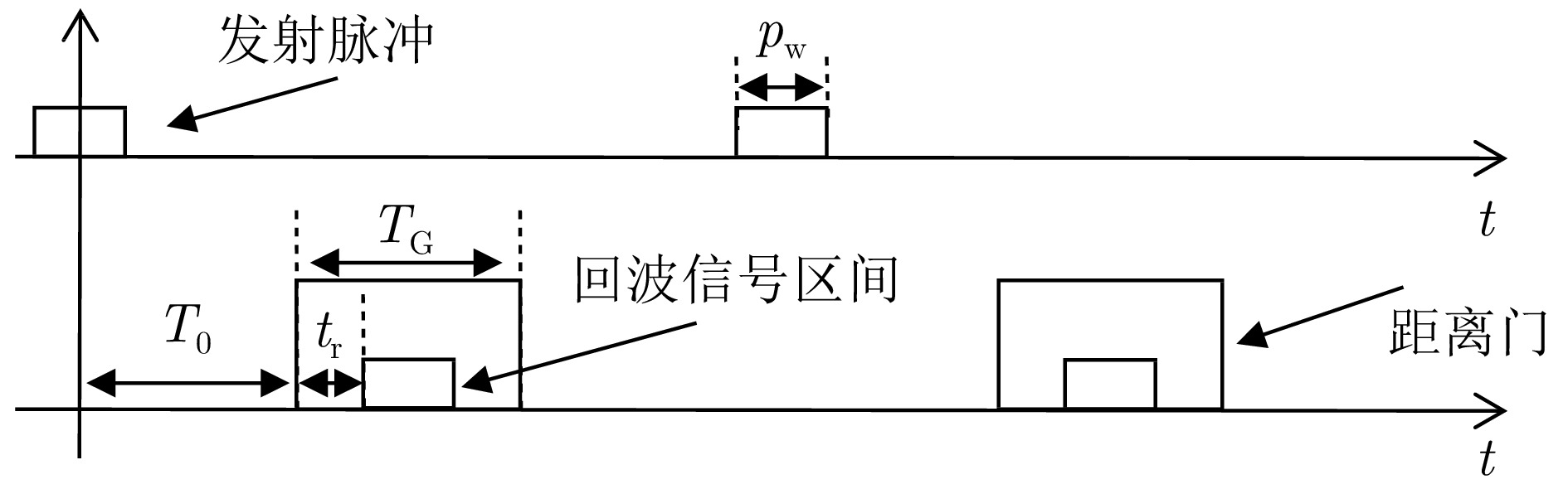
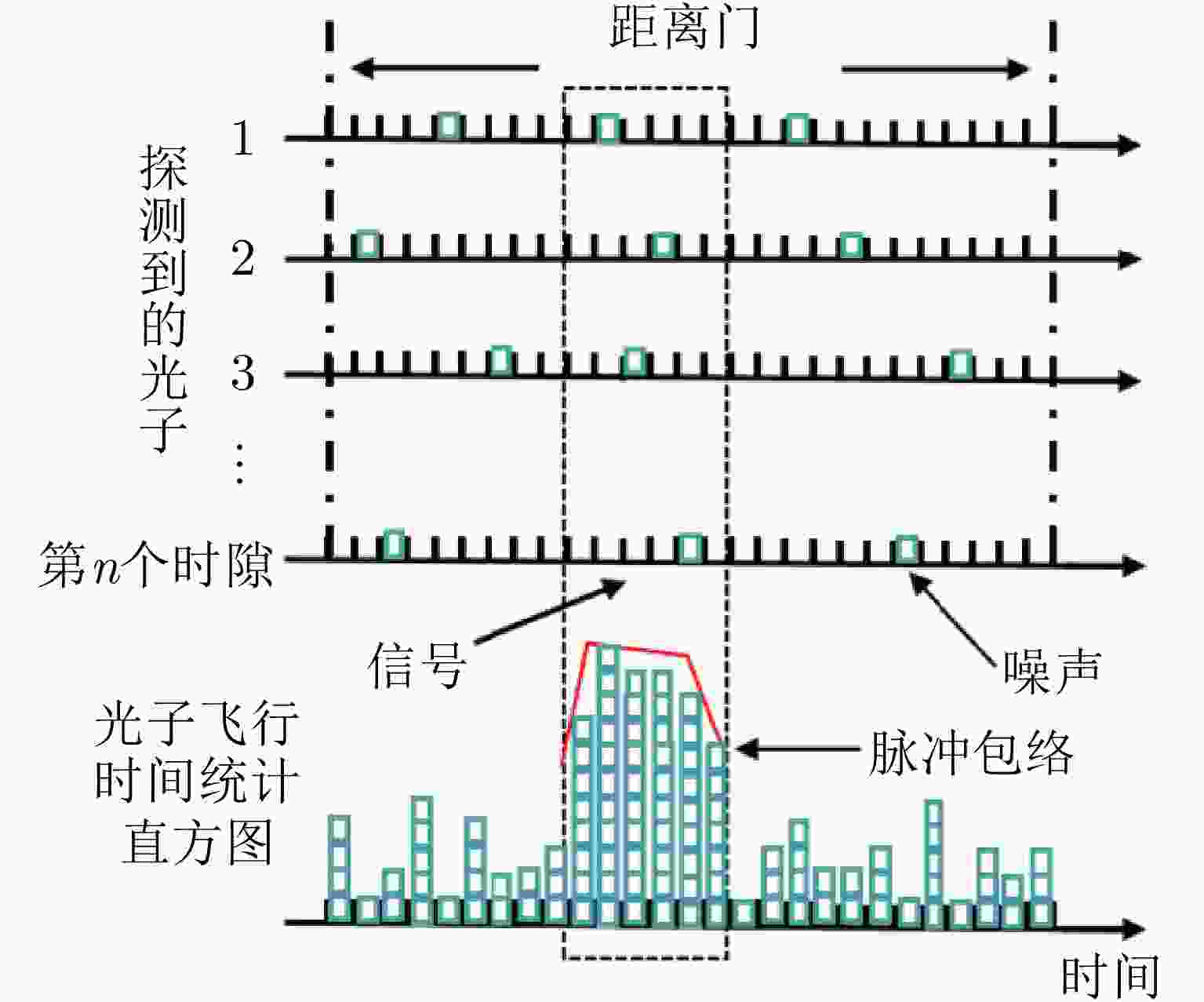
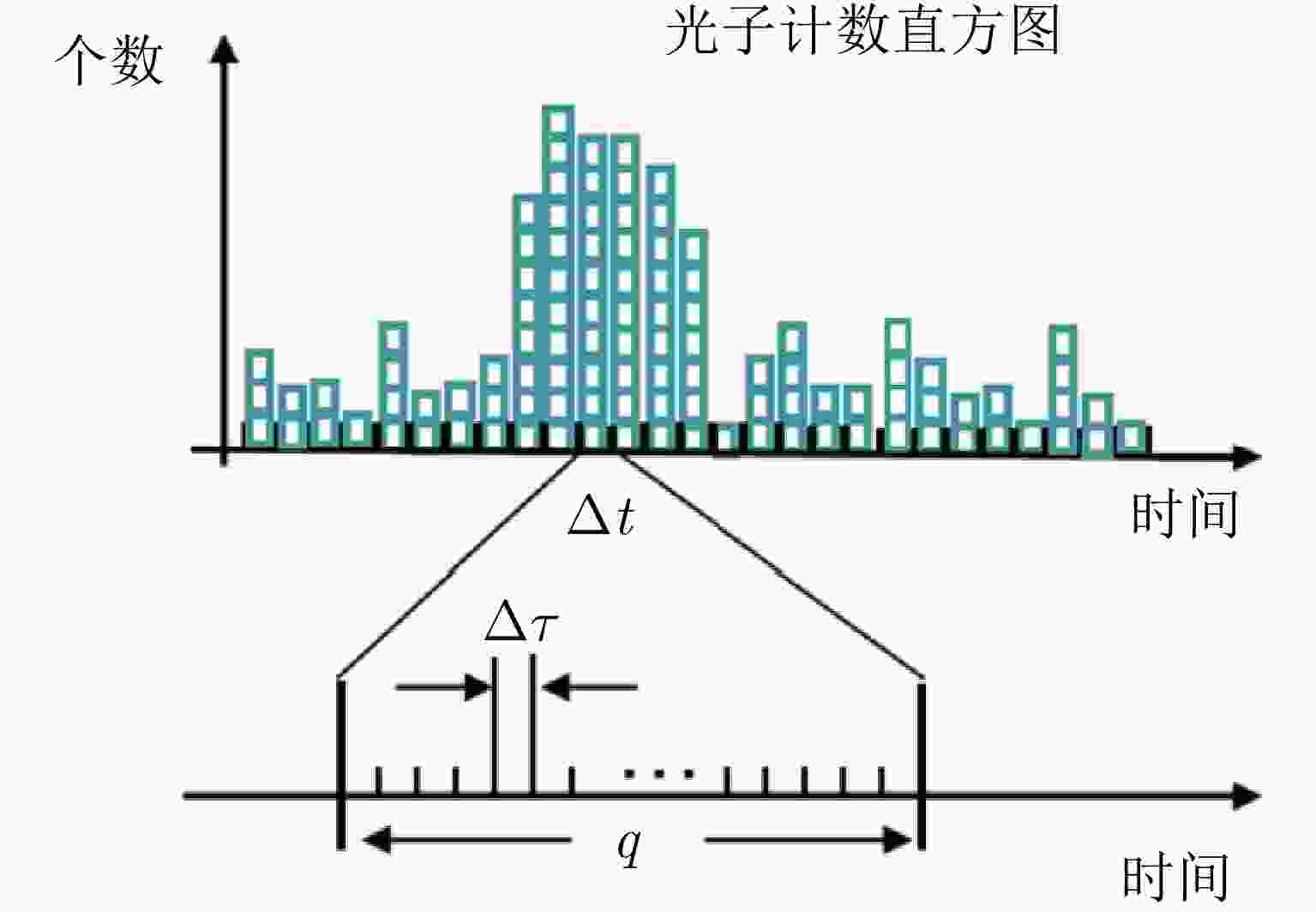
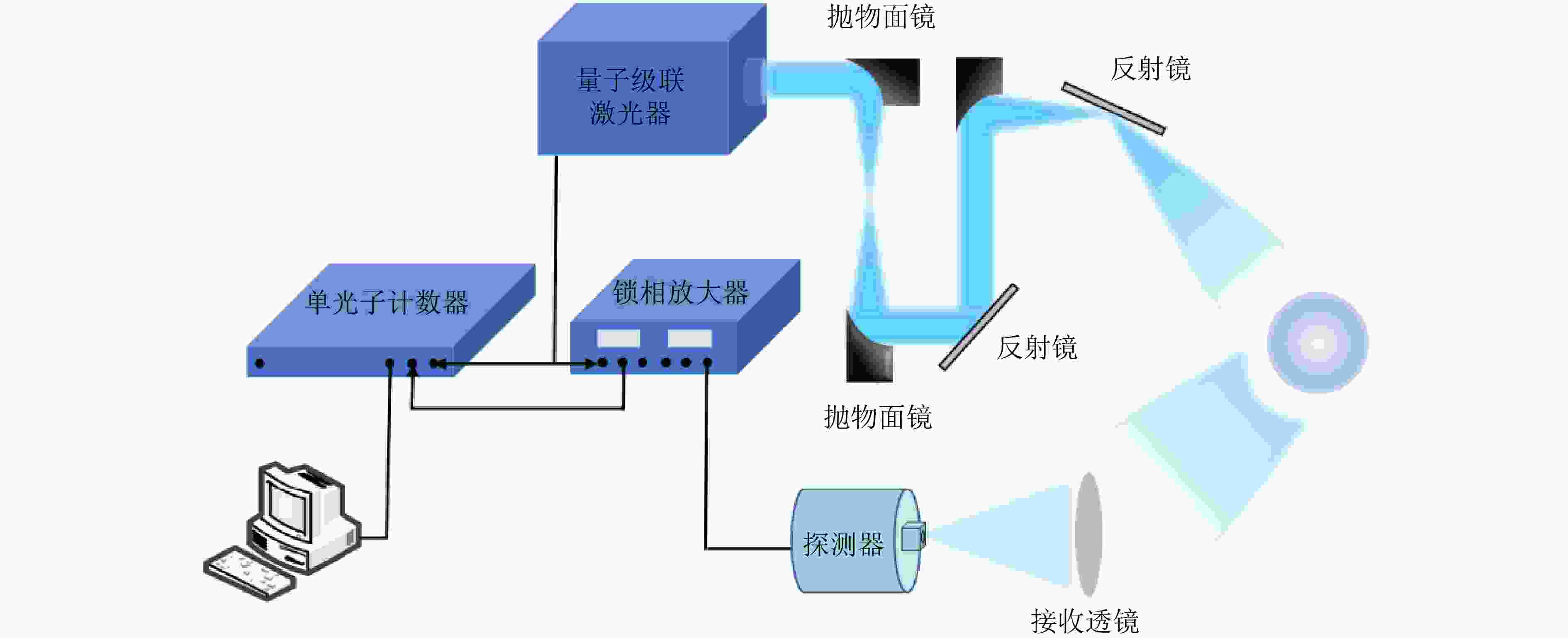
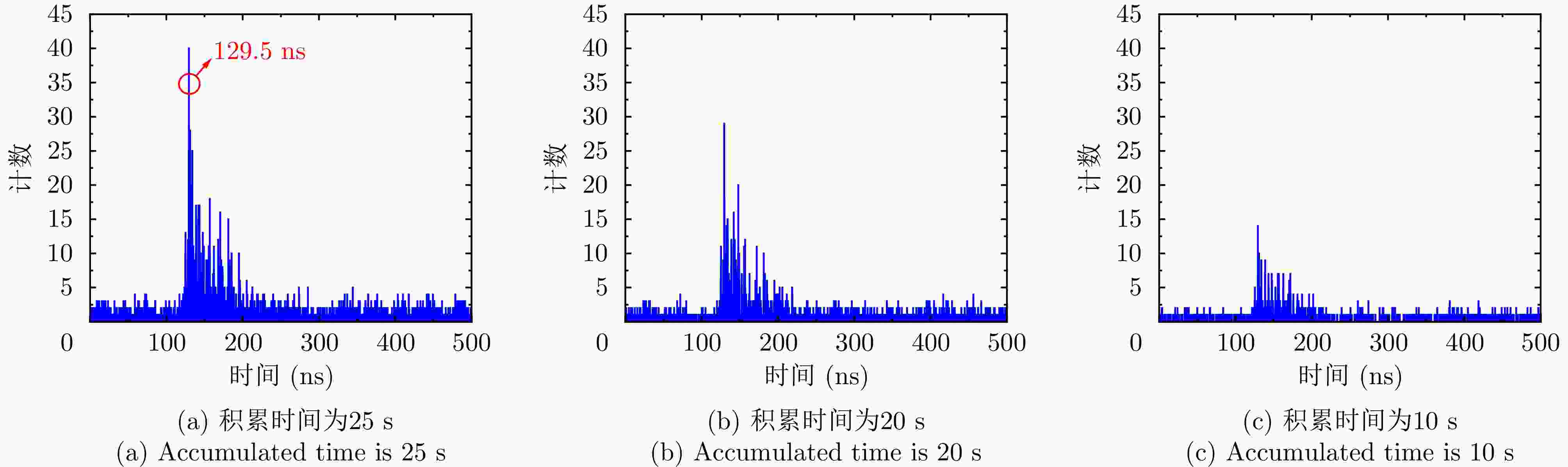
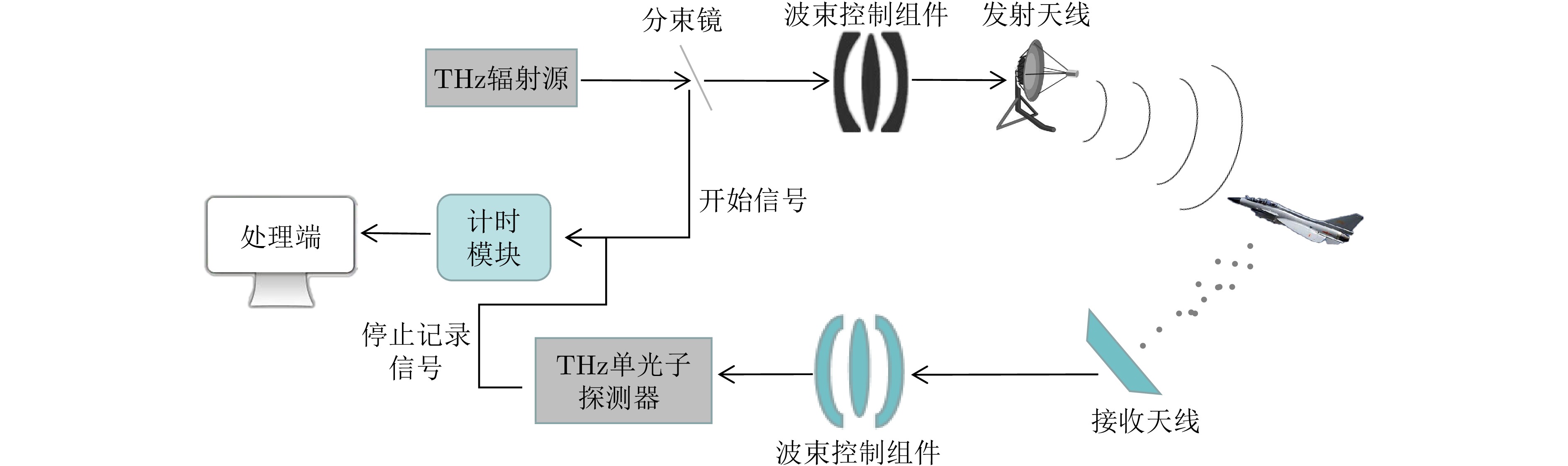
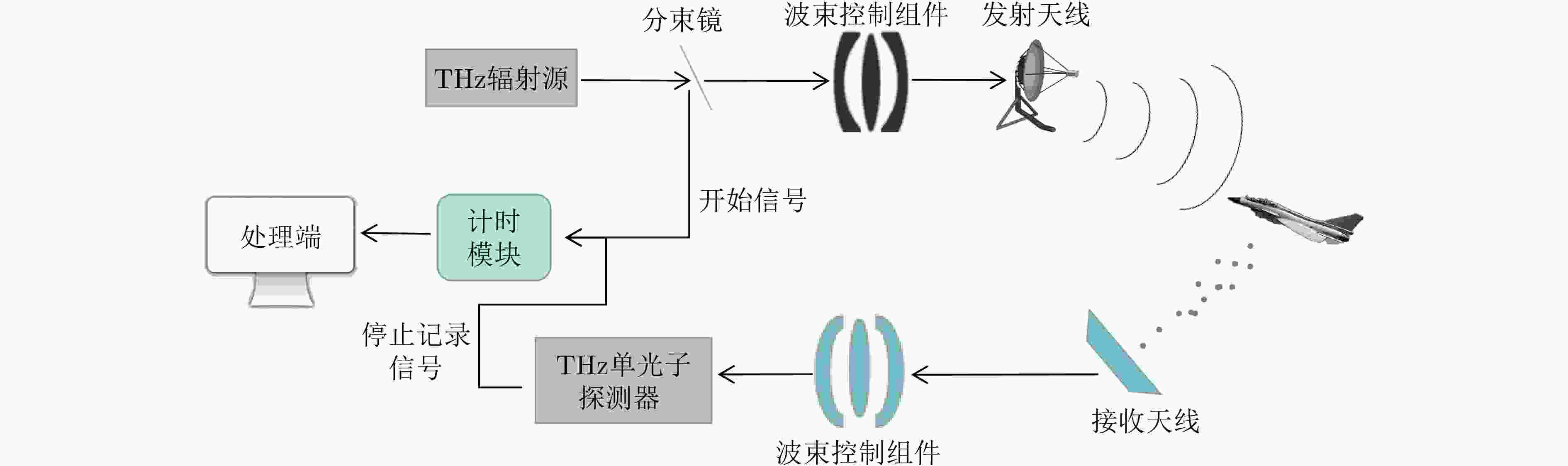
近年来，随着一系列太赫兹领域新技术和新材料的发展进步，太赫兹雷达探测技术得以迅猛发展。然而对于远距离非合作目标探测，现有太赫兹雷达受限于发射机功率、大气衰减效应等因素，雷达回波能量微弱，雷达最大探测距离受限，难以满足对目标的预警探测需求^[1]。

单光子又称为光量子，其能量为$hv$，其中h为普朗克常量，v为电磁波频率。一般而言，光子频率越高越容易被探测到。目前已报道的太赫兹单光子探测器典型的有半导体量子点探测器(Quantum Dot Detector, QDD)^[2−5]、量子阱探测器^[6−9]以及超导量子电容探测器(Quantum Capacitor Detector, QCD)^[10−12]等。与传统雷达接收机相比，单光子探测器具有极低的噪声水平和极高的探测灵敏度^[13]，能够检测到仅有少量光子的回波信号，利用单光子探测器替代传统雷达接收机，可显著提升雷达系统的探测精度和作用距离。受单光子探测器发展的驱动，太赫兹单光子雷达在接收端用单光子探测器代替传统雷达接收机，结合光子计数技术等信号处理手段实现目标探测，有望解决现有太赫兹雷达对远距离非合作目标作用距离不足的问题。

目前国内外对单光子雷达的研究主要集中在光学频段^[14−20]，这主要得益于光学领域材料的突破以及硬件的成熟。在太赫兹探测技术相关领域，国内外科研人员的研究主要集中于太赫兹大功率信号的产生^[21−24]或者单光子信号的探测^[25,26]。由于光子能量低，并且难以突破材料的瓶颈，太赫兹单光子探测器的研发难度非常高。迄今为止，太赫兹单光子探测器仍不成熟，也未见太赫兹单光子雷达探测系统集成的公开报道，仅有一些理论探索研究成果。文献[27]提出了太赫兹单光子雷达直接探测与外差探测两种系统实现方式，分析了当前太赫兹单光子雷达探测技术面临的关键问题，最后讨论了其在诸多领域的潜在应用。文献[28]首次研究了太赫兹频率下的外差单光子雷达，提出了目标距离和多普勒频率的估计方法，并通过推导概率密度函数对其性能进行了分析。以上成果具有较强的创新，但其探测模型并不完善，且未考虑探测器典型参数——死时间的影响，以及脉冲积累数、最小可检测信噪比等因素对检测概率、虚警概率的影响。对此本文基于光子计数技术，提出了太赫兹单光子雷达的直接探测模型，研究了其目标探测性能，并在太赫兹频段开展了原理验证实验。

2.   信号光子计数统计规律与探测模型

2.1   雷达工作流程与探测器工作原理

太赫兹单光子雷达直接探测工作流程如图1所示。太赫兹辐射源发射大功率太赫兹脉冲信号，经分束镜后，部分脉冲作为计时模块的开始信号，其余大部分脉冲信号经调制后照射至目标区域，回波光子到达雷达接收端后，触发太赫兹单光子探测器产生光子计数事件，计时模块输出对应光子的飞行时间，经过多次脉冲积累得到脉冲飞行时间直方图，处理后实现目标的精确测距。

图  1  太赫兹单光子雷达直接探测方式工作流程

Figure  1.  Workflow of the direct detection method of terahertz single-photon radar

下载: 全尺寸图片 幻灯片

QCD的超导吸收栅是铝纳米线形成的栅格结构，当入射的光子能量大于铝的超导能隙时，吸收栅中的库珀对会被拆散并产生多个准粒子^[26]。准粒子通过隧道结隧穿到超导岛上，导致超导岛的量子电容发生偏移，射频谐振器与库珀对箱(Single Cooper-pair Box, SCB)相耦合用于读取超导岛的量子电容的变化。每一次准粒子隧穿事件都会在读出电路产生对应的电压信号，表示探测器探测到了一个光子。由于当前器件的限制，探测器并不能精确区分究竟有几个光子同时产生了一次触发，仅能判断到达探测器光子的有无。

实际上，并非到达探测器的每个回波光子都能成功激发准粒子隧穿事件，探测器的光子探测效率$\eta$为成功产生光子计数事件的个数与入射光子数的比值^[26]。图2中${\eta _{\mathrm{a}}}$指探测器的吸收栅吸收入射光子的效率，${\eta _{\text{q}}}$指吸收光子后发生准粒子隧穿事件的效率，$\eta = {\eta _{\mathrm{a}}}{\eta _{\text{q}}}$。${K_{\text{s}}}$和${K_{{\text{n1}}}}$分别表示到达探测器的平均的信号光子数与外部噪声光子数，以效率$\eta$分别转变为平均光子计数事件${N_{\mathrm{s}}}$与${N_{{\text{n1}}}}$。${N_{{\text{n2}}}}$与${N_{\text{n}}}$分别表示平均的内部噪声光子计数事件和总噪声光子计数事件，${N_{\text{s}}} = \eta {K_{\text{s}}}$, ${N_{\text{n}}} = \eta {K_{{\text{n1}}}} + {N_{{\text{n2}}}}$。

图  2  超导量子电容探测器工作原理

Figure  2.  Operation principle of QCD

下载: 全尺寸图片 幻灯片

探测器产生一次光子计数事件后，会有一段时间无法再次工作，这个时间间隔${t_{\text{d}}}$就是探测器的死时间。探测器的死时间会限制最大饱和计数率，也即限制了探测器的动态范围。死时间将会影响太赫兹单光子雷达的探测性能，本文将在第3节给出具体分析。

2.2   信号光子的统计分布规律

对于微波而言，电磁波波长远大于目标表面微米量级的粗糙度，目标的粗糙度可以忽略，但对于太赫兹波，波长与粗糙度几乎为同等量级，因此必须考虑目标的粗糙度对电磁波散射的影响。在传统的雷达系统中，由于回波相对较强，对应的回波光子数很大，因此其宏观的回波能量的统计特性大多服从高斯分布。而在单光子量级的探测中，到达探测器的回波光子数极少，此时信号的光子计数事件次数不一定服从高斯分布。因此有必要明确经由目标反射后的信号光子到达探测器后，产生光子计数事件的统计分布规律。

探测器光子计数个数的分布规律主要取决于两个过程：发射信号经由目标反射到达探测器接收平面；到达探测器接收孔径的光子被探测器吸收后产生光子计数事件。

2.2.1   回波信号的能量概率密度

若目标表面是理想光滑的^[29]，则探测器接收到的由镜面目标反射的回波信号能量概率密度$p(W) = \delta (W - {W_0})$，其中，$\delta$表示冲激函数，${W_0}$为到达探测器接收面的信号能量。

若目标表面相对粗糙，则接收平面任意点的能量密度$w(u,v)$的概率密度函数为

其中，${I_0}(x)$为第1类贝塞尔函数，$\sigma _{\text{w}}^2 = {{T{\sigma ^2}}}/{{{z_0}}}$，$\bar w_0$表示接收孔径任意点能量的均值${\bar w_0} = E[e_{\text{r}}^2 \cdot T/(2{z_0})]$，${e_{\text{r}}}$是电压值，T是脉冲持续时间，${z_0}$为与介质阻抗相关的常数，${\sigma ^2}$与目标的表面粗糙度相关。

当${{{e_{\text{r}}}\sqrt {w \cdot 2T/{z_0}} }}/{{\sigma _{\text{w}}^2}} \ll 1$时：

接收平面接收到的总能量：$W = \displaystyle\iint_{{A_{\text{R}}}} w(u,v) {\mathrm{d}}u{\mathrm{d}}v = \displaystyle\sum\nolimits_{i = 1}^{{M_{\text{n}}}} {{w_i}}$，其中，${M_{\text{n}}}$可以解释为接收面接收到的相互独立的噪声的区域数量，也可以理解为接收到信号的自由度^[30]。总能量W的概率密度函数为

均值为$E(W) = {M_{\text{n}}}\sigma _{\mathrm{w}}^2 + {M_{\text{n}}}{\bar w_0}$。

2.2.2   回波信号光子计数事件的统计规律

根据光子的半经典理论^[30,31]—光子入射的概率在任何增量时间间隔是正比于在该时间间隔期间入射的电磁波能量；并且假设：(1)随着时间间隔的减小，在此时间段内多于一个光子入射的概率可以忽略不计；(2)任意两个无重叠的时间段内是否有入射的光子信号在统计上是独立的。

已知回波在探测器所探测到的光子个数分布为泊松分布^[30]，即若入射能量为W，产生k个光子事件的概率为

其中，$\bar N = {{\eta W}}/({{hv}})$，$\bar N$表示发生的光子计数事件的平均次数，也即探测到的光子的平均个数。$\eta$为探测器的光子探测效率。如果入射的能量大小随机波动，那么探测到的光子数可以由统计量的集合平均表示，即$\bar N = {{\eta E(W)}}/({{hv}} )$，$E(W)$为入射总能量的统计平均。

若发射信号经理想光滑表面的目标反射，探测器探测到k个信号光子的概率为

当发射信号经粗糙表面的目标反射后，若${M_{\text{n}}}\bar w \to 0$，即接收孔径内探测到的光子数目趋近于0时，${\bar N_{\mathrm{s}}} = {{\eta E(W)}}/({{hv}}) \approx {{\eta {M_{\text{n}}}\sigma _{\text{w}}^2}}/({{hv}} )$，探测器探测到k个信号光子的概率为

当${M_{\text{n}}} \gg {\bar N_{\text{s}}}$，即每个独立单元的平均信号光电子数远远小于1时，${P_{\mathrm{s}}}(k) \approx {{\bar N_{\text{s}}^k}}/{{k!}}\exp ( - {\bar N_{\text{s}}})$，粗糙目标回波产生的信号光子计数统计可以近似为泊松分布。

本节根据光子的半经典理论，分析了镜面和粗糙表面的目标下探测器产生信号光子计数事件的统计分布规律。一般而言，脉冲信号经由表面光滑的目标反射后，探测到的信号光子统计分布服从泊松分布。对于粗糙目标，回波信号光子计数事件统计服从负二项分布，但单光子探测过程中每次探测的平均信号光电子数远远小于1，即${\bar N_{\mathrm{s}}}/{M_{\text{n}}} \ll 1$，此时负二项分布近似为泊松分布，因此采用泊松分布模型对目标的回波信号进行分析。

2.3   由噪声产生的光子计数事件统计规律

雷达探测过程中的噪声主要来源于两个方面：内部噪声和外部噪声。传统雷达的1/f噪声和热噪声等内部噪声是由器件的低频噪声和电路中电子热运动造成的，可以认为是电子带来的噪声。而单光子探测器内部噪声主要包括范诺噪声(Fano noise)、相位噪声(phase noise)和暗计数等^[25]，是由光子的量子涨落和对非信号光子的误判带来的噪声。单光子探测外部噪声主要为目标背景的热辐射以及发射信号的后向散射噪声两种，内部噪声和外部噪声相互独立，一般情况下均可看作具有稳定平均值的泊松随机过程。因此总的噪声也服从泊松分布，探测到k个噪声光子的概率为${P_{\text{n}}}(k) = {{{{({N_{\text{n}}})}^k}}}/{{k!}} \exp ( - {N_{\text{n}}})$，${N_{\text{n}}}$表示在探测时间T内探测器探测到的总的平均噪声光子数。设噪声光子计数事件的产生速率为一个定值，探测器每秒响应的噪声平均光子计数事件个数表示为${\lambda _{\text{n}}} = {N_{\text{n}}}/T$。

2.4   探测模型的建立

假设太赫兹单光子雷达的平均发射功率为${P_{\text{t}}}$，发射前端增益为${G_{\text{t}}}$，探测目标与雷达距离为R，目标雷达横截面积为$\sigma$，接收孔径有效面积为${A_{\text{e}}}$，孔径效率为${\rho _{\mathrm{a}}}$，系统损耗为L，则雷达系统接收到的回波功率可表示为

那么探测时间T内能够探测到的平均信号光子数${N_{\text{s}}} = \eta {P_{\text{r}}}T/hv$。雷达的灵敏度${S_{i\min }}$由探测器的等效噪声功率(Noise Equivalent Power, NEP)以及测量带宽${B_{\text{W}}}$确定^[26]：

其中，最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$由系统探测概率与虚警概率决定。${R_{{\text{SN}}}}$可以表示为时间轴上信号所在区间中，信号与噪声分别产生的光子计数次数的比值：

其中，$E({P_{\text{s}}})$与$E({P_{\text{n}}})$分别为脉冲信号的峰值功率与总噪声的平均功率，${p_{\text{w}}}{\lambda _{\text{n}}}$为信号回波所在时间区间内的噪声平均光子计数事件次数。

太赫兹单光子雷达探测过程中目标回波引起的光子计数事件次数的分布近似为泊松分布。由于信号、外部噪声和内部噪声三者相互独立，因此三者同时发生在探测器内部的光子计数过程也是一个泊松分布。模型建立未考虑时间抖动。

单光子雷达系统工作时序如图3所示，将距离选通门内的时间轴离散化，分为${{{T_{\text{G}}}} \mathord{\left/ {\vphantom {{{T_{\text{G}}}} {\Delta \tau }}} \right. } {\Delta \tau }}$个具有相同大小的时隙($\Delta \tau$对应于探测器计时时钟的分辨率)。第n个时隙$\Delta {\tau _n}$中光子的探测概率可以表示为${p_{{\text{d0}}}}\left( n \right) = {p_{\text{r}}}\left( n \right) \cdot {p_{\text{t}}}\left( n \right)$，其中，${p_{\text{r}}}$表示探测器能够对回波光子进行响应的概率，即探测器从死区恢复、处于待激发状态的概率，${p_{\text{r}}}(1) = 1$，

图  3  单光子雷达系统工作时序

Figure  3.  Working sequence of single-photon radar

下载: 全尺寸图片 幻灯片

${p_{\text{t}}}\left( n \right)$表示$\Delta {\tau _n}$中光子计数事件的触发概率，${p_{\text{t}}}\left( n \right) = 1 - \exp ( - {m_{{\text{sn}}}}(n))$。${m_{{\text{sn}}}}$为信号与噪声共同引起的平均光子计数事件在时间轴上的分布表达式：

其中，${m_{\text{n}}} = {\lambda _{\text{n}}} \cdot \Delta \tau$, $\displaystyle\sum\nolimits_n {{m_{\text{s}}}(n)} = {N_{\text{s}}} = \eta {K_{\text{s}}}$。

则${p_{{\text{d0}}}}\left( n \right)$可以改写为

单脉冲探测的虚警概率${P_{{\text{fa1}}}}$与检测概率${P_{{\text{d1}}}}$为

其中，$\left\lfloor\cdot \right\rfloor$表示向下取整。为了提高雷达探测的检测概率和降低虚警概率，采用光子计数技术对回波脉冲串进行能量积累，光子计数积累过程如图4所示。太赫兹单光子雷达每产生一个光子计数事件，就意味着探测到了对应某个计时通道的一个光子。经由目标反射的光子集中分布在回波区间，而噪声光子却因其随机性散布在整个时间轴。由于信号脉宽远大于时隙$\Delta \tau$，信号光子计数事件可能在信号区间内的任意位置产生，因此少次累积探测并不能直接体现出信号的相关性，只有当探测次数逐渐增大，光子计数分布直方图的回波区间才会呈现出与脉冲包络相关的形状，通过对直方图的处理就能到脉冲精确的飞行时间。

图  4  光子计数积累过程示意图

Figure  4.  Schematic diagram of photon counting accumulation process

下载: 全尺寸图片 幻灯片

本文脉冲飞行时间直方图的组距等于子区间$\Delta t$，$\Delta t$中包含$q = \Delta t/\Delta \tau$个时隙，如图5所示。单脉冲探测时第n个子区间$\Delta {t_n}$中光子探测概率可以表示为

图  5  一个子区间$\Delta t$包含q个时隙

Figure  5.  A sub-interval $\Delta t$ contains q intervals

下载: 全尺寸图片 幻灯片

若脉冲累计测量次数为M次，对于给定的平均噪声水平${\lambda _{\text{n}}}$和最大可容忍虚警概率${P_{{\text{FA}}}}$，设判定阈值为${M_{\mathrm{t}}} \in \mathbb{N}$，第n个子区间判定有目标的概率${P_{{M}}}(n)$为

满足要求的最小阈值${M_{\text{t}}}$的计算公式为

检测概率为

设置主要仿真参数：雷达工作频率$f = 4{\text{ THz}}$，脉宽${p_{\text{w}}}{\text{ = 2 }}{\text{ μs}}$，探测器光子探测效率$\eta = 0.9$，死时间${t_{\text{d}}}{\text{ = 20 }} {\text{ μs}}$, $\Delta \tau = 1{\text{ ns}}$, $\Delta t = {\text{100 ns}}$, $M = 1000$, $R = 1100{\text{ m}}$, ${T_{\text{G}}}{\text{ = 20 }} {\text{ μs}}$，总的噪声功率为$3 \times {10^{ - 16}}{\text{ W}}$，回波功率为$1.5 \times {10^{ - 15}}{\text{ W}}$，得到脉冲飞行时间直方图如图6所示，可以看出仿真结果与理论模型曲线相符合。

图  6  脉冲飞行时间直方图

Figure  6.  The time-of-flight histogram

下载: 全尺寸图片 幻灯片

3.   探测模型的性能分析

为简化分析，设发射信号为理想矩形脉冲，仅考虑单脉冲检测。死时间是单光子探测器特有的性能参数，由于死时间的不同，雷达的探测性能发生变化。按在距离门内是否可以探测到多个光子，死时间的大小可划分为：${t_{\text{d}}} = 0$，${t_{\text{d}}} \ge {T_{\text{G}}}$以及不包括以上两种的第3种情况。那么探测模型可分为以下3种：

(1) 当死时间${t_{\text{d}}}$相对于发射信号的脉宽可忽略时，近似看作${t_{\text{d}}} = 0$。从距离门起点至回波到达后，探测到光子的次数只与回波和噪声的能量有关。$\Delta {\tau _n}$内回波光子待触发的概率${p_{\text{r}}} = 1$，探测到光子的概率${p_{{\text{d0}}}}\left( n \right) = 1 - \exp ( - m(n))$。单脉冲探测的虚警概率与检测概率为

(2) 若死时间不可忽略，且回波所在区间与第1个死时间区间不重合时，如图7(b)所示。从距离门起点至回波到达后，探测到光子的次数可以为多次。此时某回波区间的光子探测概率受到该区间以及之前区间的平均光子计数次数的影响。该区间内的光子探测概率并无精简的数学公式，只能根据模型求其数值解。

图  7  探测模型的3种情况

Figure  7.  The detection model divided into the three cases

下载: 全尺寸图片 幻灯片

(3) 若死时间不可忽略，且第1个死时间区间可以覆盖回波区间时，如图7(c)所示。从距离门起点至回波到达后，最多只能探测到一个光子。虽然探测器在回波到达后仍可能探测到光子，但其均为噪声引起的，并且对目标区间的探测概率无影响，因此这种情况可归为${t_{\text{d}}} \ge {T_{\text{G}}}$。$\Delta {\tau _n}$发生光子计数事件的概率可化简为

主要仿真参数设置为${R_{{\text{SN}}}} = 2$, ${\lambda _{\text{n}}}{\text{ = 0}}{\text{.1 MHz}}$, ${p_{\text{w}}}{\text{ = 2 }} {\text{ μs}}$, $\Delta t = {\text{0}}{\text{.2 }} {\text{ μs}}$。图8(a)展示了单次探测时不同死时间下各个子区间内的探测概率分布情况，可以发现，死时间越大，回波区间的探测概率越小，这是由于死时间的大小直接影响了回波区间的待激发概率。图8(b)和图8(c)表明了回波相对距离门起点的飞行时间不同时各个子区间的探测概率。其他条件一定时，回波越靠近距离门起点，检测概率越大；当目标飞行时间大于死时间时，回波区间的探测概率与区间位置无明显关系。

图  8  死时间与回波位置影响下的各个时间区间内探测概率${p_{\text{d}}}$的分布

Figure  8.  The distribution of ${p_{\text{d}}}$ in each interval under different ${t_{\text{d}}}$ and ${t_{\text{r}}}$

下载: 全尺寸图片 幻灯片

3.1   子区间的取值对检测概率影响

单次探测时划分的子区间大小对检测概率并无影响；当进行多脉冲积累时，不同的判定阈值以及子区间大小均会对检测概率造成影响。若直接对得到的直方图进行处理，由于探测器时间分辨率$\Delta \tau$在纳秒量级，探测需要进行大量的脉冲积累才能够将信号从噪声中区分出来。若在时间轴上取合适的$\Delta t$，则可以在提高检测概率的同时减小脉冲积累数M，节省雷达的探测时间。

如图9所示，参数${t_{\text{f}}}$表示回波信号前沿在所处子区间的位置，即脉冲以脉冲前沿所在的子区间起点为零点的相对飞行时间。

图  9  脉冲回波前沿在所对应子区间的位置示意图

Figure  9.  Schematic diagram of the position of the pulse echo front in its corresponding sub-interval

下载: 全尺寸图片 幻灯片

图10表示回波脉冲前沿在某一固定区间内，检测概率随比值${t_{\text{f}}}/\Delta t$的变化趋势，仿真参数设置为$M = 100$, ${t_{\text{r}}}{\text{ = 8 }} {\text{ μs}}$, ${p_{\text{w}}} = \Delta t$, ${P_{{\text{FA}}}} = {10^{ - 4}}$，其余参数与之前设置相同。可以看出：无死时间的影响下，随着比值${t_{\text{f}}}/\Delta t$越来越大，检测概率先增大后减小，检测概率最小值出现在${t_{\text{f}}}/\Delta t = 0.5$处。随着死时间增大，检测概率的最低点将会向右偏移。

图  10  检测概率${P_{\text{D}}}$随比值${t_{\text{f}}}/\Delta t$的变化关系

Figure  10.  The detection probability ${P_{\text{D}}}$ as a function of ratio ${t_{\text{f}}}/\Delta t$

下载: 全尺寸图片 幻灯片

绘制不同情况下目标检测概率随所划分区间取值$\Delta t$的变化趋势如图11所示，设${R_{{\text{SN}}}} = 2$, ${t_{\text{d}}} = 3{\text{ }} {\text{μs}}$, ${t_{\mathrm{r}}} = 8{\text{ }}{\text{μs}}$，其中飞行时间参数${t_{\mathrm{r}}}$的设置是为了确保划分后某一区间的起点与回波脉冲前沿重合，即${t_{\text{f}}} = 0$。图11(a)和图11(b)均表明只有当$\Delta t = {p_{\text{w}}}$时，检测概率才能够达到最大。图11(c)可以看出：随着积累数M的增大，$\Delta t$的一些取值都会无限趋于1。因此只有在较少的脉冲积累探测时，划分区间大小的取值才需严格等于脉宽。图中噪声光子率函数表示单光子探测器每秒探测到的噪声光子个数。

图  11  目标检测概率随所划分区间取值$\Delta t$的变化趋势

Figure  11.  Detection probability as a function of $\Delta t$ with different simulations

下载: 全尺寸图片 幻灯片

由于回波区间位置在距离门内是任意的，当以脉宽大小离散时间轴时，回波位置与划分区间不一定重合。本文通过调整第1个划分区间的大小，使得之后的某一区间与回波位置重合。图12为调整前后检测概率对比，明显看出调整后的检测概率在回波所处距离门一些位置有了很大提升。

图  12  检测概率随脉冲飞行时间的变化曲线(t_d=3 μs)

Figure  12.  Detection probability as a function of ${t_{\text{r}}}$ (t_d=3 μs)

下载: 全尺寸图片 幻灯片

因此，在进行目标探测时，应使时间轴上划分的子区间大小等于发射信号的脉宽，并且应适当调整第一个区间大小，使得某一区间与目标回波区间尽量重合，这种处理能够提高目标的检测概率，同时也能减少雷达探测所需要的脉冲数。

3.2   回波在距离门的相对位置对探测性能影响

为简化分析，仅考虑单脉冲探测时的检测概率和虚警概率，设${p_{\text{w}}} = 2{\text{ }} {\text{μs}}$, ${T_{\text{G}}} = 20{\text{ }}{\text{μs}}$。

(1) 当死时间${t_{\text{d}}} = 0$时，目标检测概率与回波在距离门内的位置无关，目标的检测概率随信号平均光子数增大而增大，随噪声平均光子数的减小而增大。

(2) 当死时间${t_{\text{d}}} \ge {T_{\text{G}}}$时，目标的检测概率会明显受到距离门内回波位置的影响。定义脉冲在距离门内的飞行时间与距离门的比值为${r_{\text{t}}} = {t_{\text{r}}}/{T_{\text{G}}}$。

当${r_{\text{t}}} = 0$时，即回波脉冲前沿与距离门起点重合，图13(a)表明当噪声一定，检测概率随着平均信号光子数的增大而增大并会逐渐趋于一个定值，虚警概率仅与距离门内的噪声光子数以及死时间有关。当信号光子数较少时，随着噪声增大检测概率会略微有一点提升，这是由于回波所在区间的噪声也会引起探测器产生光子计数事件，回波所在区间内总光子数增加，使得该区间内的检测概率提高。随着信号光子数的增大，噪声对检测概率的影响逐渐减小。

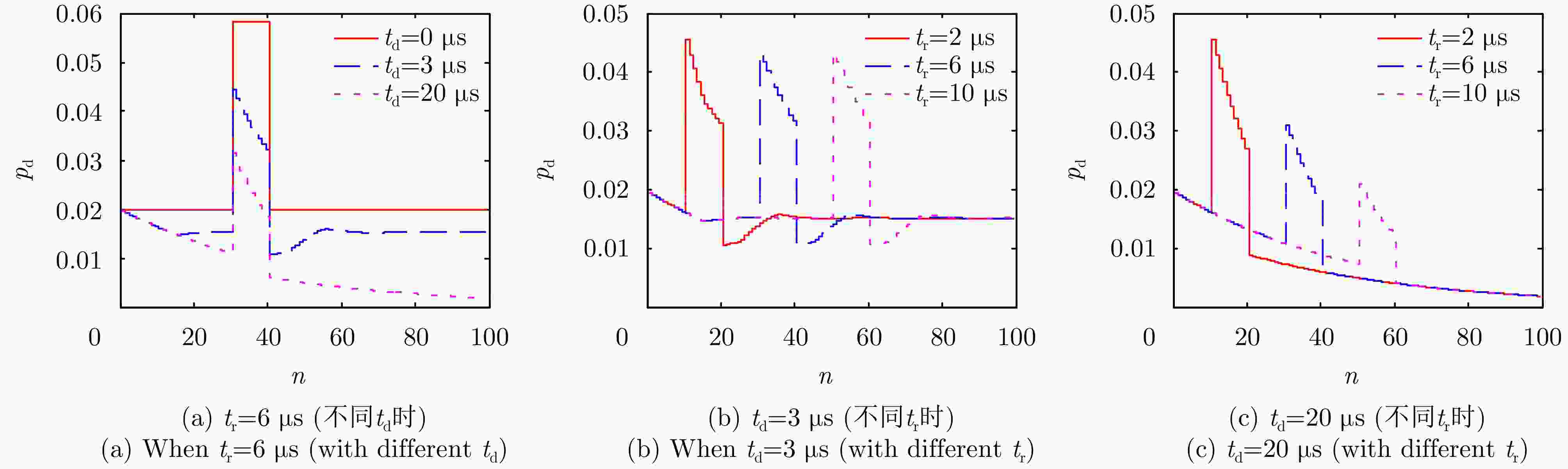
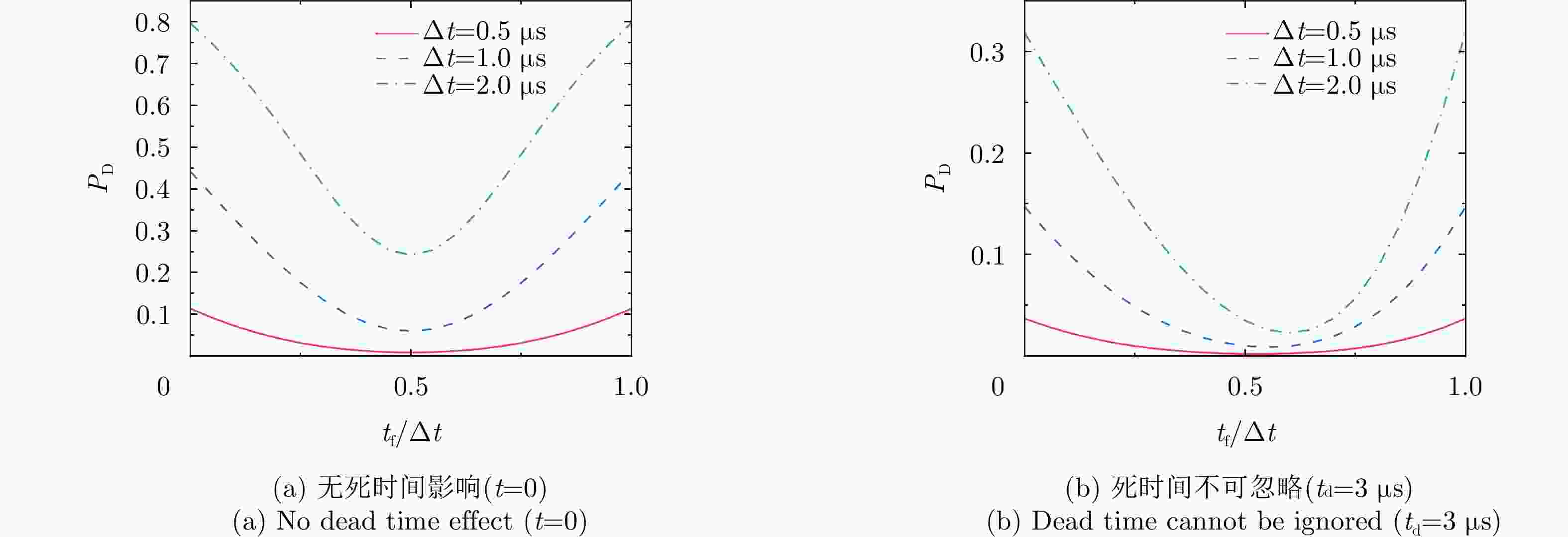
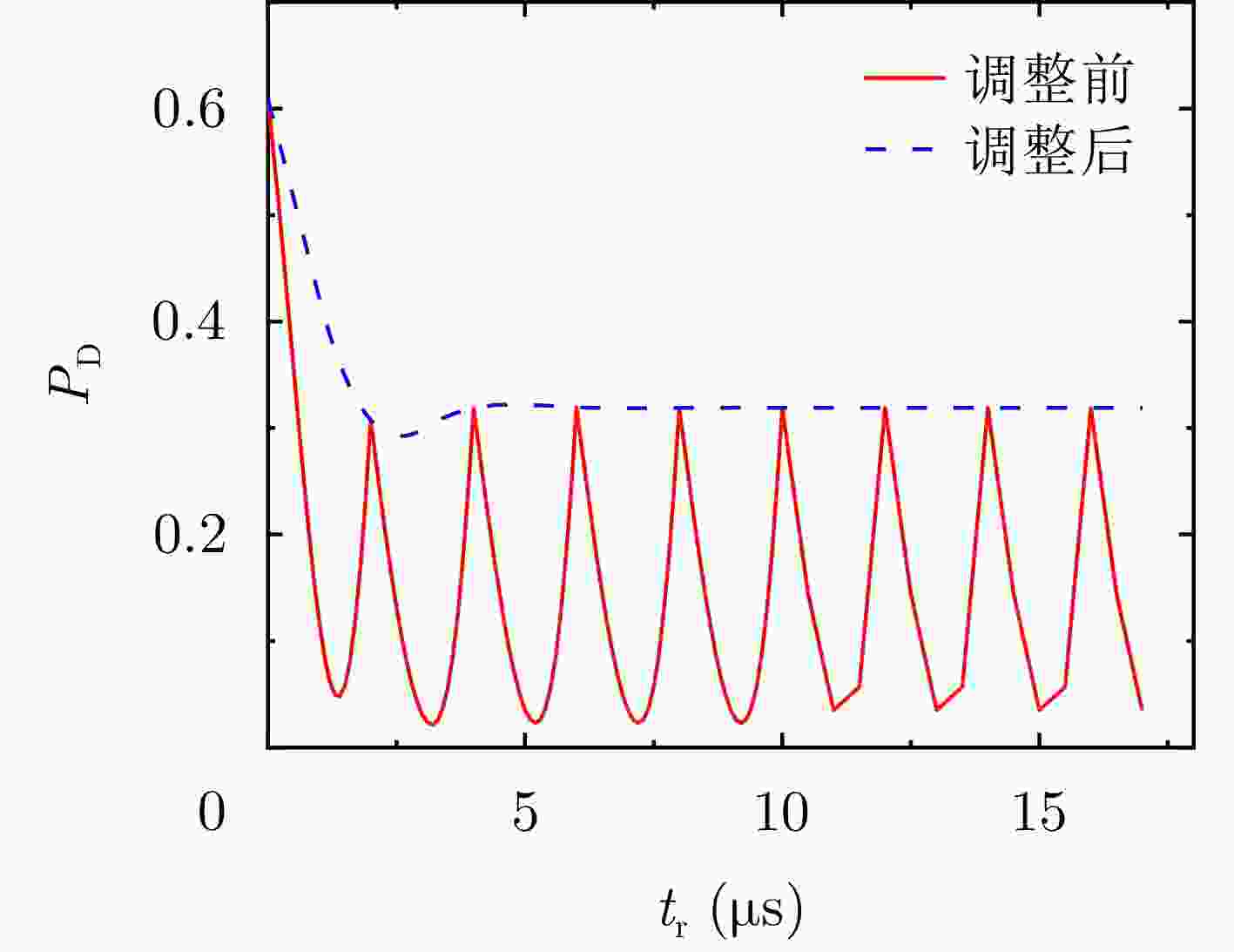
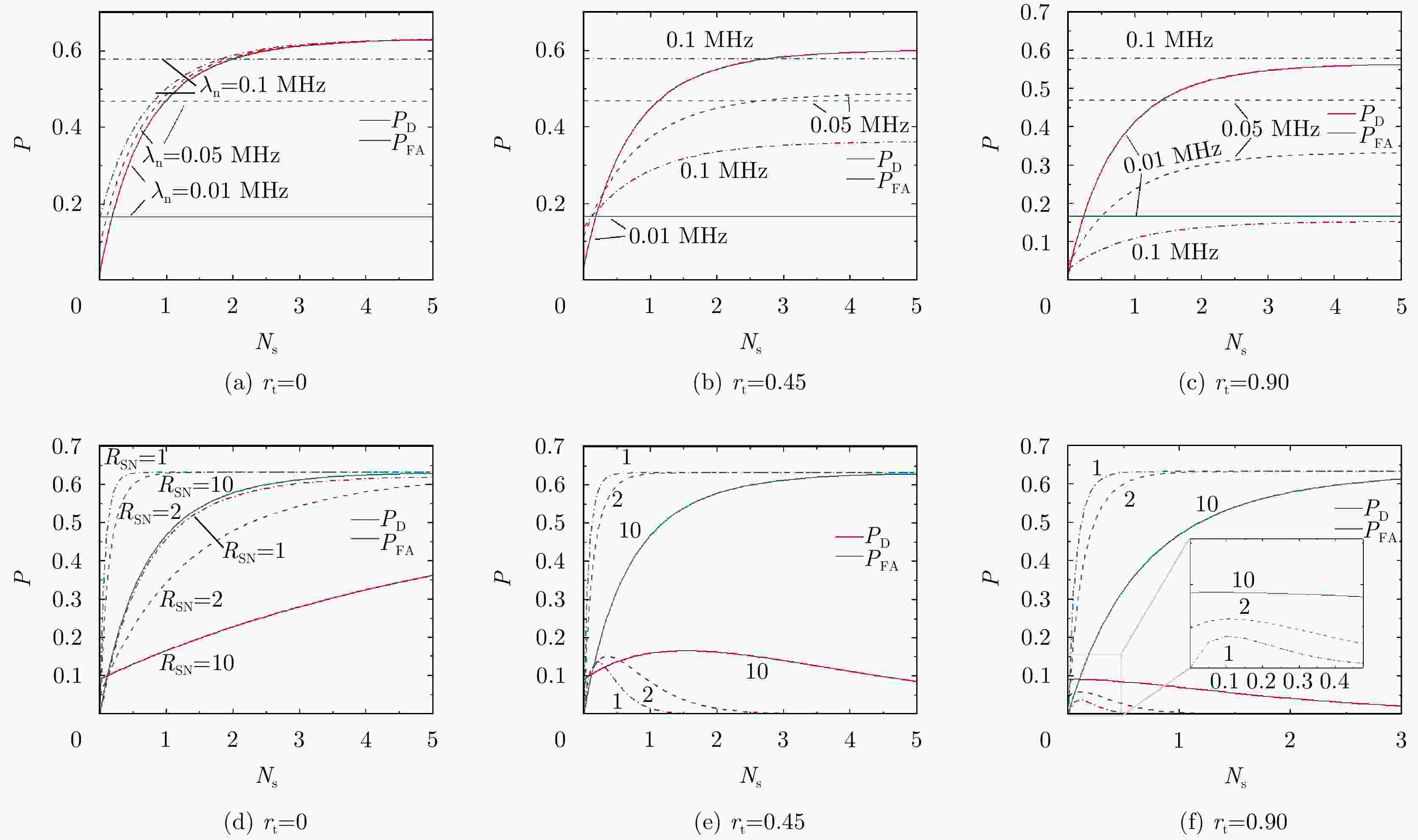
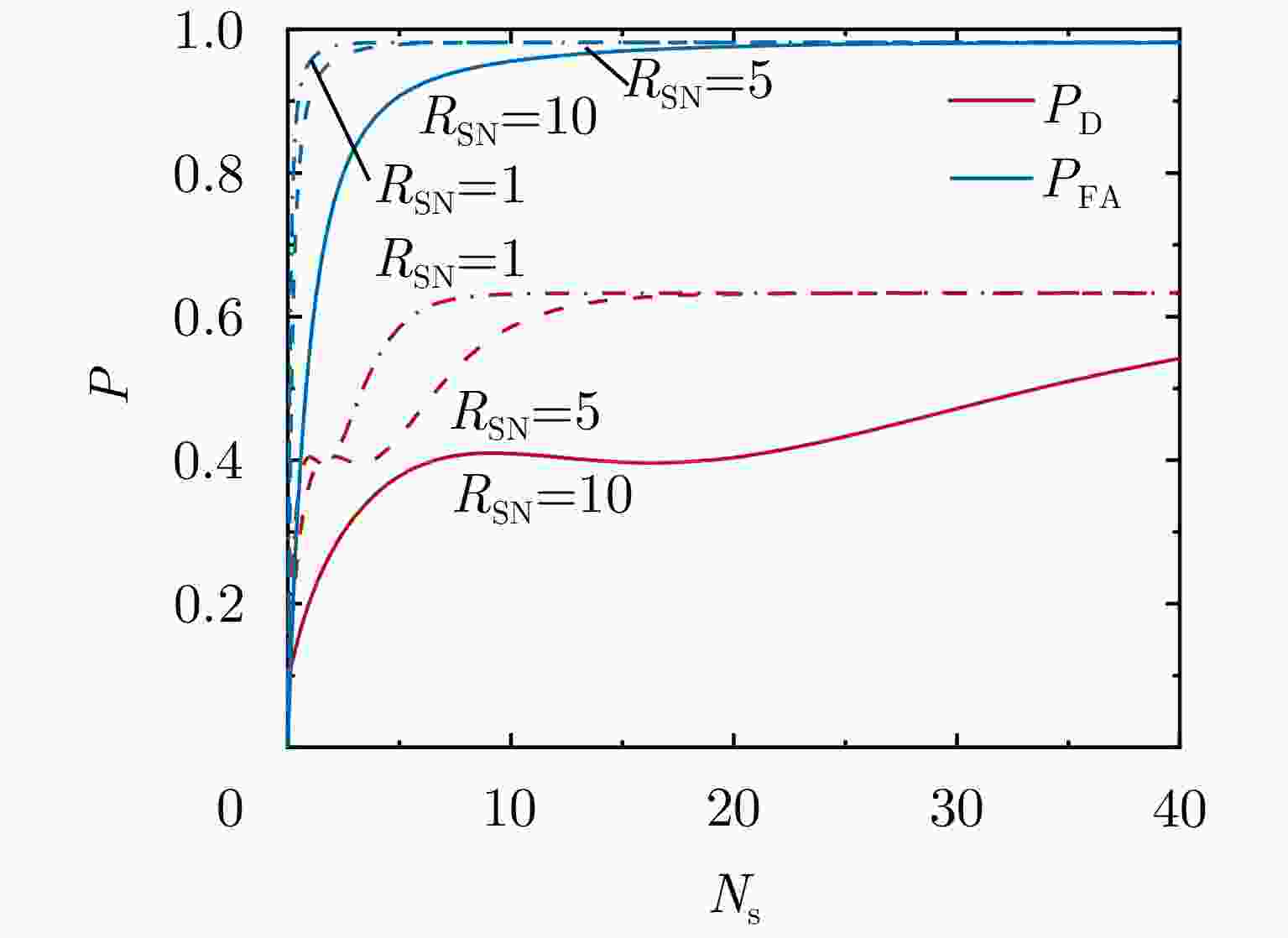
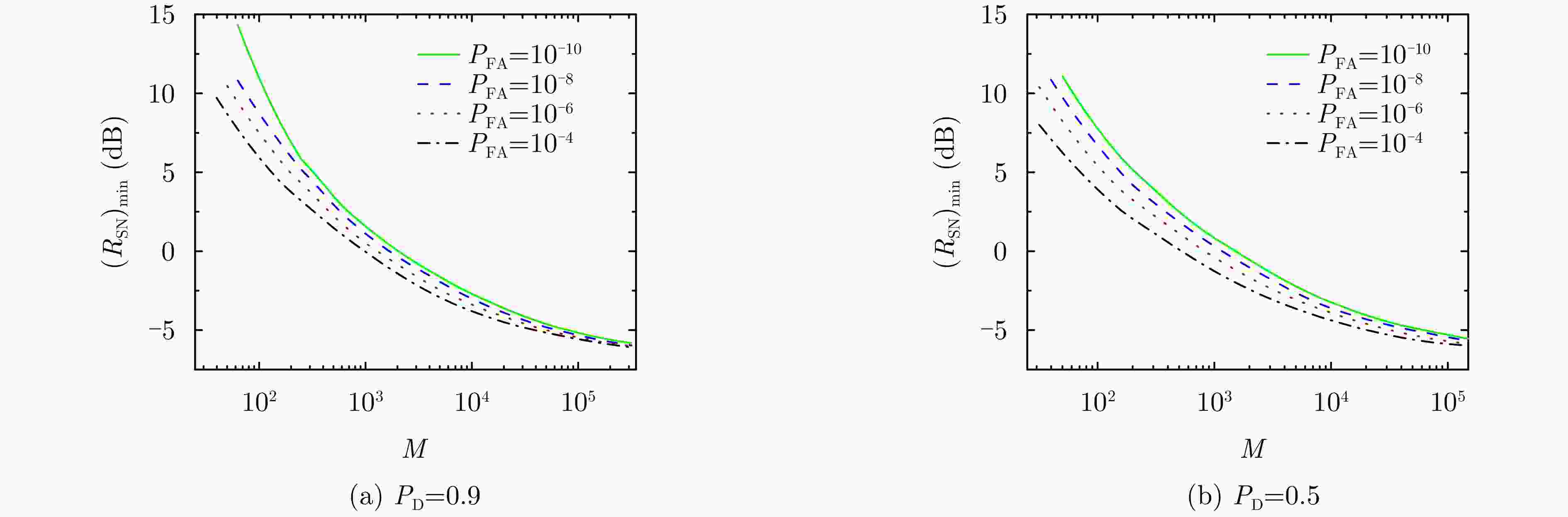
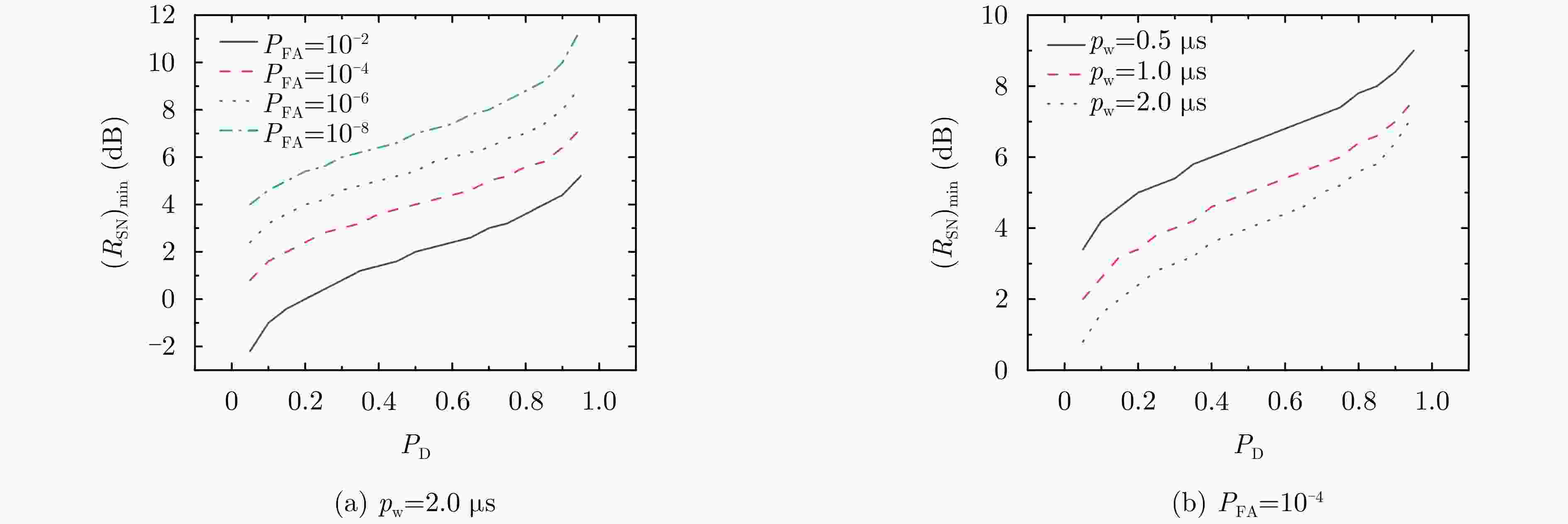
图  13  单脉冲探测时检测概率和虚警概率随信号平均光子数的变化曲线((a)、(b)和(c)中曲线分别以噪声光子率${\lambda _{\text{n}}}$：$0.01{\text{ MHz}}$(点划线)，$0.05{\text{ MHz}}$(划线)，$0.1{\text{ MHz}}$(实线)区分；(d)、(e)和(f)中曲线分别以信噪比${R_{{\text{SN}}}}$：1(点划线)，2(划线)，10(实线)区分)

Figure  13.  The detection probability and false alarm probability versus the mean signal photons${N_{\text{s}}}$ (the curves Fig. (a), Fig. (b) and Fig. (c) are differentiated by the noise photon rate function ${\lambda _{\text{n}}}$ marked with $0.01{\text{ MHz}}$ (dotted line), $0.05{\text{ MHz}}$ (dotted line), $0.1{\text{ MHz}}$ (solid line); The curves from Fig. (d), Fig. (e) and Fig. (f) are differentiated by the signal to noise ratio ${R_{{\text{SN}}}}$ marked with 1 (dotted line), 2 (dotted line), 10 (solid line))

下载: 全尺寸图片 幻灯片

当${r_{\text{t}}} = 0.45$时，如图13(b)所示，检测概率随着信号平均光子数的增大而增大并逐渐趋于一个定值$\exp ( - {r_{\text{t}}}{\lambda _{\text{n}}}{T_{\text{G}}})$。当信号平均光子数较小时，检测概率随噪声光子率函数增大而增大，这是因为到达回波区间的光子主要为噪声光子，检测概率主要受回波区间的触发概率${p_{\text{t}}}(n) = 1 - \exp ( - {m_{{\text{sn}}}}(n))$的影响；当信号光子数较大时，检测概率主要受回波区间的待激发概率${p_{\text{r}}} = \exp ( - {r_{\text{t}}}{\lambda _{\text{n}}}{T_{\text{G}}})$的影响，其随噪声光子率函数增大而减小。

当${r_{\text{t}}} = 0.90$时，回波脉冲下降沿与距离门终点重合，此时回波与距离门起点之间的噪声光子数最多，检测概率受噪声的影响最大。

图13(d)、图13(e)和图13(f)分别展示了不同回波位置下，保持${R_{{\text{SN}}}}$不变时探测概率随信号平均光子数的变化趋势。当${r_{{\mathrm{t}}} } = 0$，${R_{{\text{SN}}}}$一定时，检测概率与虚警概率均随信号平均光子数的增大而增大并趋于一个定值。当${r_{\text{t}}} \ne 0$，${R_{{\text{SN}}}}$一定时，信号光子数为某一值${N_{{\text{s0}}}}$时检测概率取得最大值，${N_{{\text{s0}}}}$随着${R_{{\text{SN}}}}$的增大而增大。这是由于检测概率是由回波区间的待激发概率和光子触发概率共同决定的，待触发概率与噪声光子数成反比，光子触发概率与噪声光子数成正比，随着信号平均光子数的增大，检测概率主要分别受到待激发概率和光子触发概率的影响。由式(12)可知，虚警概率主要是由在距离门范围内非回波信号区域的噪声光子导致的，在实验中由于距离门范围远大于脉冲宽度，因此虚警概率也大于检测概率。实验结果为单光子探测距离门的设计提供了指导思路。

(3) 当回波区间与第1个死时间区间不重合，且死时间不可忽略时，目标的检测概率只能根据数学表达式求其数值解。当回波区间位于距离门中间位置时，检测概率随信号光子数的变化曲线如图14所示。可以看出，随着信号光子数的增大，单次探测的检测概率先增大后减小，最终再次增大并趋于一个定值。

图  14  单脉冲探测时检测概率(P_D)和虚警概率(P_FA)随信号平均光子数的变化曲线

Figure  14.  The detection probability (P_D) and false alarm probability (P_FA) versus the mean signal photons ${N_{\text{s}}}$

下载: 全尺寸图片 幻灯片

因此，为提高目标的检测概率，进行探测时应尽可能使回波处于距离门靠前位置，但这需要目标距离的先验信息；还可以调节发射脉冲的能量或在接收端前添加适当衰减片使信号平均光子数达到最优来提高检测概率。

3.3   最小可检测信噪比分析

由雷达方程得到雷达的最大作用距离${R_{\max }}$：

由式(18)可知雷达最大探测距离${R_{\max }}$的分析可以转化成对其最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$的分析。由于探测模型公式的计算较为复杂，因此在计算${({R_{{\text{SN}}}})_{\min }}$时采用了数值近似的方法：首先在已知最大可容忍虚警概率后，求出经M次积累的判定阈值，再遍历${R_{{\text{SN}}}}$值，求出所要求的检测概率下，M次探测积累所对应的最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$。设置仿真参数为${t_{\text{r}}}{\text{ = 9 }} {\text{μs}}$, ${t_{\text{d}}} = 3{\text{ }} {\text{μs}}$, ${p_{\text{w}}}{\text{ = 2 }} {\text{μs}}$, ${\lambda _{\text{n}}} = 0.1{\text{ MHz}}$, ${T_{\text{G}}}{\text{ = 20 }} {\text{μs}}$，得到在给定${P_{{\text{FA}}}}$情况下的最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$随脉冲积累数M的变化曲线如图15所示。图15分别对应${P_{\text{D}}} = 0.9$和${P_{\text{D}}} = 0.5$。由结果可知，与传统雷达一致，单光子探测的最小可检测信噪比随脉冲积累数的增大而逐渐减小。

图  15  给定${P_{{\text{FA}}}}$情况下最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$随脉冲积累数M的变化曲线

Figure  15.  The ${({R_{{\text{SN}}}})_{\min }}$ as a function of the pulse accumulation number M under different ${P_{{\text{FA}}}}$

下载: 全尺寸图片 幻灯片

绘制不同虚警概率以及不同脉宽下，最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$随检测概率的变化关系如图16所示，仿真参数设置为${t_{\text{r}}}{\text{ = 9 }} {\text{ μs}}$, ${t_{\text{d}}} = 3{\text{ }} {\text{μs}}$, $M = 100$, ${\lambda _{\text{n}}} = 0.1{\text{ MHz}}$。可以看出：信噪比一定，虚警概率越小，检测概率越小；脉宽越大，检测概率越大。

图  16  最小可检测信噪比${({R_{{\text{SN}}}})_{\min }}$随检测概率${P_{\text{D}}}$的变化关系

Figure  16.  ${({R_{{\text{SN}}}})_{\min }}$ as a function of ${P_{\text{D}}}$

下载: 全尺寸图片 幻灯片

4.   光子计数目标探测原理验证实验

为验证太赫兹单光子雷达直接探测原理的可行性，本文在4.3 THz频段开展了基于光子计数的目标探测原理验证实验。由于当前太赫兹单光子探测器件发展尚未成熟，只能工作在极低温(≤10 K)的稀释制冷机中，难以直接搭建雷达接收机，因此选用测辐射热计(bolometer)探测器代替太赫兹单光子探测器进行验证。在实际的太赫兹单光子雷达系统中，通过太赫兹单光子探测器探测到回波光子后输出脉冲信号，由鉴别器输出太赫兹脉冲发射时刻与探测器单光子接收时刻的时间差，并通过计数器在相应的时间单元进行计数，通过一定时间积累后，得到飞行时间计数统计直方图计算实现对目标的高精度测距。利用bolometer代替太赫兹单光子探测器进行飞行时间计数的区别在于接收的回波未达到单光子量级，是对回波脉冲进行响应，且探测器没有死时间概念，探测机理与单光子探测器不同。但利用单光子探测器与bolometer检测都是对飞行时间进行测量，且bolometer与单光子探测器对雷达目标回波的响应均为电脉冲信号，并通过单光子计数器检测电脉冲信号进行计数统计。而单光子计数太赫兹雷达的目标信息反演主要依赖于单光子统计计数结果，因此通过对回波脉冲的飞行时间计数可以用于验证光子计数雷达的目标探测的原理可行性以及对统计直方图结果的信号处理的准确性。

基于光子计数的直接探测实验系统框图如图17所示，使用中心频率在4.3 THz的量子级联激光器(QCL)作为太赫兹辐射源，经过离轴抛物面镜、反射镜等组件进行波束整形后照射目标。同时QCL提供两路脉冲电信号，一路作为参考信号输入至锁相放大器，另外一路作为计时开始信号输入至单光子计数器。经目标反射的回波通过一个透镜进行聚焦接收，聚焦后的太赫兹波束入射到Nb₅N₆微测辐射热计(micro-bolometer)探测器并转换为脉冲电信号输入锁相放大器。锁相放大器的作用是提取与发射脉冲同频率的信号并进行放大，经放大后的脉冲信号输入至单光子计数器作为计时结束信号。通过对单光子计数器输出的计时开始信号与计时结束信号的时间差进行统计，得到飞行时间计数直方图，进而实现对目标的高精度测距。

图  17  基于光子计数的直接探测实验系统框图

Figure  17.  Schematic of the direct detection experimental system based on photon counting

下载: 全尺寸图片 幻灯片

QCL的输出太赫兹脉冲宽度设置为10 μs，重复频率为2 kHz。实验采用准单站设计，目标距离接收透镜的距离约为35 cm，QCL到最后一个反射镜的光程经测量约为24 cm，接收透镜到探测器的距离约为16 cm，光子飞行总光程为1.1 m。单光子计数器对脉冲的上升沿进行触发，探测时隙设置为200 ps，积累时间分别为25 s, 20 s和10 s，响应电信号延迟100 ns便于观察信号。单光子计数器输出的时间分辨统计直方图结果如图18所示。

图  18  不同积累时间下单光子计数器输出的时间分辨统计直方图

Figure  18.  Time resolution histogram for the output of the single-photon counter in different accumulated time

下载: 全尺寸图片 幻灯片

分析时间统计直方图可知，经过长时间积累，计时开始信号与计时结束信号的时间差约为29.5 ns，包含了探测器、锁相放大器以及光子计数器等器件的响应时间以及太赫兹光子飞行时间。通过将探测器放置QCL波束出口处对器件响应时间进行多次测量，得到平均响应时间约为26 ns。因此，得到太赫兹光子飞行时间约为3.5 ns，计算得到飞行距离约为1.05 m，与实际距离的误差为0.05 m。可以发现，在不同积累时间下均得到近似相同的测距结果，表明了结果的有效性。但随着积累时间的增加，探测的有效脉冲计数也增加，信号的信噪比也逐渐增大，因此目标探测概率也逐渐增大，有效验证了单光子探测模型的对应结论。在实验过程中，通过长时间的积累可有效提高统计时间信号的信噪比，提高测距的准确度。而当脉冲数M太少时，将降低目标检测的信噪比，可能导致目标无法有效检测。测距精度由分辨时间单元决定，分辨时间单元越小则测距精度提高。实验通过将目标放置在不同的位置，测量得到多组测距结果，均实现了目标的高精度测距，保证了测距结果的有效性。因此，通过对太赫兹回波脉冲飞行时间进行计数，实现了目标的高精度测距，有效验证了太赫兹单光子飞行时间测距的原理可行性。

5.   结语

本文提出了一种单光子计数太赫兹雷达目标探测模型，通过分析回波产生的光子计数事件的分布规律，结合QCD特点和光子计数技术，对太赫兹单光子雷达的探测性能展开了研究。基于太赫兹光子探测概率，推导得到了太赫兹单光子雷达目标检测性能数学表达式，并通过仿真实验对目标检测性能进行了验证和分析。根据距离门内探测到的光子个数的不同建立了3种典型模型，并分别研究了信噪比与回波位置对检测性能的影响，得到了信噪比一定、回波位于距离门不同位置时，能使检测概率达到最大的回波光子数，同时计算获得了雷达最小可检测信噪比随脉冲积累数的关系。最后，开展了太赫兹雷达光子计数目标探测原理验证实验，有效验证了太赫兹单光子飞行时间测距的原理有效性，为太赫兹频段超灵敏探测技术及单光子雷达系统的发展提供技术支撑。未来，随着太赫兹频段单光子探测器器件研制水平的逐步成熟，可以构建更为完善的太赫兹单光子雷达系统，并开展典型场景下目标探测性能验证实验。

致谢 感谢南京大学和中国科学院上海微系统与信息技术研究所在实验验证方面提供的帮助。