Adaptive Screening Approach of Training Data with an Unknown Number of Outliers(in English)
-
摘要: 在雷达目标多通道自适应检测场景下,诸多非均匀背景因素易导致异常值干扰,使得辅助数据独立同分布条件难以满足,已有辅助数据筛选方法往往假定异常值个数已知,在个数未知的情况下面临较大性能损失。为此,该文研究了异常值个数未知情况下辅助数据自适应筛选方法。首先,在杂噪协方差矩阵已知条件下,建立了异常数据集合的最大似然估计,基于广义内积对辅助数据进行初步排序,将异常数据集合的最大似然估计过程简化为异常值个数估计。其次,利用快速最大似然方法进行未知协方差矩阵估计,提出了未知异常值个数下辅助数据自适应筛选方法。进一步地,为降低异常值对初步排序性能的不利干扰,基于归一化采样协方差矩阵设计了归一化广义内积形式,并结合迭代估计方式,对前述辅助数据自适应筛选流程进行改进。仿真结果表明,与广义内积相比,采用归一化广义内积可获得更高的筛选精度,采用较小迭代次数即可获得稳定的归一化信干比改善;与已有辅助数据筛选方法相比,该文所提方法在异常值个数未知条件下具有更好的筛选性能。Abstract: In multichannel adaptive radar target detection, diverse nonhomogeneous background factors can cause considerable outlier interference, making it challenging to meet the requirements of independent and identically distributed training data. Current methods for screening training data rely on prior knowledge of the number of outliers, often leading to poor performance in real-world scenarios where this number is usually unknown. This paper addresses these issues by focusing on adaptive training data screening when the number of outliers is unknown. First, the outlier set is estimated using maximum likelihood estimation, assuming known covariance matrices of clutter and noise. In particular, the training data is initially ranked based on the generalized inner product of each range cell data, approximately transforming the maximum likelihood estimation of the outlier set to the estimation of the number of outliers. Second, a fast maximum likelihood estimation algorithm is employed to calculate the unknown covariance matrix, and an adaptive screening approach is designed for scenarios with an unspecified number of outliers. Furthermore, to address the adverse effects of outliers on ranking performance, a normalized generalized inner product form is devised utilizing the normalized sampling covariance matrix. This form is subsequently incorporated into an iterative estimation procedure to improve the adaptive screening accuracy of training data. Simulation results demonstrate that the screening accuracy of the normalized generalized inner product exceeds that of the generalized inner product. Moreover, through even a small number of reiterations, maintaining a consistent enhancement in terms of the Normalized Signal-to-Interference Ratio (NSIR) is still possible. Compared with existing methods, the proposed algorithm considerably improves screening performance, especially when the number of outliers is unknown.
-
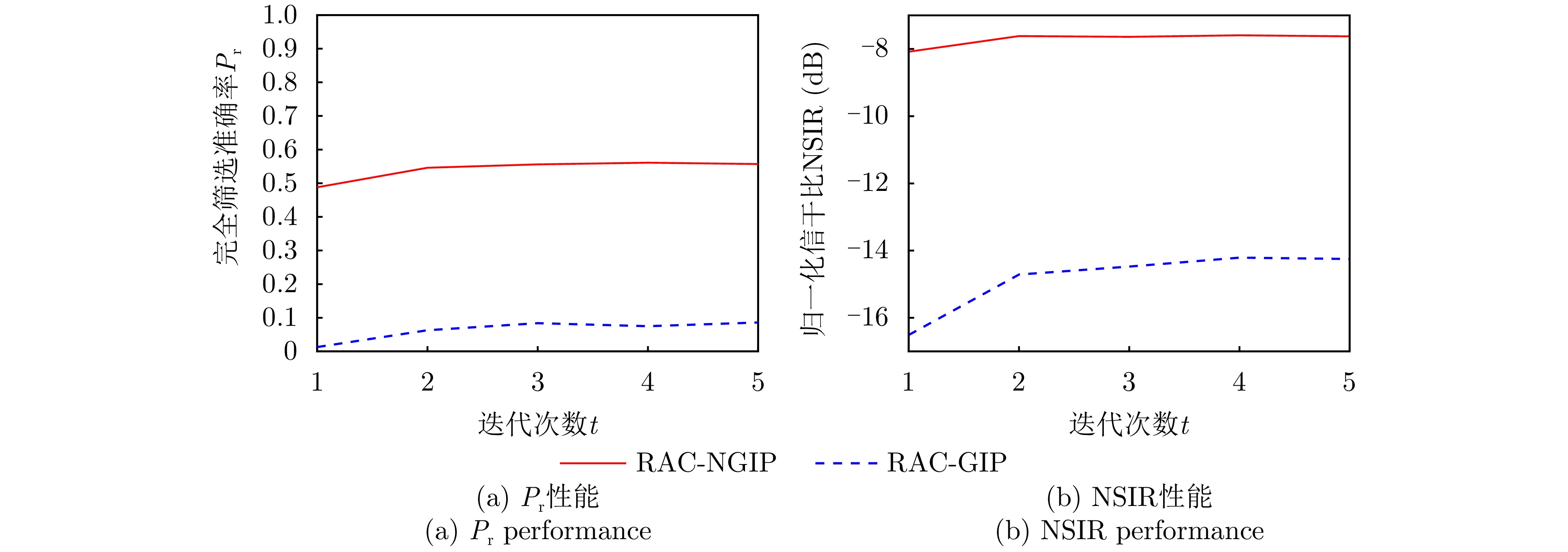
图 1 RAC-NGIP与RAC-GIP方法
${P_{\mathrm{r}}}$ 和NSIR随t的变化曲线($N = 8,{\text{ }}R = 12,{\text{ }}m = 4,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 1.
${P_{\mathrm{r}}}$ and NSIR versus t of the RAC-NGIP and RAC-GIP with$N = 8,{\text{ }}R = 12,{\text{ }}m = 4,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 2 不同自适应筛选方法
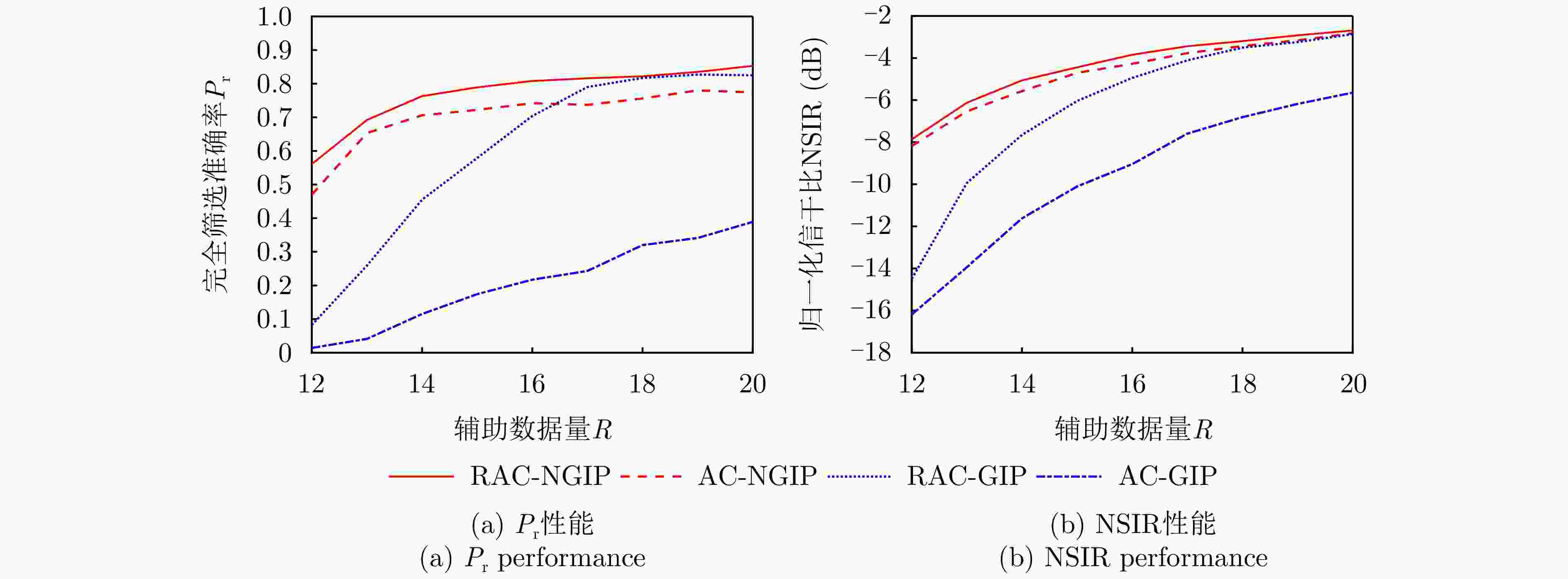
${P_{\mathrm{r}}}$ 和NSIR随R的变化曲线($N = 8,{\text{ }}m = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 2.
${P_{\mathrm{r}}}$ and NSIR versus R of different methods with$N = 8,{\text{ }}m = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 3 不同自适应筛选方法
${P_{\mathrm{r}}}$ 和NSIR随N的变化曲线($R = 12,{\text{ }}m = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 3.
${P_{\mathrm{r}}}$ and NSIR versus N of different methods with$R = 12,{\text{ }}m = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 4 不同自适应筛选方法
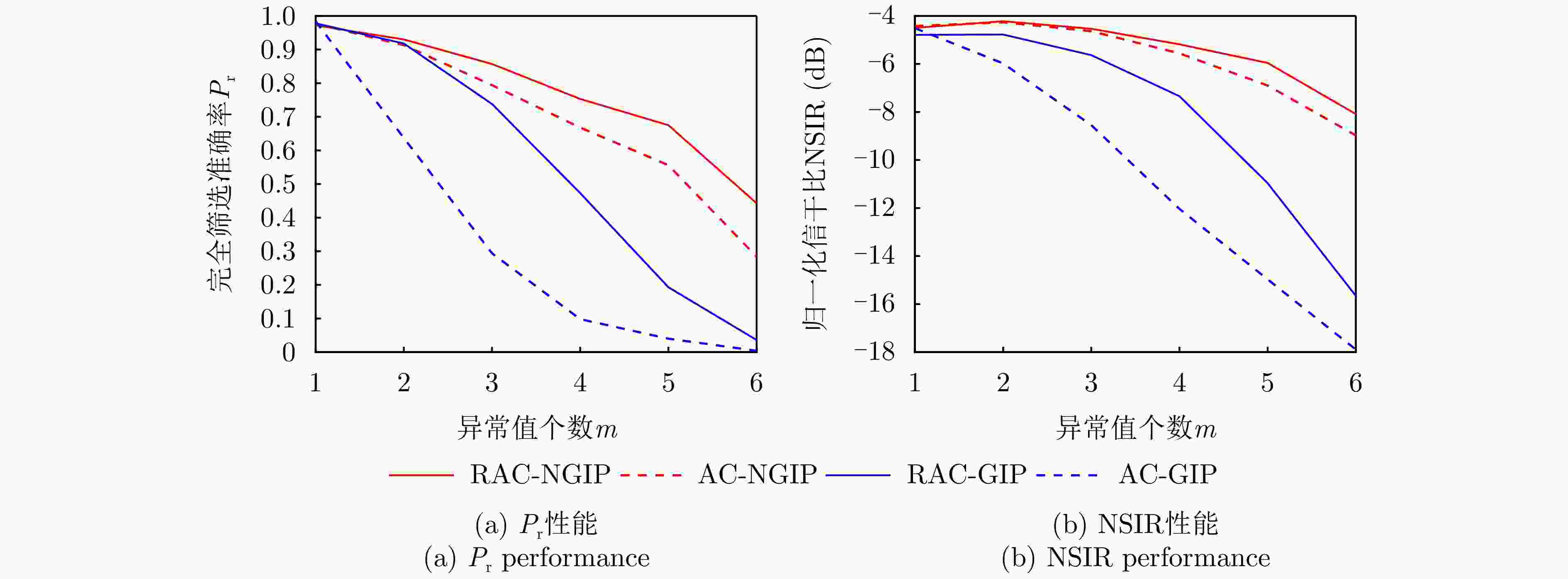
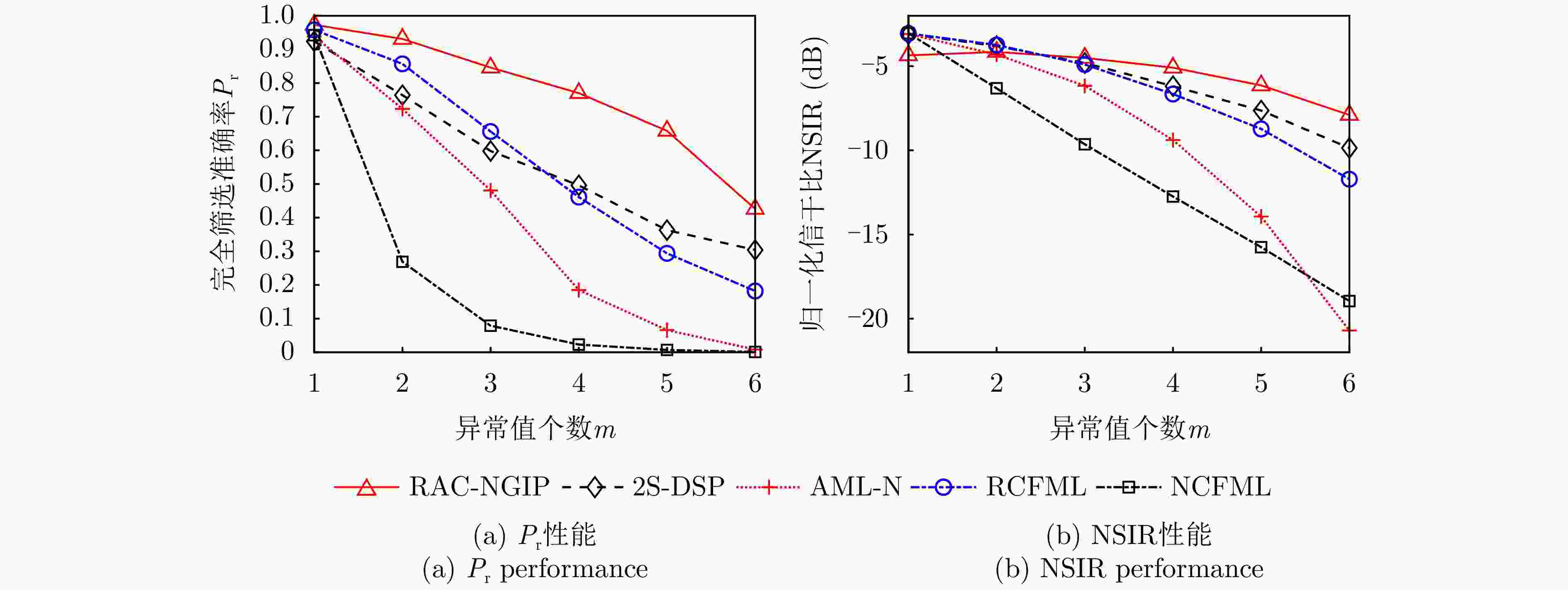
${P_{\mathrm{r}}}$ 和NSIR随m的变化曲线($N = 8,{\text{ }}R = 14,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 4.
${P_{\mathrm{r}}}$ and NSIR versus m of different methods with$N = 8,{\text{ }}R = 14,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 5 当
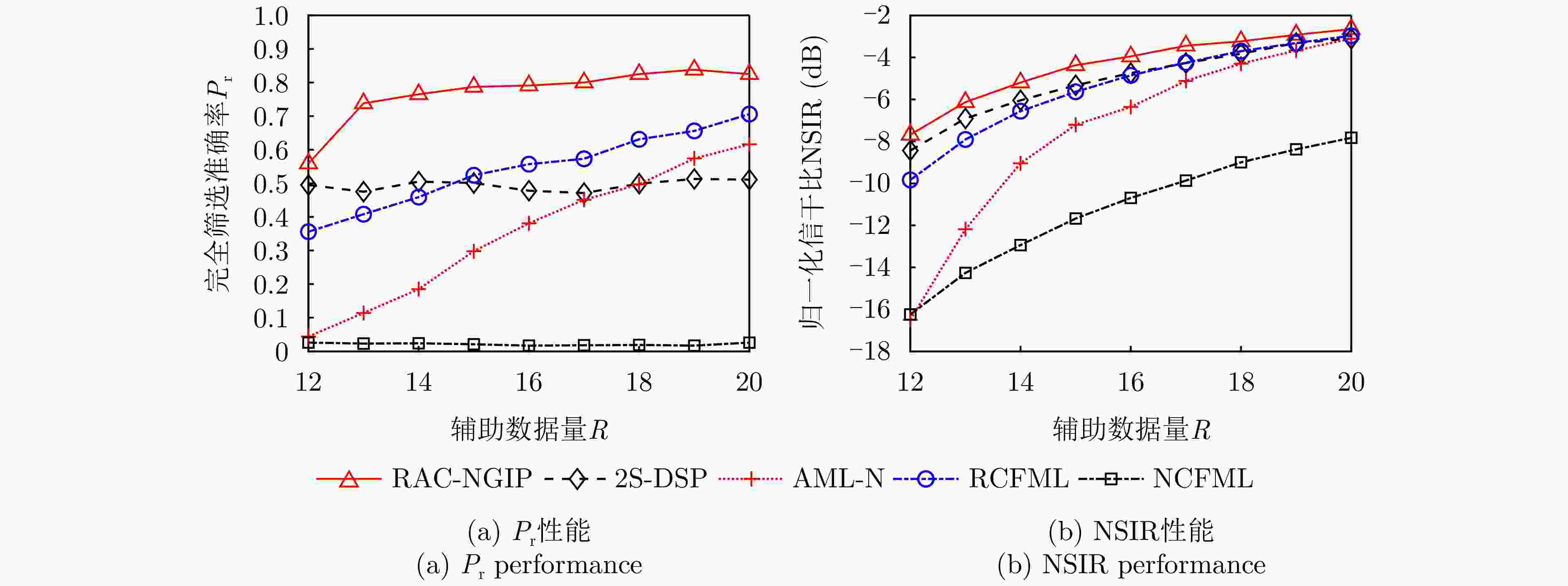
${m_0} < m$ 时,不同筛选方法${P_{\mathrm{r}}}$ 和NSIR随R的变化曲线($N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 3,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 5.
${P_{\mathrm{r}}}$ and NSIR versus R of different methods for${m_0} < m$ with$N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 3,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 6 当
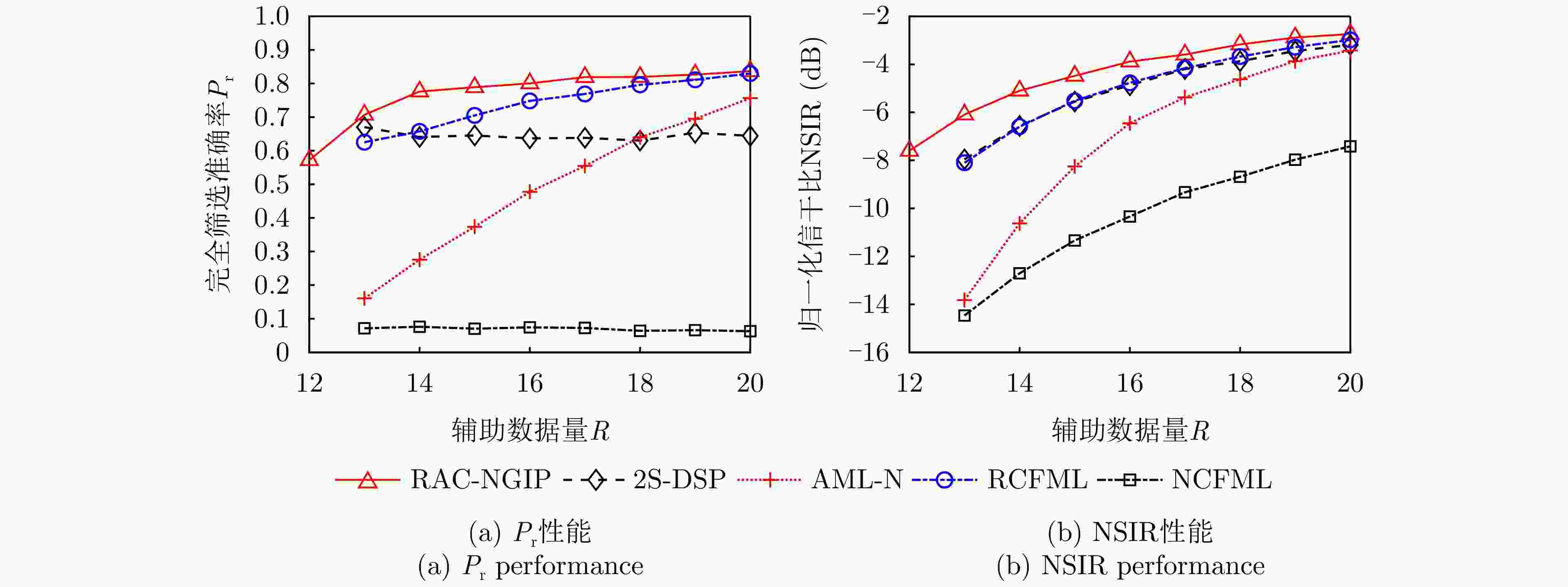
${m_0} = m$ 时,不同筛选方法${P_{\mathrm{r}}}$ 和NSIR随R的变化曲线($N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 6.
${P_{\mathrm{r}}}$ and NSIR versus R of different methods for${m_0} = m$ with$N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 4,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 7 当
${m_0} > m$ 时,不同筛选方法${P_{\mathrm{r}}}$ 和NSIR随R的变化曲线($N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 5,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 7.
${P_{\mathrm{r}}}$ and NSIR versus R of different methods for${m_0} > m$ with$N = 8,{\text{ }}m = 4,{\text{ }}{m_0} = 5,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 图 8 当
${m_0} = m$ 时,不同筛选方法${P_{\mathrm{r}}}$ 和NSIR随m的变化曲线($N = 8,{\text{ }}R = 14,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ )Figure 8.
${P_{\mathrm{r}}}$ and NSIR versus m of different methods for${m_0} = m$ with$N = 8,{\text{ }}R = 14,{\text{ }}T = 2,{\text{ }}{\mathrm{CNR}} = 10\;{\mathrm{dB}},{\text{ }}{\mathrm{ONR}} = 20\;{\mathrm{dB}}$ 1 RAC-NGIP方法
1. RAC-NGIP method
输入:$N \times R$维辅助数据Z,最大迭代次数T
输出:异常数据集合$ {\hat \varOmega _0} $1: $t = 1$
2: $ \hat {\boldsymbol{M}}_{{\mathrm{N}}0}^{(1)} \leftarrow $式(19)3: FOR $i = 1:R$ 4: $ \omega _i^{(t)} \leftarrow $式(20) 5: END
6: 对$ \omega _i^{(t)} $从大到小排序,提取索引序列$\{ (1),(2), \cdots ,(R)\} $7: FOR ${m_p} = 1:R$
8: $ {\hat \varOmega _p} = \{ (1),(2), \cdots ,({m_p})\} $9: $ \varOmega - {\hat \varOmega _p} = \{ ({m_p} + 1),({m_p} + 2), \cdots ,(R)\} $ 10: $ {\hat {\boldsymbol{S}}_{p1}} $, $ {\hat {\boldsymbol{S}}_{p2}} \leftarrow $式(8) 11: $ {{\boldsymbol{M}}_{{\mathrm{S}}1}} $, $ {{\boldsymbol{M}}_{{\mathrm{S}}2}} \leftarrow $式(12) 12: $ {\hat {\boldsymbol{M}}_{p1}} $, $ {\hat {\boldsymbol{M}}_{p2}} \leftarrow $式(14) 13: $ f\left({\boldsymbol{Z}}\left| {{{\hat {\boldsymbol{M}}}_{p1}},{{\hat {\boldsymbol{M}}}_{p2}};{H_p}} \right.,{m_p}\right) \leftarrow $式(15) 14: END 15: $ {\hat m^{(t)}} \leftarrow $式(16) 16: $ \hat \varOmega _0^{(t)} = \left\{ (1),(2), \cdots ,({\hat m^{(t)}})\right\} $ 17: $t \leftarrow t + 1$
18: $ \hat {\boldsymbol{M}}_{{\mathrm{N}}0}^{(t)} \leftarrow $式(21)19: REPEAT 步骤3—步骤18 until $t > T$
20: $ {\hat \varOmega _0} = \hat \varOmega _0^{(T)} $表 1 本文所提的辅助数据自适应筛选方法简要总结
Table 1. Brief summary of methods proposed in this paper
方法 简要说明 计算复杂度 AC-GIP 异常值个数未知的非迭代估计方法,采用GIP筛选处理对辅助数据进行初步排序 $ {O}\left( {{N^2}{R^2} + 3{N^3}R - 4{N^4}} \right) $ AC-NGIP 异常值个数未知的非迭代估计方法,采用NGIP筛选处理对辅助数据进行初步排序 $ {O}\left( {{N^2}{R^2} + 3{N^3}R - 4{N^4}} \right) $ RAC-GIP 异常值个数未知条件下,以AC-GIP为基础,对异常值集合进行迭代估计 $ {O}\left( {T{N^2}{R^2} + 3T{N^3}R - 4T{N^4}} \right) $ RAC-NGIP 异常值个数未知条件下,以AC-NGIP为基础,对异常值集合进行迭代估计 $ {O}\left( {T{N^2}{R^2} + 3T{N^3}R - 4T{N^4}} \right) $ 1 RAC-NGIP method
Input: $N \times R$-dimensional training data Z , maximum number
of iterations TOutput: Outlier data set $ {\hat \varOmega _0} $ 1: $t = 1$ 2: Calculate $ \hat {\boldsymbol{M}}_{{\mathrm{N}}0}^{(1)} $ according to Eq. (19) 3: FOR $i = 1:R$ 4: Calculate $ \omega _i^{(t)} $ according to Eq. (20) 5: END 6: Sort $ \omega _i^{(t)} $ from large to small and extract the index
sequence $\{ (1),(2), \cdots ,(R)\} $7: FOR ${m_p} = 1:R$ 8: $ {\hat \varOmega _p} = \{ (1),(2), \cdots ,({m_p})\} $ 9: $ \varOmega - {\hat \varOmega _p} = \{ ({m_p} + 1),({m_p} + 2), \ldots ,(R)\} $ 10: Calculate $ {\hat {\boldsymbol{S}}_{p1}} $, $ {\hat {\boldsymbol{S}}_{p2}} $ according to Eq. (8) 11: Calculate $ {{\boldsymbol{M}}_{{\mathrm{S}}1}} $, $ {{\boldsymbol{M}}_{{\mathrm{S}}2}} $ according to Eq. (12) 12: Calculate $ {\hat {\boldsymbol{M}}_{p1}} $, $ {\hat {\boldsymbol{M}}_{p2}} $ according to Eq. (14) 13: Calculate the generalized likelihood function
$ {{f}}({\boldsymbol{Z}}\left| {{{\hat {\boldsymbol{M}}}_{p1}},{{\hat {\boldsymbol{M}}}_{p2}};{H_p}} \right.,{m_p}) $ according to Eq. (15)14: END 15: Obtain $ {\hat m^{(t)}} $ by maximizing the generalized likelihood
function according to Eq. (16)16: $ \hat \varOmega _0^{(t)} = \{ (1),(2), \cdots ,({\hat m^{(t)}})\} $ 17: $t \leftarrow t + 1$ 18: Update $ \hat {\boldsymbol{M}}_{{\mathrm{N}}0}^{(t)} $ according to Eq. (21) 19: Repeat Steps 3—18 until the stopping condition $t > T$ is
met20: $ {\hat \varOmega _0} = \hat \varOmega _0^{(T)} $ 表 1 Brief summary of the methods proposed in this work
Method Brief description Computational complexity AC-GIP Noniterative estimation method for an unknown number of outliers. It uses the GIP
screening process to preliminarily rank the training data$ {O}\left( {{N^2}{R^2} + 3{N^3}R - 4{N^4}} \right) $ AC-NGIP Noniterative estimation method for an unknown number of outliers. It uses the NGIP
screening process to preliminarily rank the training data$ {O}\left( {{N^2}{R^2} + 3{N^3}R - 4{N^4}} \right) $ RAC-GIP Under the condition of an unknown number of outliers, it is based on the AC-GIP
and iteratively estimates the outlier set$ {O}\left( {T{N^2}{R^2} + 3T{N^3}R - 4T{N^4}} \right) $ RAC-NGIP Under the condition of an unknown number of outliers, it is based on the AC-NGIP
and iteratively estimates the outlier set$ {O}\left( {T{N^2}{R^2} + 3T{N^3}R - 4T{N^4}} \right) $ -
[1] 王永良, 刘维建, 谢文冲, 等. 机载雷达空时自适应检测方法研究进展[J]. 雷达学报, 2014, 3(2): 201–207. doi: 10.3724/SP.J.1300.2014.13081.WANG Yongliang, LIU Weijian, XIE Wenchong, et al. Research progress of space-time adaptive detection for airborne radar[J]. Journal of Radars, 2014, 3(2): 201–207. doi: 10.3724/SP.J.1300.2014.13081. [2] 李海, 刘新龙, 周盟, 等. 基于修正自适应匹配滤波器的机动目标检测方法[J]. 雷达学报, 2015, 4(5): 552–559. doi: 10.12000/JR15105.LI Hai, LIU Xinlong, ZHOU Meng, et al. Detection of maneuvering target based on modified AMF[J]. Journal of Radars, 2015, 4(5): 552–559. doi: 10.12000/JR15105. [3] DUAN Jia, WU Yifeng, DENG Xiaobo, et al. Robust clutter suppression in heterogeneous environments based on multi frames and similarities[J]. Multidimensional Systems and Signal Processing, 2022, 33(1): 167–180. doi: 10.1007/s11045-021-00792-x. [4] LU Shuping, YI Wei, LIU Weijian, et al. Data-dependent clustering-CFAR detector in heterogeneous environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 476–485. doi: 10.1109/TAES.2017.2740065. [5] 高永婵, 潘丽燕, 李亚超, 等. 空/时对称阵列雷达非高斯杂波背景下多秩距离扩展目标检测方法[J]. 雷达学报, 2022, 11(5): 765–777. doi: 10.12000/JR22013.GAO Yongchan, PAN Liyan, LI Yachao, et al. Multi-rank range-spread target detection method for space/time symmetric array radar under non-Gaussian clutter background[J]. Journal of Radars, 2022, 11(5): 765–777. doi: 10.12000/JR22013. [6] 简涛, 王哲昊, 王海鹏, 等. 基于损失加权修正的舰船目标HRRP小样本元学习识别方法[J]. 信号处理, 2022, 38(12): 2460–2468. doi: 10.16798/j.issn.1003-0530.2022.12.002.JIAN Tao, WANG Zhehao, WANG Haipeng, et al. Ship target HRRP meta-learning recognition with small samples based on loss weighted correction[J]. Journal of Signal Processing, 2022, 38(12): 2460–2468. doi: 10.16798/j.issn.1003-0530.2022.12.002. [7] ZHANG Xinying and WANG Tong. A novel training samples selection method for space-time adaptive processing[C]. The 4th International Conference on Electronic Engineering and Informatics, Guiyang, China, 2022: 1–4. [8] GUO Qiang, LIU Lichao, KALIUZHNYI M, et al. STAP training samples selection based on GIP and volume cross correlation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4028205. doi: 10.1109/LGRS.2022.3218670. [9] MELVIN W L, WICKS M C, and BROWN R D. Assessment of multichannel airborne radar measurements for analysis and design of space-time processing architectures and algorithms[C]. The 1996 IEEE National Radar Conference, Ann Arbor, USA, 1996: 130–135. doi: 10.1109/NRC.1996.510669. [10] MELVIN W L and WICKS M C. Improving practical space-time adaptive radar[C]. The 1997 IEEE National Radar Conference, Syracuse, USA, 1997: 48–53. doi: 10.1109/NRC.1997.588124. [11] GERLACH K. Outlier resistant adaptive matched filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 885–901. doi: 10.1109/TAES.2002.1039406. [12] CONTE E, DE MAIO A, FARINA A, et al. Design and analysis of a knowledge-aided radar detector for Doppler processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1058–1079. doi: 10.1109/TAES.2006.248200. [13] HAN Sudan, DE MAIO A, CAROTENUTO V, et al. Censoring outliers in radar data: An approximate ML approach and its analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(2): 534–546. doi: 10.1109/TAES.2018.2852418. [14] KARBASI S M. Joint likelihood estimation and model order selection for outlier censoring[J]. IET Radar, Sonar & Navigation, 2021, 15(6): 561–573. doi: 10.1049/rsn2.12072. [15] STEINER M and GERLACH K. Fast converging adaptive processor or a structured covariance matrix[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4): 1115–1126. doi: 10.1109/7.892662. [16] YANG Xiaopeng, LIU Yongxu, and LONG Teng. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing[J]. IET Radar, Sonar & Navigation, 2013, 7(1): 47–54. doi: 10.1049/iet-rsn.2011.0404. [17] CONTE E, LOPS M, and RICCI G. Adaptive detection schemes in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1058–1069. doi: 10.1109/7.722671. [18] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893. [19] LI Zhihui, LIU Hanwei, ZHANG Yongshun, et al. Robust nonhomogeneous training samples detection method for space-time adaptive processing radar using sparse-recovery with knowledge-aided[J]. Journal of Applied Remote Sensing, 2017, 11(4): 045013. doi: 10.1117/1.JRS.11.045013. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公





 下载:
下载: