Recent Advances in Multi-radar Collaborative Surveillance: Cognitive Tracking and Resource Scheduling Algorithms(in English)
-
摘要: 多雷达协同探测技术通过有机地联动多部雷达,形成广域分布的探测构型,可充分获取空间、频率分集等探测增益,显著提升雷达系统的目标探测性能和电磁干扰环境顽存能力,是雷达技术领域重点发展的方向之一。近年来,国内外针对多雷达协同探测技术开展了广泛研究,在系统架构设计、信号处理、资源调度等技术方向积累了诸多研究成果。该文首先总结了多雷达协同探测技术的概念内涵,阐述了其基于信号处理闭环反馈的协同机制,分析了其实现过程中所面临的技术挑战;随后,聚焦于认知跟踪与资源调度算法,从内涵特点、系统构成、跟踪模型、信息融合、性能评估、调度算法、优化准则、认知流程等方面进行了技术总结,并分析了协同认知跟踪及其与系统资源调度的关系;接着从雷达资源要素、信息融合架构、跟踪性能指标、资源调度模型、复杂任务场景5个方面梳理和总结了协同认知跟踪与资源调度算法近年来的研究进展;最后总结全文并展望了该领域未来技术的发展趋势,旨在为后续的相关技术研究提供参考。Abstract: Multi-Radar Collaborative Surveillance (MRCS) technology enables a geographically distributed detection configuration through the linkage of multiple radars, which can fully obtain detection gains in terms of spatial and frequency diversity, thereby enhancing the detection performance and viability of radar systems in the context of complex electromagnetic environments. MRCS is one of the key development directions in radar technology and has received extensive attention in recent years. Considerable research on MRCS has been conducted, and numerous achievements in system architecture design, signal processing, and resource scheduling for MRCS have been accumulated. This paper first summarizes the concept of MRCS technology, elaborates on the signal processing-based closed-loop mechanism of cognitive collaboration, and analyzes the challenges faced in the process of MRCS’s implementation. Then, the paper focuses on cognitive tracking and resource scheduling algorithms and implements the technical summary regarding the connotation characteristics, system configuration, tracking model, information fusion, performance evaluation, resource scheduling algorithm, optimization criteria, and cognitive process of cognitive tracking. The relevance between multi-radar cognitive tracking and its system resource scheduling is further analyzed. Subsequently, the recent research trends of cognitive tracking and resource scheduling algorithms are identified and summarized in terms of five aspects: radar resource elements, information fusion architectures, tracking performance indicators, resource scheduling models, and complex task scenarios. Finally, the full text is summarized and future technology in this field is explored to provide a reference for subsequent research on related technologies.
-
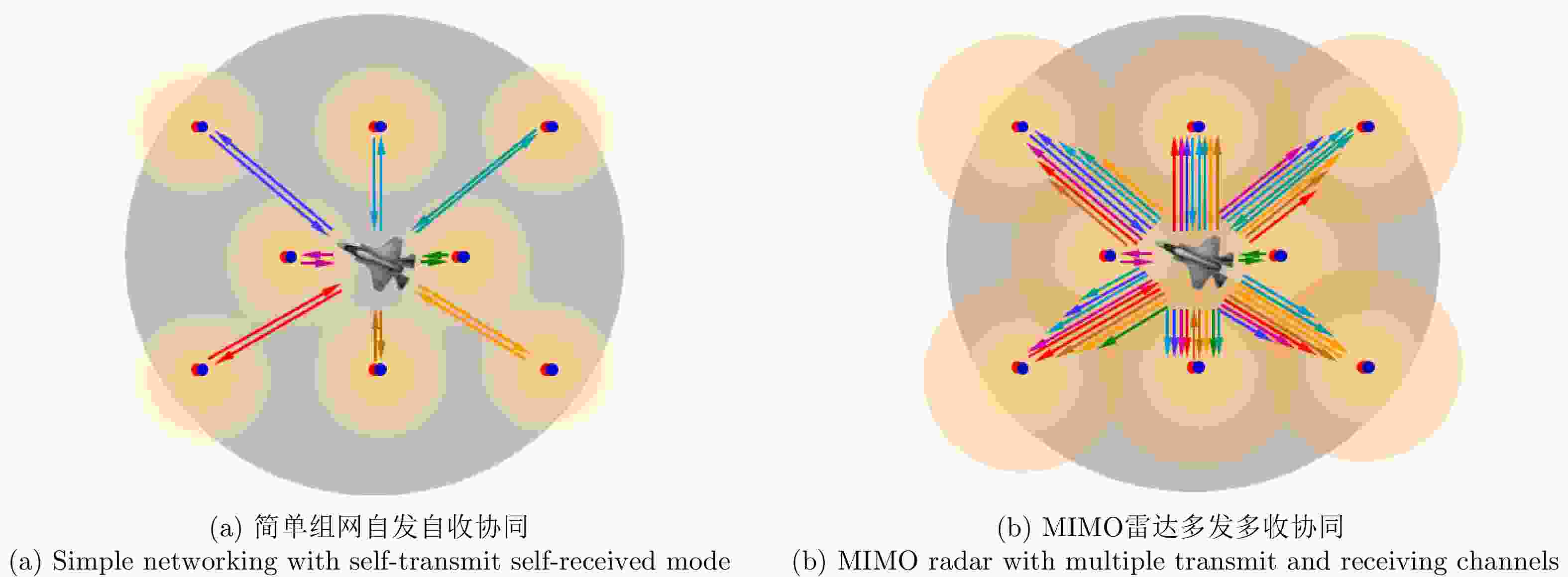
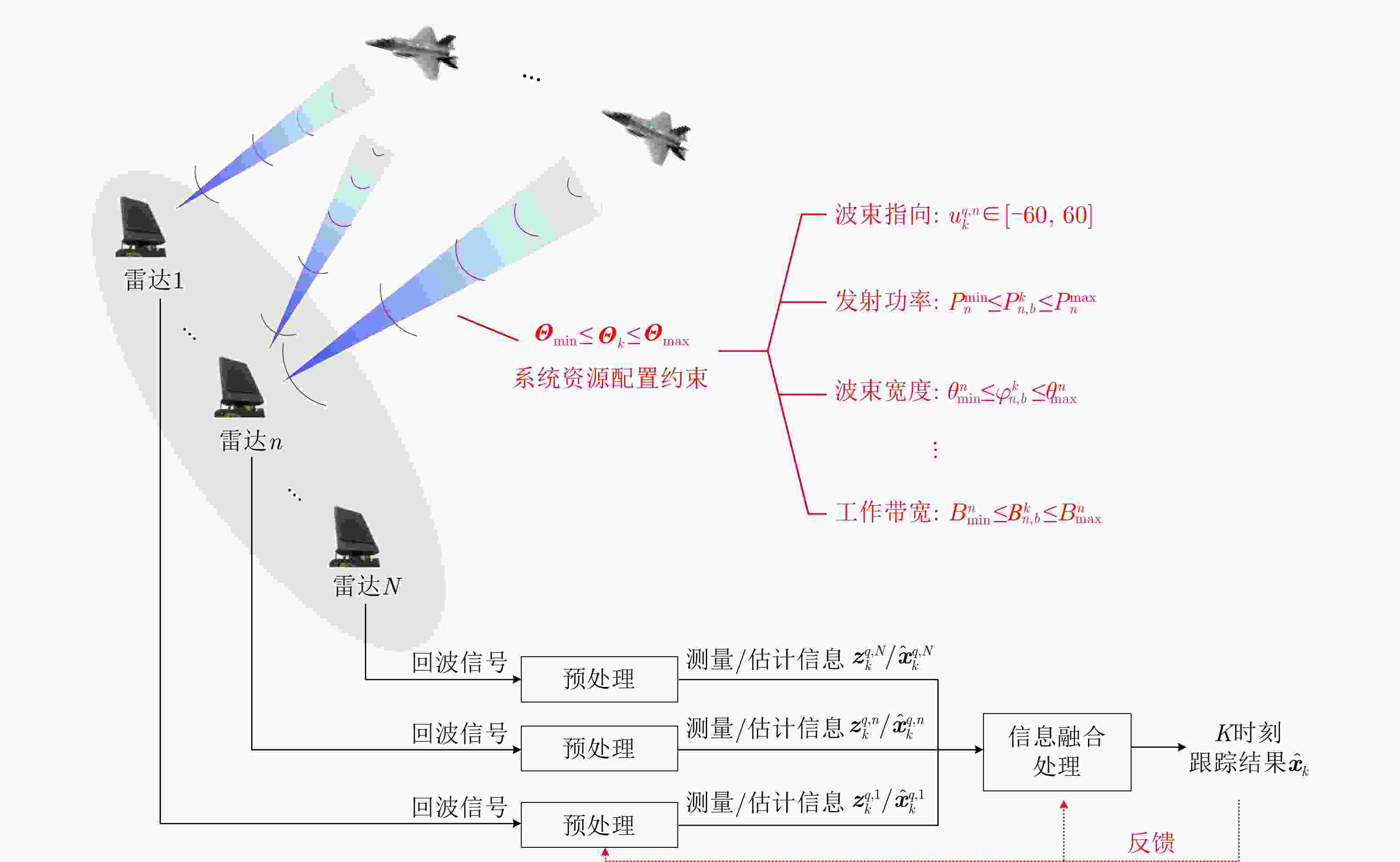
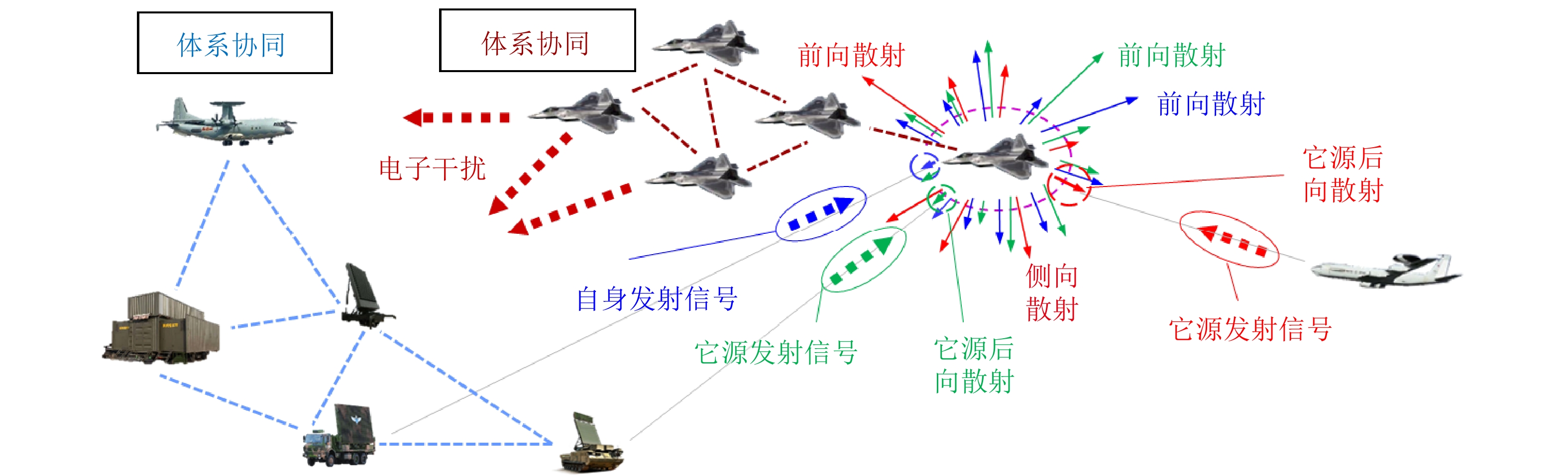
图 2 Schematic diagram of MRCS systems, in which the blue and red dots represent the transmit and receiving antennas, respectively; Arrows of different colors represent the signal transmission and receiving paths of different frequencies, polarization angles, etc. Brown shadows indicate the sensing performance coverage
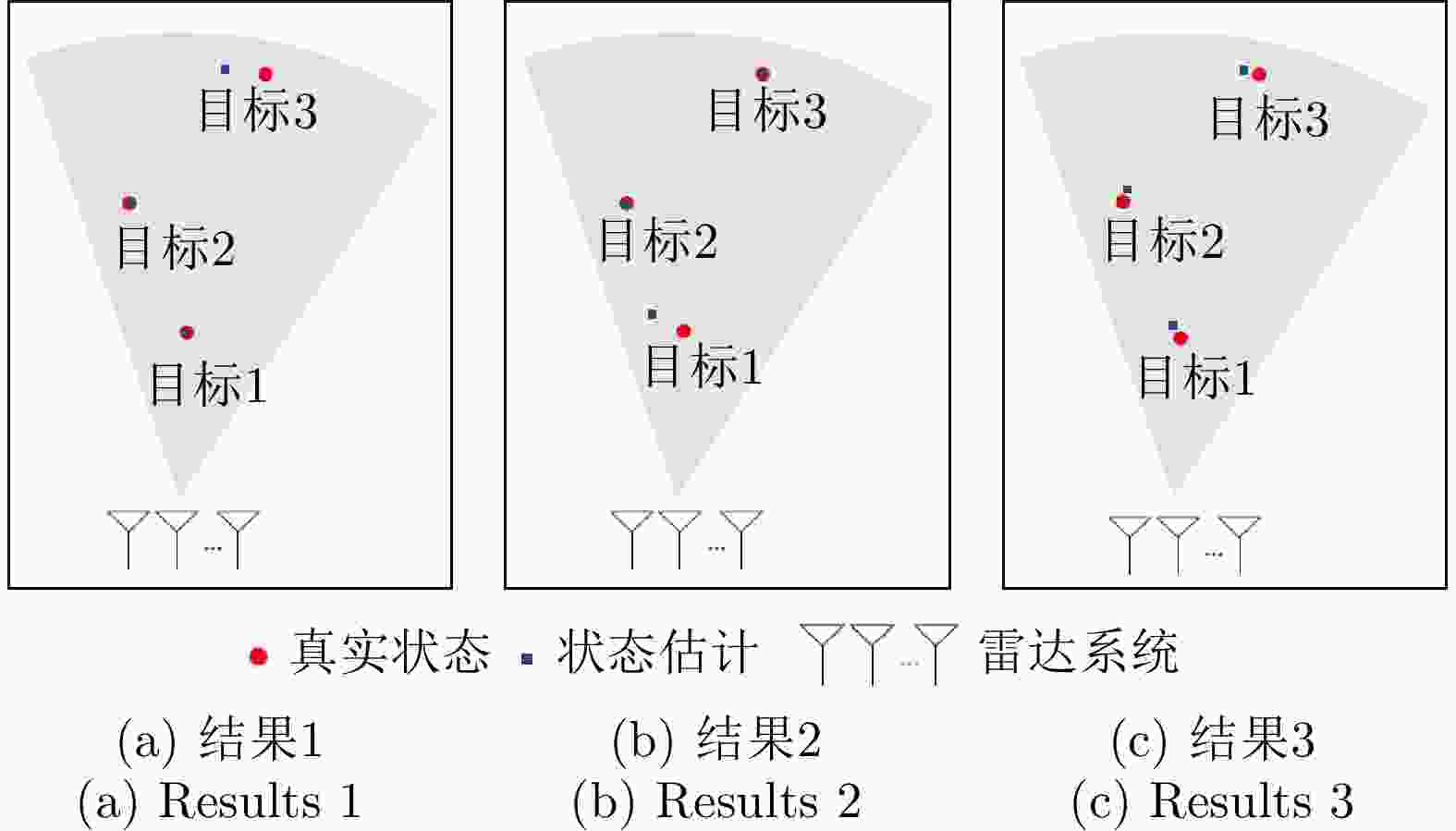
图 11 Three possible results of target state estimation [ 126]
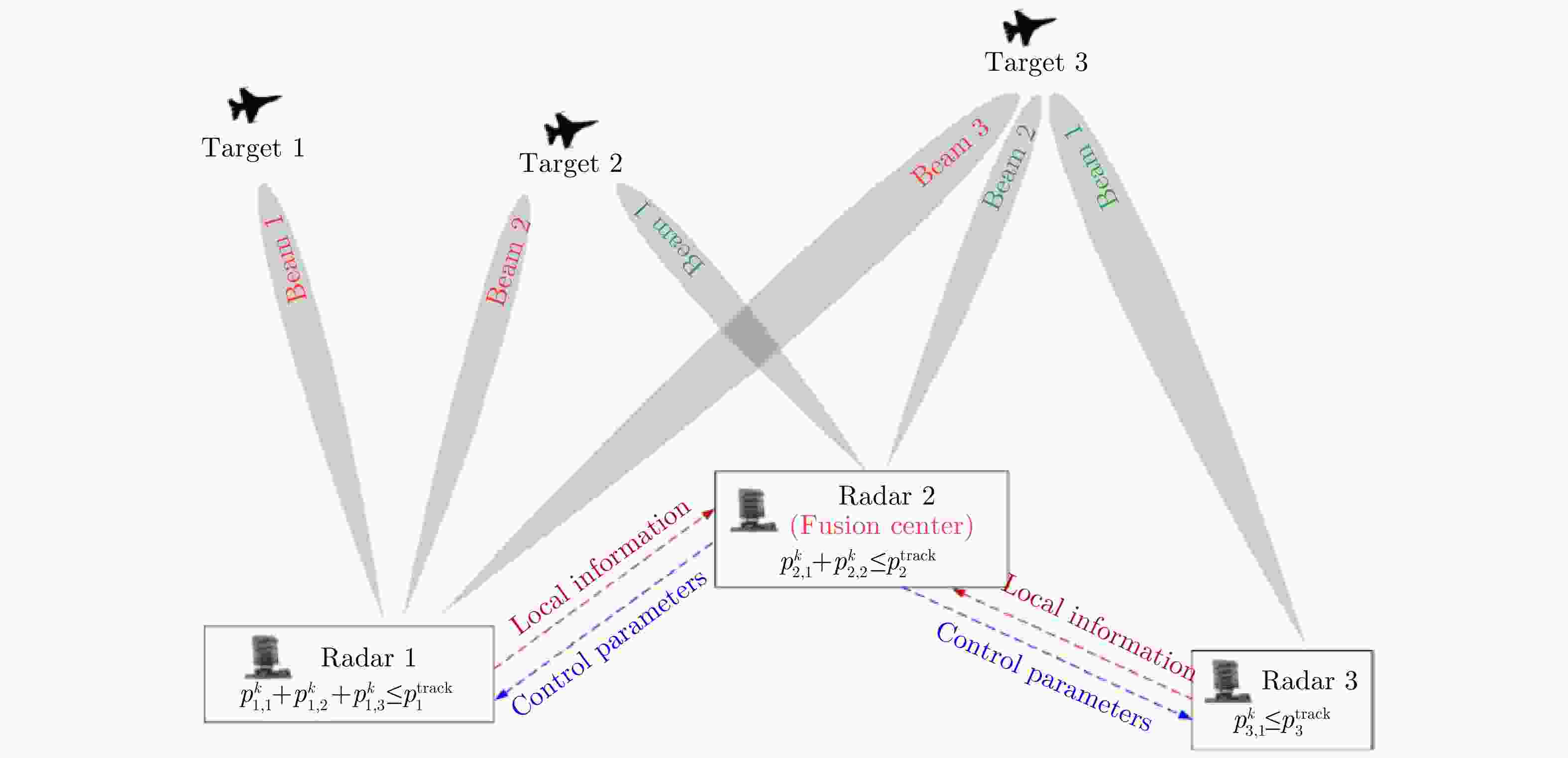
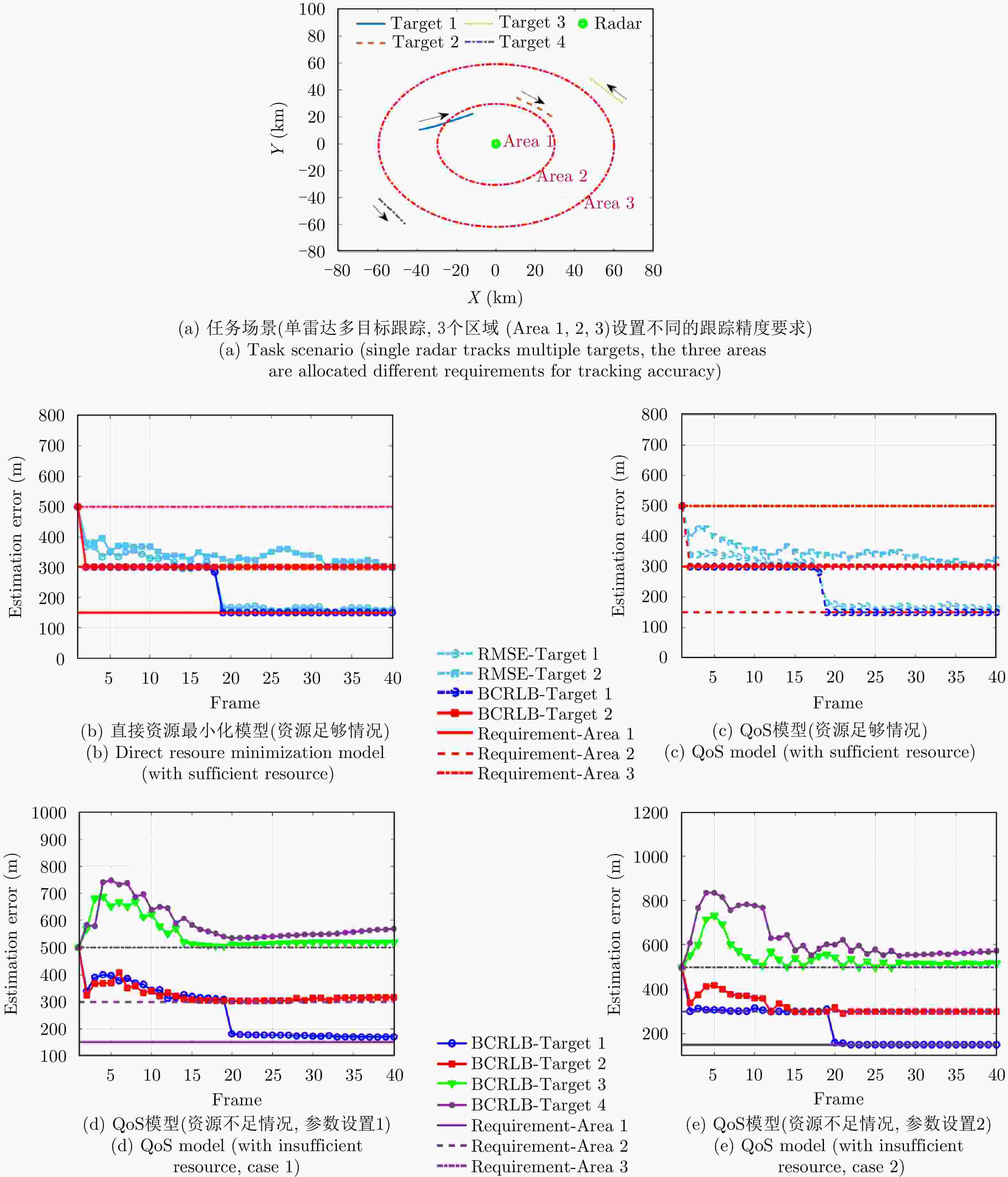
图 12 Multi-target tracking scenario using netter MIMO radar [ 23] (with 3 radars tracking 4 targets simultaneously. The surveillance is divided into 3 parts in terms of the distance from the radar system, and the closer the distance, the higher the expected tracking accuracy
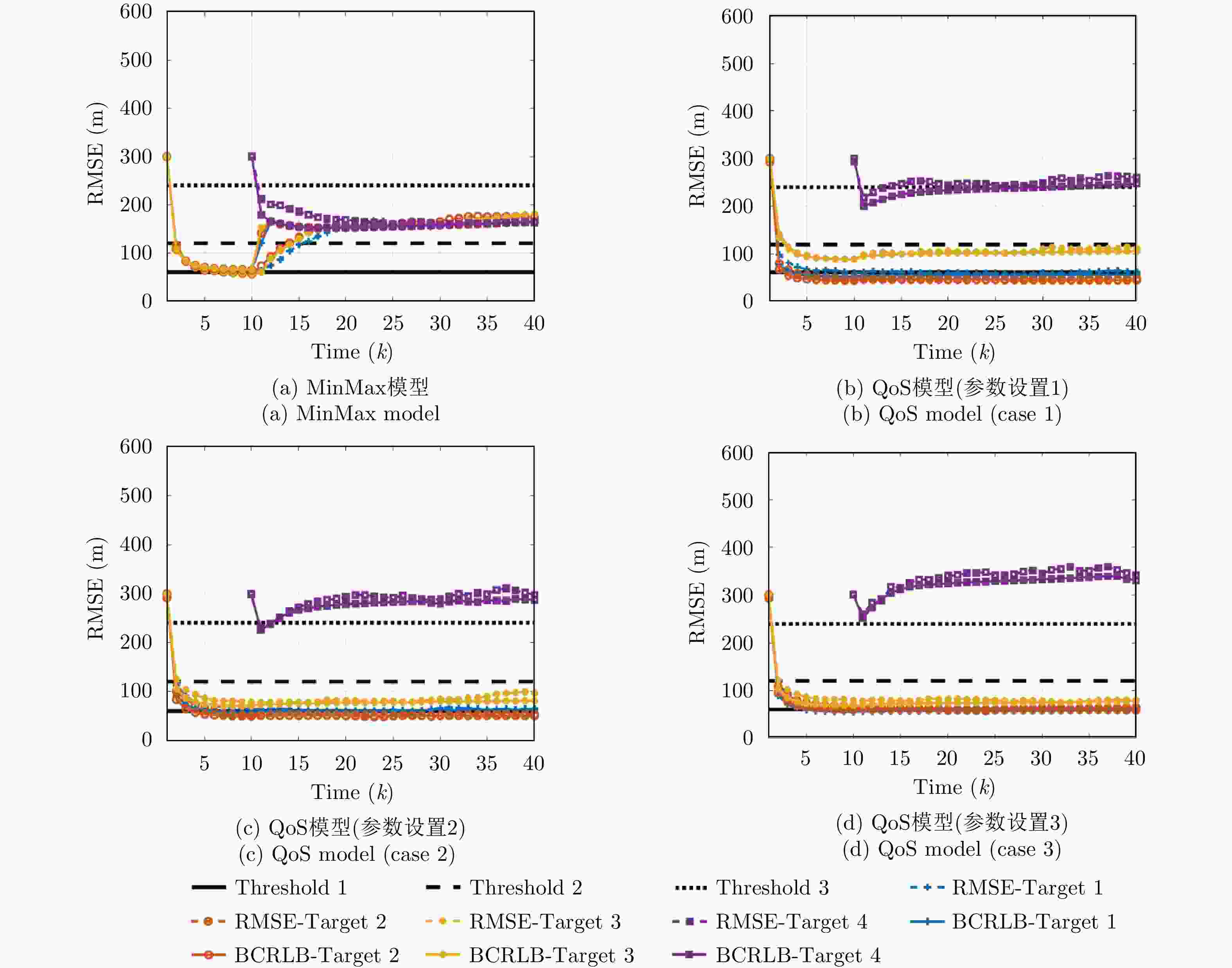
图 13 Multi-target tracking performance comparison between MinMax and QoS models [ 23] (in which RMSE-Target i and BCRLB-Target i represent the root mean-square-error and PCRLB of target i, and Threshold is the corresponding performance requirement)
图 14 Resource allocation comparison between MinMax and QoS models [ 23] (the change of radar beam and transmit power with time)
图 15 Multi-target tracking performance comparison between Direct resource minimization and QoS models [ 33] (with 4 targets to be tracked, in which RMSE-Target i and BCRLB-Target i represent the root mean-square-error and PCRLB of target i, and Requirement is the performance requirement)
参数 $\left[ {\eta _k^1,\eta _k^2,\eta _k^3,\eta _k^4} \right]$ $\left[ {{\varpi ^1},{\varpi ^2},{\varpi ^3},{\varpi ^4}} \right]$ 参数设置1 [60 m, 60 m, 120 m, 240 m] [0.25, 0.25, 0.25, 0.25] 参数设置2 [60 m, 60 m, 60 m, 240 m] [0.25, 0.25, 0.25, 0.25] 参数设置3 [60 m, 60 m, 60 m, 240 m] [0.40, 0.10, 0.40, 0.10] 表 1 The 3 different parameter settings for the QoS model in Ref. [ 23]
$ \left[\eta _{k}^{1},\eta _{k}^{2},\eta _{k}^{3},\eta _{k}^{4}\right] $ $ \left[{\varpi }^{1},{\varpi }^{2},{\varpi }^{3},{\varpi }^{4}\right] $ Setting 1 [60 m, 60 m, 120 m, 240 m] [0.25, 0.25, 0.25, 0.25] Setting 2 [60 m, 60 m, 60 m, 240 m] [0.25, 0.25, 0.25, 0.25] Setting 3 [60 m, 60 m, 60 m, 240 m] [0.40, 0.10, 0.40, 0.10] -
[1] 丁建江. 预警装备组网协同探测模型及应用[J]. 现代雷达, 2020, 42(12): 13–18. doi: 10.16592/j.cnki.1004-7859.2020.12.003.DING Jianjiang. Model and application of the synergy-netted detection for early warning equipment[J]. Modern Radar, 2020, 42(12): 13–18. doi: 10.16592/j.cnki.1004-7859.2020.12.003. [2] 董晓龙, 吴季, 姜景山. 微波辐射计用于隐身目标探测的性能分析[J]. 系统工程与电子技术, 2001, 23(3): 54–57. doi: 10.3321/j.issn:1001-506X.2001.03.016.DONG Xiaolong, WU Ji, and JIANG Jingshan. The performance of the detection of stealthy targets by microwave radiometer[J]. Systems Engineering and Electronics, 2001, 23(3): 54–57. doi: 10.3321/j.issn:1001-506X.2001.03.016. [3] DERHAM T, WOODBRIDGE K, GRIFFITHS H, et al. The design and development of an experimental netted radar system[C]. 2003 International Conference on Radar (IEEE Cat. No. 03EX695), Adelaide, Australia, 2003: 293–298. [4] BAKER C J and HUME A L. Netted radar sensing[J]. IEEE Aerospace and Electronic Systems Magazine, 2003, 18(2): 3–6. doi: 10.1109/MAES.2003.1183861. [5] 杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 1(1): 19–27. doi: 10.3724/SP.J.1300.2012.20010.YANG Jianyu. Development laws and macro trends analysis of radar technology[J]. Journal of Radars, 2012, 1(1): 19–27. doi: 10.3724/SP.J.1300.2012.20010. [6] 周琳. 雷达组网协同探测系统技术架构设计[J]. 现代雷达, 2020, 42(12): 19–23. doi: 10.16592/j.cnki.1004-7859.2020.12.004.ZHOU Lin. Technical architecture design of radar network cooperative detection system[J]. Modern Radar, 2020, 42(12): 19–23. doi: 10.16592/j.cnki.1004-7859.2020.12.004. [7] 王小军, 张修社, 胡小全, 等. 基于杀伤链感知的动态可重构作战体系结构[J]. 现代导航, 2020, 11(4): 235–243, 249. doi: 10.3969/j.issn.1674-7976.2020.04.001.WANG Xiaojun, ZHANG Xiushe, HU Xiaoquan, et al. Dynamic reconfigurable combat architecture based on kill chain perception[J]. Modern Navigation, 2020, 11(4): 235–243, 249. doi: 10.3969/j.issn.1674-7976.2020.04.001. [8] 刘宏伟, 严峻坤, 周生华. 网络化雷达协同探测技术[J]. 现代雷达, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002.LIU Hongwei, YAN Junkun, and ZHOU Shenghua. Collaborative detection technology of netted radar[J]. Modern Radar, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002. [9] 马林, 周琳. 预警系统协同探测技术研究[J]. 现代雷达, 2020, 42(12): 1–6. doi: 10.16592/j.cnki.1004-7859.2020.12.001.MA Lin and ZHOU Lin. A study on collaborative detection technology of early warning system[J]. Modern Radar, 2020, 42(12): 1–6. doi: 10.16592/j.cnki.1004-7859.2020.12.001. [10] 葛建军, 李春霞. 探测体系能力生成理论及方法[J]. 雷达科学与技术, 2018, 16(3): 237–241, 248. doi: 10.3969/j.issn.1672-2337.2018.03.001.GE Jianjun and LI Chunxia. Theory and method for capability generation of detection system[J]. Radar Science and Technology, 2018, 16(3): 237–241, 248. doi: 10.3969/j.issn.1672-2337.2018.03.001. [11] 丁建江. 组网协同探测闭环与预案的设计[J]. 雷达科学与技术, 2021, 19(1): 7–13. doi: 10.3969/j.issn.1672-2337.2021.01.002.DING Jianjiang. Design of the closed-loop and pre-arranged planning for synergy-netted detection[J]. Radar Science and Technology, 2021, 19(1): 7–13. doi: 10.3969/j.issn.1672-2337.2021.01.002. [12] DAVIS M S, SHOWMAN G A, and LANTERMAN A D. Coherent MIMO radar: The phased array and orthogonal waveforms[J]. IEEE Aerospace and Electronic Systems Magazine, 2014, 29(8): 76–91. doi: 10.1109/MAES.2014.130148. [13] 陈金立, 顾红, 苏卫民, 等. 基于发射分集的MIMO雷达相参信号处理方法[J]. 系统工程与电子技术, 2009, 31(8): 1836–1841. doi: 10.3321/j.issn:1001-506X.2009.08.013.CHEN Jinli, GU Hong, SU Weimin, et al. Method of coherent signal processing for MIMO radar based on transmitting diversity[J]. Systems Engineering and Electronics, 2009, 31(8): 1836–1841. doi: 10.3321/j.issn:1001-506X.2009.08.013. [14] 鲁耀兵, 张履谦, 周荫清, 等. 分布式阵列相参合成雷达技术研究[J]. 系统工程与电子技术, 2013, 35(8): 1657–1662. doi: 10.3969/j.issn.1001-506X.2013.08.12.LU Yaobing, ZHANG Lüqian, ZHOU Yinqing, et al. Study on distributed aperture coherence-synthetic radar technology[J]. Systems Engineering and Electronics, 2013, 35(8): 1657–1662. doi: 10.3969/j.issn.1001-506X.2013.08.12. [15] 米闯. 分布式阵列相参合成雷达的发射相参相关研究[D]. [硕士论文], 西安电子科技大学, 2014.MI Chuang. Study on transmit coherence of distributed aperture coherence-synthetic radar[D]. [Master dissertation], Xidian University, 2014. [16] HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448. [17] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars—models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813. [18] 向龙, 丁建江, 周芬, 等. 协同探测群柔性架构分析与设计[J]. 现代雷达, 2022, 44(4): 1–5. doi: 10.16592/j.cnki.1004-7859.2022.04.001.XIANG Long, DING Jianjiang, ZHOU Fen, et al. Analysis and design for the flexible architecture of synergy-netted detection cluster[J]. Modern Radar, 2022, 44(4): 1–5. doi: 10.16592/j.cnki.1004-7859.2022.04.001. [19] HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335. [20] CHARLISH A, HOFFMANN F, DEGEN C, et al. The development from adaptive to cognitive radar resource management[J]. IEEE Aerospace and Electronic Systems Magazine, 2020, 35(6): 8–19. doi: 10.1109/MAES.2019.2957847. [21] BRYANT D J. Rethinking OODA: Toward a modern cognitive framework of command decision making[J]. Military Psychology, 2006, 18(3): 183–206. doi: 10.1207/s15327876mp1803_1. [22] ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188. doi: 10.1109/78.978374. [23] YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587. [24] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part I. Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333–1364. doi: 10.1109/TAES.2003.1261132. [25] YAN Junkun, JIAO Hao, PU Wenqiang, et al. Radar sensor network resource allocation for fused target tracking: A brief review[J]. Information Fusion, 2022, 86/87: 104–115. doi: 10.1016/j.inffus.2022.06.009. [26] LIGGINS M E, CHONG C Y, KADAR I, et al. Distributed fusion architectures and algorithms for target tracking[J]. Proceedings of the IEEE, 1997, 85(1): 95–107. doi: 10.1109/JPROC.1997.554211. [27] HAYKIN S, HUBER K, and CHEN Zhe. Bayesian sequential state estimation for MIMO wireless communications[J]. Proceedings of the IEEE, 2004, 92(3): 439–454. doi: 10.1109/JPROC.2003.823143. [28] SÄRKKÄ S. Bayesian Filtering and Smoothing[M]. Cambridge: Cambridge University Press, 2013: 17–24. [29] LI Xueting, ZHANG Tianxian, YI Wei, et al. Radar selection based on the measurement information and the measurement compensation for target tracking in radar network[J]. IEEE Sensors Journal, 2019, 19(18): 7923–7935. doi: 10.1109/JSEN.2019.2918866. [30] SHI Chenguang, ZHOU Jianjiang, and WANG Fei. Low probability of intercept optimization for radar network based on mutual information[C]. 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 2014: 683–687. [31] GODRICH H, HAIMOVICH A M, and BLUM R S. Target localization accuracy gain in MIMO radar-based systems[J]. IEEE Transactions on Information Theory, 2010, 56(6): 2783–2803. doi: 10.1109/TIT.2010.2046246. [32] TICHAVSKY P, MURAVCHIK C H, and NEHORAI A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1386–1396. doi: 10.1109/78.668800. [33] YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519. [34] YUAN Ye, YI Wei, and VARSHNEY P K. Exponential mixture density based approximation to posterior cramér-rao lower bound for distributed target tracking[J]. IEEE Transactions on Signal Processing, 2022, 70: 862–877. doi: 10.1109/TSP.2022.3148540. [35] ZHANG Haowei, LIU Weijian, SHI Junpeng, et al. Joint detection threshold optimization and illumination time allocation strategy for cognitive tracking in a networked radar system[J]. IEEE Transactions on Signal Processing, 2022, 70: 5833–5847. doi: 10.1109/TSP.2022.3188205. [36] 王祥丽, 易伟, 孔令讲. 基于多目标跟踪的相控阵雷达波束和驻留时间联合分配方法[J]. 雷达学报, 2017, 6(6): 602–610. doi: 10.12000/JR17045.WANG Xiangli, YI Wei, and KONG Lingjiang. Joint beam selection and dwell time allocation for multi-target tracking in phased array radar system[J]. Journal of Radars, 2017, 6(6): 602–610. doi: 10.12000/JR17045. [37] YAN Junkun, PU Wenqiang, LIU Hongwei, et al. Cooperative target assignment and dwell allocation for multiple target tracking in phased array radar network[J]. Signal Processing, 2017, 141: 74–83. doi: 10.1016/j.sigpro.2017.05.014. [38] YAN Junkun, PU Wenqiang, DAI Jinhui, et al. Resource allocation for search and track application in phased array radar based on Pareto bi-objective optimization[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3487–3499. doi: 10.1109/TVT.2019.2894960. [39] SHI Chenguang, DING Lintao, WANG Fei, et al. Joint target assignment and resource optimization framework for multitarget tracking in phased array radar network[J]. IEEE Systems Journal, 2021, 15(3): 4379–4390. doi: 10.1109/JSYST.2020.3025867. [40] YUAN Ye, YI Wei, and KONG Lingjiang. Joint tracking sequence and dwell time allocation for multi-target tracking with phased array radar[J]. Signal Processing, 2021, 192: 108374. doi: 10.1016/j.sigpro.2021.108374. [41] KIRUBARAJAN T, BAR-SHALOM Y, BLAIR W D, et al. IMMPDA solution to benchmark for radar resource allocation and tracking in the presence of ECM[C]. 1997 European Control Conference (ECC), Brussels, Belgium, 1997: 2967–2972. [42] BLAIR W D and WATSON G A. Benchmark problem for radar resource allocation and tracking maneuvering targets in the presence of ECM[R]. Naval Surface Warfare Center Dahlgren Division, Dahlgren, VA, 1996. [43] MOO P W and DING Zhen. Coordinated radar resource management for networked phased array radars[J]. IET Radar, Sonar & Navigation, 2015, 9(8): 1009–1020. doi: 10.1049/iet-rsn.2013.0368. [44] LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812. [45] YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint beam selection and power allocation for multiple target tracking in netted colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2016, 64(24): 6417–6427. doi: 10.1109/TSP.2016.2607147. [46] YAN Junkun, LIU Hongwei, JIU Bo, et al. Simultaneous multibeam resource allocation scheme for multiple target tracking[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3110–3122. doi: 10.1109/TSP.2015.2417504. [47] YAN Junkun, LIU Hongwei, JIU Bo, et al. Joint detection and tracking processing algorithm for target tracking in multiple radar system[J]. IEEE Sensors Journal, 2015, 15(11): 6534–6541. doi: 10.1109/JSEN.2015.2461435. [48] CHENG Ting, LI Shuyi, and ZHANG Jie. Adaptive resource management in multiple targets tracking for co-located multiple input multiple output radar[J]. IET Radar, Sonar & Navigation, 2018, 12(9): 1038–1045. doi: 10.1049/iet-rsn.2018.5153. [49] ZHANG Weiwei, SHI Chenguang, and ZHOU Jianjiang. Power minimization-based joint resource allocation algorithm for target localization in noncoherent distributed MIMO radar system[J]. IEEE Systems Journal, 2022, 16(2): 2183–2194. doi: 10.1109/JSYST.2021.3126152. [50] SHI Chenguang, DING Lintao, WANG Fei, et al. Low probability of intercept-based collaborative power and bandwidth allocation strategy for multi-target tracking in distributed radar network system[J]. IEEE Sensors Journal, 2020, 20(12): 6367–6377. doi: 10.1109/JSEN.2020.2977328. [51] REN Haiwei, YI Wei, LU Xiujuan, et al. Online beam scheduling for multi-target tracking in linear wireless array radar[C]. 2021 CIE International Conference on Radar (Radar), Haikou, China, 2021: 2553–2558. [52] SUN Hao, LI Ming, ZUO Lei, et al. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems[J]. IEEE Signal Processing Letters, 2021, 28: 1863–1867. doi: 10.1109/LSP.2021.3108675. [53] CHEN Haowen, TA Shiying, and SUN Bin. Cooperative game approach to power allocation for target tracking in distributed MIMO radar sensor networks[J]. IEEE Sensors Journal, 2015, 15(10): 5423–5432. doi: 10.1109/JSEN.2015.2431261. [54] 胡捍英, 孙扬, 郑娜娥. 多目标速度估计的分布式MIMO雷达资源分配算法[J]. 电子与信息学报, 2016, 38(10): 2453–2460. doi: 10.11999/JEIT151452.HU Hanying, SUN Yang, and ZHENG Na’e. Resource allocation approach in distributed MIMO radar with multiple targets for velocity estimation[J]. Journal of Electronics & Information Technology, 2016, 38(10): 2453–2460. doi: 10.11999/JEIT151452. [55] ZHANG Haowei, XIE Junwei, GE Jiaang, et al. Finite sensor selection algorithm in distributed MIMO radar for joint target tracking and detection[J]. Journal of Systems Engineering and Electronics, 2020, 31(2): 290–302. doi: 10.23919/JSEE.2020.000007. [56] XIE Mingchi, YI Wei, KONG Lingjiang, et al. Receive-beam resource allocation for multiple target tracking with distributed MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2421–2436. doi: 10.1109/TAES.2018.2818579. [57] LIU Xinghua, XU Zhenhai, DONG Wei, et al. Cognitive resource allocation for target tracking in location-aware radar networks[J]. IEEE Signal Processing Letters, 2020, 27: 650–654. doi: 10.1109/LSP.2020.2987208. [58] WANG Wenqin. Moving-target tracking by cognitive RF stealth radar using frequency diverse array antenna[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 3764–3773. doi: 10.1109/TGRS.2016.2527057. [59] LIU Pengfei, LIU Yimin, HUANG Tianyao, et al. Decentralized automotive radar spectrum allocation to avoid mutual interference using reinforcement learning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 190–205. doi: 10.1109/TAES.2020.3011869. [60] DURST S and BRÜGGENWIRTH S. Quality of service based radar resource management using deep reinforcement learning[C]. 2021 IEEE Radar Conference (RadarConf21), Atlanta, USA, 2021: 1–6. [61] GARCIA N, HAIMOVICH A M, COULON M, et al. Resource allocation in MIMO radar with multiple targets for non-coherent localization[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2656–2666. doi: 10.1109/TSP.2014.2315169. [62] CIUONZO D, JAVADI S H, MOHAMMADI A, et al. Bandwidth-constrained decentralized detection of an unknown vector signal via multisensor fusion[J]. IEEE Transactions on Signal and Information Processing over Networks, 2020, 6: 744–758. doi: 10.1109/TSIPN.2020.3037832. [63] SELVI E, BUEHRER R M, MARTONE A, et al. Reinforcement learning for adaptable bandwidth tracking radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3904–3921. doi: 10.1109/TAES.2020.2987443. [64] SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1316–1330. doi: 10.1109/TSP.2017.2770086. [65] BELL K L, BAKER C J, SMITH G E, et al. Cognitive radar framework for target detection and tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1427–1439. doi: 10.1109/JSTSP.2015.2465304. [66] WANG Fangzhou and LI Hongbin. Joint power allocation for radar and communication co-existence[J]. IEEE Signal Processing Letters, 2019, 26(11): 1608–1612. doi: 10.1109/LSP.2019.2941087. [67] SHI Chenguang, WANG Yijie, WANG Fei, et al. Joint optimization scheme for subcarrier selection and power allocation in multicarrier dual-function radar-communication system[J]. IEEE Systems Journal, 2021, 15(1): 947–958. doi: 10.1109/JSYST.2020.2984637. [68] VAN CHIEN T, BJÖRNSON E, and LARSSON E G. Joint power allocation and load balancing optimization for energy-efficient cell-free massive MIMO networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(10): 6798–6812. doi: 10.1109/TWC.2020.3006083. [69] DING Lintao, SHI Chenguang, QIU Wei, et al. Joint dwell time and bandwidth optimization for multi-target tracking in radar network based on low probability of intercept[J]. Sensors, 2020, 20(5): 1269. doi: 10.3390/s20051269. [70] LIU Xinghua, XU Zhenhai, WANG Luoshengbin, et al. Cognitive dwell time allocation for distributed radar sensor networks tracking via cone programming[J]. IEEE Sensors Journal, 2020, 20(10): 5092–5101. doi: 10.1109/JSEN.2020.2970280. [71] MIR H S and GUITOUNI A. Variable dwell time task scheduling for multifunction radar[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 463–472. doi: 10.1109/TASE.2013.2285014. [72] WATSON G A and BLAIR W D. Tracking performance of a phased array radar with revisit time controlled using the IMM algorithm[C]. 1994 IEEE National Radar Conference, Atlanta, USA, 1994: 160–165. [73] SHI Yuchun, JIU Bo, YAN Junkun, et al. Data-driven radar selection and power allocation method for target tracking in multiple radar system[J]. IEEE Sensors Journal, 2021, 21(17): 19296–19306. doi: 10.1109/JSEN.2021.3087747. [74] MOHAMMADI A and ASIF A. Decentralized sensor selection based on the distributed posterior Cramér-Rao lower bound[C]. 2012 15th International Conference on Information Fusion, Singapore, 2012: 1668–1675. [75] SHEN Xiaojing and VARSHNEY P K. Sensor selection based on generalized information gain for target tracking in large sensor networks[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 363–375. doi: 10.1109/TSP.2013.2289881. [76] ZOU Yi and CHAKRABARTY K. Sensor deployment and target localization in distributed sensor networks[J]. ACM Transactions on Embedded Computing Systems, 2004, 3(1): 61–91. doi: 10.1145/972627.972631. [77] CHAVALI P and NEHORAI A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 715–729. doi: 10.1109/TSP.2011.2174989. [78] SUN Bin, CHEN Haowen, WEI Xizhang, et al. Power allocation for range-only localisation in distributed multiple-input multiple-output radar networks - a cooperative game approach[J]. IET Radar Sonar & Navigation, 2014, 8(7): 708–718. [79] YUAN Ye, YI Wei, KIRUBARAJAN T, et al. Scaled accuracy based power allocation for multi-target tracking with colocated MIMO radars[J]. Signal Processing, 2019, 158: 227–240. doi: 10.1016/j.sigpro.2019.01.014. [80] XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 729–743. doi: 10.1109/TSP.2017.2777394. [81] ZHANG Haowei, ZONG Binfeng, and XIE Junwei. Power and bandwidth allocation for multi-target tracking in collocated MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(9): 9795–9806. doi: 10.1109/TVT.2020.3002899. [82] SU Yang, CHENG Ting, HE Zishu, et al. Adaptive resource management for multi-target tracking in co-located MIMO radar based on time-space joint allocation[J]. Journal of Systems Engineering and Electronics, 2020, 31(5): 916–927. doi: 10.23919/JSEE.2020.000061. [83] ZHANG Haowei, LIU Weijian, XIE Junwei, et al. Joint subarray selection and power allocation for cognitive target tracking in large-scale MIMO radar networks[J]. IEEE Systems Journal, 2020, 14(2): 2569–2580. doi: 10.1109/JSYST.2019.2960401. [84] MA Botao, CHEN Haowen, SUN Bin, et al. A joint scheme of antenna selection and power allocation for Localization in MIMO radar sensor networks[J]. IEEE communications letters, 2014, 18(12): 2225–2228. doi: 10.1109/LCOMM.2014.2365206. [85] KATSILIERIS F, DRIESSEN H, and YAROVOY A. Threat-based sensor management for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 2772–2785. doi: 10.1109/TAES.2015.140052. [86] SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869. [87] JIN Biao, KUANG Xiaofei, LIU Shujin, et al. Joint allocation of transmit power and signal bandwidth for distributed cognitive tracking radar network using cooperative game[J]. Digital Signal Processing, 2023, 135: 103964. doi: 10.1016/j.dsp.2023.103964. [88] 孟令同, 易伟, 孔令讲. 动平台分布式雷达系统协同跟踪路径优化算法[J]. 信号处理, 2018, 34(11): 1321–1329. doi: 10.16798/j.issn.1003-0530.2018.11.007.MENG Lingtong, YI Wei, and KONG Lingjiang. Path optimization method of distributed radar system with moving platform for cooperative target tracking[J]. Journal of Signal Processing, 2018, 34(11): 1321–1329. doi: 10.16798/j.issn.1003-0530.2018.11.007. [89] TANG Yaoying, WANG Yao, and SHAO Xuehui. Mobile sensor path planning for multi-region surveillance with different mission importances[C]. 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 2019: 1–5. [90] LU Xiujuan, KONG Lingjiang, SUN Jun, et al. Joint online route planning and power allocation for multitarget tracking in airborne radar systems[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. [91] 严俊坤, 白舸, 黄佳沁, 等. 多机雷达协同区域动态覆盖航迹优化方法[J]. 雷达学报, 2023, 12(3): 541–549. doi: 10.12000/JR22196.YAN Junkun, BAI Ge, HUANG Jiaqin, et al. Flight path optimization method for dynamic area coverage based on multi-aircraft Radars[J]. Journal of Radars, 2023, 12(3): 541–549. doi: 10.12000/JR22196. [92] DAI Jinhui, PU Wenqiang, YAN Junkun, et al. Multi-UAV collaborative trajectory optimization for asynchronous 3-D passive multitarget tracking[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5101116. doi: 10.1109/TGRS.2023.3239952. [93] DING Lintao, SHI Chenguang, and ZHOU Jianjiang. Collaborative route optimization and resource management strategy for multi-target tracking in airborne radar system[J]. Digital Signal Processing, 2023, 138: 104051. doi: 10.1016/j.dsp.2023.104051. [94] YAN Junkun, HE Tao, MA Lin, et al. Maneuvering resource allocation for coordinated target tracking in airborne radar network[J]. IEEE Transactions on Signal Processing, 2023, 71: 1563–1573. doi: 10.1109/TSP.2023.3265882. [95] YI Jianxin, WAN Xianrong, LEUNG H, et al. Joint placement of transmitters and receivers for distributed MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 122–134. doi: 10.1109/TAES.2017.2649338. [96] LIANG Junli, HUAN Mingsai, DENG Xiaobo, et al. Optimal transmitter and receiver placement for localizing 2D interested-region target with constrained sensor regions[J]. Signal Processing, 2021, 183: 108032. doi: 10.1016/j.sigpro.2021.108032. [97] WANG Yao, ZHOU Tao, and YI Wei. Geometric optimization of distributed MIMO radar system for accurate localization in multiple key subareas[J]. Signal Processing, 2022, 201: 108689. doi: 10.1016/j.sigpro.2022.108689. [98] QI Cheng, XIE Junwei, and ZHANG Haowei. Joint antenna placement and power allocation for target detection in a distributed MIMO radar network[J]. Remote Sensing, 2022, 14(11): 2650. doi: 10.3390/rs14112650. [99] YANG Chengxin, WANG Yao, and YI Wei. Network architecture optimization for area surveillance in multi-static radar systems[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. [100] HERNANDEZ M L, KIRUBARAJAN T, and BAR-SHALOM Y. Multisensor resource deployment using posterior Cramer-Rao bounds[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(2): 399–416. doi: 10.1109/TAES.2004.1309993. [101] THARMARASA R, KIRUBARAJAN T, and HERNANDEZ M. Large-scale optimal sensor array management for multitarget tracking[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(5): 803–814. doi: 10.1109/TSMCC.2007.901003. [102] YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint threshold adjustment and power allocation for cognitive target tracking in asynchronous radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3094–3106. doi: 10.1109/TSP.2017.2679693. [103] YAN Junkun, PU Wenqiang, ZHOU Shenghua, et al. Optimal resource allocation for asynchronous multiple targets tracking in heterogeneous radar networks[J]. IEEE Transactions on Signal Processing, 2020, 68: 4055–4068. doi: 10.1109/TSP.2020.3007313. [104] WU Linlong, MISHRA K V, SHANKAR M R B, et al. Resource allocation in heterogeneously-distributed joint radar-communications under asynchronous Bayesian tracking framework[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(7): 2026–2042. doi: 10.1109/JSAC.2022.3157371. [105] MOHAMMADI A and ASIF A. Decentralized conditional posterior Cramér-Rao lower bound for nonlinear distributed estimation[J]. IEEE Signal Processing Letters, 2013, 20(2): 165–168. doi: 10.1109/LSP.2012.2235430. [106] CHEN Junting, DAI Wenhan, SHEN Yuan, et al. Resource management games for distributed network localization[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(2): 317–329. doi: 10.1109/JSAC.2017.2659318. [107] LU Yanxi, HE Zishu, CHENG Ziyang, et al. Adaptive resource allocation in decentralized colocated MIMO radar network for multiple targets tracking[C]. 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, USA, 2018: 152–157. [108] JIANG Xinyue, YI Wei, YUAN Ye, et al. Network cost based node selection strategy for multiple target tracking in netted radar system[C]. 2019 IEEE Radar Conference (RadarConf), Boston, USA, 2019: 1–6. [109] DELIGIANNIS A, PANOUI A, LAMBOTHARAN S, et al. Game-theoretic power allocation and the nash equilibrium analysis for a multistatic MIMO radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6397–6408. doi: 10.1109/TSP.2017.2755591. [110] OZDEMIR O, NIU Ruixin, and VARSHNEY P K. Tracking in wireless sensor networks using particle filtering: Physical layer considerations[J]. IEEE Transactions on Signal Processing, 2009, 57(5): 1987–1999. doi: 10.1109/TSP.2009.2014818. [111] YUAN Ye, YI Wei, CHOI W, et al. Dynamic quantizer design for target tracking for wireless sensor network with imperfect channels[J]. IEEE Transactions on Wireless Communications, 2023, 22(3): 1695–1711. doi: 10.1109/TWC.2022.3206493. [112] 高晓光, 李飞, 万开方. 数据丢包环境下的多传感器协同跟踪策略研究[J]. 系统工程与电子技术, 2018, 40(11): 2450–2458. doi: 10.3969/j.issn.1001-506X.2018.11.10.GAO Xiaoguang, LI Fei, and WAN Kaifang. Research on multi-sensor cooperative tracking strategy in data packet loss environment[J]. Systems Engineering and Electronics, 2018, 40(11): 2450–2458. doi: 10.3969/j.issn.1001-506X.2018.11.10. [113] ZUO Lei, HU Juan, SUN Hao, et al. Resource allocation for target tracking in multiple radar architectures over lossy networks[J]. Signal Processing, 2023, 208: 108973. doi: 10.1016/j.sigpro.2023.108973. [114] HURTADO M, ZHAO Tong, and NEHORAI A. Adaptive polarized waveform design for target tracking based on sequential Bayesian inference[J]. IEEE Transactions on Signal Processing, 2008, 56(3): 1120–1133. doi: 10.1109/TSP.2007.909044. [115] HUE C, LE CADRE J P, and PEREZ P. Posterior Cramer-Rao bounds for multi-target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 37–49. doi: 10.1109/TAES.2006.1603404. [116] YAN Junkun, JIU Bo, LIU Hongwei, et al. Prior knowledge-based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter[J]. IEEE Transactions on Signal Processing, 2015, 63(2): 512–527. doi: 10.1109/TSP.2014.2371774. [117] GROSSI E, LOPS M, and VENTURINO L. Joint design of surveillance radar and MIMO communication in cluttered environments[J]. IEEE Transactions on Signal Processing, 2020, 68: 1544–1557. doi: 10.1109/TSP.2020.2974708. [118] FARINA A, RISTIC B, and TIMMONERI L. Cramer-Rao bound for nonlinear filtering with Pd<1 and its application to target tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(8): 1916–1924. doi: 10.1109/TSP.2002.800411. [119] ZUO Long, NIU Ruixin, and VARSHNEY P K. Conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 1–14. doi: 10.1109/TSP.2010.2080268. [120] ZHENG Yujiao, OZDEMIR O, NIU Ruixin, et al. New conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(10): 5549–5556. doi: 10.1109/TSP.2012.2205686. [121] SUN Jun, YI Wei, VARSHNEY P K, et al. Resource scheduling for multi-target tracking in multi-radar systems with imperfect detection[J]. IEEE Transactions on Signal Processing, 2022, 70: 3878–3893. doi: 10.1109/TSP.2022.3191800. [122] SUN Jun, YUAN Ye, WANG Yao, et al. Enumeration PCRLB-based power allocation for multitarget tracking with colocated MIMO radar systems in clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 1–18. doi: 10.1109/TGRS.2023.3278727. [123] MOHAMMADI A and ASIF A. Distributed posterior Cramér-Rao lower bound for nonlinear sequential Bayesian estimation[C]. 2012 IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hoboken, USA, 2012: 509–512. [124] SUN Wei, YI Wei, XIE Mingchi, et al. Adaptive node and power simultaneous scheduling strategy for target tracking in distributed multiple radar systems[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–6. [125] WANG Xiangli, YI Wei, XIE Mingchi, et al. Time management for target tracking based on the predicted Bayesian Cramer-Rao lower bound in phase array radar system[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–5. [126] 袁野. 面向认知跟踪的无线分布式雷达资源闭环调度方法研究[D]. [博士论文], 电子科技大学, 2022.YUAN Ye. Research on closed-form resource allocation for wireless distributed radars with cognitive tracking[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2022. [127] SCHUHMACHER D, VO B T, and VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447–3457. doi: 10.1109/TSP.2008.920469. [128] IRCI A, SARANLI A, and BAYKAL B. Study on Q-RAM and feasible directions based methods for resource management in phased array radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1848–1864. doi: 10.1109/TAES.2010.5595599. [129] CHARLISH A and HOFFMANN F. Cognitive Radar Management[M]. KLEMM R. Novel Radar Techniques and Applications Volume 2: Waveform Diversity and Cognitive Radar. Oxford, U.K.: IET, 2017: 157–193. [130] GODRICH H, PETROPULU A P, and POOR H V. Power allocation strategies for target localization in distributed multiple-radar architectures[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3226–3240. doi: 10.1109/TSP.2011.2144976. [131] YAN Junkun, PU Wenqiang, LIU Hongwei, et al. Robust chance constrained power allocation scheme for multiple target localization in colocated MIMO radar system[J]. IEEE Transactions on Signal Processing, 2018, 66(15): 3946–3957. doi: 10.1109/TSP.2018.2841865. [132] WANG Xiangli, YI Wei, XIE Mingchi, et al. A joint beam and dwell time allocation strategy for multiple target tracking based on phase array radar system[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–5. [133] SHI Chenguang, WANG Fei, SALOUS S, et al. Joint subcarrier assignment and power allocation strategy for integrated radar and communications system based on power minimization[J]. IEEE Sensors Journal, 2019, 19(23): 11167–11179. doi: 10.1109/JSEN.2019.2935760. [134] YAN Junkun, DAI Jinhui, PU Wenqiang, et al. Target capacity based resource optimization for multiple target tracking in radar network[J]. IEEE Transactions on Signal Processing, 2021, 69: 2410–2421. doi: 10.1109/TSP.2021.3071173. [135] XIONG Kui, ZHANG Tianxian, CUI Guolong, et al. Coalition game of radar network for multitarget tracking via model-based multiagent reinforcement learning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(3): 2123–2140. doi: 10.1109/TAES.2022.3208865. [136] HAN Qinghua, PAN Minghai, LONG Weijun, et al. Joint adaptive sampling interval and power allocation for maneuvering target tracking in a multiple opportunistic array radar system[J]. Sensors, 2020, 20(4): 981. doi: 10.3390/s20040981. [137] ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227. [138] DAI Jinhui, YAN Junkun, PU Wenqiang, et al. Adaptive channel assignment for maneuvering target tracking in multistatic passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(3): 2780–2793. doi: 10.1109/TAES.2022.3218610. [139] XU Gongguo, SHAN Ganlin, and DUAN Xiusheng. Sensor scheduling for ground maneuvering target tracking in presence of detection blind zone[J]. Journal of Systems Engineering and Electronics, 2020, 31(4): 692–702. doi: 10.23919/JSEE.2020.000044. [140] 耿文东. 基于相控阵雷达的群目标准自适应调度策略研究[J]. 雷达科学与技术, 2013, 11(2): 125–129. doi: 10.3969/j.issn.1672-2337.2013.02.003.GENG Wendong. Research on quasi-adaptive scheduling strategy for tracking group target in phased array radar[J]. Radar Science and Technology, 2013, 11(2): 125–129. doi: 10.3969/j.issn.1672-2337.2013.02.003. [141] CAO Lanying and HE Kefeng. Time resource scheduling algorithm for multiple target tracking in jamming[C]. IET International Radar Conference 2013, Xi’an, China, 2013: 1–4. [142] ZHANG Haowei, YAN Junkun, LIU Weijian, et al. Array scheduling with power and bandwidth allocation for simultaneous multibeam tracking low-angle targets in a VHF-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023. [143] LU Xiujuan, XU Zhenchang, REN Haiwei, et al. LPI-based resource allocation strategy for target tracking in the moving airborne radar network[C]. 2022 IEEE Radar Conference (RadarConf22), New York City, USA, 2022: 1–6. [144] 李正杰, 谢军伟, 张浩为, 等. 一种低截获背景下的集中式MIMO雷达快速功率分配算法[J]. 雷达学报, 2013, 12(3): 602–612. doi: 10.12000/JR22203.LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. A fast power allocation algorithm in collocated MIMO radar under low intercept background[J]. Journal of Radars, 2013, 12(3): 602–612. doi: 10.12000/JR22203. [145] 廖雯雯, 程婷, 何子述. MIMO雷达射频隐身性能优化的目标跟踪算法[J]. 航空学报, 2014, 35(4): 1134–1141. doi: 10.7527/S1000-6893.2013.0368.LIAO Wenwen, CHENG Ting, and HE Zishu. A target tracking algorithm for RF stealth performance optimization of MIMO radar[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 1134–1141. doi: 10.7527/S1000-6893.2013.0368. [146] LU Xiujuan, YI Wei, and KONG Lingjiang. LPI-based transmit resource scheduling for target tracking with distributed MIMO radar systems[J]. IEEE Transactions on Vehicular Technology, 2023: 1–15. [147] SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Low probability of intercept-based optimal power allocation scheme for an integrated multistatic radar and communication system[J]. IEEE Systems Journal, 2020, 14(1): 983–994. doi: 10.1109/JSYST.2019.2931754. [148] 周颖, 施龙飞, 陈明辉, 等. 密集干扰环境下相控阵雷达资源管理优化研究[J]. 电子学报, 2005, 33(6): 999–1003. doi: 10.3321/j.issn:0372-2112.2005.06.010.ZHOU Ying, SHI Longfei, CHEN Minghui, et al. Optimized resource management for phased array radar in dense jamming[J]. Acta Electronica Sinica, 2005, 33(6): 999–1003. doi: 10.3321/j.issn:0372-2112.2005.06.010. [149] TAO Tingbao, ZHANG Gong, and LEUNG H. An optimal algorithm of time resource for multi-target tracking under active oppressive jamming[C]. 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 2019: 1–6. [150] LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Joint beam selection and power allocation in cognitive collocated MIMO radar for potential guidance application under oppressive jamming[J]. Digital Signal Processing, 2022, 127: 103579. doi: 10.1016/j.dsp.2022.103579. [151] ZHANG Haowei, LIU Weijian, ZHANG Qiliang, et al. Joint resource optimization for a distributed MIMO radar when tracking multiple targets in the presence of deception jamming[J]. Signal Processing, 2022, 200: 108641. doi: 10.1016/j.sigpro.2022.108641. [152] 赫彬, 苏洪涛. 认知雷达抗干扰中的博弈论分析综述[J]. 电子与信息学报, 2021, 43(5): 1199–1211. doi: 10.11999/JEIT200843.HE Bin and SU Hongtao. A review of game theory analysis in cognitive radar anti-jamming[J]. Journal of Electronics & Information Technology, 2021, 43(5): 1199–1211. doi: 10.11999/JEIT200843. [153] SONG Xiufeng, WILLETT P, ZHOU Shengli, et al. The MIMO radar and jammer games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687–699. doi: 10.1109/TSP.2011.2169251. [154] ZHANG Xiaobo, WANG Hai, RUAN Lang, et al. Joint channel and power optimisation for multi-user anti-jamming communications: A dual mode Q-learning approach[J]. IET Communications, 2022, 16(6): 619–633. doi: 10.1049/cmu2.12339. [155] AILIYA, YI Wei, and VARSHNEY P K. Adaptation of frequency hopping interval for radar anti-jamming based on reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2022, 71(12): 12434–12449. doi: 10.1109/TVT.2022.3197425. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: