基于高斯混合聚类的阵列干涉SAR三维成像

李杭; 梁兴东; 张福博; 吴一戎

doi:10.12000/JR17020

基于高斯混合聚类的阵列干涉SAR三维成像

DOI: 10.12000/JR17020

李杭^1,2,3,,
梁兴东^1,2, ,,
张福博^1,2,,
吴一戎^1,2,

1.
微波成像技术重点实验室北京 100190
2.
中国科学院电子学研究所北京 100190
3.
中国科学院大学北京 100049

基金项目: 国家部委基金

详细信息

作者简介:
李杭：李杭(1989–)，男，江苏人，学士，中国科学技术大学；博士生，中国科学院电子学研究所；研究方向为阵列干涉SAR高精度3维成像。E-mail: aaronli@mail.ustc.edu.cn

梁兴东(1973–)，男，陕西人，博士，北京理工大学；研究员，中国科学院电子学研究所；研究方向为高分辨率合成孔径雷达系统、干涉合成孔径雷达、成像处理及应用、实时数字信号处理。E-mail: xdliang@mail.ie.ac.cn

张福博(1988–)，男，河北人，博士，中国科学院电子学研究所；助理研究员，研究方向为多通道SAR 3维重建、新体制雷达、阵列雷达信号处理。E-mail: zhangfubo8866@126.com

吴一戎(1963–)，男，安徽人，博士，中国科学院电子学研究所；研究员，中国科学院院士，中国科学院电子学研究所；研究方向为微波成像理论、微波成像技术和雷达信号处理。E-mail: wyr@mail.ie.ac.cn

通讯作者:
梁兴东 xdliang@mail.ie.ac.cn

中图分类号: TN957.52
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程
- 收稿日期: 2017-03-03
- 修回日期: 2017-04-10
- 网络出版日期: 2017-12-01

3D Imaging for Array InSAR Based on Gaussian Mixture Model Clustering

Li Hang^{1,2,3
,},
Liang Xingdong^{1,2
, ,},
Zhang Fubo^{1,2
,},
Wu Yirong^{1,2
,}

1.
Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China
2.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Ministries Foundation

摘要

摘要:
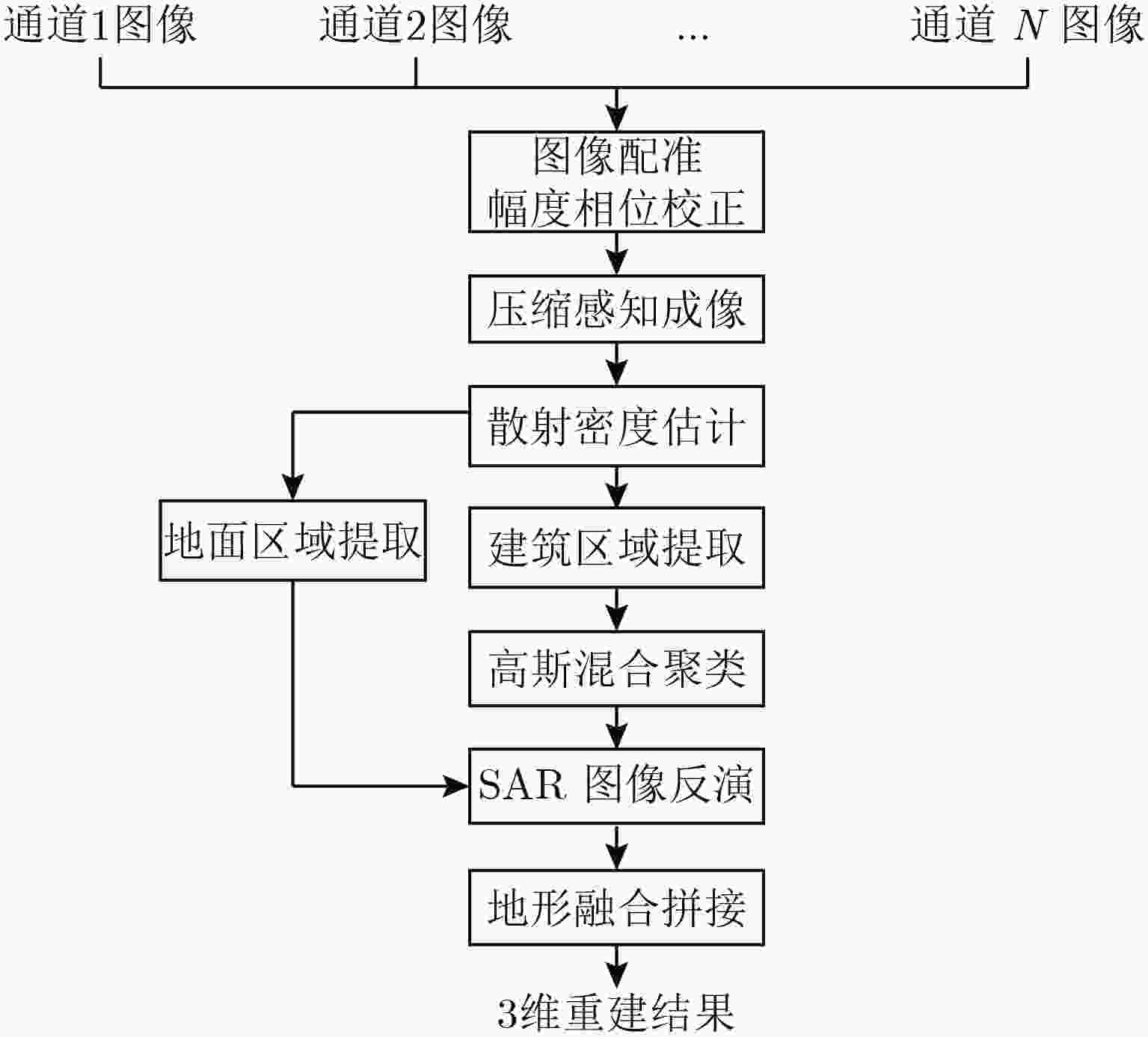
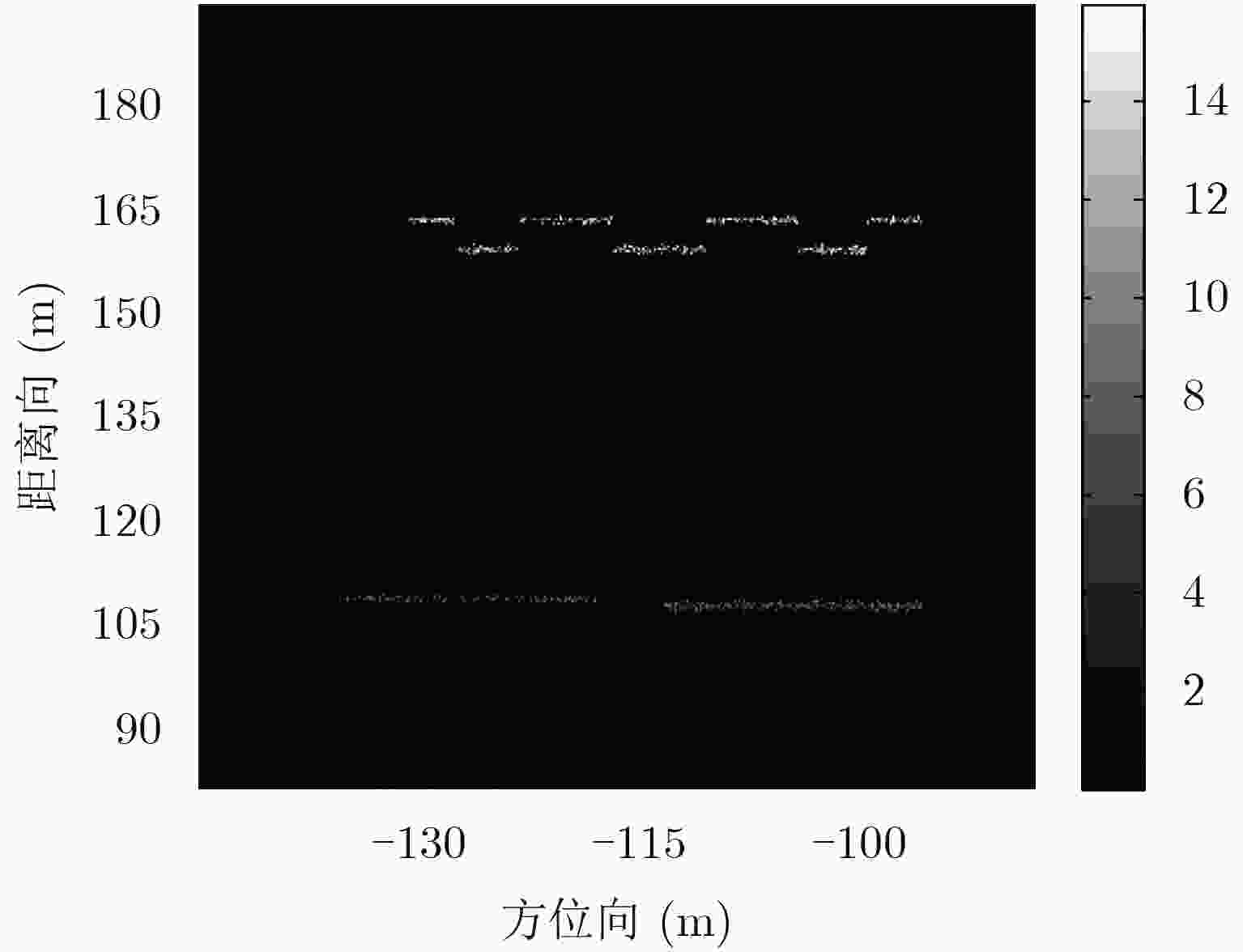
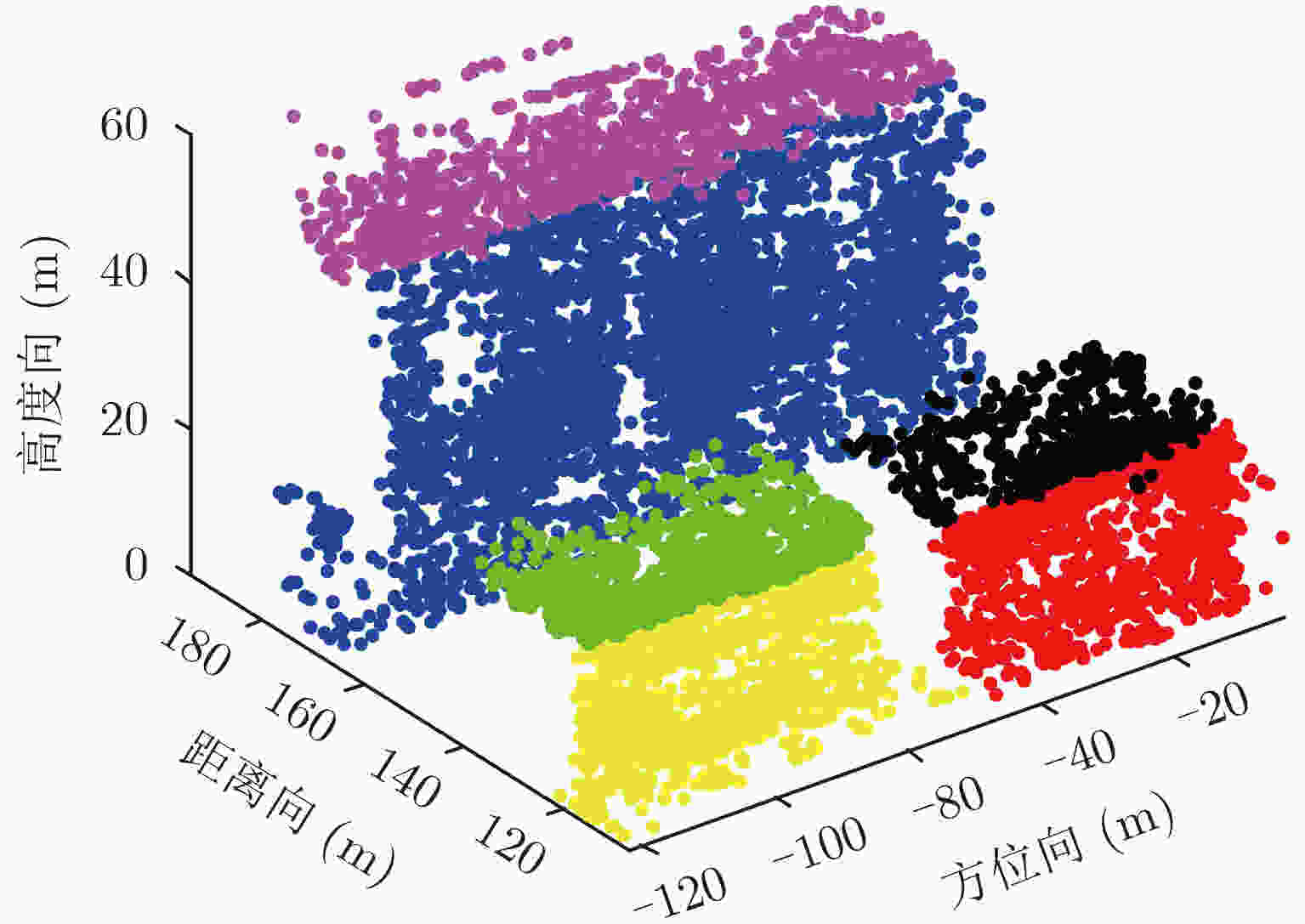
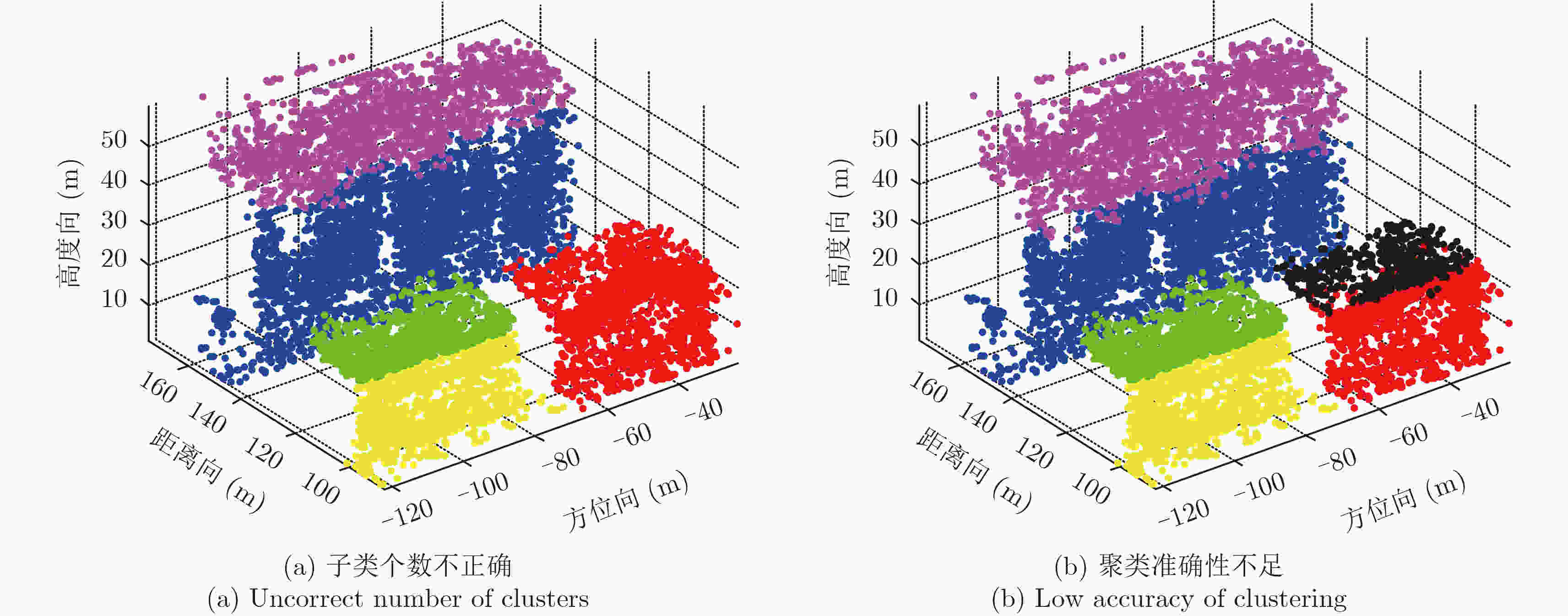
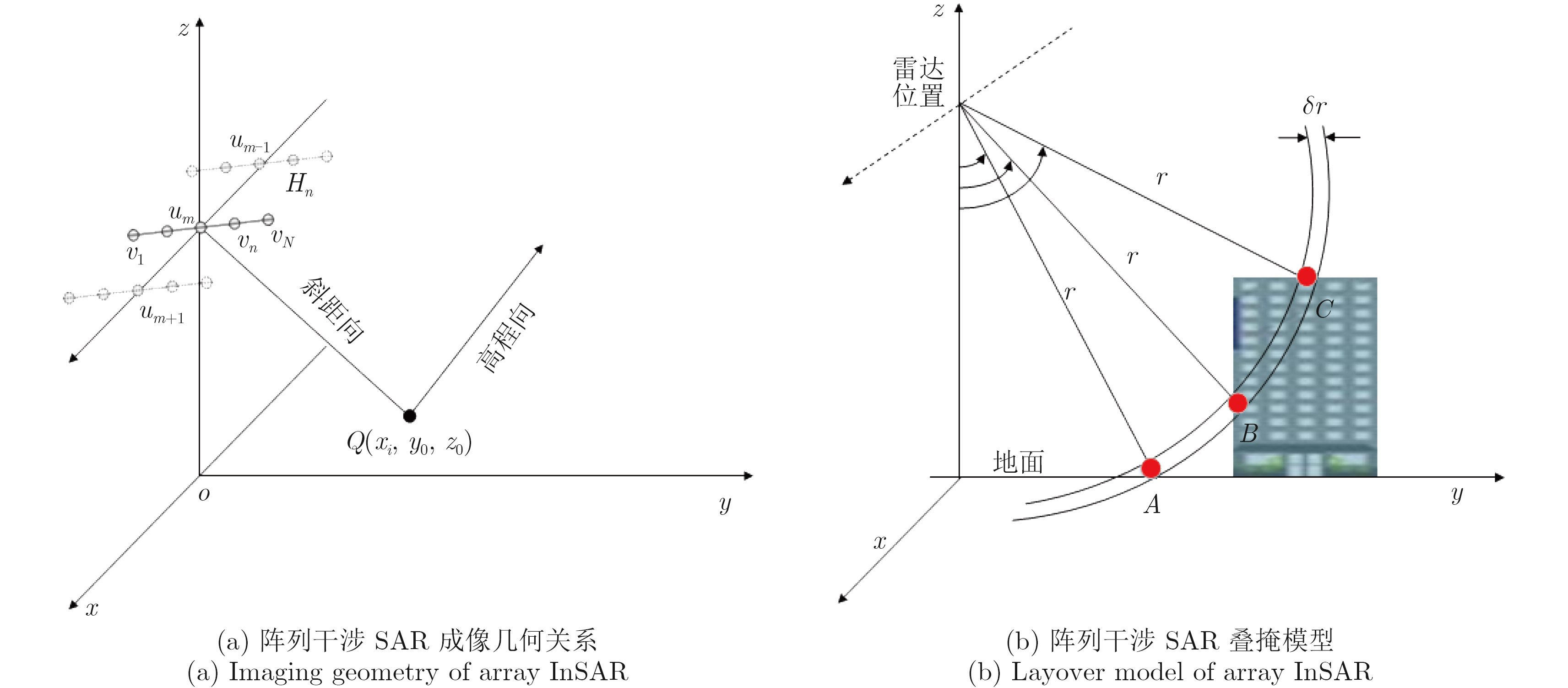
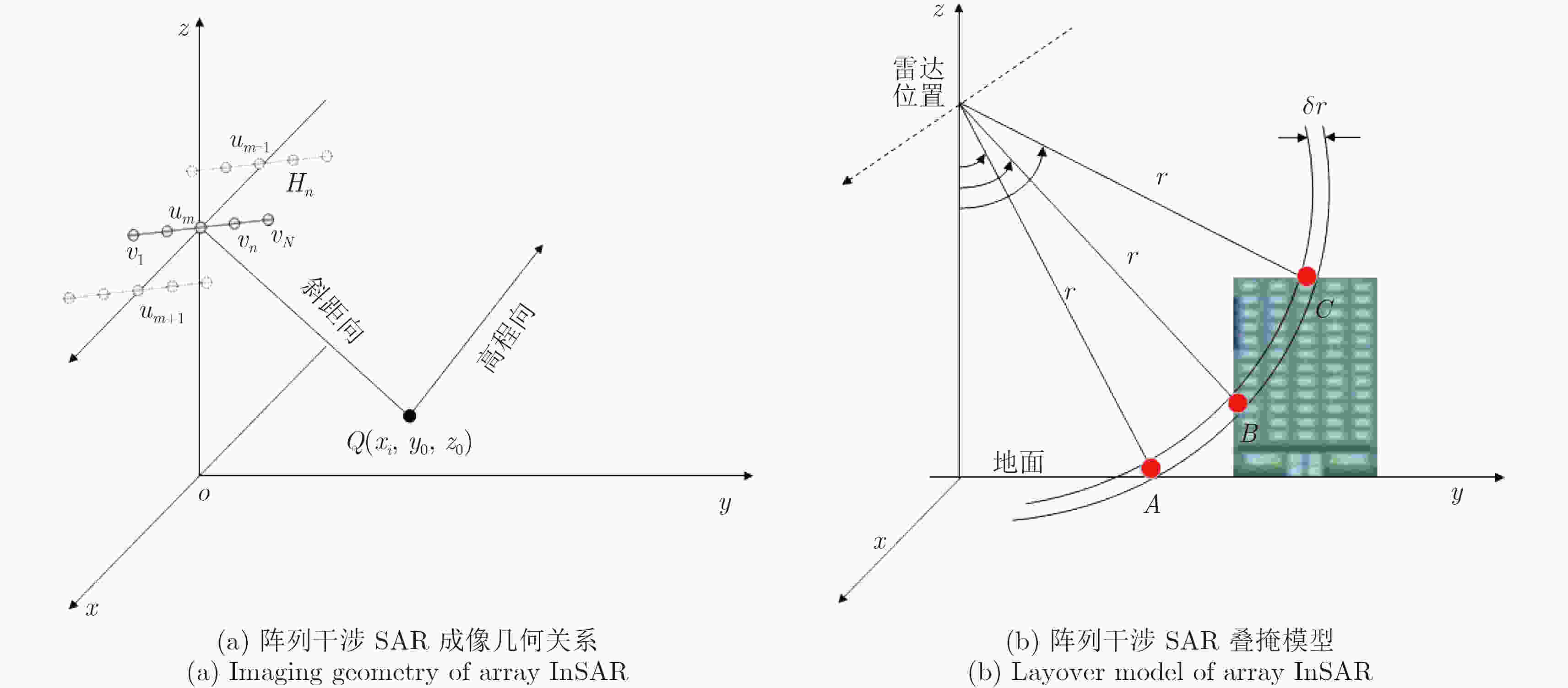
阵列干涉SAR具备高程分辨能力，单次航过即可生成观测场景的3维点云分布，解决叠掩问题。但是，由于阵列干涉SAR阵元数目有限、基线长度较短，高程向分辨率受到限制，加之城区建筑物的叠掩现象，常规方法重建结果定位精度较差，难以提取建筑物有效特征。针对这个问题，该文提出了一种基于高斯混合聚类的阵列干涉SAR 3维成像方法，首先通过基于压缩感知(Compressive Sensing, CS)的超分辨算法获得场景区域的3维点云分布，然后利用密度估计方法提取出建筑物的散射点，之后使用高斯混合模型(Gaussian Mixture Model, GMM)对建筑物3维点云进行聚类，最后利用系统参数完成各个区域的SAR图像反演，实现建筑物的3维成像。通过国内首次机载阵列干涉SAR实验的实际数据，验证了该文算法的有效性，并获得了真实的建筑物3维成像结果。
- 3维成像 /
- 阵列干涉SAR /
- 叠掩现象 /
- 压缩感知 /
- 高斯混合模型聚类
Abstract:
Array InSAR can generate 3D point clouds with the use of SAR images of the observed scene, which are obtained using multiple channels in a single flight. Its resolution power in elevation enables one to solve the layover problem. However, due to the limited number of arrays and the short baseline length, the resolution power in elevation is restricted. Together with the layover phenomenon of the urban buildings, the result of 3D reconstruction suffers from poor accuracy in positioning, and it is difficult to extract the effective characteristics of the buildings. In view of this situation, this paper proposed a 3D reconstruction method of array InSAR based on Gaussian mixture model clustering. First, the 3D point clouds of the observed scene are obtained by an algorithm with super-resolution based on compressive sensing, and then the scatters of buildings are extracted by density estimation; after which the method of Gaussian mixture model clustering is used to classify the 3D point clouds of the buildings. Finally, the inverse SAR images of each region are obtained by using the system parameters, and the 3D reconstruction of the buildings is completed. Based on the actual data of the first domestic 3D imaging experiment by airborne array InSAR, the validity of the algorithm is confirmed and the 3D imaging results of the buildings are obtained.
- 3D reconstruction /
- Array InSAR /
- Layover phenomenon /
- Compressive Sensing (CS) /
- Gaussian Mixture Model clustering (GMM clustering)

HTML全文

图 1 阵列干涉SAR成像模型

Figure 1. Array InSAR imaging model

下载: 全尺寸图片幻灯片

图 2 观测场景光学图像

Figure 2. Optical image of the observed scene

下载: 全尺寸图片幻灯片

图 3 观测场景原始3维点云

Figure 3. Orginal 3D point clouds of the observed scene

下载: 全尺寸图片幻灯片

图 4 算法流程图

Figure 4. Workflow of proposed approach

下载: 全尺寸图片幻灯片

图 5 观测场景散射点密度图

Figure 5. Scatterer density map of the observed scene

下载: 全尺寸图片幻灯片

图 6 观测场景建筑物提取结果

Figure 6. Extracted building results of the observed scene

下载: 全尺寸图片幻灯片

图 7 不同窗口/阈值性能曲线图

Figure 7. Performance curve map with varying TH and GA parameters

下载: 全尺寸图片幻灯片

图 8 子类个数与偏差度关系图

Figure 8. Dispersion plot with number of clusters

下载: 全尺寸图片幻灯片

图 9 建筑物区域聚类结果

Figure 9. Clustered result of building areas

下载: 全尺寸图片幻灯片

图 10 K-means聚类结果

Figure 10. Clustered results of K-means

下载: 全尺寸图片幻灯片

图 11 各区域反演SAR图像

Figure 11. Inversed SAR images of all aeras

下载: 全尺寸图片幻灯片

图 12 地面区域SAR图像

Figure 12. Inversed SAR images of the ground

下载: 全尺寸图片幻灯片

图 13 观测场景2维SAR图像

Figure 13. 2D SAR image of the observed scene

下载: 全尺寸图片幻灯片

图 14 观测场景干涉相位图

Figure 14. Interferometric phase image of the observed scene

下载: 全尺寸图片幻灯片

图 15 观测场景3维成像结果

Figure 15. 3D imaging result of the observed scene

下载: 全尺寸图片幻灯片

表 1 阵列干涉SAR系统参数

Table 1. System parameters of array InSAR

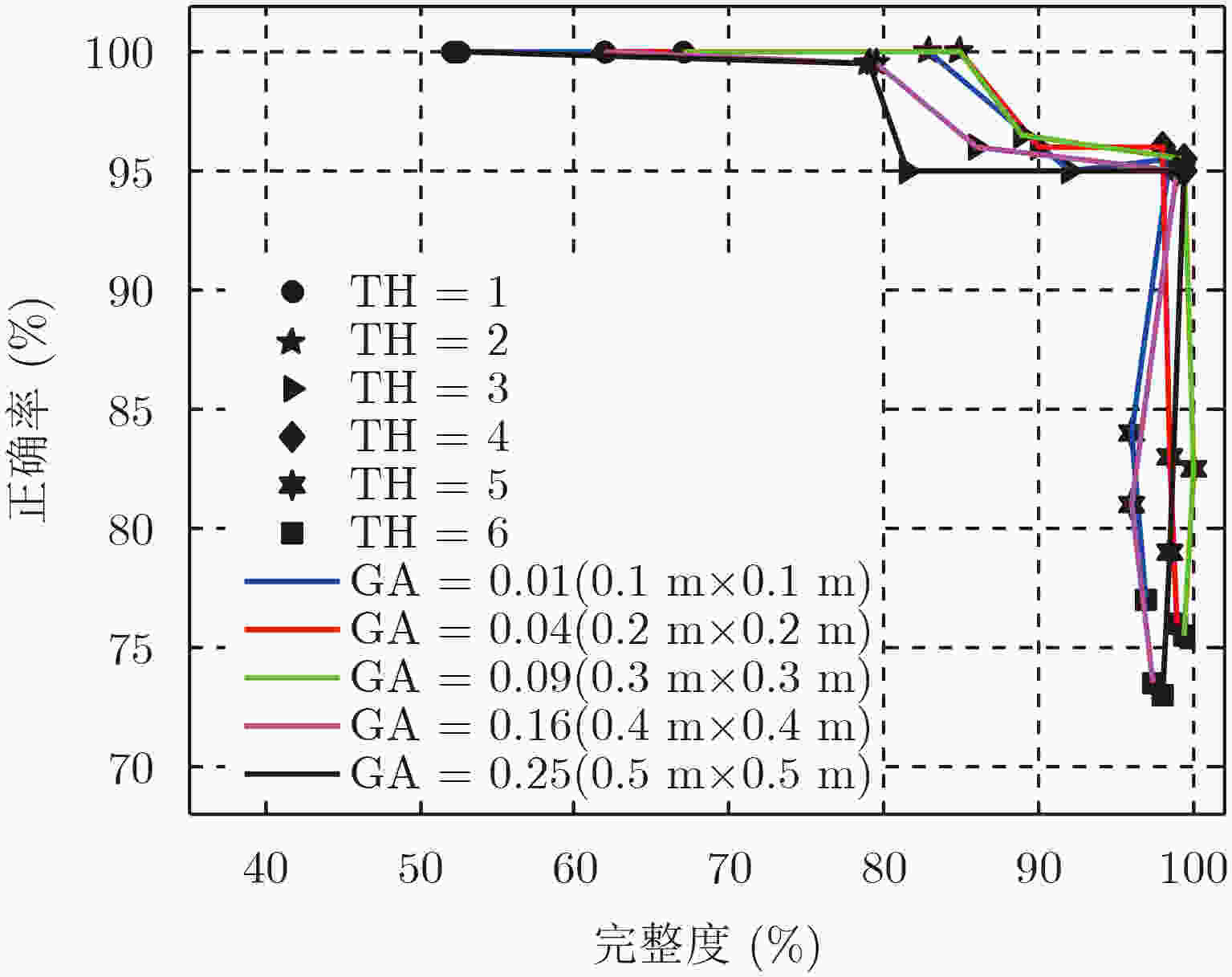
项目	参数
载频(GHz)	15
发射信号带宽(MHz)	500
脉冲重复频率(kHz)	1
载机高度(m)	600
飞行速度(m/s)	70
方位波束宽度(°)	2
距离波束宽度(°)	27
中心下视角(°)	25

下载: 导出CSV

表 2 不同窗口/阈值质量评价表

Table 2. Quality evaluation with varying TH and GA parameters

TH (点数/dm²)	GA (dm²)
TH (点数/dm²)	1×1	2×2	3×3	4×4	5×5
1	75.12	74.88	74.37	71.89	71.75
2	81.27	81.86	81.73	77.71	78.07
3	94.12	93.84	94.82	94.63	94.08
4	87.48	86.32	86.40	81.98	77.56
5	81.89	84.77	84.68	78.29	77.91
6	67.23	63.02	67.14	60.62	51.83

下载: 导出CSV

参考文献(20)

[1]	Morishita Y and Hanssen R F. Temporal decorrelation in L-, C-, and X-band satellite radar interferometry for pasture on drained peat soils[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 1096–1104. DOI: 10.1109/TGRS.2014.2333814.
[2]	张福博. 阵列干涉SAR三维重建信号处理技术研究[D]. [博士论文], 中国科学院大学, 2015. Zhang Fubo. Research on signal processing of 3-D reconstruction in linear array Synthetic Aperture Radar interferometry[D]. [Ph.D.dissertation], Institute of Electronics, Chinese Acedamy of Science, 2015.
[3]	Knaell K K and Cardillo G P. Radar tomography for the generation of three-dimensional images[J]. IEE Proceedings-Radar, Sonar and Navigation, 1995, 142(2): 54–60. DOI: 10.1049/ip-rsn:19951791.
[4]	Wang Bin, Wang Yanping, Hong Wen, et al.. Application of spatial spectrum estimation technique in multibaseline SAR for layover solution[C]. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Boston, USA, 2008: III-1139–III-1142.
[5]	王爱春, 向茂生. 基于块压缩感知的SAR层析成像方法[J]. 雷达学报, 2016, 5(1): 57–64. DOI: 10.12000/JR16006. Wang Aichun and Xiang Maosheng. SAR tomography based on block compressive sensing[J]. Journal of Radars, 2016, 5(1): 57–64. DOI: 10.12000/JR16006.
[6]	Reigber A and Moreira A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. DOI: 10.1109/36.868873.
[7]	Zhu Xiaoxiang and Bamler R. Tomographic SAR inversion by L₁-norm regularization—the compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. DOI: 10.1109/TGRS.2010.2048117.
[8]	Zhu Xiaoxiang and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. DOI: 10.1109/TGRS.2011.2160183.
[9]	Zivkovic Z. Improved adaptive Gaussian mixture model for background subtraction[C]. Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 2004, 2: 28–31.
[10]	Budillon A, Evangelista A, and Schirinzi G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488–499. DOI: 10.1109/TGRS.2010.2054099.
[11]	Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI: 10.1109/TIT.2006.871582.
[12]	张福博, 梁兴东, 吴一戎. 一种基于地形驻点分割的多通道SAR三维重建方法[J]. 电子与信息学报, 2015, 37(10): 2287–2293. DOI: 10.11999/JEIT150244. Zhang Fu-bo, Liang Xing-dong, and Wu Yi-rong. 3-D reconstruction for multi-channel SAR interferometry using terrain stagnation point based division[J]. Journal of Electronics &Information Technology, 2015, 37(10): 2287–2293. DOI: 10.11999/JEIT150244.
[13]	廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 123–129. DOI: 10.12000/JR15031. Liao Ming-sheng, Wei Lian-huan, Wang Zi-yun, et al. Compressive sensing in high-resolution 3D SAR tomography of urban scenarios[J]. Journal of Radars, 2015, 4(2): 123–129. DOI: 10.12000/JR15031.
[14]	Zhu Xiaoxiang and Shahzad M. Facade reconstruction using multiview spaceborne TomoSAR point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3541–3552. DOI: 10.1109/TGRS.2013.2273619.
[15]	Sithole G and Vosselman G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85–101. DOI: 10.1016/j.isprsjprs.2004.05.004.
[16]	Vosselman G. Slope based filtering of laser altimetry data[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(B3/2), Part 3: 935–942.
[17]	Rottensteiner F and Briese C. A new method for building extraction in urban areas from high-resolution LIDAR data[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2002, 34(3/A): 295–301.
[18]	Vrieze S I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC)[J]. Psychological Methods, 2012, 17(2): 228–243. DOI: 10.1037/a0027127.
[19]	Moon T K. The expectation-maximization algorithm[J]. IEEE Signal Processing Magazine, 1996, 13(6): 47–60. DOI: 10.1109/79.543975.
[20]	Sampath A and Shan Jie. Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1554–1567. DOI: 10.1109/TGRS.2009.2030180.