基于马尔科夫判别谱聚类的极化SAR图像分类方法

张向荣; 于心源; 唐旭; 侯彪; 焦李成

doi:10.12000/JR19059

基于马尔科夫判别谱聚类的极化SAR图像分类方法

DOI: 10.12000/JR19059

西安电子科技大学人工智能学院，智能感知与图像理解教育部重点实验室，国际智能感知与计算联合研究中心西安 710071

基金项目: 国家自然科学基金(61772400)，陕西省重点研发计划(2019ZDLGY03-08)

详细信息

作者简介:
张向荣(1978–)，女，西安电子科技大学人工智能学院，教授/博导，IEEE高级会员，IEEE GRSS西安分会副主席。主要从事遥感影像智能解译、机器学习、模式识别相关方向研究。E-mail: xrzhang@mail.xidian.edu.cn

于心源(1993–)，女，西安电子科技大学研究生。研究领域为极化SAR图像处理、机器学习等

唐　旭(1985–)，男，西安电子科技大学人工智能学院讲师，IEEE会员。主要从事遥感影像内容解译方向的研究

侯　彪(1974–)，男，西安电子科技大学人工智能学院，教授/博导，IEEE会员。从事人工智能、类脑计算、遥感脑、图像和视频分析、智能教育等研究

焦李成(1959–)，男，西安电子科技大学人工智能学院，教授/博导，IEEE Fellow, IEEE GRSS西安分会主席，IEEE Transactions on Geoscience and Remote Sensing副主编。主要从事人工智能相关领域的研究

通讯作者:
张向荣　xrzhang@mail.xidian.edu.cn

中图分类号: TN958
计量
- 文章访问数: 2587
- HTML全文浏览量: 868
- PDF下载量: 250
- 被引次数: 7
出版历程
- 收稿日期: 2019-06-01
- 修回日期: 2019-07-22
- 网络出版日期: 2019-08-28

PolSAR Image Classification Method Based on Markov Discriminant Spectral Clustering

Artificial Intelligence Institute, Xidian University, Key Laboratory of Intelligent Perception and Image Understanding of Ministry of Education, International Research Center for Intelligent Perception and Computation, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (61772400), The Key Research and Development Plans of Shaanxi Province (2019ZDLGY03-08)

More Information

Corresponding author: ZHANG Xiangrong, xrzhang@mail.xidian.edu.cn

摘要

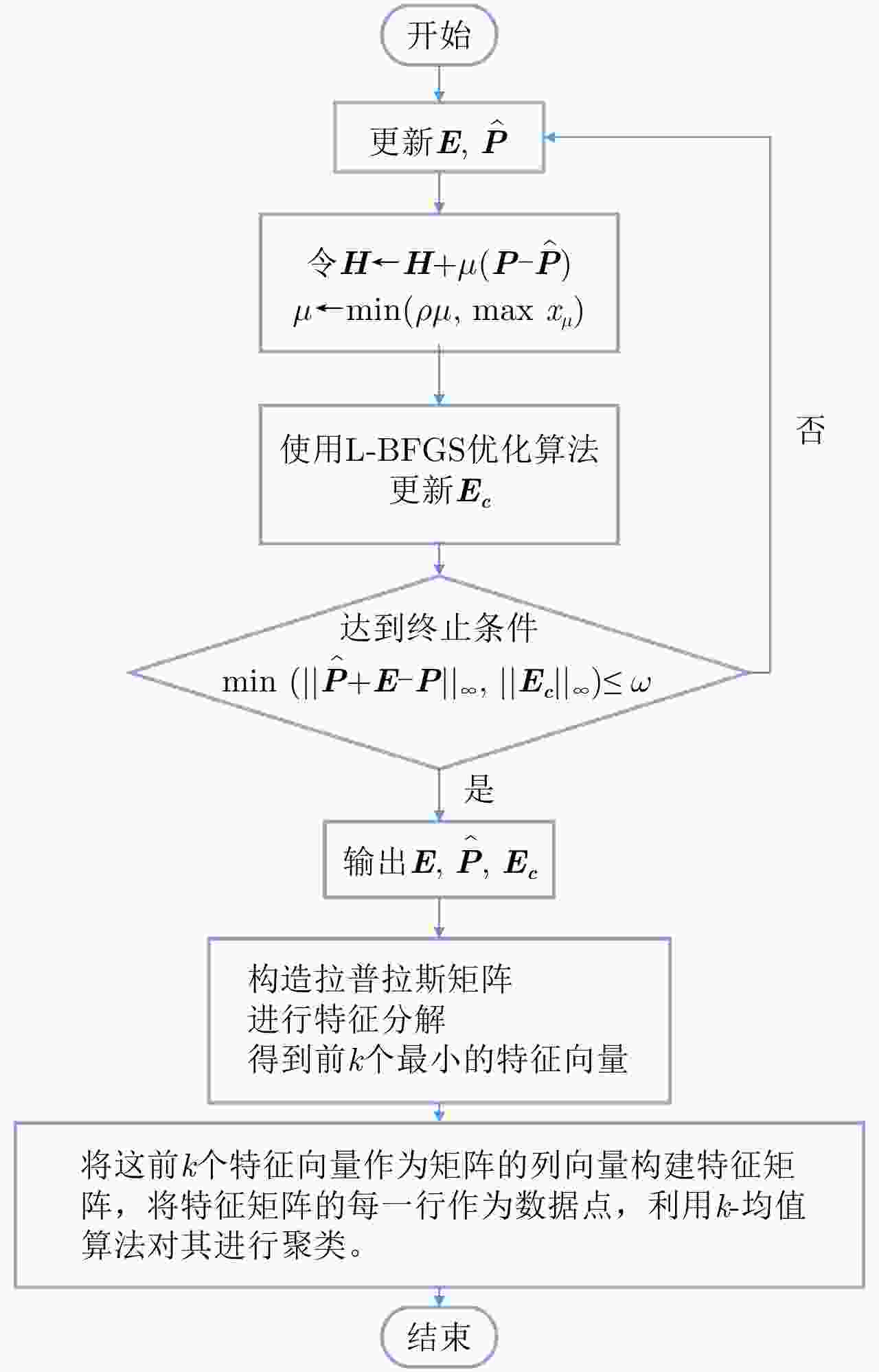
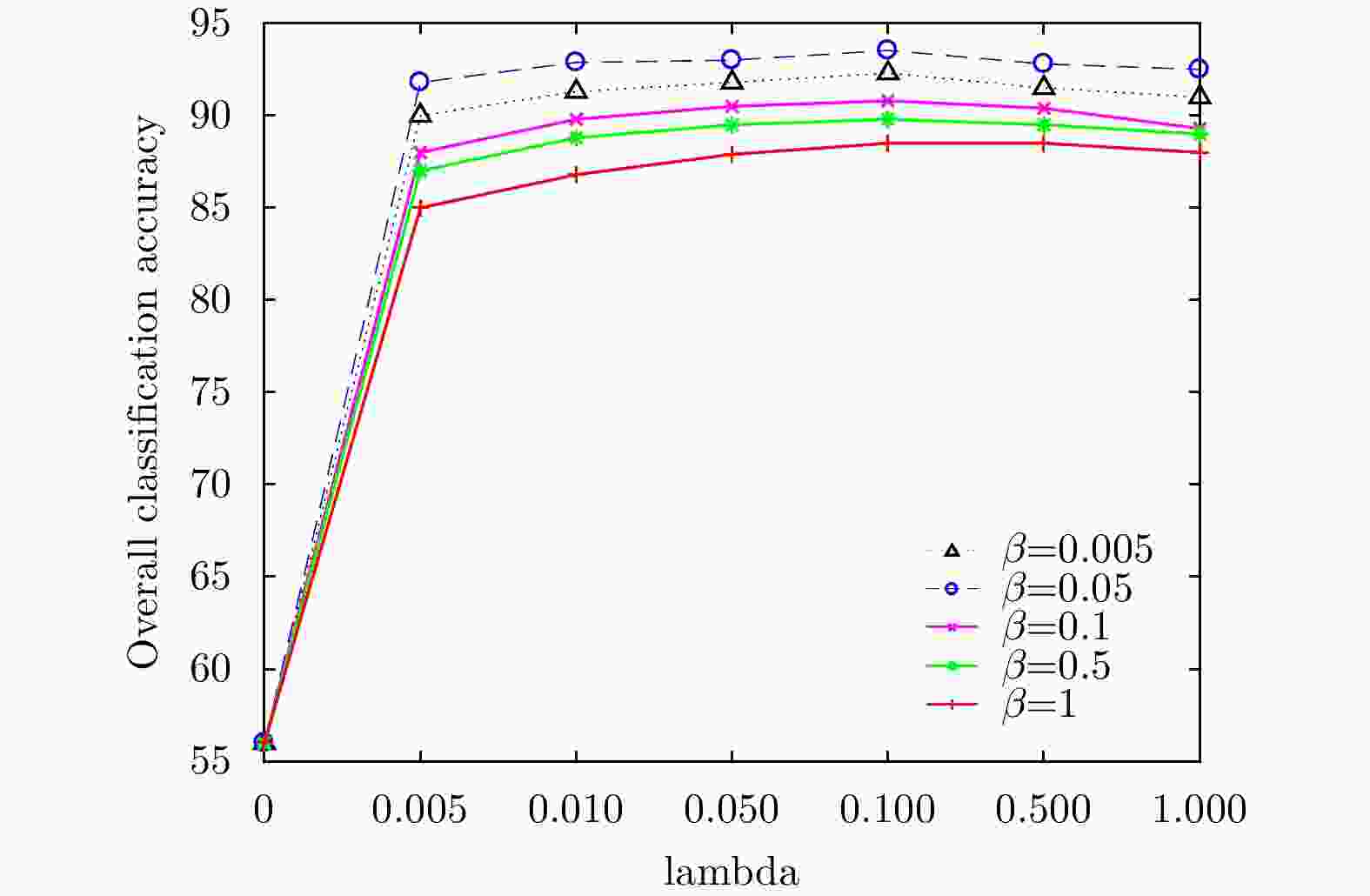
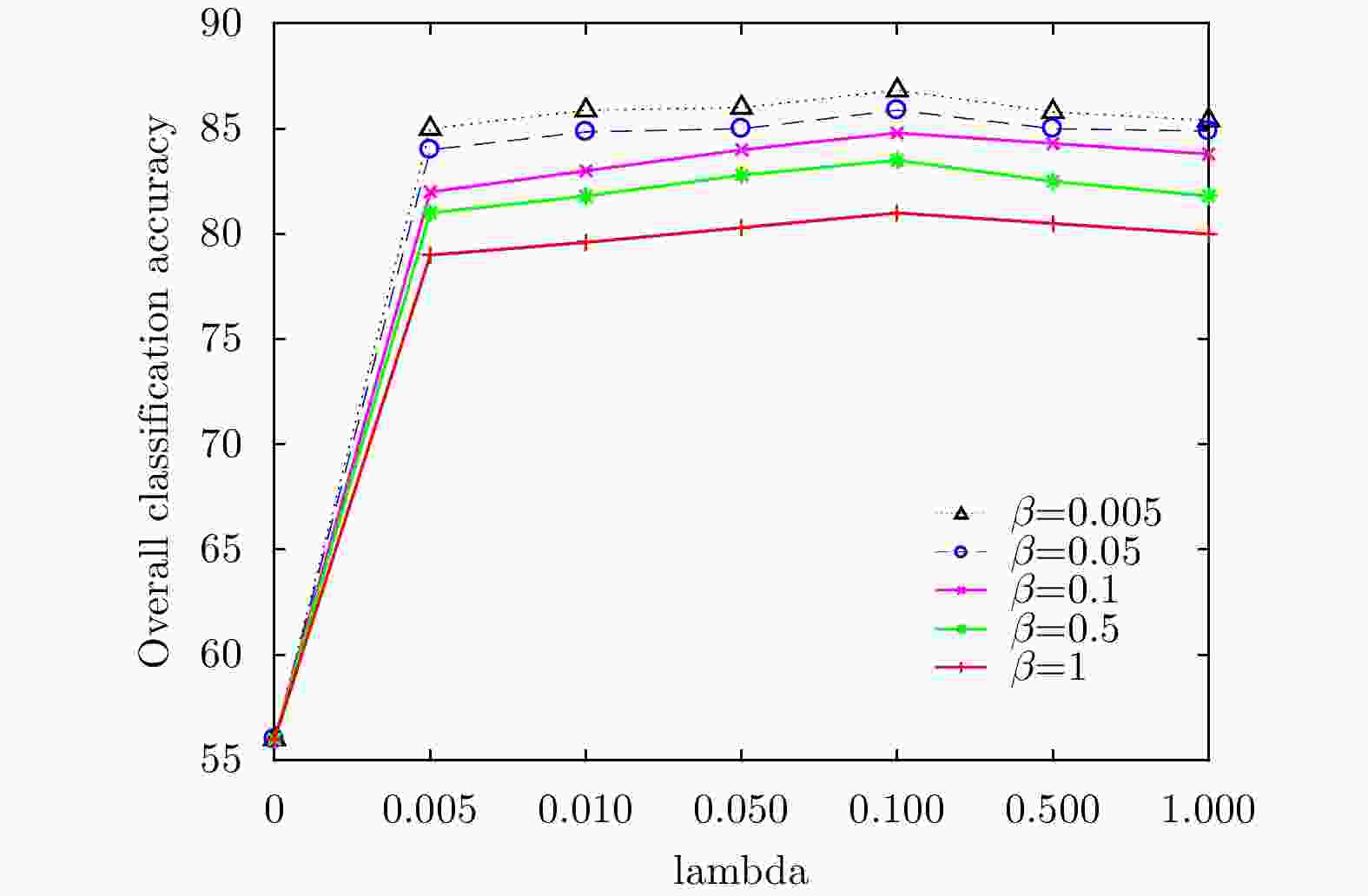
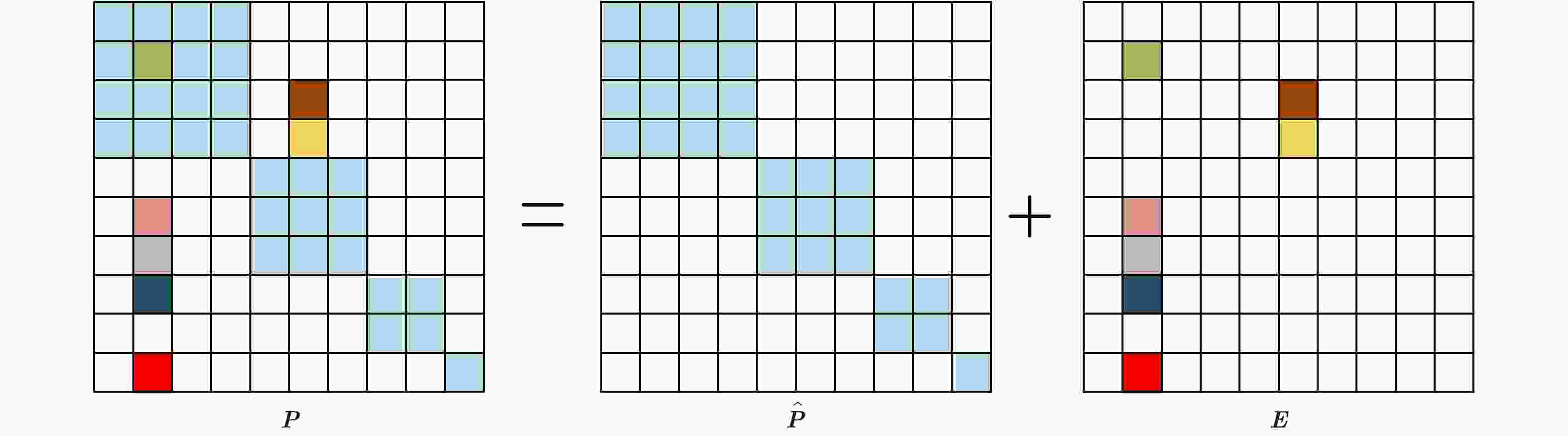
摘要: 该文针对现有的谱聚类方法用于极化SAR图像分类时精度较低的问题，提出一种基于马尔科夫的判别谱聚类方法(MDSC)，具有低秩和稀疏分解的特点。该方法首先恢复一个真实的低秩概率转移矩阵，将其作为标准马尔科夫谱聚类方法的输入，以减少噪声对分类结果的影响；然后在目标函数中引入判别信息，使极化SAR图像的数据信息能够得到更加充分地利用；最后采用增广拉格朗日乘子法来解决低秩和概率单纯形约束下的目标函数优化问题。在荷兰小农田、德国、西安和荷兰大农田4个不同数据集上的实验证明，该方法具有较好的准确率，且参数敏感性较低，表现出了良好的分类性能。
- 极化SAR /
- 谱聚类 /
- 判别谱聚类 /
- 多视角谱聚类
Abstract: Due to the existing spectral clustering methods have low accuracy for PolSAR image classification, a Markov-based Discriminative Spectral Clustering(MDSC) method is proposed, which has the characteristics of low-rank and sparse decomposition. Firstly, a real low-rank probability transfer matrix is restored as an input to the standard Markov spectral clustering method to reduce the influence of noise on the classification result. Then the discriminative information is introduced into the objective function to make the polarimetric SAR image data can be more fully used. Finally, the augmented Lagrangian multiplier method is used to solve the objective function optimization problem under low-rank and probability simplex constraints. Experiments on three different data sets of Flevoland, Oberpfaffenhofen, and Xi’an show that our method has good accuracy and low sensitivity, which having a good classification performance.
- PolSAR /
- Spectral clustering /
- Discriminant spectral clustering /
- Multi-view spectral clustering

HTML全文

图 1 真实的概率转移矩阵构造概图

Figure 1. Real probability transfer matrix construction profile

下载: 全尺寸图片幻灯片

图 2 本文算法框架图

Figure 2. Algorithm frame diagram

下载: 全尺寸图片幻灯片

图 3 荷兰Flevoland地区农田小图的伪彩图、类标图以及不同算法的分类结果图

Figure 3. Pseudo-color map, class diagram and classification results of different algorithms for farmland maps in the Flevoland region of the Netherlands

下载: 全尺寸图片幻灯片

图 4 德国Oberpfaffenhofen地区数据的伪彩图、类标图以及不同算法的分类结果图

Figure 4. Pseudo-color map, class diagram and data classification results of different algorithms in the Oberpfaffenhofen region of Germany

下载: 全尺寸图片幻灯片

图 5 西安地区数据的伪彩图、类标图以及不同算法的分类结果图

Figure 5. Pseudo-color map, class diagram and data classification results of different algorithms in Xi’an area

下载: 全尺寸图片幻灯片

图 6 荷兰 Flevoland 地区大农田数据的伪彩图、类标图以及不同算法的分类结果图

Figure 6. Pseudo-color map, class diagram and classification results of different algorithms for large farmland data in the Flevoland region of the Netherlands

下载: 全尺寸图片幻灯片

图 7 荷兰小农田中不同 $\lambda$ 和 $\beta$ 下的分类结果图

Figure 7. Classification results of different $\lambda$ and $\beta$ below in small Dutch farmland

下载: 全尺寸图片幻灯片

图 10 不同正则项参数 $\xi$ 的分类结果图

Figure 10. Classification results of different regular item parameter $\xi$

下载: 全尺寸图片幻灯片

图 8 德国地区中不同 $\lambda$ 和 $\beta$ 下的分类结果

Figure 8. Classification results for different $\lambda$ and $\beta$ below in the German region

下载: 全尺寸图片幻灯片

图 9 西安地区中不同 $\lambda$ 和 $\beta$ 下的分类结果图

Figure 9. Classification results of different $\lambda$ and $\beta$ subordinates in Xi’an area

下载: 全尺寸图片幻灯片

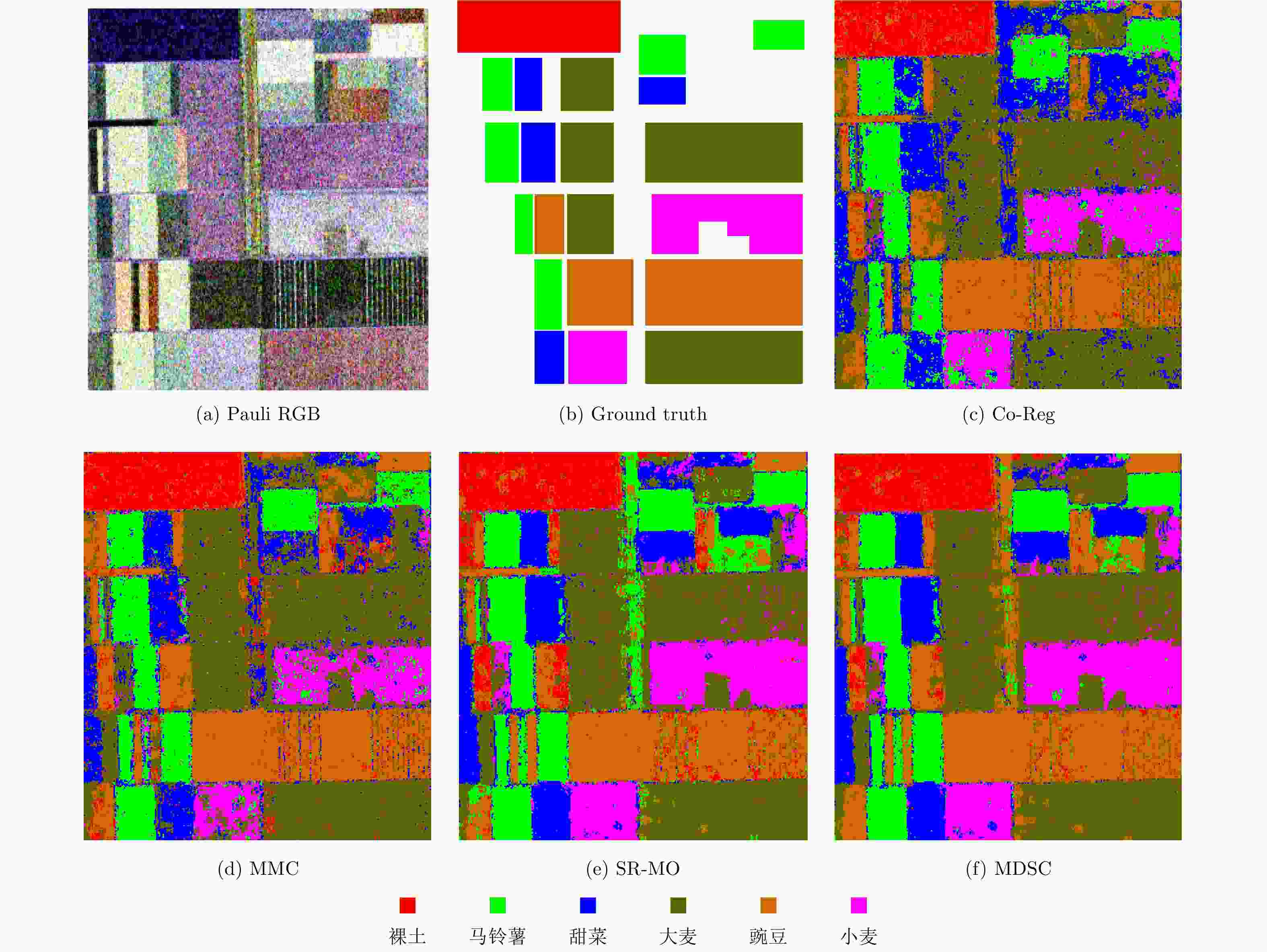
表 1 4种算法对Flevoland小农田图的分类结果

Table 1. Classification results of four algorithms for Flevoland small farmland map

	裸土	土豆	甜菜	大麦	豌豆	小麦	OA	AA	Kappa
Co-Reg	0.8860	0.9452	0.7551	0.7906	0.8262	0.8960	0.8400	0.8498	0.8775
MMC	0.9180	0.9580	0.7242	0.9623	0.8756	0.6994	0.8708	0.8396	0.9005
SR-MO	0.9034	0.9049	0.8845	0.9561	0.8362	0.9554	0.9130	0.9067	0.9331
本文算法	0.9048	0.9088	0.8834	0.9604	0.8920	0.9382	0.9243	0.9146	0.9418

下载: 导出CSV

表 2 4种算法对德国Oberpfaffenhofen地区的分类结果

Table 2. Classification results of four algorithms for the Oberpfaffenhofen region of Germany

	Co-Reg	MMC	SR-MO	本文算法
农田	0.6111	0.6018	0.6859	0.7016
居民区	0.6072	0.6521	0.7336	0.7389
林地	0.8162	0.7993	0.9055	0.9108
道路	0.5311	0.5681	0.6049	0.6418
其他	0.8791	0.8789	0.8673	0.8814
OA	0.7363	0.7471	0.7822	0.7974
AA	0.6889	0.7000	0.7594	0.7749
Kappa	0.6170	0.6348	0.6920	0.7205

下载: 导出CSV

表 3 4种算法对西安地区的分类结果

Table 3. Classification results of four algorithms for Xi’an area

	Co-Reg	MMC	SR-MO	本文算法
河流	0.9372	0.8876	0.9189	0.8890
城区	0.7300	0.6622	0.8128	0.8550
植被	0.6876	0.8052	0.8006	0.8555
OA	0.7400	0.7670	0.8227	0.8503
AA	0.7259	0.7584	0.8136	0.8436
Kappa	0.7341	0.7710	0.8071	0.8471

下载: 导出CSV

表 4 4种算法对荷兰 Flevoland 地区大农田图的分类结果

Table 4. Classification results of four algorithms for large farmland maps in the Flevoland region of the Netherlands

	Co-Reg	MMC	SR-MO	本文算法
蚕豆	0.7459	0.8942	0.9614	0.9584
油菜籽	0.1393	0.7194	0.7094	0.8337
裸地	0.2056	0.9616	0.9541	0.9583
土豆	0.2479	0.8912	0.8796	0.9086
甜菜	0.1079	0.9481	0.9656	0.9515
小麦2	0.2427	0.6251	0.8525	0.7941
豌豆	0.7932	0.9517	0.8887	0.9571
小麦3	0.5412	0.9231	0.9180	0.9300
苜蓿	0.9541	0.8940	0.8391	0.9284
大麦	0.9226	0.6311	0.9660	0.8524
小麦	0.1158	0.8458	0.8660	0.8796
草地	0.3944	0.6459	0.7470	0.8773
森林	0.4041	0.8833	0.8329	0.9122
水域	0.5403	0.9757	0.9035	0.9620
建筑物	0.5954	0.7761	0.5865	0.7912
OA	0.4204	0.8441	0.8501	0.8923
AA	0.4165	0.8398	0.8697	0.9043
Kappa	0.4269	0.8409	0.8441	0.9136

下载: 导出CSV

参考文献(13)

[1]	邹焕新, 罗天成, 张月, 等. 基于组合条件随机场的极化SAR图像监督地物分类[J]. 雷达学报, 2017, 6(5): 541–553. doi: 10.12000/JR16109 ZOU Huanxin, LUO Tiancheng, ZHANG Yue, et al. Combined conditional random fields model for supervised PolSAR images classification[J]. Journal of Radars, 2017, 6(5): 541–553. doi: 10.12000/JR16109
[2]	FREEMAN A and DURDEN S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963–973. doi: 10.1109/36.673687
[3]	BUONO A, NUNZIATA F, MIGLIACCIO M, et al. Classification of the Yellow River delta area using fully polarimetric SAR measurements[J]. International Journal of Remote Sensing, 2017, 38(23): 6714–6734. doi: 10.1080/01431161.2017.1363437
[4]	JOULIN A, BACH F, and PONCE J. Discriminative clustering for image co-segmentation[C]. Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, USA, 2010: 1943–1950.
[5]	HARALICK R M, SHANMUGAM K, and DINSTEIN I. Textural features for image classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1973, SMC-3(6): 610–621. doi: 10.1109/TSMC.1973.4309314
[6]	RATHA D, BHATTACHARYA A, and FRERY A C. Unsupervised classification of PolSAR data using a scattering similarity measure derived from a geodesic distance[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(1): 151–155. doi: 10.1109/LGRS.2017.2778749
[7]	AHMED N and CAMPBELL M. Variational Bayesian learning of probabilistic discriminative models with latent softmax variables[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3143–3153. doi: 10.1109/TSP.2011.2144587
[8]	LIN Zhouchen, CHEN Minming, and MA Ya. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Eprint Arxiv, 2010(9): 26.
[9]	XIA Rongkai, PAN Yan, DU Lei, et al. Robust multi-view spectral clustering via low-rank and sparse decomposition[C]. Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, 2014: 2149–2155.
[10]	CAI Jianfeng, CANDÈS E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970
[11]	ZHU Ciyou, BYRD R H, LU Peihuang, et al. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization[J]. ACM Transactions on Mathematical Software, 1997, 23(4): 550–560. doi: 10.1145/279232.279236
[12]	KUMAR Y, MULLER U, BEN J, et al. spectral clustering MIT Press[C]. 24th Annual Conference on Neural Information Processing Systems, Vancouver, Canada, 2010.
[13]	MATSUGU M, MORI K, ISHII M, et al. Convolutional spiking neural network model for robust face detection[C]. Proceedings of the 9th International Conference on Neural Information Processing, Singapore, Singapore, 2002: 660–664.

施引文献

期刊类型引用(2)

1.	赵泉华，杜耀西，李玉，王光辉. 一种高分辨率SAR图像统计建模方法. 测绘科学. 2022(03): 65-74 . 百度学术
2.	刘旭，李玲玲，刘芳，杨淑媛，侯彪，焦李成. 基于散射图卷积网络的PolSAR影像地物分类. 中国科学:信息科学. 2022(10): 1900-1914 . 百度学术