- Home
- Articles & Issues
-
Data
- Dataset of Radar Detecting Sea
- SAR Dataset
- SARGroundObjectsTypes
- SARMV3D
- AIRSAT Constellation SAR Land Cover Classification Dataset
- 3DRIED
- UWB-HA4D
- LLS-LFMCWR
- FAIR-CSAR
- MSAR
- SDD-SAR
- FUSAR
- SpaceborneSAR3Dimaging
- Sea-land Segmentation
- SAR Multi-domain Ship Detection Dataset
- SAR-Airport
- Hilly and mountainous farmland time-series SAR and ground quadrat dataset
- SAR images for interference detection and suppression
- HP-SAR Evaluation & Analytical Dataset
- GDHuiYan-ATRNet
- Multi-System Maritime Low Observable Target Dataset
- DatasetinthePaper
- DatasetintheCompetition
- Report
- Course
- About
- Publish
- Editorial Board
- Chinese
| Citation: | LIU Che, YANG Kaiqiao, BAO Jianghan, et al. Recent progress in intelligent electromagnetic computing[J]. Journal of Radars, 2023, 12(4): 657–683. doi: 10.12000/JR23133 |
Recent Progress in Intelligent Electromagnetic Computing(in English)
DOI: 10.12000/JR23133 CSTR: 32380.14.jr23133
More Information-
Abstract
Since the introduction of Maxwell’s equations in the 19th century, computational electromagnetics has dramatically increased development. This growth can be attributed to the evolution of numerical algorithms, such as the finite difference method, finite element method, method of moments, and high-frequency approximation methods. These numerical techniques have become a crucial foundation of modern electronic and information engineering. Artificial intelligence has recently witnessed considerable development in electromagnetics; the rapid growth within this field owes itself to its robust modeling and inferential capability. This advancement has given rise to the emerging field of intelligent electromagnetic computing, which has captured the attention of numerous researchers. Remarkable achievements include electromagnetic modeling and simulation, analysis and synthesis of new electromagnetic materials and devices, and detection and perception. These contributions have injected fresh insights into the realm of electromagnetics. This paper discusses recent advances in intelligent electromagnetic computing to highlight new perspectives and avenues in research in this emerging field.
-

-
References
[1] “电磁计算”专刊编委会. 电磁计算方法研究进展综述[J]. 电波科学学报, 2020, 35(1): 13–25. doi: 10.13443/j.cjors.2019110301.The Editorial Board of Special Issue for “Computational Electromagnetics”. Progress in computational electromagnetic methods[J]. Chinese Journal of Radio Science, 2020, 35(1): 13–25. doi: 10.13443/j.cjors.2019110301.[2] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354–359. doi: 10.1038/nature24270.[3] JUMPER J, EVANS R, PRITZEL A, et al. Highly accurate protein structure prediction with AlphaFold[J]. Nature, 2021, 596(7873): 583–589. doi: 10.1038/s41586-021-03819-2.[4] BI Kaifeng, XIE Lingxi, ZHANG Hengheng, et al. Accurate medium-range global weather forecasting with 3D neural networks[J]. Nature, 2023, 619(7970): 533–538. doi: 10.1038/s41586-023-06185-3.[5] ZHANG Yuchen, LONG Mingsheng, CHEN Kaiyuan, et al. Skilful nowcasting of extreme precipitation with NowcastNet[J]. Nature, 2023, 619(7970): 526–532. doi: 10.1038/S41586-023-06184-4.[6] FAWZI A, BALOG M, HUANG A, et al. Discovering faster matrix multiplication algorithms with reinforcement learning[J]. Nature, 2022, 610(7930): 47–53. doi: 10.1038/s41586-022-05172-4.[7] ZHU Shiqiang, YU Ting, XU Tao, et al. Intelligent computing: The latest advances, challenges, and future[J]. Intelligent Computing, 2023, 2: 0006. doi: 10.34133/icomputing.0006.[8] HORNIK K, STINCHCOMBE M, and WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359–366. doi: 10.1016/0893-6080(89)90020-8.[9] MA Qian, LIU Che, XIAO Qiang, et al. Information metasurfaces and intelligent metasurfaces[J]. Photonics Insights, 2022, 1(1): R01. doi: 10.3788/PI.2022.R01.[10] CHEVALIER M W, LUEBBERS R J, and CABLE V P. FDTD local grid with material traverse[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 411–421. doi: 10.1109/8.558656.[11] JIN Jianming. The Finite Element Method in Electromagnetics[M]. 3rd ed. Hoboken: John Wiley & Sons, 2014.[12] HARRINGTON R F. The method of moments in electromagnetics[J]. Journal of Electromagnetic Waves and Applications, 1987, 1(3): 181–200. doi: 10.1163/156939387X00018.[13] LING H, CHOU R C, and LEE S W. Shooting and bouncing rays: Calculating the RCS of an arbitrarily shaped cavity[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(2): 194–205. doi: 10.1109/8.18706.[14] SCHÜTT K T, GASTEGGER M, TKATCHENKO A, et al. Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions[J]. Nature Communications, 2019, 10(1): 5024. doi: 10.1038/s41467-019-12875-2.[15] NOÉ F, OLSSON S, KÖHLER J, et al. Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning[J]. Science, 2019, 365(6457): eaaw1147. doi: 10.1126/science.aaw1147.[16] MOMENI A and FLEURY R. Electromagnetic wave-based extreme deep learning with nonlinear time-Floquet entanglement[J]. Nature Communications, 2022, 13(1): 2651. doi: 10.1038/s41467-022-30297-5.[17] GIANNAKIS I, GIANNOPOULOS A, and WARREN C. A machine learning-based fast-forward solver for ground penetrating radar with application to full-waveform inversion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(7): 4417–4426. doi: 10.1109/TGRS.2019.2891206.[18] YAO Heming and JIANG Lijun. Machine learning based neural network solving methods for the FDTD method[C]. 2018 IEEE International Symposium on Antennas and Propagation, Boston, USA, 2018: 2321–2322.[19] QI Shutong, WANG Yinpeng, LI Yongzhong, et al. Two-dimensional electromagnetic solver based on deep learning technique[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2020, 5: 83–88. doi: 10.1109/JMMCT.2020.2995811.[20] SHAN Tao, TANG Wei, DANG Xunwang, et al. Study on a fast solver for Poisson’s equation based on deep learning technique[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(9): 6725–6733. doi: 10.1109/TAP.2020.2985172.[21] NOAKOASTEEN O, WANG Shu, PENG Zhen, et al. Physics-informed deep neural networks for transient electromagnetic analysis[J]. IEEE Open Journal of Antennas and Propagation, 2020, 1: 404–412. doi: 10.1109/OJAP.2020.3013830.[22] MA Zhenchao, XU Kuiwen, SONG Rencheng, et al. Learning-based fast electromagnetic scattering solver through generative adversarial network[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(4): 2194–2208. doi: 10.1109/TAP.2020.3026447.[23] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672–2680.[24] ZHANG Wenwei, KONG Dehua, HE Xiaoyang, et al. A machine learning method for 2-D scattered far-field prediction based on wave coefficients[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(5): 1174–1178. doi: 10.1109/LAWP.2023.3235928.[25] KONG Dehua, ZHANG Wenwei, HE Xiaoyang, et al. Intelligent prediction for scattering properties based on multihead attention and target inherent feature parameter[J]. IEEE Transactions on Antennas and Propagation, 2023, 71(6): 5504–5509. doi: 10.1109/TAP.2023.3262341.[26] YIN Tiantian, WANG Chaofu, XU Kuiwen, et al. Electric flux density learning method for solving 3-D electromagnetic scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(7): 5144–5155. doi: 10.1109/TAP.2022.3145486.[27] YAO Heming and JIANG Lijun. Machine-learning-based PML for the FDTD method[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(1): 192–196. doi: 10.1109/LAWP.2018.2885570.[28] YAO Heming and JIANG Lijun. Enhanced PML based on the long short term memory network for the FDTD method[J]. IEEE Access, 2020, 8: 21028–21035. doi: 10.1109/ACCESS.2020.2969569.[29] HUGHES T W, WILLIAMSON I A D, MINKOV M, et al. Wave physics as an analog recurrent neural network[J]. Science Advances, 2019, 5(12): eaay6946. doi: 10.1126/sciadv.aay6946.[30] FENG Naixing, CHEN Yingshi, ZHANG Yuxian, et al. An expedient DDF-based implementation of perfectly matched monolayer[J]. IEEE Microwave and Wireless Components Letters, 2021, 31(6): 541–544. doi: 10.1109/LMWC.2021.3062645.[31] SUN Jiajing, SUN Sheng, CHEN Y P, et al. Machine-learning-based hybrid method for the multilevel fast multipole algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(12): 2177–2181. doi: 10.1109/LAWP.2020.3026822.[32] HAO Wenqu, CHEN Y P, CHEN Peiyao, et al. Solving two-dimensional scattering from multiple dielectric cylinders by artificial neural network accelerated numerical green’s function[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(5): 783–787. doi: 10.1109/LAWP.2021.3063133.[33] GUO Rui, LIN Zhichao, SHAN Tao, et al. Solving combined field integral equation with deep neural network for 2-D conducting object[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(4): 538–542. doi: 10.1109/LAWP.2021.3056460.[34] GUO Rui, SHAN Tao, SONG Xiaoqian, et al. Physics embedded deep neural network for solving volume integral equation: 2-D case[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(8): 6135–6147. doi: 10.1109/TAP.2021.3070152.[35] XUE Bowen, GUO Rui, LI Maokun, et al. Deep-learning-equipped iterative solution of electromagnetic scattering from dielectric objects[J]. IEEE Transactions on Antennas and Propagation, 2023, 71(7): 5954–5966. doi: 10.1109/TAP.2023.3264701.[36] RAISSI M, PERDIKARIS P, and KARNIADAKIS G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686–707. doi: 10.1016/j.jcp.2018.10.045.[37] LIM J and PSALTIS D. MaxwellNet: Physics-driven deep neural network training based on Maxwell's equations[J]. APL Photonics, 2022, 7(1): 011301. doi: 10.1063/5.0071616.[38] GIGLI C, SABA A, AYOUB A B, et al. Predicting nonlinear optical scattering with physics-driven neural networks[J]. APL Photonics, 2023, 8(2): 026105. doi: 10.1063/5.0119186.[39] FUJITA K. Electromagnetic field computation of multilayer vacuum chambers with physics-informed neural networks[J]. Frontiers in Physics, 2022, 10: 967645. doi: 10.3389/fphy.2022.967645.[40] CHEN Mingkun, LUPOIU R, MAO Chenkai, et al. WaveY-Net: Physics-augmented deep-learning for high-speed electromagnetic simulation and optimization[C]. SPIE 12011, High Contrast Metastructures XI, San Francisco, USA, 2022: 120110C.[41] LU Lu, JIN Pengzhan, PANG Guofei, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021, 3(3): 218–229. doi: 10.1038/s42256-021-00302-5.[42] LU Lu, MENG Xuhui, MAO Zhiping, et al. DeepXDE: A deep learning library for solving differential equations[J]. Siam Review, 2021, 63(1): 208–228. doi: 10.1137/19M1274067.[43] GUPTA G, XIAO Xiongye, and BOGDAN P. Multiwavelet-based operator learning for differential equations[C]. 35th Conference on Neural Information Processing Systems, 2021, 34: 24048–24062.[44] LI Zongyi, KOVACHKI N, AZIZZADENESHELI K, et al. Fourier neural operator for parametric partial differential equations[C]. 9th International Conference on Learning Representations, Austria, 2021.[45] AUGENSTEIN Y, REPÄN T, and ROCKSTUHL C. Neural operator-based surrogate solver for free-form electromagnetic inverse design[J]. ACS Photonics, 2023, 10(5): 1547–1557. doi: 10.1021/acsphotonics.3c00156.[46] PENG Zhong, YANG Bo, XU Yixian, et al. Rapid surrogate modeling of electromagnetic data in frequency domain using neural operator[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 2007912. doi: 10.1109/TGRS.2022.3222507.[47] PATHAK J, SUBRAMANIAN S, HARRINGTON P, et al. FourCastNet: A global data-driven high-resolution weather model using adaptive Fourier neural operators[J]. arXiv: 2202.11214, 2022.[48] GUIBAS J, MARDANI M, LI Zongyi, et al. Adaptive Fourier neural operators: Efficient token mixers for transformers[C]. 10th International Conference on Learning Representations (ICLR), Virtual, Online, 2022.[49] 许威威, 周漾, 吴鸿智, 等. 可微绘制技术研究进展[J]. 中国图象图形学报, 2021, 26(6): 1521–1535. doi: 10.11834/jig.200853.XU Weiwei, ZHOU Yang, WU Hongzhi, et al. Differential rendering: A survey[J]. Journal of Image and Graphics, 2021, 26(6): 1521–1535. doi: 10.11834/jig.200853.[50] GUO Liangshuai, LI Maokun, XU Shenheng, et al. Electromagnetic modeling using an FDTD-equivalent recurrent convolution neural network: Accurate computing on a deep learning framework[J]. IEEE Antennas and Propagation Magazine, 2023, 65(1): 93–102. doi: 10.1109/MAP.2021.3127514.[51] HU Yanyan, JIN Yuchen, WU Xuqing, et al. A theory-guided deep neural network for time domain electromagnetic simulation and inversion using a differentiable programming platform[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(1): 767–772. doi: 10.1109/TAP.2021.3098585.[52] FU Shilei and XU Feng. Differentiable SAR renderer and image-based target reconstruction[J]. IEEE Transactions on Image Processing, 2022, 31: 6679–6693. doi: 10.1109/TIP.2022.3215069.[53] LOPER M M and BLACK M J. OpenDR: An approximate differentiable renderer[C]. 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 154–169.[54] CHEN Wenzheng, GAO Jun, LING Huan, et al. Learning to predict 3D objects with an interpolation-based differentiable renderer[C]. 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 862.[55] MARKLEIN R, MAYER K, HANNEMANN R, et al. Linear and nonlinear inversion algorithms applied in nondestructive evaluation[J]. Inverse Problems, 2002, 18(6): 1733–1759. doi: 10.1088/0266-5611/18/6/319.[56] ZOUGHI R and KHARKOVSKY S. Microwave and millimetre wave sensors for crack detection[J]. Fatigue &Fracture of Engineering Materials &Structures, 2008, 31(8): 695–713. doi: 10.1111/j.1460-2695.2008.01255.x.[57] NEAL A. Ground-penetrating radar and its use in sedimentology: Principles, problems and progress[J]. Earth-Science Reviews, 2004, 66(3/4): 261–330. doi: 10.1016/j.earscirev.2004.01.004.[58] ABUBAKAR A, HABASHY T M, DRUSKIN V L, et al. 2.5D forward and inverse modeling for interpreting low-frequency electromagnetic measurements[J]. Geophysics, 2008, 73(4): F165–F177. doi: 10.1190/1.2937466.[59] BOND E J, LI Xu, HAGNESS S C, et al. Microwave imaging via space-time beamforming for early detection of breast cancer[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(8): 1690–1705. doi: 10.1109/TAP.2003.815446.[60] NIKOLOVA N K. Microwave imaging for breast cancer[J]. IEEE Microwave Magazine, 2011, 12(7): 78–94. doi: 10.1109/MMM.2011.942702.[61] SHEEN D M, MCMAKIN D L, and HALL T E. Three-dimensional millimeter-wave imaging for concealed weapon detection[J]. IEEE Transactions on Microwave Theory and Techniques, 2001, 49(9): 1581–1592. doi: 10.1109/22.942570.[62] ZHUGE Xiaodong and YAROVOY A G. A sparse aperture MIMO-SAR-based UWB imaging system for concealed weapon detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 509–518. doi: 10.1109/TGRS.2010.2053038.[63] VAN DEN BERG P M and KLEINMAN R E. A contrast source inversion method[J]. Inverse Problems, 1997, 13(6): 1607–1620. doi: 10.1088/0266-5611/13/6/013.[64] VAN DEN BERG P M, ABUBAKAR A, and FOKKEMA J T. Multiplicative regularization for contrast profile inversion[J]. Radio Science, 2003, 38(2): 8022. doi: 10.1029/2001RS002555.[65] CHEW W C and WANG Yiming. Reconstruction of two-dimensional permittivity distribution using the distorted Born iterative method[J]. IEEE Transactions on Medical Imaging, 1990, 9(2): 218–225. doi: 10.1109/42.56334.[66] LI Lianlin, WANG Longgang, DING Jun, et al. A probabilistic model for the nonlinear electromagnetic inverse scattering: TM case[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(11): 5984–5991. doi: 10.1109/TAP.2017.2751654.[67] PASTORINO M. Stochastic optimization methods applied to microwave imaging: A review[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3): 538–548. doi: 10.1109/TAP.2007.891568.[68] SALUCCI M, ARREBOLA M, SHAN Tao, et al. Artificial intelligence: New frontiers in real-time inverse scattering and electromagnetic imaging[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(8): 6349–6364. doi: 10.1109/TAP.2022.3177556.[69] SUN Yu, XIA Zhihao, and KAMILOV U S. Efficient and accurate inversion of multiple scattering with deep learning[J]. Optics Express, 2018, 26(11): 14678–14688. doi: 10.1364/OE.26.014678.[70] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241.[71] WEI Zhun and CHEN Xudong. Deep-learning schemes for full-wave nonlinear inverse scattering problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(4): 1849–1860. doi: 10.1109/TGRS.2018.2869221.[72] XU Kuiwen, WU Liang, YE Xiuzhu, et al. Deep learning-based inversion methods for solving inverse scattering problems with phaseless data[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(11): 7457–7470. doi: 10.1109/TAP.2020.2998171.[73] ZHANG Huanhuan, YAO Heming, JIANG Lijun, et al. Enhanced two-step deep-learning approach for electromagnetic-inverse-scattering problems: Frequency extrapolation and scatterer reconstruction[J]. IEEE Transactions on Antennas and Propagation, 2023, 71(2): 1662–1672. doi: 10.1109/TAP.2022.3225532.[74] ZHOU Yulong, ZHONG Yu, WEI Zhun, et al. An improved deep learning scheme for solving 2-D and 3-D inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(5): 2853–2863. doi: 10.1109/TAP.2020.3027898.[75] ZHONG Yu, LAMBERT M, LESSELIER D, et al. A new integral equation method to solve highly nonlinear inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(5): 1788–1799. doi: 10.1109/TAP.2016.2535492.[76] GUO Liang, SONG Guanfeng, and WU Hongsheng. Complex-valued pix2pix-deep neural network for nonlinear electromagnetic inverse scattering[J]. Electronics, 2021, 10(6): 752. doi: 10.3390/electronics10060752.[77] ISOLA P, ZHU Junyan, ZHOU Tinghui, et al. Image-to-image translation with conditional adversarial networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 5967–5976.[78] SONG Rencheng, HUANG Youyou, YE Xiuzhu, et al. Learning-based inversion method for solving electromagnetic inverse scattering with mixed boundary conditions[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(8): 6218–6228. doi: 10.1109/TAP.2021.3139645.[79] LI Lianlin, WANG Longgang, TEIXEIRA F L, et al. DeepNIS: Deep neural network for nonlinear electromagnetic inverse scattering[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(3): 1819–1825. doi: 10.1109/TAP.2018.2885437.[80] WEI Zhun and CHEN Xudong. Physics-inspired convolutional neural network for solving full-wave inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(9): 6138–6148. doi: 10.1109/TAP.2019.2922779.[81] GUO Rui, JIA Zekui, SONG Xiaoqian, et al. Pixel- and model-based microwave inversion with supervised descent method for dielectric targets[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(12): 8114–8126. doi: 10.1109/TAP.2020.2999741.[82] GUO Rui, LIN Zhichao, SHAN Tao, et al. Physics embedded deep neural network for solving full-wave inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(8): 6148–6159. doi: 10.1109/TAP.2021.3102135.[83] LIU Che, ZHANG Hongrui, LI Lianlin, et al. Towards intelligent electromagnetic inverse scattering using deep learning techniques and information metasurfaces[J]. IEEE Journal of Microwaves, 2023, 3(1): 509–522. doi: 10.1109/JMW.2022.3225999.[84] ZHU Junyan, PARK T, ISOLA P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2242–2251.[85] ZHANG Hongrui, CHEN Yanjin, CUI Tiejun, et al. Probabilistic deep learning solutions to electromagnetic inverse scattering problems using conditional renormalization group flow[J]. IEEE Transactions on Microwave Theory and Techniques, 2022, 70(11): 4955–4965. doi: 10.1109/TMTT.2022.3205890.[86] CHEN Yanjin, ZHANG Hongrui, CUI Tiejun, et al. A mesh-free 3-D deep learning electromagnetic inversion method based on point clouds[J]. IEEE Transactions on Microwave Theory and Techniques, 2023.[87] VESELAGO V G. The electrodynamics of substances with simultaneously negative values of ε and μ[J]. Soviet Physics Uspekhi, 1968, 10(4): 509–514. doi: 10.1070/PU1968v010n04ABEH003699.[88] PARAZZOLI C G, GREEGOR R B, LI K, et al. Experimental verification and simulation of negative index of refraction using Snell’s law[J]. Physical Review Letters, 2003, 90(10): 107401. doi: 10.1103/PhysRevLett.90.107401.[89] DRACHEV V P, CAI W, CHETTIAR U, et al. Experimental verification of an optical negative-index material[J]. Laser Physics Letters, 2006, 3(1): 49–55. doi: 10.1002/lapl.200510062.[90] LIU Ruopeng, CHENG Qiang, HAND T, et al. Experimental demonstration of electromagnetic tunneling through an epsilon-near-zero metamaterial at microwave frequencies[J]. Physical Review Letters, 2008, 100(2): 023903. doi: 10.1103/PhysRevLett.100.023903.[91] KUNDTZ N and SMITH D R. Extreme-angle broadband metamaterial lens[J]. Nature Materials, 2010, 9(2): 129–132. doi: 10.1038/nmat2610.[92] CUI Tiejun, QI Meiqing, WAN Xiang, et al. Coding metamaterials, digital metamaterials and programmable metamaterials[J]. Light:Science &Applications, 2014, 3(10): e218. doi: 10.1038/lsa.2014.99.[93] CUI Tiejun, LI Lianlin, LIU Shuo, et al. Information metamaterial systems[J]. iScience, 2020, 23(8): 101403. doi: 10.1016/j.isci.2020.101403.[94] CUI Tiejun, LIU Shuo, and ZHANG Lei. Information metamaterials and metasurfaces[J]. Journal of Materials Chemistry C, 2017, 5(15): 3644–3668. doi: 10.1039/C7TC00548B.[95] LI Lianlin and CUI Tiejun. Information metamaterials - from effective media to real-time information processing systems[J]. Nanophotonics, 2019, 8(5): 703–724. doi: 10.1515/nanoph-2019-0006.[96] CUI Tiejun, LIU Shuo, and LI Lianlin. Information entropy of coding metasurface[J]. Light:Science &Applications, 2016, 5(11): e16172. doi: 10.1038/lsa.2016.172.[97] 刘彻, 马骞, 李廉林, 等. 人工智能超材料[J]. 光学学报, 2021, 41(8): 0823004. doi: 10.3788/AOS202141.0823004.LIU Che, MA Qian, LI Lianlin, et al. Artificial intelligence metamaterials[J]. Acta Optica Sinica, 2021, 41(8): 0823004. doi: 10.3788/AOS202141.0823004.[98] SHAN Tao, PAN Xiaotian, LI Maokun, et al. Coding programmable metasurfaces based on deep learning techniques[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2020, 10(1): 114–125. doi: 10.1109/JETCAS.2020.2972764.[99] LI Shangyang, LIU Zhuoyang, FU Shilei, et al. Intelligent beamforming via physics-inspired neural networks on programmable metasurface[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(6): 4589–4599. doi: 10.1109/TAP.2022.3140891.[100] LIU Che, YU Wenming, MA Qian, et al. Intelligent coding metasurface holograms by physics-assisted unsupervised generative adversarial network[J]. Photonics Research, 2021, 9(4): B159–B167. doi: 10.1364/PRJ.416287.[101] CHEN Xiaoqing, ZHANG Lei, and CUI Tiejun. Intelligent autoencoder for space-time-coding digital metasurfaces[J]. Applied Physics Letters, 2023, 122(16): 161702. doi: 10.1063/5.0132635.[102] QIAN Chao, ZHENG Bin, SHEN Yichen, et al. Deep-learning-enabled self-adaptive microwave cloak without human intervention[J]. Nature Photonics, 2020, 14(6): 383–390. doi: 10.1038/s41566-020-0604-2.[103] JIA Yuetian, QIAN Chao, FAN Zhixiang, et al. A knowledge-inherited learning for intelligent metasurface design and assembly[J]. Light:Science &Applications, 2023, 12(1): 82. doi: 10.1038/s41377-023-01131-4.[104] REN Haoran, LI Xiangping, ZHANG Qiming, et al. On-chip noninterference angular momentum multiplexing of broadband light[J]. Science, 2016, 352(6287): 805–809. doi: 10.1126/science.aaf1112.[105] LIN Xing, RIVENSON Y, YARDIMCI N T, et al. All-optical machine learning using diffractive deep neural networks[J]. Science, 2018, 361(6406): 1004–1008. doi: 10.1126/science.aat8084.[106] KHORAM E, CHEN Ang, LIU Dianjing, et al. Nanophotonic media for artificial neural inference[J]. Photonics Research, 2019, 7(8): 823–827. doi: 10.1364/PRJ.7.000823.[107] LIU Che, MA Qian, LUO Zhangjie, et al. A programmable diffractive deep neural network based on a digital-coding metasurface array[J]. Nature Electronics, 2022, 5(2): 113–122. doi: 10.1038/s41928-022-00719-9.[108] PENDRY J B, MARTÍN-MORENO L, and GARCIA-VIDAL F J. Mimicking surface plasmons with structured surfaces[J]. Science, 2004, 305(5685): 847–848. doi: 10.1126/science.1098999.[109] GAO Xinxin, MA Qian, GU Ze, et al. Programmable surface plasmonic neural networks for microwave detection and processing[J]. Nature Electronics, 2023, 6(4): 319–328. doi: 10.1038/s41928-023-00951-x.[110] 李廉林, 崔铁军. 智能电磁感知的若干进展[J]. 雷达学报, 2021, 10(2): 183–190. doi: 10.12000/JR21049.LI Lianlin and CUI Tiejun. Recent progress in intelligent electromagnetic sensing[J]. Journal of Radars, 2021, 10(2): 183–190. doi: 10.12000/JR21049.[111] ZHAO Hanting, HU Shengguo, ZHANG Hongrui, et al. Intelligent indoor metasurface robotics[J]. National Science Review, 2023, 10(8): nwac266. doi: 10.1093/NSR/NWAC266.[112] WANG Zhuo, ZHANG Hongrui, ZHAO Hanting, et al. Multi-task and multi-scale intelligent electromagnetic sensing with distributed multi-frequency reprogrammable metasurfaces[J]. Advanced Optical Materials, 2023: 2203153.[113] LI Weihan, MA Qian, LIU Che, et al. Intelligent metasurface system for automatic tracking of moving targets and wireless communications based on computer vision[J]. Nature Communications, 2023, 14(1): 989. doi: 10.1038/s41467-023-36645-3. -
Proportional views

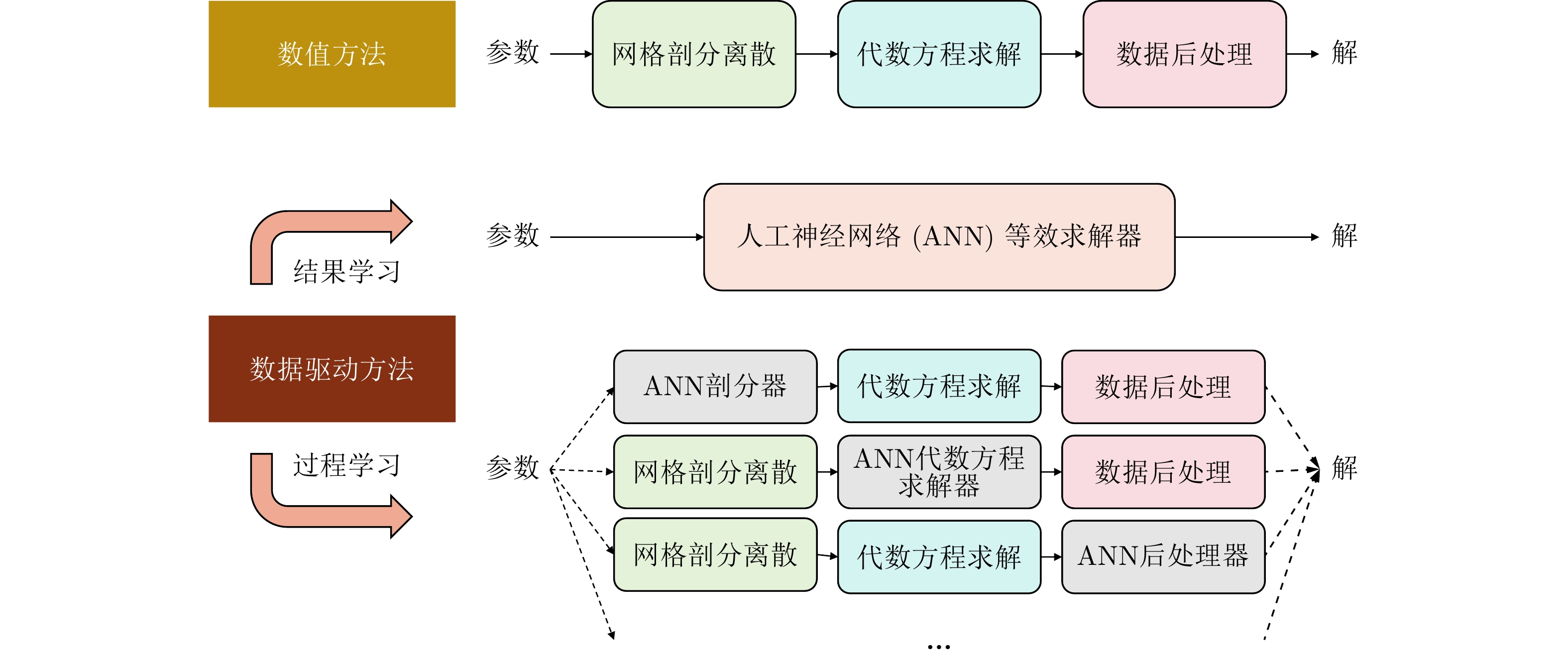
- Figure 1. The classification of data-driven forward electromagnetic computing
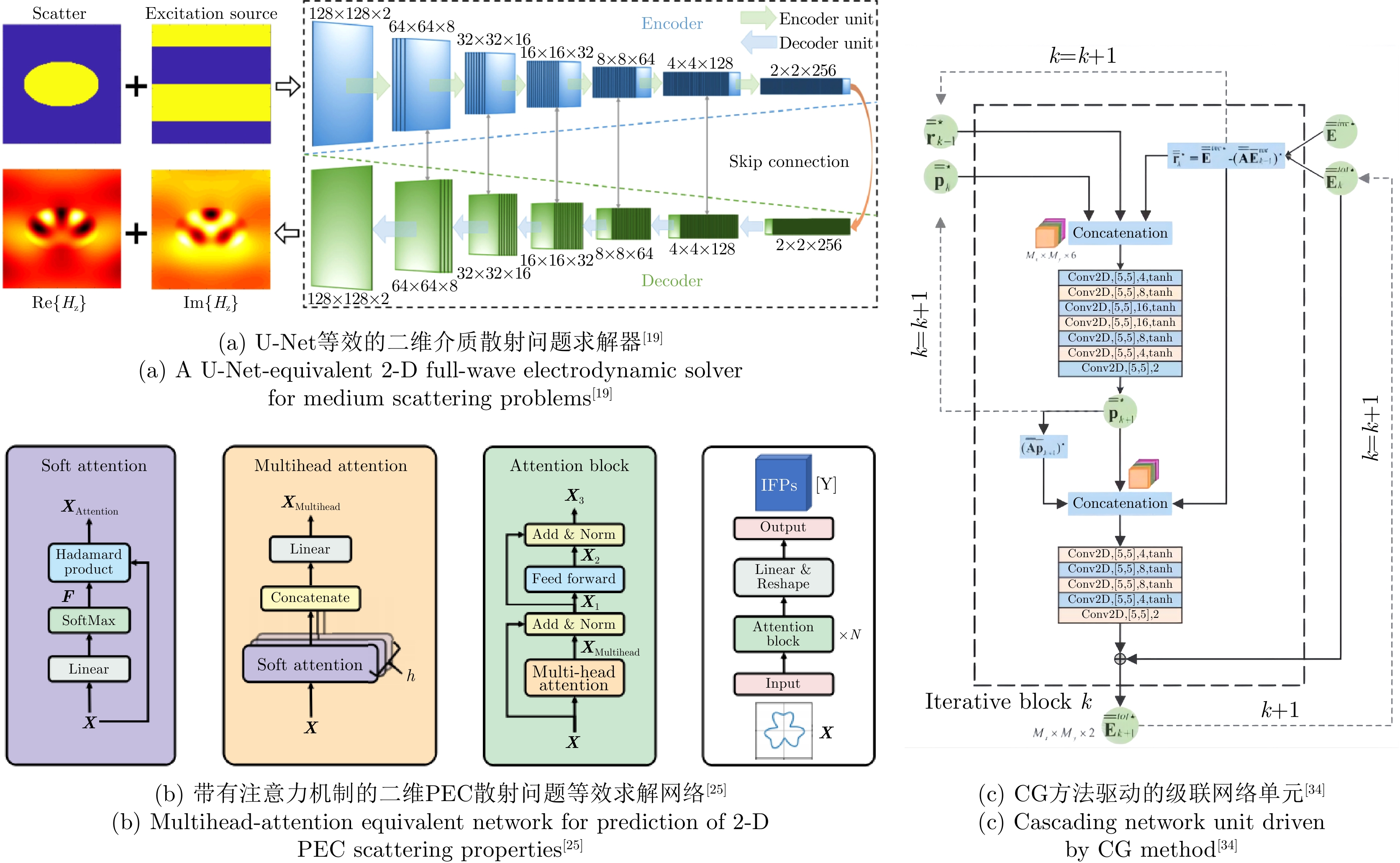
- Figure 2. Several research results of data-driven forward electromagnetic computing
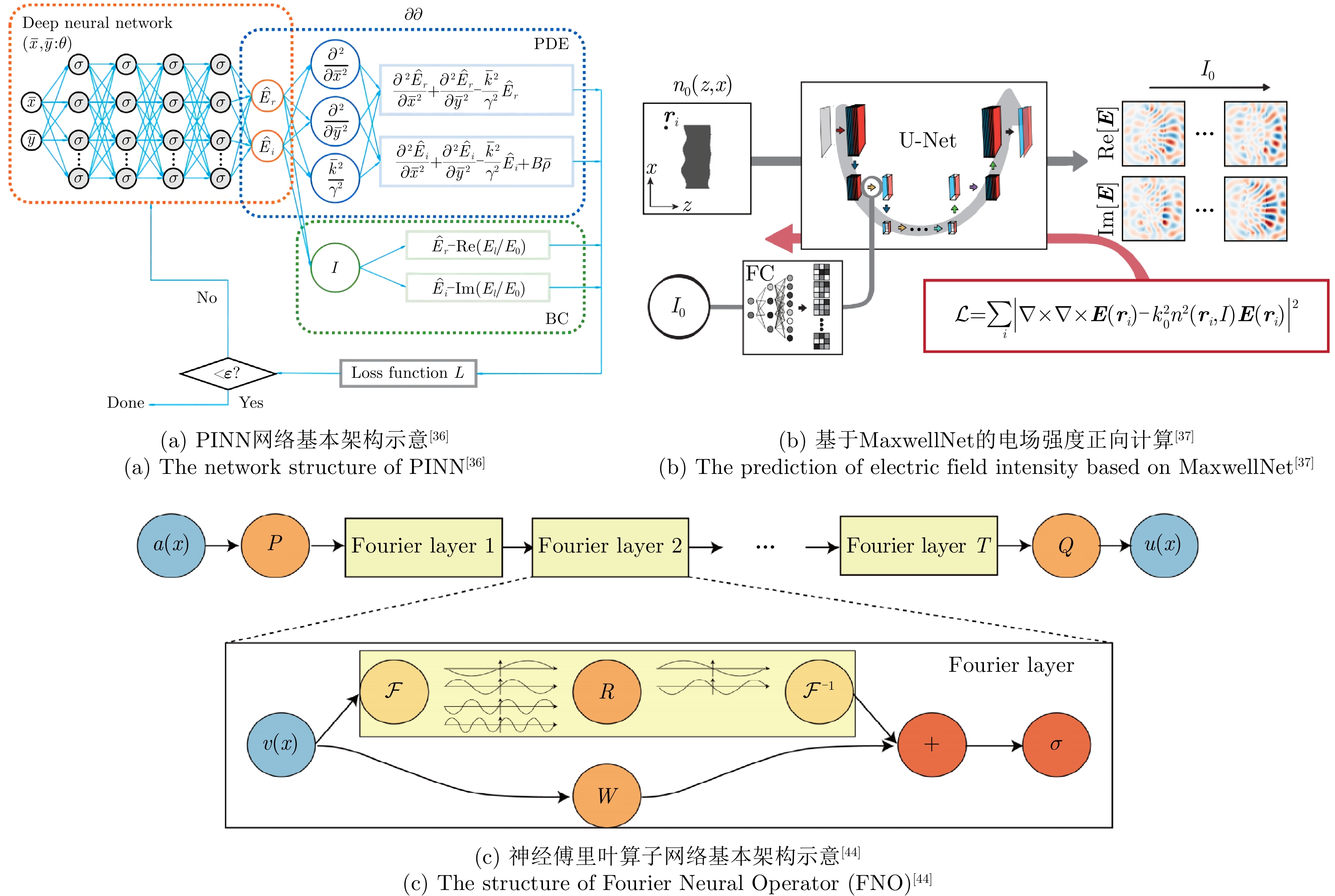
- Figure 3. Several research results of PINN based and operator-learning based forward computing
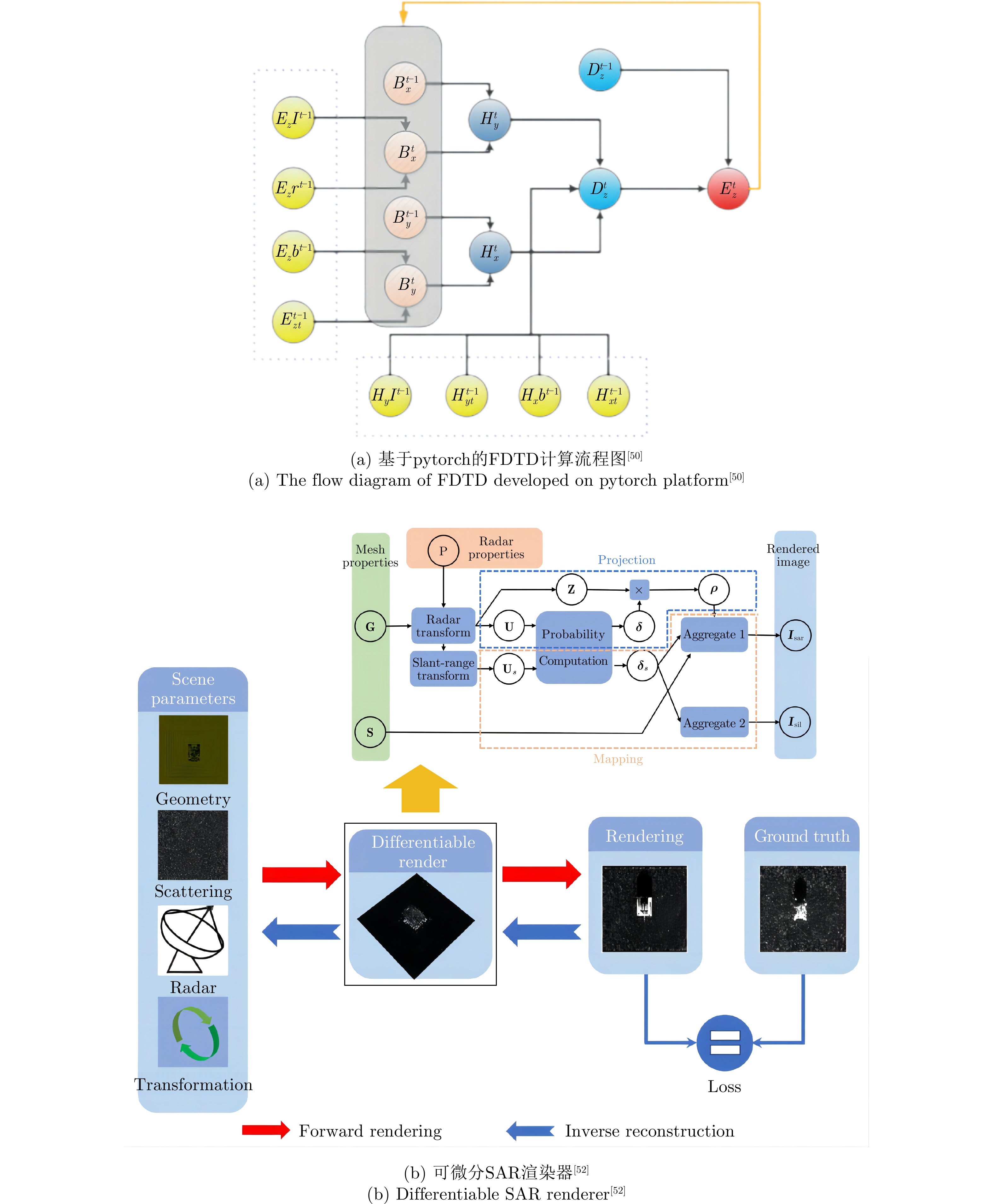
- Figure 4. Several research results of differentiable forward electromagnetic computing
- Figure 5. Reverse intelligent electromagnetic imaging based on U-Net
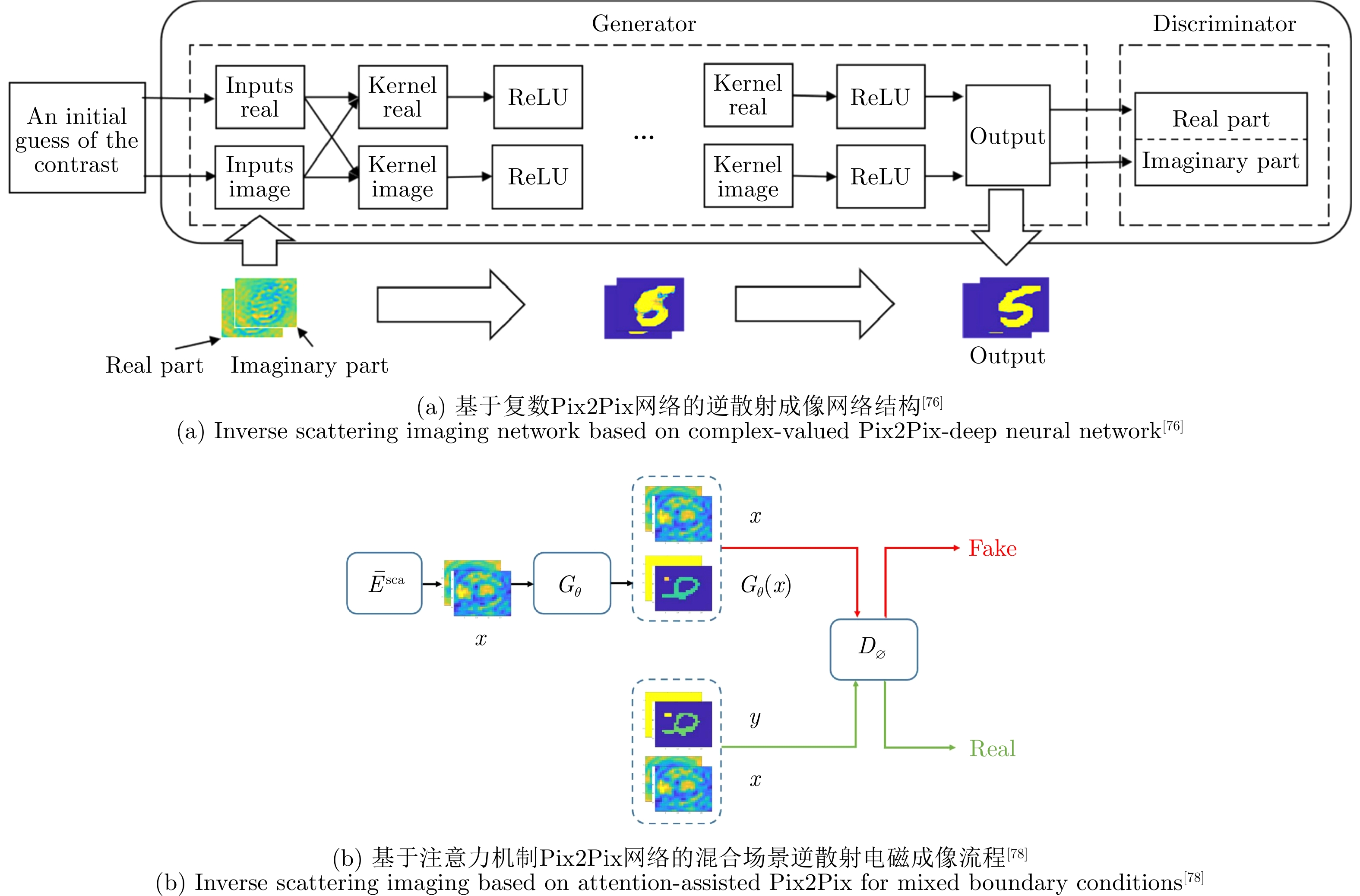
- Figure 6. Reverse intelligent electromagnetic imaging based on Pix2Pix
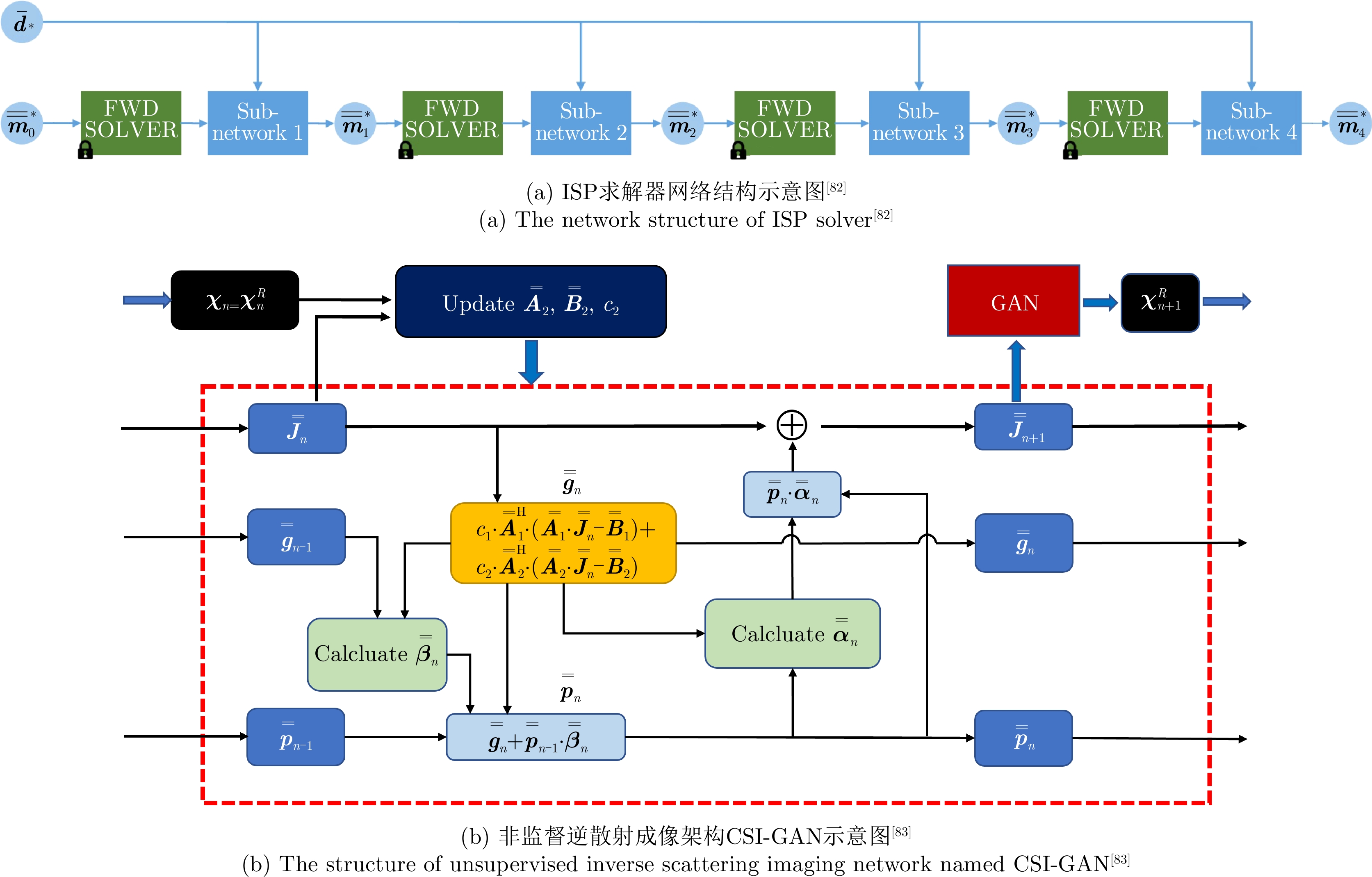
- Figure 7. End-to-end reverse intelligent electromagnetic imaging inspired by iterative optimization methods
- Figure 8. Iterative intelligent electromagnetic imaging
- Figure 9. A mesh-free 3-D deep learning electromagnetic inversion method based on point clouds[86]
- Figure 10.
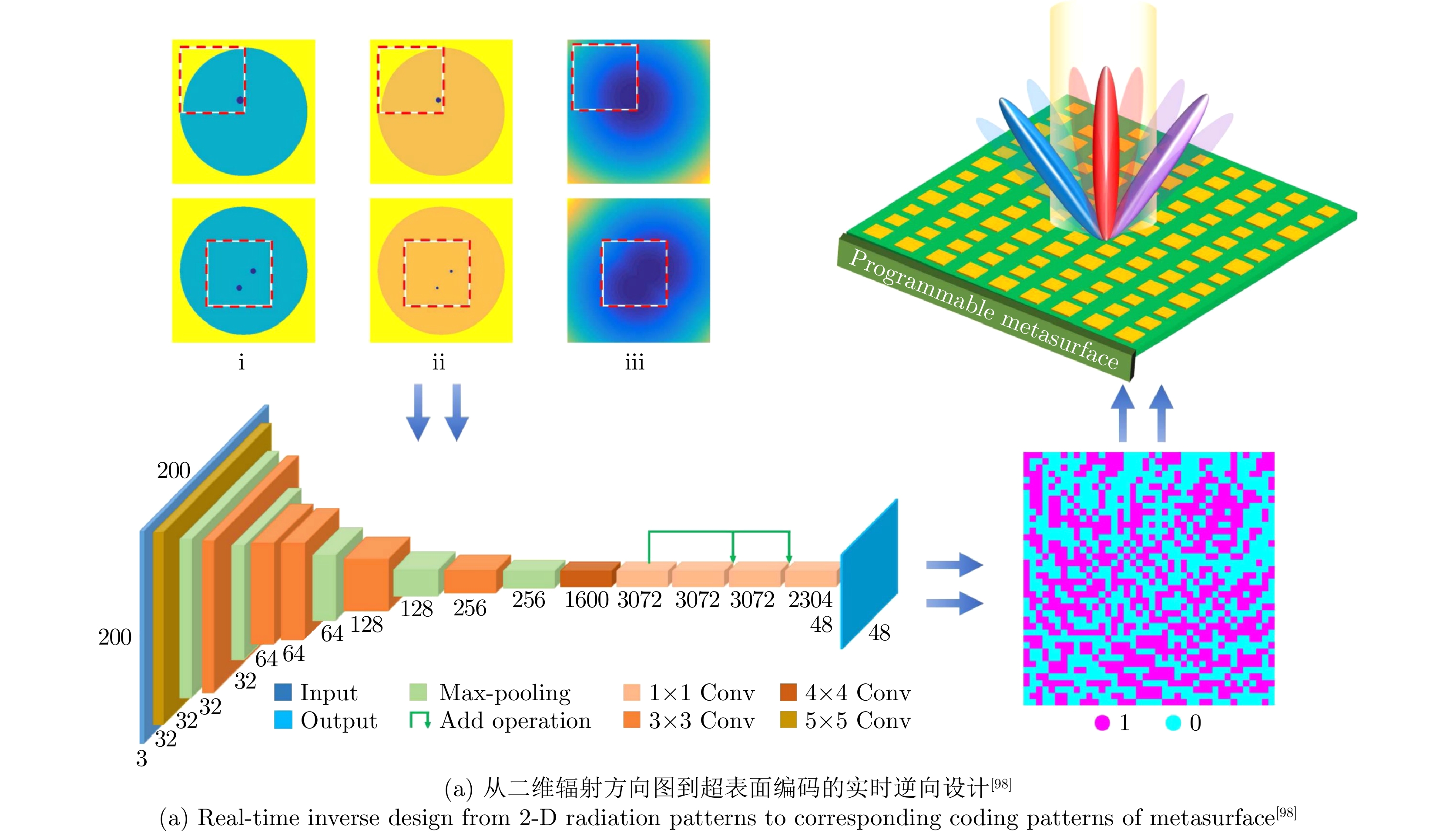
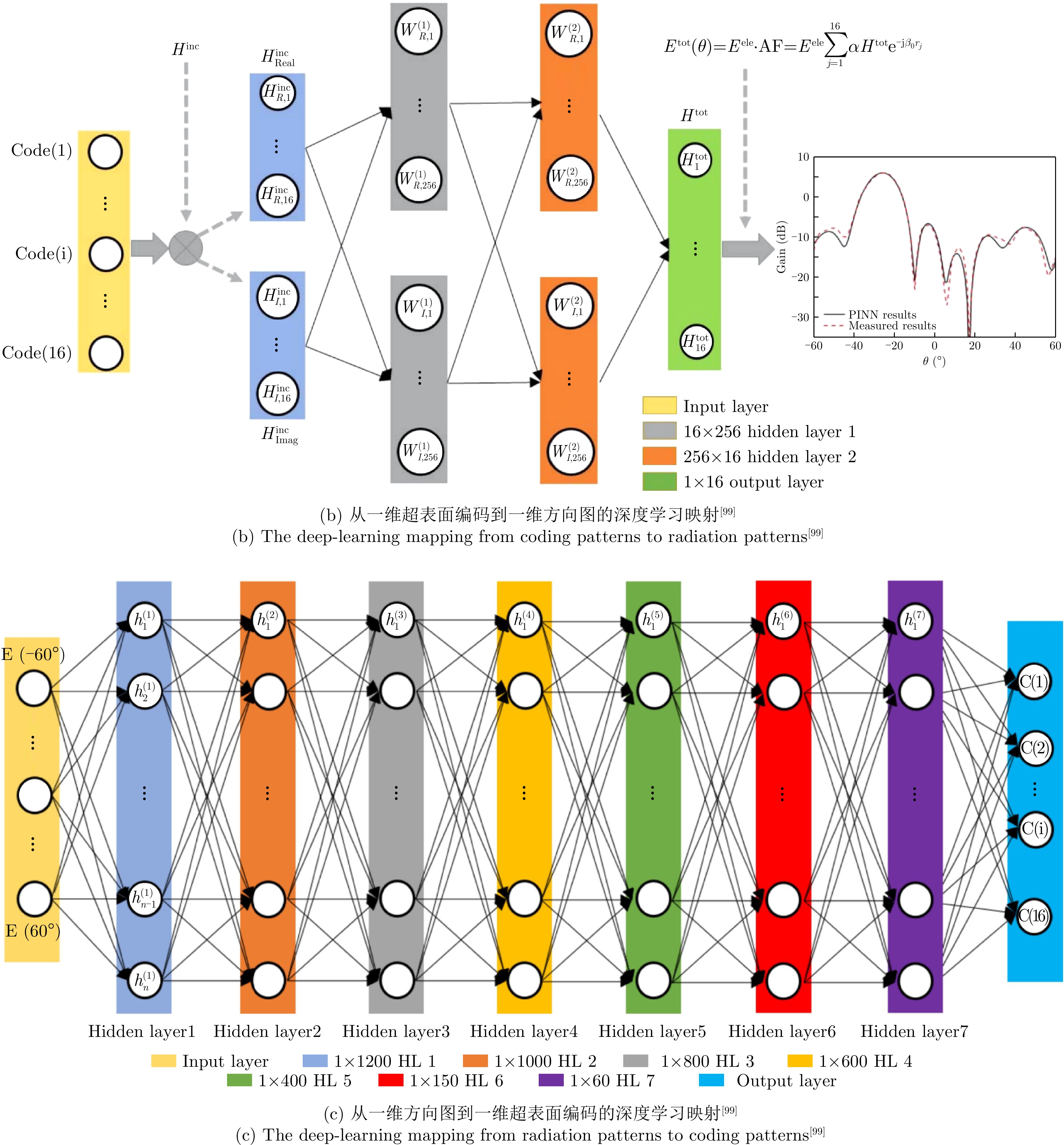
- Figure 10. Intelligent design of radiation patterns based on information metamaterial
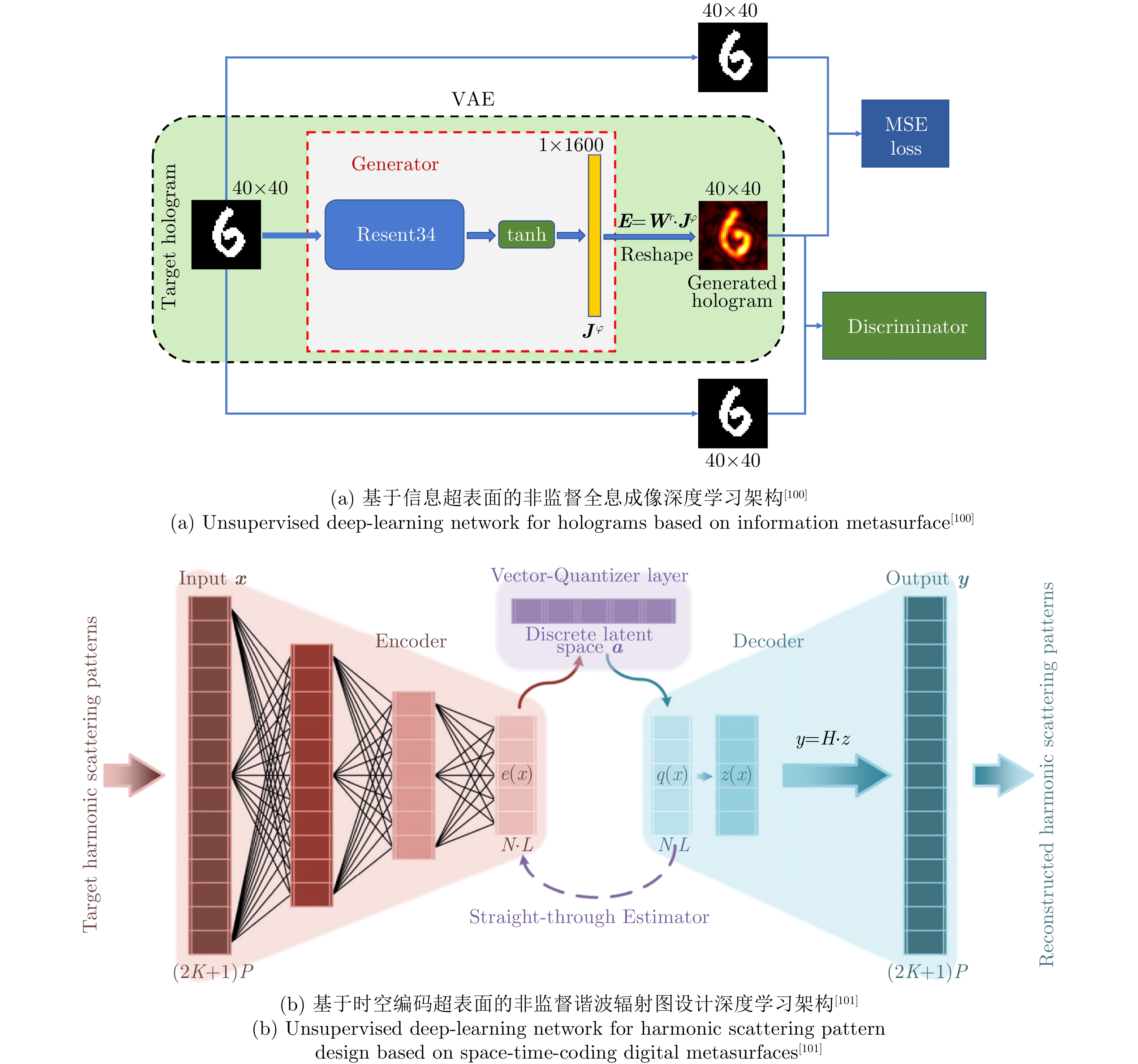
- Figure 11. Unsupervised intelligent design based on information metamaterial
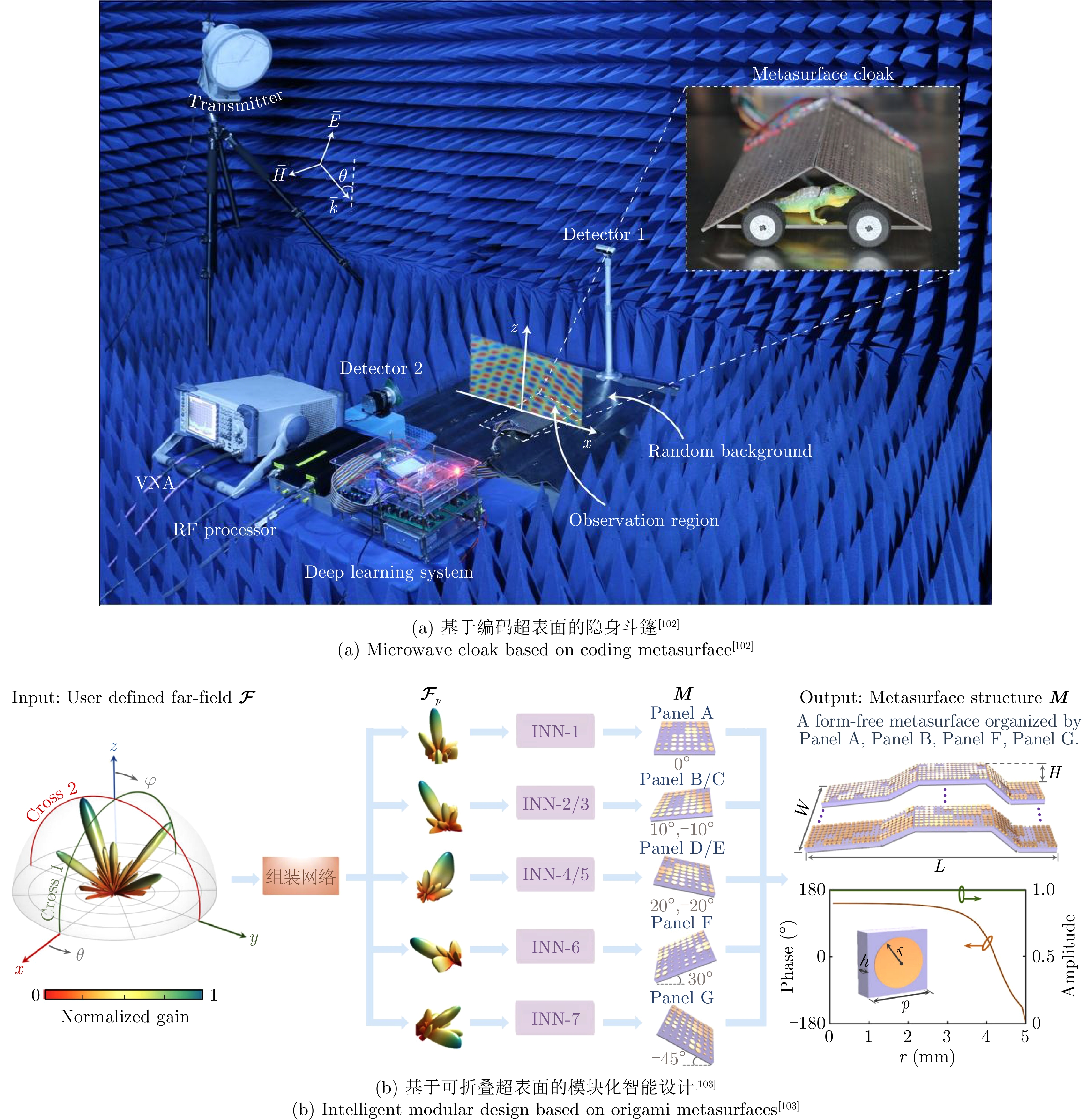
- Figure 12. Intelligent design of information metamaterial for complex systems
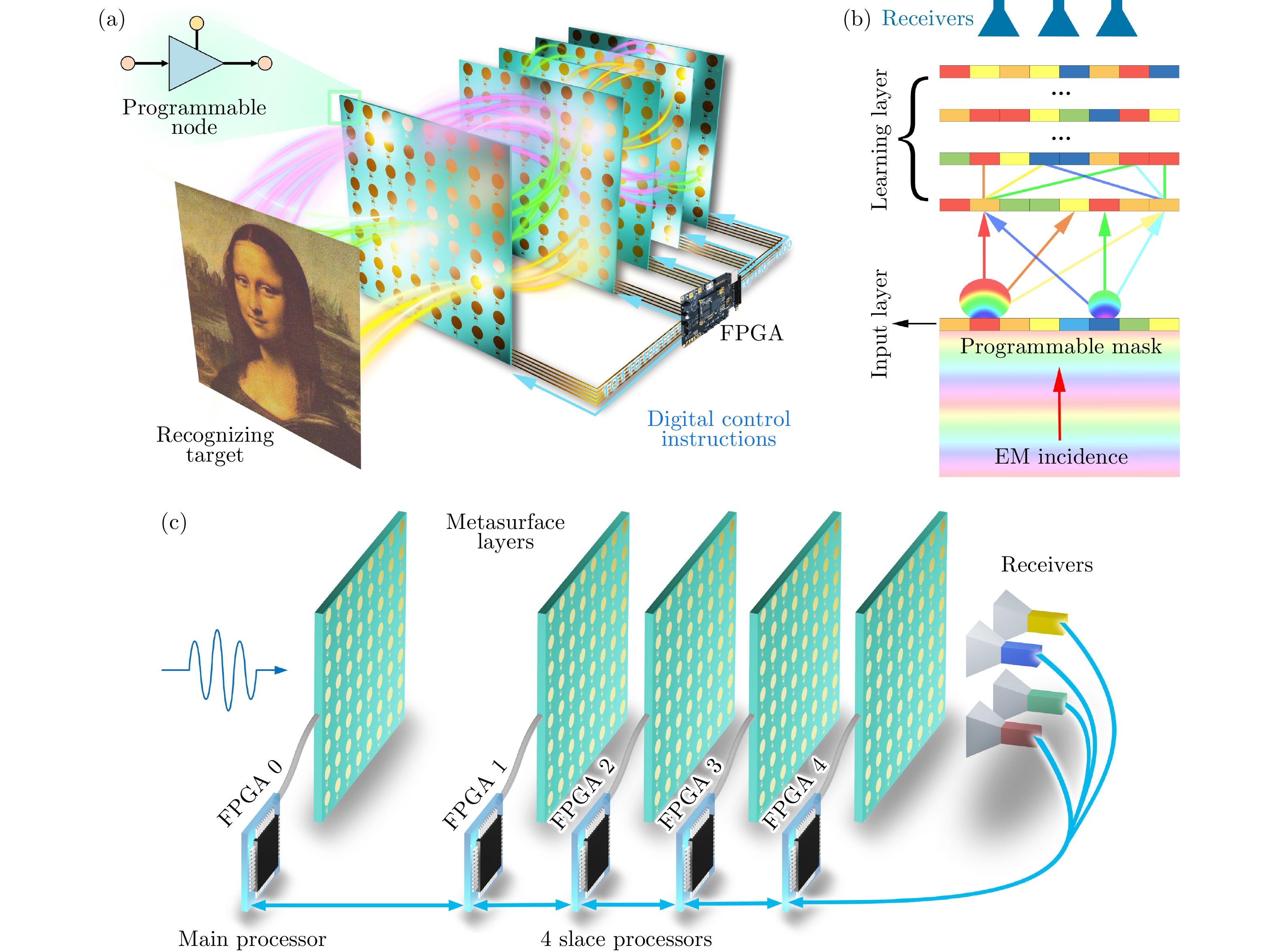
- Figure 13. The Working Principle of Programmable Artificial Intelligence Machine (PIAM)[107]
- Figure 14. Programmable Surface Plasmonic Neural Networks (SPNN)[109]
- Figure 15. Intelligent indoor metasurface robotics (I2MR)[111]
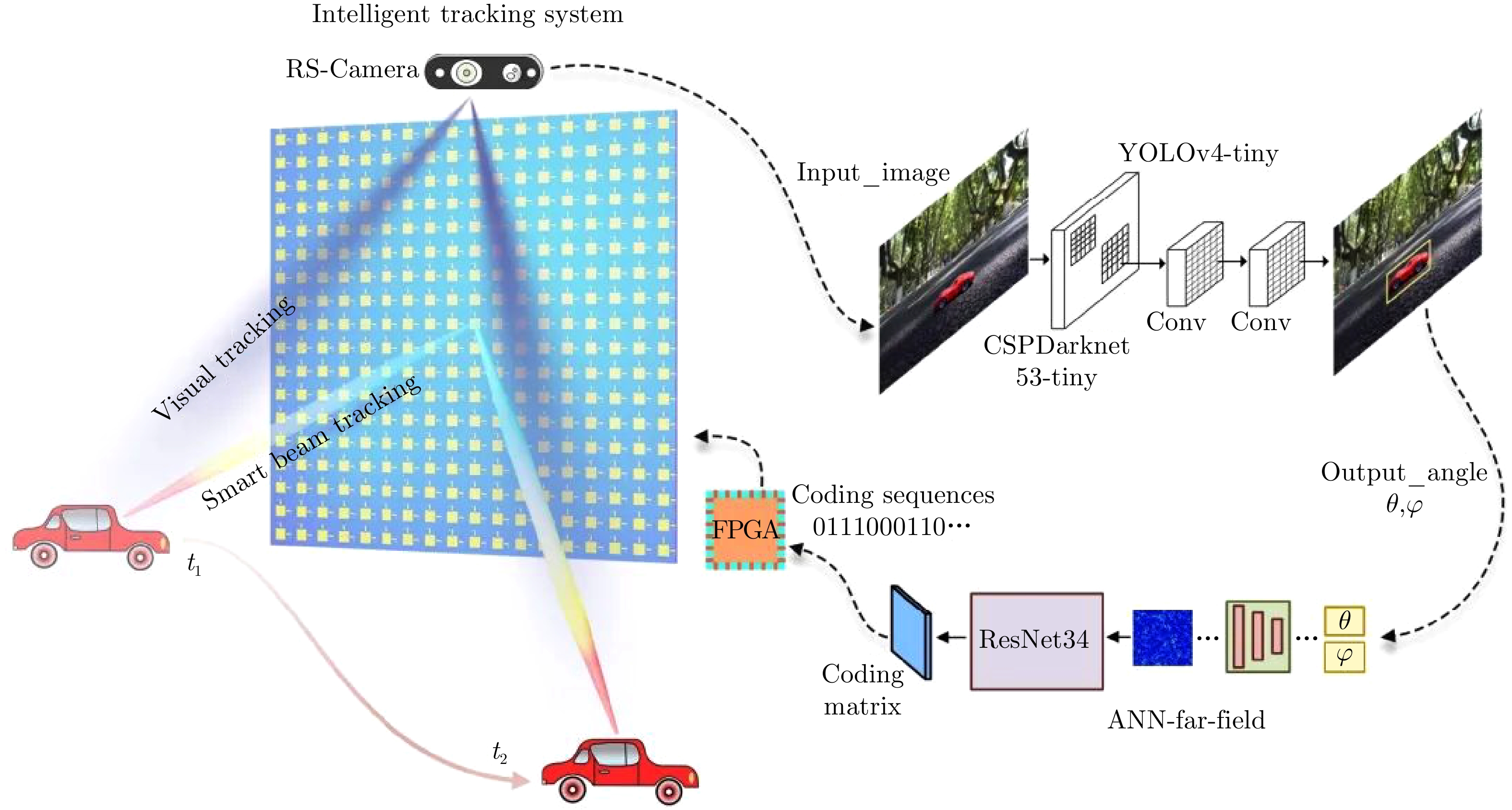
- Figure 16. The working principle of intelligent metasurface system for automatic tracking of moving targets and wireless communications based on computer vision[113]
- Figure 1.
- Figure 2.
- Figure 3.
- Figure 4.
- Figure 5.
- Figure 6.
- Figure 7.
- Figure 8.
- Figure 9.
- Figure 10.
- Figure 11.
- Figure 12.
- Figure 13.
- Figure 14.
- Figure 15.
- Figure 16.
- Figure 17.
- Figure 18.
- Figure 19.


 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work




 DownLoad:
DownLoad: