Submit Manuscript
Peer Review
Editor Work
| Citation: | GAO Xiangying, ZHAO Yongjun, LIU Zhixin, et al. Robust source localization using TDOA and FDOA with receiver location errors[J]. Journal of Radars, 2020, 9(5): 916–924. doi: 10.12000/JR20039
|
Robust Source Localization Using TDOA and FDOA with Receiver Location Errors
doi: 10.12000/JR20039
More Information-
Abstract
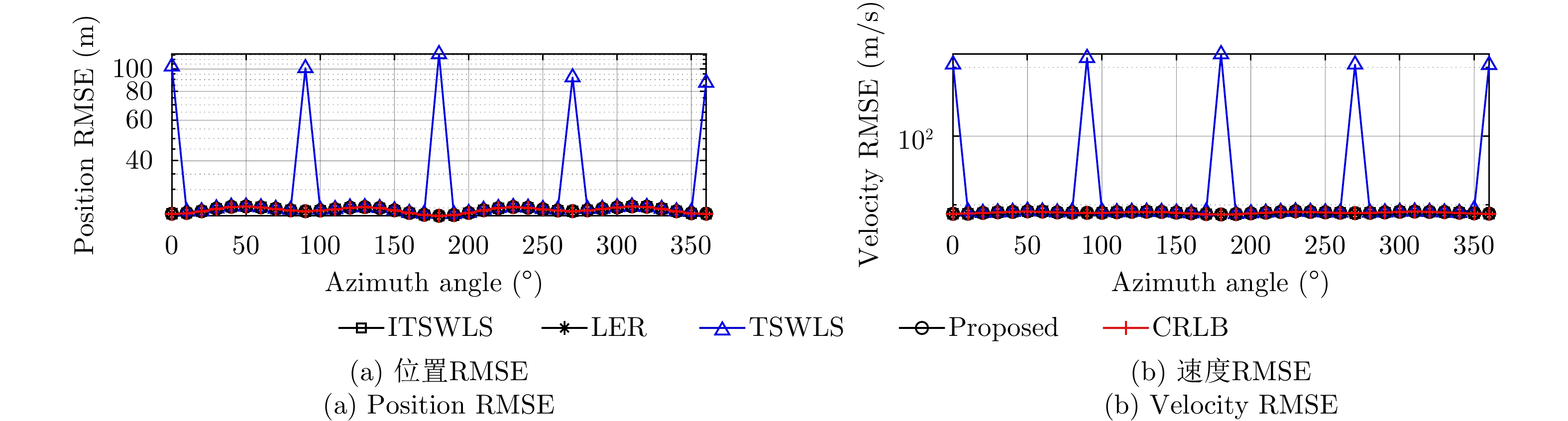
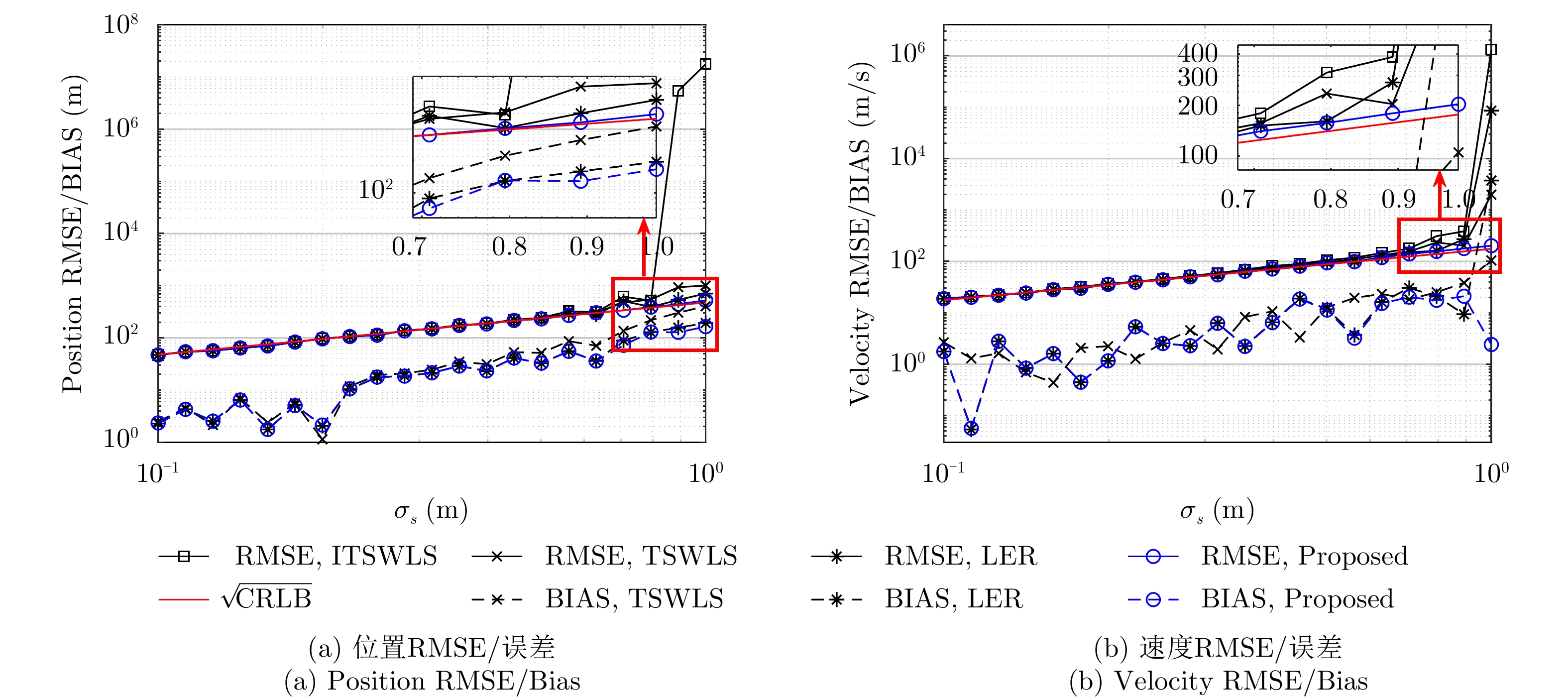
To address the low location accuracy and poor robustness of existing methods, error correction to improve the Stage 2 of the original Two-Stage Weighted Least Squares (TSWLS)-based methods is proposed, which involves a robust moving source localization method with high accuracy based on Time Difference Of Arrival (TDOA) and Frequency Difference Of Arrival (FDOA) in the presence of receiver location errors. This newly proposed Stage 2 performs Taylor expansion on the nuisance variables introduced in Stage 1 to construct the error correction equation, thereby avoiding the rank deficiency problem and nonlinear mathematical operations in the original TSWLS-based methods; and improving the robustness and location accuracy of the method. Theoretical analysis indicates that the proposed method can attain the Cramer-Rao Lower Bound (CRLB) under small noise condition. Simulation results show the proposed method has stronger localization robustness and better anti-noise performance over the existing methods under the common level of receiver location and measurement error.
-
-
References
[1] 田中成, 刘聪锋. 无源定位技术[M]. 北京: 国防工业出版社, 2015: 8–12.TIAN Zhongcheng and LIU Congfeng. Passive Locating Technology[M]. Beijing: National Defense Industry Press, 2015: 8–12.[2] 孙霆, 董春曦. 传感器参数误差下的运动目标TDOA/FDOA无源定位算法[J]. 航空学报, 2020, 41(2): 323317. doi: 10.7527/S1000-7527.2019.23317SUN Ting and DONG Chunxi. TDOA/FDOA passive localization algorithm for moving target with sensor parameter errors[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(2): 323317. doi: 10.7527/S1000-7527.2019.23317[3] LIU Congfeng, YANG Jie, and WANG Fengshuai. Joint TDOA and AOA location algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 183–188. doi: 10.1109/JSEE.2013.00023[4] CHEN Xin, WANG Ding, LIU Ruirui, et al. Structural total least squares algorithm for locating multiple disjoint sources based on AOA/TOA/FOA in the presence of system error[J]. Frontiers of Information Technology & Electronic Engineering, 2018, 19(7): 917–936. doi: 10.1631/FITEE.&1700735[5] LIU Zhixin, HU Dexiu, ZHAO Yongjun, et al. Computationally efficient TDOA, FDOA and differential Doppler rate estimation algorithm for passive emitter localization[J]. Digital Signal Processing, 2020, 96: 102598. doi: 10.1016/j.dsp.2019.102598[6] LIU Zhixin, WANG Rui, and ZHAO Yongjun. Computationally efficient TDOA and FDOA estimation algorithm in passive emitter localisation[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1731–1740. doi: 10.1049/&iet-rsn.2019.0101[7] KIM D G, PARK G H, KIM H N, et al. Computationally efficient TDOA/FDOA estimation for unknown communication signals in electronic warfare systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 77–89. doi: 10.1109/TAES.2017.2735118[8] YU H, HYANG G, and GAO J. Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J]. IET Radar, Sonar & Navigation, 2012, 6(9): 891–899.[9] HO K C, LU Xiaoning, and KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684–696. doi: 10.1109/TSP.2006.885744[10] NOROOZI A, OVEIS A H, HOSSEINI S M, et al. Improved algebraic solution for source localization from TDOA and FDOA measurements[J]. IEEE Wireless Communications Letters, 2018, 7(3): 352–355. doi: 10.1109/LWC.2017.2777995[11] LIU Yang, GUO Fucheng, YANG Le, et al. An improved algebraic solution for TDOA localization with sensor position errors[J]. IEEE Communications Letters, 2015, 19(12): 2218–2221. doi: 10.1109/LCOMM.2015.2486769[12] 刘洋, 杨乐, 郭福成, 等. 基于定位误差修正的运动目标TDOA/FDOA无源定位方法[J]. 航空学报, 2015, 36(5): 1617–1626.LIU Yang, YANG Le, GUO Fucheng, et al. Moving targets TDOA/FDOA passive localization algorithm based on localization error refinement[J]. Acta Aeronauticaet Astronautica Sinica, 2015, 36(5): 1617–1626.[13] SORENSON H W. Parameter Estimation: Principles and Problems[M]. New York: Marcel Dekker Inc., 1980.[14] LIU Zhixin, HU Dexiu, ZHAO Yongsheng, et al. An algebraic method for moving source localization using TDOA, FDOA, and differential Doppler rate measurements with receiver location errors[J]. EURASIP Journal on Advances in Signal Processing, 2019, 2019(1): 25. doi: 10.1186/s13634-019-0621-9[15] LIU Zhixin, HU Dexiu, ZHAO Yongsheng, et al. An improved closed-form method for moving source localization using TDOA, FDOAs, differential Doppler rate measurements[J]. IEICE Transactions on Communications, 2019, E102. B(6): 1219–1228. doi: 10.1587/transcom.&2018ebp3249 -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. Performance comparison among different methods
- Figure 2. Robustness comparison among different methods