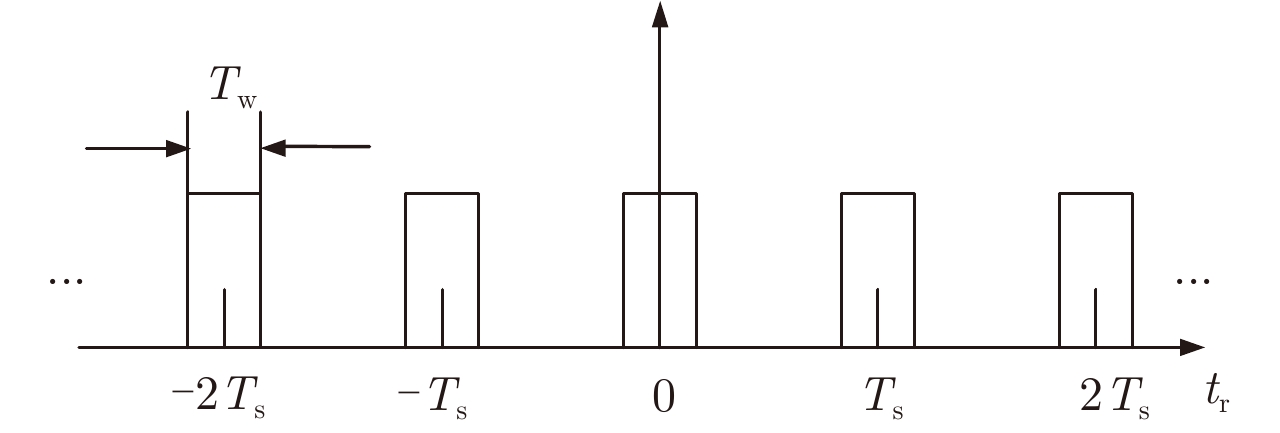
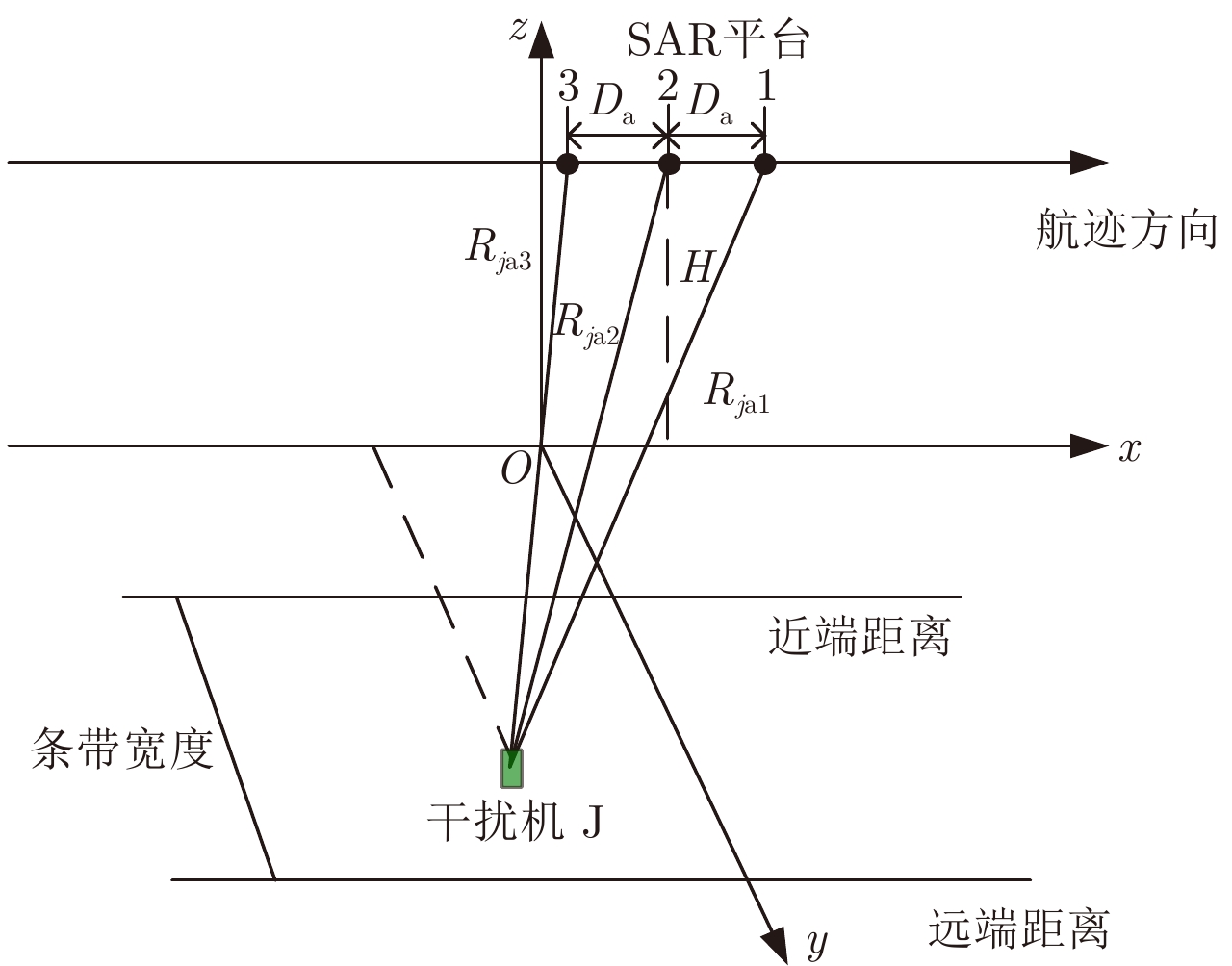
| [1] |
Zhang Xue-pan, Liao Gui-sheng, Zhu Sheng-qi, et al. Geometry-information-aided efficient motion parameter estimation for moving-target imaging and location[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 155–159. DOI: 10.1109/LGRS.2014.2329941 |
| [2] |
Huang Long, Dong Chun-xi, Shen Zhi-bo, et al. The influence of rebound jamming on SAR GMTI[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 399–403. DOI: 10.1109/LGRS.2014.2345091 |
| [3] |
Zhang Shuang-xi, Xing Meng-dao, Xia Xiang-gen, et al. Robust clutter suppression and moving target imaging approach for multichannel in azimuth high-resolution and wide-swath synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 687–709. DOI: 10.1109/TGRS.2014.2327031 |
| [4] |
李兵, 洪文. 合成孔径雷达噪声干扰研究[J]. 电子学报, 2005, 32(12): 2035–2037
Li Bing and Hong Wen. Study of noise jamming to SAR[J]. Acta Electronica Sinica, 2005, 32(12): 2035–2037
|
| [5] |
蔡幸福, 宋建社, 郑永安, 等. 二维间歇采样延迟转发SAR干扰技术及其应用[J]. 系统工程与电子技术, 2015, 37(3): 566–571
Cai Xing-fu, Song Jian-she, Zheng Yong-an, et al. SAR jamming technology based on 2-D intermittent sampling delay repeater and its application[J]. Systems Engineering and Electronics, 2015, 37(3): 566–571
|
| [6] |
黄龙, 董春曦, 赵国庆. 利用多干扰机对抗SAR双通道干扰对消技术的研究[J]. 电子与信息学报, 2014, 36(4): 904–907
Huang Long, Dong Chun-xi, and Zhao Guo-qing. Investigation on countermeasure against SAR dual-channel cancellation technique with multi-jammers[J]. Journal of Electronics&Information Technology, 2014, 36(4): 904–907
|
| [7] |
黄龙, 董春曦, 沈志博, 等. 多天线干扰机对抗InSAR双通道干扰对消的研究[J]. 电子与信息学报, 2015, 37(4): 913–918 doi: 10.11999/JEIT140769Huang Long, Dong Chun-xi, Shen Zhi-bo, et al. Investigation on countermeasure against InSAR dual-channel cancellation technique with multi-antenna jammer[J]. Journal of Electronics& Information Technology, 2015, 37(4): 913–918. DOI: 10.11999/JEIT140769 |
| [8] |
Wu Xiao-fang, Wang Xue-song, and Liang Jing-xiu. Modulation jamming method for high-vivid false uniformly-moving targets against SAR-GMTI[J]. Journal of Astronautics, 2012, 33(10): 1472–1479. DOI: 10.3873/j.issn.1000-1328.2012.10.016 |
| [9] |
吴晓芳, 梁景修, 王雪松, 等. SAR-GMTI匀加速运动假目标有源调制干扰方法[J]. 宇航学报, 2012, 33(6): 761–768
Wu Xiao-fang, Liang Jing-xiu, Wang Xue-song, et al. Modulation jamming method of active false uniformly-accelerating targets against SAR-GMTI[J]. Journal of Astronautics, 2012, 33(6): 761–768
|
| [10] |
王雪松, 刘建成, 张文明, 等. 间歇采样转发干扰的数学原理[J]. 中国科学E辑: 信息科学, 2006, 36(8): 891–901
Wang Xue-song, Liu Jian-cheng, Zhang Wen-ming, et al. Mathematical principles of intermittent sampling repeater jamming[J]. Science in China Series E:Information Sciences, 2006, 36(8): 891–901
|
| [11] |
孙光才, 周峰, 邢孟道. 一种SAR-GMTI的无源压制性干扰方法[J]. 系统工程与电子技术, 2010, 32(1): 39–45
Sun Guang-cai, Zhou Feng, and Xing Meng-dao. New passive barrage jamming method for SAR-GMTI[J]. Systems Engineering and Electronics, 2010, 32(1): 39–45
|
| [12] |
周阳, 房明星, 毕大平, 等. 旋转角反射器阵列对SAR-GMTI的无源遮蔽干扰方法[J]. 探测与控制学报, 2017, 39(2): 87–93
Zhou Yang, Fang Ming-xing, Bi Da-ping, et al. A passive shading jamming method to SAR-GMTI using array rotating angular reflectors[J]. Journal of Detection&Control, 2017, 39(2): 87–93
|
| [13] |
吴晓芳, 王雪松, 卢焕章. 对SAR的间歇采样转发干扰研究[J]. 宇航学报, 2009, 30(5): 2043–2049
Wu Xiao-fang, Wang Xue-song, and Lu Huan-zhang. Study of intermittent sampling repeater jamming to SAR[J]. Journal of Astronautics, 2009, 30(5): 2043–2049
|
| [14] |
Sjögren T K, Vu V T, Pettersson M I, et al. Suppression of clutter in multichannel SAR GMTI[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4005–4013. DOI: 10.1109/TGRS.2013.2278701 |
| [15] |
周阳, 毕大平, 房明星, 等. 对SAR-GMTI的运动调制-步进移频复合干扰[J]. 信号处理, 2016, 32(12): 1468–1477
Zhou Yang, Bi Da-ping, Fang Ming-xing, et al. A motion modulated and step frequency shifting compound interference to SAR-GMTI[J]. Journal of Signal Processing, 2016, 32(12): 1468–1477
|


 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work

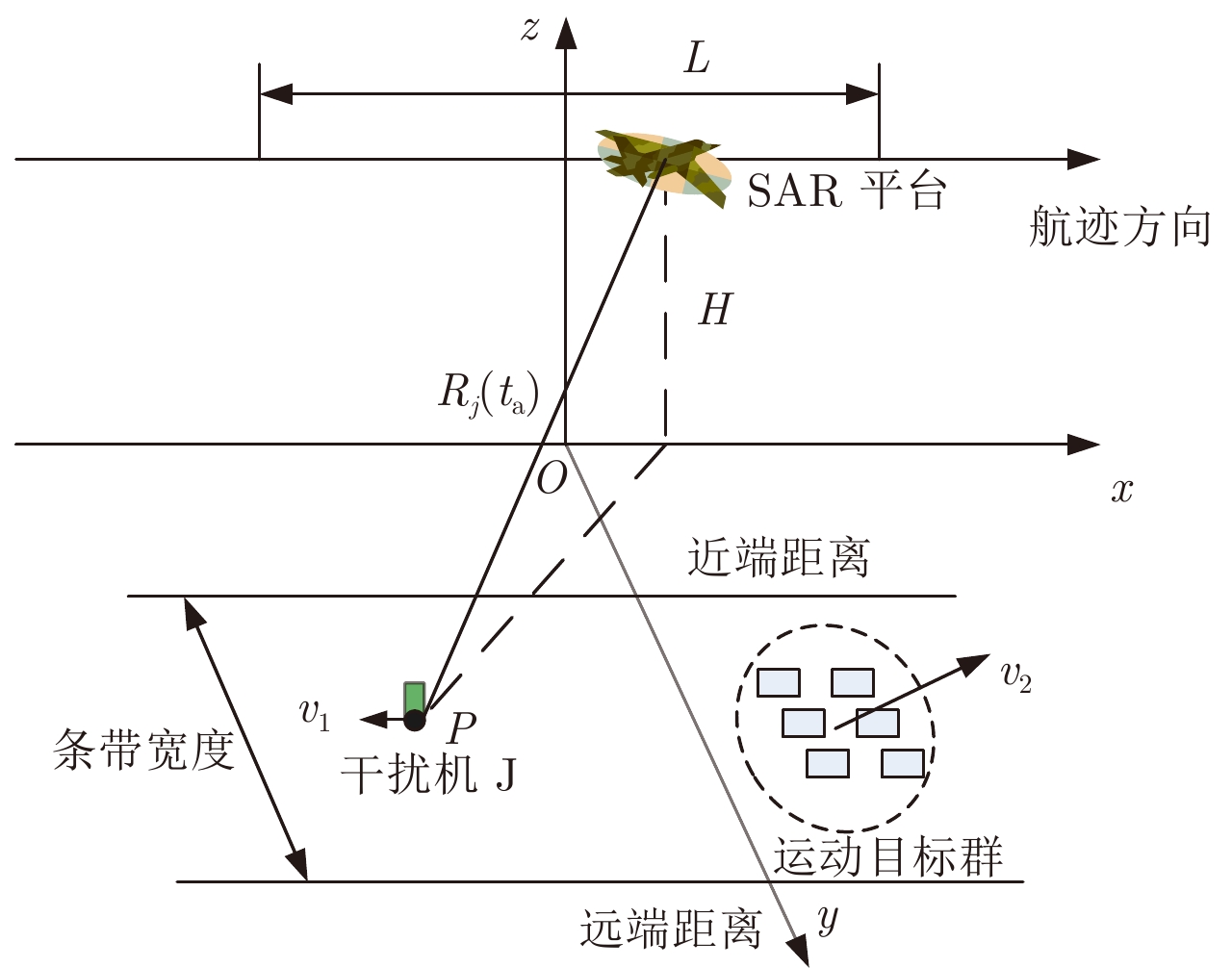



 DownLoad:
DownLoad: