1.   引言

非视距(Non-Line-Of-Sight, NLOS)三维成像雷达是一种新兴的雷达探测技术，可利用多径电磁散射信号重建隐藏目标的高精度三维图像，实现视距(Line-Of-Sight, LOS)路径外的环境探测感知^[1]，在自动驾驶、反恐安防、城市作战等领域具有重要的应用价值。在城市作战等应用中，目标通常隐藏在视距范围之外，传统视距雷达直接利用视距路径回波进行成像，需要抑制非视距回波提高成像质量，故无法感知视距范围之外的隐匿目标。如何挖掘雷达多径散射回波特性，实现非视距回波的良好聚焦，是近年非视距测隐藏目标探测成像的重要目标^[2]。与视距三维成像雷达^[3−5]不同，非视距三维成像雷达接收到的隐藏目标回波通常伴随着多次散射、绕射或穿透传播，其成像处理需考虑能量衰减、多径效应、杂波干扰等因素影响；另外，非视距遮蔽引入的孔径缩减及多反射面引入的回波相位误差，也会导致隐匿目标成像精度和质量降低。因此，传统成像处理方法并不能直接用于非视距雷达的高精度三维成像，亟需研究一些新的高精度成像方法。

非视距成像的概念在2006年率先出现在光学成像领域^[6]，已成为近年光学及雷达感知领域的研究热点之一。目前，光学非视距重构技术主要可分为3种：基于光子的飞行时间(Time-Of-Flight, TOF)^[6]、基于相干性的散斑反演^[7]和基于光子强度信息的阴影利用技术^[8]，相关试验均可以获得高质量的隐匿目标三维成像结果^[9,10]。然而，光学非视距成像方法存在明显不足：硬件昂贵复杂、天气依赖性强、观测范围有限等，例如观察场景通常只有平方米级，限制了其在全天时、全天候、大规模场景成像的应用。此外，近几年相关学者也提出了多种基于非光学传感器的NLOS成像方法，如声信号^[11]和Wi-Fi信号^[12]，但同样也面临应用场景有限、成像分辨率低和受环境干扰等问题，难以满足城市作战、自动驾驶等大区域场景隐藏目标高精度三维重构的需求。对比上述光声非视距三维成像技术，雷达具有全天时、全天候、系统成本低、大规模观测和成像分辨率高等优势，在非视距目标探测、定位和成像等方面更具应用潜力^[13,14]。

在非视距雷达探测与成像方面，围绕典型城市建筑结构和场景，近年研究人员提出了多种拐角场景非视距雷达检测和成像技术^[15−22]。例如，Sume等人^[16]利用短时傅里叶变换分析了墙角后隐蔽人体走动和呼吸产生的微多普勒信号，并结合运动目标指示技术提出了一种快速目标距离轨迹检测算法；Li等人^[19]建立了多目标场景下多路径传播模型，提出了一种椭圆交叉定位方法来获得多路径重构图像的位置，并基于相似性准则最终确定了多目标的实际位置。Wei等人^[1]也验证了毫米波雷达非视距三维成像的可行性，提出了一种基于反射面镜像后向投影(Mirror-Symmetry Back-Projection, MSBP)的隐匿目标三维成像算法，在进行非视距目标三维重构的同时可以恢复其真实位置，并搭建了非视距三维成像实验系统进行了试验验证；另外，结合NLOS成像模型与逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像，Wen等人^[23]也探讨了运动目标的非视距成像，提出了一种基于距离迁徙算法(Range Migration Algorithm, RMA)的隐藏运动目标成像方法。仇晓兰等人^[24]针对合成孔径雷达层析成像(TomoSAR)三维成像模式，提出了一种基于多径散射补偿的非视距三维成像方法，实现了TomoSAR模式下非视距目标三维成像与定位，并利用4通道无人机载SAR系统验证了方法的有效性。综上可知，利用雷达多径散射回波进行隐匿目标探测与成像是可行的，但是上述方法主要基于经典的匹配滤波(Matchened Filtering, MF)理论，采用后向投影(Back-Projection, BP)^[25]和RMA^[26,27]等改进方法实现非视距目标的二维或三维成像，存在成像精度低、旁瓣串扰严重、图像信噪比低等问题，难以实现孔径受限及稀疏阵列天线下非视距目标的高精度三维成像。

2010年以来，压缩感知稀疏重构是提高孔径受限及稀疏阵列天线下雷达成像质量的一种重要途径^[28−32]。Baraniuk等人^[33]于2007年首次在SAR系统中引入稀疏重构技术，实现了欠采样条件下目标的高分辨成像。针对传统SAR成像结果中的散焦和模糊问题，文献[34]利用压缩感知技术从稀疏孔径数据中恢复了无模糊图像。Pu等人^[35]提出了一种联合稀疏成像及运动误差补偿的成像算法，改善了双基前视SAR成像中的运动误差空变问题。SAR数据稀疏采样会破坏信号相干性，降低成像聚焦精度，研究人员将自聚焦过程引入稀疏贝叶斯成像中，获得了自聚焦高精度图像^[36]。然而，上述视距雷达稀疏成像方法针对视距场景及回波模型成像，直接应用于NLOS应用场景会存在模型失配、成像精度低和算法自适应差等问题，如非视距回波测量矩阵由多个路径反射延时相位构成，并且反射面会引入相位误差，为隐藏目标高精度三维重构带来挑战。因此，需结合非视距三维雷达成像模型及多径散射特性，研究适用的高效率高分辨稀疏成像算法。

为了实现非视距成像雷达隐藏目标的三维精确重构，围绕多路径回波分离、反射面相位误差等问题，本文结合拐角(Looking Around Corner, LAC)场景中隐藏目标的参数化多径传播模型，提出了一种基于迭代稀疏重构的非视距隐藏目标三维成像雷达精确重构方法，命名为NSIR (Non-line-of-sight Sparse Iterative Reconstruction)。针对墙体多径反射导致的目标边缘信息模糊问题，该算法引入了全变分(Total Variation, TV)算子^[37,38]增强目标边缘特征的提取能力；针对实际场景中粗糙反射面多次散射引入的非视距回波相位误差问题，该算法构建了耦合多径反射面相位误差的全变分多约束优化求解模型，进一步引入最小均方误差的相位误差估计方法提升非视距隐藏目标聚焦能力；另外，该方法结合频域快速成像算子与分裂Bregman方法，保证稀疏重构质量的同时显著提高成像效率。最后，搭建了毫米波雷达非视距成像实验系统，采集了多组真实场景回波数据并对所提方法进行了验证分析。

2.   非视距雷达3D成像模型

2.1   非视距成像模型

非视距雷达三维成像的基本原理与视距雷达相似，主要利用宽带信号实现距离向高分辨，利用合成孔径或天线阵列实现方位/俯仰二维分辨率，成像几何模型如图1所示。其中，场景包含两个墙面W₁和W₂，目标位于墙面W₂后面的非视距区域，为简化分析假设两个墙面均为理想光滑墙面，电磁波在反射墙面上发生镜面反射。令${{\boldsymbol{P}}_{\text{a}}}\left( r \right) = \left( {{x_r},{y_r},{z_r}} \right)$表示第r个天线阵元的位置，${{\boldsymbol{P}}_{\text{t}}}\left( s \right) = \left( {{x_s},{y_s},{z_s}} \right)$表示非视距隐匿目标散射点s的位置，${{\boldsymbol{P}}_{\text{t}}}\left( s \right)$相对于墙面W₁的镜像投影位置为${\boldsymbol{P}}'_{\text{t}}{}\left( s \right) = \left( {x'_s ,y'_s ,z'_s } \right)$，雷达到非视距目标的距离历史${{\boldsymbol{R}}_{{\text{rs}}}}$可表示为

图  1  NLOS雷达3D成像几何模型

Figure  1.  NLOS radar 3D imaging geometry model

下载: 全尺寸图片 幻灯片

其中，$\delta \left( {\boldsymbol{R}} \right)$是由反射墙面引入的距离误差，本文暂不考虑。${{\boldsymbol{R}}_{{\text{LOS}}}}$和${{\boldsymbol{R}}_{{\text{NLOS}}}}$分别是阵列平面到反射面W₁和W₁到隐藏目标T的传播路径。${{\boldsymbol{P}}_{\text{w}}}$为反射区域的空间坐标。${N_r}$是天线阵列平面上的雷达收发阵元总数，${N_s}$是隐藏目标在成像空间中的散射点总数。

假设雷达发射调频连续波(Frequency Modulated Continuous Wave, FMCW)，则总的接收回波信号由视距和非视距两部分组成，可以写为

其中，${{\boldsymbol{S}}_{{\text{LOS}}}}$表示视距直接回波，${{\boldsymbol{S}}_{{\text{NLOS}}}}\left( {{\boldsymbol{P}}_{\text{t}}^s} \right)$表示隐藏目标散射点${\boldsymbol{P}}_{\text{t}}^s$的非视距多路径回波，$\Upsilon \left( {{\boldsymbol{P}}_{\text{t}}^s} \right)$代表双向反射函数且受毫米波频段、反射墙面材质和表面粗糙度等因素决定，$\sigma$和$\sigma \left( {{\boldsymbol{P}}_{\text{t}}^s} \right)$分别表示视距和非视距散射点的散射系数，$\tau$表示散射点对应的延时，K为信号调频斜率，${f_0}$是载波频率。

回波信号经过脉冲压缩和距离徙动矫正后，式(2)可转换成

其中，l表示距离单元格索引，${\text{sinc}}\left( l \right)$为距离包络。与传统视距雷达成像不同，针对非视距雷达三维成像，需要提取非视距回波进行独立的误差补偿及聚焦成像。

RMA算法作为近场三维SAR全息成像常用的算法，具有成像处理效率高、计算步骤简单、可靠性强等优点。在提取了非视距回波之后，本文参考传统的RMA快速成像算法，将非视距隐匿目标的聚焦信号和近似回波表示为

其中，${\text{F}}{{\text{T}}_{{\text{2D}}}}\left( \cdot \right)$和${\text{FT}}_{{\text{2D}}}^{ - 1}\left( \cdot \right)$表示二维傅里叶变换及其逆变换，${k_{{y}}}$为空间波数在距离方向的分量，${y{'}}$表示距离方向上第l个切片的距离，${\mathcal{F}^{ - 1}}\left\{ {\boldsymbol{Y}} \right\}$和$\mathcal{F}\left\{ {\boldsymbol{X}} \right\}$为频域快速成像算子，分别近似为傅里叶变换和傅里叶逆变换运算。依据文献[39]，非视距隐匿目标的稀疏成像处理可采用该频域快速成像算子进行重构，以提升重构的效率。

由于遮蔽墙面、反射墙面等影响，雷达非视距区域的有效观测孔径通常要小于视距孔径长度。其有效观测孔径的长度与成像场景结构$\varOmega$、目标到遮蔽墙面和反射墙面的距离${d_{\text{w}}}$及雷达波束入射角度${\theta _{\text{a}}}$等多个因素相关。设非视距雷达方位向和俯仰向的有效孔径长度为${L_{{x}}}$和${L_{{z}}}$，则非视距雷达三维成像的分辨率为

其中，$\lambda$为信号波长，${R_{{\text{rs}}}}$为雷达到非视距目标的距离，${L_{\text{r}}}$为真实孔径长度，c为光速，B为信号带宽。从式(5)可知，非视距三维成像的方位和俯仰成像分辨率通常是空变，并且大于视距成像，若要实现高分辨成像，需要采用高分辨成像方法进行非视距目标的三维重构。

2.2   非视距雷达3D成像问题阐述

根据文献[40]，存在粗糙墙面反射的隐藏目标多路径回波，则会存在电磁波的幅度衰减和相位误差，其双向反射函数如下表述：

其中，$\varsigma \left( {{\boldsymbol{P}}_{\text{t}}^s} \right)$服从方差为$\delta$的瑞利分布，$\Delta \phi$为反射墙面引入的相位误差，$\Delta \phi$服从$\left( { - \pi ,\pi } \right)$上的均匀分布。具体分布如下：

其中，方差$\delta$具体值与反射墙面不平整度相关。因此对于非视距雷达回波建模和成像，需要结合墙面的双向反射函数特性。

依据式(7)，假设非视距回波已被精确提取，其回波可表示为矩阵向量乘积的线性测量模型

其中，y为提取的非视距回波向量化表示，${\boldsymbol{\chi }}$是成像空间中隐藏目标散射系数，H为信号测量矩阵，n代表噪声向量。为了简化分析，不考虑反射墙面引入的幅度变化$\varsigma \left( {{\boldsymbol{P}}_{\text{t}}^s} \right)$，上述模型可以进一步表示为

与传统视距线性测量模型相比，式(9)中的非视距多路径回波由于和其他反射或散射信号混合，导致其难以被区分和提取；反射面引入的随机相位误差$\Delta \phi$也为精确重构提出了更高的算法要求。

依据压缩感知稀疏重构理论，式(9)中的目标求解可以表征为一个多约束的最优化问题

其中，${{\boldsymbol{E}}^{\boldsymbol{S}}}$是散射场，${{\boldsymbol{G}}_{\boldsymbol{S}}}\left( \cdot \right)$表示将散射场与入射场近似为一个病态线性关系，${{\boldsymbol{E}}^i}$是入射场，$\mathcal{R}\left( {\boldsymbol{y}} \right)$为约束项， $\lambda$为平衡各个约束项的参数。将原始信号重构问题转化为线性约束最优化求解问题，再通过正则化方法即可求解目标散射系数。针对式(10)，正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)、迭代阈值收缩算法(Iterative Shrinkage-Thresholding Algorithm, ISTA)和稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)的方法均可求解。这些方法各具优缺点，选择哪种方法取决于特定场景的需求，对于非视距隐藏目标的精确重构问题，还需要设计更加合适的求解框架。

3.   非视距雷达3D精确重构方法

3.1   精确重构总体框架

针对式(10)的多约束最优化问题，本文采用一种基于分裂Bregman的稀疏重构框架进行求解，主要通过对正则项进行改进，将式(10)变化为TV正则化问题，再联合目标固有稀疏性及随机相位误差补偿技术对隐藏目标实现高精度重构。具体的求解最优问题表示如下：

其中，${\boldsymbol{\alpha }}$表示隐藏目标散射系数，${\left\|{\boldsymbol{ \alpha}} \right\|_p}$为正则化约束项，本文基于非视距成像特性，构造L1及TV范数约束。

本文方法隐藏目标重构总体思路与框图如图2所示，该方法主要步骤可分为3部分：多路径回波提取、TV稀疏重构及自聚焦相位补偿。

图  2  回波提取及NSIR重构流程

Figure  2.  Echo extraction and NSIR reconstruction process

下载: 全尺寸图片 幻灯片

3.2   多路径回波提取

由于视距回波直接到达雷达接收器，其距离历史较短。通过对信号的时间延迟进行分析，可以区分视距回波和经过反射、折射或绕射等路径到达的多路径非视距回波。为了有效提取非视距回波，本文采用时间差分与物理模型相结合的方法(Time Difference-Physical Models, TD-PME)区分视距回波和非视距回波。TD-PME方法采用粗成像-先验信息辅助判定-非视距回波提取的思路：首先结合视距环境和理论模型划分成像视距区域和非视距区域，其次对非视距区域的回波进行检索，以滤除虚假目标干扰并确定隐藏目标虚像，最后根据时间差分的性质提取目标多路径回波。

从不同散射路径分析，视距/非视距单次散射和多次散射目标距离历史可以表示为

其中，${R_{{\text{rs}}}}$和$R'_{{\text{is}}}$分别是雷达与目标、目标与目标之间的距离。LOS区域主要由单次散射回波组成，而NLOS区域主要为多次散射回波表征。${R_{\text{D}}} = {R_{{\text{ri}}}} + R'_{{\text{is}}}{} + {R_{{\text{jr}}}} + {R_{\text{E}}}$为多径散射的主路径，${R_{\text{E}}}$表示场景内部多次散射路径。建立LOS和NLOS耦合散射回波模型

其中，${\sigma _{\text{S}}}$和${\sigma _{\text{D}}}$分别为3次散射和多次散射的目标散射系数，G表示空间格林函数。

首先对雷达回波进行二维距离向粗成像，计算不同目标t到雷达阵列的距离并结合视距环境结构划分视距区域及非视距区域

其中，${I_\varOmega }$代表当前目标所在区域，${\varOmega _{{\text{NLOS}}}}$和${\varOmega _{{\text{LOS}}}}$分别表示非视距区域及视距区域，${R_{\text{T}}} = {\left\| {{{\boldsymbol{P}}_{\text{a}}} - {{\boldsymbol{P}}_{\text{w}}}} \right\|_2}$是雷达阵列到反射墙面的距离。确定非视距区域后，检索区域内的隐藏目标，确定其到雷达的距离历史。

对雷达接收回波进行脉冲压缩，距离聚焦后的脉压图可以提供不同多径回波的距离单元位置并推断出回波距离历史：

其中，${y_r}$为隐藏目标第r条路径对应的距离历史，${m_r}$是对应脉压图中第r条路径虚像的距离索引，q是FFT点数。由非视距区域隐藏目标的距离历史可以倒推出对应的距离门，即可区分出非视距目标的多路径回波。

非视距目标提取多路径回波方法TD-PME的过程如算法1所示。

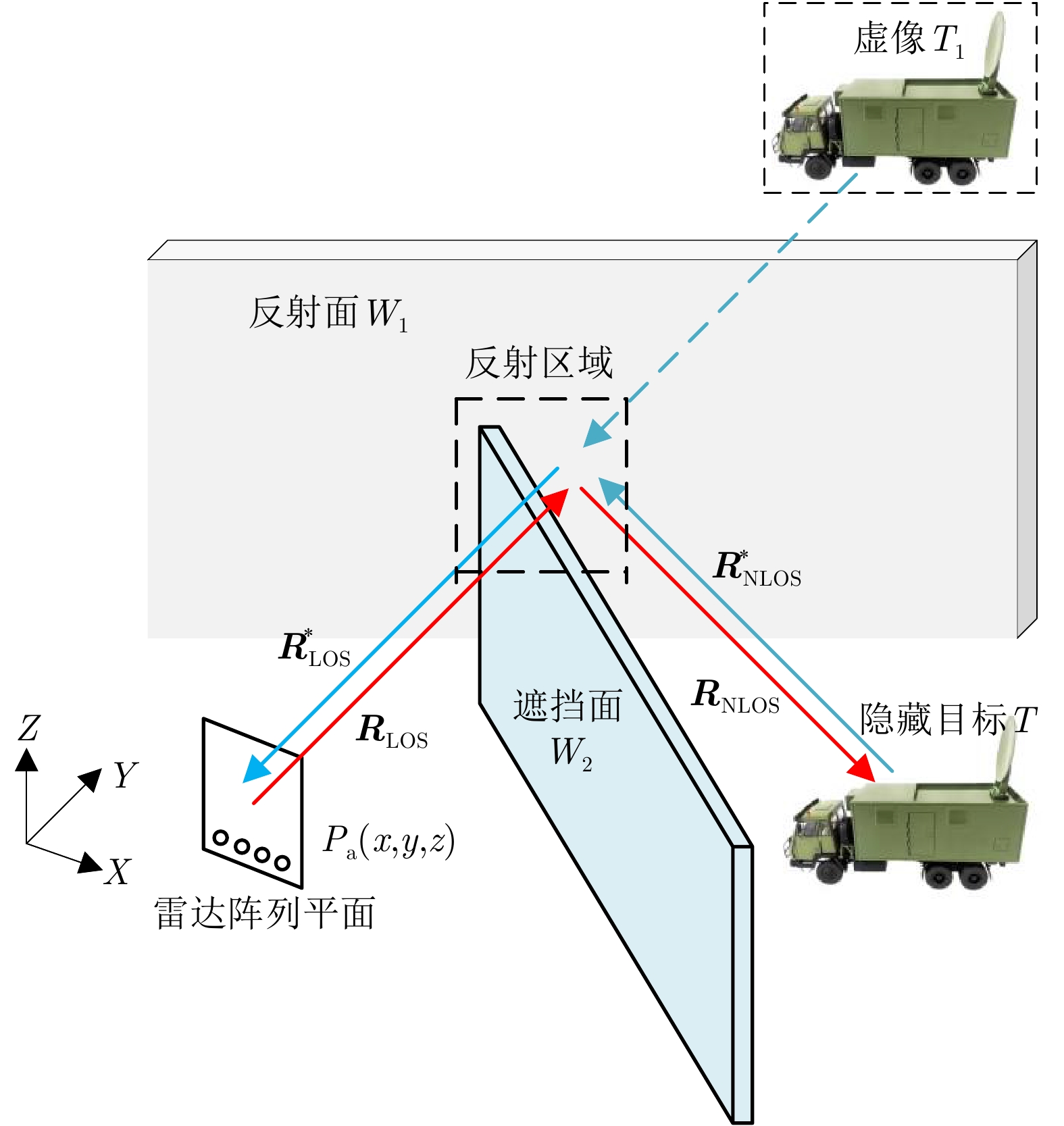
1  NLOS目标多路径回波提取

1.  Extraction of NLOS target echoes

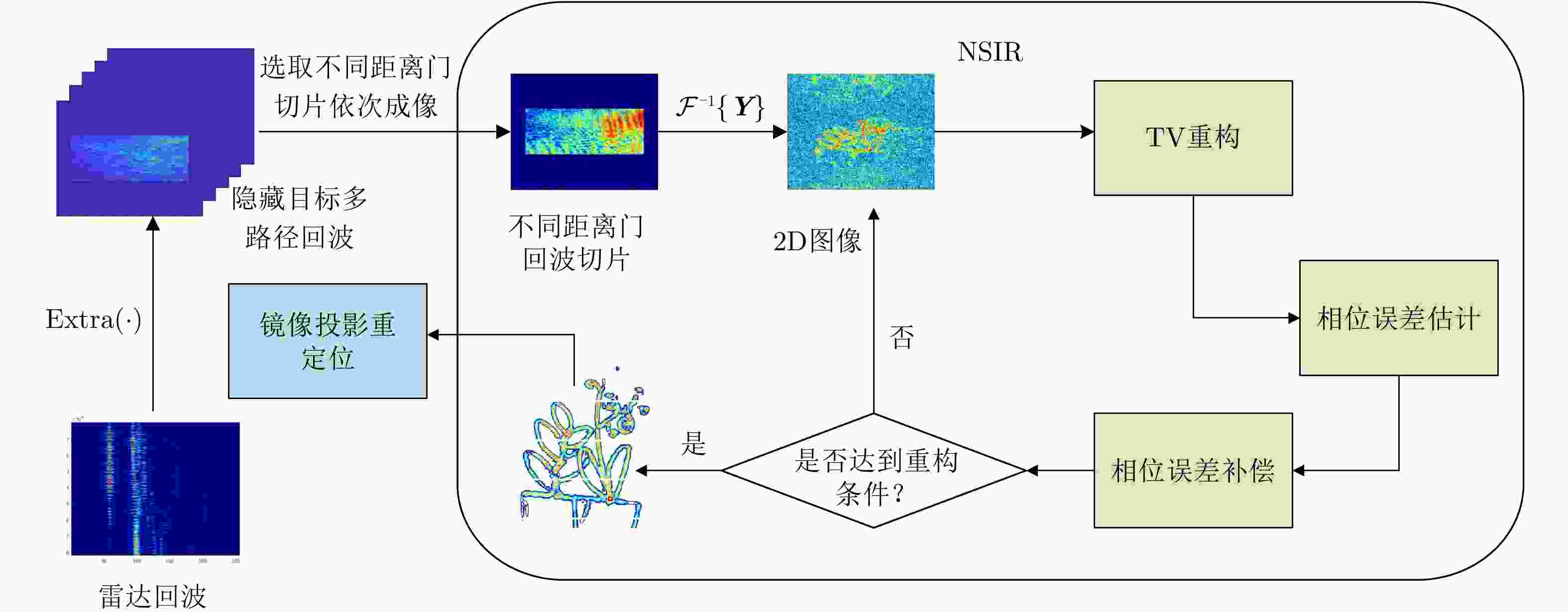
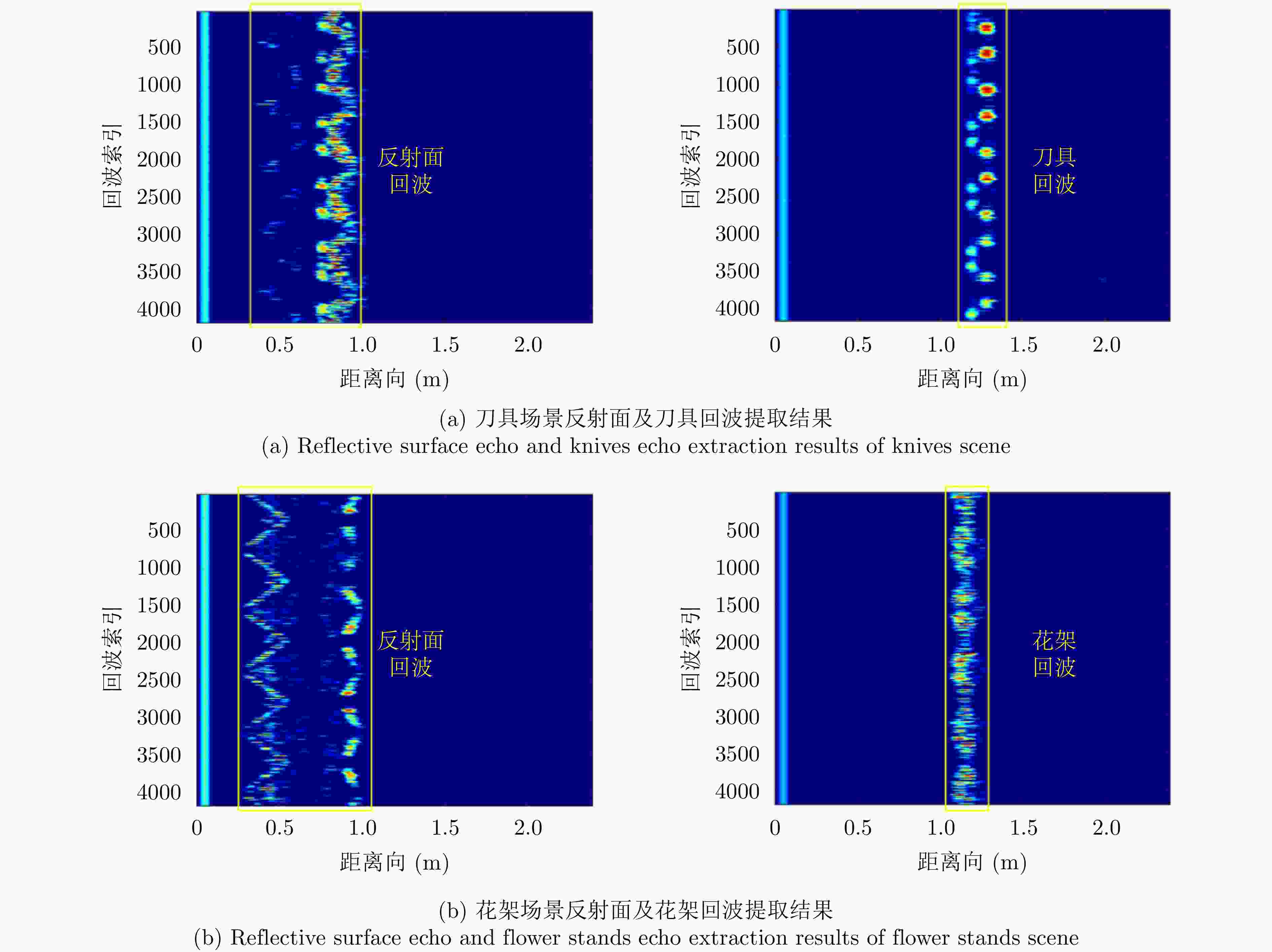
输入：LOS环境结构，雷达回波E；
输出：NLOS目标多径回波；
RMA粗成像：${{\boldsymbol{I}}_{{\text{RMA}}}} = {\mathcal{G}_{{\text{RMA}}}}\left( {\boldsymbol{E}} \right)$；
结合RMA成像结果与LOS环境布局分析，确定NLOS区域及隐藏 　目标：${\varOmega _{{\mathrm{all}}}}\mathop \to \limits^f {\varOmega _{{\mathrm{NLOS}}}}$；
距离聚焦：${P_{\text{c}}} = {\text{FFT}}\left( {{\boldsymbol{E}},q} \right)$；
计算隐藏目标对应时延及距离：${y_r} = \left( {\dfrac{{{m_r}}}{{{f_0} \times T \times q}}} \right) \times \dfrac{{\mathrm{c}}}{2}$；
根据镜像对称原理，确定同一目标不同虚像对应的回波；
根据距离历史提取对应回波：${\text{Extra}}\left( {\boldsymbol{E}} \right) \to {{\boldsymbol{E}}_{{\text{NLOS}}}}$；
返回隐藏目标的多径回波。

下载: 导出CSV 

| 显示表格

3.3   TV重构及误差补偿

针对多约束的最优化问题(11)，为了简便分析，先不考虑相位误差存在的情况，本文通过L1正则化和TV正则化约束求解

其中，$\lambda$为正则化系数，${\left\| \cdot \right\|_1}$为向量1范数，${\left\| \cdot \right\|_{{\text{TV}}}}$为TV范数。通常，上述优化问题求解需采用大量向量和矩阵运算，而且测量矩阵构造需占用大量内存，导致计算复杂度高，难以在大规模成像场景应用。为提高成像效率、减少内存占用，本算法引入RMA频域快速成像算子，将式(16)转化为算子表征的最优化问题：

其中，${\boldsymbol{X}}={\left[{\alpha }_{1},{\alpha }_{2},\cdots ,{\alpha }_{{N}_{r}}\right]}^{{\mathrm{T}}}\in {{\mathbb{C}}}^{N\times N}$为散射系数的矩阵形式，$N = \sqrt {{N_r}}$，${\left\| {\boldsymbol{X}} \right\|_{{\text{TV}}}}$的定义如下：

其中，

其中，$\left[ {i,j} \right]$表示矩阵的第i行第j列，${\boldsymbol{X}}\left[ {i,j} \right]$是X的复值元素，$|\cdot|$表示取模运算。

引入辅助变量${{\boldsymbol{d}}_1} = \nabla {\boldsymbol{X}}$, ${{\boldsymbol{d}}_2} = {\boldsymbol{X}}$

其中，$\nabla {\boldsymbol{X}}$代表散射系数矩阵X的梯度。分裂Bregman框架是求解式(20)的有效方法之一，引入Bregman参数${{\boldsymbol{b}}_1}$和${{\boldsymbol{b}}_2}$，用来权衡散射系数变量的更新。

通过交替迭代的方式得到最优解：

其中，式(22)为${l_2}$范数问题，可以直接求解：

其中，$\Delta \left( {\boldsymbol{X}} \right) = \nabla \left( {\nabla \left( {\boldsymbol{X}} \right)} \right)$。

其中，$\mathcal{T}\left( {{x_i},\rho } \right)$表达式如下：

上述即无相位误差估计及补偿的NSIR算法求解过程。在距离向脉压和徙动校正后，隐藏目标回波已经在距离方向上完成聚焦，不考虑距离方向上的相位误差，三维成像问题可转化为目标区域距离门回波切片的若干二维自聚焦成像问题。

反射面引入的相位误差可简化为二维相位误差，记x方向上的相位误差为${{\mathrm{e}}^{{\mathrm{j}}{\varPsi _{{x}}}}}$，z方向上的相位误差为${{\mathrm{e}}^{{\mathrm{j}}{\varPsi _{{z}}}}}$，则隐藏目标回波信号模型可表示为

其中，${{\boldsymbol{S}}_{\text{e}}}$为含有相位误差的回波矩阵，进一步建立式(28)修正公式：

从含有相位误差的回波矩阵${{\boldsymbol{S}}_{\text{e}}}$中同时估计${{\boldsymbol{\varLambda}} _{{z}}}$, ${{\boldsymbol{\varLambda}} _{{x}}}$和X，即可完成自聚焦成像。此时，原优化问题(17)可表示为

采用块坐标下降法，固定一个矩阵${{\boldsymbol{\varLambda }}_{{x}}}$或${{\boldsymbol{\varLambda}} _{{z}}}$来估计另一个相位误差矩阵，交替估计X, ${{\boldsymbol{\varLambda }}_{{z}}}$和${{\boldsymbol{\varLambda }}_{{x}}}$以求解问题(29)。为了公式推导的简洁，省略固定矩阵${{\boldsymbol{\varLambda}} _{{x}}}$，以求解${{\boldsymbol{\varLambda}} _{{z}}}$为例：

由式(24)推导过程可知，X可以通过式(31)迭代步骤得到：

在求解${{\boldsymbol{\varLambda}} _{{z}}}$时，可将隐藏目标散射系数矩阵X视为固定的常数矩阵。可以推导得到${{{\varPsi }}_{{z}}}$的最优值：

其中，${\text{angle}}\left( \cdot \right)$为复变量相位提取算子。同理，可得

综上，目标散射系数X的最终迭代过程如下：

算法2总结了NSIR成像处理流程。

2  三维雷达自聚焦成像算法NSIR

2.  3D radar autofocusing imaging algorithm NSIR

输入：隐藏目标回波${{\boldsymbol{S}}_{\text{e}}} \in {\mathbb{C}^{{N_x} \times {N_z} \times R}}$，参数$\lambda$, ${\gamma _1}$和${\gamma _2}$；
输出：稀疏成像结果${\boldsymbol{X}} \in {\mathbb{C}^{R \times N \times N}}$；
初始化：${\boldsymbol{X}}^0 = {\boldsymbol{b}}_1^0 = {\boldsymbol{b}}_2^0 = {\boldsymbol{d}}_1^0 = {\boldsymbol{d}}_2^0 = 0$, ${\boldsymbol{Y}} = {{\boldsymbol{S}}_{\text{e}}}$；
循环开始
(1) 根据式(34)，重构${\boldsymbol{X}}^{k + 1}$；
(2) 更新辅助变量：${\boldsymbol{d}}_1^{k + 1} = \mathcal{T}\left( {\nabla {\boldsymbol{X}}^{k + 1} + {\boldsymbol{b}}_1^k,1/{\gamma _1}} \right)$, 　${\boldsymbol{d}}_2^{k + 1} = \mathcal{T}\left( {{\boldsymbol{X}}^{k + 1} + {\boldsymbol{b}}_2^k,1/{\gamma _2}} \right)$；
(3) 更新参数：${\boldsymbol{b}}_1^{k + 1} = {\boldsymbol{b}}_1^k + \nabla {\boldsymbol{X}}^{k + 1} - {\boldsymbol{d}}_1^{k + 1}$, 　${\boldsymbol{b}}_2^{k + 1} = {\boldsymbol{b}}_2^k + {\boldsymbol{X}}^{k + 1} - {\boldsymbol{d}}_2^{k + 1}$；
(4) 由式(32)、式(33)估计相位误差, $t = t + 1$；
(5) 迭代判定：若$k \le T$，则重复(1)—(5)；否则，结束循环。
循环结束

下载: 导出CSV 

| 显示表格

4.   实测验证和分析

为了验证非视距三维雷达成像性能，本文通过多组近场毫米波三维成像实测实验验证所提NSIR算法的有效性，本文采用对比方法为3种成像算法：基于匹配滤波理论的BP^[23]及RMA^[24,25]、稀疏成像算法ISTA。其中，ISTA与NSIR最大迭代次数均设置为15，迭代误差门限设置均为1E–5，ISTA迭代门限设置为0.1，NSIR参数分别设置为$\lambda = 0.18$, ${\gamma _1} = 0.7$, ${\gamma _2} = 7$。不同参数选择对成像质量影响较大，本文参数可采用L-curve方法选出^[41,42]。

为了定量分析算法性能，本文选取图像熵(Image Entropy, ENT)、图像对比度(Image Contrast, IC)等2个指标评价成像质量。

其中，$M \times N$是重构图像X的维度，$g = \displaystyle\sum\nolimits_{n = 0}^{N - 1} \cdot \displaystyle\sum\nolimits_{m = 0}^{M - 1} {\left| {{\boldsymbol{X}}\left( {m,n} \right)} \right|} ^2$表示图像的总能量。一般来说，ENT值越低，图像聚焦性越好，而IC值越高，说明图像中重构目标与背景差异越明显、视觉区分度更高。

如图3所示，本文构建一个毫米波三维成像平台，其主要由高精度导轨、AWR2243毫米波雷达和数据采集模块DCA1000等3部分组成。高精度导轨控制雷达进行平面扫描，用来实现方位向大虚拟孔径。设计了两组非视距成像实验场景，隐藏目标分别为金属刀具和金属花架。其中，X-Z平面表示虚拟天线阵列的位置，Y轴对应距离方向，黄线和蓝线分别代表电磁波探测隐藏目标的路径。为了减少环境杂波的干扰，场景周围布置了毫米波吸波材料。天线阵列与反射墙面之间的夹角约为45°。系统具体参数设置如表1。

图  3  实验平台及实验场景

Figure  3.  Experimental platform and experimental scenes

下载: 全尺寸图片 幻灯片

表  1  实测系统参数

Table  1.  Parameters in real experiments

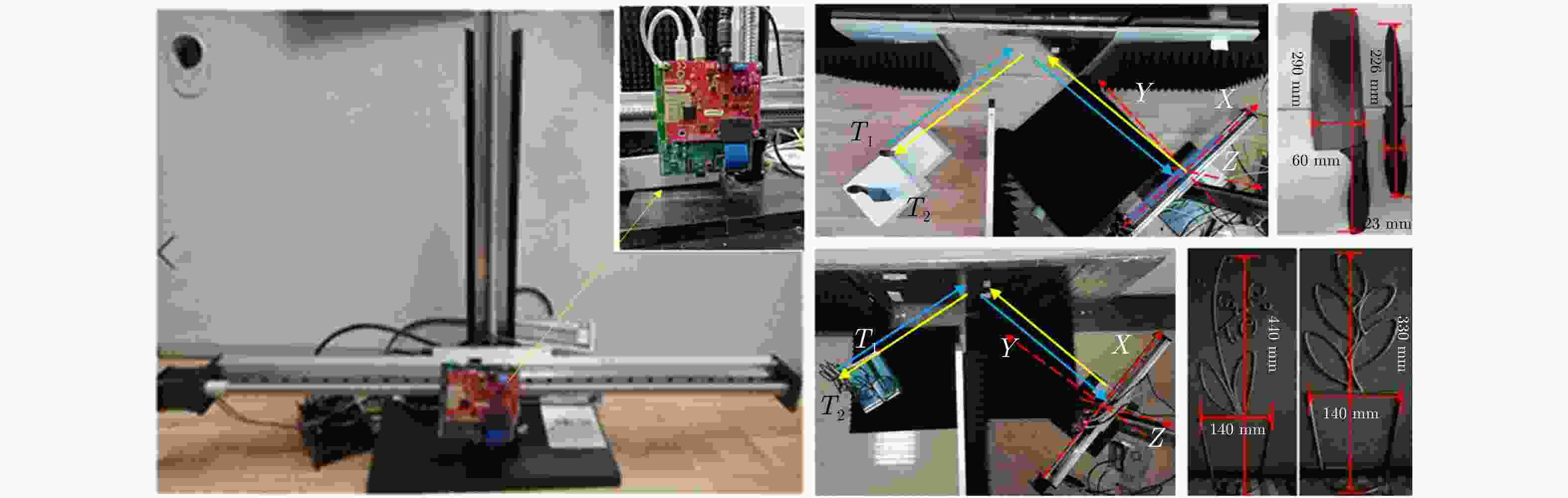
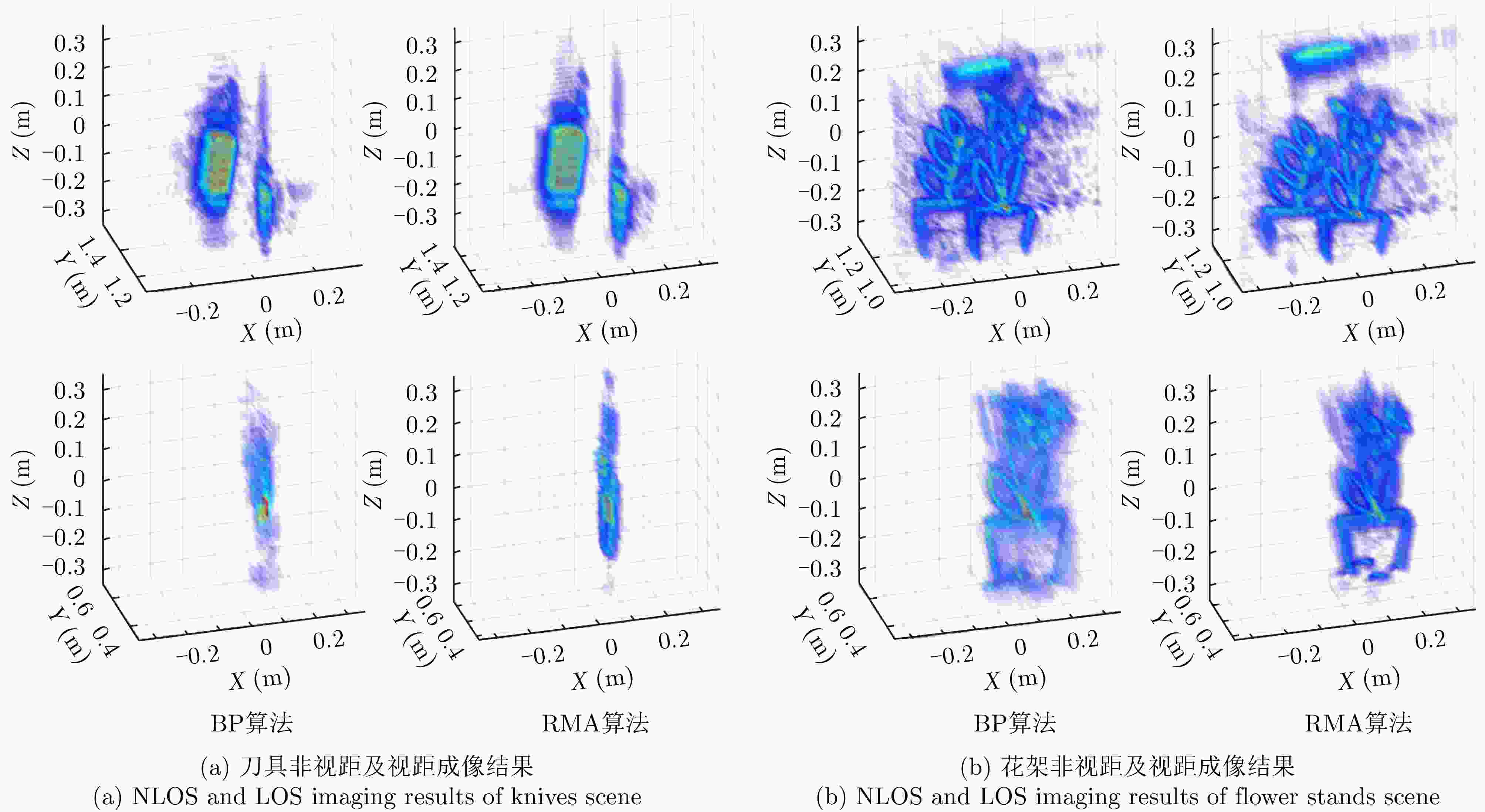
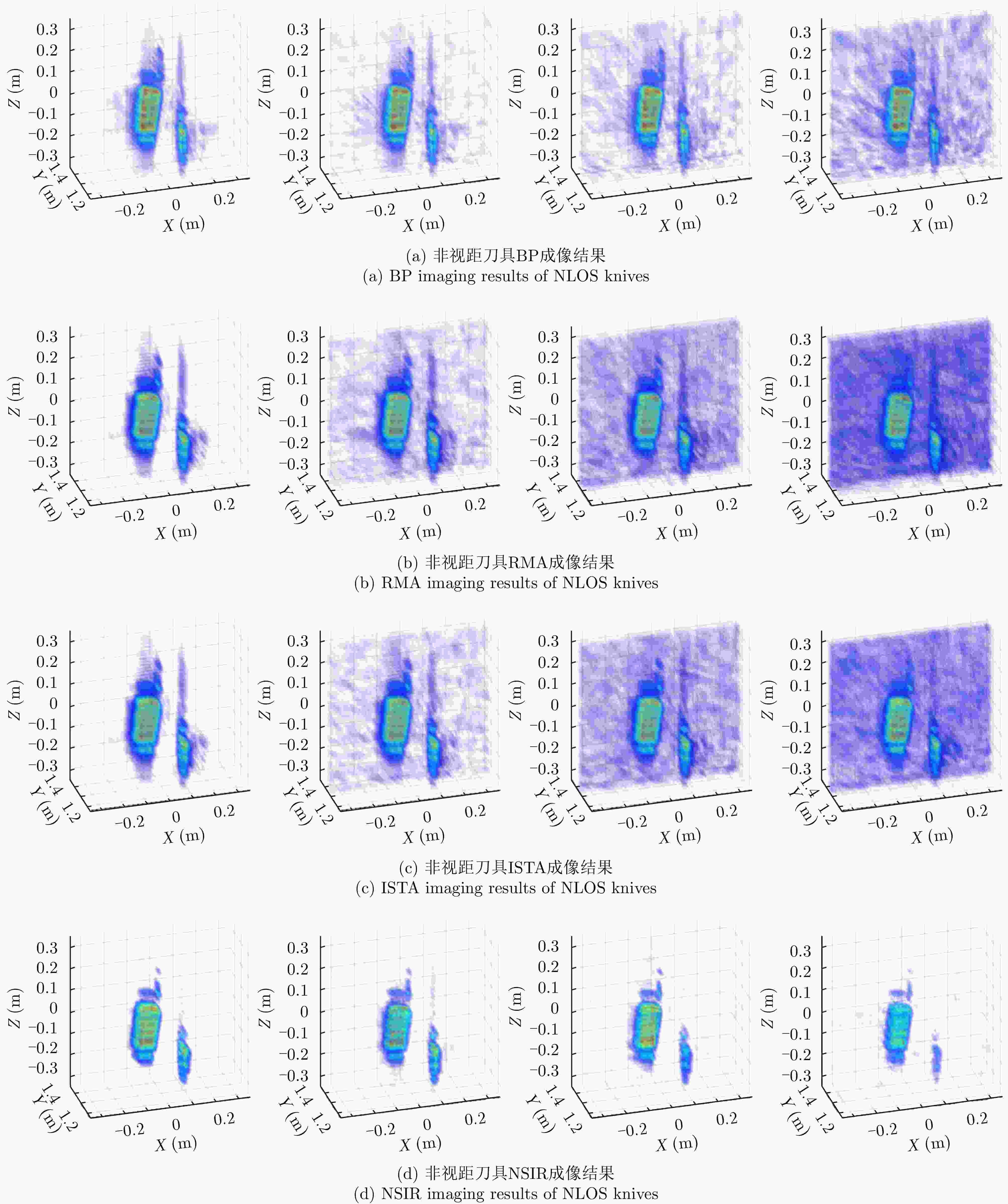
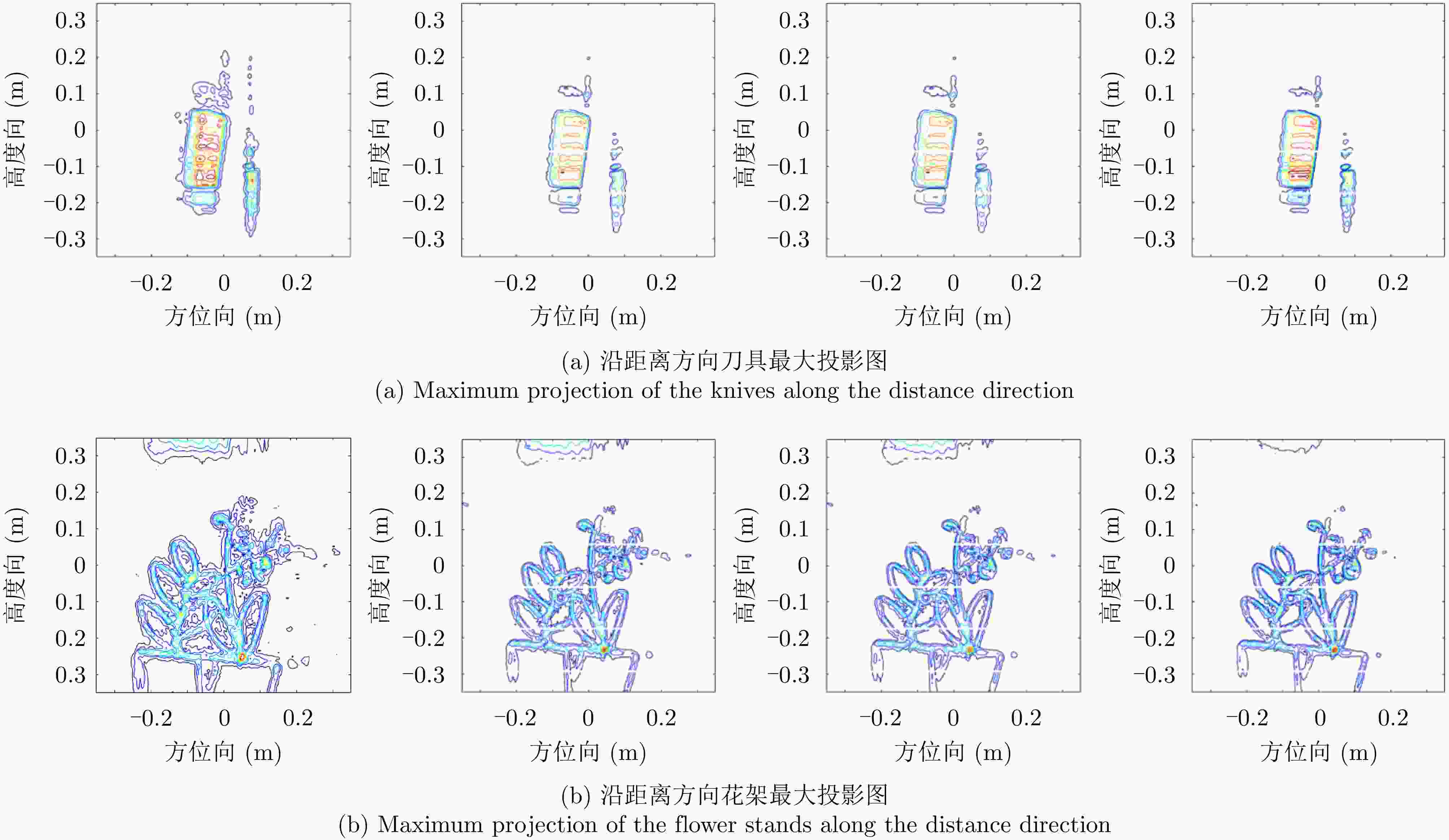
参数	实测系统值
载频(GHz)	79
带宽(GHz)	3.998
孔径尺寸(cm)	40×40
采样间隔(mm)	x: 1; z: 2
脉冲发射间隔(ms)	50

下载: 导出CSV 

| 显示表格

图4为X-Y平面(方位-距离)二维非视距成像结果。在金属刀具场景中，雷达位于坐标原点，反射墙面位于y=–1.1x+0.55平面，将目标场景分为视距区域和非视距区域。由成像结果可见，两个金属刀具目标清晰可见、位于反射面后的非视距区域，其图像目标散射区坐标与场景真实位置关于反射面对称，此外反射面及环境干扰引入了虚假目标。金属花架成像结果中，反射墙面位于y=–1.28x+0.6平面，花架聚焦在非视距区域。刀具虚像距离雷达阵列1.2 m附近，花架虚像在距离雷达阵列1.2～1.4 m位置处，成像结果与模型分析一致。

图  4  实验场景2D成像

Figure  4.  2D imaging of experimental scenes

下载: 全尺寸图片 幻灯片

图5为第100～110行脉压回波。结合图4信息，金属刀具回波和花架回波位于反射面回波之后，可确定回波具体位置。由于小刀散射区域小于菜刀，且二者径向距离不同，其回波位于不同距离门。场景中，两个铁质花架目标在回波域相互融合，其原因是花架尺寸较大且二者距离较小。对此本文将采用所提TD-PME方法，分离非视距目标多径回波，实现精确三维成像。

图  5  距离向脉冲压缩结果

Figure  5.  Results of range compression

下载: 全尺寸图片 幻灯片

结合实验场景2D成像结果，采用TD-PME方法分别提取1.2 m和1.3 m处的虚像回波。其结果如图6所示，反射面回波和隐藏目标回波被分离出来。

图  6  多路径回波提取结果

Figure  6.  Multipath echo extraction results

下载: 全尺寸图片 幻灯片

为了体现非视距环境所带来的分辨率低、旁瓣高等成像问题，本文对隐藏目标进行了传统算法成像结果对比，如图7所示。视距环境成像得到的图像目标背景更为干净，噪声、旁瓣和杂波干扰更低，成像质量更高。非视距环境下刀具目标带有较高的旁瓣，花架目标被淹没在背景噪声中，成像质量较视距环境下的更低。由于实验环境经过毫米波吸波材料的优化，可以认为隐藏目标成像质量的下降与反射墙面有关。在对隐藏目标非视距多路径回波提取之后，如何克服反射墙面导致的成像质量下降、实现隐藏目标高精度重构是本文NSIR算法的主要工作。

图  7  金属刀具及金属花架非视距及视距成像结果对比(第1行为非视距成像结果，第2行为视距成像结果，采样率均为100%)

Figure  7.  Comparison of the NLOS and LOS imaging results of the metal knives and the metal flower stands (the first line is the NLOS imaging result, the second line is the LOS imaging result, the sampling rate is 100%)

下载: 全尺寸图片 幻灯片

首先，为了分析算法对平面目标的成像性，在100%, 70%, 50%和30%采样率下对刀具进行成像对比，BP, RMA, ISTA和本文NSIR算法成像结果如图8所示。三维成像网格尺寸为512×31×512，成像空间大小固定为70 cm×30 cm×70 cm。可以看出，BP, RMA和ISTA算法随着采样率的下降，出现明显的旁瓣，背景杂波增加，重构质量显著下降；NSIR算法随着采样率的下降基本上仍能保持金属刀具的轮廓清晰、背景干净，说明不同采样率下本文NSIR算法均能获得较高的重构精度。验证了NSIR在低采样率下对平面目标的良好重构性能。

图  8  不同采样率下，4种算法的非视距金属刀具成像结果对比(从左至右：采样率分别为100%, 70%, 50%和30%)

Figure  8.  Comparison of NLOS metal knives imaging results of four algorithms with different sampling rates (from left to right: sampling rates of 100%, 70%, 50%, and 30%, respectively)

下载: 全尺寸图片 幻灯片

其次，为了分析算法对强边缘目标的成像性能，验证NSIR算法中TV正则化对隐藏目标的边缘特征提取能力，本文在一个边缘信息丰富的金属花架上进行了三维重构实验。图9展示了不同算法的成像结果。即使在全采样情况下，BP, RMA和ISTA成像结果也受到严重的旁瓣和杂波干扰，花架细节部分被噪声污染严重。相比之下，NSIR算法有效地抑制了图像旁瓣，滤除了大量的背景杂波，相较于另外3种算法所获得的花架结果更加清晰、轮廓重构更加精确，显著提高了重构质量。在低采样率下，NSIR仍然恢复了目标细节轮廓。

图  9  不同采样率下，4种算法的非视距金属花架成像结果对比((从左至右：采样率分别为100%, 70%, 50%和30%)

Figure  9.  Comparison of NLOS metal flower stands imaging results of four algorithms with different sampling rates (from left to right: sampling rates of 100%, 70%, 50%, and 30%, respectively)

下载: 全尺寸图片 幻灯片

此外，为了更好地展示不同算法对两种非视距目标的轮廓细节重构效果，本文给出了100%采样率下沿距离方向的最大投影结果，如图10所示。结果表明，NSIR重构了两种目标的轮廓特征，对目标细节刻画效果更好。在全采样情况下，NSIR对金属刀具的聚焦性最强，对金属花架的轮廓和纹理重构效果最好。相较于其他3种算法，NSIR有效地抑制了散乱点和背景中的旁瓣与噪声。

图  10  在全采样率下，4种算法的最大投影结果对比(从左往右分别对应BP, RMA, ISTA和NSIR)

Figure  10.  At the full sampling rate, the maximum projection results of the four algorithms are compared (from left to right, corresponding to BP, RMA, ISTA and NSIR)

下载: 全尺寸图片 幻灯片

表2提供了两组实验中不同算法成像结果的数值评估。与BP, RMA和ISTA算法相比，在两组隐藏目标不同采样率情况下的成像结果数值评估中，NSIR都获得了更低的图像熵和更高的图像对比度，表明其成像质量更好。此外，该表记录了各个算法成像所需时长。其中，BP算法重构所需时间最长，这是由于BP算法极高的计算复杂度导致的。RMA算法重构速度最快，基于频域快速成像算子的ISTA算法和NSIR算法重构时长依次增加。

表  2  不同算法下的实测实验数值评估结果

Table  2.  Numerical evaluation results of real experiments with different algorithms

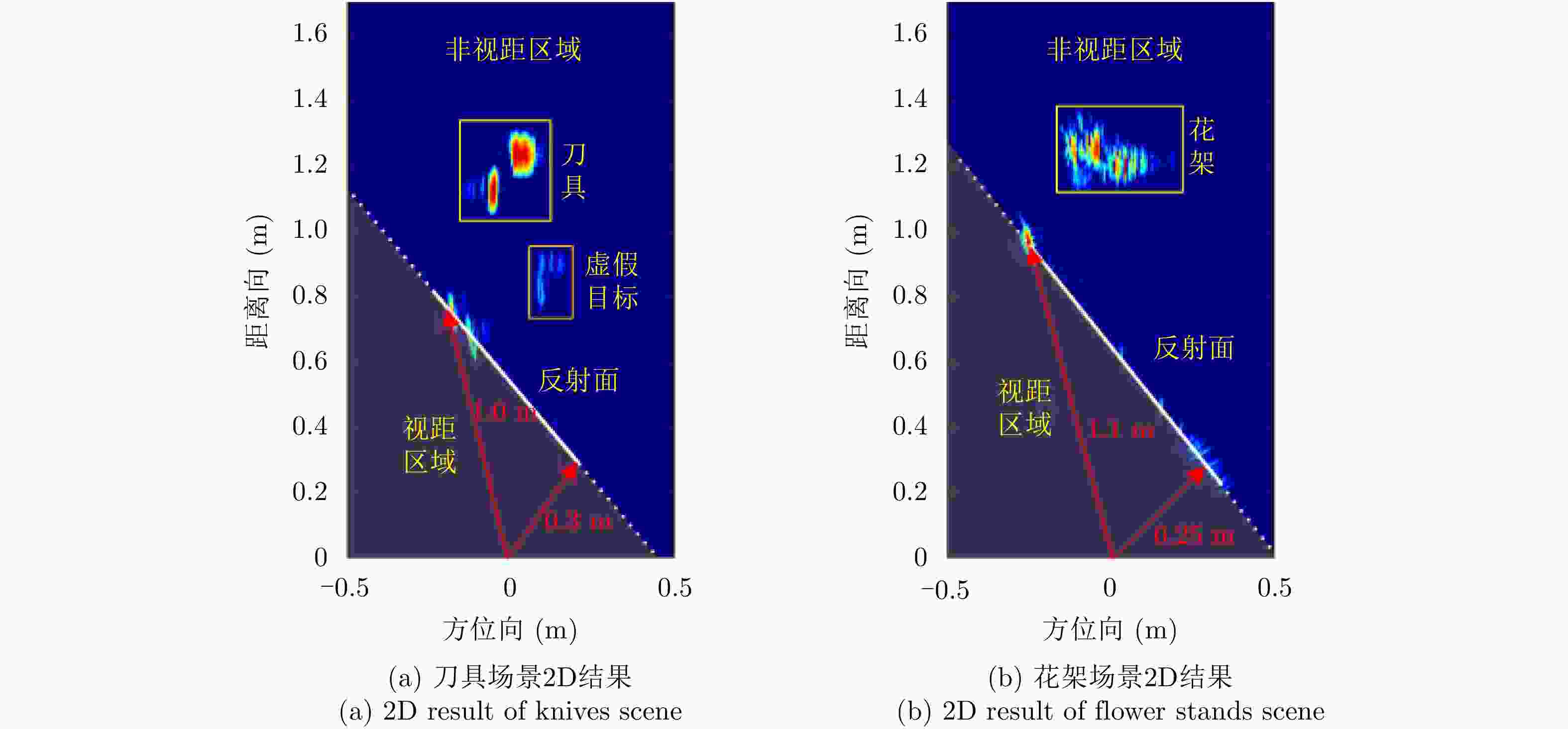
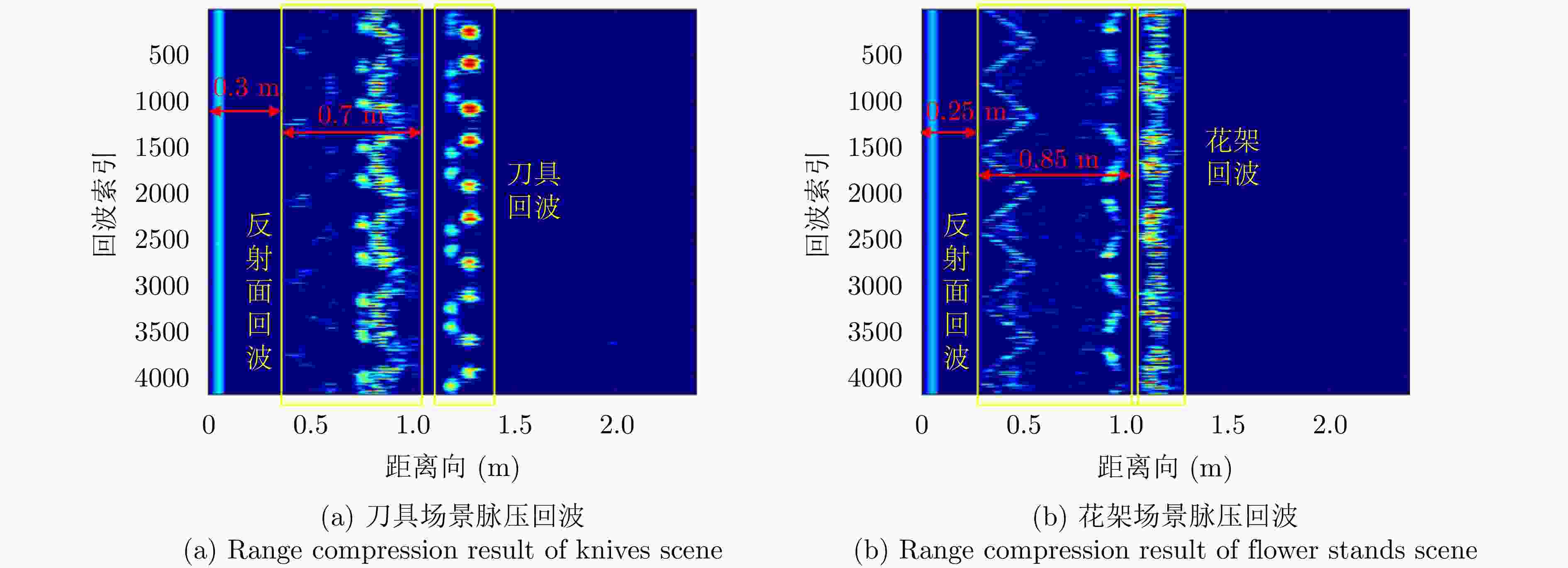
目标	采样率(%)	BP				RMA				ISTA				NSIR
		ENT	IC	Time (s)		ENT	IC	Time (s)		ENT	IC		Time (s)	ENT	IC	Time (s)
金属刀具	100	11.03	8.74	810.56		10.70	8.41	1.05		10.65	8.48		14.69	10.24	11.05	76.94
	70	11.15	8.62	625.30		11.06	7.91	1.06		10.944	8.06		17.58	10.78	11.75	124.38
	50	11.27	8.50	308.45		11.39	7.30	1.06		11.237	7.54		17.82	10.00	11.64	77.447
	30	11.49	8.12	183.67		11.92	6.19	1.15		11.572	6.79		20.49	9.93	12.08	131.58
金属花架	100	11.25	7.25	251.61		11.93	5.23	0.99		11.61	5.73		23.96	10.71	9.07	80.96
	70	11.50	6.82	169.20		12.41	4.56	1.00		11.83	5.44		24.61	10.44	12.08	80.18
	50	11.75	5.13	120.88		12.78	3.98	0.98		12.05	5.16		24.48	10.06	16.30	77.25
	30	11.10	4.23	73.76		13.23	3.04	0.99		12.26	4.76		24.53	8.59	45.89	77.98

下载: 导出CSV 

| 显示表格

5.   结语

针对非视距雷达隐匿目标的三维高精度成像问题，本文提出了一种多约束联合优化的隐藏目标精确重构算法NSIR。首先，采用TD-PME回波分离方法对雷达回波进行预处理并提取隐藏目标的多路径回波；随后，引入${l_1}$范数及TV范数约束构建稀疏成像和相位误差联合正则化估计模型，采用块坐标下降框架对相位误差及散射系数进行迭代求解，实现墙面多次反射相位误差下隐藏目标的高精度成像。此外，本文算法也引入RMA频域快速成像算子，避免了成像过程中的大规模矩阵-向量运算，降低了内存消耗并提高了成像效率。最后，通过实测实验验证所提方法的隐藏目标高精度成像性能。实验结果表明，对于非视距隐匿目标，所提方法具有较高的成像质量及成像效率。然而，目前本文考虑的非视距成像场景较为简单，后续将继续研究逼近实际场景的回波精确提取、非视距信息挖掘、多路径微弱回波增强及复杂反射面相位误差补偿等非视距高精度成像关键问题。