作者中心
专家审稿
责编办公
编辑办公
High-resolution Imaging Method for Through-the-wall Radar Based on Transfer Learning with Simulation Samples
-
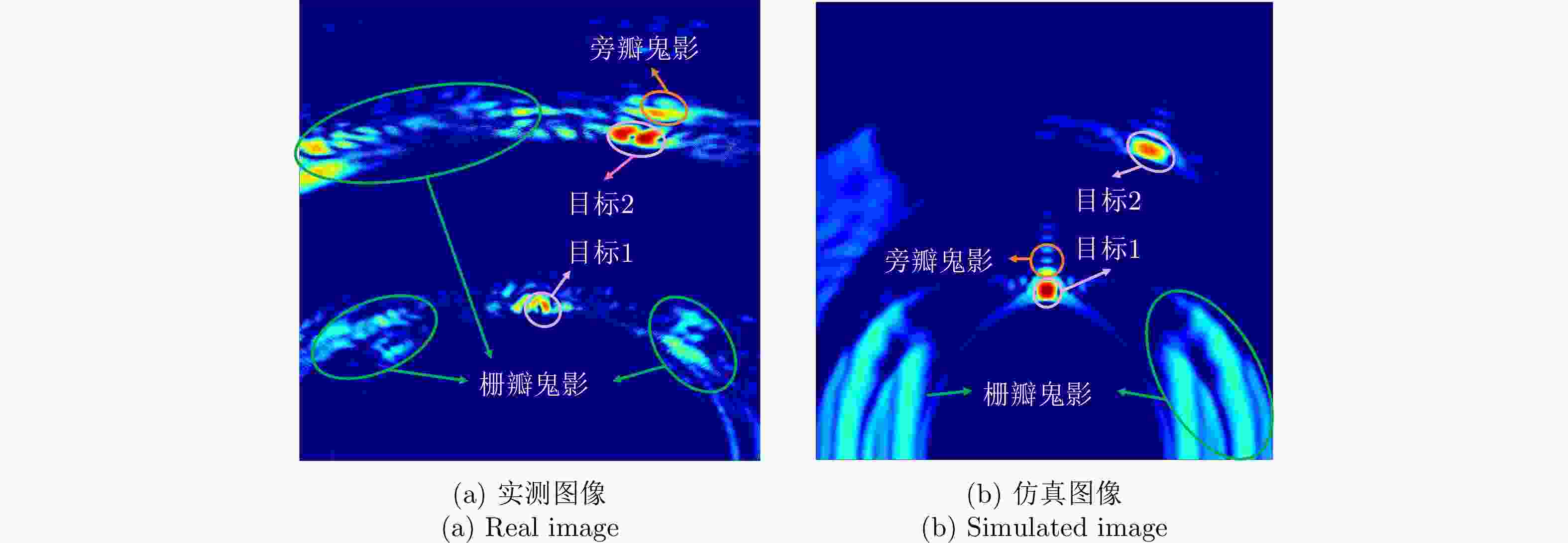
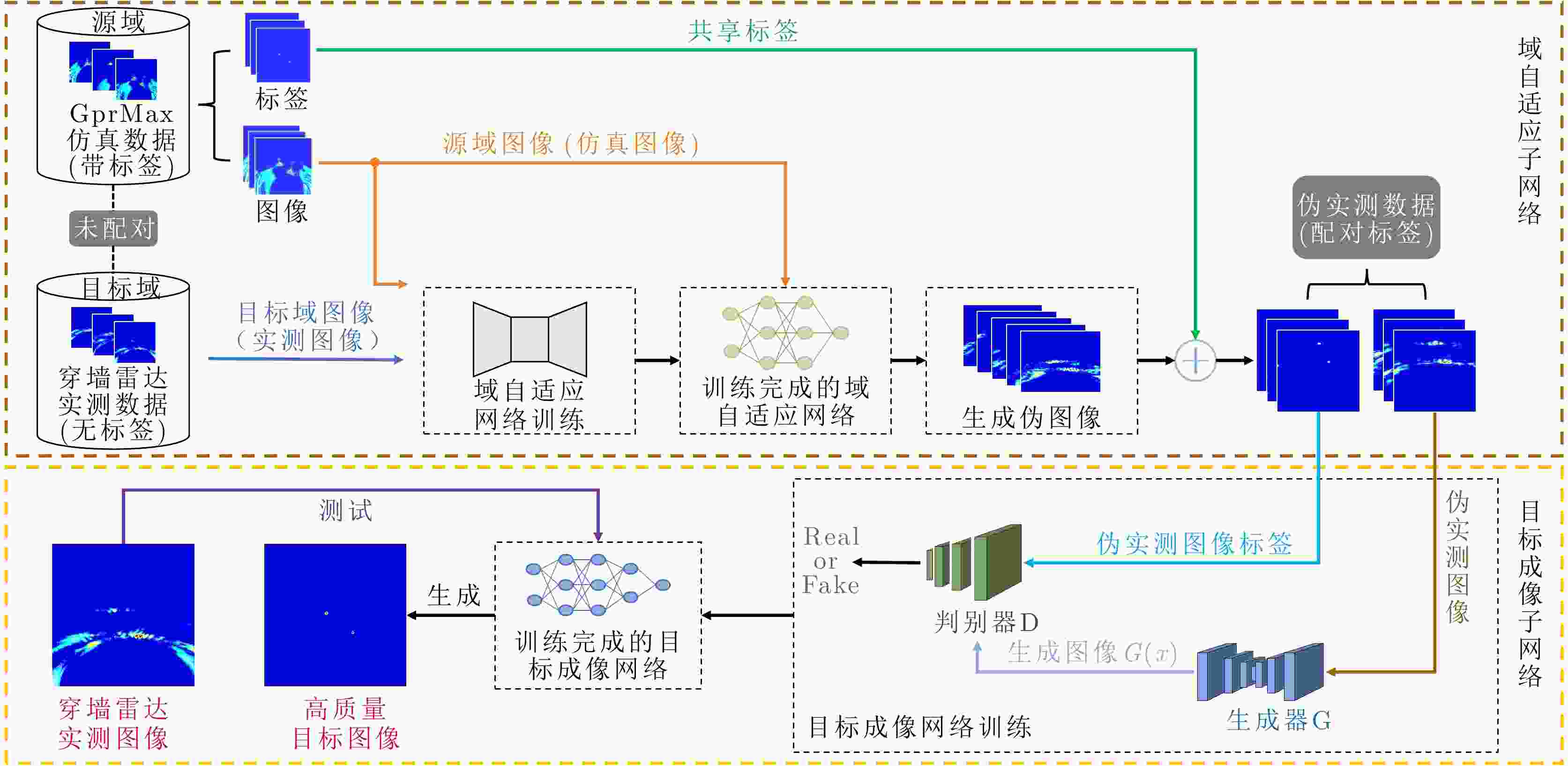
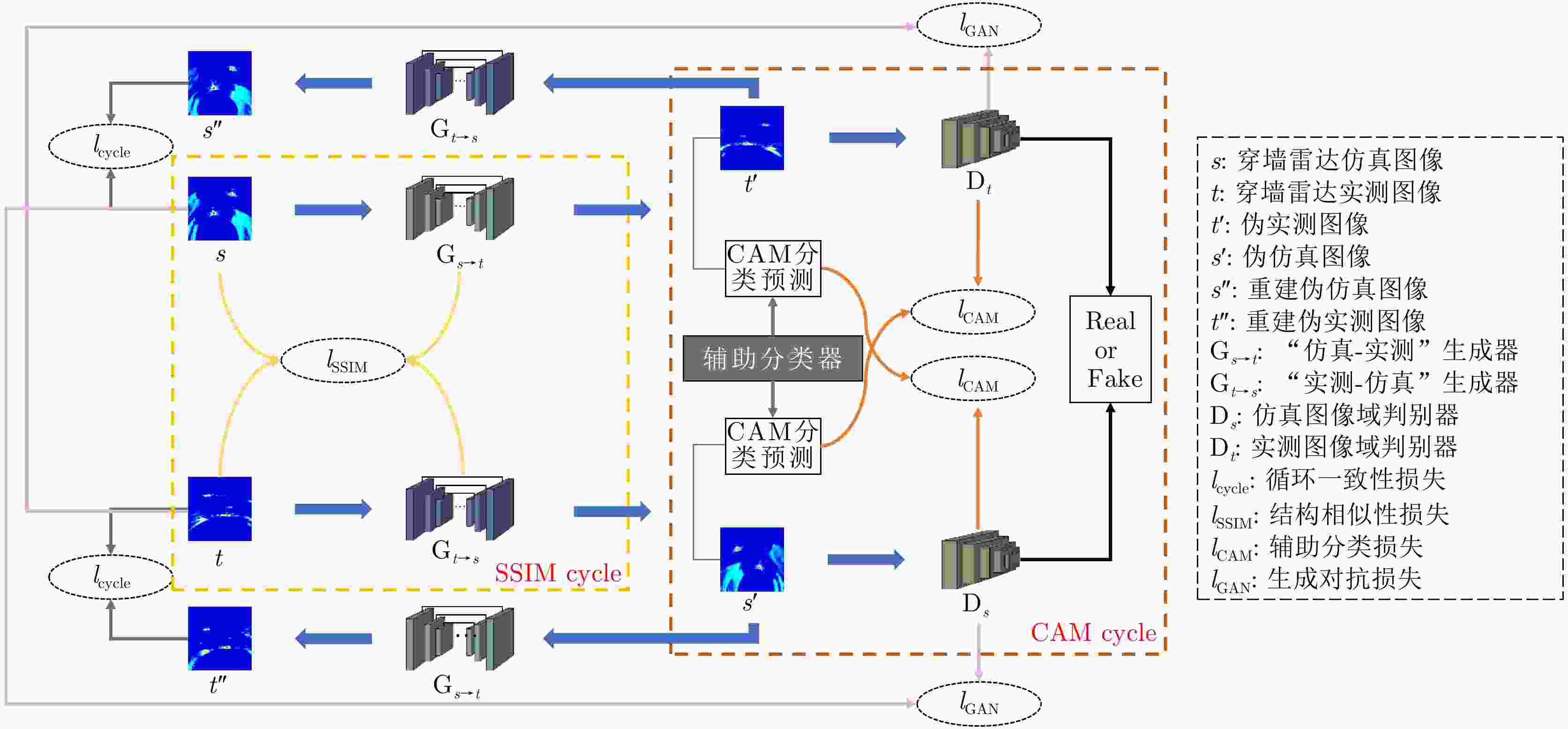
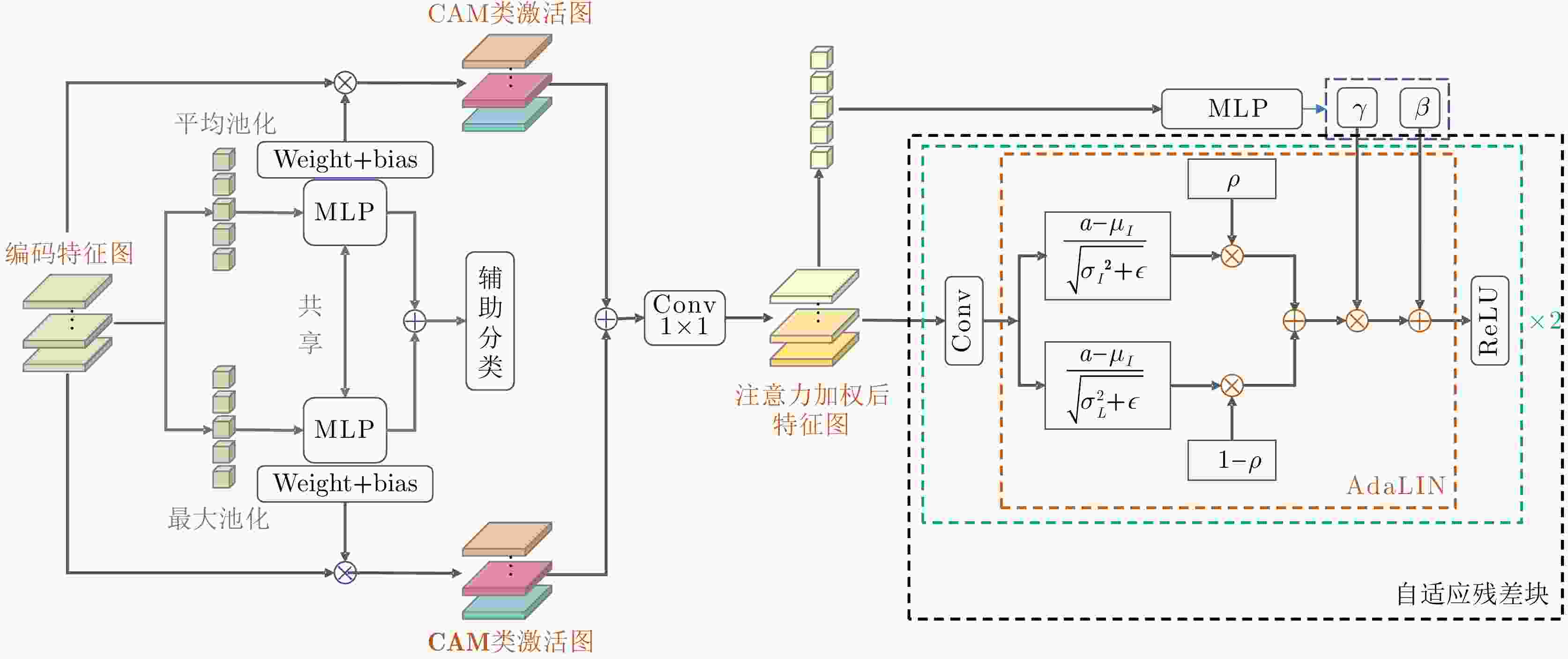
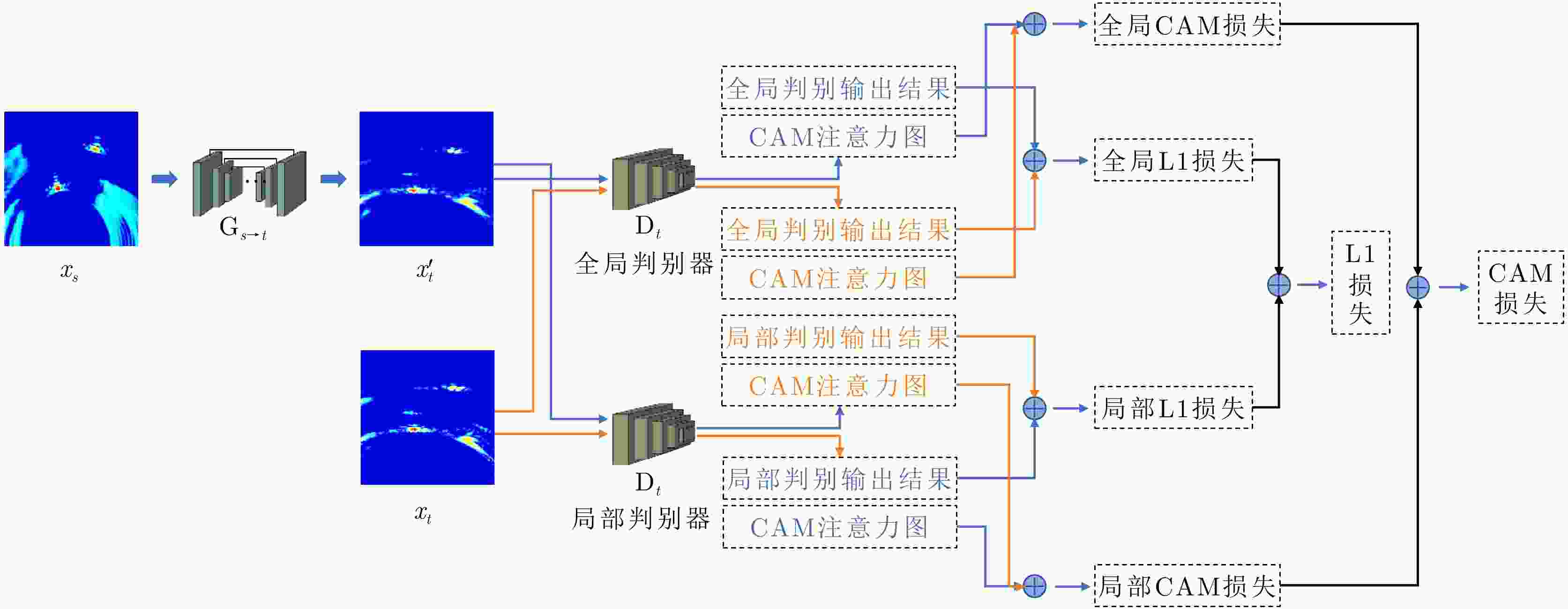
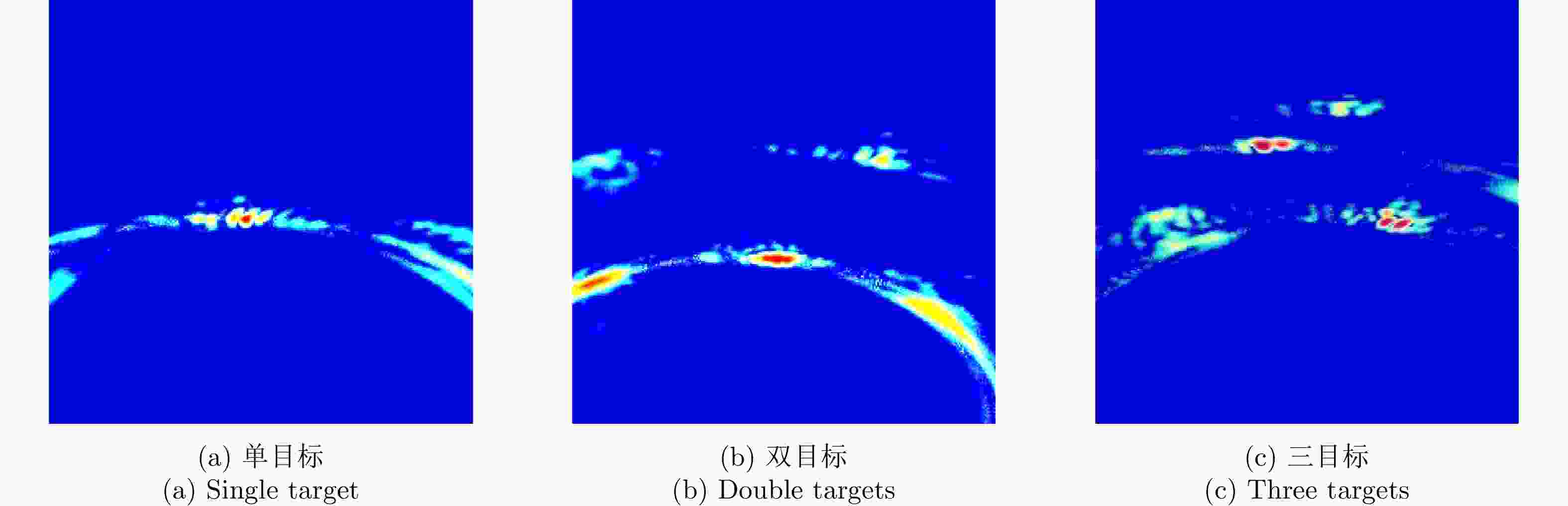
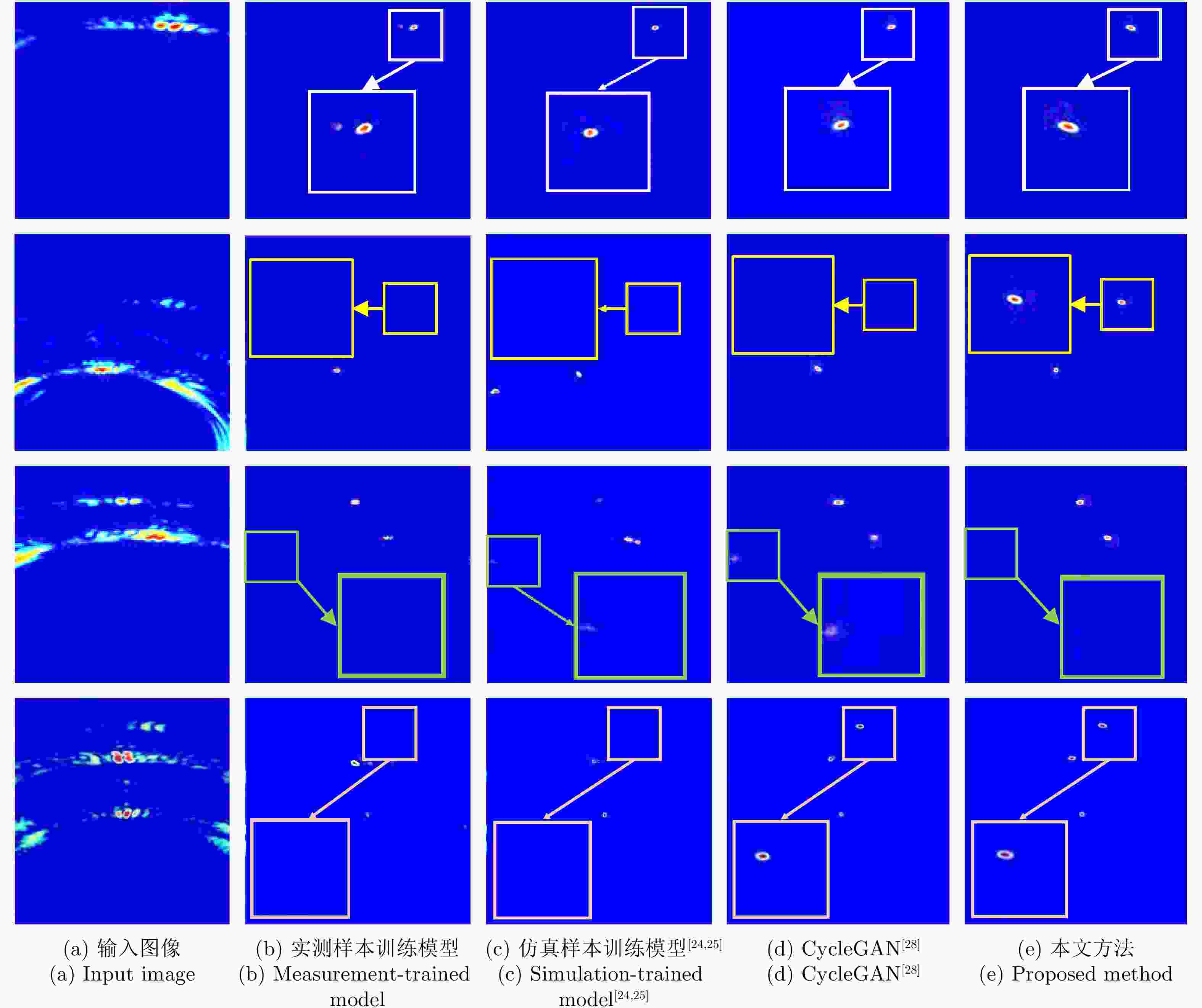
摘要: 针对带标注实测样本受限情况下的遮蔽多目标高分辨成像问题，提出一种基于迁移学习的穿墙雷达成像方法。首先，搭建生成对抗子网络实现带标签仿真数据到实测数据的迁移，解决带标签数据制作困难的问题；然后，联合使用注意力机制、自适应残差块及多尺度判别器提高图像迁移质量，引入结构一致性损失函数减小图像间的感知差异；最后，利用带标签数据训练穿墙雷达目标成像子网络，实现穿墙雷达多目标高分辨成像。实验结果表明，所提方法能有效缩小仿真图像和实测图像域间差异，实现穿墙雷达带标签伪实测图像生成，系统性解决了穿墙雷达遮蔽目标成像面临的旁/栅瓣鬼影干扰、目标图像散焦、多目标互扰等问题，在单、双和三目标场景下成像准确率分别达到98.24%, 90.97%和55.17%，相比于传统CycleGAN方法，所提方法成像准确率分别提升了2.29%, 40.28%和15.51%。Abstract: This paper addresses the problem of high-resolution imaging of shadowed multiple-targets with limited labeled data, by proposing a transfer-learning-based method for through-the-wall radar imaging. First, a generative adversarial sub-network is developed to facilitate the migration of labeled simulation data to measured data, overcoming the difficulty of generating labeled data. This method incorporates an attention mechanism, adaptive residual blocks, and a multi-scale discriminator to improve the quality of image migration. It also incorporates a structural consistency loss function to minimize perceptual differences between images. Finally, the labeled data are used to train the through-the-wall radar target-imaging sub-network, achieving high-resolution imaging of multiple targets through walls. Experimental results show that the proposed method effectively reduces discrepancies between simulated and obtained images, and generates pseudo-measured images with labels. It systematically addresses issues such as side/grating ghost interference, target image defocusing, and multi-target mutual interference, significantly improving the multi-target imaging quality of the through-the-wall radar. The imaging accuracy achieved is 98.24%, 90.97% and 55.17% for single, double, and triple-target scenarios, respectively. Compared with CycleGAN, the imaging accuracy for the corresponding scenarios is improved by 2.29%, 40.28% and 15.51%, respectively.
-
图 1 MIMO穿墙成像雷达模型
Figure 1. A simple of Multiple-Input Multiple-Output (MIMO) Through-the-Wall Radar Imaging (TWRI)
图 11 迁移学习结果(黄色圆圈标记生成图像纹理差异部分)
Figure 11. Transfer learning results (yellow circle marking generates texture differences in the image)
图 12 训练过程中图像FID得分(虚线为训练过程中实际FID得分曲线，实线表示经平滑处理后的FID得分曲线)
Figure 12. FID Score during training (the dotted line is the actual FID score curve during the training process, and the solid line represents the FID score curve after smoothing)
图 13 不同方法训练目标成像网络的成像测试结果(图中大方框图像是小方框的放大图像)
Figure 13. Target imaging results of different method (the large box image in the figure is an enlarged image of the small box)
表 1 仿真参数设置
Table 1. Parameter setting
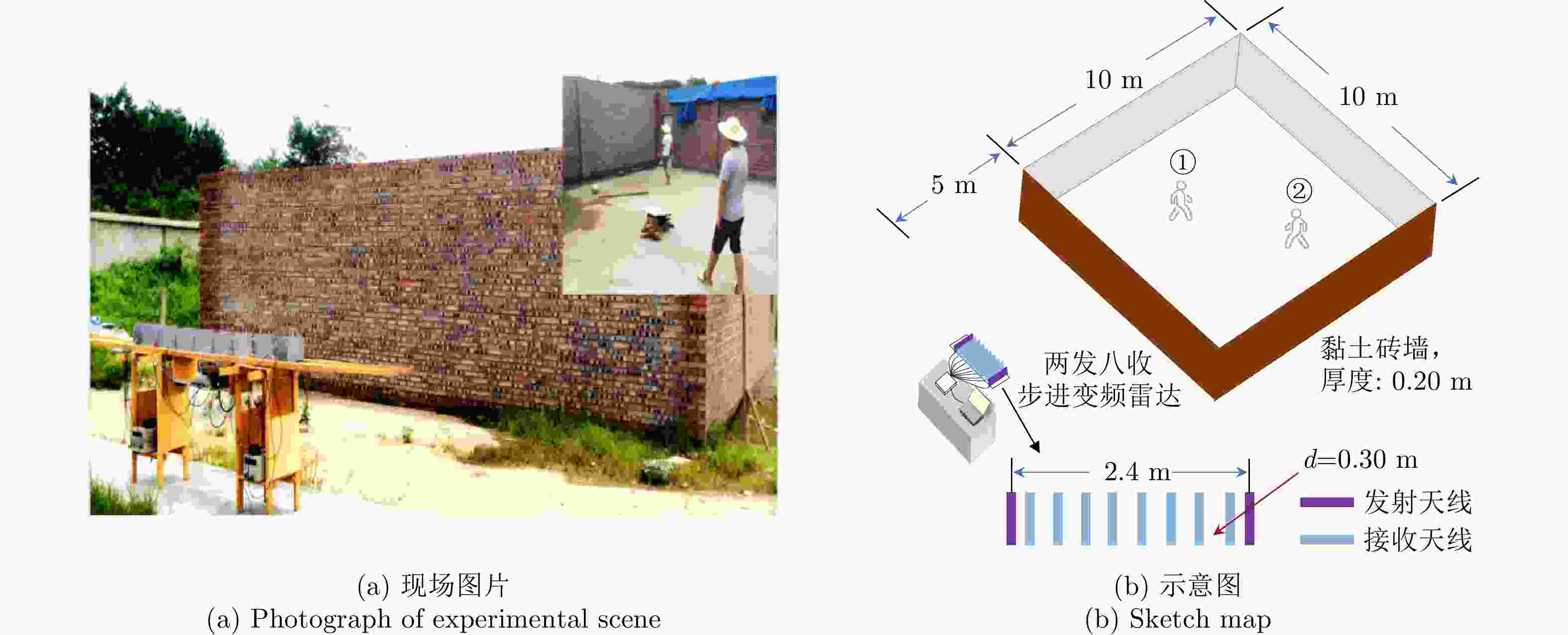
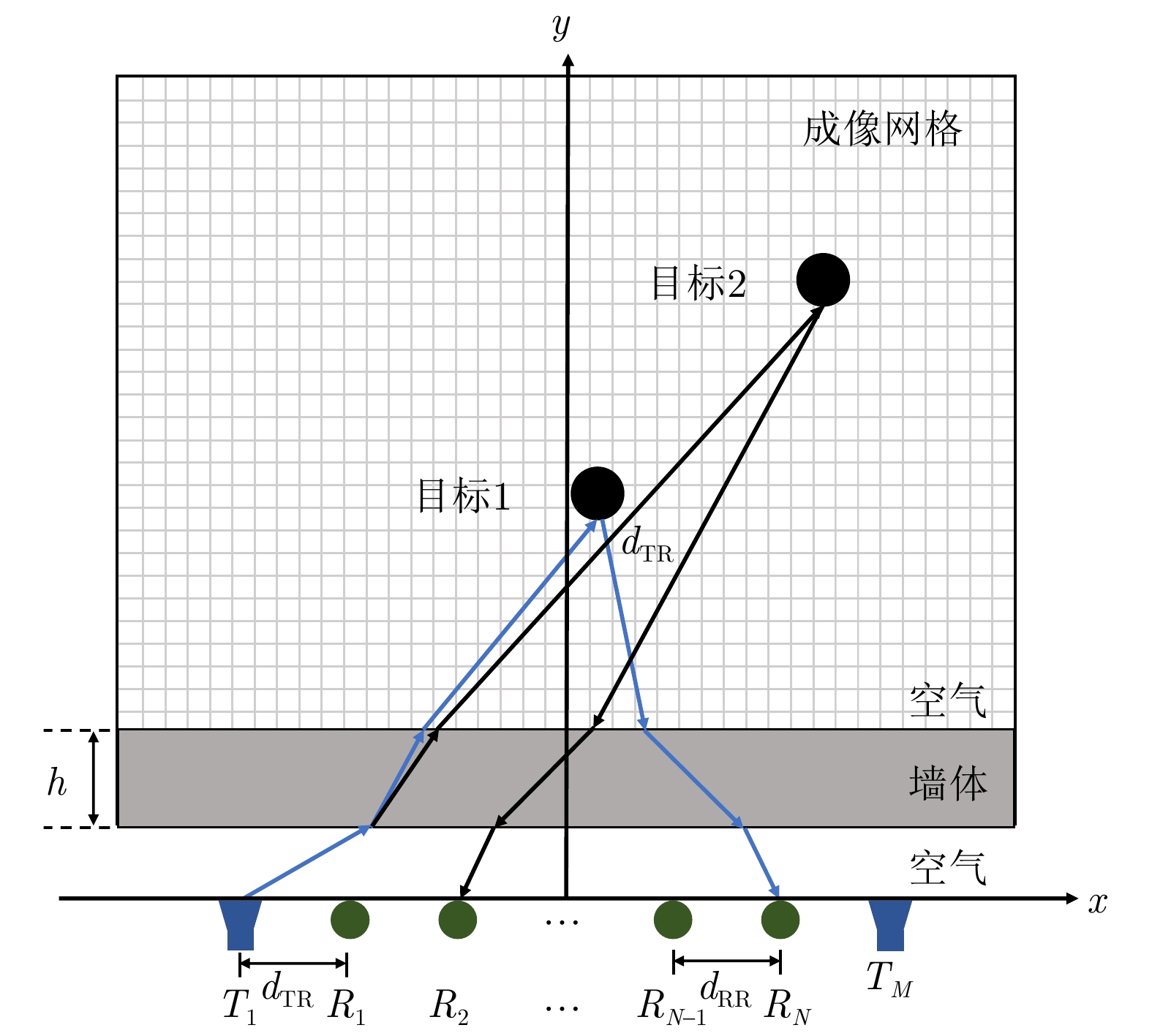
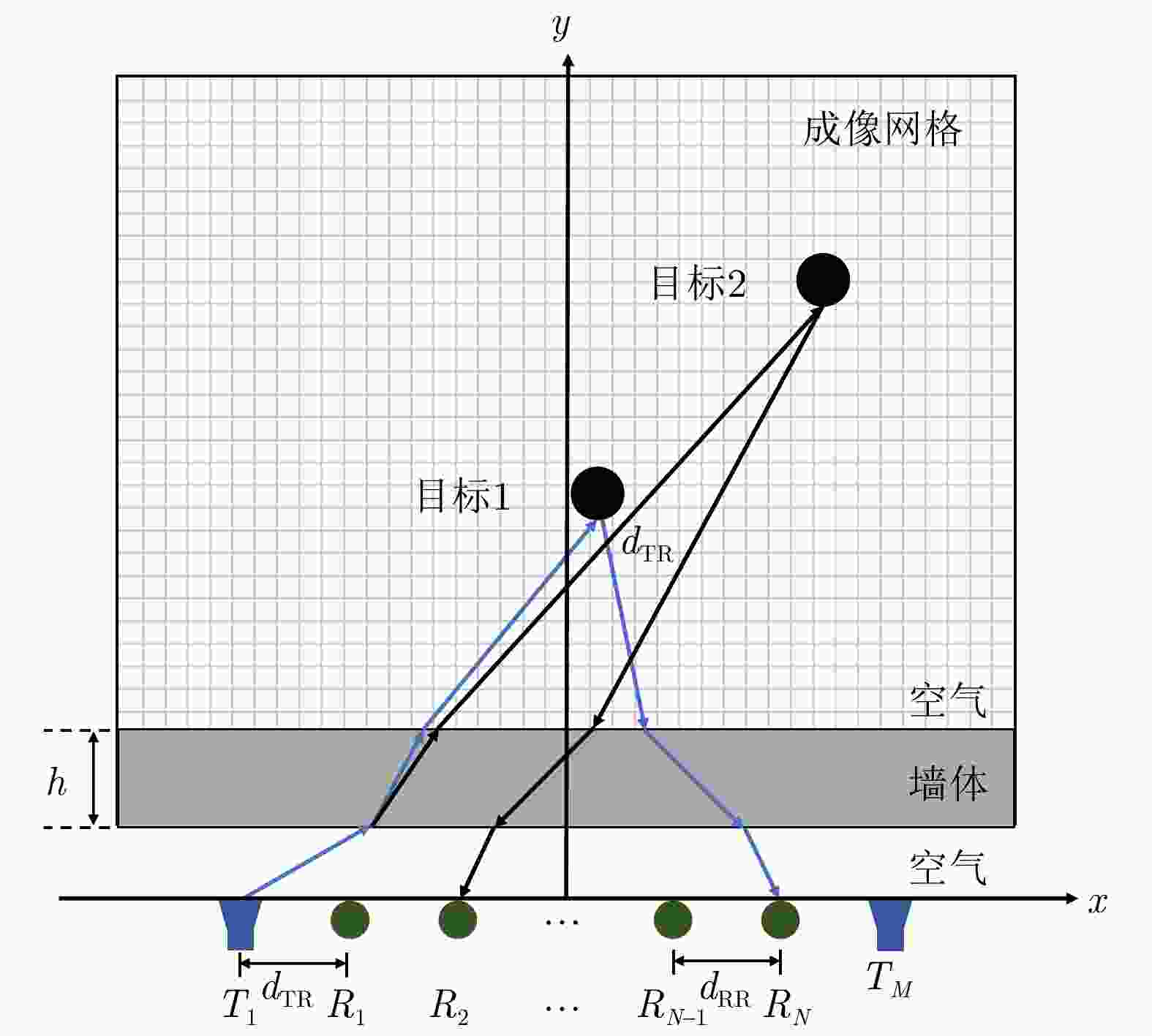
参数 取值 参数 取值 中心频率f 1.5 GHz 墙体电导率${\sigma _{\mathrm{w}}}$ 0.1 S/m 带宽B 1 GHz 人体目标半径r 10 cm 墙体厚度h 0.2 cm 目标介电常数${\varepsilon _{\mathrm{r}}}$ 55 发射阵元和相邻接收阵元间距${d_{{\mathrm{TR}}}}$ 0.15 接收阵元间距${d_{{\mathrm{RR}}}}$ 0.3 发射天线数量M 2 接收天线数量N 8 墙体介电常数${\varepsilon _{\mathrm{w}}}$ 5.0 目标电导率${\sigma _{\mathrm{r}}}$ 1.05 S/m 
下载: 导出CSV
表 2 实验环境详细参数
Table 2. Detailed parameters of experimental environment
实验环境 版本 操作系统 Windows 10专业版64位 CPU Intel(R) Core(TM) i7-10700K CPU @ 3.80 GHz GPU NAVIDIA RTX 3090 Pytorch 1.10.2 CUDA 11.6
下载: 导出CSV
-
[1] AMIN M G. Through-The-Wall Radar Imaging[M]. Boca Raton, USA: CRC Press, 2017: 7–11. doi: 10.1201/9781315218144. [2] NKWARI P K M, SINHA S, and FERREIRA H C. Through-the-wall radar imaging: A review[J]. IETE Technical Review, 2018, 35(6): 631–639. doi: 10.1080/02564602.2017.1364146. [3] 金添, 宋勇平, 崔国龙, 等. 低频电磁波建筑物内部结构透视技术研究进展[J]. 雷达学报, 2021, 10(3): 342–359. doi: 10.12000/JR20119.JIN Tian, SONG Yongping, CUI Guolong, et al. Advances on penetrating imaging of building layout technique using low frequency radio waves[J]. Journal of Radars, 2021, 10(3): 342–359. doi: 10.12000/JR20119. [4] CUI Guolong, KONG Lingjiang, and YANG Jianyu. A back-projection algorithm to stepped-frequency synthetic aperture through-the-wall radar imaging[C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 123–126. doi: 10.1109/APSAR.2007.4418570. [5] 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展(科普类)[J]. 雷达学报, 2014, 3(4): 383–395. doi: 10.3724/SP.J.1300.2014.14105.WU Yirong, HONG Wen, ZHANG Bingchen, et al. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383–395. doi: 10.3724/SP.J.1300.2014.14105. [6] YOOON Y S and AMIN M G. Through-the-wall radar imaging using compressive sensing along temporal frequency domain[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, USA, 2010: 2806–2809. doi: 10.1109/ICASSP.2010.5496199. [7] LI Minchao, XI Xiaoli, SONG Zhongguo, et al. Multitarget time-reversal radar imaging method based on high-resolution hyperbolic radon transform[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1–5. doi: 10.1109/LGRS.2021.3054119. [8] ODEDO V C, YAVUZ M E, COSTEN F, et al. Time reversal technique based on spatiotemporal windows for through the wall imaging[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(6): 3065–3072. doi: 10.1109/TAP.2017.2696421. [9] LI Lianlin, ZHANG Wenji, and LI Fang. A novel autofocusing approach for real-time through-wall imaging under unknown wall characteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 423–431. doi: 10.1109/TGRS.2009.2024686. [10] JIA Yong, GUO Yong, CHEN Shengyi, et al. Multipath ghost and side/grating lobe suppression based on stacked generative adversarial nets in MIMO through-wall radar imaging[J]. IEEE Access, 2019, 7: 143367–143380. doi: 10.1109/ACCESS.2019.2945859. [11] CHEN Guohao, CUI Guolong, KONG Lingjiang, et al. Robust multiple human targets tracking for through-wall imaging radar[C]. 2018 21st International Conference on Information Fusion, Cambridge, UK, 2018: 1–5. doi: 10.23919/ICIF.2018.8455343. [12] JIA Yong, KONG Lingjiang, YANG Xiaobo, et al. Target detection in multi-channel through-wall-radar imaging[C]. 2012 IEEE Radar Conference, Atlanta, USA, 2012: 539–542. doi: 10.1109/RADAR.2012.6212199. [13] 姚雪, 孔令讲, 易川, 等. 一种适用于穿墙雷达成像的墙体补偿算法[J]. 雷达科学与技术, 2014, 12(6): 654–658. doi: 10.3969/j.issn.1672-2337.2014.06.017.YAO Xue, KONG Lingjiang, YI Chuan, et al. A new wall compensation algorithm for through-the-wall radar imaging[J]. Radar Science and Technology, 2014, 12(6): 654–658. doi: 10.3969/j.issn.1672-2337.2014.06.017. [14] LI Shiyong, AMIN M G, AN Qiang, et al. 2-D coherence factor for sidelobe and ghost suppressions in radar imaging[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(2): 1204–1209. doi: 10.1109/TAP.2019.2938581. [15] LU Biying, SUN Xin, ZHAO Yang, et al. Phase coherence factor for mitigation of sidelobe artifacts in through-the-wall radar imaging[J]. Journal of Electromagnetic Waves and Applications, 2013, 27(6): 716–725. doi: 10.1080/09205071.2013.774111. [16] LIU Jiangang, JIA Yong, KONG Lingjiang, et al. Sign-coherence-factor-based suppression for grating lobes in through-wall radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(11): 1681–1685. doi: 10.1109/LGRS.2016.2603982. [17] AN Qiang, HORRFAR A, ZHANG Wenji, et al. Range coherence factor for down range sidelobes suppression in radar imaging through multilayered dielectric media[J]. IEEE Access, 2019, 7: 66910–66918. doi: 10.1109/ACCESS.2019.2911693. [18] SENG C H, BOUZERDOUM A, AMIN M G, et al. Two-stage fuzzy fusion with applications to through-the-wall radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 687–691. doi: 10.1109/LGRS.2012.2218570. [19] SENG C H, BOUZERDOUM A, AMIN M G, et al. Probabilistic fuzzy image fusion approach for radar through wall sensing[J]. IEEE Transactions on Image Processing, 2013, 22(12): 4938–4951. doi: 10.1109/TIP.2013.2279953. [20] JIA Yong, ZHONG Xiaoling, LIU Jiangang, et al. Single-side two-location spotlight imaging for building based on MIMO through-wall-radar[J]. Sensors, 2016, 16(9): 1441. doi: 10.3390/s16091441. [21] LI Huquan, CUI Guolong, GUO Shisheng, et al. Human target detection based on FCN for through-the-wall radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(9): 1565–1569. doi: 10.1109/LGRS.2020.3006077. [22] QU Lele, WANG Changan, YANG Tianhong, et al. Enhanced through-the-wall radar imaging based on deep layer aggregation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4023705. doi: 10.1109/LGRS.2022.3171714. [23] VISHWAKARMA S and RAM S S. Mitigation of through-wall distortions of frontal radar images using denoising autoencoders[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6650–6663. doi: 10.1109/TGRS.2020.2978440. [24] ZHANG Huiyuan, SONG Ruiyuan, CHEN Shengyi, et al. Target imaging based on generative adversarial nets in through-wall radar imaging[C]. International Conference on Control, Automation and Information Sciences, Chengdu, China, 2019: 1–6. doi: 10.1109/ICCAIS46528.2019.9074694. [25] JIA Yong, SONG Ruiyuan, CHEN Shengyi, et al. Preliminary results of multipath ghost suppression based on generative adversarial nets in TWRI[C]. IEEE 4th International Conference on Signal and Image Processing, Wuxi, China, 2019: 208–212. doi: 10.1109/SIPROCESS.2019.8868597. [26] HUANG Shaoyin, QIAN Jiang, WANG Yong, et al. Through-the-wall radar super-resolution imaging based on cascade U-net[C]. IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 2933–2936. doi: 10.1109/IGARSS.2019.8900569. [27] GAMIN Y, USTINOVA E, AJAKAN H, et al. Domain-adversarial training of neural networks[J]. The Journal of Machine Learning Research, 2016, 17(59): 1–35. doi: 10.48550/arXiv.1505.07818. [28] ZHU Junyan, PAKR T, ISOLA P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2242–2251. doi: 10.1109/ICCV.2017.244. [29] JANA R and KOCUR D. Compensation of wall effect for through wall tracking of moving targets[J]. Radioengineering, 2009, 18(2): 189–195. [30] 范苍宁, 刘鹏, 肖婷, 等. 深度域适应综述: 一般情况与复杂情况[J]. 自动化学报, 2021, 47(3): 515–548. doi: 10.16383/j.aas.c200238.FAN Cangning, LIU Peng, XIAO Ting, et al. A review of deep domain adaptation: General situation and complex situation[J]. Acta Automatica Sinica, 2021, 47(3): 515–548. doi: 10.16383/j.aas.c200238. [31] KIM J, KIM M, KANG H, et al. U-GAT-IT: Unsupervised generative attentional networks with adaptive layer-instance normalization for image-to-image translation[C]. 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [32] ULYANOV D, VEDALDI A, and LEMPITSKY V. Instance normalization: The missing ingredient for fast stylization[EB/OL]. https://arXiv.org/abs/1607.08022, 2016. [33] BA J L, KIROS J R, and HINTON G E. Layer normalization[EB/OL]. https://arXiv.org/abs/1607.06450, 2016. [34] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [35] SHORTEN C and KHOSHGOFTAAR T M. A survey on image data augmentation for deep learning[J]. Journal of Big Data, 2019, 6(1): 60. doi: 10.1186/s40537-019-0197-0. [36] WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861. [37] HEUSEL M, RAMSAUER H, UNTERTHINER T, et al. GANs trained by a two time-scale update rule converge to a local nash equilibrium[C]. 31st Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6629–6640. doi: 10.5555/3295222.3295408. [38] WANG Qiang and BI Sheng. Prediction of the PSNR quality of decoded images in fractal image coding[J]. Mathematical Problems in Engineering, 2016, 2016: 2159703. doi: 10.1155/2016/2159703. -
图(13) / 表(4)
计量
- 文章访问数: 431
- HTML全文浏览量: 196
- PDF下载量: 127
- 被引次数: 0
