-
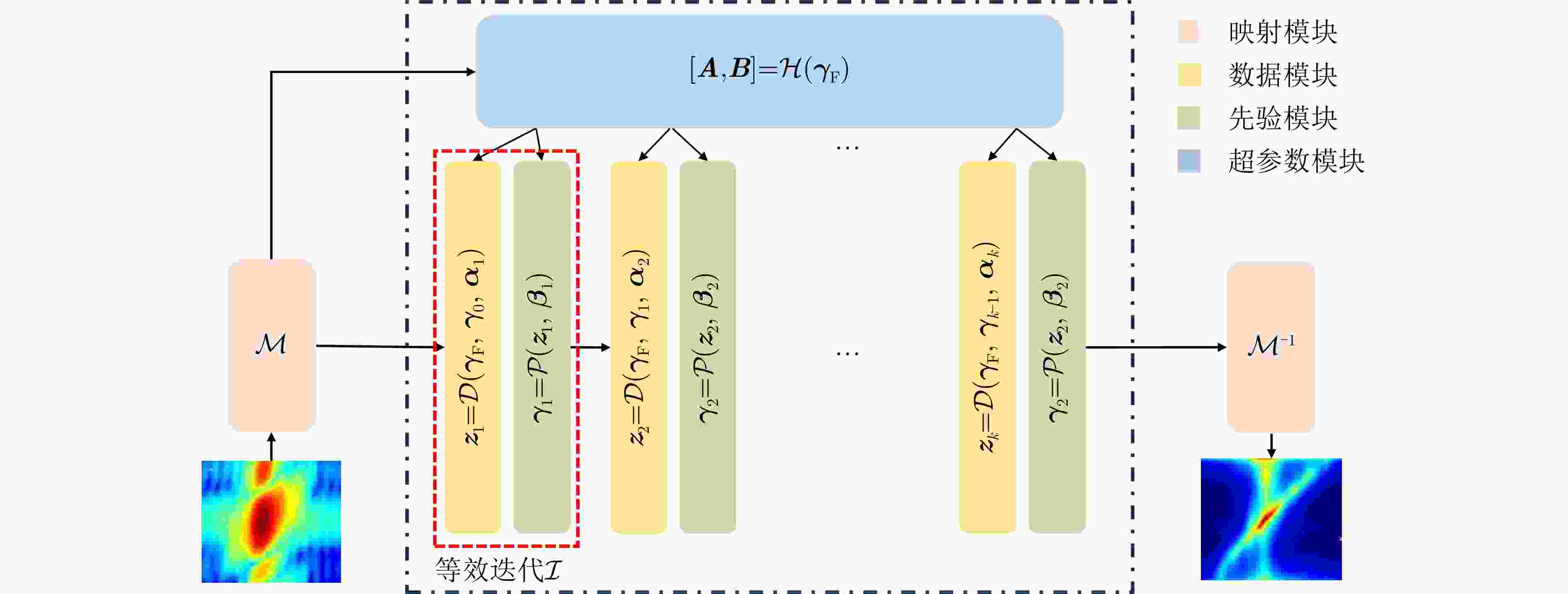
摘要: 在实际应用中,空时自适应处理(STAP)算法的性能受限于足够多独立同分布(IID)样本的获取。然而,目前可有效减少IID样本需求的算法仍面临一些问题。针对这些问题,该文融合数据驱动和模型驱动思想,构建了具有明确数学含义的多模块深度卷积神经网络(MDCNN),实现了小样本条件下对杂波协方差矩阵快速、准确、稳定估计。所构建MDCNN网络由映射模块、数据模块、先验模块和超参数模块组成。其中,前后端映射模块分别对应数据的预处理和后处理;单组数据模块和先验模块共同完成一次迭代优化,网络主体由多组数据模块和先验模块构成,可实现多次等效迭代优化;超参数模块则用来调整等效迭代中可训练参数。上述子模块均具有明确数学表述和物理含义,因此所构造网络具有良好的可解释性。实测数据处理结果表明,在实际非均匀杂波环境下该文所提方法杂波抑制性能优于现有典型小样本STAP方法,且运算时间较后者大幅降低。
-
关键词:
- 多模块深度卷积神经网络 /
- 空时自适应处理 /
- 稀疏恢复 /
- 非均匀杂波 /
- 杂波抑制
Abstract: In practical settings, the efficacy of Space-Time Adaptive Processing (STAP) algorithms relies on acquiring sufficient Independent Identically Distributed (IID) samples. However, sparse recovery STAP method encounters challenges like model parameter dependence and high computational complexity. Furthermore, current deep learning STAP methods lack interpretability, posing significant hurdles in debugging and practical applications for the network. In response to these challenges, this paper introduces an innovative method: a Multi-module Deep Convolutional Neural Network (MDCNN). This network blends data- and model-driven techniques to precisely estimate clutter covariance matrices, particularly in scenarios where training samples are limited. MDCNN is built based on four key modules: mapping, data, priori and hyperparameter modules. The front- and back-end mapping modules manage the pre- and post-processing of data, respectively. During each equivalent iteration, a group of data and priori modules collaborate. The core network is formed by multiple groups of these two modules, enabling multiple equivalent iterative optimizations. Further, the hyperparameter module adjusts the trainable parameters in equivalent iterations. These modules are developed with precise mathematical expressions and practical interpretations, remarkably improving the network’s interpretability. Performance evaluation using real data demonstrates that our proposed method slightly outperforms existing small-sample STAP methods in nonhomogeneous clutter environments while significantly reducing computational time. -
表 1 MCARM数据雷达系统参数
Table 1. MCARM data radar system parameters
参数 数值 飞行高度 3060 m飞行速度 100.2 m/s 载波频率 1240 MHz工作波长 0.2419 m主波束方位角 0° 主波束俯仰角 5.4° 载机偏航角 –7.3° 相参脉冲数 16 阵元误差 1%~2% 峰值辐射功率 25 kW 不模糊距离门 630个 系统损耗 8 dB 表 2 运算复杂度分析
Table 2. Analysis of computational complexity
方法 运算复杂度 运行时间(s) FOCUSS $ O\left( {\left( {NK{N_{\text{S}}}{N_{\text{D}}} + {{\left( {NK} \right)}^3} + 3{{\left( {NK} \right)}^3}{N_{\text{S}}}{N_{\text{D}}} + 2NK{{\left( {{N_{\text{S}}}{N_{\text{D}}}} \right)}^2}} \right){I_{{\text{SBL}}}}} \right) $ 61.870 SBL $ O\left( {\left( {NK{N_{\text{S}}}{N_{\text{D}}} + {{\left( {NK} \right)}^3} + 2{{\left( {NK} \right)}^2}{N_{\text{S}}}{N_{\text{D}}} + NK{{\left( {{N_{\text{S}}}{N_{\text{D}}}} \right)}^2}} \right){I_{{\text{FOC}}}}} \right) $ 130.400 CNN $ O\left( {{\text{28777}}{N_{\text{S}}}{N_{\text{D}}}} \right) $ 0.003 MDCNN $ O\left( {{\text{12960}}{N_{\text{S}}}{N_{\text{D}}}} \right) $ 0.002 -
[1] 谢文冲, 王永良, 熊元燚. 机载雷达空时自适应处理[M]. 北京: 清华大学出版社, 2024: 1–8.XIE Wenchong, WANG Yongliang, and XIONG Yuanyi. Airborne Radar Space-time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2024: 1–8. [2] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073.XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073. [3] BRENNAN L E and REED L S. Theory of adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 237–252. doi: 10.1109/TAES.1973.309792. [4] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893. [5] WANG Yongliang, CHEN Jianwen, BAO Zheng, et al. Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 70–81. doi: 10.1109/TAES.2003.1188894. [6] DIPIETRO R C. Extended factored space-time processing for airborne radar systems[C]. The 26th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1992, 1: 425–430. doi: 10.1109/ACSSC.1992.269236. [7] DUAN Keqing, XU Hong, YUAN Huadong, et al. Reduced-DOF three-dimensional STAP via subarray synthesis for nonsidelooking planar array airborne radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3311–3325. doi: 10.1109/TAES.2019.2958174. [8] MELVIN W L and GUERCI J R. Knowledge-aided signal processing: A new paradigm for radar and other advanced sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 983–996. doi: 10.1109/TAES.2006.248215. [9] MELVIN W L and SHOWMAN G A. An approach to knowledge-aided covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1021–1042. doi: 10.1109/TAES.2006.248216. [10] YANG Zhaocheng, DE LAMARE R C, and LIU Weijian. Sparsity-based STAP using alternating direction method with gain/phase errors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2756–2768. doi: 10.1109/TAES.2017.2714938. [11] DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183. [12] CUI Ning, XING Kun, YU Zhongjun, et al. Reduced-complexity subarray-level sparse recovery STAP for multichannel airborne radar WGMTI application[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6292–6313. doi: 10.1109/TAES.2023.3274104. [13] WANG Degen, WANG Tong, CUI Weichen, et al. A clutter suppression algorithm via enhanced sparse Bayesian learning for airborne radar[J]. IEEE Sensors Journal, 2023, 23(10): 10900–10911. doi: 10.1109/JSEN.2023.3263919. [14] DUAN Keqing, CHEN Hui, XIE Wenchong, et al. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP[J]. IET Radar, Sonar & Navigation, 2022, 16(2): 193–207. doi: 10.1049/rsn2.12176. [15] VENKATASUBRAMANIAN S, WONGKAMTHONG C, SOLTANI M, et al. Toward data-driven STAP radar[C]. 2022 IEEE Radar Conference (RadarConf22), New York, USA, 2022: 1–5. doi: 10.1109/RadarConf2248738.2022.9764354. [16] LIU Jing, LIAO Guisheng, XU Jingwei, et al. Autoencoder neural network-based STAP algorithm for airborne radar with inadequate training samples[J]. Remote Sensing, 2022, 14(23): 6021. doi: 10.3390/rs14236021. [17] 王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040.WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040. [18] YANG Yan, SUN Jian, LI Huibin, et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(3): 521–538. doi: 10.1109/TPAMI.2018.2883941. [19] MA Jiawei, LIU Xiaoyang, SHOU Zheng, et al. Deep tensor ADMM-net for snapshot compressive imaging[C]. The IEEE/CVF International Conference on Computer Vision, Seoul, Korea (South), 2019: 10222–10231. doi: 10.1109/ICCV.2019.01032. [20] MARQUES E C, MACIEL N, NAVINER L, et al. Deep learning approaches for sparse recovery in compressive sensing[C]. 2019 11th International Symposium on Image and Signal Processing and Analysis (ISPA), Dubrovnik, Croatia, 2019: 129–134. doi: 10.1109/ISPA.2019.8868841. [21] ZHANG Kai, VAN GOOL L, and TIMOFTE R. Deep unfolding network for image super-resolution[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 3214–3223. doi: 10.1109/CVPR42600.2020.00328. [22] BEN SAHEL Y, BRYAN J P, CLEARY B, et al. Deep unrolled recovery in sparse biological imaging: Achieving fast, accurate results[J]. IEEE Signal Processing Magazine, 2022, 39(2): 45–57. doi: 10.1109/MSP.2021.3129995. [23] ZOU Bo, WANG Xin, FENG Weike, et al. DU-CG-STAP method based on sparse recovery and unsupervised learning for airborne radar clutter suppression[J]. Remote Sensing, 2022, 14(14): 3472. doi: 10.3390/rs14143472. [24] 朱晗归, 冯为可, 冯存前, 等. 机载雷达深度展开空时自适应处理方法[J]. 雷达学报, 2022, 11(4): 676–691. doi: 10.12000/JR22051.ZHU Hangui, FENG Weike, FENG Cunqian, et al. Deep unfolding based space-time adaptive processing method for airborne radar[J]. Journal of Radars, 2022, 11(4): 676–691. doi: 10.12000/JR22051. [25] SANYAL P K. STAP processing monostatic and bistatic MCARM data[R]. MITRE Technical Report AFRL-SN-RS-TR-1999-197, 1999. [26] 周宇, 张林让, 刘楠, 等. 非均匀环境下利用杂波脊信息的杂波滤除方法研究[J]. 电子与信息学报, 2010, 32(6): 1332–1337. doi: 10.3724/SP.J.1146.2009.01104.ZHOU Yu, ZHANG Linrang, LIU Nan, et al. Study on exploring knowledge of the clutter ridge for clutter suppression in heterogeneous environments[J]. Journal of Electronics & Information Technology, 2010, 32(6): 1332–1337. doi: 10.3724/SP.J.1146.2009.01104. [27] SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: