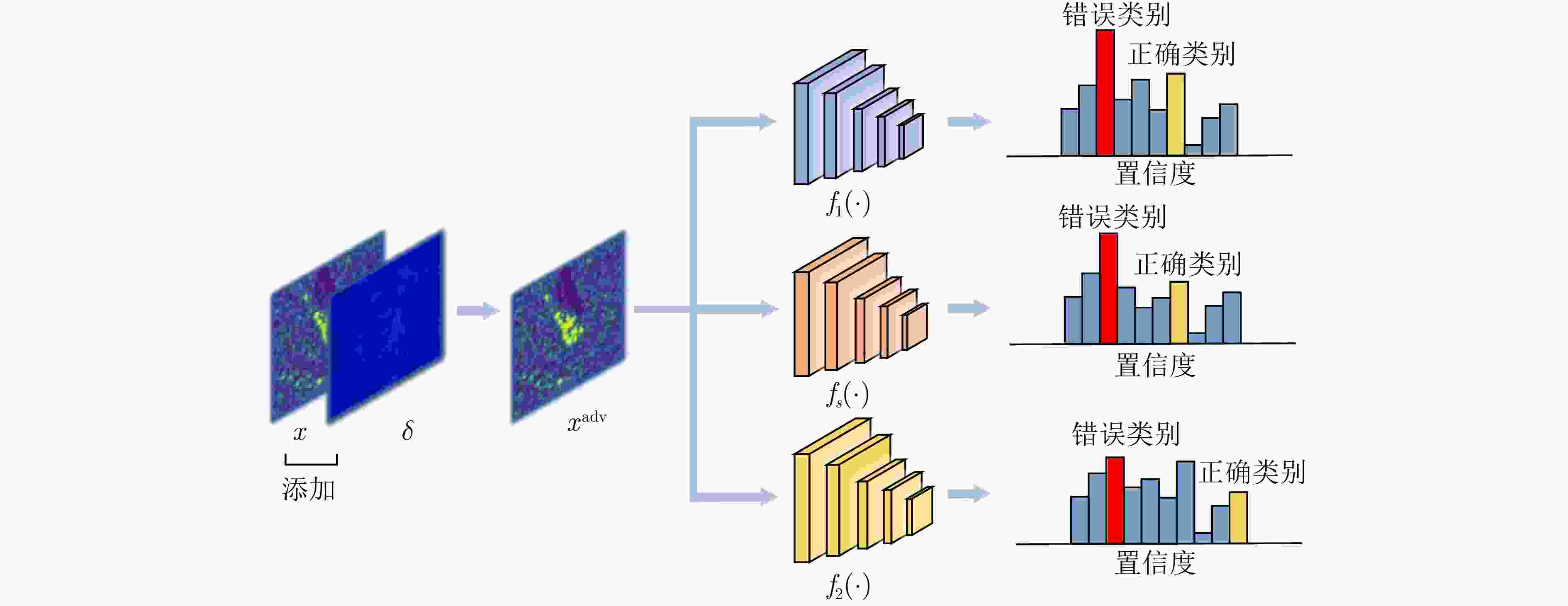
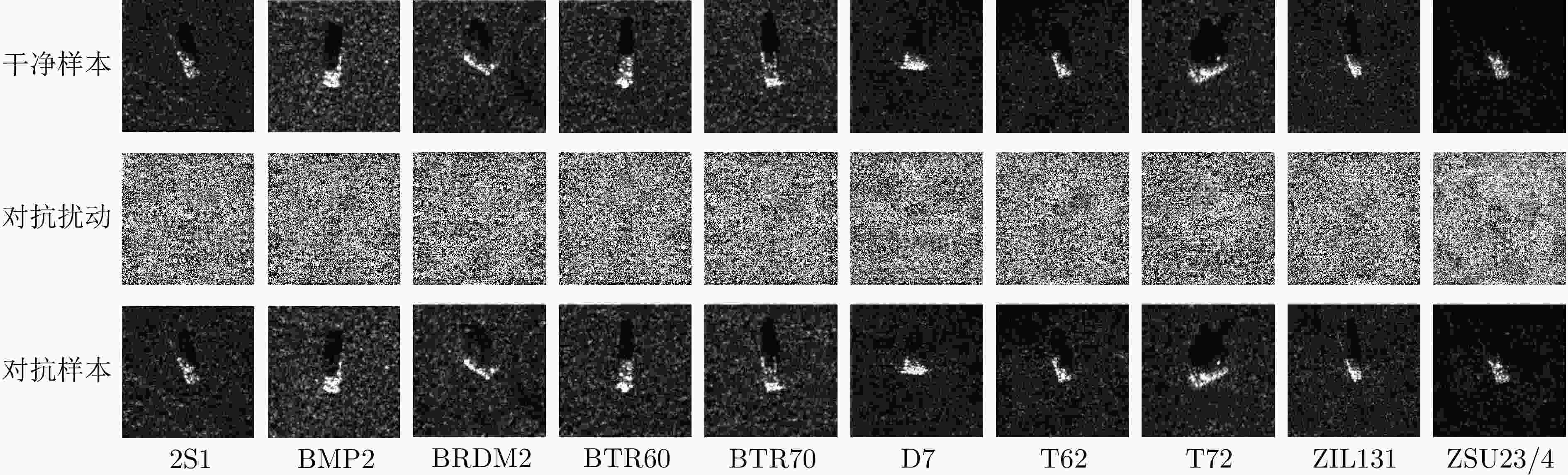
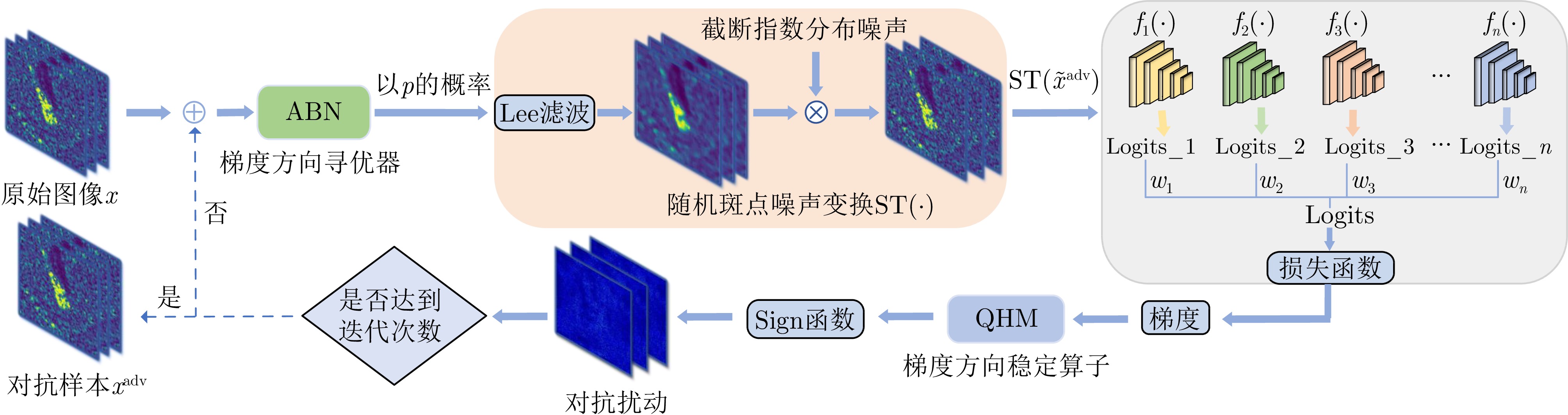
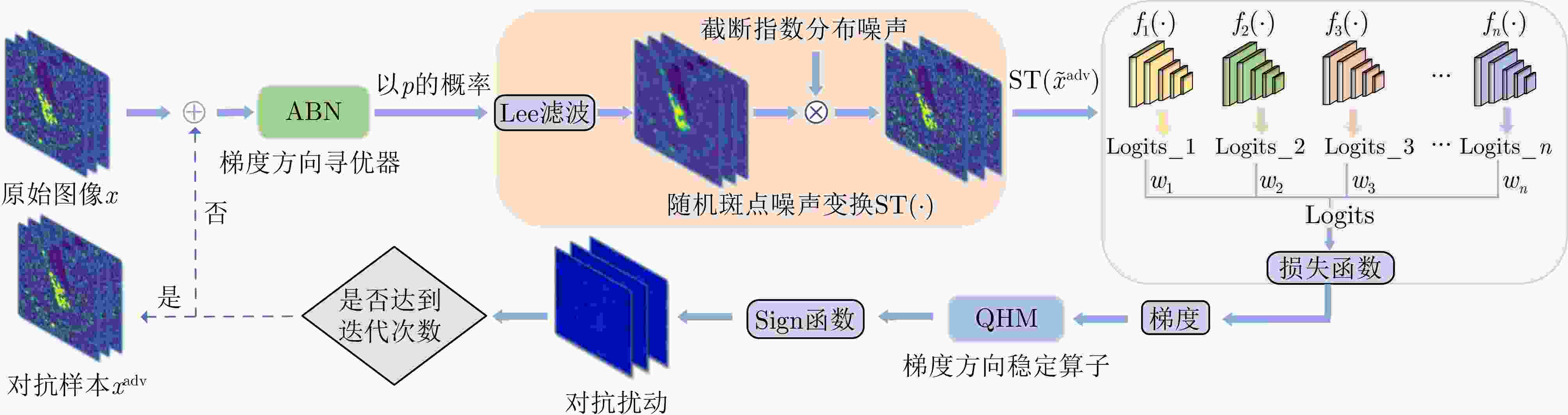
-
摘要: 合成孔径雷达自动目标识别(SAR-ATR)领域缺乏有效的黑盒攻击算法,为此,该文结合动量迭代快速梯度符号(MI-FGSM)思想提出了一种基于迁移的黑盒攻击算法。首先结合SAR图像特性进行随机斑点噪声变换,缓解模型对斑点噪声的过拟合,提高算法的泛化性能;然后设计了能够快速寻找最优梯度下降方向的ABN寻优器,通过模型梯度快速收敛提升算法攻击有效性;最后引入拟双曲动量算子获得稳定的模型梯度下降方向,使梯度在快速收敛过程中避免陷入局部最优,进一步增强对抗样本的黑盒攻击成功率。通过仿真实验表明,与现有的对抗攻击算法相比,该文算法在MSTAR和FUSAR-Ship数据集上对主流的SAR-ATR深度神经网络的集成模型黑盒攻击成功率分别提高了3%~55%和6.0%~57.5%,而且生成的对抗样本具有高度的隐蔽性。Abstract: The field of Synthetic Aperture Radar Automatic Target Recognition (SAR-ATR) lacks effective black-box attack algorithms. Therefore, this research proposes a migration-based black-box attack algorithm by combining the idea of the Momentum Iterative Fast Gradient Sign Method (MI-FGSM). First, random speckle noise transformation is performed according to the characteristics of SAR images to alleviate model overfitting to the speckle noise and improve the generalization performance of the algorithm. Second, an AdaBelief-Nesterov optimizer is designed to rapidly find the optimal gradient descent direction, and the attack effectiveness of the algorithm is improved through a rapid convergence of the model gradient. Finally, a quasihyperbolic momentum operator is introduced to obtain a stable model gradient descent direction so that the gradient can avoid falling into a local optimum during the rapid convergence and to further enhance the success rate of black-box attacks on adversarial examples. Simulation experiments show that compared with existing adversarial attack algorithms, the proposed algorithm improves the ensemble model black-box attack success rate of mainstream SAR-ATR deep neural networks by 3%~55% and 6.0%~57.5% on the MSTAR and FUSAR-Ship datasets, respectively; the generated adversarial examples are highly concealable.
-
1 基于迁移的SAR-ATR黑盒攻击算法
1. SAR-ATR Transfer-based Black-box Attack Algorithm (TBAA)
输入:干净样本x,K个深度神经网络模型${f_1},{f_2},\cdots,{f_K}$,对应
的网络模型逻辑值${l_1},{l_2},\cdots,{l_K}$以及相应的网络模型集成权重
${w_1},{w_2},\cdots,{w_K}$,扰动量大小$\varepsilon $,步长$\alpha $,迭代次数T,系数$v,\beta $,
${\beta _1}$和${\beta _2}$输出:对抗样本${x^{{\text{adv}}}}$ 步骤1 $\alpha \leftarrow \varepsilon /T,{g_0} \leftarrow 0,{m_0} \leftarrow 0,{n_0} \leftarrow 0$ 步骤2 ${g_0} \leftarrow 0,{m_0} \leftarrow 0,{s_0} \leftarrow 0,x_0^{{\text{adv}}} \leftarrow x$ 步骤3 For $t = 0$ to $T - 1$ do 步骤4 Update ${m_t}$ by ${m_t} = {\beta _1} \cdot {m_{t - 1}} + (1 - {\beta _1}){g_t}$ 步骤5 Update ${\hat m_t} = \dfrac{{{m_t}}}{{1 - \beta _1^t}}$ 步骤6 Update ${s_t} = {\beta _2} \cdot {s_{t - 1}} + (1 - {\beta _2}){({\hat g_t} - {m_t})^2}$ 步骤7 Update ${\hat s_t} = \dfrac{{{s_t} + \zeta }}{{1 - \beta _2^t}}$ 步骤8 $ \tilde x_t^{{\text{adv}}} = x_t^{{\text{adv}}} + \dfrac{\alpha }{{\sqrt {{{\hat s}_t} + \zeta } }}{\hat m_t} $ 步骤9 $l(\tilde x_t^{{\text{adv}}}) = \sum\limits_{k = 1}^K {{w_k}{l_k}\left( {{\text{ST}}(\tilde x_t^{{\text{adv}}};p)} \right)} $ 步骤10 Update $g_t^*$ by $ g_t^* = {\nabla _{x_t^{{\text{adv}}}}}J\left( {{\text{ST}}(\tilde x_t^{{\text{adv}}};p),y} \right) $ 步骤11 Update ${g_{t + 1}}$ by ${g_{t + 1}} = \beta {g_t} + (1 - \beta ) \cdot \dfrac{{g_t^*}}{{{{\left\| {g_t^*} \right\|}_1}}}$ 步骤12 Update ${\tilde g_{t + 1}}$ by ${\tilde g_{t + 1}} = (1 - v){g_{t + 1}} + v \cdot \dfrac{{g_t^*}}{{{{\left\| {g_t^*} \right\|}_1}}}$ 步骤13 $x_{t + 1}^{{\text{adv}}} = {\mathrm{Clip}}_x^\varepsilon \left\{ {x_t^{{\text{adv}}} + \alpha \cdot {\mathrm{sign}}({{\tilde g}_{t + 1}})} \right\}$ 步骤14 End for 步骤15 Return $x_t^{{\text{adv}}} = x_{t + 1}^{{\text{adv}}}$ 表 1 MSTAR数据中SOC下的SAR图像类别与样本数量
Table 1. SAR image categories and number of samples under SOC in MSTAR dataset
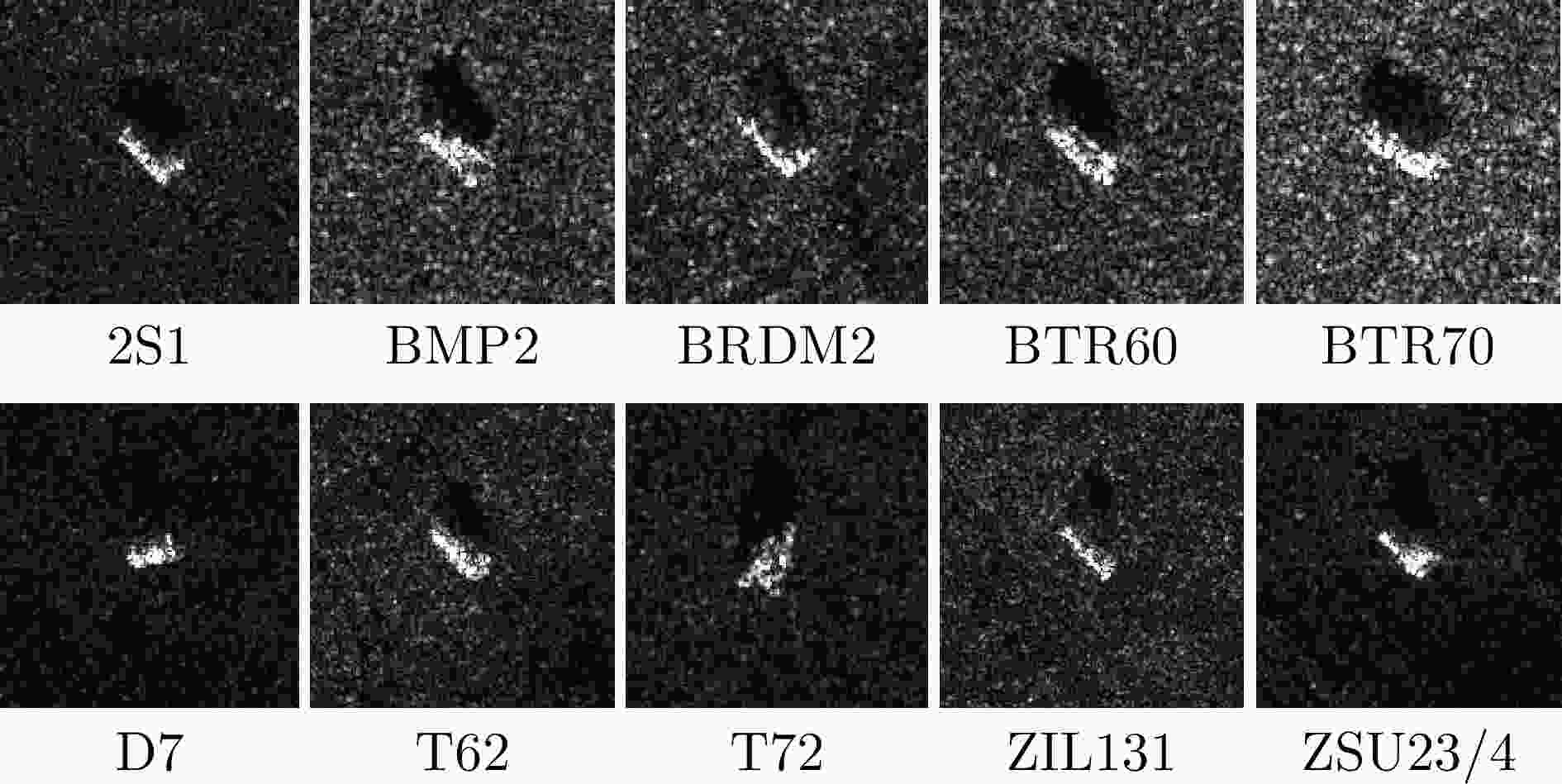
目标类别 训练集 测试集 俯仰角(°) 数量 俯仰角(°) 数量 2S1 17 299 15 274 BRDM2 17 298 15 274 BTR60 17 233 15 195 D7 17 299 15 274 T62 17 299 15 273 ZIL131 17 299 15 274 BMP2 17 233 15 195 ZSU23/4 17 299 15 274 T72 17 232 15 196 BTR70 17 233 15 196 表 2 FUSAR-Ship数据集中SAR图像类别与样本数量
Table 2. SAR image categories and number of samples in FUSAR-Ship dataset
目标类别 训练集数量 测试集数量 BulkCarrier 97 25 CargoShip 126 32 Fishing 75 19 Tanker 36 10 表 3 模型识别精度
Table 3. Model recognition accuracy
模型 MSTAR ACC (%) FUSAR-Ship ACC (%) AlexNet 95.1 69.47 VGG16 95.6 70.23 ResNet18 96.6 68.10 ResNet50 97.7 — InceptionV3 99.1 — A-ConvNet 99.8 — MobileNet 97.8 — SqueezeNet 95.4 72.25 PVTv2 98.8 — MobileViTv2 99.4 72.70 表 4 MSTAR数据集单模型攻击成功率(%)
Table 4. Single model attack success rate on the MSTAR dataset (%)
代理模型 攻击算法 受害者模型 AlexNet VGGNet16 ResNet18 ResNet50 InceptionV3 A-ConvNet MobileNet SqueezeNet PVTv2 MobileViTv2 AlexNet MI-FGSM 100* 10.9 12.0 9.0 5.0 28.0 35.0 18.9 14.0 19.6 NAM 100* 12.0 13.0 10.0 6.9 36.0 37.0 22.9 20.7 22.0 VMI-FGSM 100* 19.5 19.5 17.0 6.0 29.5 39.5 27.0 40.5 21.5 DI-FGSM 100* 21.0 26.5 16.0 7.5 29.5 43.5 32.5 32.0 20.5 Attack-Unet-GAN 98.69* 7.0 8.0 7.5 4.0 20.5 32.5 14.5 12.5 9.5 Fast C&W 100* 4.5 7.0 6.0 3.0 17.5 19.5 12.5 8.0 3.5 TBAA 100* 23.5 29.0 20.4 14.5 64.0 53.4 33.9 56.0 32.8 VGGNet16 MI-FGSM 61.0 100* 58.0 56.0 40.0 55.0 41.0 43.0 26.0 30.0 NAM 60.0 100* 61.0 59.0 42.0 61.0 45.0 47.0 31.0 35.0 VMI-FGSM 62.5 100* 59.5 58.5 42.5 57.5 41.0 46.5 38.5 38.5 DI-FGSM 63.5 100* 60.5 67.5 46.5 59.5 42.5 48.0 37.5 38.5 Attack-Unet-GAN 53.0 100* 40.5 32.5 24.5 32.5 38.5 39.0 23.0 24.5 Fast C&W 44.5 100* 31.0 37.5 24.0 31.5 22.0 24.5 13.5 14.5 TBAA 69.5 100* 72.0 78.5 56.9 74.0 56.5 63.5 48.0 48.5 ResNet18 MI-FGSM 13.0 9.9 100* 20.9 13.9 39.0 26.0 15.0 14.0 5.0 NAM 15.0 9.0 100* 20.9 16.0 38.0 31.0 17.0 21.0 5.3 VMI-FGSM 17.0 16.5 100* 25.0 15.8 45.5 31.5 25.0 32.5 10.5 DI-FGSM 18.0 14.0 100* 21.0 19.0 41.0 29.5 30.0 23.5 8.6 Attack-Unet-GAN 12.5 6.5 100* 11.5 5.0 19.5 18.5 11.5 11.0 3.0 Fast C&W 10.0 4.0 100* 6.0 3.0 9.0 11.5 12.0 13.5 4.0 TBAA 29.0 19.0 100* 25.0 35.5 64.0 42.5 30.0 54.0 24.0 ResNet50 MI-FGSM 8.0 12.0 10.5 100* 21.0 16.0 22.9 10.0 12.0 9.0 NAM 10.0 14.0 14.0 100* 22.0 27.0 24.0 13.0 17.0 14.9 VMI-FGSM 19.5 19.0 14.5 100* 22.0 33.0 33.5 21.0 28.5 13.5 DI-FGSM 19.5 19.0 22.5 100* 23.5 26.5 23.0 22.5 28.0 11.5 Attack-Unet-GAN 6.5 10.5 6.5 100* 7.0 15.0 18.0 8.0 8.0 7.0 Fast C&W 5.0 4.5 7.5 100* 13.0 7.5 10.5 7.5 10.5 6.0 TBAA 24.5 19.9 27.5 100* 27.4 48.5 44.9 25.5 43.9 22.0 InceptionV3 MI-FGSM 29.0 31.4 65.5 38.0 100* 65.0 31.0 39.0 12.0 28.0 NAM 36.0 35.0 67.9 42.0 100* 66.9 33.9 41.9 18.0 29.5 VMI-FGSM 33.0 31.5 52.5 39.0 100* 68.5 34.0 43.0 30.0 29.5 DI-FGSM 34.0 34.5 56.0 41.0 100* 66.0 33.5 41.5 23.5 28.5 Attack-Unet-GAN 20.6 24.5 53.0 31.0 100* 32.5 25.0 26.5 9.0 24.5 Fast C&W 11.0 16.5 30.0 28.0 100* 20.0 12.0 15.0 10.5 16.5 TBAA 41.0 50.0 73.5 52.0 100* 76.5 49.5 47.0 45.9 43.9 A-ConvNet MI-FGSM 19.9 15.5 29.5 20.9 11.5 100* 29.0 15.0 21.9 9.0 NAM 23.5 17.5 35.5 24.5 18.9 100* 32.5 18.0 24.0 13.0 VMI-FGSM 25.5 19.0 37.0 25.5 19.5 100* 36.5 31.0 31.0 12.5 DI-FGSM 28.0 17.5 37.0 23.0 21.5 100* 36.5 29.5 26.5 10.5 Attack-Unet-GAN 10.8 5.6 9.0 13.0 7.0 98.0* 11.6 11.0 14.7 8.0 Fast C&W 11.5 4.0 8.5 5.0 3.0 97.5* 10.5 12.5 13.5 4.0 TBAA 29.5 21.9 40.5 30.5 24.5 100* 38.0 32.9 36.0 24.0 MobileNet MI-FGSM 16.0 15.1 10.0 15.0 15.6 18.0 100* 18.9 8.0 9.0 NAM 18.0 14.9 12.0 18.9 18.9 25.0 100* 26.9 9.5 10.5 VMI-FGSM 21.0 18.0 12.0 18.0 21.5 23.0 100* 23.5 22.0 14.0 DI-FGSM 19.0 17.5 10.5 17.5 18.0 19.5 100* 20.5 22.0 14.5 Attack-Unet-GAN 9.0 3.5 7.5 7.8 2.5 12.5 100* 11.0 7.3 5.0 Fast C&W 10.0 4.0 6.0 5.0 3.0 7.0 100* 10.0 6.5 4.0 TBAA 24.0 20.5 18.9 26.0 25.4 32.9 100* 30.0 24.0 25.0 SqueezeNet MI-FGSM 19.5 9.5 20.5 18.0 6.0 40.5 31.4 100* 18.0 18.0 NAM 18.5 10.3 20.9 19.5 6.5 40.5 32.9 100* 24.0 21.0 VMI-FGSM 26.5 15.5 28.5 25.5 11.0 42.5 32.0 100* 28.5 19.5 DI-FGSM 21.0 11.5 30.5 22.5 12.0 41.0 31.5 100* 23.0 21.5 Attack-Unet-GAN 13.0 8.0 16.5 17.0 4.5 17.5 17.0 100* 12.5 14.5 Fast C&W 10.0 4.5 7.0 5.5 3.0 18.0 10.0 100* 13.5 14.0 TBAA 28.0 18.5 32.5 31.0 12.5 53.5 38.5 100* 41.9 39.0 PVTv2 MI-FGSM 10.0 7.3 9.0 12.0 15.5 6.0 18.0 7.8 100* 11.3 NAM 13.0 3.5 10.7 13.5 21.5 10.4 19.9 9.0 100* 18.5 VMI-FGSM 12.0 12.0 9.5 20.0 22.5 16.0 23.0 11.0 100* 19.5 DI-FGSM 11.0 13.5 11.0 15.0 23.5 12.0 23.5 12.6 100* 13.0 Attack-Unet-GAN 8.5 5.0 7.5 7.9 12.5 3.5 11.6 4.5 100* 9.0 Fast C&W 10.0 4.0 6.5 4.5 13.0 5.5 9.0 3.7 100* 4.0 TBAA 26.0 23.0 22.0 27.0 35.0 28.9 37.0 25.0 100* 32.0 MobileViTv2 MI-FGSM 14.0 16.0 19.0 18.3 7.9 43.8 30.0 18.0 52.0 100* NAM 21.4 24.0 26.2 20.7 11.6 47.8 33.9 25.4 58.0 100* VMI-FGSM 21.0 25.0 29.0 21.5 11.5 45.0 35.0 27.0 56.0 99.5* DI-FGSM 22.5 23.1 29.0 24.0 10.5 46.3 38.0 27.5 58.5 98.0* Attack-Unet-GAN 11.0 6.5 14.0 11.5 5.5 29.0 15.5 15.0 46.0 100* Fast C&W 11.0 4.0 8.5 5.5 3.0 17.5 10.5 11.5 45.0 99.5* TBAA 40.0 31.9 33.9 35.9 20.3 66.0 48.0 45.9 65.9 100* 注:标红字体为最优值,标蓝字体为次优值。*表示白盒攻击成功率,其余数值表示黑盒攻击成功率。 表 5 FUSAR-Ship数据集单模型攻击成功率(%)
Table 5. Single model attack success rate on the FUSAR-Ship dataset (%)
代理模型 攻击算法 受害者模型 AlexNet VGGNet16 ResNet18 SqueezeNet MobileViTv2 AlexNet MI-FGSM 100* 38.00 40.00 33.90 68.00 NAM 100* 48.00 62.00 45.90 76.00 VMI-FGSM 100* 47.10 63.60 42.60 70.00 DI-FGSM 98.41* 47.40 63.56 44.93 74.94 Attack-Unet-GAN 100* 23.80 33.20 15.60 30.00 Fast C&W 99.96* 18.70 29.10 12.40 24.00 TBAA 100* 60.00 84.00 56.00 80.00 VGGNet16 MI-FGSM 28.00 100* 24.00 40.00 46.00 NAM 33.90 100* 30.00 38.00 50.00 VMI-FGSM 33.90 98.62* 28.10 42.80 52.40 DI-FGSM 37.60 98.76* 36.60 42.40 52.60 Attack-Unet-GAN 13.50 100* 20.40 24.00 26.00 Fast C&W 9.30 99.96* 19.60 22.90 24.00 TBAA 43.90 100* 48.00 62.00 56.00 ResNet18 MI-FGSM 6.00 7.90 100* 15.90 40.00 NAM 7.90 9.90 100* 21.90 50.00 VMI-FGSM 9.30 10.60 100* 28.60 53.80 DI-FGSM 13.50 12.80 99.96* 29.91 54.60 Attack-Unet-GAN 4.50 5.60 100* 10.40 17.80 Fast C&W 5.30 6.20 99.98* 6.70 12.90 TBAA 38.00 18.00 100* 50.00 60.00 SqueezeNet MI-FGSM 16.00 9.90 28.00 100* 45.90 NAM 21.90 14.00 43.90 100* 56.00 VMI-FGSM 25.10 19.30 44.20 99.86* 53.30 DI-FGSM 25.07 16.32 45.39 99.59* 59.40 Attack-Unet-GAN 14.50 7.90 22.00 100* 28.00 Fast C&W 10.10 6.30 20.10 98.69* 26.90 TBAA 39.90 31.90 65.90 100* 64.00 MobileViTv2 MI-FGSM 4.00 7.90 42.00 21.90 100* NAM 9.00 16.00 48.00 26.00 100* VMI-FGSM 12.80 23.50 45.90 24.10 100* DI-FGSM 13.20 18.60 47.00 26.40 99.52* Attack-Unet-GAN 2.90 5.30 25.60 18.00 100* Fast C&W 2.60 4.20 21.60 14.60 100* TBAA 24.00 16.00 67.90 43.90 100* 注:标红字体为最优值,标蓝字体为次优值。*表示白盒攻击成功率,其余数值表示黑盒攻击成功率。 表 6 集成模型攻击成功率(%)
Table 6. Ensemble model attack success rate (%)
数据集 攻击算法 AlexNet VGGNet16 ResNet18 ResNet50 InceptionV3 A-ConvNet MobileNet SqueezeNet PVTv2 MobileViTv2 MSTAR MI-FGSM 62.9 39.0 52.0 65.0 42.0 67.9 50.0 51.5 68.0 46.0 NAM 63.1 41.5 68.2 70.5 45.0 75.7 53.2 54.0 75.6 51.4 VMI-FGSM 66.4 43.5 72.5 65.8 46.5 74.6 52.0 53.0 76.3 56.0 DI-FGSM 69.0 44.3 74.0 70.0 50.3 76.0 55.0 55.8 70.0 51.0 Attack-Unet-GAN 53.6 30.5 47.0 35.0 30.0 35.0 41.0 43.0 52.3 31.0 Fast C&W 46.0 26.8 35.0 38.0 28.0 33.0 28.5 30.0 51.0 24.0 TBAA 72.0 62.0 86.0 88.0 70.0 88.0 70.0 66.0 92.0 78.0 FUSAR-
ShipMI-FGSM 31.9 40.9 48.0 — — — — 45.9 — 71.9 NAM 34.5 50.5 68.5 — — — — 48.5 — 78.0 VMI-FGSM 35.8 53.2 67.0 — — — — 51.3 — 76.5 DI-FGSM 36.0 56.0 68.0 — — — — 50.0 — 78.0 Attack-Unet-GAN 16.0 25.0 38.0 — — — — 28.5 — 38.4 Fast C&W 12.5 22.5 34.2 — — — — 26.0 — 32.0 TBAA 70.0 62.0 86.0 — — — — 64.0 — 88.0 注:标红数字为最优值,标蓝数字为次优值。 表 7 消融实验方法设置
Table 7. Ablation experiment method setup
攻击算法 QHM ABN ST MI-FGSM — — — AN-QHMI-FGSM √ — — ABN-QHMI-FGSM √ √ — TBAA √ √ √ 表 8 消融实验攻击成功率(%)
Table 8. Ablation experiment attack success rate (%)
数据集 攻击算法 AlexNet VGGNet16 ResNet18 ResNet50 InceptionV3 A-ConvNet MobileNet SqueezeNet PVTv2 MobileViTv2 MSTAR MI-FGSM 62.9 39.0 52.0 65.0 42.0 67.9 50.0 51.5 68.0 46 AN-QHMI-FGSM 65.7 48.0 75.0 78.0 56.0 82.0 56.0 57.2 82.0 58.0 ABN-QHMI-FGSM 69.3 51.6 82.0 81.0 63.0 85.2 68.3 60.8 88.3 69.5 TBAA 72.0 62.0 86.0 88.0 70.0 88.0 70.0 66.0 92.0 78.0 FUSAR-
ShipMI-FGSM 31.9 40.9 38.0 — — — — 45.9 — 71.9 AN-QHMI-FGSM 36.9 52.0 76.0 — — — — 50.0 — 81.6 ABN-QHMI-FGSM 43.9 59.9 81.5 — — — — 52.0 — 85.0 TBAA 70.0 62.0 86.0 — — — — 64.0 — 88.0 注:标红数字为最优值,标蓝数字为次优值。 表 9 MSTAR数据集在集成模型攻击下原始SAR图像和SAR对抗样本的平均结构相似度
Table 9. ASS of original SAR images and SAR adversarial examples under ensemble model attack on MSTAR dataset
攻击算法 AlexNet VGGNet16 ResNet18 ResNet50 InceptionV3 A-ConvNet MobileNet SqueezeNet PVTv2 MobileViTv2 Mean MI-FGSM 0.951 0.959 0.968 0.976 0.970 0.962 0.969 0.960 0.963 0.960 0.9638 NAM 0.962 0.965 0.971 0.978 0.973 0.967 0.973 0.966 0.968 0.962 0.9685 VMI-FGSM 0.965 0.961 0.972 0.976 0.975 0.969 0.977 0.967 0.969 0.965 0.9696 DI-FGSM 0.960 0.970 0.974 0.974 0.976 0.971 0.979 0.974 0.970 0.963 0.9711 Attack-Unet-
GAN0.968 0.975 0.975 0.978 0.978 0.974 0.982 0.975 0.972 0.968 0.9745 Fast C&W 0.969 0.974 0.976 0.979 0.979 0.974 0.980 0.975 0.971 0.967 0.9744 TBAA 0.969 0.975 0.979 0.981 0.978 0.975 0.981 0.973 0.972 0.967 0.9750 注:标红数字为最优值,标蓝数字为次优值。 表 10 对抗样本生成效率(s)
Table 10. Adversarial examples generation efficiency (s)
攻击方法 VGGNet16 ResNet18 ResNet50 InceptionV3 A-ConvNet MobileNet Squeezenet Ensemble MI-FGSM 0.2970 0.2404 0.3621 0.5217 0.1797 0.3258 0.2550 1.8953 NAM 0.3014 0.2410 0.3623 0.5303 0.1822 0.3248 0.2257 1.8973 VMI-FGSM 0.2980 0.2498 0.3625 0.5289 0.1826 0.3289 0.2274 1.9766 DI-FGSM 0.2984 0.2485 0.3623 0.5280 0.1823 0.3283 0.2294 1.9795 Attack-Unet-GAN 0.0052 0.0052 0.0052 0.0052 0.0052 0.0052 0.0052 0.0052 Fast C&W 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 TBAA 0.3588 0.3046 0.4159 0.5676 0.2456 0.3876 0.2824 2.1357 注:标红数字为最大值,标蓝数字为最小值。 -
[1] XU Yan and SCOOT K A. Sea ice and open water classification of SAR imagery using CNN-based transfer learning[C]. 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 2017: 3262–3265. doi: 10.1109/IGARSS.2017.8127693. [2] ZHANG Yue, SUN Xian, SUN Hao, et al. High resolution SAR image classification with deeper convolutional neural network[C]. International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018: 2374–2377. doi: 10.1109/IGARSS.2018.8518829. [3] SHAO Jiaqi, QU Changwen, and LI Jianwei. A performance analysis of convolutional neural network models in SAR target recognition[C]. 2017 SAR in Big Data Era: Models, Methods and Applications, Beijing, China, 2017: 1–6. doi: 10.1109/BIGSARDATA.2017.8124917. [4] ZHANG Ming, AN Jubai, YU Dahua, et al. Convolutional neural network with attention mechanism for SAR automatic target recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4004205. doi: 10.1109/LGRS.2020.3031593. [5] CHEN Sizhe, WANG Haipeng, XU Feng, et al. Target classification using the deep convolutional networks for SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4806–4817. doi: 10.1109/TGRS.2016.2551720. [6] 徐丰, 王海鹏, 金亚秋. 深度学习在SAR目标识别与地物分类中的应用[J]. 雷达学报, 2017, 6(2): 136–148. doi: 10.12000/JR16130.XU Feng, WANG Haipeng, and JIN Yaqiu. Deep learning as applied in SAR target recognition and terrain classification[J]. Journal of Radars, 2017, 6(2): 136–148. doi: 10.12000/JR16130. [7] 吕艺璇, 王智睿, 王佩瑾, 等. 基于散射信息和元学习的SAR图像飞机目标识别[J]. 雷达学报, 2022, 11(4): 652–665. doi: 10.12000/JR22044.LYU Yixuan, WANG Zhirui, WANG Peijin, et al. Scattering information and meta-learning based SAR images interpretation for aircraft target recognition[J]. Journal of Radars, 2022, 11(4): 652–665. doi: 10.12000/JR22044. [8] HUANG Teng, ZHANG Qixiang, LIU Jiabao, et al. Adversarial attacks on deep-learning-based SAR image target recognition[J]. Journal of Network and Computer Applications, 2020, 162: 102632. doi: 10.1016/j.jnca.2020.102632. [9] 孙浩, 陈进, 雷琳, 等. 深度卷积神经网络图像识别模型对抗鲁棒性技术综述[J]. 雷达学报, 2021, 10(4): 571–594. doi: 10.12000/JR21048.SUN Hao, CHEN Jin, LEI Lin, et al. Adversarial robustness of deep convolutional neural network-based image recognition models: A review[J]. Journal of Radars, 2021, 10(4): 571–594. doi: 10.12000/JR21048. [10] 高勋章, 张志伟, 刘梅, 等. 雷达像智能识别对抗研究进展[J]. 雷达学报, 2023, 12(4): 696–712. doi: 10.12000/JR23098.GAO Xunzhang, ZHANG Zhiwei, LIU Mei, et al. Intelligent radar image recognition countermeasures: A review[J]. Journal of Radars, 2023, 12(4): 696–712. doi: 10.12000/JR23098. [11] SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]. The 2nd International Conference on Learning Representations, Banff, Canada, 2014. [12] GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. The 3rd International Conference on Learning Representations, San Diego, CA, USA, 2015: 1050. [13] KURAKIN A, GOODFELLOW L J, and BENGIO S. Adversarial examples in the physical world[C]. The 5th International Conference on Learning Representations, Toulon, France, 2017: 99–112. [14] PAPERNOT N, MCDANIEL P, JHA S, et al. The limitations of deep learning in adversarial settings[C]. 2016 IEEE European Symposium on Security and Privacy, Saarbruecken, Germany, 2016: 372–387. doi: 10.1109/EuroSP.2016.36. [15] BRENDEL W, RAUBER J, and BETHGE M. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [16] CARLINI N and WAGNER D. Towards evaluating the robustness of neural networks[C]. 2017 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 2017: 39–57. doi: 10.1109/SP.2017.49. [17] SU Jiawei, VARGAS D V, and SAKURAI K. One pixel attack for fooling deep neural networks[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(5): 828–841. doi: 10.1109/TEVC.2019.2890858. [18] CHEN Pinyu, ZHANG Huan, SHARMA Y, et al. ZOO: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models[C]. The 10th ACM Workshop on Artificial Intelligence and Security, Dallas, USA, 2017: 15–26. doi: 10.1145/3128572.3140448. [19] CHEN Jianbo, JORDAN M I, and WAINWRIGHT M J. HopSkipJumpAttack: A query-efficient decision-based attack[C]. 2020 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 2020: 1277–1294. doi: 10.1109/SP40000.2020.00045. [20] DONG Yinpeng, LIAO Fengzhou, PANG Tianyu, et al. Boosting adversarial attacks with momentum[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 2018: 9185–9193. doi: 10.1109/CVPR.2018.00957. [21] ZHAO Haojun, LIN Yun, GAO Song, et al. Evaluating and improving adversarial attacks on DNN-based modulation recognition[C]. GLOBECOM 2020–2020 IEEE Global Communications Conference, Taipei, China, 2020: 1–5. doi: 10.1109/GLOBECOM42002.2020.9322088. [22] WANG Xiaosen and HE Kun. Enhancing the transferability of adversarial attacks through variance tuning[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 2021: 1924–1933. doi: 10.1109/CVPR46437.2021.00196. [23] XIE Cihang, ZHANG Zhishuai, ZHOU Yuyin, et al. Improving transferability of adversarial examples with input diversity[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 2019: 2725–2734. doi: 10.1109/CVPR.2019.00284. [24] CZAJA W, FENDLEY N, PEKALA M J, et al. Adversarial examples in remote sensing[C]. The 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, USA, 2018: 408–411. doi: 10.1145/3274895.3274904. [25] CHEN Li, XU Zewei, LI Qi, et al. An empirical study of adversarial examples on remote sensing image scene classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7419–7433. doi: 10.1109/TGRS.2021.3051641. [26] DU Chuan, HUO Chaoying, ZHANG Lei, et al. Fast C&W: A fast adversarial attack algorithm to fool SAR target recognition with deep convolutional neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4010005. doi: 10.1109/LGRS.2021.3058011. [27] DU Chuan and ZHANG Lei. Adversarial attack for SAR target recognition based on UNet-generative adversarial network[J]. Remote Sensing, 2021, 13(21): 4358. doi: 10.3390/rs13214358. [28] ZHOU Junfan, SUN Hao, and KUANG Gangyao. Template-based universal adversarial perturbation for SAR target classification[C]. The 8th China High Resolution Earth Observation Conference, Singapore, Singapore, 2023: 351–360. doi: 10.1007/978-981-19-8202-6_32. [29] XIA Weijie, LIU Zhe, and LI Yi. SAR-PeGA: A generation method of adversarial examples for SAR image target recognition network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(2): 1910–1920. doi: 10.1109/TAES.2022.3206261. [30] PENG Bowen, PENG Bo, ZHOU Jie, et al. Scattering model guided adversarial examples for SAR target recognition: Attack and defense[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5236217. doi: 10.1109/TGRS.2022.3213305. [31] HANSEN L K and SALAMON P. Neural network ensembles[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(10): 993–1001. doi: 10.1109/34.58871. [32] DING Jun, CHEN Bo, LIU Hongwei, et al. Convolutional neural network with data augmentation for SAR target recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 364–368. doi: 10.1109/LGRS.2015.2513754. [33] LEE J S. Digital image enhancement and noise filtering by use of local statistics[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980, PAMI-2(2): 165–168. doi: 10.1109/TPAMI.1980.4766994. [34] ZHUANG Juntang, TANG T, DING Yifan, et al. AdaBelief optimizer: Adapting stepsizes by the belief in observed gradients[C]. The 34th International Conference on Neural Information Processing Systems, 2020: 795–806. [35] NESTEROV Y. A method for unconstrained convex minimization problem with the rate of convergence[J]. Mathematics, 1983, 269: 543–547. [36] MA J and YARATS D. Quasi-hyperbolic momentum and Adam for deep learning[C]. The 7th International Conference on Learning Representations, New Orleans, LA, USA, 2019: 1–38. [37] KEYDEL E R, LEE S W, and MOORE J T. MSTAR extended operating conditions: A tutorial[C]. SPIE 2757, Algorithms for Synthetic Aperture Radar Imagery III, Orlando, USA, 1996: 228–242. doi: 10.1117/12.242059. [38] HOU Xiyue, AO Wei, SONG Qian, et al. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition[J]. Science China Information Sciences, 2020, 63(4): 140303. doi: 10.1007/s11432-019-2772-5. [39] KRIZHEVSKY A, SUTSKEVER I, and HINTON G E. ImageNet classification with deep convolutional neural networks[C]. The 25th International Conference on Neural Information Processing Systems, Lake Tahoe, USA, 2012: 1106–1114. [40] SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. The 3rd International Conference on Learning Representations, San Diego, CA, USA, 2015. [41] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [42] SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 2818–2826. doi: 10.1109/CVPR.2016.308. [43] HOWARD A G, ZHU Menglong, CHEN Bo, et al. MobileNets: Efficient convolutional neural networks for mobile vision applications[EB/OL]. https://arxiv.org/abs/1704.04861, 2017. [44] IANDOLA F N, HAN Song, MOSKEWICZ M W, et al. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size[EB/OL]. https://arxiv.org/abs/1602.07360, 2016. [45] WANG Wenhai, XIE Enze, LI Xiang, et al. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 2021: 548–558. doi: 10.1109/ICCV48922.2021.00061. [46] MEHTA S and RASTEGARI M. MobileViT: Light-weight, general-purpose, and mobile-friendly vision transformer[C]. The Tenth International Conference on Learning Representations, 2022. [47] KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. The 3rd International Conference on Learning Representations, San Diego, CA, USA, 2015: 1–15. [48] WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: