基于数据失真的雷达通信一体化OFDM波形设计方法

刘燕; 万显荣; 易建新

doi:10.12000/JR23205

基于数据失真的雷达通信一体化OFDM波形设计方法

DOI: 10.12000/JR23205

武汉大学电子信息学院武汉 430072

基金项目: 国家自然科学基金(61931015, 62071335, 62250024)，湖北省自然科学基金创新群体项目(2021CFA002)，中央高校自主科研项目(2042022dx0001)

详细信息

作者简介:
刘　燕，博士生，主要研究方向为新体制雷达信号处理、雷达通信一体化信号设计等

万显荣，博士，教授，博士生导师，主要研究方向为新体制雷达设计，如外辐射源雷达、高频超视距雷达系统及信号处理

易建新，博士，副研究员，主要研究方向为外辐射源雷达信号处理、目标跟踪和信息融合

通讯作者:
万显荣 xrwan@whu.edu.cn

责任主编：刘凡 Corresponding Editor: LIU Fan
中图分类号: TN958
计量
- 文章访问数: 971
- HTML全文浏览量: 342
- PDF下载量: 151
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-20
- 修回日期: 2023-12-28
- 网络出版日期: 2024-01-09
- 刊出日期: 2024-02-28

OFDM Waveform Design for Joint Radar-communication Based on Data Distortion

School of Electronic Information, Wuhan University, Wuhan 430072, China

Funds: The National Natural Science Foundation of China (61931015, 62071335, 62250024), The Innovation Group Project of Natural Science Foundation of Hubei Province (2021CFA002), The Fundamental Research Funds for the Central Universities of China (2042022dx0001)

More Information

Corresponding author: WAN Xianrong, xrwan@whu.edu.cn

摘要

摘要: 正交频分复用(OFDM)波形设计是实现雷达通信一体化的物理层关键技术之一。OFDM波形通常存在峰均功率比(PAPR)高，以及波形自相关旁瓣电平高的问题。该文针对现有联合降低PAPR和自相关旁瓣方法存在的通信速率下降问题，提出了一种基于数据失真的一体化波形设计方法。该文还将通信数据的误差矢量幅度作为优化目标之一，降低了数据失真引起的通信误码率。首先，构建了PAPR约束下最小化积分旁瓣比和误差矢量幅度的优化模型。其次，根据调制星座图特点，通过外围星座调制的数据失真和所有调制数据失真，将多目标高维非凸优化问题转化为两个单目标优化子问题，分别采取凸松弛操作和交替方向乘子法(ADMM)求解简化后的子问题，得到低积分旁瓣比波形和PAPR约束下的低误差矢量幅度波形。仿真结果表明该方法设计的一体化波形可满足PAPR要求，同时具有良好的感知和通信性能。
- 波形设计 /
- 雷达通信一体化 /
- 正交频分复用(OFDM) /
- 峰均功率比(PAPR) /
- 旁瓣 /
- 误差矢量幅度
Abstract: Orthogonal Frequency Division Multiplexing (OFDM) waveform design is one of the key physical layer technologies for achieving joint radar-communication. OFDM waveforms usually have issues with high Peak to Average Power Ratio (PAPR) and high waveform autocorrelation sidelobe levels. This paper proposes an integrated waveform design method based on data distortion to address the communication rate degradation problem of existing joint PAPR and autocorrelation sidelobe reduction methods. The paper also takes the Error Vector Magnitude (EVM) of communication data as one of the optimization objectives, reducing the communication bit error rate caused by data distortion. Firstly, an optimization model was constructed to minimize the Integrated Sidelobe Level Ratio (ISLR) and EVM under PAPR constraints. Secondly, based on the characteristics of the modulation constellation, the multi-objective high-dimensional non-convex optimization problem is transformed into two single objective optimization subproblems by using the data distortion of outer constellation modulation and all modulation data distortion. Convex relaxation operation and Alternating Direction Method of Multipliers (ADMM) are respectively used to solve the simplified subproblems, resulting in low ISLR waveform and low EVM waveform under PAPR constraint. The simulation results show that the integrated waveform designed by the proposed method can meet the requirements of PAPR, and has good sensing and communication performance.
- Waveform design /
- Joint radar-communication /
- Orthogonal Frequency Division Multiplexing (OFDM) /
- Peak to Average Power Ratio (PAPR) /
- Sidelobe /
- Error Vector Magnitude (EVM)

HTML全文

图 1 雷达通信一体化系统模型

Figure 1. The joint radar-communication system model

下载: 全尺寸图片幻灯片

图 2 雷达通信一体化信号结构

Figure 2. The signal structure for joint radar-communication system

下载: 全尺寸图片幻灯片

图 3 外围星座调制数据可扩展区域(16QAM)

Figure 3. Extended region of outer constellation modulation data (16QAM)

下载: 全尺寸图片幻灯片

图 4 数据失真引入的噪声频域分布

Figure 4. The frequency domain distribution of noise induced by data distortion

下载: 全尺寸图片幻灯片

图 5 不同方法的PAPR性能对比

Figure 5. The comparison of PAPR performance between different methods

下载: 全尺寸图片幻灯片

图 6 本文方法的收敛性能

Figure 6. The convergence performance of the proposed method

下载: 全尺寸图片幻灯片

图 7 不同方法的归一化周期自相关幅度对比

Figure 7. The comparison of normalized periodic autocorrelation amplitudes using different methods

下载: 全尺寸图片幻灯片

图 8 ISLR均值与迭代次数的关系

Figure 8. The relationship between the average ISLR and iteration times

下载: 全尺寸图片幻灯片

图 9 功率放大器输入输出特性

Figure 9. Input and output characteristics of power amplifiers

下载: 全尺寸图片幻灯片

图 10 不同方法的目标检测概率

Figure 10. Target detection probability of different methods

下载: 全尺寸图片幻灯片

图 11 不同方法的BER性能对比

Figure 11. The comparison of BER performance between different methods

下载: 全尺寸图片幻灯片

图 12 不同方法的频域波形

Figure 12. Frequency domain waveforms of different methods

下载: 全尺寸图片幻灯片

1 基于数据失真的一体化OFDM波形设计次优算法

1. A suboptimal algorithm for integrated OFDM waveform design based on data distortion

1. 输入：X, $ {{\boldsymbol{S}}_{\text{D}}} $, $ {{\boldsymbol{S}}_{{\text{Out}}}} $, $ {N_{{\text{int}}}} $, $ {K_{{\text{Out}}}} $, $ {K_{\text{D}}} $, $ {\alpha _1} $, $ {\alpha _2} $, $ \beta $, $ \rho $
2. 初始化：$ {{\boldsymbol{U}}^0} = {{\bf{0}}^{N \times 1}} $, $ {{\boldsymbol{V}}^0} = {{\bf{0}}^{LN \times 1}} $
优化变量$ {{\boldsymbol{C}}_{{\text{Out}}}} $：
3. 计算$ {\left\| {\left( {{\boldsymbol{X}} + {{\boldsymbol{C}}_{{\mathrm{Out}}}}} \right)} \right\|^{{\text{2,sub}}}} $，通过$ \left\\| {{{\boldsymbol{F}}^{\text{H}}}{\boldsymbol{X}}} \right\\|_2^2 $近似$ r\left( 0 \right) $，解问题(13)；
4. 计算${\boldsymbol{\hat x}}_{{\text{Out}}}^{{\text{sub}}}$，通过式(14)在集合$\varOmega $中搜索；
优化变量$ {{\boldsymbol{C}}_{\text{D}}} $：
5. for $ {k_{\text{D}}} = 0,1,\cdots,{K_{\text{D}}} - 1 $
6. 　更新$ {\boldsymbol{C}}_{\rm D}^{{k_{\rm D}} + 1} $，通过式(23)和式(24)解式(21)；
7. 　更新$ {\boldsymbol{\bar x}}_L^{{k_{\rm D}} + 1} $，通过式(31)和式(32)解式(25)；
8. 　更新$ {\boldsymbol{U}}_{}^{{k_{\rm D}} + 1} $，通过式(19)；
9. 　更新$ {\boldsymbol{V}}_{}^{{k_{\rm D}} + 1} $，通过式(20)；
10. end for
11. 输出：优化后的一体化波形$ {\boldsymbol{\bar x}}_L^{{\text{sub}}} $，通过式(33)。

下载: 导出CSV

表 1 仿真参数

Table 1. Simulation parameters

参数	数值
OFDM符号数	2000
OFDM子载波数N	512
保护带宽的空子载波数	50
CP长度${N_{{\text{CP}}}} $	128
数据子载波调制方式	16QAM
感兴趣距离单元数${N_{{\text{int}}}} $	100
功率约束$ {\alpha _1} $	2
功率约束$ {\alpha _2} $	0.12
PAPR约束$ \beta $	5 dB
惩罚参数$ \rho $	200
备选信号个数$ {K_{{\text{Out}}}} $	100
ADMM迭代次数$ {K_{\text{D}}} $	10

下载: 导出CSV

表 2 不同方法的ISLR均值(dB)

Table 2. The average ISLR of different methods (dB)

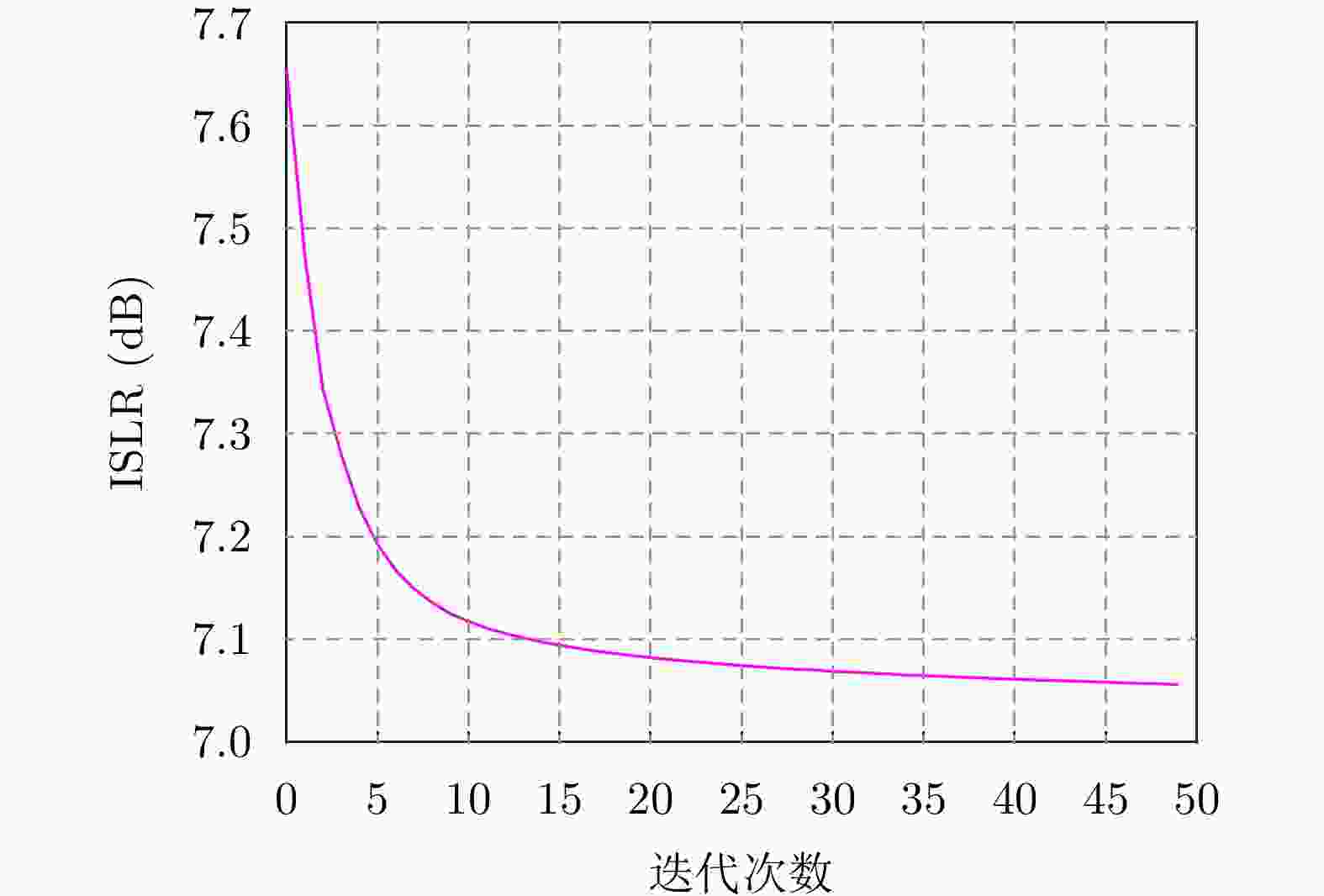
方法	ISLR
原始信号	9.00
ICF方法	9.14
New-ICF方法	9.12
ACE方法	9.42
TR-LNCA方法	8.23
本文方法	7.12

下载: 导出CSV

参考文献(40)

[1]	刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467–484. doi: 10.12000/JR20113 LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communication spectrum sharing and integration: Overview and prospect[J]. Journal of Radars, 2021, 10(3): 467–484. doi: 10.12000/JR20113
[2]	余显祥, 姚雪, 杨婧, 等. 面向感知应用的通感一体化信号设计技术与综述[J]. 雷达学报, 2023, 12(2): 247–261. doi: 10.12000/JR23015 YU Xianxiang, YAO Xue, YANG Jing, et al. Radar-centric DFRC signal design: Overview and future research avenues[J]. Journal of Radars, 2023, 12(2): 247–261. doi: 10.12000/JR23015
[3]	兰岚, 廖桂生, 许京伟, 等. 基于频率分集阵列的多功能一体化波形设计与信号处理方法[J]. 雷达学报, 2022, 11(5): 850–870. doi: 10.12000/JR22163 LAN Lan, LIAO Guisheng, XU Jingwei, et al. Waveform design and signal processing method of a multifunctional integrated system based on a frequency diverse array[J]. Journal of Radars, 2022, 11(5): 850–870. doi: 10.12000/JR22163
[4]	马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146 MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146
[5]	HWANG T, YANG Chenyang, WU Gang, et al. OFDM and its wireless applications: A survey[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4): 1673–1694. doi: 10.1109/TVT.2008.2004555
[6]	XU Zhaoyi and PETROPULU A. A bandwidth efficient dual-function radar communication system based on a MIMO radar using OFDM waveforms[J]. IEEE Transactions on Signal Processing, 2023, 71: 401–416. doi: 10.1109/TSP.2023.3241779
[7]	肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展趋势[J]. 电子与信息学报, 2019, 41(3): 739–750. doi: 10.11999/JEIT180515 XIAO Bo, HUO Kai, and LIU Yongxiang. Development and prospect of radar and communication integration[J]. Journal of Electronics & Information Technology, 2019, 41(3): 739–750. doi: 10.11999/JEIT180515
[8]	吴文俊, 唐波, 汤俊, 等. 杂波环境中雷达通信一体化系统波形设计算法研究[J]. 雷达学报, 2022, 11(4): 570–580. doi: 10.12000/JR22105 WU Wenjun, TANG Bo, TANG Jun, et al. Waveform design for dual-function radar-communication systems in clutter[J]. Journal of Radars, 2022, 11(4): 570–580. doi: 10.12000/JR22105
[9]	NI Zhitong, ZHANG J A, WU Kai, et al. Uplink sensing using CSI ratio in perceptive mobile networks[J]. IEEE Transactions on Signal Processing, 2023, 71: 2699–2712. doi: 10.1109/TSP.2023.3294626
[10]	COLONE F, FILIPPINI F, and PASTINA D. Passive radar: Past, present, and future challenges[J]. IEEE Aerospace and Electronic Systems Magazine, 2023, 38(1): 54–69. doi: 10.1109/MAES.2022.3221685
[11]	万显荣, 易建新, 占伟杰, 等. 基于多照射源的被动雷达研究进展与发展趋势[J]. 雷达学报, 2020, 9(6): 939–958. doi: 10.12000/JR20143 WAN Xianrong, YI Jianxin, ZHAN Weijie, et al. Research progress and development trend of the multi-illuminator-based passive radar[J]. Journal of Radars, 2020, 9(6): 939–958. doi: 10.12000/JR20143
[12]	RAHMATALLAH Y and MOHAN S. Peak-to-average power ratio reduction in OFDM systems: A survey and taxonomy[J]. IEEE Communications Surveys & Tutorials, 2013, 15(4): 1567–1592. doi: 10.1109/SURV.2013.021313.00164
[13]	ARMSTRONG J. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering[J]. Electronics Letters, 2002, 38(5): 246–247. doi: 10.1049/el:20020175
[14]	WANG Y C and LUO Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]. IEEE Transactions on Communications, 2011, 59(1): 33–37. doi: 10.1109/TCOMM.2010.102910.090040
[15]	TANG Bo, QIN Kaiyu, ZHANG Xiangyin, et al. A clipping-noise compression method to reduce PAPR of OFDM Signals[J]. IEEE Communications Letters, 2019, 23(8): 1389–1392. doi: 10.1109/LCOMM.2019.2916052
[16]	SOHN I and KIM S C. Neural network based simplified clipping and filtering technique for PAPR reduction of OFDM signals[J]. IEEE Communications Letters, 2015, 19(8): 1438–1441. doi: 10.1109/LCOMM.2015.2441065
[17]	KRONGOLD B S and JONES D L. PAR reduction in OFDM via active constellation extension[J]. IEEE Transactions on Broadcasting, 2003, 49(3): 258–268. doi: 10.1109/TBC.2003.817088
[18]	LI Haibo, JIANG Tao, and ZHOU Yang. An improved tone reservation scheme with fast convergence for PAPR reduction in OFDM systems[J]. IEEE Transactions on Broadcasting, 2011, 57(4): 902–906. doi: 10.1109/TBC.2011.2169622
[19]	NI Chunxing, MA Yahui, and JIANG Tao. A novel adaptive tone reservation scheme for PAPR reduction in large-scale multi-user MIMO-OFDM systems[J]. IEEE Wireless Communications Letters, 2016, 5(5): 480–483. doi: 10.1109/LWC.2016.2588489
[20]	WU Wenhua, CAO Yunhe, WANG Shenghua, et al. Joint optimization of PAPR reduction based on modified TR scheme for MIMO-OFDM radar[J]. Digital Signal Processing, 2018, 80: 27–36. doi: 10.1016/j.dsp.2018.05.008
[21]	ZHANG Siyu and SHAHRRAVA B. A SLM scheme for PAPR reduction in Polar coded OFDM-IM systems without using side information[J]. IEEE Transactions on Broadcasting, 2021, 67(2): 463–472. doi: 10.1109/TBC.2020.3039696
[22]	季策, 祝雯靖, 魏颖, 等. 降低OFDM系统PAPR的改进SLM算法[J]. 通信学报, 2018, 39(4): 152–158. doi: 10.11959/j.issn.1000-436x.2018059 JI Ce, ZHU Wenjing, WEI Ying, et al. Improved SLM algorithm for PAPR reduction in OFDM system[J]. Journal on Communications, 2018, 39(4): 152–158. doi: 10.11959/j.issn.1000-436x.2018059
[23]	王鑫海, 王超宇, 张宁, 等. 一种相位域低积分旁瓣雷达波形优化方法[J]. 雷达学报, 2022, 11(2): 255–263. doi: 10.12000/JR21137 WANG Xinhai, WANG Chaoyu, ZHANG Ning, et al. Phase-only method for designing a unimodular radar waveform with low ISL[J]. Journal of Radars, 2022, 11(2): 255–263. doi: 10.12000/JR21137
[24]	LELLOUCH G, MISHRA A K, and INGGS M. Design of OFDM radar pulses using genetic algorithm based techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1953–1966. doi: 10.1109/TAES.2016.140671
[25]	TSAI L S, CHUNG W H, and SHIU D S. Synthesizing low autocorrelation and low PAPR OFDM sequences under spectral constraints through convex optimization and GS algorithm[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2234–2243. doi: 10.1109/TSP.2011.2108652
[26]	STOICA P, HE Hao, and LI Jian. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1415–1425. doi: 10.1109/TSP.2009.2012562
[27]	周凯, 李德鑫, 粟毅, 等. 雷达脉冲压缩低旁瓣发射波形和非匹配滤波联合设计方法[J]. 电子学报, 2021, 49(9): 1701–1707. doi: 10.12263/DZXB.20201405 ZHOU Kai, LI Deixin, SU Yi, et al. Joint design of transmitted waveform and mismatched filter sup-pressing radar pulse compression sidelobe level[J]. Acta Electronica Sinica, 2021, 49(9): 1701–1707. doi: 10.12263/DZXB.20201405
[28]	ZHOU Shenghua, LIANG Xueling, YU Yao, et al. Joint radar-communications Co-Use waveform design using optimized phase perturbation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1227–1240. doi: 10.1109/TAES.2019.2909254
[29]	BARUFFA G, RUGINI L, FRESCURA F, et al. Low-complexity PAPR reduction by coded data insertion on DVB-T2 reserved carriers[J]. IEEE Access, 2023, 11: 73377–73393. doi: 10.1109/ACCESS.2023.3296256
[30]	BULUSU S S K C, CRUSSIÈRE M, HÉLARD J F, et al. Quasi-optimal tone reservation PAPR reduction algorithm for next generation broadcasting systems: A performance/complexity/latency tradeoff with testbed implementation[J]. IEEE Transactions on Broadcasting, 2018, 64(4): 883–899. doi: 10.1109/TBC.2018.2811623
[31]	HUANG Yixuan, HU Su, MA Shiyong, et al. Designing low-PAPR waveform for OFDM-based RadCom systems[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 6979–6993. doi: 10.1109/TWC.2022.3153606
[32]	VARSHNEY P, BABU P, and STOICA P. Low-PAPR OFDM waveform design for radar and communication systems[J]. IEEE Transactions on Radar Systems, 2023, 1: 69–74. doi: 10.1109/TRS.2023.3275210
[33]	WEN Cai, HUANG Yan, ZHENG Le, et al. Transmit waveform design for dual-function radar-communication systems via hybrid linear-nonlinear precoding[J]. IEEE Transactions on Signal Processing, 2023, 71: 2130–2145. doi: 10.1109/TSP.2023.3278858
[34]	WANG Luqing and TELLAMBURA C. A simplified clipping and filtering technique for PAR reduction in OFDM systems[J]. IEEE Signal Processing Letters, 2005, 12(6): 453–456. doi: 10.1109/LSP.2005.847886
[35]	JIANG Tao and WU Yiyan. An overview: Peak-to-average power ratio reduction techniques for OFDM signals[J]. IEEE Transactions on Broadcasting, 2008, 54(2): 257–268. doi: 10.1109/TBC.2008.915770
[36]	杨婧, 余显祥, 沙明辉, 等. MIMO系统探通一体化信号矩阵设计方法[J]. 雷达学报, 2023, 12(2): 262–274. doi: 10.12000/JR22087 YANG Jing, YU Xianxiang, SHA Minghui, et al. Dual function radar and communication signal matrix design method for MIMO system[J]. Journal of Radars, 2023, 12(2): 262–274. doi: 10.12000/JR22087
[37]	LIU Shuang, WANG Yajun, LIAN Zhuxian, et al. Joint suppression of PAPR and OOB radiation for OFDM systems[J]. IEEE Transactions on Broadcasting, 2023, 69(2): 528–537. doi: 10.1109/TBC.2023.3243410
[38]	WANG Yongchao, WANG Yanjiao, and SHI Qingjiang. Optimized signal distortion for PAPR reduction of OFDM signals with IFFT/FFT complexity via ADMM approaches[J]. IEEE Transactions on Signal Processing, 2019, 67(2): 399–414. doi: 10.1109/TSP.2018.2880711
[39]	GRANT M and BOYD S. CVX: Matlab software for disciplined convex programming, version 2.2[EB/OL]. http://cvxr.com/cvx, 2020.
[40]	DU Zhen, LIU Fan, XIONG Yifeng, et al. Probabilistic constellation shaping for OFDM-based ISAC signaling[EB/OL]. http://arxiv.org/abs/2310.18090, 2023.