Filter Bank Multi-carrier Waveform Design for Low Probability of Intercepting Joint Radar and Communication System
-
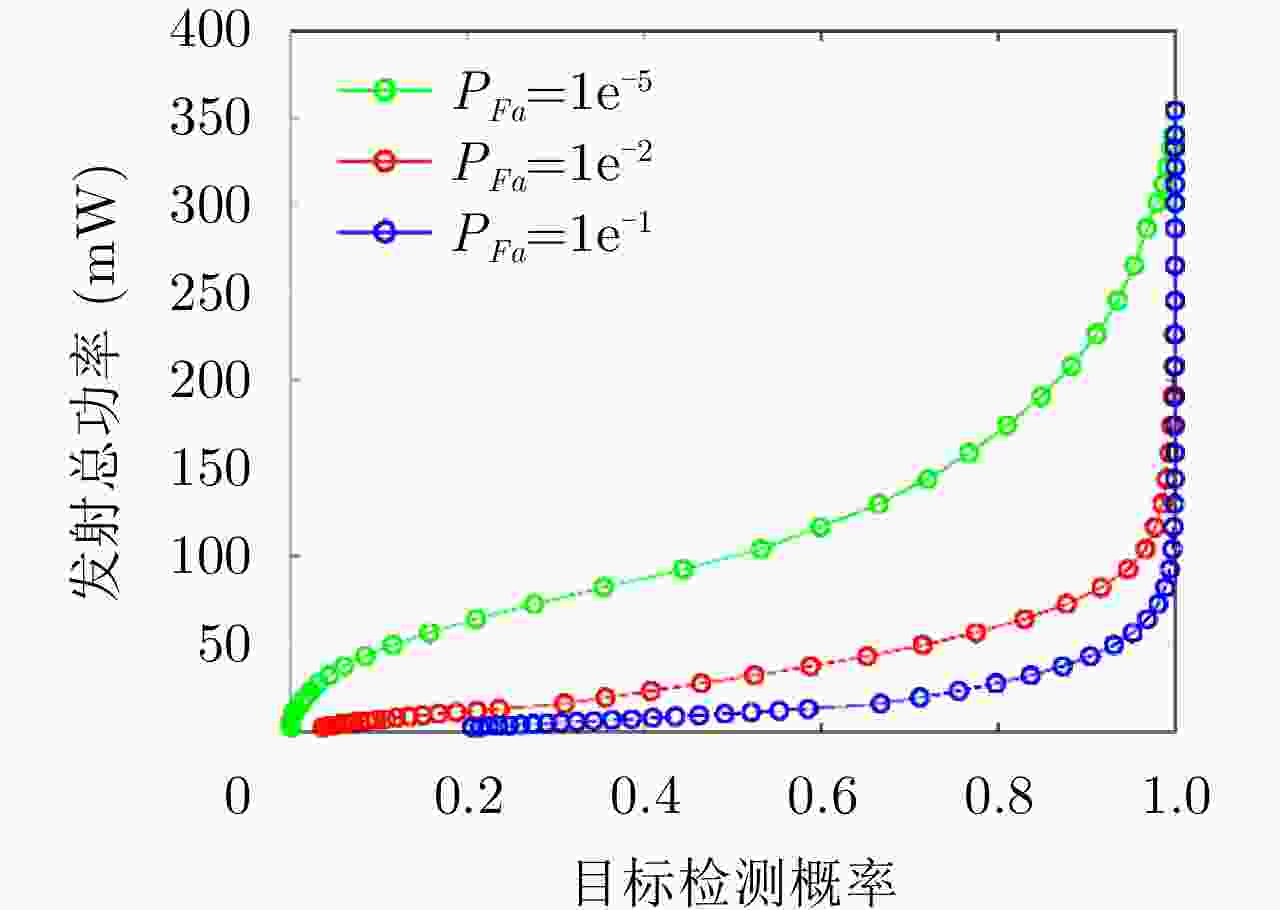
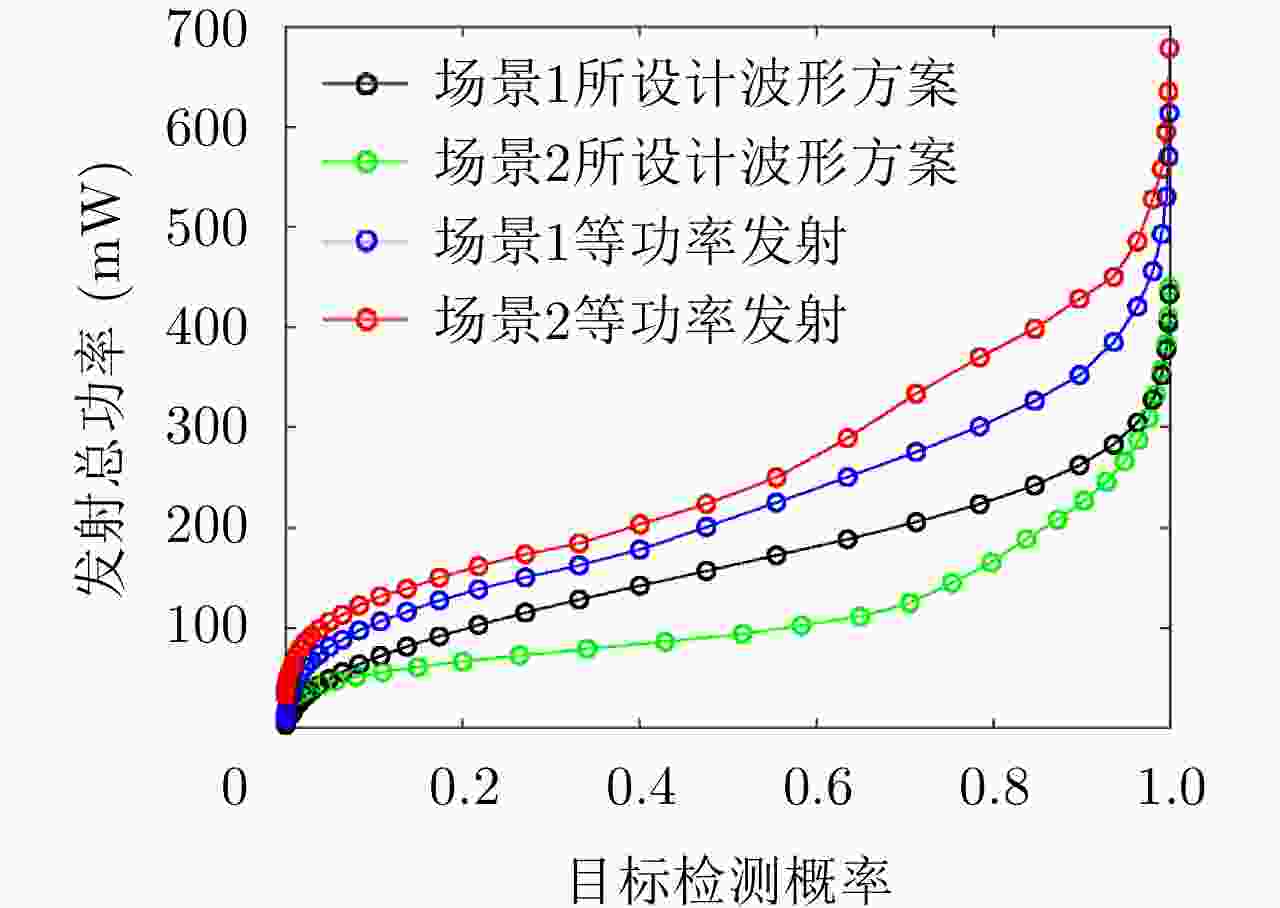
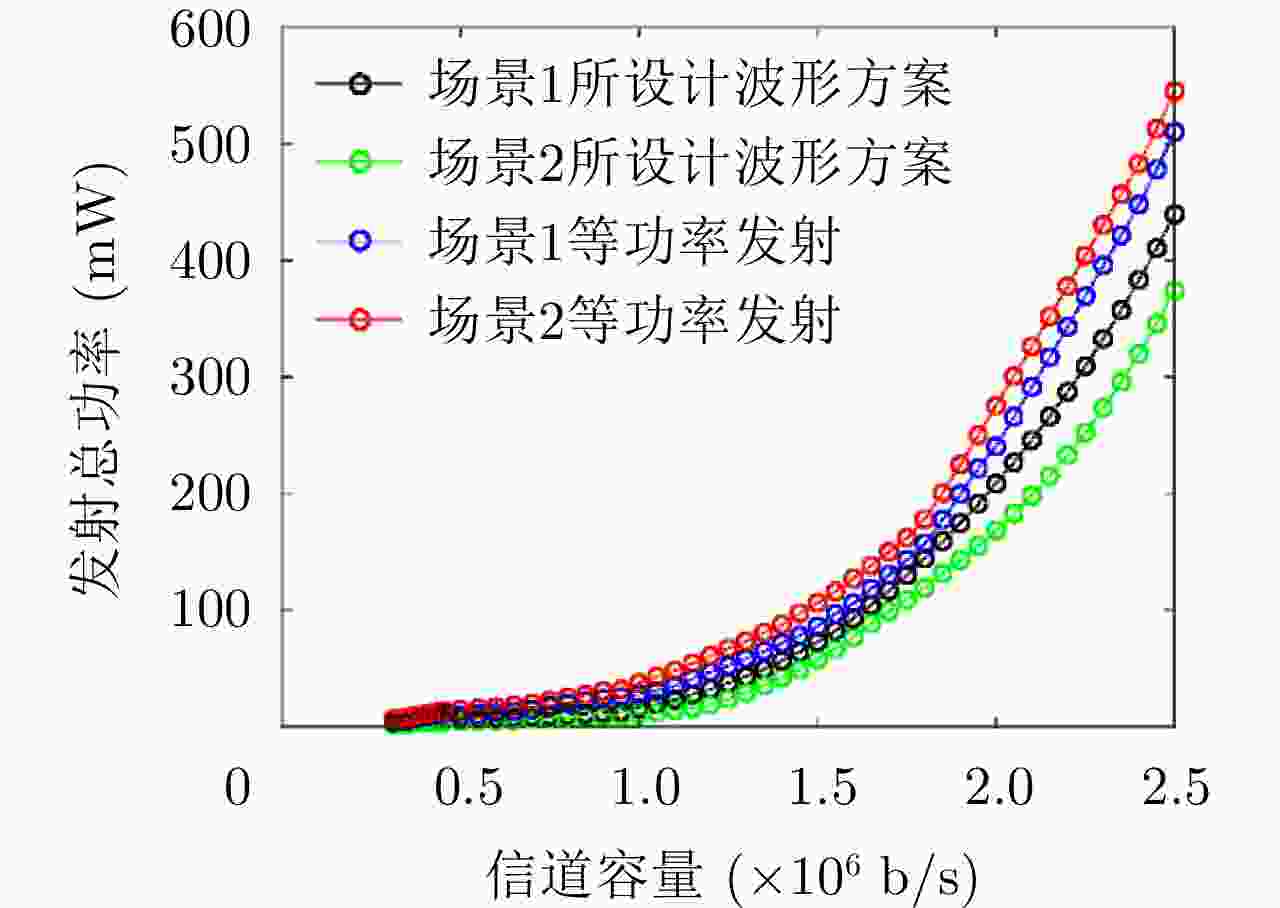
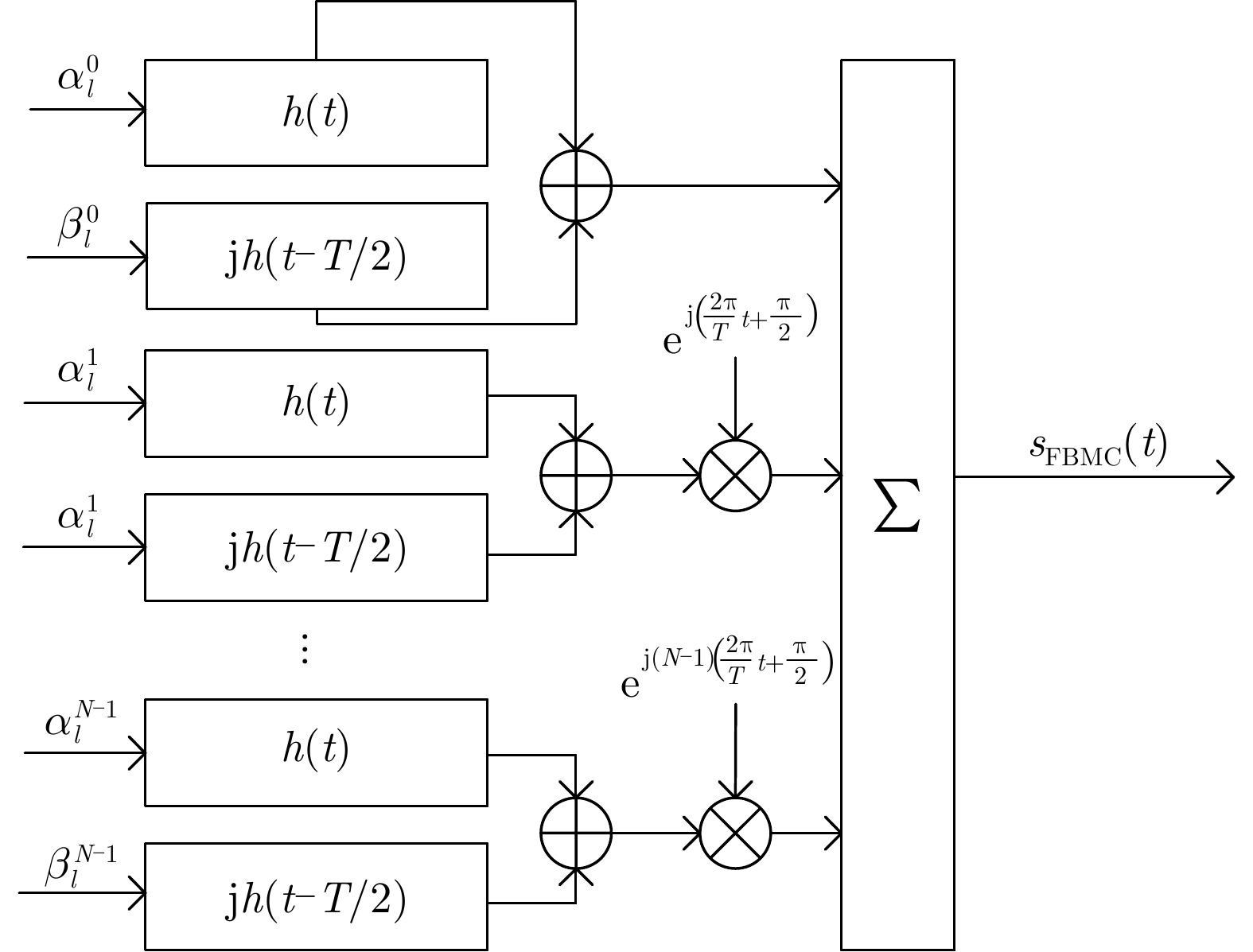
摘要: 针对正交频分复用(OFDM)雷达通信一体化波形方案中循环前缀引起的弱回波掩盖问题和敌方战场低截获概率问题,该文提出了基于滤波器组的多载波偏移正交幅度调制(FBMC-OQAM)的低截获雷达通信一体化波形设计方案。分别构建FBMC雷达通信一体化波形与目标检测概率、通信信道容量之间的数学模型,在保证一定系统雷达与通信性能的条件约束下,设计最小化系统总发射功率联合优化问题,优化各个子载波发射功率分配方案。该算法利用测量值和信道状态信息,对下一个脉冲的发射波形参数进行优化设计,实现自适应传输。此外,从平均模糊函数角度分析了FBMC作为雷达信号的可行性和优势。仿真结果表明,与等功率分配方案相比,该文提出的功率分配方案可有效降低一体化系统总发射功率,从而实现低截获性能,并且FBMC波形可有效降低循环前缀引起的距离旁瓣,提高雷达分辨率与信息速率。Abstract: Cyclic prefixes in joint radar and communication systems based on Orthogonal Frequency Division Multiplexing (OFDM) and low probability of interception lead to weak radar echo masking on the battlefield. To address this problem, a low probability of interception waveform design scheme based on Filter Bank Multi-Carrier (FBMC) with Offset Quadrature Amplitude Modulation (FBMC-OQAM) is proposed in this paper. Mathematical models for the FBMC joint radar and communication waveform, target detection probability, and communication channel capacity are established. Under the radar and communication performance constraints required by the system, a joint optimization problem of minimizing the total transmitted power of the system is designed, and the subcarrier and power allocation scheme are optimized. Furthermore, the proposed algorithm can realize adaptive transmission where the parameters of the transmitting waveform can be optimally designed for the next pulse by utilizing the measured values of the current signal and the channel state information. Moreover, the feasibility and advantages of FBMC as the radar signal are analyzed based on the average ambiguity function. Theoretical analysis and simulation experiments show that the power allocation scheme proposed in this paper can effectively reduce the total transmitted power of the system, to achieve low interception performance compared with the equal power allocation. The FBMC waveform can effectively reduce the sidelobes caused by cyclic prefixes, which improves the radar resolution and information rate.
-
表 1 多载波波形仿真参数设置
Table 1. Multi-Carrier waveform parameters setting
波形 符号
周期子载
波数CP长度 符号
数调制方式 滤波器 OFDM 1.65 μs 64 0 4 16QAM 矩形窗 CP-OFDM 2.07 μs 80 0.42 μs 4 16QAM 矩形窗 FBMC-OQAM 0.83 μs 64 0 4 16QAM PHDYAS K=4 表 2 PHDYAS滤波器系数
Table 2. PHDYAS filter coefficients
参数 数值 参数 数值 K 4 ${H_1}$ 0.971960 ${H_0}$ 1 ${H_2}$ $\sqrt 2 /2$ ${H_3}$ 0.235147 表 3 参数
${\boldsymbol{\lambda }}$ 与${\boldsymbol{\eta }}$ 仿真参数设置Table 3.
${\boldsymbol{\lambda }}$ and${\boldsymbol{\eta }}$ parameters setting参数 子信道1 子信道2 子信道3 子信道4 场景1$ {\boldsymbol{\lambda }} $ –0.1369–0.0619i 0.3611+0.2125i 0.0075–0.0921i 0.2667–0.2076i 场景1${\boldsymbol{\eta }}$ –0.046+0.1705i 0.0304+0.1136i 0.0609+0.2273i 0.1218–0.4546i 场景2$ {\boldsymbol{\lambda }} $ 0.6288–0.1170i 0.1064+0.0408i 0.0617+0.0590i 0.0449+0.1549i 场景2${\boldsymbol{\eta }}$ 0.5520+0.1479i 0.0370–0.1380i 0.2070+0.0055i 0.0018–0.0690i -
[1] CALDWELL D, FREDA J, and GOLDSTEIN L J. China maritime report No. 5: China’s dreadnought? The PLA Navy’s type 055 cruiser and its implications for the future maritime security environment[R]. CMSI China Maritime Reports. 5, 2020. [2] MCCASLIN I B and ERICKSON A S. The Impact of Xi-Era Reforms on the Chinese Navy[M]. SAUNDERS P C, DING A S, SCOBELL A, et al. Chairman Xi Remakes the PLA: Assessing Chinese Military Reforms. Washington: National Defense University Press, 2018. [3] MCMAHON B, LAPIERRE R, MACCABE A, et al. ORCHESTRA: Optimizable RF converged hardware expression of a scalable transmit/receive architecture[C]. 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, USA, 2018: 2139–2140. [4] MENZEL W. Millimeter-wave radar for civil applications[C]. The 7th European Radar Conference, Paris, France, 2010: 89–92. [5] ERDELJ M, NATALIZIO E, CHOWDHURY K R, et al. Help from the sky: Leveraging UAVs for disaster management[J]. IEEE Pervasive Computing, 2017, 16(1): 24–32. doi: 10.1109/MPRV.2017.11 [6] YANG Chouchang and SHAO Huairong. WiFi-based indoor positioning[J]. IEEE Communications Magazine, 2015, 53(3): 150–157. doi: 10.1109/MCOM.2015.7060497 [7] MISHRA K V, SHANKAR M R B, KOIVUNEN V, et al. Toward millimeter-wave joint radar communications: A signal processing perspective[J]. IEEE Signal Processing Magazine, 2019, 36(5): 100–114. doi: 10.1109/MSP.2019.2913173 [8] 马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint Radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radar, 2022, 11(2): 198–212. doi: 10.12000/JR21146 [9] 刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467–484. doi: 10.12000/JR20113LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communication spectrum sharing and integration: overview and prospect[J]. Journal of Radar, 2021, 10(3): 467–484. doi: 10.12000/JR20113 [10] ZHANG Qiuyue, ZHOU Yu, ZHANG Linrang, et al. Circulating code array for a dual-function radar-communications system[J]. IEEE Sensors Journal, 2020, 20(2): 786–798. doi: 10.1109/JSEN.2019.2944470 [11] BEKAR M, BAKER C J, HOARE E G, et al. Joint MIMO Radar and communication system using a PSK-LFM waveform With TDM and CDM approaches[J]. IEEE Sensors Journal, 2021, 21(5): 6115–6124. doi: 10.1109/JSEN.2020.3043085 [12] 杨慧婷, 周宇, 谷亚彬, 等. 参数调制多载波雷达通信共享信号设计[J]. 雷达学报, 2019, 8(1): 54–63. doi: 10.12000/JR18001YANG Huiting, ZHOU Yu, GU Yabin, et al. Design of integrated Radar and communication signal based on multicarrier parameter modulation signal[J]. Journal of Radar, 2019, 8(1): 54–63. doi: 10.12000/JR18001 [13] LEVANON N. Multifrequency complementary phase-coded radar signal[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(6): 276–284. doi: 10.1049/ip-rsn:20000734 [14] MOZESON E and LEVANON N. Multicarrier radar signals with low peak-to-mean envelope power ratio[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(2): 71–77. doi: 10.1049/ip-rsn:20030263 [15] STURM C and WIESBECK W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing[J]. Proceedings of the IEEE, 2011, 99(7): 1236–1259. doi: 10.1109/JPROC.2011.2131110 [16] LIU Yongjun, LIAO Guisheng, XU Jingwei, et al. Adaptive OFDM integrated radar and communications waveform design based on information theory[J]. IEEE Communications Letters, 2017, 21(10): 2174–2177. doi: 10.1109/LCOMM.2017.2723890 [17] FARHANG-BOROUJENY B. OFDM versus filter bank multicarrier[J]. IEEE Signal Processing Magazine, 2011, 28(3): 92–112. doi: 10.1109/MSP.2011.940267 [18] PACE P E. Detecting and Classifying Low Probability of Intercept Radar[M]. 2nd ed. Norwood: Artech House, 2009: 231–245. [19] SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Low probability of intercept-based optimal power allocation scheme for an integrated multistatic radar and communication system[J]. IEEE Systems Journal, 2020, 14(1): 983–994. doi: 10.1109/JSYST.2019.2931754 [20] SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Low probability of intercept based multicarrier radar jamming power allocation for joint radar and wireless communications systems[J]. IET Radar, Sonar & Navigation, 2017, 11(5): 802–811. doi: 10.1049/iet-rsn.2016.0362 [21] JAMAL H and MATOLAK D W. Dual-polarization FBMC for improved performance in wireless communication systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 349–358. doi: 10.1109/TVT.2018.2879573 [22] MADHOW U. Fundamentals of Digital Communication[M]. Cambridge: Cambridge University Press, 2008: 213–243. [23] KNOTT E F, SHAEFFER J F, and TULEY M T. Radar Cross Section[M]. 2nd ed. SciTech Publishing, 2004: 23–45. [24] SEN S, TANG Gongguo, and NEHORAI A. Multiobjective optimization of OFDM radar waveform for target detection[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 639–652. doi: 10.1109/TSP.2010.2089628 [25] KAY S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. Englewood Cliffs: Prentice-Hall, 1993: 125–132. [26] LEVANON N and MOZESON E. Radar Signals[M]. New York: John Wiley & Sons, 2004: 211–232. [27] AUSLANDER L and TOLIMIERI R. Characterizing the radar ambiguity functions[J]. IEEE Transactions on Information Theory, 1984, 30(6): 832–836. doi: 10.1109/TIT.1984.1056980 [28] SKOLNIK M I. Introduction to Radar Systems[M]. New York: McGraw-Hill, 1980. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: