基于联合邻域像素结构化低秩的层析SAR三维成像方法

周弘昊; 刘艳阳; 李涛; 崔硕; 徐刚; 邢孟道

doi:10.12000/JR25092

基于联合邻域像素结构化低秩的层析SAR三维成像方法

DOI: 10.12000/JR25092 CSTR: 32380.14.JR25092

周弘昊¹,
刘艳阳²,
李涛³,
崔硕¹,
徐刚^1, ,,
邢孟道^{4, 5}

1.
东南大学毫米波全国重点实验室南京 210096
2.
上海卫星工程研究所上海 201109
3.
自然资源部国土卫星遥感应用中心北京 100048
4.
西安电子科技大学雷达信号处理全国重点实验室西安 710071
5.
西安电子科技大学前沿交叉研究院西安 710071

基金项目: 国家自然科学基金(62071113)，江苏省优秀青年基金(BK20211559)，中央高校基本科研业务费专项资金资助(2242022k60008)

详细信息

作者简介:
周弘昊，博士生，主要研究方向为SAR三维成像处理

刘艳阳，博士，高级工程师，研究方向为星载SAR/InSAR系统仿真与信号处理

李　涛，博士，副研究员，主要研究方向为SAR卫星地形测绘及形变监测等研究工作

崔　硕，博士生，主要研究方向为阵列SAR三维成像处理

徐　刚，博士，教授，主要研究方向为雷达信号处理、雷达高分辨成像以及毫米波雷达成像等

邢孟道，博士，教授，主要研究方向为SAR/ISAR成像、稀疏信号处理

通讯作者:
徐刚 xugang0102@126.com

责任主编：XXX Corresponding Editor: XXX
中图分类号: TN957.52
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
出版历程

Structured Low-Rankness Method of Joint Neighboring Pixels for Tomographic SAR 3D Imaging

ZHOU Honghao¹,
LIU Yanyang²,
LI Tao³,
CUI Shuo¹,
XU Gang^{1
, ,},
XING Mengdao^{4, 5}

1.
State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 210096, China
2.
Shanghai Institute of Satellite Engineering, Shanghai 201109, China
3.
Land Satellite Remote Sensing Application Center, Ministry of Natural Resources of P.R., Beijing 100048, China
4.
National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China
5.
Academy of Advanced Interdisciplinary Research, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (62071113), The Natural Science Foundation of Jiangsu Province (BK20211559), The Fundamental Research Funds for the Central Universities (2242022k60008)

摘要

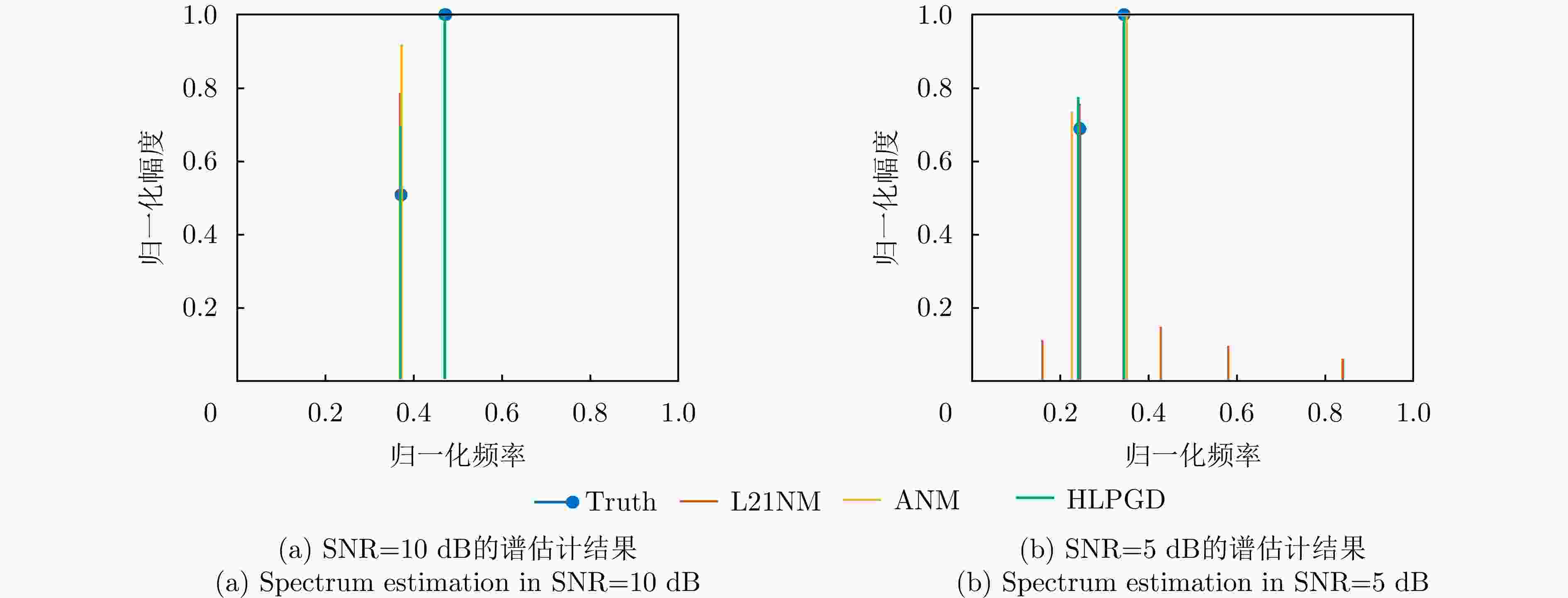
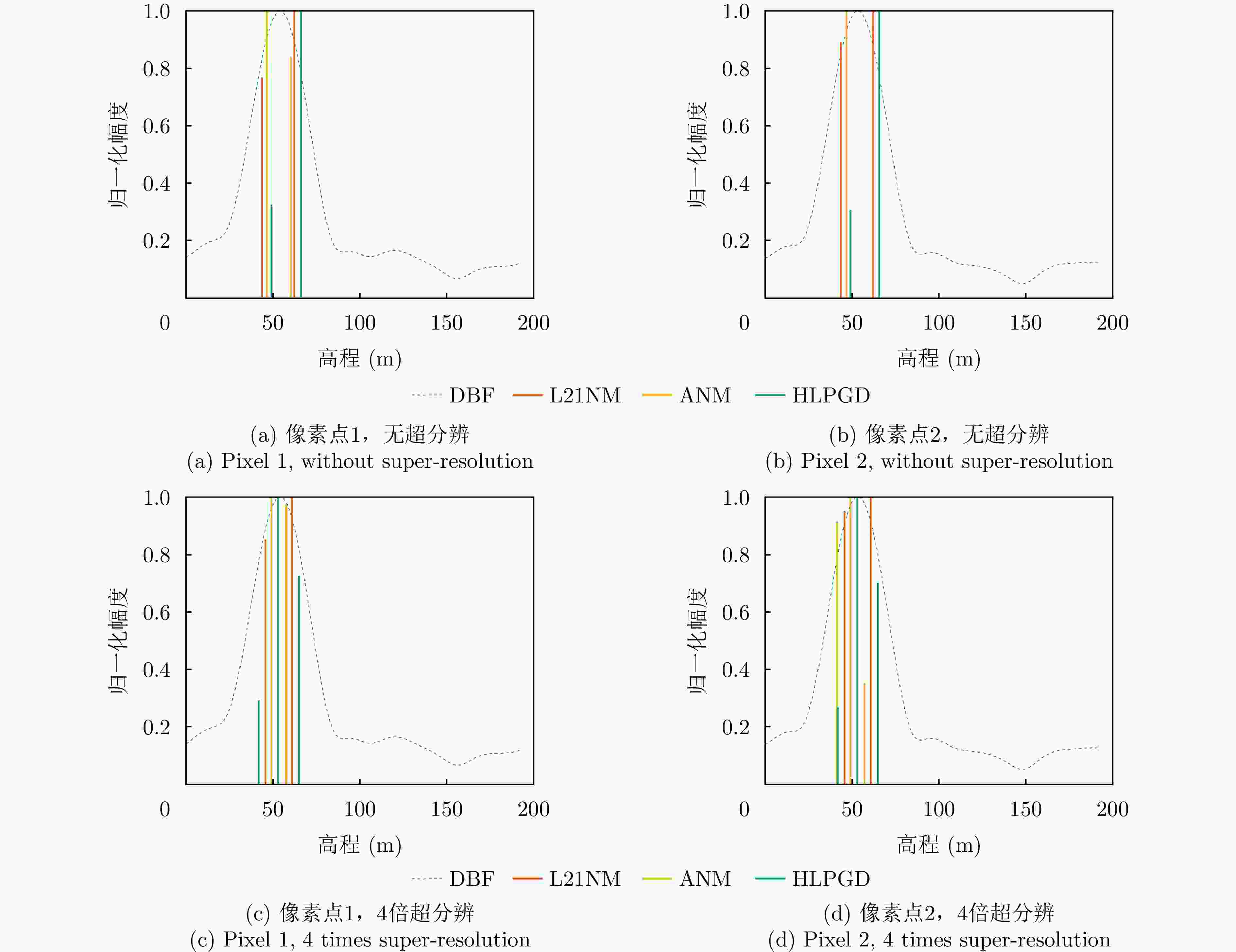
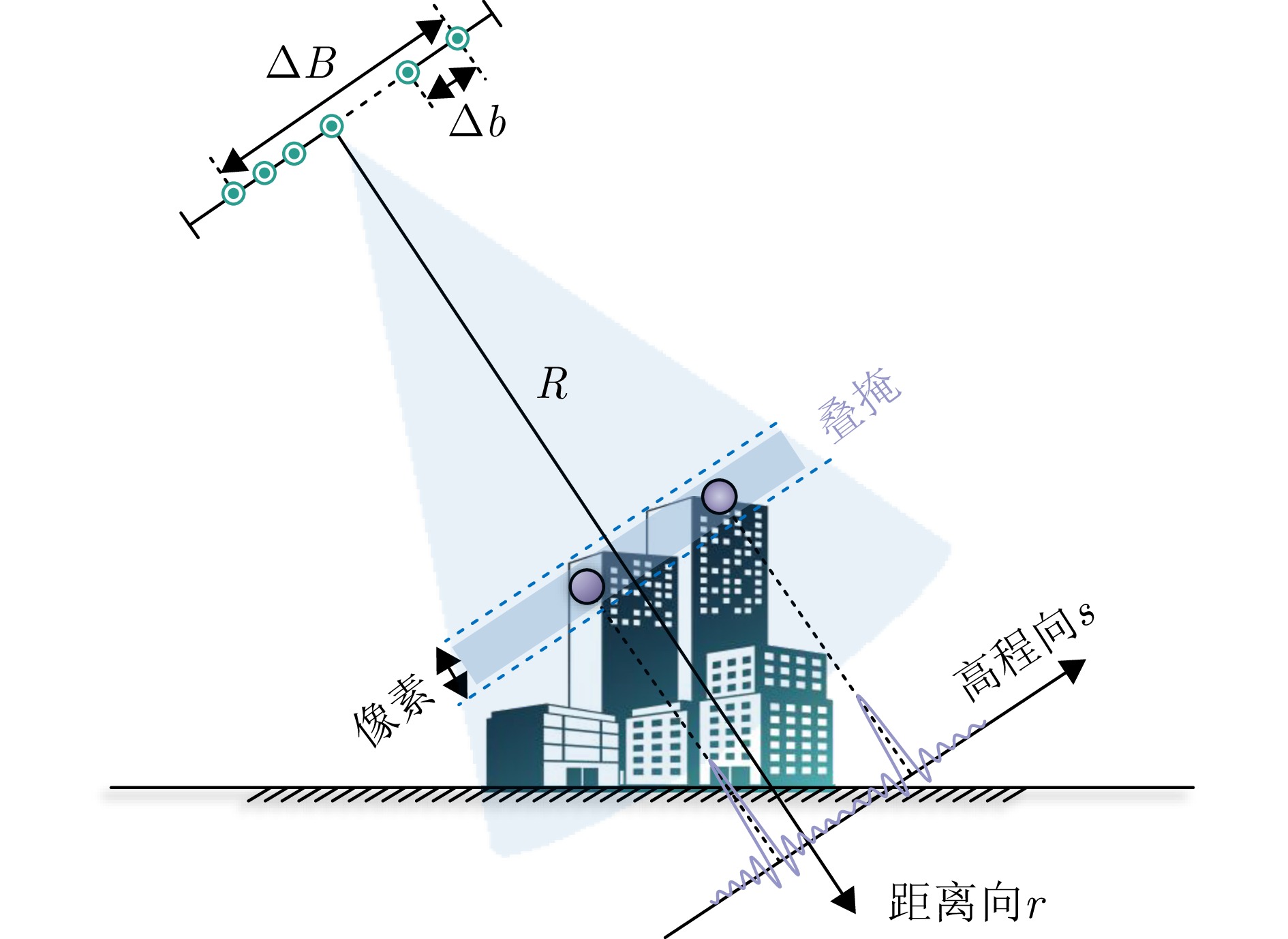
摘要: 层析合成孔径雷达(TomoSAR)三维成像能够克服场景叠掩、投影几何失真等问题，具有重要的科学研究和应用价值。由于TomoSAR高程分辨率受到高程向孔径限制，通常利用压缩感知等超分辨算法提升三维成像性能。然而，传统压缩感知方法需预先划分离散网格导致存在网格失配等问题，同时在通道数少、信噪比低等限制条件下，成像分辨精度受限。针对以上问题，本文提出了一种基于联合邻域像素结构化低秩的层析SAR超分辨三维成像方法，通过增强信号内部结构性表征以增加有效样本数量，提高三维重建性能。具体而言，基于邻域像素高程一致性假设，可联合邻域像素稀疏特性构建无网格结构化低秩非凸优化模型，以增强信号内部结构表征并克服传统稀疏网格化的缺陷。此外采用投影梯度下降算法进行高效求解，引入非相干可行域约束，有效降低重构性能对采样位置的依赖性。最后，利用仿真数据、实测SARMV3D-1.0机载阵列数据和陆地探测一号卫星数据进行了验证。实验结果表明，所提方法在三维重建精度和稳定性方面均显著优于现有大多数主流方法。
- 三维SAR /
- 联合邻域 /
- 超分辨 /
- 结构化低秩 /
- 陆地探测一号
Abstract: Tomographic SAR (TomoSAR) has significant value in scientific research and applications, as it enables three-dimensional (3D) imaging to address limitations such as scene overlay and projection geometric distortion. The elevation resolution of TomoSAR is limited by the aperture in the elevation direction. Consequently, super-resolution algorithms such as compressive sensing (CS) are generally used to enhance the performance of 3D imaging. However, conventional CS methods suffer from grid mismatch issues due to predefined discrete grids, which lead to limited resolution under practical constraints, such as limited channels and low signal-to-noise ratios. To address these limitations, a novel, gridless, super-resolution algorithm based on the structured low-rankness of joint neighboring pixels is proposed herein for tomographic 3D SAR Imaging. By enhancing the intrinsic structural observation, the efficacy of the model for 3D reconstruction can be effectively improved by increasing the number of valid observations. Specifically, a gridless, structured, low-rank, non-convex optimization model is constructed by leveraging the joint sparse characteristics of neighboring pixels, overcoming the limitations of traditional sparse grid-based approaches. Furthermore, an efficient solution is achieved using a projected gradient descent algorithm, and the dependence of the reconstruction performance on the sampling positions is reduced by introducing an incoherent feasible region constraint. Finally, the superiority of the proposed algorithm is validated through both simulation and analysis of real measured datasets, including the SARMV3D-1.0 airborne array dataset and spaceborne LuTan-1 dataset. The proposed algorithm achieves superior 3D reconstruction accuracy and stability compared to most existing state-of-the-art methods.
- 3-D SAR /
- Joint neighboring pixels /
- Super-resolution /
- Structured low-rankness /
- LuTan-1

HTML全文

图 1 TomoSAR三维成像几何模型

Figure 1. TomoSAR 3-D geometric model

下载: 全尺寸图片幻灯片

图 2 HLPGD算法示意图

Figure 2. Schematic diagram of HLPGD algorithm

下载: 全尺寸图片幻灯片

图 3 点目标仿真结果

Figure 3. Point target simulation results

下载: 全尺寸图片幻灯片

图 4 超分辨成功率相变图

Figure 4. PTD results of super-resolution success rate

下载: 全尺寸图片幻灯片

图 5 测试区域的SAR图像和对应的光学影像

Figure 5. SAR image and Optical image of the test area

下载: 全尺寸图片幻灯片

图 6 机载数据谱估计超分辨结果

Figure 6. Spectrum super-resolution results of airborne dataset

下载: 全尺寸图片幻灯片

图 7 HLPGD算法收敛迭代曲线

Figure 7. Convergence iteration curve of HLPGD algorithm

下载: 全尺寸图片幻灯片

图 8 机载数据建筑三维重建结果

Figure 8. TomoSAR results of the building of airborne dataset

下载: 全尺寸图片幻灯片

图 9 陆探数据集测试区域的SAR图像和对应的光学图像

Figure 9. SAR image and corresponding Optical image of the test area of the LuTan-1 Dataset

下载: 全尺寸图片幻灯片

图 10 12非均匀通道和38均匀通道分布

Figure 10. 12 irregular and 38 uniform channel configurations

下载: 全尺寸图片幻灯片

图 11 陆探数据谱估计结果

Figure 11. Spectrum estimation results of the LuTan-1 Dataset

下载: 全尺寸图片幻灯片

图 12 陆探数据城区三维重建结果

Figure 12. TomoSAR results of the urban area in LuTan-1 Dataset

下载: 全尺寸图片幻灯片

图 13 三维重建结果细节展示

Figure 13. The details of TomoSAR results

下载: 全尺寸图片幻灯片

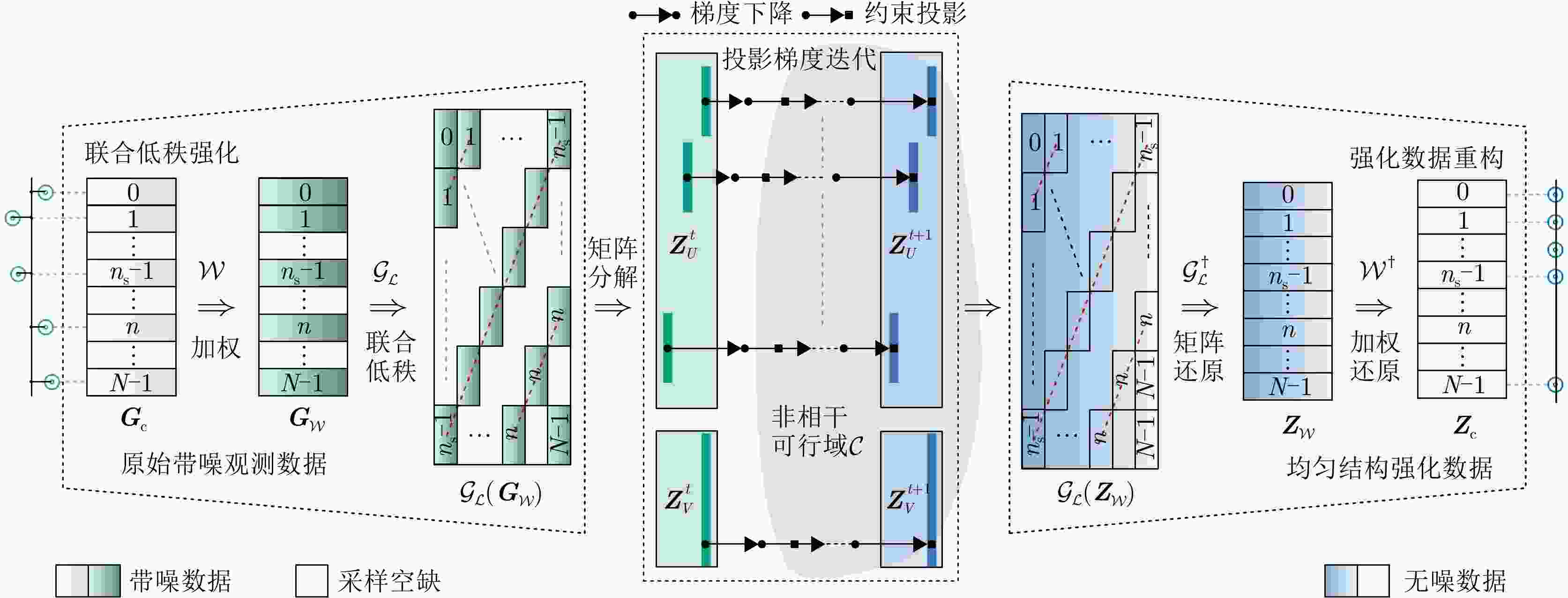
表 1 HLPGD超分辨算法流程

Table 1. The process of HLPGD super-resolution algorithm

算法：HLPGD
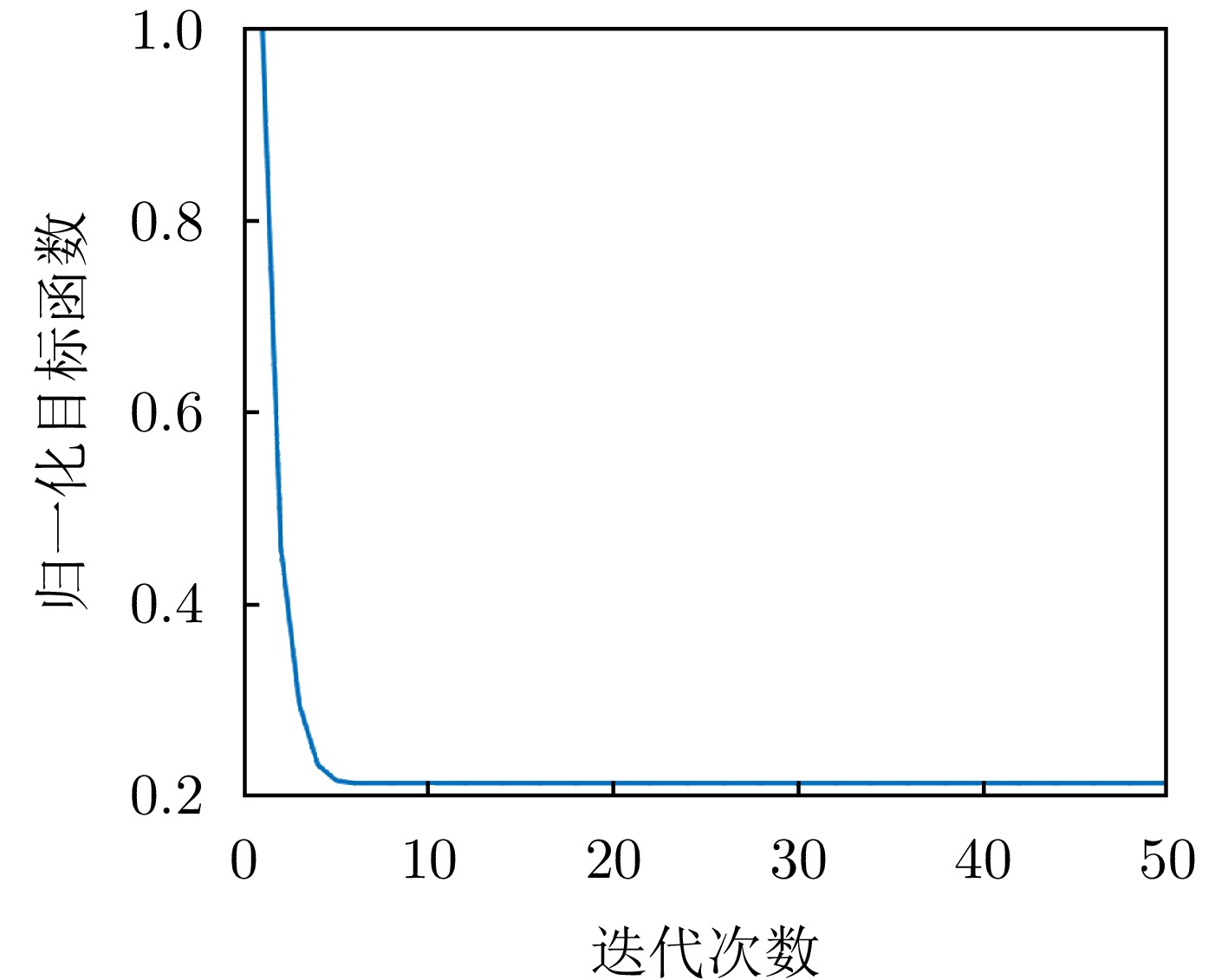
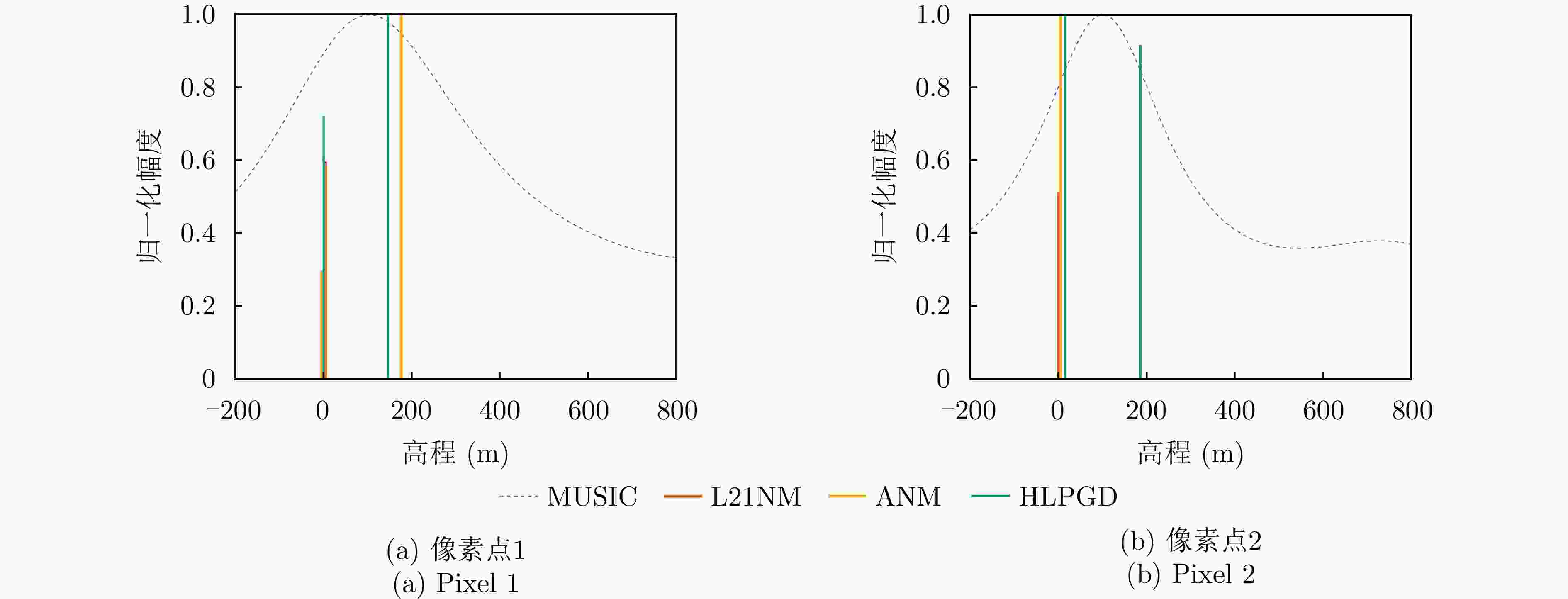
(1) 算法输入：邻域多像素观测矩阵$ {{\boldsymbol{G}}_{\text{c}}} $，采样算子$ {P_\Omega } $，梯度下降步长$ \eta $，最大迭代次数${T_{\max }}$；
(2) 变量初值：$ [{\boldsymbol{U}},{\boldsymbol{\varSigma}} ,{\boldsymbol{V}}] = {{\mathrm{SVD}}} ({{\boldsymbol{G}}_{\text{c}}}) $，$ {\boldsymbol{Z}}_U^0 = {\boldsymbol{U}}{{\boldsymbol{\varSigma}} ^{\tfrac{1}{2}}} $，$ {\boldsymbol{Z}}_V^0 = {\boldsymbol{V}}{{\boldsymbol{\varSigma}} ^{\tfrac{1}{2}}} $；
(3) 迭代求解：For count $t = 1:{T_{\max }}$
$ {\boldsymbol{Z}}_U^{t + 1} = {{\boldsymbol{P}}_\mathcal{C}}({\boldsymbol{Z}}_U^t - \eta \nabla F({\boldsymbol{Z}}_U^t)) $
$ {\boldsymbol{Z}}_V^{t + 1} = {P_\mathcal{C}}({\boldsymbol{Z}}_V^t - \eta \nabla F({\boldsymbol{Z}}_V^t)) $ end
(4) 数据重构：得到收敛值$ \tilde Z_U^{} $和$ \tilde Z_V^{} $，并根据$ {\hat Z_{\text{c}}} = \mathcal{W}_{}^\dagger (\mathcal{G}_\mathcal{L}^\dagger ({\tilde Z_U}\tilde Z_V^{\text{H}})) $重构无噪声多像素信号矩阵；
(5) 频率估计：对$ {\hat {\boldsymbol{Z}}_{\text{c}}} $使用Root-MUSIC算法进行高程频率超分辨估计；
(6) 点云滤波：利用式(21)进行超分辨模型定阶实现有效点筛选；
(7) 算法输出：高程频率$\{ {f_1},{f_2},\cdots\} $。

下载: 导出CSV

表 2 机载数据集雷达系统参数

Table 2. Radar system parameters of Airborne data

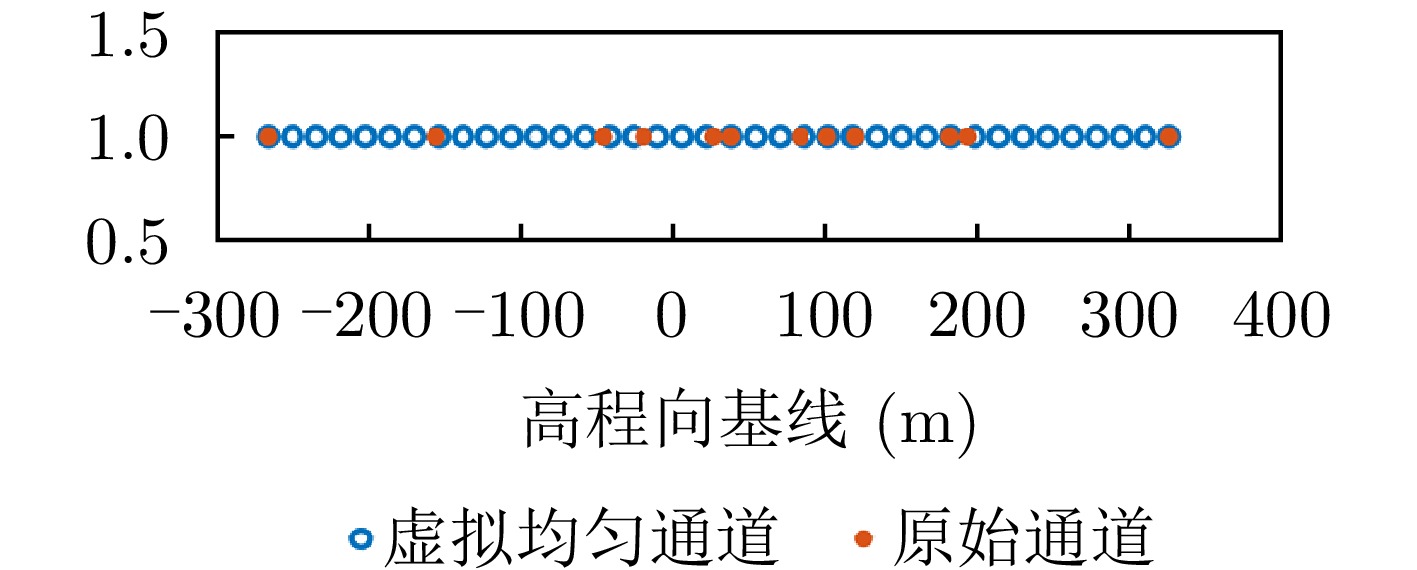
参数	数值	参数	数值
阵列通道数	8	信号波长	0.021 m
图像大小	1200×3100	方位分辨率	0.073 m
下视角	32.00°	距离分辨率	0.150 m
平台高度	1.67 km	高程分辨率	26.73 m

下载: 导出CSV

表 3 星载陆探一号卫星数据集雷达系统参数

Table 3. Radar system parameters of Spaceborne data of LuTan-1 satellites

参数	数值	参数	数值
观测航过数	12	信号波长	0.238 m
图像大小	2880×3200	方位分辨率	1.67 m
下视角	51.67°	距离分辨率	1.87 m
轨道高度	607 km	高程分辨率	182.4 m

下载: 导出CSV

表 4 实测数据超分辨成像指标汇总

Table 4. Summary of super-resolution imaging metrics of measured data

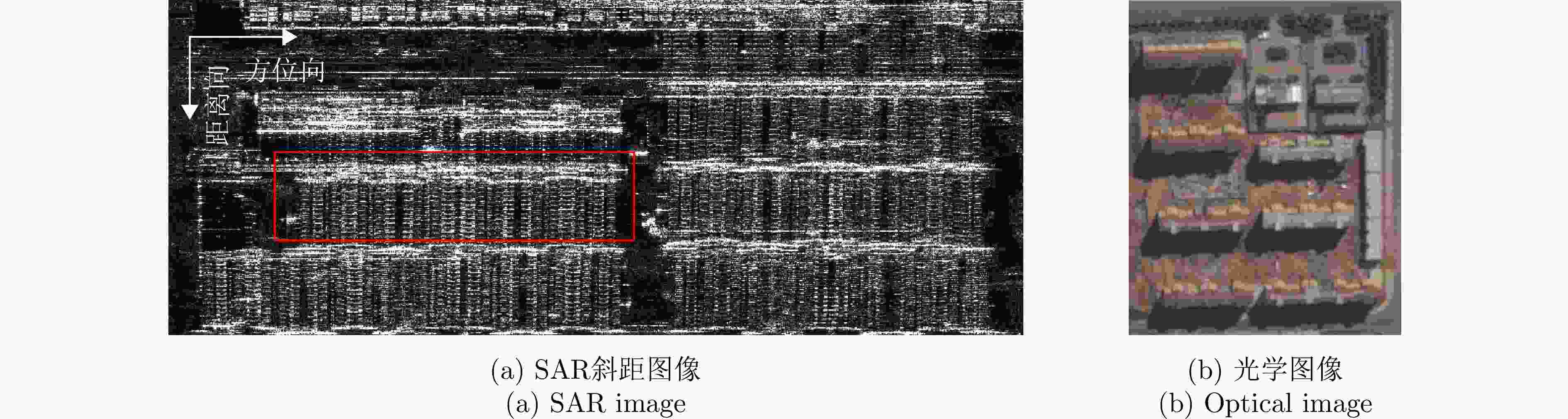
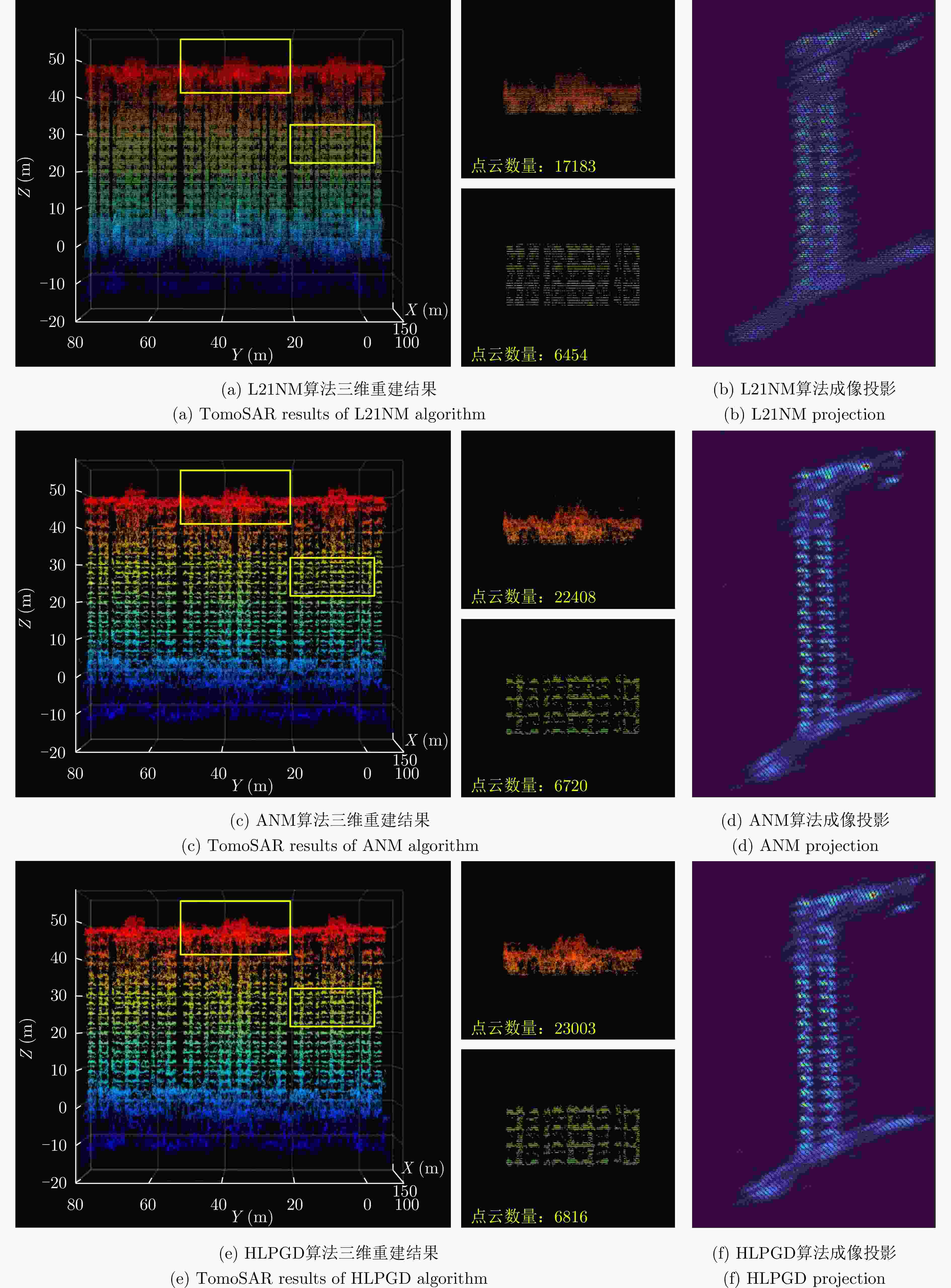
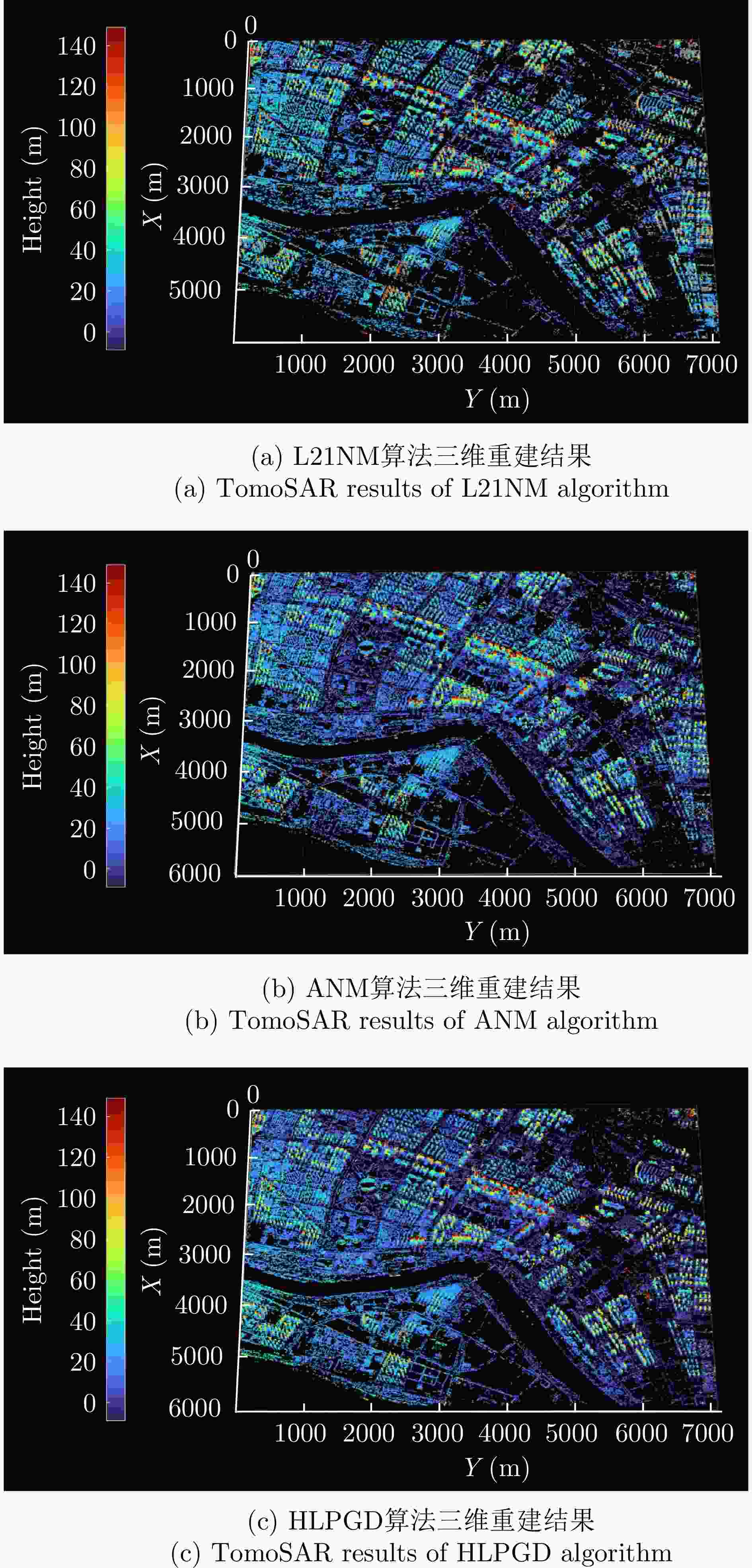
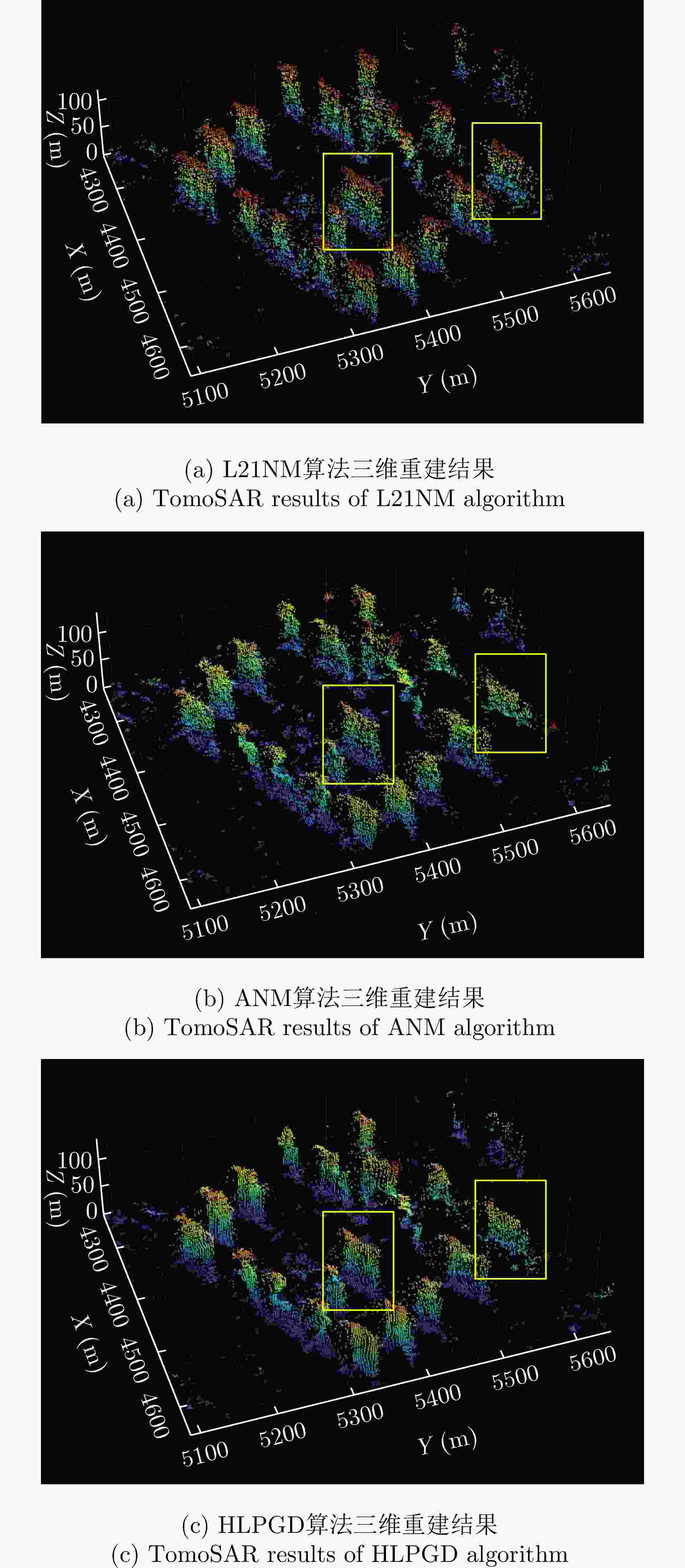
算法	Ku波段机载数据集(运城)		L波段星载数据集(南京)
算法	处理时间(min)	三维点云重建数	处理时间(min)	三维点云重建数
L21NM	284.14	232181	5705.5	657863
ANM	11.12	247352	851.3	772789
HLPGD	8.98	276915	709.5	823788

下载: 导出CSV

参考文献(39)

[1]	FORNARO G, LOMBARDINI F, and SERAFINO F. Three-dimensional multipass SAR focusing: experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 702–714. doi: 10.1109/TGRS.2005.843567.
[2]	REIGBER A, MOREIRA A, and PAPATHANASSIOU K P. First demonstration of airborne SAR tomography using multibaseline L-band data[C]. IEEE International Geoscience and Remote Sensing Symposium. Hamburg, Germany, 1999: 44-46(1). doi: 10.1109/IGARSS.1999.773395.
[3]	FORNARO G and SERAFINO F. Imaging of single and double scatterers in urban areas via SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3497–3505. doi: 10.1109/TGRS.2006.881748.
[4]	丁赤飚, 仇晓兰, 徐丰, 等. 合成孔径雷达三维成像——从层析、阵列到微波视觉[J]. 雷达学报, 2019, 8(6): 693–709. DING Chibiao, QIU Xiaolan, XU Feng, et al. Synthetic aperture radar three-dimensional imaging: from TomoSAR and array InSAR to microwave vision[J]. Journal of Radars, 2019, 8(6): 693–709.
[5]	WANG C, LI Z, HAI Y, et al. Multistatic TomoSAR 3D Imaging Technique via Matrix Completion for Structured Targets[J]. IEEE Transactions on Geoscience and Remote Sensing. doi: 10.1109/TGRS.2025.3563481.
[6]	毕辉, 金双, 王潇, 等. 基于高分三号SAR数据的城市建筑高分辨率高维成像[J]. 雷达学报, 2022, 11(1): 40–51. BI Hui, JIN Shuang, WANG Xiao, et al. High-resolution high-dimensional imaging of urban building based on GaoFen-3 SAR Data[J]. Journal of Radars, 2022, 11(1): 40–51.
[7]	ZHU X X and BAMLER R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. doi: 10.1109/TGRS.2010.2050487.
[8]	ZHU X X and BAMLER R. Superresolving SAR tomography for multidimensional imaging of urban areas: compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. doi: 10.1109/MSP.2014.2312098.
[9]	RAMBOUR C, DENIS L, TUPIN F, et al. Introducing spatial regularization in SAR tomography reconstruction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8600–8617. doi: 10.1109/TGRS.2019.2921756.
[10]	YANG Z and XIE L. On gridless sparse methods for line spectral estimation from complete and incomplete data[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3139–3153. doi: 10.1109/TSP.2015.2420541.
[11]	LI Y and CHI Y. Off-the-grid line spectrum denoising and estimation with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2016, 64(5): 1257–1269. doi: 10.1109/TSP.2015.2496294.
[12]	杜邦, 仇晓兰, 张柘, 等. 基于扰动的结合Off-grid目标的层析SAR三维成像方法[J]. 雷达学报, 2022, 11(1): 62–70. DU Bang, QIU Xiaolan, ZHANG Zhe, et al. TomoSAR 3D imaging method incorporating off-grid targets based on perturbation[J]. Journal of Radars, 2022, 11(1): 62–70.
[13]	CANDÈS E and FERNANDEZ-GRANDA C. Towards a mathematical theory of super-resolution[J]. Communications on Pure and Applied Mathematics, 2014, 67(6): 906–956. doi: 10.1002/cpa.21455.
[14]	CHI Y and FERREIRA D. Harnessing Sparsity Over the Continuum: Atomic norm minimization for superresolution[J]. IEEE Signal Processing Magazine, 2020, 37(2): 39–57. doi: 10.1109/MSP.2019.2962209.
[15]	YANG Z, XIE L and ZHANG C, Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference[J]. IEEE Transactions on Signal Processing, 2013, doi: 10.1109/TSP.2012.2222378.
[16]	TANG G, BHASKAR B N SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451.
[17]	WANG X and XU F. Tomographic SAR inversion by atomic-norm minimization—The gridless compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5239113. doi: 10.1109/TGRS.2022.3223524.
[18]	WANG X and XU F. Efficient ADMM algorithm for atomic norm minimization in SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5211415. doi: 10.1109/TGRS.2024.3395510.
[19]	GAO S, ZHANG B, XU G, et al. A robust super-resolution gridless imaging framework for UAV-borne SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5210917. doi: 10.1109/TGRS.2024.3393972.
[20]	ZHANG B, XU G, YU H, et al. Array 3-D SAR tomography using robust gridless compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5205013. doi: 10.1109/TGRS.2023.3259980.
[21]	LIU M, WANG Y, DING Z, et al. Atomic norm minimization based fast off-grid tomographic SAR imaging with nonuniform sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5203517. doi: 10.1109/TGRS.2024.3358863.
[22]	SHAO M, ZHANG Z, LI J, et al. TADCG: A novel gridless tomographic SAR imaging approach based on the alternate descent conditional gradient algorithm with robustness and efficiency[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5201213. doi: 10.1109/TGRS.2023.3345454.
[23]	ZHANG S, HAO Y, WANG M, et al. Multichannel Hankel matrix completion through nonconvex optimization[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(4): 617–632. doi: 10.1109/JSTSP.2018.2827299.
[24]	CHEN Y and CHI Y. Robust spectral compressed sensing via structured matrix completion[J]. IEEE Transactions on Information Theory, 2014, 60(10): 6576–6601. doi: 10.1109/TIT.2014.2343623.
[25]	CAI J F, WANG T and WEI K. Spectral compressed sensing via projected gradient descent[J]. SIAM Journal on Optimization, 2018, 28(3): 2625–2653. doi: 10.1137/17M1141394.
[26]	LI J, CUI W and ZHANG X. Projected gradient descent for spectral compressed sensing via symmetric Hankel factorization[J]. IEEE Transactions on Signal Processing, 2024, 72: 1590–1606. doi: 10.1109/TSP.2024.3378004.
[27]	仇晓兰, 焦泽坤, 彭凌霄, 等. SARMV3D-1.0: SAR微波视觉三维成像数据集[J]. 雷达学报, 2021, 10(4): 485–498. QIU Xiaolan, JIAO Zekun, PENG Lingxiao, et al. SARMV3D-1.0: A SAR microwave vision 3D imaging dataset[J]. Journal of Radars, 2021, 10(4): 485–498.
[28]	ZHU X X, GE N and SHAHZAD M. Joint sparsity in SAR tomography for urban mapping[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1498–1509. doi: 10.1109/JSTSP.2015.2469646.
[29]	XU G, ZHANG B, YU H, et al. Sparse synthetic aperture radar imaging from compressed sensing and machine learning: Theories, applications, and trends[J]. IEEE Geoscience and Remote Sensing Magazine, 2022, 10(4): 32–69. doi: 10.1109/MGRS.2022.3218801.
[30]	杨磊,王腾腾,陈英杰,等. 低秩矩阵补全高分辨SAR成像特征重建[J]. 电子与信息学报, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992. YANG Lei, WANG Tengteng, CHEN Yingjie, et al. Feature reconstruction of high-resolution SAR imagery based on low rank matrix completion[J]. Journal of Electronics and Information Technology, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992.
[31]	MAO S and CHEN J. Blind super-resolution of point sources via projected gradient descent[J]. IEEE Transactions on Signal Processing, 2022, 70: 4649–4664. doi: 10.1109/TSP.2022.3209006.
[32]	VU T and RAICH R. On asymptotic linear convergence of projected gradient descent for constrained least squares[J]. IEEE Transactions on Signal Processing, 2022, 70: 4061–4076. doi: 10.1109/TSP.2022.3192142.
[33]	RAO B D and HARI K V S. Performance analysis of Root-MUSIC[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(12): 1939–1949. doi: 10.1109/29.45540.
[34]	BUDILLON A and SCHIRINZI G. GLRT based on support estimation for multiple scatterers detection in SAR tomography[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1086–1094. doi: 10.1109/JSTARS.2015.2494376.
[35]	任烨仙, 徐丰. 若干层析SAR成像方法在解叠掩性能上的对比分析[J]. 雷达学报, 2022, 11(1): 71–82. REN Yexian and XU Feng. Comparative analysis of layover resolution performance for TomoSAR imaging methods[J]. Journal of Radars, 2022, 11(1): 71–82.
[36]	姬昂, 裴昊, 张邦杰, 等. 阵列SAR高分辨三维成像与点云聚类研究[J]. 电子与信息学报, 2024, 46(5): 2087–2094. JI Ang, PEI Hao, ZHANG Bangjie, et al. High-resolution 3D imaging and point cloud clustering for array SAR[J]. Journal of Electronics & Information Technology, 2024, 46(5): 2087–2094.
[37]	任子帅, 张照, 高雨欣, 等. 基于自适应高程约束的TomoSAR三维成像[J]. 雷达学报, 2023, 12(5): 1056–1068. doi: 10.12000/JR23111. REN Zishuai, ZHANG Zhao, GAO Yuxin, et al. Three-dimensional imaging of tomographic SAR based on adaptive elevation constraint[J]. Journal of Radars, 2023, 12(5): 1056–1068. doi: 10.12000/JR23111.
[38]	LI T, ZHANG Y, WANG L, et al. First application demonstrations of Lu Tan-1 SAR satellites[C]. 2023 SAR in Big Data Era (BIGSARDATA). Beijing, China, 2023: 1-4. doi: 10.1109/BIGSARDATA59007.2023.10294711.
[39]	XU G, CHEN Y, JI A, et al. 3-D high-resolution imaging and array calibration of ground-based millimeter-wave MIMO radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2024, 72(8): 4919–4931. doi: 10.1109/TMTT.2024.3352406.