基于多域联合直达波估计的建筑布局层析成像方法

李念; 刘杰; 于君明; 朱智豪; 刘剑光; 郭世盛; 陈家辉; 崔国龙; 孔令讲; 杨晓波

doi:10.12000/JR24220

基于多域联合直达波估计的建筑布局层析成像方法

DOI: 10.12000/JR24220

1.
电子科技大学信息与通信工程学院成都 611731
2.
中国电子科技集团公司第二十七研究所郑州 450047

基金项目: 国家自然科学基金(62401098, 62371110)

详细信息

作者简介:
李念，博士生，主要研究方向为穿墙雷达成像和射频无线电层析成像

刘杰，研究员，主要研究方向为航天测控与卫星应用

于君明，研究员，主要研究方向为SAR成像处理及遥感应用

朱智豪，博士生，主要研究方向为阵列信号处理与非直视目标探测技术

刘剑光，高工，主要研究方向为计算机软件应用

郭世盛，博士，研究员，主要研究方向为城市环境目标探测、基于雷达的人体行为识别等

陈家辉，博士，师资博士后，主要研究方向为雷达非直视隐蔽探测

崔国龙，博士，教授，主要研究方向为最优化理论和算法、雷达目标检测理论、波形多样性以及城市环境目标探测等

孔令讲，博士，教授，主要研究方向为新体制雷达、统计信号处理、优化理论和算法、雷达信号处理、非合作信号处理技术和自适应阵列信号处理及城市环境目标探测等

杨晓波，教授，主要研究方向为雷达隐蔽探测与成像、太赫兹雷达等

通讯作者:
陈家辉 chenjiahui@uestc.edu.cn

责任主编：杨小鹏 Corresponding Editor: YANG Xiaopeng
中图分类号: TN957.52
计量
- 文章访问数: 15
- HTML全文浏览量: 12
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-06

Building Layout Tomography Method Based on Joint Multidomain Direct Wave Estimation

1.
School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
2.
The 27th Research Institute of China Electronics Technology Group Corporation, Zhengzhou 450047, China

Funds: The National Natural Science Foundation of China (62401098, 62371110)

More Information

Corresponding author: CHEN Jiahui, chenjiahui@uestc.edu.cn

摘要

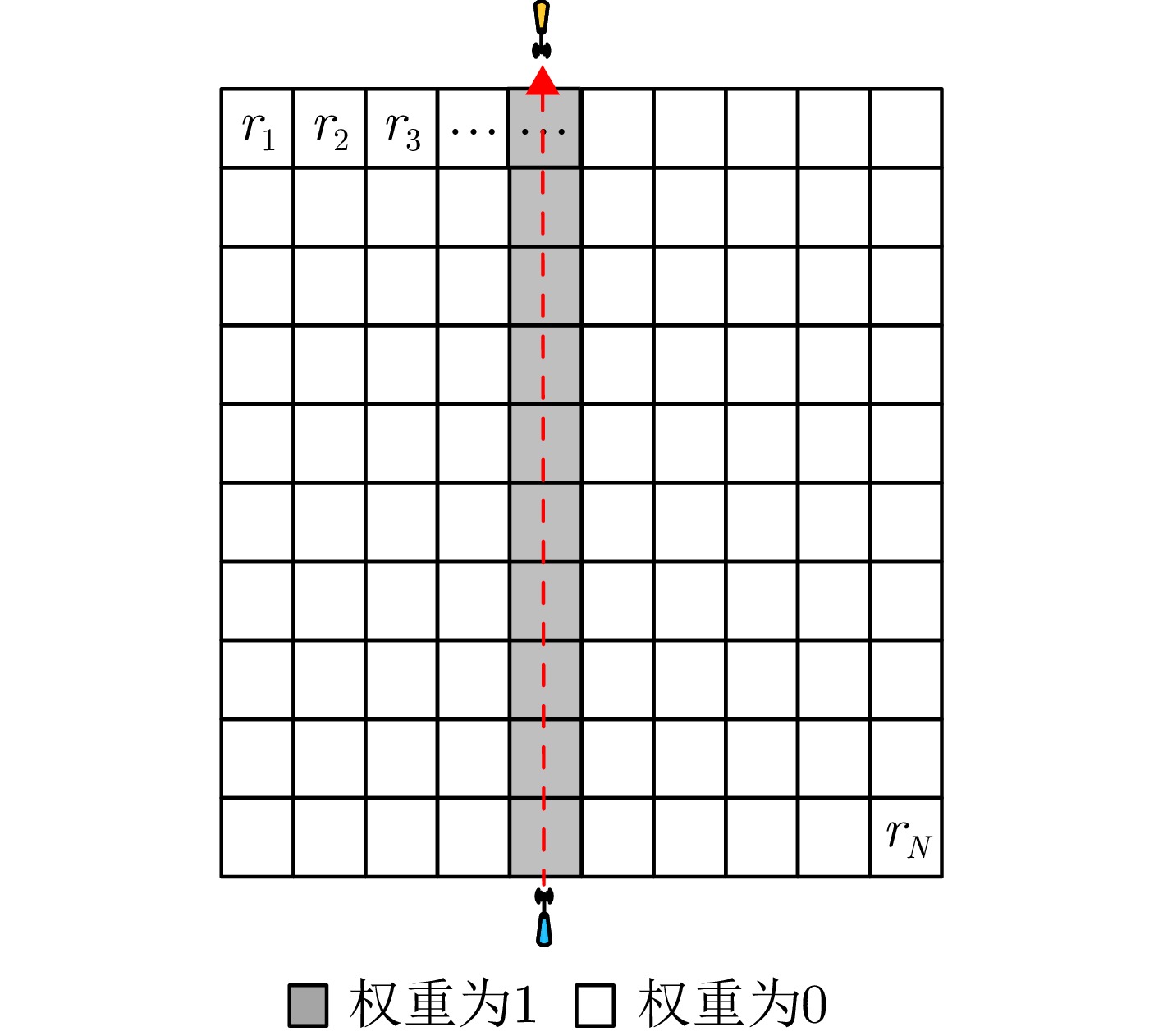
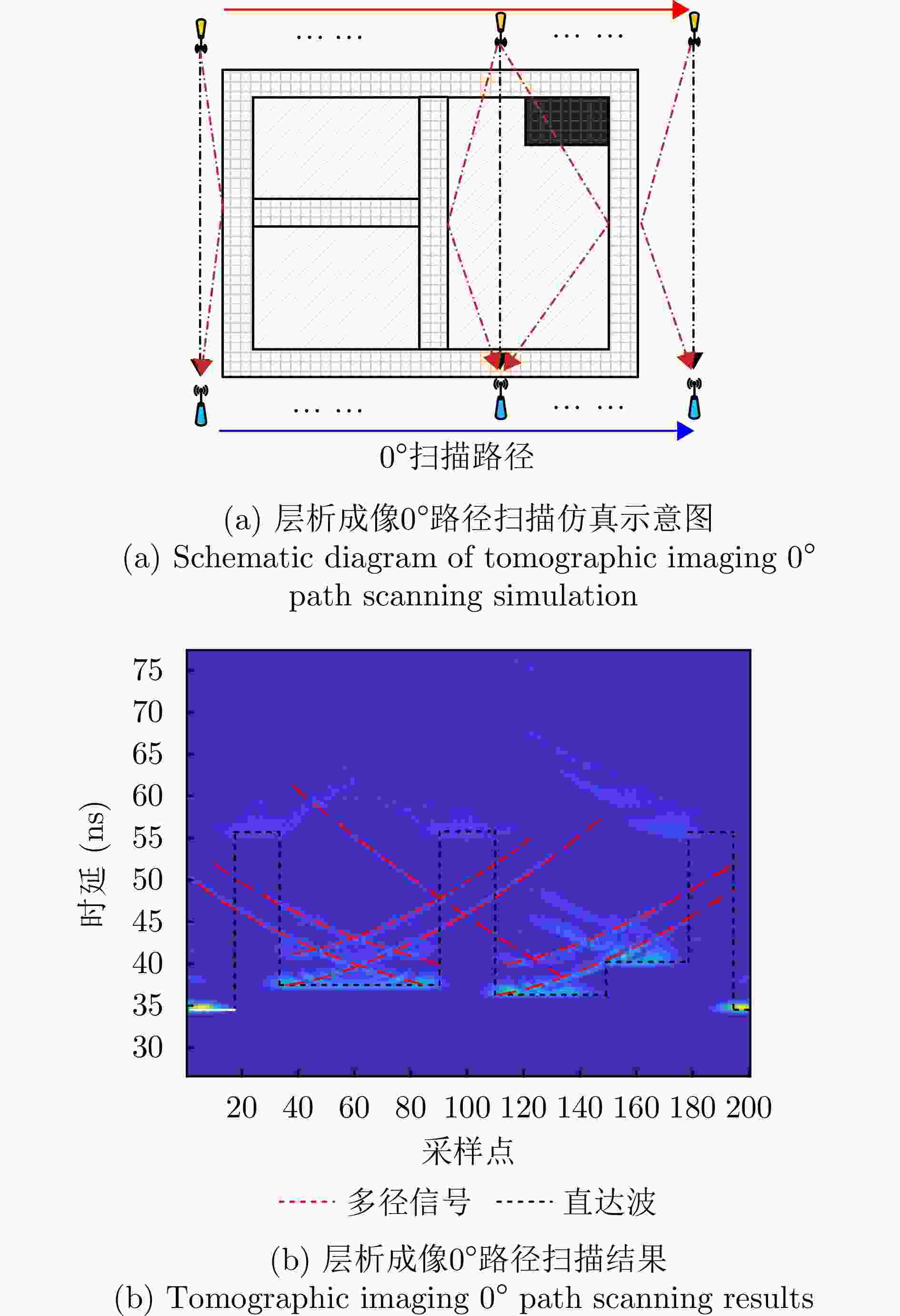
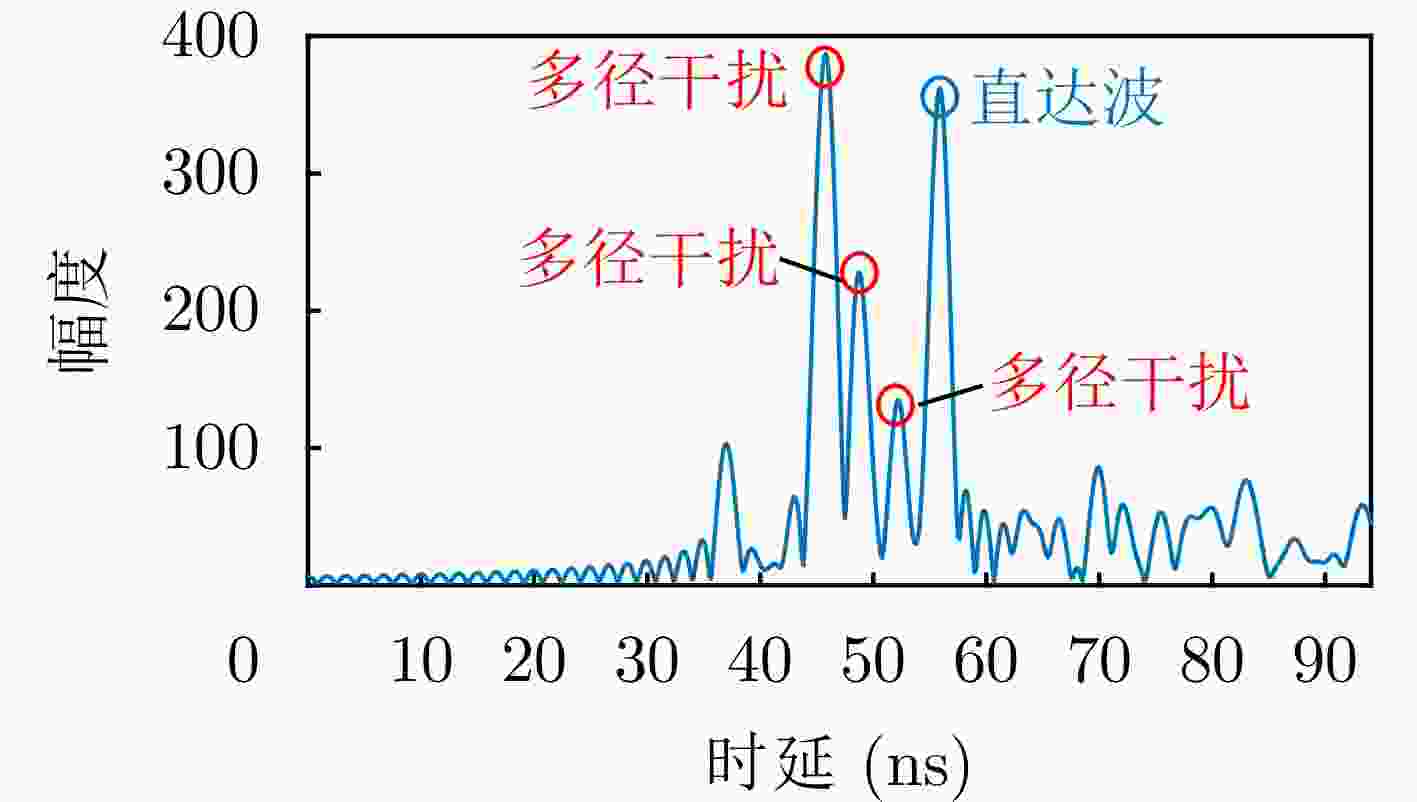
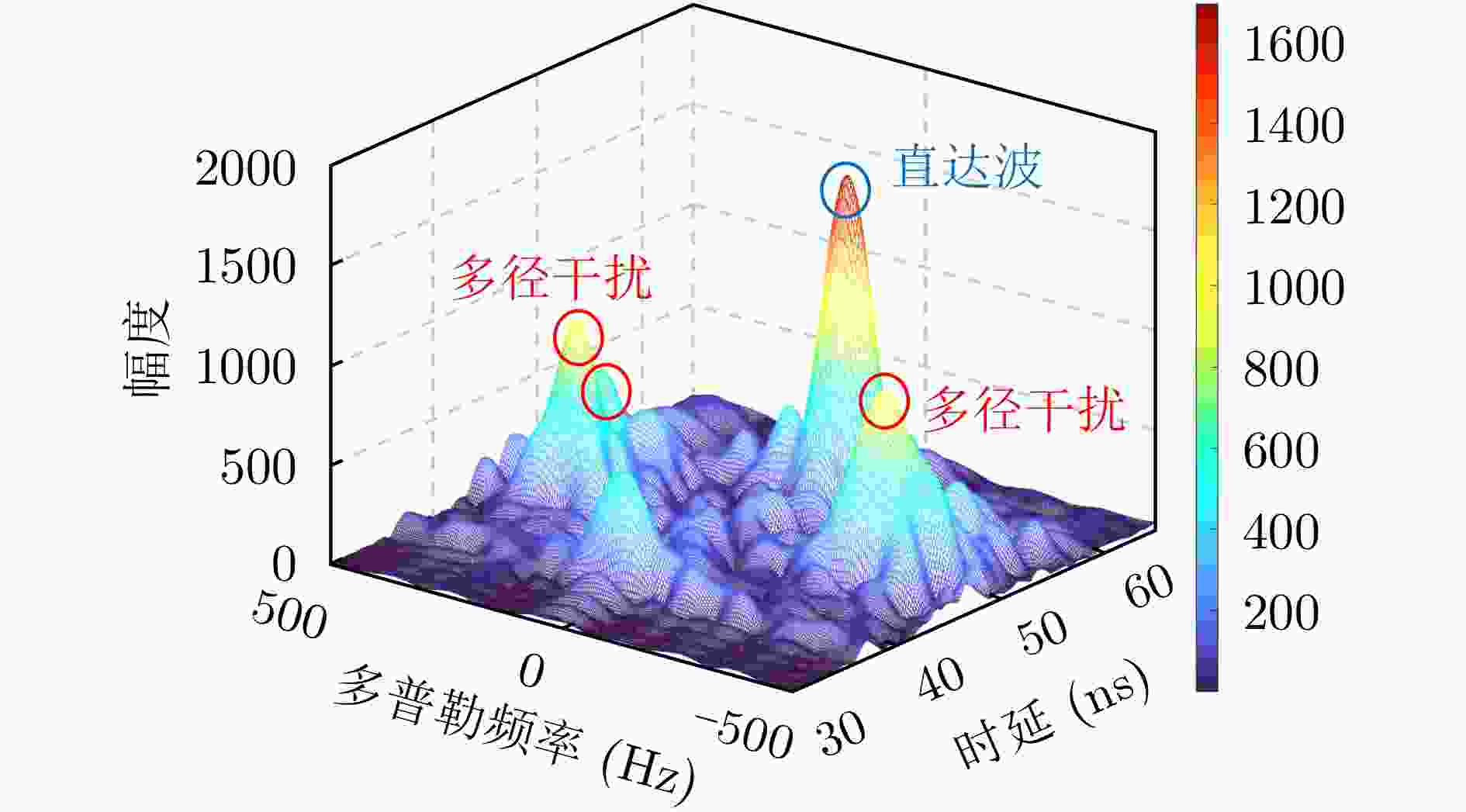
摘要: 在进入陌生建筑物之前掌握其内部结构信息，能够为反恐作战、灾害救援、监视管控等多种应用提供支持，具有重要的现实意义和研究价值。为实现建筑布局结构信息获取，该文开展了基于多域联合直达波估计的建筑布局层析成像方法研究。首先，建立了线性近似模型，实现了直达波信号传播时延与未知建筑布局图像之间的映射关系；在此模型基础上，分析了在层析成像模式下直达波信号与多径信号在快时间域、慢时间域与多普勒域中的分布特性，提出了一种基于多域联合的直达波估计算法，实现了多径干扰抑制与直达波信号精确估计；此外，提出了一种总变分约束的投影矩阵自适应修正代数重建算法，提升了有限数据下的建筑布局反演质量；最后，电磁仿真与实测实验结果证明了所提出的建筑布局层析成像方法的有效性，其重建结果的结构相似性指标分别可达到91.2%和81.7%，显著优于现有建筑布局层析成像方法。
- 建筑布局层析成像 /
- 直达波估计 /
- 代数重建技术 /
- 总变分约束 /
- 投影矩阵自适应修正
Abstract: Obtaining internal layout information before entering unfamiliar buildings is crucial for various applications, such as counter-terrorism operations, disaster relief, and surveillance, highlighting its great practical significance and research value. To enable the acquisition of the building layout information, this paper presents a building layout tomography method based on joint multidomain direct wave estimation. First, a linear approximation model is established to map the relationship between the propagation delay of direct wave signals and the layout of the unknown building. Using this model, the distribution characteristics of direct wave and multipath signals in the fast-time, slow-time, and Doppler domains are analyzed in the tomographic imaging mode. A joint multidomain direct wave estimation algorithm is then proposed to achieve the suppression of multipath interference and precise estimation of direct wave signals. Additionally, a projection matrix adaptive correction algebraic reconstruction algorithm with total variation constraints is proposed, which enhances building layout inversion quality under limited data scenarios. Finally, electromagnetic simulation and experimental results demonstrate the effectiveness of the proposed building layout tomography method, with structural similarity indices of 91.2% and 81.7% for the reconstructed results, significantly outperforming existing building layout tomography methods.

HTML全文

图 1 射频层析成像示意图

Figure 1. Schematic diagram of RTI

下载: 全尺寸图片幻灯片

图 2 线性层析投影模型示意图

Figure 2. Schematic diagram of linear tomographic projection model

下载: 全尺寸图片幻灯片

图 3 直达波与多径信号对比示意图

Figure 3. Comparison diagram of propagation time between direct wave and multipath propagation

下载: 全尺寸图片幻灯片

图 4 第96个采样点脉冲压缩结果

Figure 4. The 96th sampling point pulse compression result

下载: 全尺寸图片幻灯片

图 5 第91～101个采样点R-D谱结果

Figure 5. R-D spectrum results of sampling points 91th～101th

下载: 全尺寸图片幻灯片

图 6 多径抑制结果

Figure 6. Multipath suppression results

下载: 全尺寸图片幻灯片

图 7 仿真场景图

Figure 7. Simulation scene diagram

下载: 全尺寸图片幻灯片

图 8 0°路径观测数据估计结果

Figure 8. Observation data estimation results of 0 ° path

下载: 全尺寸图片幻灯片

图 9 仿真场景重建结果

Figure 9. Simulation scene reconstruction results

下载: 全尺寸图片幻灯片

图 10 合成孔径成像结果

Figure 10. Synthetic aperture imaging results

下载: 全尺寸图片幻灯片

图 11 –10 dB～10 dB信噪比下不同方法重建结果对比

Figure 11. Comparison of reconstruction results using different methods at SNR ranging from –10 dB to 10 dB

下载: 全尺寸图片幻灯片

图 12 实测场景图

Figure 12. Actual scene diagram

下载: 全尺寸图片幻灯片

图 13 实测场景重建结果

Figure 13. Real scene reconstruction results

下载: 全尺寸图片幻灯片

表 1 PMAM-ART-TV算法流程

Table 1. PMAM-ART-TV algorithm Flow

输入： P, A，初始化$ {\boldsymbol{O}}=0 $，外部停止标准${\varepsilon _o}$，内部停止标准　${\varepsilon _i}$，外部迭代次数$t = 0$，外部最大迭代次数$ {T_o} $，内部最大迭代　次数${T_i}$
输出: $ \tilde{{\boldsymbol{O}}}={\boldsymbol{O}}^{t} $
repeat
1、代数重建迭代：
$k = 0$
求解式(16)、式(17)更新$ \Delta C_{}^{k + 1} $
求解式(18)更新$ {\boldsymbol{O}}_n^{k + 1} $
$ k = k + 1 $
直到$k = {T_i}$或者$ \Vert {{\boldsymbol{O}}}^{k+1}-{{\boldsymbol{O}}}^{k}\Vert \le {\varepsilon }_{i} $，输出$ {{{\boldsymbol{O}}}_{ART}} $
2、总变分约束迭代：
$k = 0$,$ {{\boldsymbol{O}}} = {{{\boldsymbol{O}}}_{ART}} $, $ {{{\boldsymbol{u}}}^k} = 0 $
求解式(23)更新$ {{{\boldsymbol{u}}}^{k + 1}} $
求解式(24)更新${{\boldsymbol{b}}}_x^{k + 1}$, ${{\boldsymbol{b}}}_y^{k + 1}$
求解式(25)更新$ {{\boldsymbol{d}}}_x^{k + 1} $, $ {{\boldsymbol{d}}}_y^{k + 1} $
$ {{\boldsymbol{O}}} = {{{\boldsymbol{u}}}^{k + 1}} $, $ k = k + 1 $
直到$k = {T_i}$或者$ \Vert {{\boldsymbol{O}}}^{k+1}-{{\boldsymbol{O}}}^{k}\Vert \le {\varepsilon }_{i} $，输出O
3、更新投影矩阵
求解式(28)更新A, $ {{{\boldsymbol{O}}}^{t + 1}} $, $t = t + 1$
until直到$t = {T_o}$或者$ \Vert {{\boldsymbol{O}}}^{t+1}-{{\boldsymbol{O}}}^{t}\Vert \le {\varepsilon }_{o} $

下载: 导出CSV

表 2 仿真参数

Table 2. Simulation parameters

类型	仿真参数	数值
信号参数	发射信号	步进频信号
	中心频率	1.5 GHz
	带宽	600 MHz
	单频点持续时间	100 us
扫描参数	采样路径长度	10 m
	采样路径数目	4组
	采样间隔	0.05 m
场景参数	场景尺寸	2 m×2 m
	墙体厚度	0.20 m
	相对介电常数	4
	电导率	0.01 S/m

下载: 导出CSV

表 3 观测数据误差对比

Table 3. Comparison of observation data errors

观测数据	RMSE
RSSI^[15]	0.367
MAE^[18]	0.219
MD-DE	0.138

下载: 导出CSV

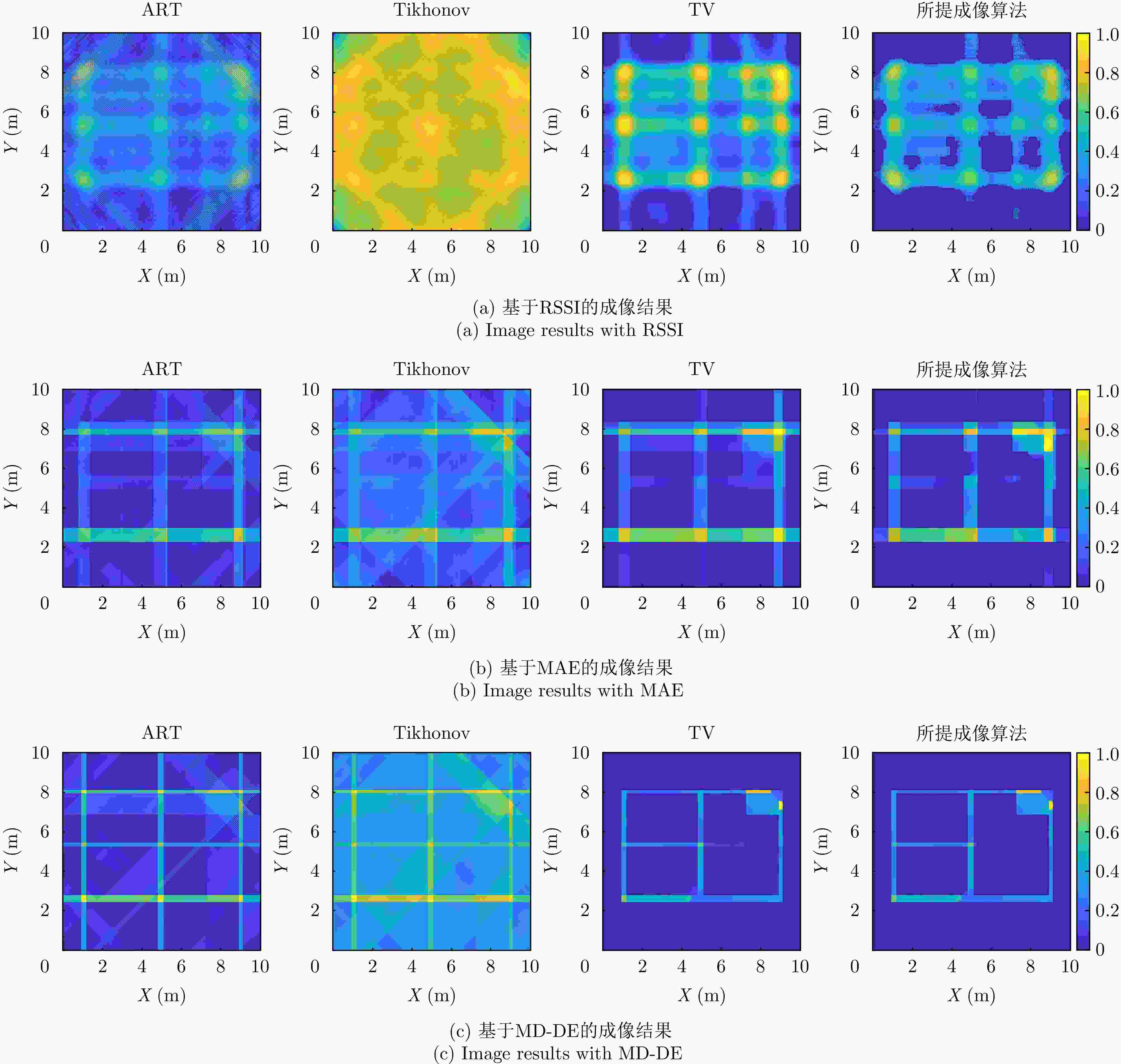
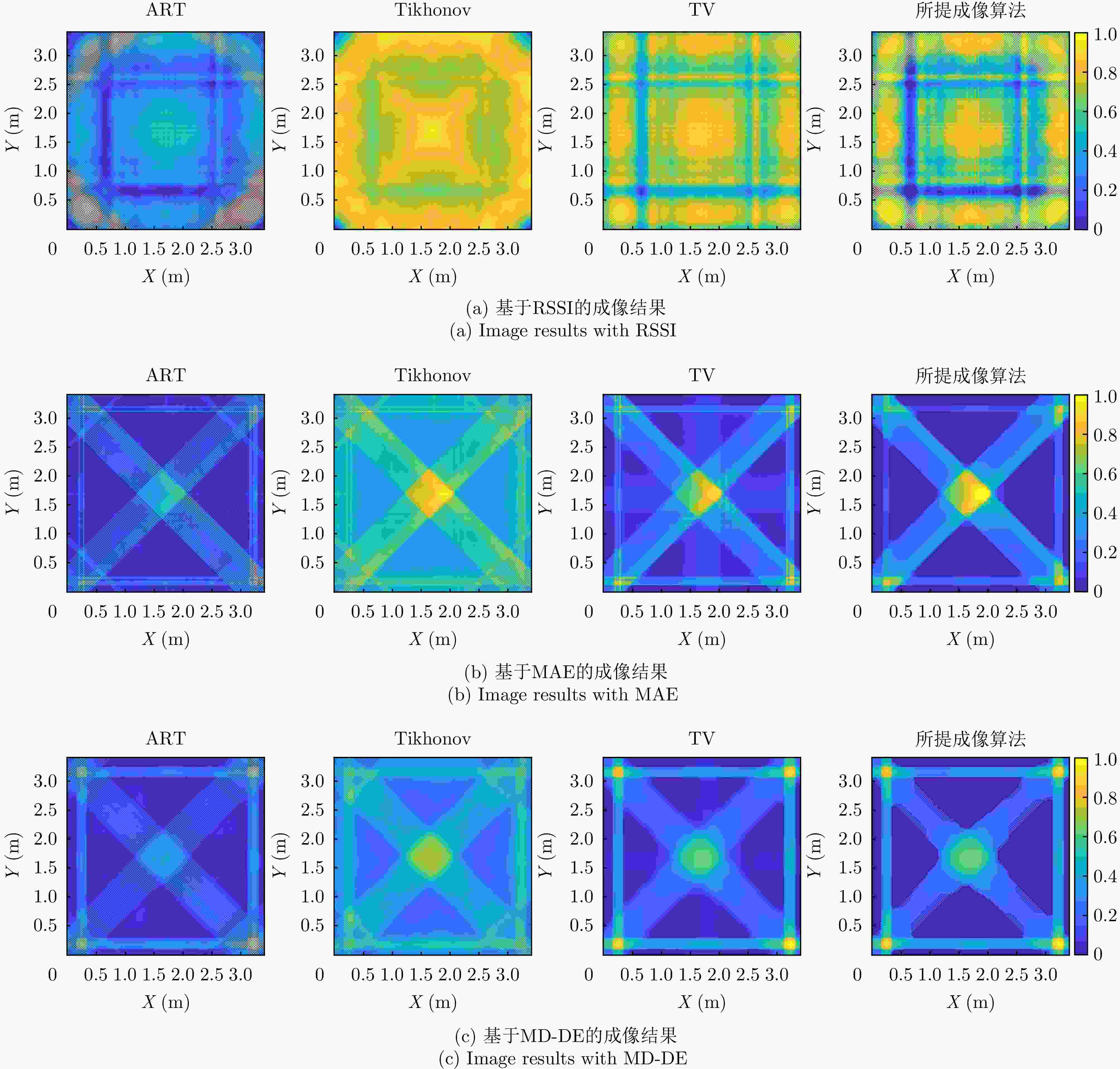
表 4 仿真成像结果SSIM指标对比

Table 4. Comparison of SSIM indicators in simulation imaging results

	ART	Tikhonov	TV	PMAM-ART-TV
RSSI	30.8%	28.7%	48.9%	68.5%
MAE	34.1%	51.4%	72.8%	86.2%
MD-DE	40.6%	58.9%	88.9%	91.2%

下载: 导出CSV

表 5 雷达系统参数

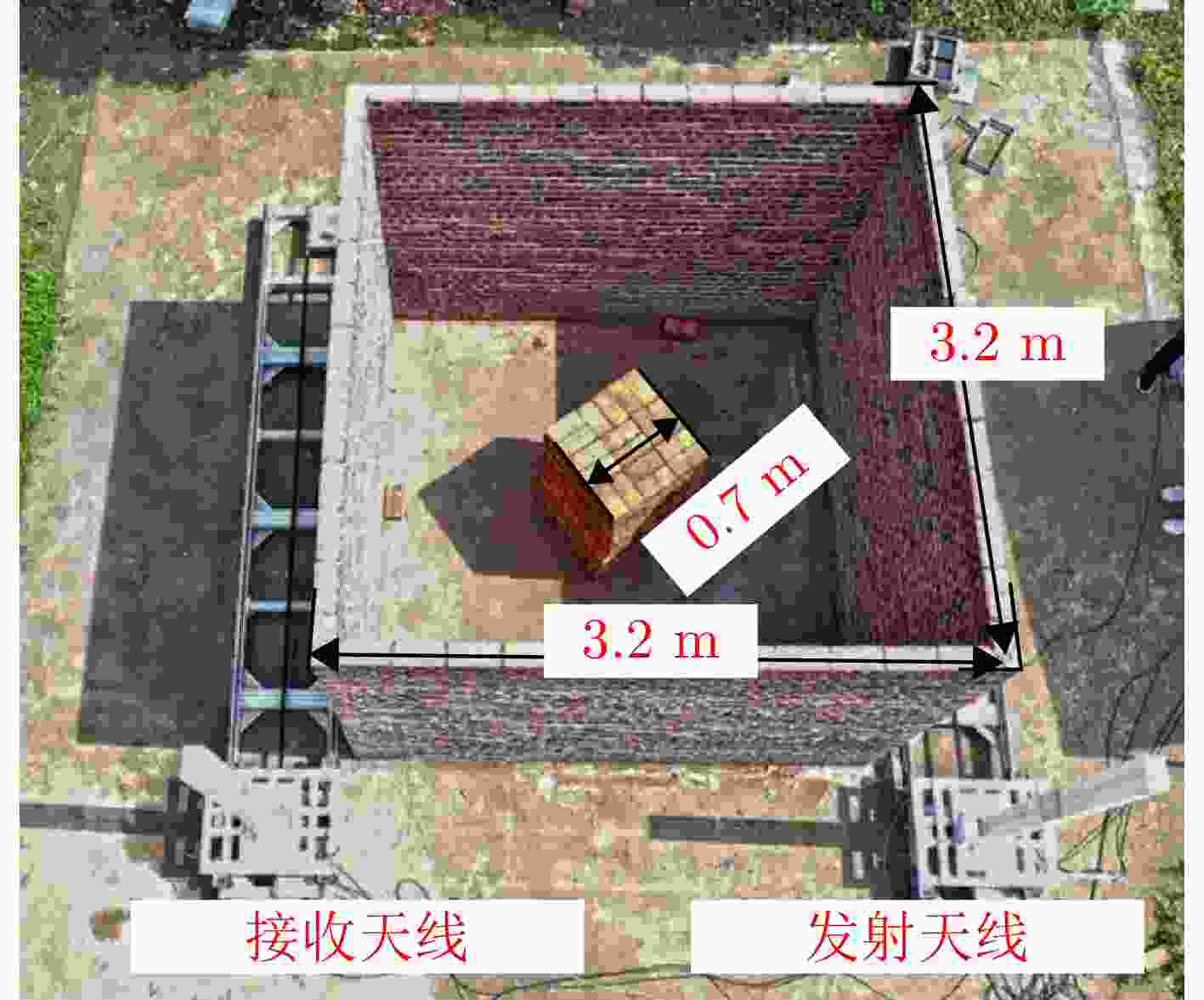
Table 5. Radar system parameters

参数名称	数值
中心频率	1.9 GHz
带宽	600 MHz
频率步进	2 MHz
频点持续时间	100 μs

下载: 导出CSV

表 6 实测成像结果SSIM指标对比

Table 6. Comparison of SSIM indicators in actual imaging results

	ART	Tikhonov	TV	PMAM-ART-TV
RSSI	31.4%	30.6%	31.2%	31.7%
MAE	43.9%	49.8%	73.6%	75.5%
MD-DE	46.3%	56.6%	78.6%	81.7%

下载: 导出CSV

参考文献(28)

[1]	金添, 宋勇平, 崔国龙, 等. 低频电磁波建筑物内部结构透视技术研究进展[J]. 雷达学报, 2021, 10(3): 342–359. doi: 10.12000/JR20119. JIN Tian, SONG Yongping, CUI Guolong, et al. Advances on penetrating imaging of building layout technique using low frequency radio waves[J]. Journal of Radars, 2021, 10(3): 342–359. doi: 10.12000/JR20119.
[2]	AHMAD F and AMIN M G. Noncoherent approach to through-the-wall radar localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4): 1405–1419. doi: 10.1109/TAES.2006.314581.
[3]	崔国龙. 超宽带穿墙雷达合成孔径成像算法研究与实现[D]. [硕士论文], 电子科技大学, 2008: 6–16. CUI Guolong. Research and implementation of synthetic aperture imaging algorithm for ultra-wideband through-the-wall radar[D]. [Master dissertation], University of Electronic Science and Technology of China, 2008: 6–16.
[4]	NKWARI P K M, SINHA S, and FERREIRA H C. Through-the-wall radar imaging: A review[J]. IETE Technical Review, 2018, 35(6): 631–639. doi: 10.1080/02564602.2017.1364146.
[5]	GUO Shisheng, CUI Guolong, KONG Lingjiang, et al. An imaging dictionary based multipath suppression algorithm for through-wall radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 269–283. doi: 10.1109/TAES.2017.2756298.
[6]	CHEN Jiahui, GUO Shisheng, LUO Haolan, et al. Non-line-of-sight multi-target localization algorithm for driver-assistance radar system[J]. IEEE Transactions on Vehicular Technology, 2023, 72(4): 5332–5337. doi: 10.1109/TVT.2022.3227971.
[7]	CHEN Jiahui, LI Nian, GUO Shisheng, et al. Enhanced 3-D building layout tomographic imaging via tensor approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5105614. doi: 10.1109/TGRS.2024.3391282.
[8]	LI Nian, CHEN Jiahui, GUO Shisheng, et al. Building layout tomographic imaging based on MIMO-UWB radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5108713. doi: 10.1109/TGRS.2024.3435831.
[9]	NGUYEN L, RESSLER M, and SICHINA J. Sensing through the wall imaging using the Army Research Lab ultra-wideband synchronous impulse reconstruction (UWB SIRE) radar[C]. SPIE 6947, Radar Sensor Technology XII, Orlando, USA, 2008: 69470B. doi: 10.1117/12.776869.
[10]	LE C, DOGARU T, NGUYEN L, et al. Ultrawideband (UWB) radar imaging of building interior: Measurements and predictions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1409–1420. doi: 10.1109/TGRS.2009.2016653.
[11]	金添, 宋勇平. 超宽带雷达建筑物结构稀疏成像[J]. 雷达学报, 2018, 7(3): 275–284. doi: 10.12000/JR18031. JIN Tian and SONG Yongping. Sparse imaging of building layouts in ultra-wideband radar[J]. Journal of Radars, 2018, 7(3): 275–284. doi: 10.12000/JR18031.
[12]	ZHANG Yang, CHEN Jiahui, GUO Shisheng, et al. Building layout tomographic reconstruction via commercial WiFi signals[J]. IEEE Internet of Things Journal, 2021, 8(20): 15500–15511. doi: 10.1109/JIOT.2021.3073912.
[13]	MOSTOFI Y. Cooperative wireless-based obstacle/object mapping and see-through capabilities in robotic networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(5): 817–829. doi: 10.1109/TMC.2012.32.
[14]	DEPATLA S, BUCKLAND L, and MOSTOFI Y. X-Ray vision with only WiFi power measurements using Rytov wave models[J]. IEEE Transactions on Vehicular Technology, 2015, 64(4): 1376–1387. doi: 10.1109/TVT.2015.2397446.
[15]	DEPATLA S, KARANAM C R, and MOSTOFI Y. Robotic through-wall imaging: Radio-frequency imaging possibilities with unmanned vehicles[J]. IEEE Antennas and Propagation Magazine, 2017, 59(5): 47–60. doi: 10.1109/MAP.2017.2731302.
[16]	KARANAM C R and MOSTOFI Y. 3D through-wall imaging with unmanned aerial vehicles using WiFi[C]. The 16th ACM/IEEE International Conference on Information Processing in Sensor Networks, Pittsburgh, USA, 2017: 131–142. doi: 10.1145/3055031.3055084.
[17]	张扬. 建筑布局结构透视微波层析成像理论与方法[D]. [博士论文], 电子科技大学, 2022: 20–82. ZHANG Yang. Theory and method of perspective microwave tomography of building layout structure[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2022: 20–82.
[18]	GUO Qichang, LI Yanlei, LIANG Xingdong, et al. A novel CT-mode through-the-wall imaging method based on time delay estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(8): 1381–1385. doi: 10.1109/LGRS.2020.3000423.
[19]	CHEN Jiahui, ZHANG Yang, LI Huquan, et al. Ultrawideband tomographic imaging in multipath-rich environment[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 8016305. doi: 10.1109/LGRS.2021.30961830.
[20]	YASWANTH K, BHATTACHARYA S, and KHANKHOJE U K. Algebraic reconstruction techniques for inverse imaging[C]. 2016 International Conference on Electromagnetics in Advanced Applications, Cairns, Australia, 2016: 756–759. doi: 10.1109/ICEAA.2016.7731509.
[21]	ANDREU F, CASELLES V, DÍAZ J I, et al. Some qualitative properties for the total variation flow[J]. Journal of Functional Analysis, 2002, 188(2): 516–547. doi: 10.1006/jfan.2001.3829.
[22]	LI Nian, ZHAN Yang, CHEN Jiahui, et al. Building layout tomographic imaging method with sparse scan angles[C]. The 2022 IEEE 8th International Conference on Computer and Communications, Chengdu, China, 2022: 2128–2132. doi: 10.1109/ICCC56324.2022.10066042.
[23]	GOLDSTEIN T and OSHER S. The split bregman method for l1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323–343. doi: 10.1137/080725891.
[24]	OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62–66. doi: 10.1109/TSMC.1979.4310076.
[25]	WARREN C, GIANNOPOULOS A, and GIANNAKIS I. GprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar[J]. Computer Physics Communications, 2016, 209: 163–170. doi: 10.1016/j.cpc.2016.08.020.
[26]	HAMILTON B R, MA Xiaoli, BAXLEY R J, et al. Radio frequency tomography in mobile networks[C]. 2012 IEEE Statistical Signal Processing Workshop, Ann Arbor, USA, 2012: 508–511. doi: 10.1109/SSP.2012.6319745.
[27]	CHEN Jiahui, GUO Shisheng, CUI Guolong, et al. Building layout reconstruction with transmissive and reflective signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5116612. doi: 10.1109/TGRS.2022.3199270.
[28]	ZHAO Jifang, JIN Liangnian, and LIU Qinghua. Through-the-wall radar sparse imaging for building walls[J]. The Journal of Engineering, 2019, 2019(21): 7403–7405. doi: 10.1049/joe.2019.0541.