作者中心
专家审稿
责编办公
编辑办公
A Novel Method for Tracking Complex Maneuvering Star Convex Extended Targets Using Transformer Network
-
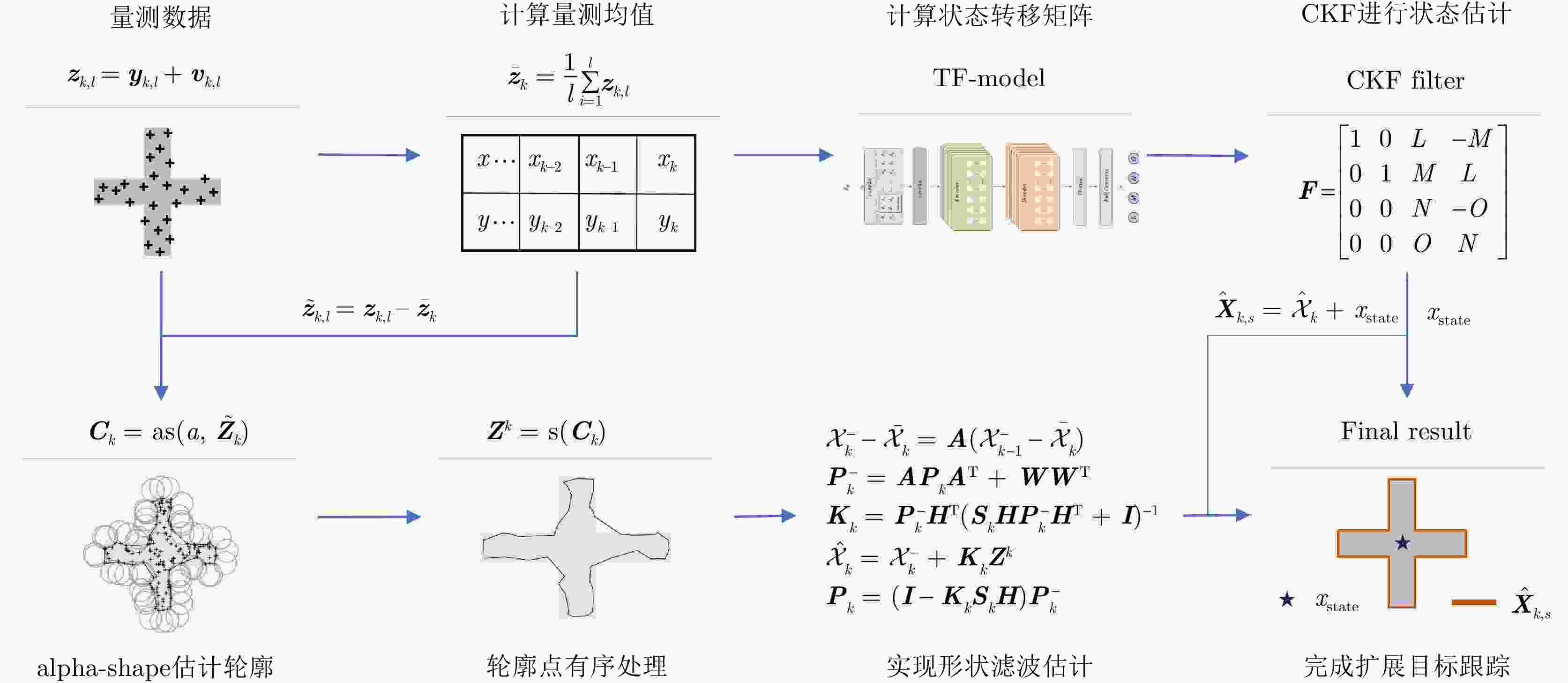
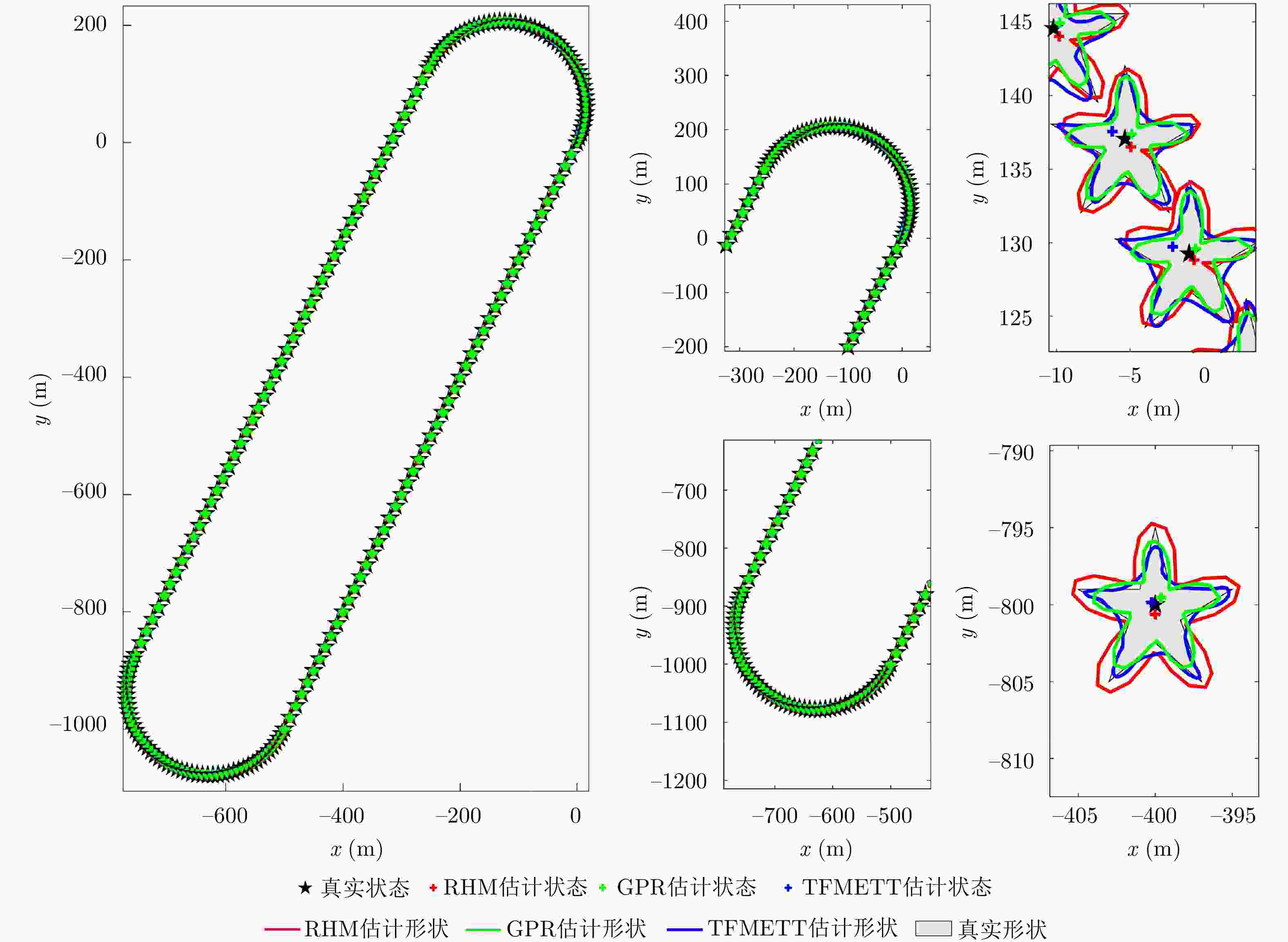
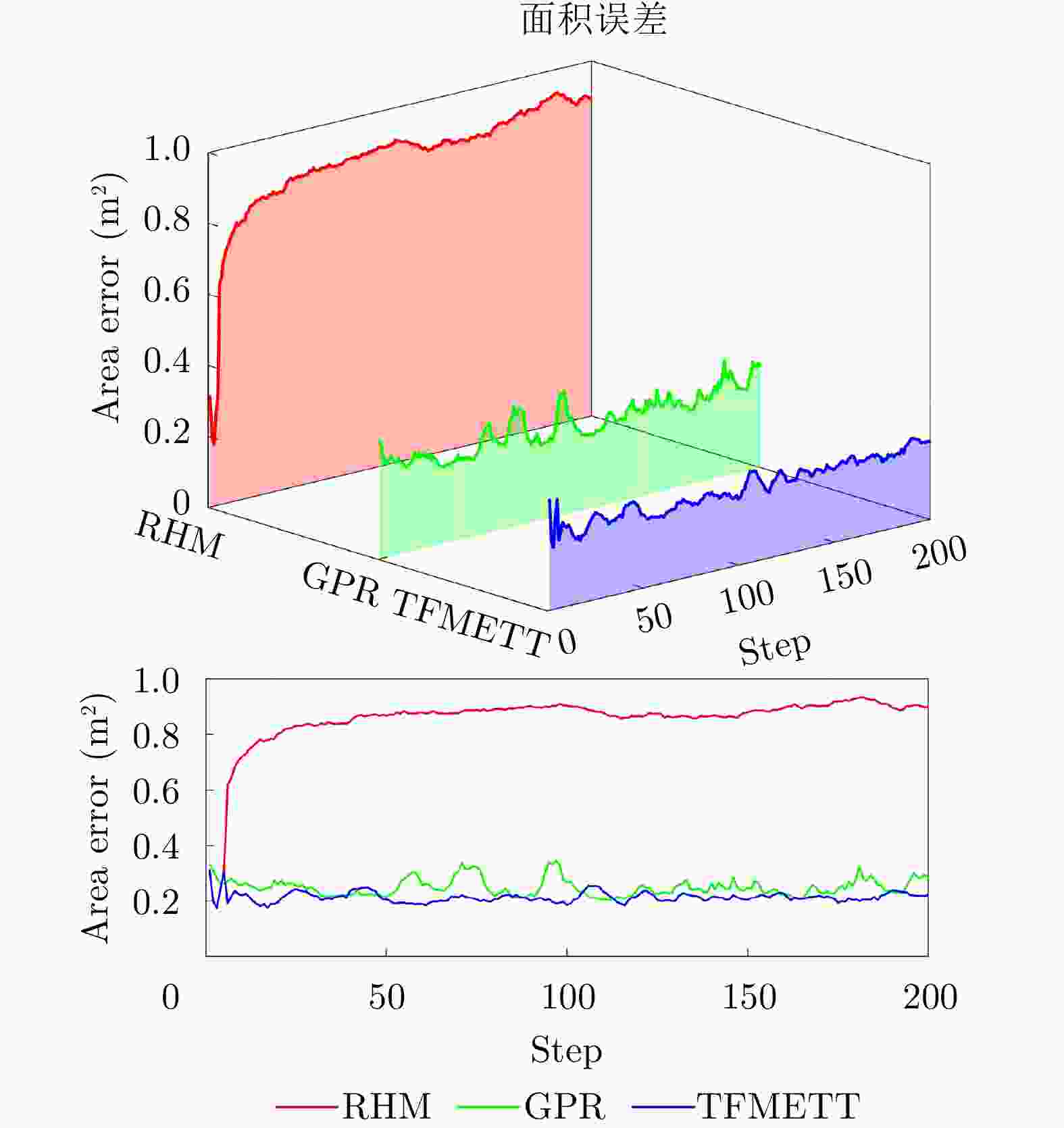
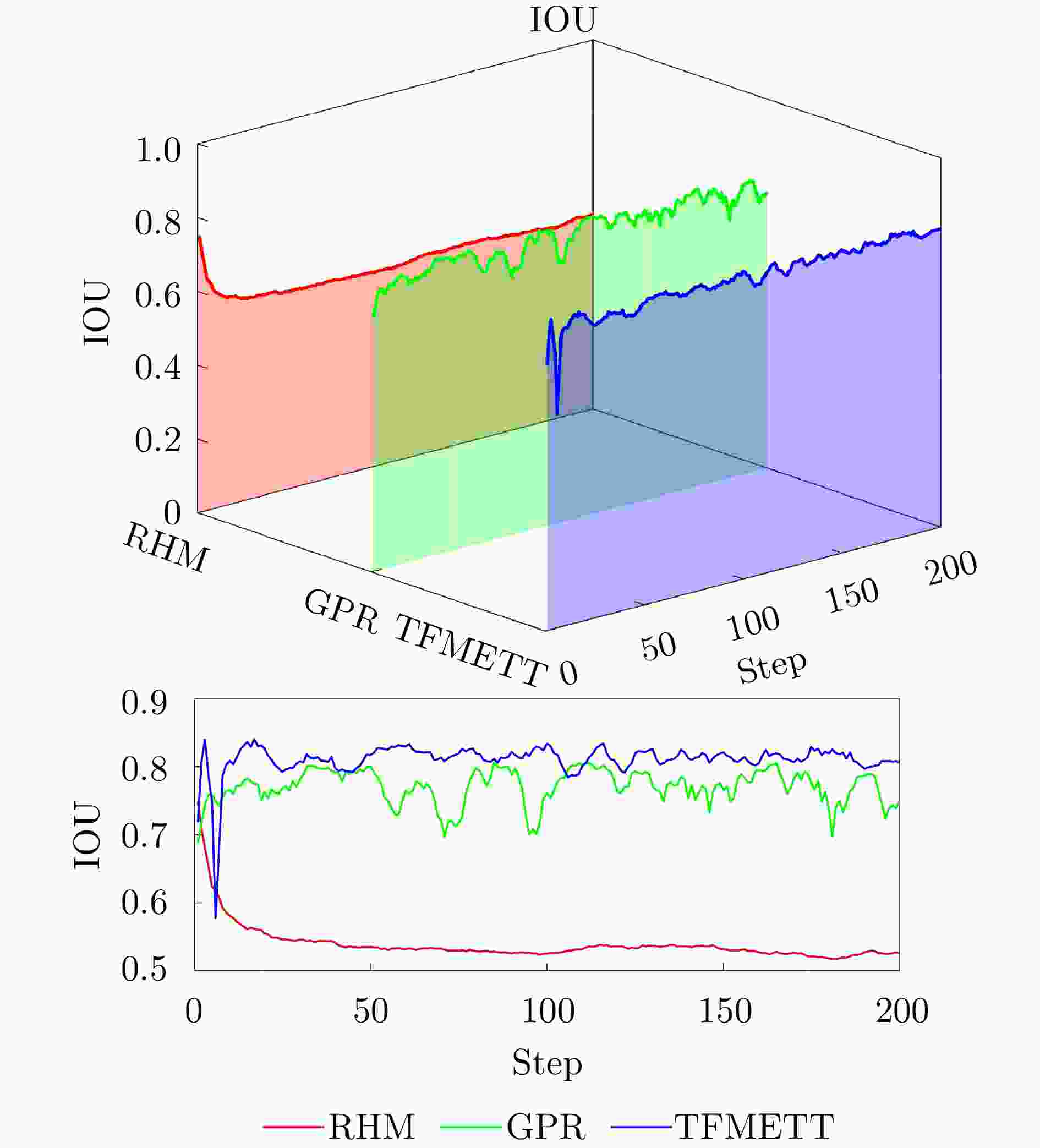
摘要: 针对复杂的机动扩展目标跟踪问题，利用Transformer网络设计了一种有效的星凸不规则形状机动扩展目标跟踪方法。首先，该文研究利用alpha-shape算法建立了星凸形状的变化模型，实现了静态场景下的星凸形扩展目标的形状估计。然后，通过对目标状态转移矩阵进行重新设计，结合Transformer网络对机动扩展目标运动状态转移矩阵进行实时估计，实现了对复杂机动目标运动过程的精准跟踪。进一步地，将估计得到的形状轮廓与运动状态进行融合，最终实现了对星凸形机动扩展目标的实时跟踪。最后，通过构造复杂的机动扩展目标跟踪场景，利用多重性能指标测试算法对形状和运动状态的综合估计性能，验证了算法的有效性。
-
关键词:
- 扩展目标跟踪 /
- 机动目标 /
- Transformer /
- 星凸形 /
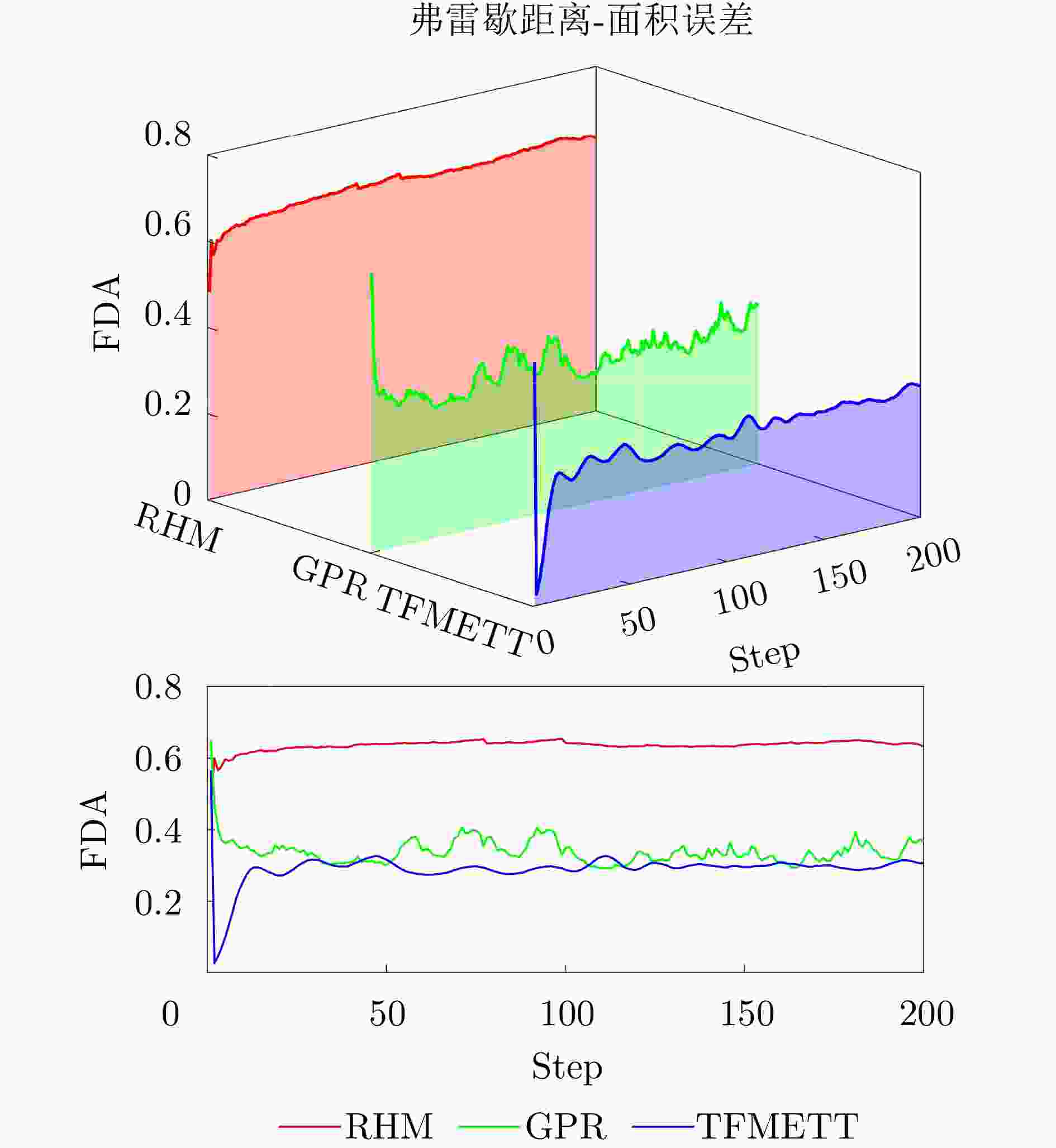
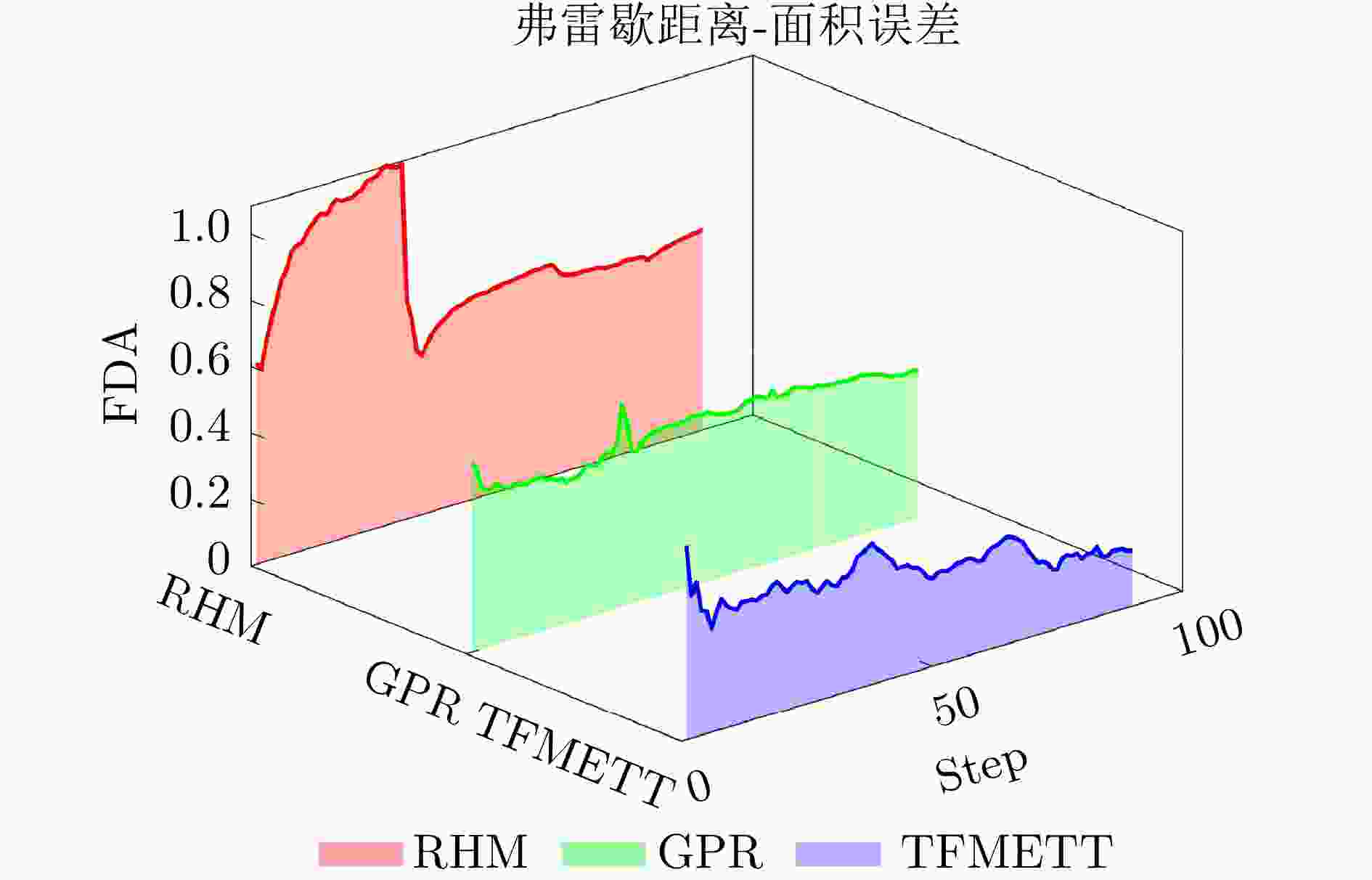
- 弗雷歇距离-面积误差
Abstract: To address the challenges in tracking complex maneuvering extended targets, an effective maneuvering extended target tracking method was proposed for irregularly shaped star-convex using a Transformer network. Initially, the alpha-shape algorithm was used to model the variations in the star-convex shape. In addition, a recursive approach was proposed to estimate the irregular shape of an extended target by detailed derivation in the Bayesian filtering framework. This approach accurately estimated the shape of a static star convex extended target. Moreover, through the structural redesign of the target state transition matrix and the real-time estimation of the maneuvering extended target’s state transition matrix using a transformer network, the accurate tracking of complex maneuvering targets was achieved. Furthermore, the real-time tracking of star convex maneuvering extended targets was achieved by fusing the estimated shape contours with motion states. This study focused on constructing certain complex maneuvering extended target tracking scenarios to assess the performance of the proposed method and the comprehensive estimation capabilities of the algorithm considering both shapes and motion states using multiple performance indicators. -
1. 引言
飞机尾流是飞机飞行时所产生的固有的流体力学现象，与周围大气相比，尾流具有独特的空气动力学特性和雷达特性，具有较强的雷达可探测性。尾流的雷达探测是航空安全、反隐身等领域的前沿研究课题。处于潮湿大气中的尾流具有较强的散射截面积(Radar Cross Section, RCS)，但受到气象杂波的影响，需要根据功率谱特性来提高可探测性。飞机尾流回波经过傅里叶变换后，其功率谱是展宽的，其检测方法包括动目标检测(Moving Target Detection, MTD)方法、谱宽检测方法、神经网络方法等，这些方法有较多局限性。在传统的MTD技术中，首先估计观测数据的功率谱，然后对各频率通道进行恒虚警率(Constant False Alarm Rate, CFAR)检测，较难对展宽的尾流功率谱进行有效积累；而谱宽检测方法在云杂波环境下虚警较高；神经网络方法需要大量的训练样本。
信息几何是在黎曼流形上采用微分几何方法研究信息领域和统计学问题的一门学科，其主要思想是把参数化的概率分布族构建为统计流形，并采用Fisher信息矩阵作为流形上的黎曼度量，以此为基础得到统计流形上的联络、曲率、测地线距离等概念，从而采用微分几何方法解决统计学中的问题。其研究对象是由概率分布族所构成的统计流形，矩阵流形就是一种重要的统计流形。与利用回波的功率谱相比，利用回波的协方差矩阵描述回波特性，其优点有：(1)不对回波进行多普勒处理，避免了多普勒处理所面临的功率谱展宽问题；(2)协方差矩阵所构成的空间在数学上为负曲率空间，适合用信息几何方法研究矩阵流形的几何结构，有利于更准确度量目标、噪声或杂波协方差矩阵间的差别。
从信息几何的角度思考问题，能为许多问题提供更加符合实际的模型框架[1]，并得出新的解决途径。1945年，印度统计学家Rao提出用Fisher信息矩阵来定义统计流形上的黎曼度量，Fisher度量与信息理论的相对熵具有紧密联系，都可以定量描述两个概率分布间可以区分的程度，从而开启了统计的几何学理论研究[2]。黎曼度量描述的是流形上切空间的性质，联络把流形上不同点处的切空间联系起来，从而使流形具有整体性。20世纪70年代，苏联数学家Chentsov引入了一族单参数的仿射联络，并证明Fisher信息与仿射联络在概率分布流形中的唯一性[3]，随后，Amari用α-仿射联络对尽可能多的统计问题进行了几何解释，取得了很大的成功，并建立了统计流形的对偶几何结构来研究信息处理，从而丰富了传统的微分几何理论，由于能够较好地描述概率分布的内在特性，微分流形的理论和方法逐步进入统计和信息处理领域[4]。有了联络，就可以定义相对于该联络的曲率，曲率描述了流形中给定区域的体积与欧氏空间中与其相当区域体积的差异程度，曲率常用于研究Jacobi场的稳定性。测地线是欧氏空间上直线段在黎曼流形上的推广，测地线是连接流形上两点的最短距离的曲线，可用于计算多元概率分布间或协方差矩阵间的测地线距离，与Kulback-Leibler分离度相比，测地线距离的优势在于它满足距离的对称性和三角不等式等重要性质[5]。实际上，测量通常含有噪声或杂波，我们需要利用统计学方法减少测量的不确定性，为了求解噪声或杂波协方差矩阵的均值，需要使目标函数，即协方差矩阵均值的经验方差，取得最小值，文献[6]利用自然梯度下降算法给出了黎曼均值的迭代计算方法，与算术均值相比，黎曼均值具有更小的经验方差。统计流形上的曲率、联络、测地线和均值等概念大大扩展了统计流形的应用范围，促进了信息几何学的产生与发展。
经过20余年的发展，信息几何学的理论迅速扩展，并在多个领域获得成功应用，已经开始应用到统计推断、控制理论、神经网络、医学成像、计算视觉、信号处理等领域[1,7]。由于较多的实际问题可以在矩阵流形上进行研究，如雷达信号处理[8,9]、矩阵方程求解[1]、医学图像处理[5,10]、流形学习、系统的稳定性与最优化等问题，将信息几何应用于矩阵流形上促进了矩阵信息几何的诞生。在用信息几何理论解决信息领域或统计学问题时，首先需要把所研究的问题构建成统计流形或矩阵流形，采用微分几何或李群方法研究流形的几何结构，从而用几何方法解决涉及的非线性问题。孙华飞等人将矩阵信息几何应用于求解矩阵方程问题，大多数矩阵方程难以得到解析解，通过将问题转化为矩阵流形上的优化问题，可以用自然梯度给出求解方案[1]。在雷达信号处理、目标检测和数据处理领域，法国Thales Air Systems研究员Barbaresco等人利用信息几何方法研究了近海小目标检测[8]、飞机尾流的检测和成像[8]、极化数据处理、STAP处理[11]等问题。文献[12]在信息几何框架下研究了雷达系统的信息分辨、信号检测、参数估计、目标跟踪等基础性和科学性问题，为雷达信号处理提供了一套全新的分析方法。总之，对于信号处理中涉及的非欧空间、非线性处理等问题，信息几何方法有优势。本文在前人研究基础上介绍了矩阵流形的几何结构，然后针对飞机尾流目标检测问题，提出了一种矩阵CFAR检测方法，分析了尾流目标的检测性能。
2. 尾流目标的多普勒特性
飞机尾流是飞机产生升力的必然产物，主要包括尾喷流和翼尖尾流两类。翼尖尾流包括两个旋向相反的漩涡，其持续时间长达数十秒到几分钟，在空间上表现为飞机后一个长的柱状分布介质目标，一般到达飞机后部百倍翼展，长达数千米，属于一种较强的湍流。欧、美、俄等对飞机尾流的关注是从航空安全领域开始的。当飞机进入前机的尾流时，会因受力不均而出现机身抖动、下沉、翻转等现象，严重时会导致飞机坠毁。飞机尾流对民用航空安全构成了巨大威胁，近年来，欧盟和美国分别投入巨资启动了SESAR (2005-2020)计划和NGATS (2005-2025)计划以提高航空安全性能[13]，飞机尾流的实时探测技术无一例外地成为各个研究计划的主要内容。从80年代开始至今，英国、法国和美国进行了多次尾流探测实验测量尾流的雷达反射率和多普勒特性，理论研究和实验结果表明，雷达能够探测到晴空尾流回波，并且能够在雨、雾等潮湿天气中有效工作，因而有望取代激光雷达成为重要的尾流探测手段。国防科技大学是国内较早从事飞机尾流探测技术研究的单位，已有周彬、李健兵、李军、刘俊凯、屈龙海、刘忠训、牛凤梁等多位博士研究尾流特性及其探测技术。
处于云、雨、雾等潮湿大气中的飞机尾流具有较强的雷达散射截面，但受到气象杂波的影响，需要根据尾流功率谱特性来提高脉冲多普勒雷达对尾流的可探测性。在潮湿大气环境下，尾流的雷达后向散射主要是由大气中的水汽微粒产生的，水气微粒的运动规律可用尾流涡旋速度模型模拟[14]，这里使用一群水汽微粒模拟尾流涡旋的运动特征，使用视频回波仿真方法对尾流回波进行建模仿真。
首先，使用一群粒子表示飞机尾流内的水汽微粒，在时刻t把所有粒子的雷达回波矢量求和，得到一个时刻尾流的合成回波矢量。t时刻离散视频回波为：
S(t)=M∑m=1Ame−jφm(t) (1) 其中，Am是第m个粒子的回波幅度，回波相位决定于粒子与雷达的距离，第m个粒子回波的相位与雷达距离的关系可表示为：
φm(t)=4πRm(t)/λw (2) 其中，
Rm(t) 为第m个粒子t时刻距雷达的距离，λw 是雷达波长。接着，假设每个粒子以Burnham-Hallock模型描述的速度做匀速圆周运动，t+1时刻运动到新的位置后，得到新的合成回波矢量
S(t+1) 。其中，每个粒子运动的Burnham-Hallock速度模型表达式为[15]：v(rm)=Γ02πrmrm2+r2c (3) 其中，
rm 表示尾涡上第m个粒子距尾涡中心的距离，rc 是尾涡的核半径，Γ0 是涡环量，表示点涡的强度，表达式为：Γ0=4MagπρVaBa (4) 式中，
Ma 为飞机重量，g为重力加速度，ρ 为室温空气密度(1.16 kg/m3)，Va 为飞机的速度，Ba 为翼展。最后，得到一个相关处理间隔内若干个时刻的回波实部和虚部，对这一复回波序列进行傅里叶变换，得到功率谱。以波音747飞机为例进行仿真。波音747的典型参数为：飞机重量
Ma=350,000kg ，飞机的速度Va=200m/s ，翼展Ba=68m ，重力加速度g=9.81m/s2 ，室温空气密度ρ=1.16kg/m3 ，计算得到Γ0=277 m2/s。一次仿真得到的飞机尾流回波如图1所示。进行多次仿真，可得到相似的归一化径向速度谱。1992年至1993年，美国通用电气公司马可尼研究中心的Sheppard使用X波段全相参脉冲多普勒雷达DX04进行了尾流雷达探测实验。在距离4.5 km处，经过相参处理，波音747飞机尾流回波接近接收机噪声电平，超过噪声尖峰2～3 dB，分析得到尾流RCS约为–73 dBsm, X波段雷达测量的功率谱如图2所示[16]。可见，视频回波建模方法仿真结果与马可尼研究中心测量的X波段功率谱具有相似的频域展宽特性，多普勒速度与尾涡旋转径向速度一致。
图 2 马可尼研究中心X波段雷达测量的功率谱[16]Figure 2. The Power Spectrum measured by the X-band radar in Marconi Research Center对于尾流目标来说，功率谱是展宽的且具有两个较大的峰值，在不同机型和不同飞行速度时，功率谱的峰值位置也不同，较难设计有效的频域CFAR检测器，特别是，需防止展宽的功率谱处于参考单元中，导致检测门限增大和检测概率降低。
3. 雷达目标回波的矩阵CFAR检测方法
设观测样本
x=[x(0)x(1)···x(n−1)]T ，传统的统计检测方法首先对观测样本提出假设：{H0:x=vH1:x=s+v (5) 式中，s为目标信号向量，
v 为噪声向量；然后从观测样本出发，制定检测准则，如奈曼-皮尔逊准则，通常可以得到似然比检测判决表达式：λ(x)=p(x|H1)p(x|H0)>η (6) 若式(6)成立，则接受H1，否则接受H0，式中，
η 为判决门限，由给定的先验条件确定。对左边的似然比进行化简，化为x的尽可能简单的表达式，称为检测统计量。假设信号和噪声都可看做零均值的高斯过程，则观测样本x服从零均值复多元高斯分布，即
p(x|R)=1πn|R|e−xHR−1x (7) 其中，R为n阶协方差矩阵。从信息几何的角度看，零均值多元复高斯分布族可以构成一个统计流形[4]
S={p(x|R)|R∈Θ} (8) 式中，
Θ⊂Cn×n 为n阶共轭对称正定矩阵空间。R为统计流形S的坐标，S又称为矩阵流形，其几何结构反应了概率密度函数族内在的本质属性。此时，H0和H1条件下的似然函数p(x|H0) 和p(x|H1) 分别对应统计流形S上的两点，将其坐标记为协方差矩阵R0和R1。在统计流形上以H0和H1条件下似然函数间的距离，或者说，以统计流形S上两点R0和R1间的距离
D(R1,R0) ，作为检测统计量，可以得到一类距离检测器，若D(R1,R0)>η (9) 则接受H1，否则接受H0，式中，
η 为根据虚警概率计算得到的判决门限。在检测器中，R0和R1分别表示噪声或杂波协方差矩阵和检测单元观测样本协方差矩阵。由式(9)，可得虚警概率和检测概率表达式
Pfa=Pr[D(R1,R0)≥η|H0] (10) Pd=Pr[D(R1,R0)>η|H1] (11) 实际中，为了满足检测器的恒虚警率特性，需要实时估计R0的值，R0的估计性能对检测性能具有重要影响。
在信息论中应用较广的距离度量是Kulback-Leibler分离度，其定义为：
KLD(R1,R0)=KLD[p(x|R1),p(x|R0)]=∫p(x|R1)lnp(x|R1)p(x|R0)dx Kulback-Leibler分离度容易计算，但也存在一定的局限性，即对于流形上相距较近的两点，它与测地线距离等价，但当两点相距较远时，由于未考虑流形的结构和连接两点的最短路径，它与测地线距离差异较大。另外，Kulback-Leibler分离度不满足距离定义的对称性、三角不等式等性质，并不是一个严格意义上的距离度量。程永强等人针对确定性信号检测和随机信号检测问题，将经典的似然比检测方法等效为统计流形上的“广义最小距离检测器”，并在信息几何框架下研究了广义似然比检测器和局部最大势检测器，从而将检测问题转变为统计流形上的几何问题来研究[12]。赵兴刚等人研究了低信杂比条件下基于Kulback-Leibler分离度的距离检测器和基于测地线距离的距离检测器，当信杂比较低时，统计流形上两假设分布间的距离很小，此时可以使用距离的近似形式来定义距离检测器，以使最终的检测器形式上更简单，更易实现[17]。这些检测器并不是严格意义上的恒虚警率(CFAR)检测器。
在雷达目标检测中，要求检测器能实时估计检测单元的杂波功率、杂波概率分布类型或其参数，以满足恒虚警率特性，为此，前人提出了单元平均CFAR、有序统计类CFAR、自适应CFAR、双参数CFAR等检测器。在信息几何框架下，将观测数据协方差矩阵构成一个统计流形，它成为一个矩阵流形，类比CFAR检测的思想，首先计算参考单元中协方差矩阵的均值，以该均值作为检测单元中噪声或杂波协方差矩阵的估计值，然后利用检测单元协方差矩阵与参考单元协方差矩阵均值间定义的距离作为检测统计量，所获得的检测器称为矩阵CFAR检测器。文献[17]在矩阵流形上，研究了黎曼度量、测地线、测地线距离，以及矩阵黎曼均值的迭代计算方法，在此基础上对矩阵CFAR进行了讨论。这里仅给出主要概念和结论。
在统计流形S上，研究流形上的几何性质。在统计流形上，Fisher信息矩阵是唯一的度量不变量[2]，通常将Fisher信息矩阵作为黎曼度量张量，直接计算或通过仿射黎曼度量计算，得到黎曼度量分量为[1]：
gij=E[∂ilnp(x|R)∂jlnp(x|R)]=⟨∂iR,∂jR⟩R=tr(R−1∂iRR−1∂jR),i,j=1,2,···,n (12) 式中，tr表示矩阵的迹。以R和
R+dR 为参数的相邻两个点p(x|R) 和p(x|R+dR) 之间的微分距离ds2 可以通过Fisher信息矩阵得到[9]：ds2=n∑i=1n∑j=1gijdθidθj=tr[R−1⋅(n∑i=1∂iRdθi)⋅R−1⋅(n∑i=1∂jRdθj)]=tr[(R−1dR)2]=‖ (13) 其中，
{\rm{d}}{{R}} = \displaystyle\sum\nolimits_{i = 1}^n {{\partial _i}{{R}}{\rm{d}}{\theta ^i}} ,{\left\| \cdot \right\|_{\rm{F}}} 为矩阵Frobenius范数。对于任意的{M} = \left[ {{m_{ij}}} \right] \in {C^{n \times n}} ，则\left\| {M} \right\|_{\rm{F}}^2 = \displaystyle\sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^n {{{\left| {{m_{ij}}} \right|}^2}} } 。流形上两点间的距离与连接两点的曲线有关，在所有可选的曲线中，使距离最短的曲线称为测地线，相应的最小距离称为测地线距离。测地线距离是欧氏空间中直线距离在流形上的推广。对于矩阵流形上的任意点
{A} \in \Theta ，设A点的切向量为{{v}} \in {{\mathop{\rm T}\nolimits} _{{A}}}\Theta ({{\mathop{\rm T}\nolimits} _{{A}}}\Theta 为A点的切空间)。利用指数映射的概念，则流形上以A为起点，沿{{v}} 方向随参数t变化的测地线[18]为：{γ} \left( t \right) = {{{A}}^{1/2}}{{\mathop{\rm e}\nolimits} ^{t{{{A}}^{ - 1/2}}{{v}}{{{A}}^{ - 1/2}}}}{{{A}}^{1/2}}, \ \ 0 \le t \le 1 (14) {γ} \left( 0 \right) = {A} ，令{γ} \left( 1 \right) = {{B}} ，可得连接两点A和B的测地线为：\begin{aligned} {γ} \left( t \right) = &{{{A}}^{1/2}}{{\mathop{\rm e}\nolimits} ^{t\log ({{{A}}^{ - 1/2}}{{B}}{{{A}}^{ - 1/2}})}}{{{A}}^{1/2}} \\ = & {{{A}}^{1/2}}{\left( {{{{A}}^{ - 1/2}}{{B}}{{{A}}^{ - 1/2}}} \right)^t}{{{A}}^{1/2}}, \;\;0 \le t \le 1 \end{aligned} (15) 沿测地线
{γ} \left( t \right) 对{\rm{d}}{s^2} 进行积分，可得A和B之间的测地线距离[8]为：\begin{aligned} D\left( {{{A}},{{B}}} \right) = &\min \int_{{A}}^{{B}} {\sqrt {{{\rm d}} {s^2}\left( {{R}} \right)} } \\ = & \int_{{γ} \left( t \right)} {\sqrt {{{\left[ {\frac{{{{\rm d}} s\left( {{{R}}\left( t \right)} \right)}}{{{\mathop{\rm d}\nolimits} t}}} \right]}^2}} } {\mathop{\rm d}\nolimits} t \\ = & {\left\| {{\rm{log}}({{{A}}^{ - 1/2}}{{B}}{{{A}}^{ - 1/2}})} \right\|_{\rm{F}}} \\ = &\sqrt {\sum\limits_{k = 1}^n {{{\ln }^2}} \left( {{\lambda _k}} \right)} \end{aligned} (16) 式中，
{{R}}\left( t \right) 表示测地线{γ} \left( t \right) 上对应点的矩阵，{\lambda _k}\left( {k = 1, ·\!·\!· ,n} \right) 为对{{{A}}^{ - 1/2}}{{B}}{{{A}}^{ - 1/2}} 进行谱分解得到的第k个特征值，利用矩阵的谱分解能够简化矩阵运算。与Kulback-Leibler分离度相比，测地线距离具有以下性质[5]：①非负性：
D\left( {{{A}},{{B}}} \right) \!\ge \! 0 ,D\left( {{{A}},{{B}}} \right) \!=\! 0 \Leftrightarrow {{A}} \!=\! {{B}} ；②对称性：
D\left( {{{A}},{{B}}} \right) = D\left( {{{B}},{{A}}} \right) ；③三角不等式：
D\left( {{{A}},{{C}}} \right) \!\le\! D\left( {{{A}},{{B}}} \right) \!+\! D\left( {{{B}},{{C}}} \right) ；④矩阵合同变换条件下不变性：D (A, B)=
D\left( {{{PA}}{{{P}}^{\rm{H}}},{{PB}}{{{P}}^{\rm{H}}}} \right) , P为n阶可逆矩阵；⑤矩阵求逆条件下不变性：
D\left( {{{A}},{{B}}} \right) = D\left( {{{{A}}^{ - 1}},{{{B}}^{ - 1}}} \right) 。这些性质使得测地线距离成为性能较好的检测统计量。
对于已知的N个矩阵
{{R}_k}\left( {k = 1,2, ·\!·\!· ,N} \right) ，其黎曼均值\bar{{R}} 是使得目标函数，即下式中均方测地线距离表示的经验方差J\left( {R} \right) = \frac{1}{N}\sum\limits_{k = 1}^N {{D^2}} \left( {{{R}_k},{R}} \right) (17) 取最小值时所对应的矩阵，即
\bar{{R}} = \arg \mathop {\min }\limits_{{{R}} \in \Theta } J\left( {R} \right) (18) 与算术均值相比，矩阵流形上的黎曼均值符合流形的几何性质，具有更高的估计精度。通常，利用目标函数
J\left( {R} \right) 对R的梯度计算局部最小值，该梯度\begin{aligned} \nabla J\left( {R} \right) & = \frac{1}{N}\sum\limits_{k = 1}^N {\nabla {D^2}} \left( {{{R}_k},{R}} \right) \\ & = \frac{1}{N}\sum\limits_{k = 1}^N {\nabla \left\| {\log \left({R}_k^{ - 1/2}{RR}_k^{ - 1/2}\right)} \right\|_{\rm F}^2} \\ & = \frac{{R}}{N}\sum\limits_{k = 1}^N {\log } \left( {{R}_k^{ - 1/2}{RR}_k^{ - 1/2}} \right) \end{aligned} (19) J\left( {R} \right) 获得局部最小值的充要条件为\nabla J\left( {R} \right) = 0 。当N > 2 时较难获得解析表达式，梯度下降算法是一种可行的计算方法。梯度下降方法的实现思想是：任意指定流形上的一个协方差矩阵作为黎曼均值的假定值，则该假定值与真实矩阵均值
\bar{{R}} 之间就确定了一条测地线{{γ} _{\bar{{R}}}}\left( t \right) ,t \ge 0 ，该测地线上任一参数t对应的协方差矩阵记为\bar{{R}}\left( t \right) ，则均值的假定值对应了\bar{{R}}\left( 0 \right) ,\bar{{R}} 对应了\bar{{R}}\left( t \right) 在终点处的取值。利用式(14)所给的测地线方程，以\bar{{R}}\left( {{t_0}} \right) ,{t_0} = 0 为初始值，切向量{ν} 为目标函数J\left( {R} \right) 在{\bar{{R}}}\left( {{t_0}} \right) 处的负梯度{ν} \!\!=\!\! - \nabla J\left[ {\bar{{R}}\left( {{t_0}} \right)} \right] ，令\tau 为增量，\tau < 1 ，可得测地线{{γ} _{\bar{{R}}}}\left( t \right) 上{t_0} + \tau 处对应的点\bar{{R}}\left( {{t_0} + \tau } \right) ，经多次迭代计算，直到目标函数J\left( {R} \right) 小于一个较小值。文献[5]和文献[6]利用梯度下降算法给出了
\bar{{R}} 的迭代计算方法，将实矩阵情况推广到复矩阵情况下，令第i次迭代计算得到的黎曼均值估计值为{\bar{{R}}_i} ，第i + 1 次迭代计算得到的黎曼均值估计值为：{\bar{{R}}_{i + 1}} \!\!=\!\! \bar{{R}}_i^{1/2}{{\mathop{\rm e}\nolimits} ^{\tiny\displaystyle\frac{\tau }{N}\sum\limits_{k = 1}^N {\log \left( {\bar{{R}}_i^{ - 1/2}{{R}_k} \bar{{R}}_i^{ - 1/2}} \right)} }}\bar{{R}}_i^{1/2},\; 0 \!\le\!\! \tau \!\le\!\! 1 \quad\ \ (20) 选择迭代的初始值
{\bar{{R}}_0} 和步长\tau ，就可以对矩阵的黎曼均值进行迭代运算。基于黎曼均值和测地线距离，矩阵CFAR检测器的框图如图3所示，其中，观测数据为根据复采样序列估计得到的样本协方差矩阵，当矩阵维数较大时，需要降低协方差矩阵的维数以提高矩阵处理的效率，滑窗中参考单元的长度为N，滑窗中的阴影部分为保护单元，RD为检测单元的协方差矩阵，
\bar{{R}} 是参考单元中的N个协方差矩阵的黎曼均值，T是根据虚警概率计算得到的检测门限。
图 3 基于信息几何的矩阵CFAR检测器框图Figure 3. Block diagram of CA-CFAR detector based on information geometry检测过程中，首先利用式(20)计算参考单元的黎曼均值
\bar{{R}} ，用于估计背景噪声或杂波协方差矩阵；然后利用式(16)计算RD和\bar{{R}} 之间的测地线距离平方作为检测统计量进行检测：{D^2}\left( {{{R}_{\rm{D}}},\bar{{R}}} \right)\mathop \gtrless \limits_{{H_0}}^{{H_1}} T (21) 由于虚警概率解析表达式难以得到，不易从理论上计算检测门限T，可利用Monte-Carlo仿真得到T。说明，为避免
D\left( {{{R}_{\rm{D}}},\bar{{R}}} \right) 中的根号运算和称呼简便，后续称{D^2}\left( {{{R}_{\rm{D}}},\bar{{R}}} \right) 为测地线距离。矩阵CFAR检测方法直接利用观测样本序列的协方差矩阵描述回波特性，并进行目标检测，协方差矩阵中包括了目标及杂波时间相关性的原始信息，有利于检测飞机尾流目标这类的多普勒展宽目标，能避免常规的多普勒处理所面临的问题。由于利用矩阵流形的结构计算参考单元的协方差矩阵均值，即满足式(18)给出的条件，该均值具有较小的经验方差，从而使得CFAR检测器具有更稳健的恒虚警特性。
需要说明的是，上面给出了一般的矩阵流形几何结构，当使用不同的统计流形的坐标、距离定义、均值定义和梯度下降算法等，能够获得不同的几何结构，同时也可以利用更多的几何结构，或采用更合适的检测策略或检测统计量，以便适应于不同的检测场景。
4. 尾流回波协方差矩阵的降低维数处理
当协方差矩阵的维数较大时，矩阵CFAR检测器的运算效率较低，不利于实时处理，因此有必要在检测性能下降较少的条件下，尽量降低协方差矩阵的维数。在对尾流回波协方差矩阵进行降维处理后，一种直观的评价标准是，降低维数之前与之后，根据相关系数估计得到的功率谱基本一致。
由于矩阵CFAR检测方法利用的是观测数据的协方差矩阵，而常规MTD检测方法利用的是观测数据的功率谱，因此这里分别给出观测数据的自相关函数和功率谱，以对两种检测方法进行对比。自相关函数和功率谱是描述脉冲序列时间相关性的两种方式，利用傅里叶变换可以将自相关函数变换为功率谱。在脉冲数为16时，在噪声中加入SNR为6 dB的仿真尾流回波，噪声和尾流回波的自相关函数如图4(a)所示，功率谱如图4(b)所示。
图 4 脉冲个数为16时的自相关函数与功率谱Figure 4. Autocorrelation function and power spectrum when the pulse number is 16当尾流目标距离雷达较远时，需要进行长时间积累，实际使用的脉冲数较多。在脉冲数为64，SNR为6 dB时，利用协方差矩阵中延迟为0至15的相关系数估计功率谱，与直接利用FFT得到的功率谱进行比较，两种方法得到的功率谱如图5所示。可见，两种方法得到的功率谱较为一致，所以可以利用相关系数进行协方差矩阵的降维处理。该矩阵降维算法的缺点是功率谱的旁瓣较高，下一步将研究性能更优的矩阵降维算法。
图 5 协方差矩阵降低维数之前与之后的功率谱Figure 5. The power spectrum before and after the covariance matrix reduces the dimension5. 噪声背景下仿真尾流回波的检测性能
下面以 64个脉冲为例，利用上节的方法降低协方差矩阵的维数为16，在矩阵流形上分析尾流目标的测地线距离随信噪比变化、黎曼均值估计性能和检测性能。
在噪声背景下，计算仿真的尾流回波的协方差矩阵与噪声的协方差矩阵间的测地线距离，对100次仿真结果进行平均，图6给出了测地线距离
{D^2}\left( {{{R}_{\rm{D}}},\bar{{R}}} \right) 随信噪比变化的曲线。测地线距离随着信噪比增大而增大，所以取适当的检测门限，在信噪比大于某一确定值时，就能够检测到尾流目标。
图 6 随SNR的变化测地线距离的变化Figure 6. The variation of geodesic distance with the variation of SNR利用仿真噪声数据对矩阵均值迭代算法的估计性能进行仿真分析，其中已知矩阵的个数N=16，选择矩阵的算术均值作为迭代算法的初始值
{\bar{{R}}_0} ，步长\tau = 0.1 ，可得协方差矩阵均值的估计性能如图7所示。由图可知，随着迭代次数的增加，均方测地线距离，即经验方法，不断减小，一般在20次迭代后，趋向于一个常数，利用梯度下降算法可以得到更符合物理意义的矩阵均值。对于仿真的噪声和尾流回波，令检测统计量为尾流回波加噪声的协方差矩阵与噪声的协方差矩阵均值间的测地线距离，利用统计方法得到检测统计量的统计直方图，以及检测门限。令虚警概率为10–4，脉冲数目为16时，通过Monte-Carlo仿真得到检测门限为44.3999；脉冲数目为64时，检测门限为11.9567；脉冲数目为256时，检测门限为2.7531。脉冲数为16, SNR为6 dB时，噪声条件下和存在尾流条件下检测统计量的统计直方图如图8(a)所示，仿真1000次，检测概率为0.59。脉冲数为64, SNR为0 dB时，噪声条件下和存在尾流条件下检测统计量的统计直方图如图8(b)所示，仿真1000次，检测概率为0.79。
图 8 有无尾流情况下检测统计量的统计直方图Figure 8. The statistical histogram of detection statistics with and without the vortex target在脉冲数分别为16, 64和256时，利用矩阵CFAR检测方法进行尾流目标检测，其中，脉冲数大于16时，均降低协方差矩阵的维数为16。随着信噪比变化，尾流目标的检测概率如图9所示，可知，脉冲数为64时与脉冲数为16时相比，以及脉冲数为256时与脉冲数为64时相比，在相同的检测概率处检测增益均提高约6 dB，增加4倍脉冲数所获得的增益相当于相参积累所获得的增益，所以利用延迟为0至15的相关系数构成16维协方差矩阵，能够达到降低协方差矩阵的维数的目的，对矩阵CFAR检测器的性能不造成影响。
图 9 基于矩阵CFAR的尾流目标的检测概率Figure 9. Detection probability of the vortex target based on matrix CFAR由图9可知，若用矩阵CFAR检测方法对尾流目标回波进行检测，在虚警概率10–4、检测概率80%、脉冲数为64时，所需信噪比约为0 dB。
常规MTD检测方法通过MTD加CFAR检测器来实现尾流目标功率谱的频域峰值检测，设定如下的假设条件：
(1) 在未知功率水平的白色高斯噪声及单脉冲平方律检测的假设下，背景功率水平由16个参考单元采样的均值估计得到，对非起伏目标，常规CA-CFAR检测器在虚警概率10–4、检测概率80%时，检测常规点目标所需的信噪比为11.6 dB；
(2) 在信噪比为0 dB时，进行100次尾流谱仿真，统计出尾流功率谱的峰值与所有功率谱值之和的比值，由统计平均可知，尾流谱的峰值约占整个尾流谱20%的功率，理论上可做出假设，由于尾流谱的展宽，导致的检测损失约7 dB；
(3) 在脉冲数为64时，经过相参积累，增益18 dB。
综上，可以近似分析出，对于尾流目标功率谱的常规MTD检测方法，在虚警概率10–4、检测概率80%、脉冲数为64时，所需信噪比约为0.6 dB。
由上面的分析可知，矩阵CFAR检测方法与常规方法相比，检测性能略有改善。另外，在信噪比为0 dB时，受噪声随机性的影响，100次仿真中有若干次，尾流目标功率谱的峰值与噪声相当，实际上常规方法的虚警概率将略高于10–4，检测性能还将低于上面的理论分析结果。更进一步，在使用常规MTD检测方法时，若参考单元选择不当，展宽的尾流目标功率谱落在参考单元中，还将抬高检测门限，导致目标遮蔽现象和检测概率下降。
矩阵CFAR检测方法直接利用观测样本序列的协方差矩阵进行尾流目标检测，避免了常规多普勒处理所面临的问题，仿真实验证明了它在尾流目标检测中具有较大优势。矩阵CFAR检测方法的缺点是运算量较大，导致较多的处理时间，有待改善实时性，可能的解决思路是通过算术均值代替黎曼均值，利用协方差矩阵为Toeplitz Hermitian正定矩阵的特点，利用矩阵谱分解方法提高矩阵运算的效率等方面。
6. 小结
飞机尾流是一种典型的角度、距离、多普勒展宽目标，同时也是一种空气介质目标，信噪比很低，针对某个特定的角度和距离单元上多普勒展宽目标的检测问题，本文研究了矩阵信息几何方法在飞机尾流目标检测中的应用。为保留原始观测信息，将协方差矩阵看作统计流形上的点，以测地线距离来定量描述目标和噪声杂波协方差矩阵间的差异，将统计检测问题转化为几何问题，提供了解决目标检测问题的一个新思路。对于功率谱展宽目标，该方法优于常规MTD检测方法。
信息几何方法在雷达目标探测技术领域的应用仍处于起步阶段，除了在尾流目标检测、近海小目标检测、短脉冲串信号检测等方面的应用，在雷达信号处理和数据处理中也具有较广的应用前景，在信息几何应用中的理论问题有待深入探讨。信息几何涉及较深的数学知识，尤其是微分几何、统计流形等方面，由于黎曼度量、测地线、测地距离、黎曼均值等几何概念的物理意义较明确，在应用中发挥了重要作用，而信息几何中更多概念的物理意义还需要深入分析。在雷达信号处理和目标检测领域中，信息几何的优势与应用条件、非高斯概率分布流形的几何结构、基于功率谱的信息几何检测器、气象杂波环境下尾流目标的信息几何检测方法、矩阵CFAR的快速算法、适用于矩阵信息几何的矩阵降维算法等方面还需要进一步研究。
-
图 2 利用alpha-shape算法提取目标形状
Figure 2. Target shape extraction using alpha-shape algorithm
图 16 形状自适应性测试的面积误差对比
Figure 16. Comparison of area errors for the shape adaptation tests
图 19 不同算法的单步运行时间对比
Figure 19. Comparison of single-step running time for different algorithms
1 结合Transformer的星凸形机动扩展目标跟踪部分伪代码
1. The pseudo-code of star convex maneuvering extended target tracking using Transformer algorithm
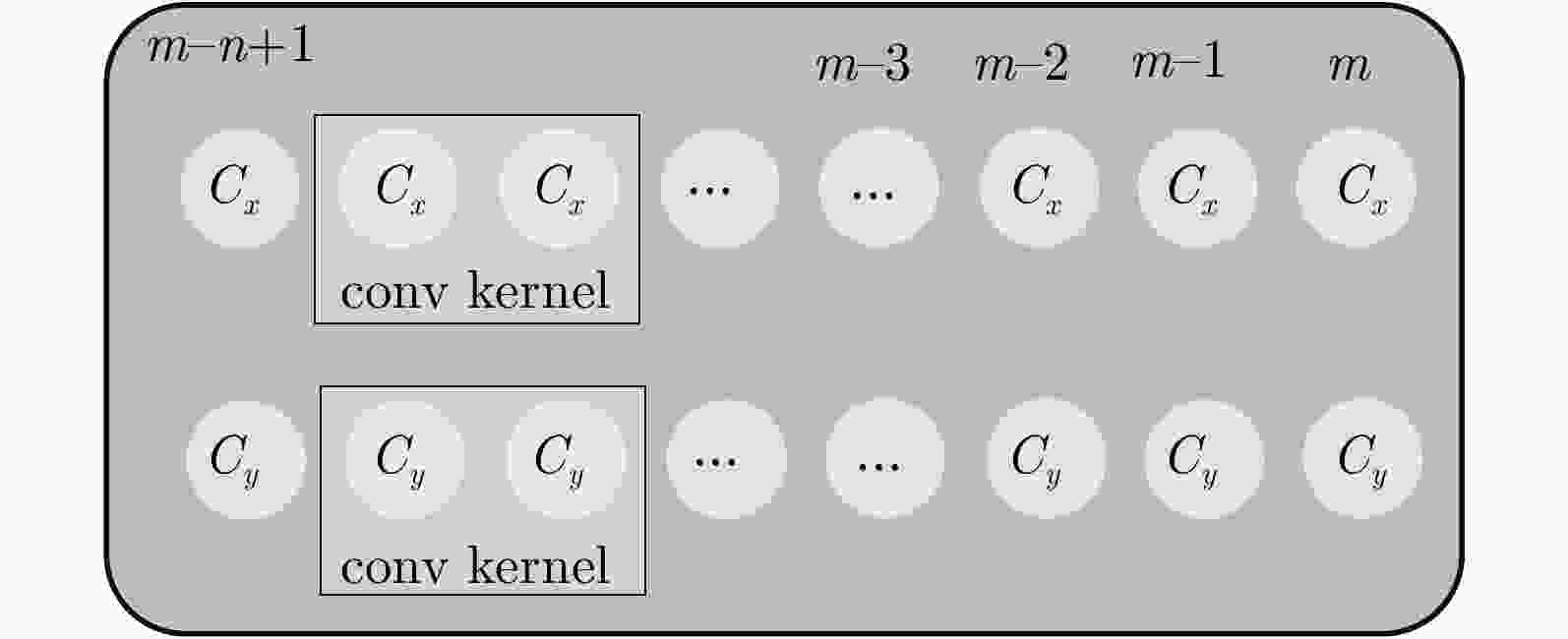
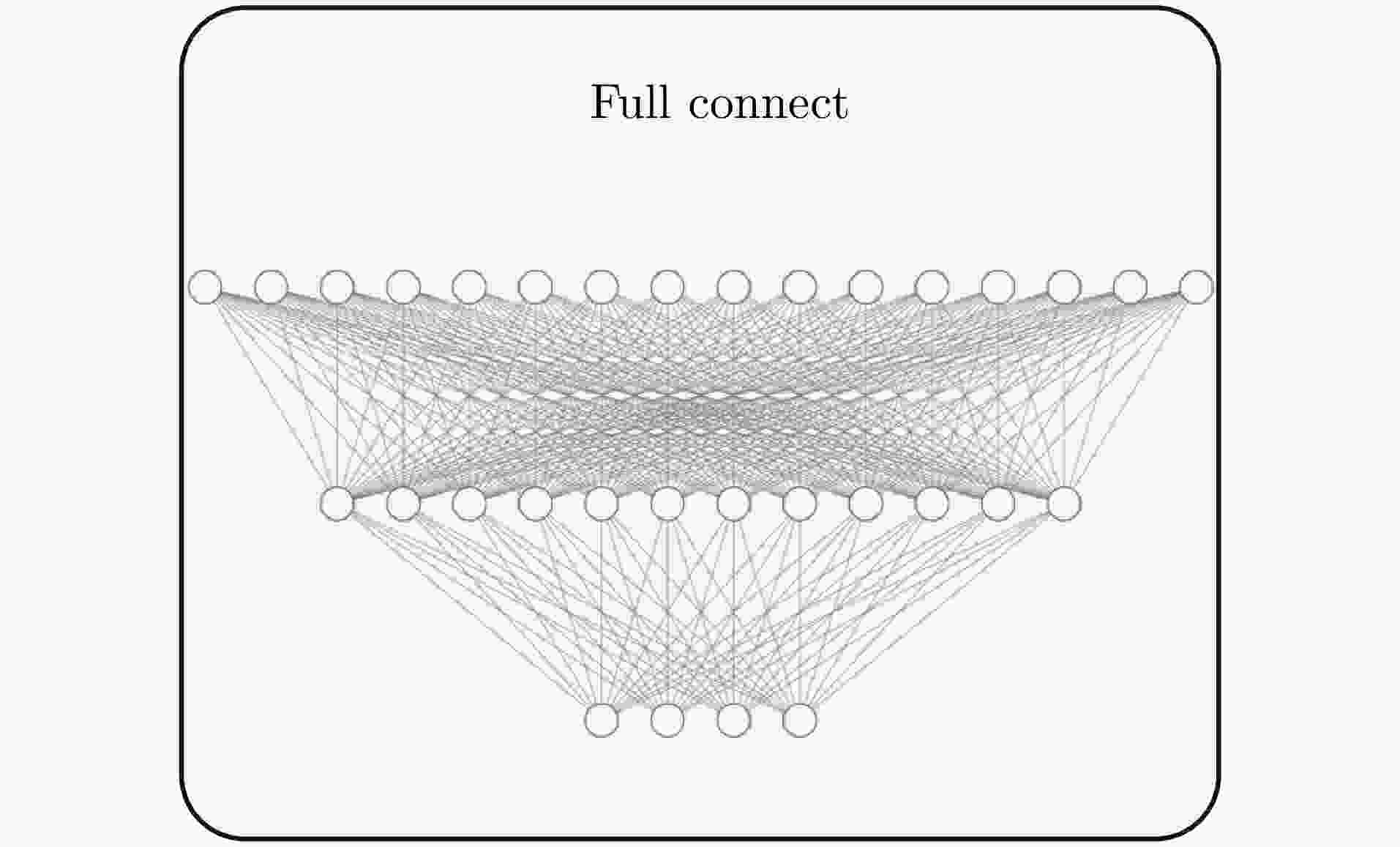
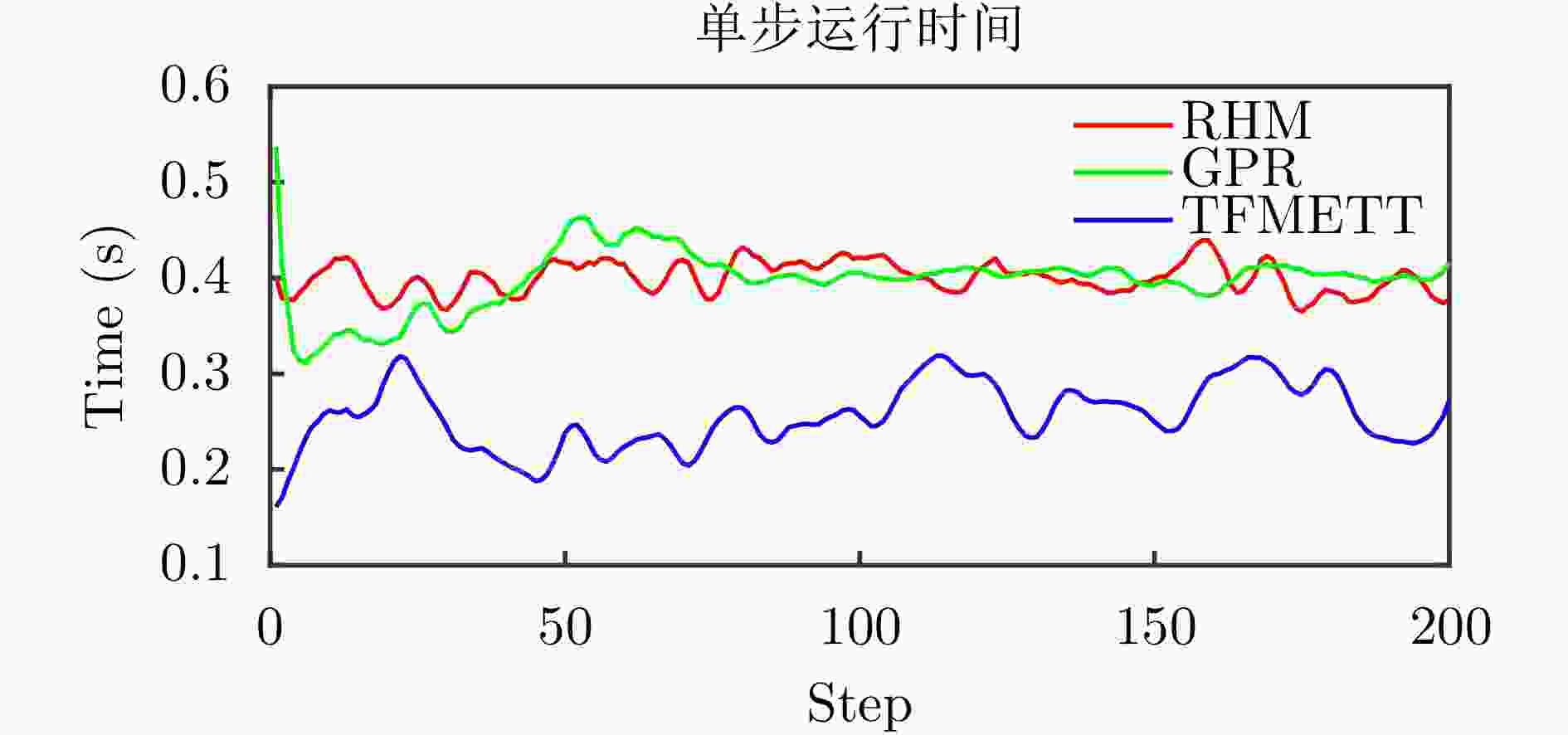
输入： {A_1},{A_2},{x_0},{P_0},{W_k},{U_k},{Q_k},{R_k},P_0^{{\text{cap}}} 步骤1：预测 for k = 1: steps % 量测集处理与形状初步处理 {{\boldsymbol{\bar z}}_k} = \dfrac{1}{l}\displaystyle\sum\limits_{i = 1}^l {{{\boldsymbol{z}}_{k,l}}} {{\boldsymbol{\tilde Z}}_k} = \{ {{\boldsymbol{\tilde z}}_{k,l}}\} {{\boldsymbol{C}}_k} = {{\mathrm{as}}} (a,{{\boldsymbol{\tilde Z}}_k}) {{\boldsymbol{Z}}^k} = {{\mathrm{s}}} ({{\boldsymbol{C}}_k}) % 静态形状预测 \mathcal{X}_k^ - - {\bar{\mathcal{X}} _k} = {\boldsymbol{A}}(\mathcal{X}_{k - 1}^ - - {\bar {\mathcal{X}} _k}) {\boldsymbol{P}}_k^ - = {\boldsymbol{A}}{{\boldsymbol{P}}_k}{{\boldsymbol{A}}^{\text{T}}} + {{\boldsymbol{W}}_k}{\boldsymbol{W}}_k^{\text{T}} % 运动状态预测 \hat \chi _{k - 1}^j = {\boldsymbol{F}}_k^i\chi _{k - 1}^j {{\boldsymbol{x}}_{k|k - 1}} = \dfrac{1}{m}\displaystyle\sum\limits_{j = 1}^m {\chi _{k - 1}^j} % 形态预测 \mathcal{X}_{k,s}^ - = \mathcal{X}_k^ - + {{\boldsymbol{x}}_{k|k - 1}} end 步骤2：更新 for k = 1: steps % 静态形状更新 {{\boldsymbol{K}}_k} = {\boldsymbol{P}}_k^ - {{\boldsymbol{H}}^{\text{T}}}{({{\boldsymbol{S}}_k}{\boldsymbol{HP}}_k^ - {{\boldsymbol{H}}^{\text{T}}} + {\boldsymbol{I}})^{ - 1}} {\hat {\mathcal{X}}_k} = \mathcal{X}_k^ - + {{\boldsymbol{K}}_k}{{\boldsymbol{Z}}^k} {{\boldsymbol{P}}_k} = ({\boldsymbol{I}} - {{\boldsymbol{K}}_k}{{\boldsymbol{S}}_k}{\boldsymbol{H}}){\boldsymbol{P}}_k^ - % 状态转移矩阵更新 {{\boldsymbol{F}}_k} = {\text{TFMETT}}({{\boldsymbol{\bar z}}_k}) % 运动状态更新 {{\boldsymbol{\hat x}}_k} = {{\boldsymbol{x}}_{k|k - 1}} + {\boldsymbol{K}}_k^{{\text{cap}}}({{\boldsymbol{\bar z}}_k} - {{\boldsymbol{z}}_{k|k - 1}}) {\boldsymbol{P}}_k^{{\text{cap}}} = {\boldsymbol{P}}_{k|k - 1}^{{\text{cap}}} - {\boldsymbol{K}}_k^{{\text{cap}}}{\boldsymbol{S}}_k^{{\text{cap}}}{\left( {{\boldsymbol{K}}_k^{{\text{cap}}}} \right)^{\text{T}}} % 形态更新 {\hat {\mathcal{X}}_{k,s}} = {\hat {\mathcal{X}}_k} + {{\boldsymbol{\hat x}}_k} end 输出：{\hat {\mathcal{X}}_{k,s}} 
下载: 导出CSV
表 1 50次蒙特卡罗仿真测试中各种算法的平均单步运行时间
Table 1. Average single-step running time of various algorithms in 50 Monte Carlo simulation tests
算法 平均单步运行时间(s) RHM 0.38 GPR 0.41 TFMETT 0.26
下载: 导出CSV
-
[1] GRANSTRÖM K and BAUM M. A tutorial on multiple extended object tracking[EB/OL]. https://www.techrxiv.org/doi/full/10.36227/techrxiv.19115858.v1, 2022. [2] LAN Jian. Extended object tracking using random matrix with extension-dependent measurement numbers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(04): 4464–4477. doi: 10.1109/TAES.2023.3241888. [3] MANNARI P, THARMARASA R, and KIRUBARAJAN T. Extended target tracking under multitarget tracking framework for convex polytope shapes[J]. Signal Processing, 2024, 217: 109321. doi: 10.1016/j.sigpro.2023.109321. [4] TAN Jintao, QI Guoqing, QI Junjie, et al. Model parameter adaptive approach of extended object tracking using random matrix and identification[C]. 2022 International Conference on Cyber-Physical Social Intelligence, Nanjing, China, 2022: 91–97. doi: 10.1109/ICCSI55536.2022.9970662. [5] BAUR T, REUTER J, ZEA A, et al. Extent estimation of sailing boats applying elliptic cones to 3D LiDAR data[C]. 2022 25th International Conference on Information Fusion (FUSION), Linksping, Sweden, 2022: 1–8. doi: 10.23919/FUSION49751.2022.9841265. [6] ZHANG Yongquan, JI Hongbing, and HU Qi. A box-particle implementation of standard PHD filter for extended target tracking[J]. Information Fusion, 2017, 34: 55–69. doi: 10.1016/j.inffus.2016.06.007. [7] ZHANG Xiaoxiao and LAN Jian. Measurement combination estimator for multisensor extended object tracking using random matrix[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(1): 698–715. doi: 10.1109/TAES.2023.3329075. [8] BAUM M and HANEBECK U D. Random hypersurface models for extended object tracking[C]. 2009 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, UAE, 2009: 178–183. doi: 10.1109/ISSPIT.2009.5407526. [9] BAUM M and HANEBECK U D. Shape tracking of extended objects and group targets with star-convex RHMs[C]. 14th International Conference on Information Fusion, Chicago, USA, 2011: 1–8. [10] YANG Jinlong, LI Peng, and GE Hongwei. Extended target shape estimation by fitting B-spline curve[J]. Journal of Applied Mathematics, 2014, 2014: 741892. doi: 10.1155/2014/741892. [11] KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042–1059. doi: 10.1109/TAES.2008.4655362. [12] FELDMANN M, FRÄNKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409–1420. doi: 10.1109/TSP.2010.2101064. [13] SWAIN A and CLARK D. Extended object filtering using spatial independent cluster processes[C]. 2010 13th International Conference on Information Fusion, Edinburgh, UK, 2010: 1–8. doi: 10.1109/ICIF.2010.5711886. [14] ABDALLAH F, GNING A, and BONNIFAIT P. Box particle filtering for nonlinear state estimation using interval analysis[J]. Automatica, 2008, 44(3): 807–815. doi: 10.1016/j.automatica.2007.07.024. [15] LAN Jian and LI Xiaorong. Tracking of maneuvering non-ellipsoidal extended object or target group using random matrix[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2450–2463. doi: 10.1109/TSP.2014.2309561. [16] LAN Jian and LI Xiaorong. Tracking of extended object or target group using random matrix—part I: New model and approach[C]. 2012 15th International Conference on Information Fusion, Singapore, Singapore, 2012: 2177–2184. [17] WAHLSTROM N and ÖZKAN E. Extended target tracking using Gaussian processes[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4165–4178. doi: 10.1109/TSP.2015.2424194. [18] LI Xiaorong and ZHANG Youmin. Multiple-model estimation with variable structure. V. Likely-model set algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 448–466. doi: 10.1109/7.845222. [19] LI Xiaorong, ZWI X, and ZWANG Y. Multiple-model estimation with variable structure. III. Model-group switching algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 225–241. doi: 10.1109/7.745694. [20] JILKOV V P, ANGELOVA D S, and SEMERDJIEV T A. Design and comparison of mode-set adaptive IMM algorithms for maneuvering target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 343–350. doi: 10.1109/7.745704. [21] 王昱淇, 卢宙, 蔡云泽. 基于一致性的分布式变结构多模型方法[J]. 自动化学报, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091.WANG Yuqi, LU Zhou, and CAI Yunze. Consensus-based distributed variable structure multiple model[J]. Acta Automatica Sinica, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091. [22] 赵楚楚, 王子微, 丁冠华, 等. 基于模糊逻辑的改进自适应IMM跟踪算法[J]. 信号处理, 2021, 37(5): 724–734. doi: 10.16798/j.issn.1003-0530.2021.05.005.ZHAO Chuchu, WANG Ziwei, DING Guanhua, et al. Fuzzy-logic adaptive IMM algorithm for target tracking[J]. Journal of Signal Processing, 2021, 37(5): 724–734. doi: 10.16798/j.issn.1003-0530.2021.05.005. [23] LIU Jingxian, YANG Shuhong, and YANG Fan. A cross-and-dot-product neural network based filtering for maneuvering-target tracking[J]. Neural Computing and Applications, 2022, 34(17): 14929–14944. doi: 10.1007/s00521-022-07338-7. [24] SONG Fei, LI Yong, CHENG Wei, et al. An improved Kalman filter based on long short-memory recurrent neural network for nonlinear radar target tracking[J]. Wireless Communications and Mobile Computing, 2022, 2022: 8280428. doi: 10.1155/2022/8280428. [25] GAO Chang, LIU Hongwei, ZHOU Shenghua, et al. Maneuvering target tracking with recurrent neural networks for radar application[C]. 2018 International Conference on Radar (RADAR), Brisbane, Australia, 2018: 1–5. doi: 10.1109/RADAR.2018.8557284. [26] YU Wanting, YU Hongyi, DU Jianping, et al. DeepGTT: A general trajectory tracking deep learning algorithm based on dynamic law learning[J]. IET Radar, Sonar & Navigation, 2021, 15(9): 1125–1150. doi: 10.1049/rsn2.12111. [27] LIU Jingxian, WANG Zulin, and XU Mai. DeepMTT: A deep learning maneuvering target-tracking algorithm based on bidirectional LSTM network[J]. Information Fusion, 2020, 53: 289–304. doi: 10.1016/j.inffus.2019.06.012. [28] JOUABER S, BONNABEL S, VELASCO-FORERO S, et al. NNAKF: A neural network adapted Kalman filter for target tracking[C]. ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Canada, 2021: 4075–4079. doi: 10.1109/ICASSP39728.2021.9414681. [29] AFTAB W and MIHAYLOVA L. A learning Gaussian process approach for maneuvering target tracking and smoothing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 278–292. doi: 10.1109/TAES.2020.3021220. [30] NEZHADARYA E, LIU Yang, and LIU Bingbing. BoxNet: A deep learning method for 2d bounding box estimation from bird’s-eye view point cloud[C]. 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 2019: 1557–1564. doi: 10.1109/IVS.2019.8814058. [31] STEUERNAGEL S, THORMANN K, and BAUM M. CNN-based shape estimation for extended object tracking using point cloud measurements[C]. 2022 25th International Conference on Information Fusion (FUSION), Linksping, Sweden, 2022: 1–8. doi: 10.23919/FUSION49751.2022.9841254. [32] BARINGOLTS T V, DOMIN D V, ZHUK S Y, et al. Adaptive algorithm of maneuvering target tracking in complex jamming situation for multifunctional radar with phased antenna array[J]. Radioelectronics and Communications Systems, 2019, 62(7): 342–355. doi: 10.3103/S0735272719070021. [33] XU Xiaolong and HARADA K. Automatic surface reconstruction with alpha-shape method[J]. The Visual Computer, 2003, 19(7): 431–443. doi: 10.1007/s00371-003-0207-1. [34] EDELSBRUNNER H, KIRKPATRICK D, and SEIDEL R. On the shape of a set of points in the plane[J]. IEEE Transactions on Information Theory, 1983, 29(4): 551–559. doi: 10.1109/TIT.1983.1056714. [35] 李世林, 李红军. 自适应步长的Alpha-shape表面重建算法[J]. 数据采集与处理, 2019, 34(3): 491–499. doi: 10.16337/j.1004-9037.2019.03.012.LI Shilin and LI Hongjun. Surface reconstruction algorithm using self-adaptive step Alpha-shape[J]. Journal of Data Acquisition and Processing, 2019, 34(3): 491–499. doi: 10.16337/j.1004-9037.2019.03.012. [36] LÜTKEPOHL H. Vector Autoregressive Models[M]. HASHIMZADE N and THORNTON M A. Handbook of Research Methods and Applications in Empirical Macroeconomics. Cheltenham: Edward Elgar, 2013: 139–164. doi: 10.4337/9780857931023.00012. [37] GHIASI G, LIN T Y, and LE Q V. DropBlock: A regularization method for convolutional networks[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 10750–10760. [38] BAI Shaojie, KOLTER J Z, and KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. https://arxiv.org/abs/1803.01271, 2018. [39] LUO Yi and MESGARANI N. Conv-TasNet: Surpassing ideal time-frequency magnitude masking for speech separation[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(8): 1256–1266. doi: 10.1109/TASLP.2019.2915167. [40] BADRINARAYANAN V, KENDALL A, and CIPOLLA R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481–2495. doi: 10.1109/TPAMI.2016.2644615. [41] CHO K, VAN MERRIËNBOER B, BAHDANAU D, et al. On the properties of neural machine translation: Encoder-decoder approaches[C]. Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 2014: 103–111. doi: 10.3115/v1/W14-4012. [42] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6000–6010. [43] SUBAKAN C, RAVANELLI M, CORNELL S, et al. Attention is all you need in speech separation[C]. ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Canada, 2021: 21–25. doi: 10.1109/ICASSP39728.2021.9413901. [44] BARRON J T. A general and adaptive robust loss function[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 4326–4334. doi: 10.1109/CVPR.2019.00446. [45] ALT H and GODAU M. Computing the Fréchet distance between two polygonal curves[J]. International Journal of Computational Geometry & Applications, 1995, 5(1/2): 75–91. doi: 10.1142/S0218195995000064. 期刊类型引用(10)
1. 管浩良，张广滨，王岩. 融合特征金字塔和自注意力机制的SAR三维点云目标识别方法. 信号处理. 2025(01): 70-83 . 
百度学术2. 李雨轩，刘峥，冉磊. 一种改进的SAR图像舰船目标超像素快速检测算法. 信号处理. 2025(01): 113-126 . 百度学术3. 王佳慧，杨果，王雨晗，毛新华. 基于MSER的车载毫米波雷达SAR图像目标检测. 现代雷达. 2025(01): 1-7 . 百度学术4. 张强，王志豪，王学谦，李刚，黄立威，宋慧娜，宋朝晖. 基于邻域显著性的可见光和SAR遥感图像海面舰船协同检测方法. 雷达学报. 2024(04): 885-903 . 
本站查看5. 何佳月，宿南，徐从安，尹璐，廖艳苹，闫奕名. 从光学到SAR：基于多级跨模态对齐的SAR图像舰船检测算法. 遥感学报. 2024(07): 1789-1801 . 百度学术6. 李家强，任梦豪，姚昌华，陈金立. 基于轻量化YOLOv5的雷达图像道路目标检测方法. 中国电子科学研究院学报. 2024(05): 393-402 . 百度学术7. 胡卫杰，刘颖冰，马飞，张帆. 基于无损压缩和量化感知的SAR舰船检测网络边缘部署. 信号处理. 2024(09): 1674-1684 . 百度学术8. 王磊，张斌，吴奇鸿. RCSA-YOLO：改进YOLOv8的SAR舰船实例分割. 计算机工程与应用. 2024(18): 103-113 . 百度学术9. 包立男，吕孝雷. 基于改进的高斯混合模型和图割模型的水体图像提取算法. 中国科学院大学学报(中英文). 2024(06): 794-802 . 百度学术10. 刘林峰，胡清平，马丽衡，张晓晖. 一种提高可见光遥感图像黑极性舰船目标检出率的方法. 光学与光电技术. 2023(04): 59-66 . 百度学术其他类型引用(12)
-
下载:
百度学术
计量
- 文章访问数: 485
- HTML全文浏览量: 194
- PDF下载量: 222
- 被引次数: 22
