作者中心
专家审稿
责编办公
编辑办公
Joint Optimization of Radar and Jammer Space-time Cooperative Beamforming for a Multitasking Dynamic Scene
-
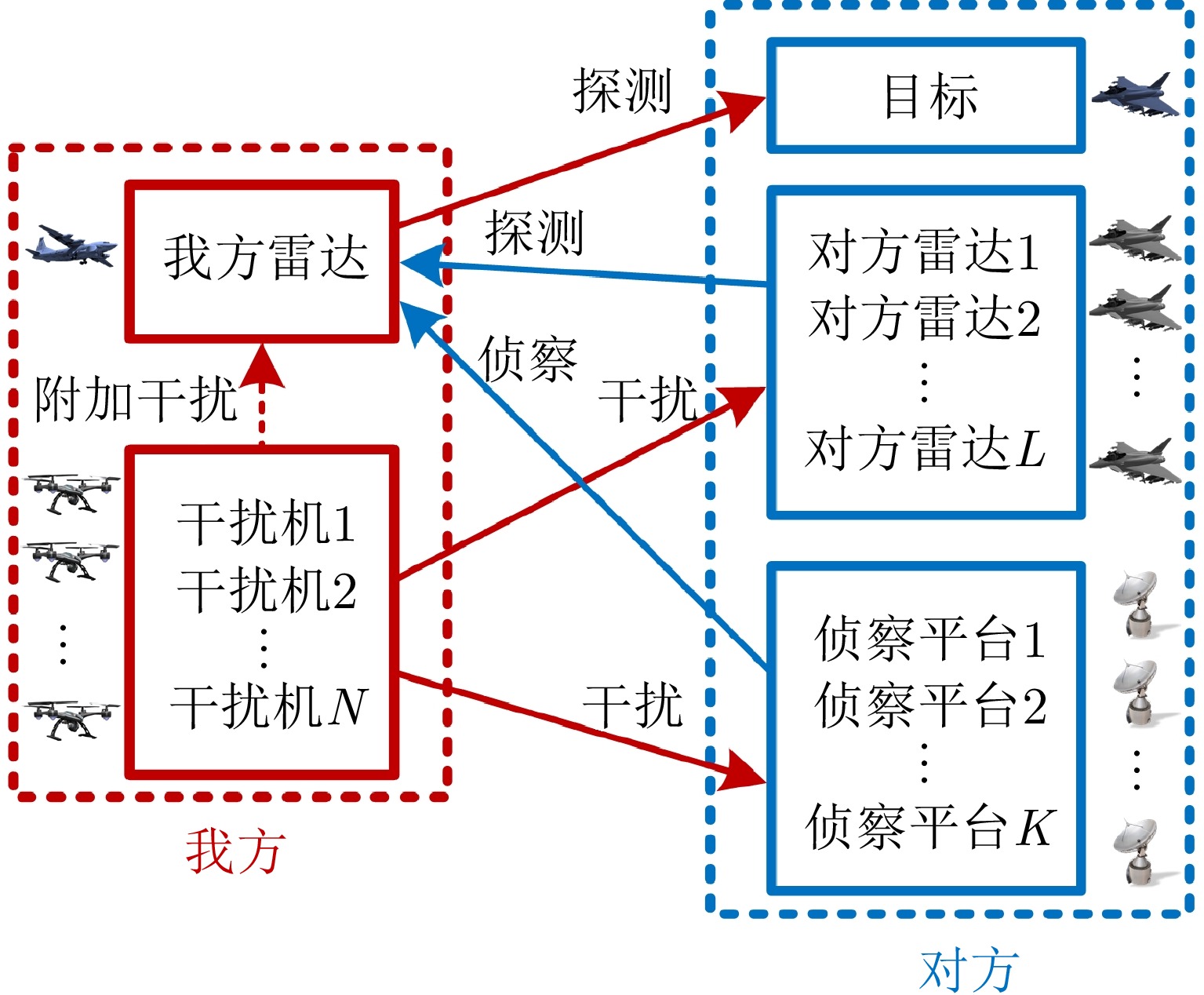
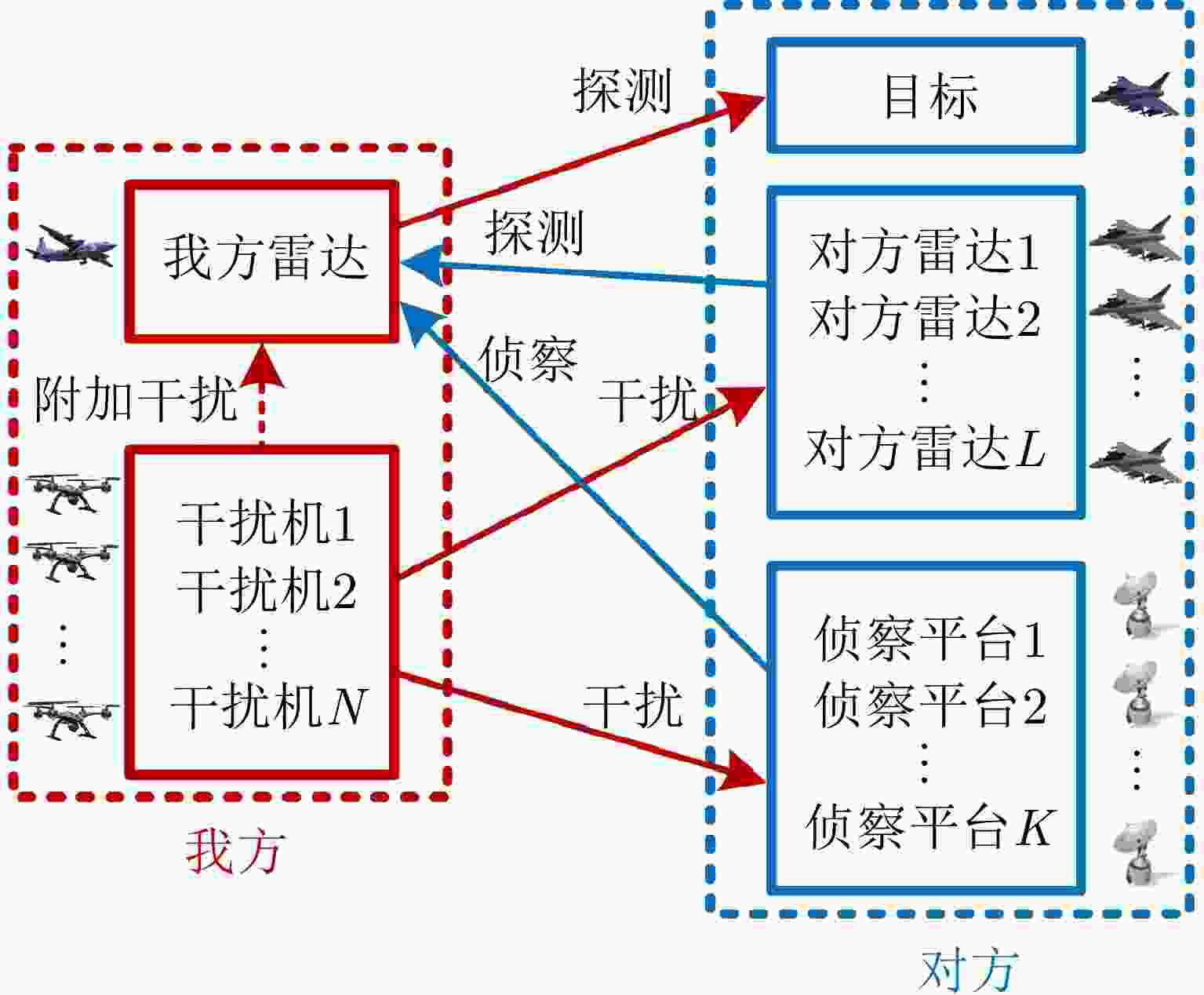
摘要: 现代雷达对抗形势复杂多变，体系与体系的作战已成为基本特点，而体系整体性能关乎着战场的主动权乃至最终的胜负。通过优化体系中雷达与干扰波束资源可以提升整体性能，获得在空间、时间域优效的低截获探测性能，然而空时域协同波束联合优化是一个复杂多参数耦合的非凸问题。该文针对空时域多任务动态场景，建立了以雷达探测性能为优化目标，以干扰性能以及能量限制为约束条件的优化模型。为求解该模型，该文提出了基于迭代优化的空时协同波束联合设计方法，即以雷达发射、接收、多干扰机发射波束交替迭代优化。其中，针对多干扰机协同优化的不定矩阵二次约束二次规划(QCQP)问题，该文基于可行点追踪-连续凸逼近(FPP-SCA)算法，在SCA算法的基础上，通过引入松弛变量与惩罚项，保证算法在合理松弛度下的可行性，解决了矩阵不定情况下难以获得可行解的问题。仿真表明，在一定的干扰机能量约束下，该文所提方法在保证雷达高性能探测目标且不受干扰情况下，同时实现了多干扰机在空时域干扰对方每个平台以掩护我方雷达探测的效果；相比传统算法，在动态场景中基于FPP-SCA算法的协同干扰具有更优效果。
-
关键词:
- 雷达与干扰资源 /
- 空时波束联合优化 /
- 多参数耦合非凸问题 /
- 迭代优化 /
- 可行点追踪-连续凸逼近(FPP-SCA)
Abstract: The modern radar confrontation situation is complex and changeable, and inter-system combat has become a basic feature. The overall system performance affects the initiative on the battlefield and even the final victory or defeat. By optimizing the beam resources of radar and jammers in a system, the overall performance can be improved, and the effective low-intercept detection effect can be obtained in the spatial and temporal domains. However, joint optimization of cooperative beamforming in the spatial and temporal domains is a nonconvex problem with complex multiparameter coupling. In this paper, an optimization model is established for a multitasking dynamic scene in the spatial and temporal domains. Radar detection performance is the optimization goal, while the interference performance and energy limitation of jammers are the constraints. To solve the model, a joint design method of space-time cooperative beamforming based on iterative optimization was proposed; that is, iterative optimization of radar transmitting, receiving, and multiple jammers transmitting beamforming vectors was alternately optimized. To solve the Quadratically Constrained Quadratic Programs (QCQP) problem with indefinite matrices for multijammer collaborative optimization, this paper is based on the Feasible-Point-Pursuit Successive Convex Approximation (FPP-SCA) algorithm. In other words, on the basis of the SCA algorithm, algorithm feasibility is ensured through reasonable relaxation by introducing relaxation variables and a penalty term, which solves the difficulty of obtaining a feasible solution when a problem contains indefinite matrices. Simulation results show that under the constraint of certain jammer energy, the proposed method achieves the effect of multiple jammers interfering with each enemy platform in the spatial and temporal domains to cover our radar detection. This effect is achieved while ensuring high-performance radar detection of the target without interference. Compared with traditional algorithms, the collaborative interference based on the FPP-SCA algorithm exhibits a better performance in the dynamic scene. -
图 2 基于迭代的波束资源联合优化算法总体框架
Figure 2. The overall framework of the joint optimization algorithm of beamforming resources based on iteration
图 3 各平台相对地面的位置及运动路线
Figure 3. The position and movement route of each platform relative to the ground
图 4 各平台相对雷达的位置及运动路线
Figure 4. The position and movement route of each platform relative to the radar
图 5 各时刻的目标函数优化过程
Figure 5. The optimization process of the objective function at each moment
图 7 各时刻干扰机发射波束权矢量(功率归一化)
Figure 7. Transmit beamforming vectors of jammers at each moment (power normalization)
图 8 侦察平台各角度上的接收功率
Figure 8. The received power of the reconnaissance platforms at all angles
图 10 对方平台在干扰机方向的接收功率
Figure 10. The received power of the opposing platforms in the direction of the jammers
图 11 雷达探测目标的信干噪比
Figure 11. The signal-to-interference plus noise ratio of the target detected by our radar
图 13 对方平台在各方向上的接收功率
Figure 13. The received power of the opposing platforms at all angles
1 基于FFP-SCA算法的干扰机发射波束权矢量优化过程
1. Optimization process of jammers’ transmit beamforming vectors based on FFP-SCA algorithm
步骤1 初始化： 设迭代次数$q = 0$，初始化M维向量${{\boldsymbol{z}}_0}$； 步骤2 循环执行： (1) 求解下式凸优化问题： $ \begin{gathered} \mathop {\min }\limits_{{{\boldsymbol{w}}_{{{\mathrm{t}}}}},{\boldsymbol{s}}} {\text{ }}{\boldsymbol{w}}_{\rm{t}}^{\rm{H}}{\boldsymbol{H}}{{\boldsymbol{w}}_{\text{t}}} + \mu \sum\limits_{m = 1}^{(K + L + N)} {{s_m}} \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{aligned} & {{\text{ }}2{{\mathrm{Re}}} \left\{ {{\boldsymbol{z}}_q^{\text{H}}( - {{\boldsymbol{P}}_k}){{\boldsymbol{w}}_{\rm{t}}}} \right\} \le - {\beta _k} + {\boldsymbol{z}}_q^{\text{H}}( - {{\boldsymbol{P}}_k}){{\boldsymbol{z}}_q} + {s_k},{\text{ }}k = 1,2, \cdots ,K} \\ & {{\text{ }}2{{\mathrm{Re}}} \left\{ {{\boldsymbol{z}}_q^{\text{H}}( - {{\boldsymbol{Q}}_l}){{\boldsymbol{w}}_{\rm{t}}}} \right\} \le - {\beta _l} + {\boldsymbol{z}}_q^{\text{H}}( - {{\boldsymbol{Q}}_l}){{\boldsymbol{z}}_q} + {s_{K + l}}{\text{, }}l = 1,2, \cdots ,L} \\ & {{\text{ }}{\boldsymbol{w}}_{\rm{t}}^{\rm{H}}{{\boldsymbol{R}}_n}{{\boldsymbol{w}}_{\rm{t}}} \le {\rho _n} + {s_{K + L + n}},{\text{ }}n = 1,2, \cdots ,N} \\ & {{\text{ }}{s_m} \ge 0,{\text{ }}m = 1,2, \cdots ,K + L + N} \end{aligned} \right.\end{gathered} $ 得到当前最优解$ {\boldsymbol{w}}_{\rm{t}}^{\text{*}} $； (2) 将第q次得到的$ {\boldsymbol{w}}_{\rm{t}}^{\text{*}} $赋值给${{\boldsymbol{z}}_{q + 1}}$； (3) 令$q = q + 1$； 直到目标函数收敛，循环结束。 
下载: 导出CSV
2 基于迭代的空域波束资源联合优化算法
2. Joint optimization algorithm of beamforming resources based on iterative optimization in the spatial domain
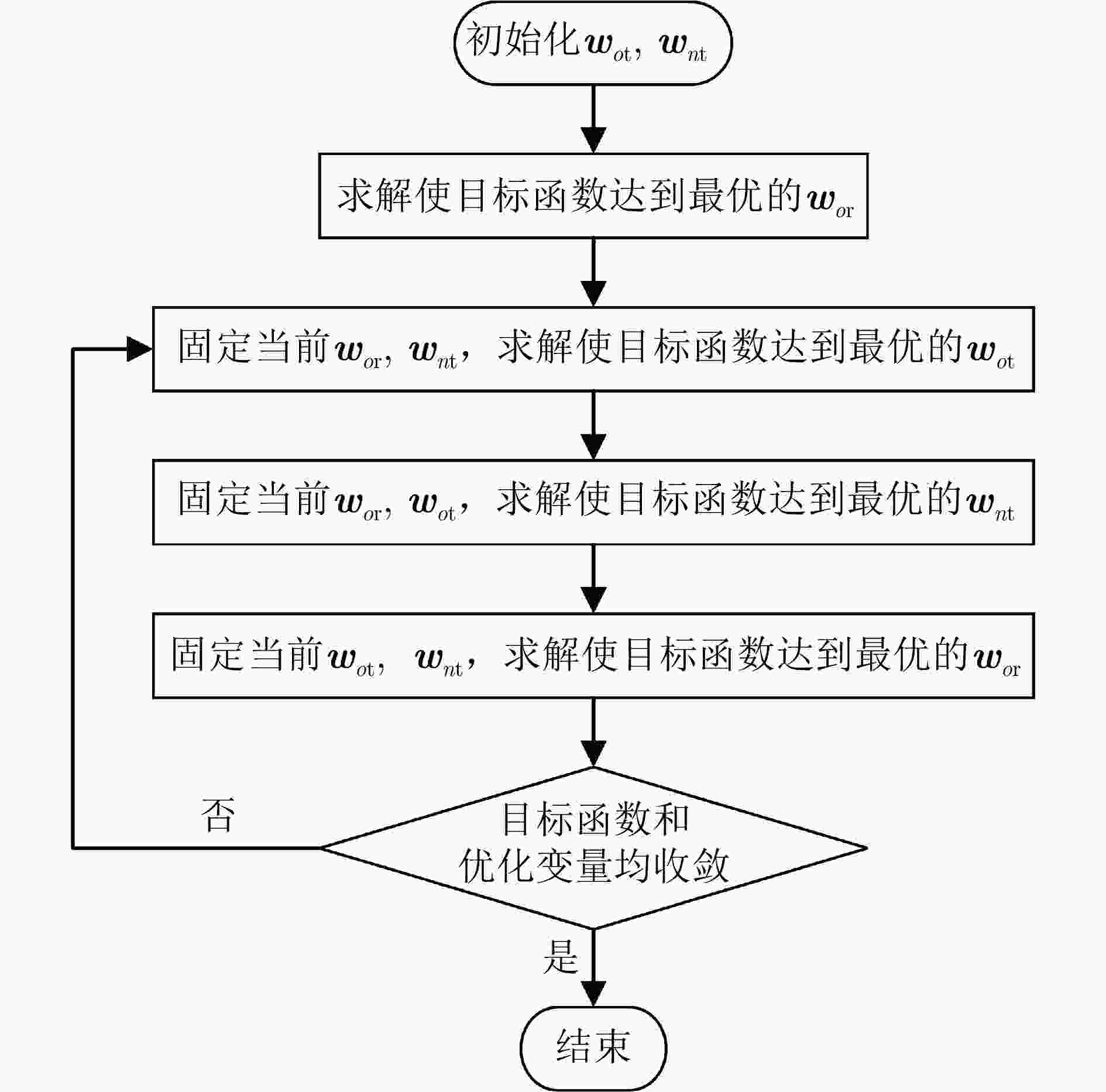
步骤1 初始化： 设置场景数据(如平台位置、阵元个数、阵元间距等)，给定$ {{\boldsymbol{w}}_{o{\rm t}}} $, $ {{\boldsymbol{w}}_{n{\rm t}}} $初值； 步骤2 执行循环： (1) 求解式(17)，得到当前最优解$ {\boldsymbol{w}}_{o{\rm r}}^{\text{*}} $：对矩阵${{\boldsymbol{B}}^{ - 1}}{\boldsymbol{A}}$进行特征值分解，最大特征值对应的特征向量即所求$ {\boldsymbol{w}}_{o{\rm r}}^{\text{*}} $； (2) 求解如式(22)所示的凸优化问题，得到当前最优解${\boldsymbol{w}}_{o{\rm t}}^{\text{*}}$； (3) 根据算法1，得到当前最优${\boldsymbol{w}}_{n{\rm t}}^{\text{*}}$； 直到目标函数收敛和优化变量收敛，循环结束； 步骤3 输出结果： 最终波束权矢量$ {\boldsymbol{w}}_{o{\rm r}}^{\text{*}} $,$ {\boldsymbol{w}}_{o{\rm t}}^{\text{*}} $和$ {\boldsymbol{w}}_{n{\rm t}}^{\text{*}} $的值即为波束资源联合优化的最优结果。
下载: 导出CSV
3 基于迭代的空时协同波束资源联合优化方法
3. Joint optimization method of space-time cooperative beamforming resources based on iterative optimization
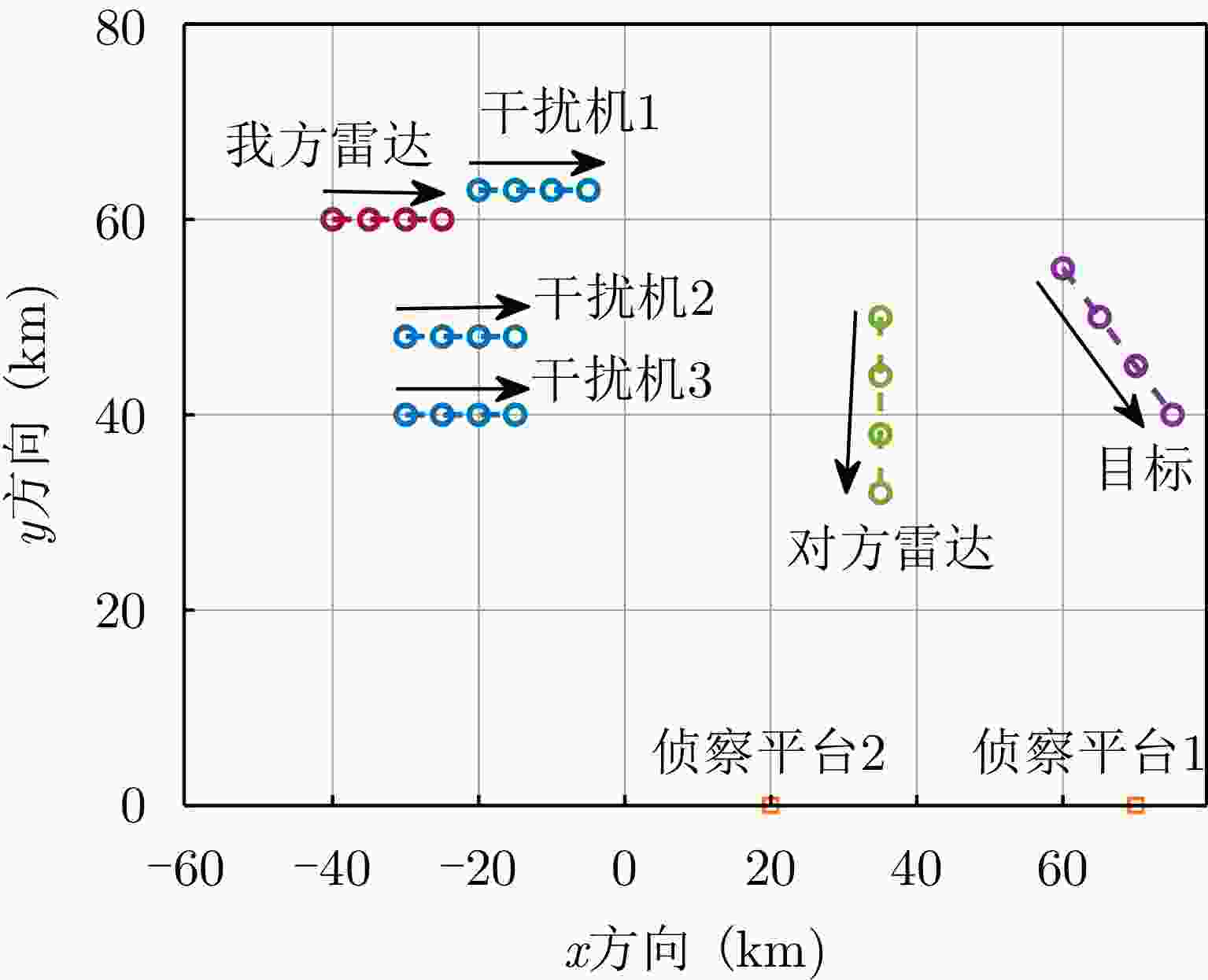
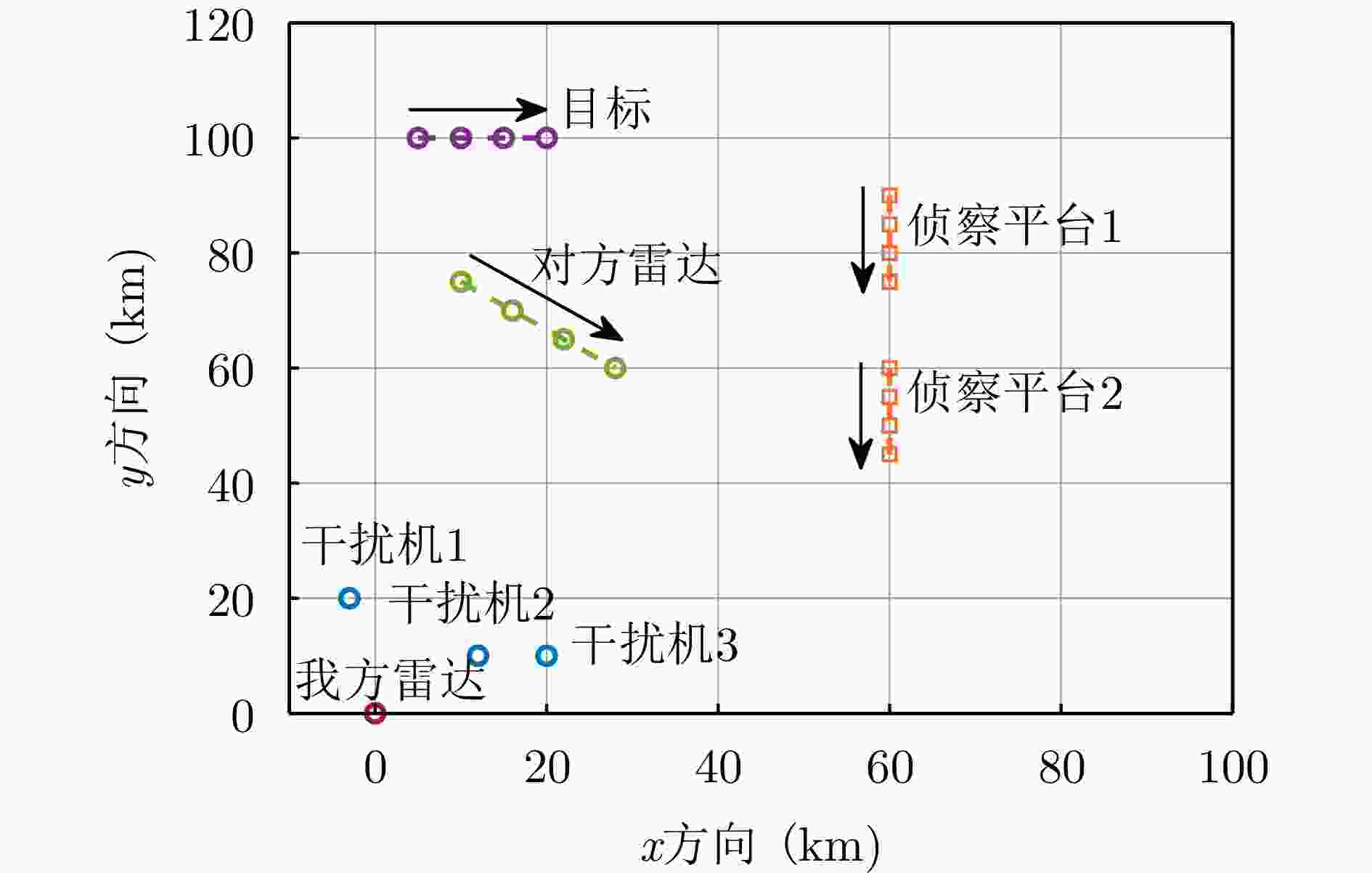
步骤1 初始化： 设置场景数据(如平台运动轨迹、阵元个数、阵元间距等)，给定$ {{\boldsymbol{w}}_{o{\rm t}}}(\tau ) $, $ {{\boldsymbol{w}}_{n{\rm t}}}(\tau ) $初值。 步骤2 执行循环： (1) 固定当前$ {{\boldsymbol{w}}_{o{\rm t}}}(\tau ) $, $ {{\boldsymbol{w}}_{n{\rm t}}}(\tau ) $，化简并求解式(2)，得到最优$ {{\boldsymbol{w}}_{o{\rm r}}^*}(\tau ) $； (2) 固定当前$ {{\boldsymbol{w}}_{o{\rm r}}}(\tau ) $, $ {{\boldsymbol{w}}_{n{\rm t}}}(\tau ) $，化简并求解式(2)，得到最优$ {{\boldsymbol{w}}_{o{\rm t}}^*}(\tau ) $； (3) 固定当前$ {{\boldsymbol{w}}_{o{\rm r}}}(\tau ) $, $ {{\boldsymbol{w}}_{o{\rm t}}}(\tau ) $，采用FPP-SCA算法求解式(35)，得到最优$ {{\boldsymbol{w}}_{n{\rm t}}^*}(\tau ) $； 直到目标函数和优化变量收敛，循环结束； 步骤3 输出结果： 当前波束权矢量$ {\boldsymbol{w}}_{o{\rm r}}^ * (\tau ) $, $ {\boldsymbol{w}}_{o{\rm t}}^ * (\tau ) $和$ {\boldsymbol{w}}_{n{\rm t}}^ * (\tau ) $的值即为运动平台的波束资源联合优化最优结果。
下载: 导出CSV
表 1 各时刻的平台坐标(km)
Table 1. The coordinates of each platform at each time (km)
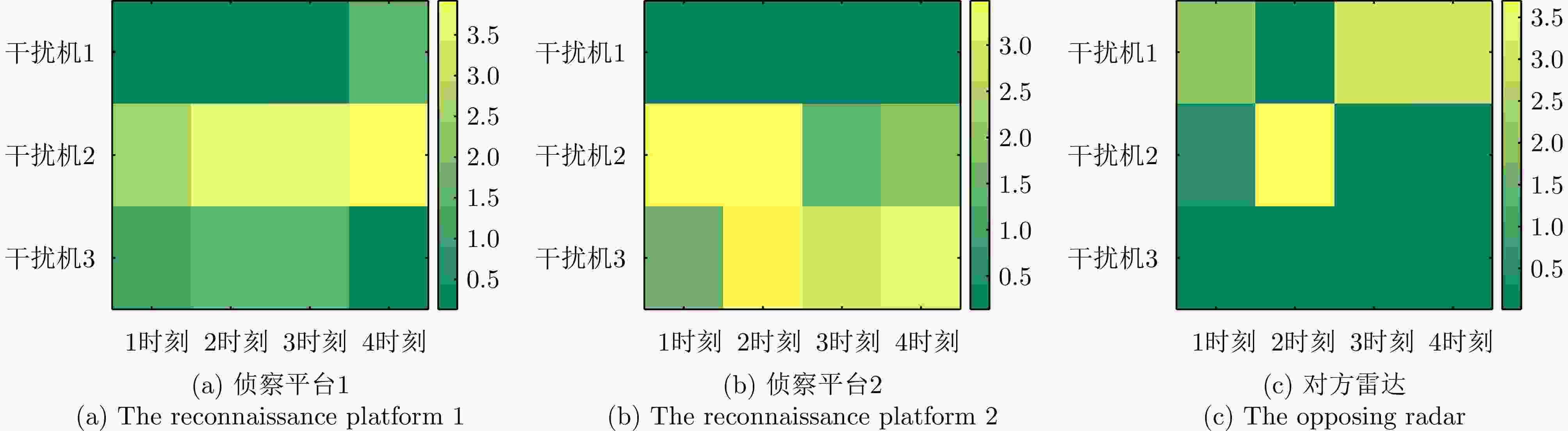
平台 $\tau = 1$时刻 $\tau = 2$时刻 $\tau = 3$时刻 $\tau = 4$时刻 目标 (5, 100) (10, 100) (15, 100) (20, 100) 对方雷达 (10, 75) (16, 70) (22, 65) (28, 60) 侦察平台1 (60, 90) (60, 85) (60, 80) (60, 75) 侦察平台2 (60, 60) (60, 55) (60, 50) (60, 45) 我方雷达 (0, 0) 干扰机1 (–3, 20) 干扰机2 (12, 10) 干扰机3 (20, 10)
下载: 导出CSV
-
[1] 赵国庆. 雷达对抗原理[M]. 2版. 西安: 西安电子科技大学出版社, 2012: 1–12.ZHAO Guoqing. Principle of Radar Countermeasure[M]. 2nd ed. Xi’an: Xidian University Press, 2012: 1–12. [2] 易伟, 袁野, 刘光宏, 等. 多雷达协同探测技术研究进展: 认知跟踪与资源调度算法[J]. 雷达学报, 2023, 12(3): 471–499. doi: 10.12000/JR23036.YI Wei, YUAN Ye, LIU Guanghong, et al. Recent advances in multi-radar collaborative surveillance: Cognitive tracking and resource scheduling algorithms[J]. Journal of Radars, 2023, 12(3): 471–499. doi: 10.12000/JR23036. [3] 王祥丽, 易伟, 孔令讲. 基于多目标跟踪的相控阵雷达波束和驻留时间联合分配方法[J]. 雷达学报, 2017, 6(6): 602–610. doi: 10.12000/JR17045.WANG Xiangli, YI Wei, and KONG Lingjiang. Joint beam selection and dwell time allocation for multi-target tracking in phased array radar system[J]. Journal of Radars, 2017, 6(6): 602–610. doi: 10.12000/JR17045. [4] HAO Guoqing, FENG Dejun, CHENG Biqin, et al. Impact analysis of passive multi-false targets to phased array radar resources[C]. 2023 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Qingdao, China, 2023: 1–3. doi: 10.1109/ICMMT58241.2023.10277047. [5] TUNCER O and CIRPAN H A. Target priority based optimisation of radar resources for networked air defence systems[J]. IET Radar, Sonar & Navigation, 2022, 16(7): 1212–1224. doi: 10.1049/rsn2.12255. [6] SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869. [7] 宋晓程, 李陟, 任海伟, 等. 目标动态威胁度驱动的分布式组网相控阵雷达资源优化分配算法[J]. 雷达学报, 2023, 12(3): 629–641. doi: 10.12000/JR22240.SONG Xiaocheng, LI Zhi, REN Haiwei, et al. Threat-driven resource allocation algorithm for distributed netted phased array radars[J]. Journal of Radars, 2023, 12(3): 629–641. doi: 10.12000/JR22240. [8] 时晨光, 董璟, 周建江. 频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法[J]. 雷达学报, 2023, 12(3): 590–601. doi: 10.12000/JR22146.SHI Chenguang, DONG Jing, and ZHOU Jianjiang. Joint transmit power and dwell time allocation for multitarget tracking in radar networks under spectral coexistence[J]. Journal of Radars, 2023, 12(3): 590–601. doi: 10.12000/JR22146. [9] YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587. [10] LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Joint beam selection and power allocation in cognitive collocated MIMO radar for potential guidance application under oppressive jamming[J]. Digital Signal Processing, 2022, 127: 103579. doi: 10.1016/j.dsp.2022.103579. [11] 张大琳, 易伟, 孔令讲. 面向组网雷达干扰任务的多干扰机资源联合优化分配方法[J]. 雷达学报, 2021, 10(4): 595–606. doi: 10.12000/JR21071.ZHANG Dalin, YI Wei, and KONG Lingjiang. Optimal joint allocation of multijammer resources for jamming netted radar system[J]. Journal of Radars, 2021, 10(4): 595–606. doi: 10.12000/JR21071. [12] YAO Zekun, TANG Chuanbin, WANG Chao, et al. Cooperative jamming resource allocation model and algorithm for netted radar[J]. Electronics Letters, 2022, 58(22): 834–836. doi: 10.1049/ell2.12611. [13] WANG Yuedong, LIANG Yan, ZHANG Huixia, et al. Domain knowledge-assisted deep reinforcement learning power allocation for MIMO radar detection[J]. IEEE Sensors Journal, 2022, 22(23): 23117–23128. doi: 10.1109/JSEN.2022.3211606. [14] 时晨光, 王奕杰, 代向荣, 等. 面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法[J]. 雷达学报, 2022, 11(5): 778–793. doi: 10.12000/JR22005.SHI Chenguang, WANG Yijie, DAI Xiangrong, et al. Joint transmit resources and trajectory planning for target tracking in airborne radar networks[J]. Journal of Radars, 2022, 11(5): 778–793. doi: 10.12000/JR22005. [15] DURST S, MARQUARDT P, and BRÜGGENWIRTH S. Quality of service based radar resource management for interference mitigation[C]. 2022 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNeT), Las Vegas, USA, 2022: 32–35. doi: 10.1109/WiSNet53095.2022.9721374. [16] YAN Junkun, JIAO Hao, PU Wenqiang, et al. Radar sensor network resource allocation for fused target tracking: A brief review[J]. Information Fusion, 2022, 86/87: 104–115. doi: 10.1016/j.inffus.2022.06.009. [17] GHADIAN M, MOFRAD R F, and ARAND B A. Robust time resource management in cognitive radar using adaptive waveform design[J]. IETE Journal of Research, 2023, 69(2): 1070–1080. doi: 10.1080/03772063.2020.1853615. [18] 王跃东, 顾以静, 梁彦, 等. 伴随压制干扰与组网雷达功率分配的深度博弈研究[J]. 雷达学报, 2023, 12(3): 642–656. doi: 10.12000/JR23023.WANG Yuedong, GU Yijing, LIANG Yan, et al. Deep game of escorting suppressive jamming and networked radar power allocation[J]. Journal of Radars, 2023, 12(3): 642–656. doi: 10.12000/JR23023. [19] DELIGIANNIS A, LAMBOTHARAN S, and CHAMBERS J A. Game theoretic analysis for MIMO radars with multiple targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 2760–2774. doi: 10.1109/TAES.2016.150699. [20] DELIGIANNIS A, PANOUI A, LAMBOTHARAN S, et al. Game-theoretic power allocation and the Nash equilibrium analysis for a multistatic MIMO radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6397–6408. doi: 10.1109/TSP.2017.2755591. [21] 赫彬, 苏洪涛. 认知雷达抗干扰中的博弈论分析综述[J]. 电子与信息学报, 2021, 43(5): 1199–1211. doi: 10.11999/JEIT200843.HE Bin and SU Hongtao. A review of game theory analysis in cognitive radar anti-jamming[J]. Journal of Electronics & Information Technology, 2021, 43(5): 1199–1211. doi: 10.11999/JEIT200843. [22] MEHANNA O, HUANG Kejun, GOPALAKRISHNAN B, et al. Feasible point pursuit and successive approximation of non-convex QCQPs[J]. IEEE Signal Processing Letters, 2015, 22(7): 804–808. doi: 10.1109/LSP.2014.2370033. [23] 任唯祎. 通信侦察信息在组网雷达对抗中的应用[D]. [硕士论文], 电子科技大学, 2021: 1. doi: 10.27005/d.cnki.gdzku.2021.002157.REN Weiyi. Application of communication reconnaissance information in radar network countermeasures[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021: 1. doi: 10.27005/d.cnki.gdzku.2021.002157. [24] 宋占福, 赵全习, 范成礼, 等. “信火一体”抗击航空兵编队突防策略分析[J]. 航空兵器, 2022, 29(4): 20–25. doi: 10.12132/ISSN.1673-5048.2021.0196.SONG Zhanfu, ZHAO Quanxi, FAN Chengli, et al. Analysis of information-firepower integration against air force formation penetration[J]. Aero Weaponry, 2022, 29(4): 20–25. doi: 10.12132/ISSN.1673-5048.2021.0196. [25] 戚志刚, 惠新成, 张卫. 天基侦察信息在航母编队信息系统中的应用[J]. 指挥信息系统与技术, 2021, 12(4): 18–22. doi: 10.15908/j.cnki.cist.2021.04.003.QI Zhigang, HUI Xincheng, and ZHANG Wei. Application of space-based reconnaissance information in aircraft carrier formation information system[J]. Command Information System and Technology, 2021, 12(4): 18–22. doi: 10.15908/j.cnki.cist.2021.04.003. [26] 张鹏程. 基于博弈的空中目标航迹预测及攻防对抗研究[D]. [硕士论文], 浙江大学, 2023: 1–45. doi: 10.27461/d.cnki.gzjdx.2023.000119.ZHANG Pengcheng. Research on game-based aerial target track prediction and confrontation[D]. [Master dissertation], Zhejiang University, 2023: 1–45. doi: 10.27461/d.cnki.gzjdx.2023.000119. [27] 王硕, 吴楠, 黄洁, 等. 基于残差修正CNN-BiLSTM的空中目标航迹短期预测算法[J]. 指挥控制与仿真, 2024, 46(1): 55–63. doi: 10.3969/j.issn.1673-3819.2024.01.007.WANG Shuo, WU Nan, HUANG Jie, et al. Short-term prediction algorithm of air target track based on residual correction CNN-BiLSTM[J]. Command Control & Simulation, 2024, 46(1): 55–63. doi: 10.3969/j.issn.1673-3819.2024.01.007. [28] 杨艳洲, 王佳雯, 张玮, 等. 国外天基信息系统装备及技术发展水平研究[J]. 现代信息科技, 2020, 4(6): 53–56, 60. doi: 10.19850/j.cnki.2096-4706.2020.06.019.YANG Yanzhou, WANG Jiawen, ZHANG Wei, et al. Research on the development level of space-based information system equipment and technology abroad[J]. Modern Information Technology, 2020, 4(6): 53–56, 60. doi: 10.19850/j.cnki.2096-4706.2020.06.019. [29] 王帅, 黄富瑜, 李婷, 等. 陆战场红外侦察告警装备作战效能评估[J]. 激光与红外, 2019, 49(3): 341–348. doi: 10.3969/j.issn.1001-5078.2019.03.013.WANG Shuai, HUANG Fuyu, LI Ting, et al. Operational effectiveness evaluation of infrared reconnaissance & warning equipment in warfield[J]. Laser & Infrared, 2019, 49(3): 341–348. doi: 10.3969/j.issn.1001-5078.2019.03.013. [30] 杨艺琼, 吴建新, 梁毅. 机载双基雷达波束域杂波抑制方法[J/OL]. 系统工程与电子技术, 1–11. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJ&filename=XTYD20230905001, 2023.YANG Yiqiong, WU Jianxin, and LIANG Yi. Airborne bistatic radar beam domain clutter suppression method[J/OL]. Systems Engineering and Electronics, 1–11. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJ&filename=XTYD20230905001, 2023. [31] 董超. 多视角广义特征值最接近支持向量机[D]. [硕士论文], 华东师范大学, 2016: 6.DONG Chao. Multi-view generalized eigenvalue proximal support vector machines[D]. [Master dissertation], East China Normal University, 2016: 6. [32] 王奇超, 文再文, 蓝光辉, 等. 优化算法的复杂度分析[J]. 中国科学: 数学, 2020, 50(9): 1271–1336. doi: 10.1360/N012018-00251.WANG Qichao, WEN Zaiwen, LAN Guanghui, et al. Complexity analysis for optimization methods[J]. Scientia Sinica Mathematica, 2020, 50(9): 1271–1336. doi: 10.1360/N012018-00251. [33] LUO Zhiquan, MA W K, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27(3): 20–34. doi: 10.1109/MSP.2010.936019. [34] RAZAVIYAYN M. Successive convex approximation: Analysis and applications[D]. [Ph.D. dissertation], University of Minnesota, 2014: 1–10. [35] FAN Tao, CUI Guolong, YU Xianxiang, et al. Joint design of intra-inter agile pulses and Doppler filter banks for Doppler ambiguous target[J]. IEEE Transactions on Signal Processing, 2024, 72: 867–882. doi: 10.1109/TSP.2024.3355768. -
图(13) / 表(4)
计量
- 文章访问数: 160
- HTML全文浏览量: 27
- PDF下载量: 24
- 被引次数: 0
