作者中心
专家审稿
责编办公
编辑办公
-
摘要: 后向投影(BP)算法是合成孔径雷达成像算法发展的重要方向之一。然而，由于BP算法具有较大的计算量，阻碍了其在工程应用上的发展。因此，近年来如何有效地提高BP算法的运算效率受到了广泛的重视。该文讨论了基于多种成像面坐标系的快速BP算法，包括距离-方位平面坐标系、地平面坐标系和非欧氏坐标系。该文首先简要介绍了原始BP算法的原理和不同坐标系对加速BP算法的影响，并对BP算法的发展历程进行梳理。然后讨论了基于不同成像面坐标系的快速BP算法的研究进展，并重点介绍了作者所在研究团队近年来在快速BP成像方面完成的研究工作。最后介绍了快速BP算法在工程上的应用，并展望了未来快速BP成像算法的研究发展趋势。Abstract: The Back Projection (BP) algorithm is an important direction in the development of synthetic aperture radar imaging algorithms. However, the large computational load of the BP algorithm has hindered its development in engineering applications. Therefore, techniques to enhance the computational efficiency of the BP algorithm have recently received widespread attention. This paper discusses the fast BP algorithm based on various imaging plane coordinate systems, including the distance-azimuth plane coordinate system, the ground plane coordinate system, and the non-Euclidean coordinate system. First, the principle of the original BP algorithm and the impact of different coordinate systems on accelerating the BP algorithm are introduced, and the development history of the BP algorithm is sorted out. Then, the research progress of the fast BP algorithm based on different imaging plane coordinate systems is examined, focusing on the recent research work completed by the author’s research team. Finally, the application of fast BP algorithm in engineering is introduced, and the research development trend of the fast BP imaging algorithm is discussed.
-
图 10 距离-方位平面坐标系成像模型
Figure 10. Imaging model in the distance-azimuth plane coordinate system
图 15 FFBP算法与CFBP算法计算量对比
Figure 15. Comparison of computational load between FFBP algorithm and CFBP algorithm
图 25 GCBP算法对地表曲面成像仿真结果
Figure 25. Simulation results of GCBP algorithm for surface imaging
表 1 各类坐标系下成像优缺点对比
Table 1. Comparison of advantages and disadvantages of imaging in various coordinate systems
坐标系 优点 缺点 局部极坐标系 可以以较低的采样率进行子孔径低分辨成像而
不会造成频谱混叠各级图像相干融合时需要进行插值操作，会使得误差积累，
分级次数越多，误差积累越大，成像质量越差全局虚拟极坐标系 不再需要进行插值处理，成像质量高 成像条件限制大，要求子图像波数谱无模糊，
并且在最后的图像融合阶段，计算量较大混合坐标系 只需对角度维进行插值，不需要对距离维插值，
减少了插值次数，提高了成像质量需要插值处理，对成像质量依旧有影响 全局直角坐标系 成像时无需插值与逐点运算，成像质量更好，
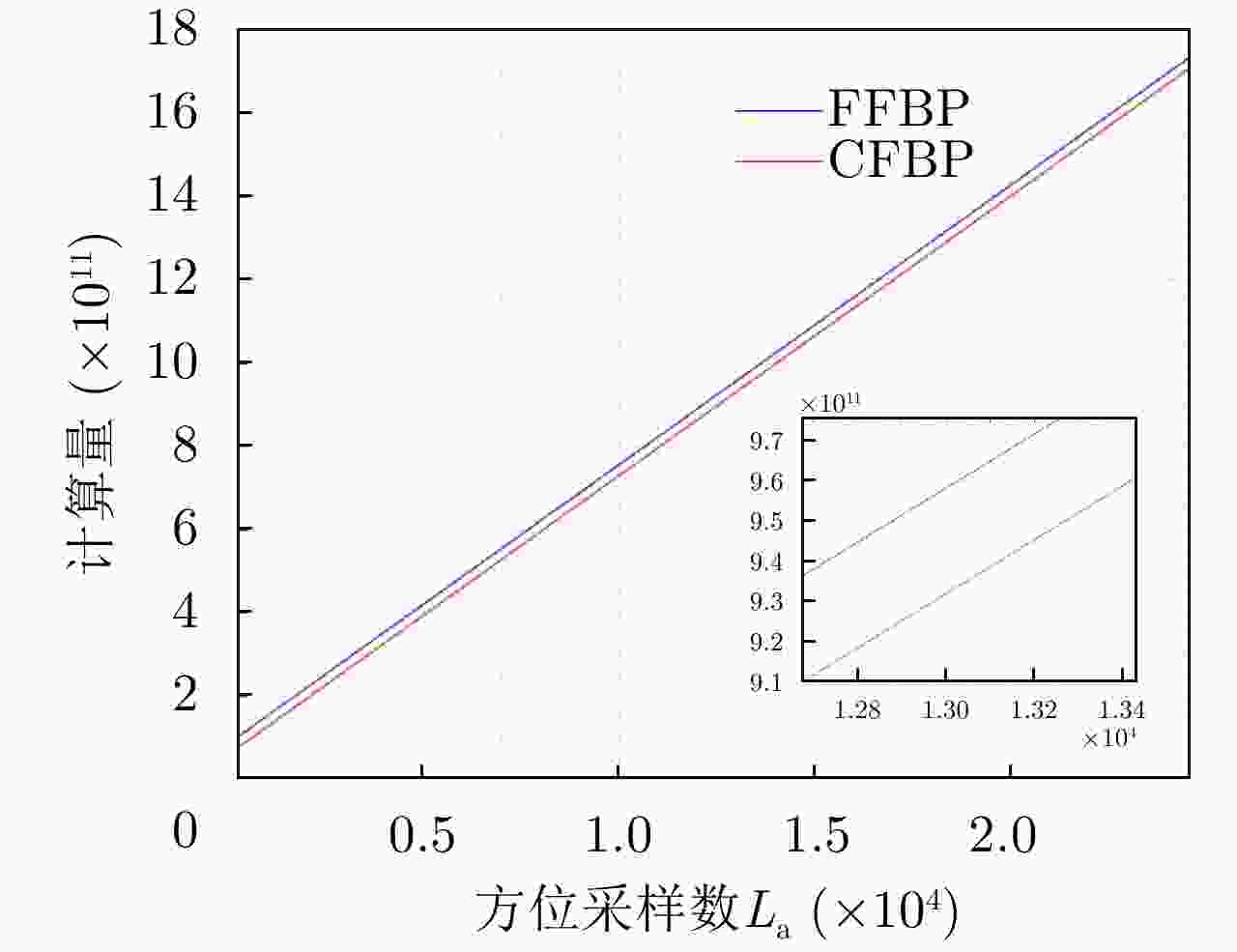
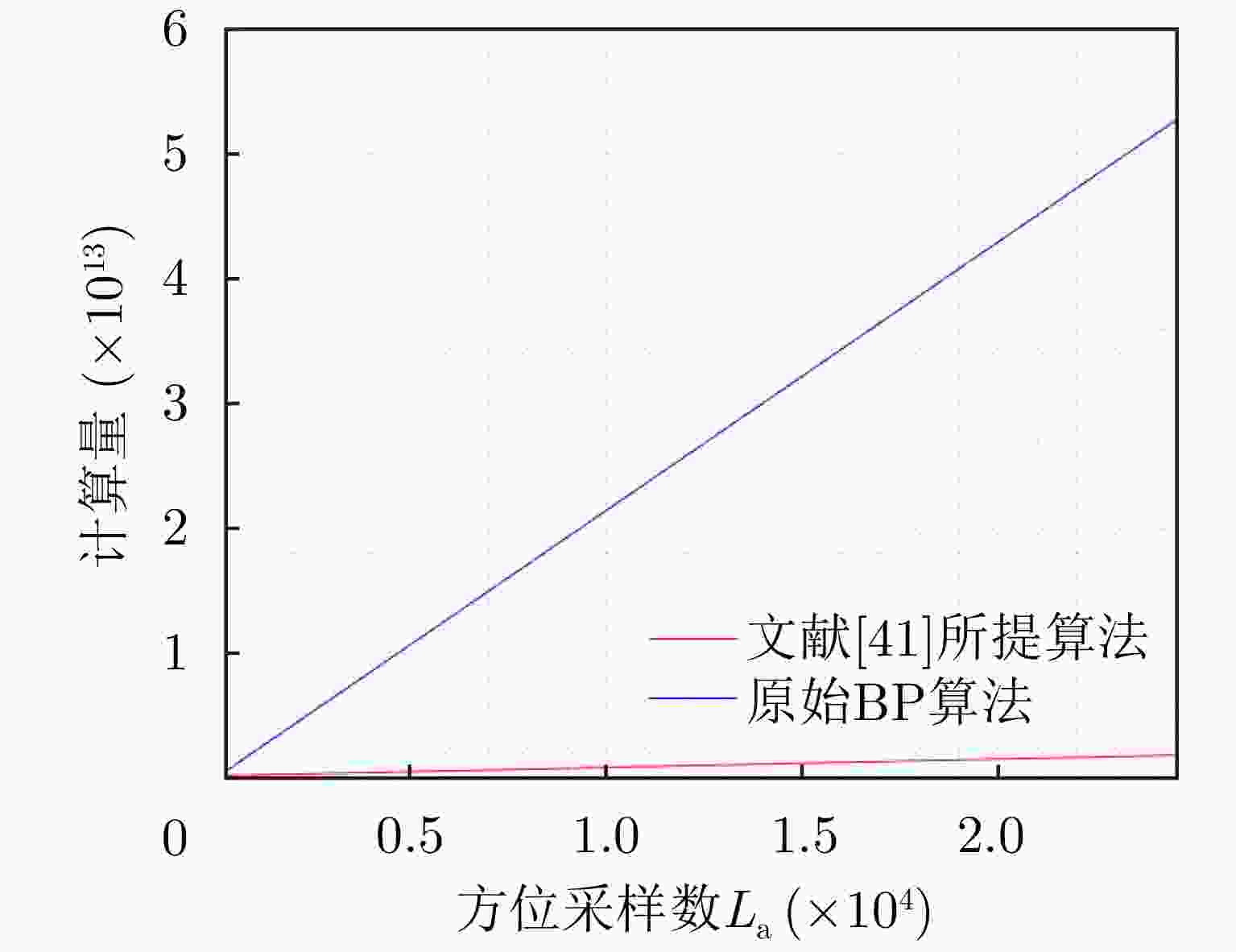
更利于工程化实现直角坐标系对子孔径图像采样率要求过高 
下载: 导出CSV
表 2 FFBP算法与CFBP算法计算量对比
Table 2. Comparison of computational burden between FFBP algorithm and CFBP algorithm
算法 计算量 FFBP $ \dfrac{{8{N^2}{L_{\text{a}}}}}{n} + 64{N^2}{\log _2}n $ CFBP $ \dfrac{{8{N^2}{L_{\text{a}}}}}{n} + \displaystyle\sum\limits_{i = 1}^{{{\log }_2}n} {\left( {{N^2}\left( \begin{gathered} 3{\log _2}\sqrt N + {\log _2}\sqrt {\frac{{N \times {2^{i - 1}}}}{n}} + \\ 2{\log _2}\sqrt {\frac{{N \times {2^i}}}{n}} + 6 \\ \end{gathered} \right)} \right)} $
下载: 导出CSV
表 3 文献[26]、文献[36]与文献[37]所提算法计算量对比
Table 3. Comparison of computational burden between algorithm Proposed in Ref. [26], Ref. [36] and Ref. [37]
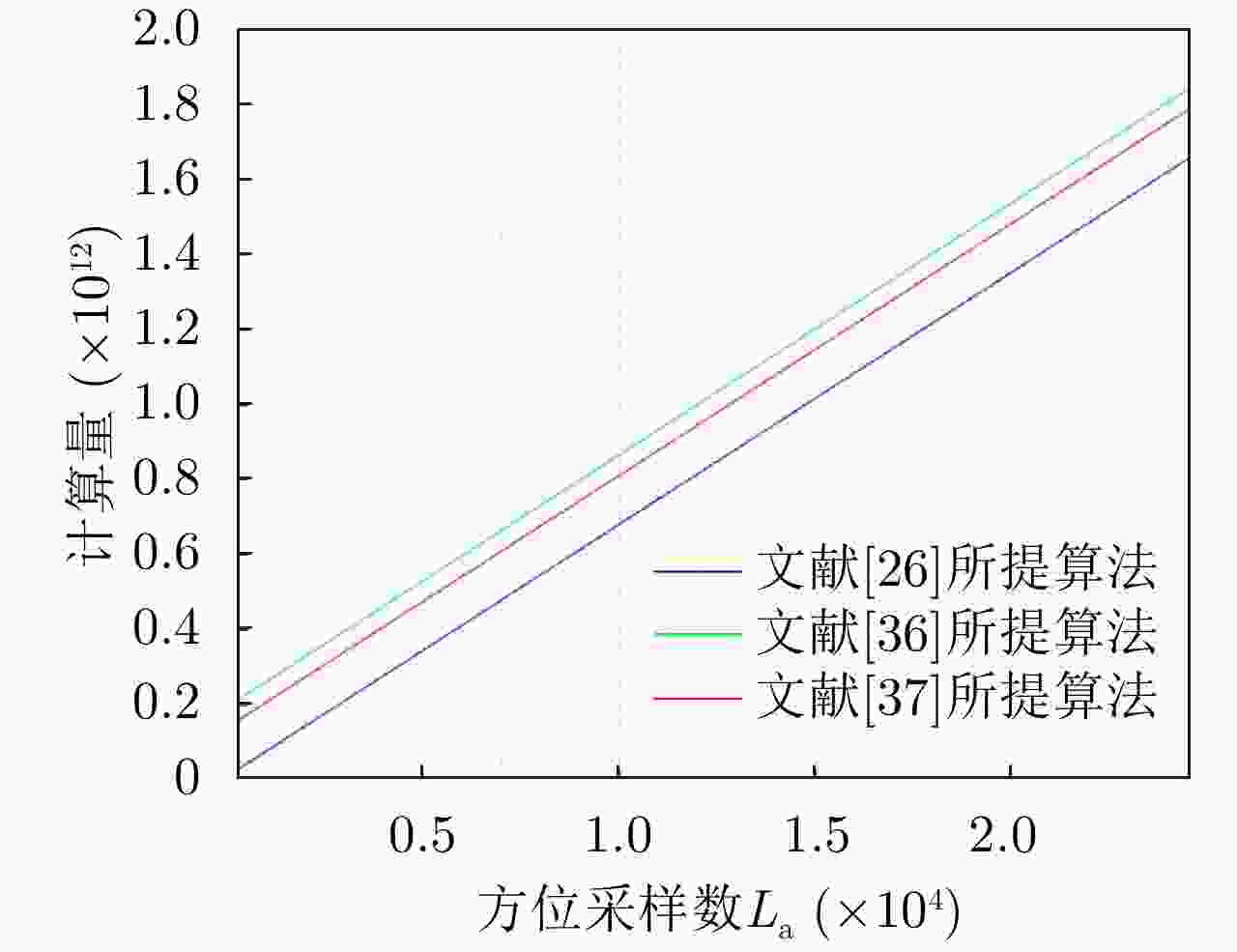
算法 计算量 文献[26]所提算法 $ \dfrac{{8{N^2}{L_{\text{a}}}}}{n} + 8{N^2}{\log _2}n $ 文献[36]所提算法 $ 50{N^2}{\log _2}N + 30{N^2} + \dfrac{{8{N^2}{L_{\text{a}}}}}{n} $ 文献[37]所提算法 $ \begin{gathered} \dfrac{{8{N^2}{L_{\text{a}}}}}{n} + \left( {2n + 2} \right){N^2} \\ +\left( {n + 1} \right){N^2}{\log _2}N - {N^2}{\log _2}\sqrt n \\ \end{gathered} $
下载: 导出CSV
表 4 文献[42]、文献[52]与文献[58]所提算法计算量对比
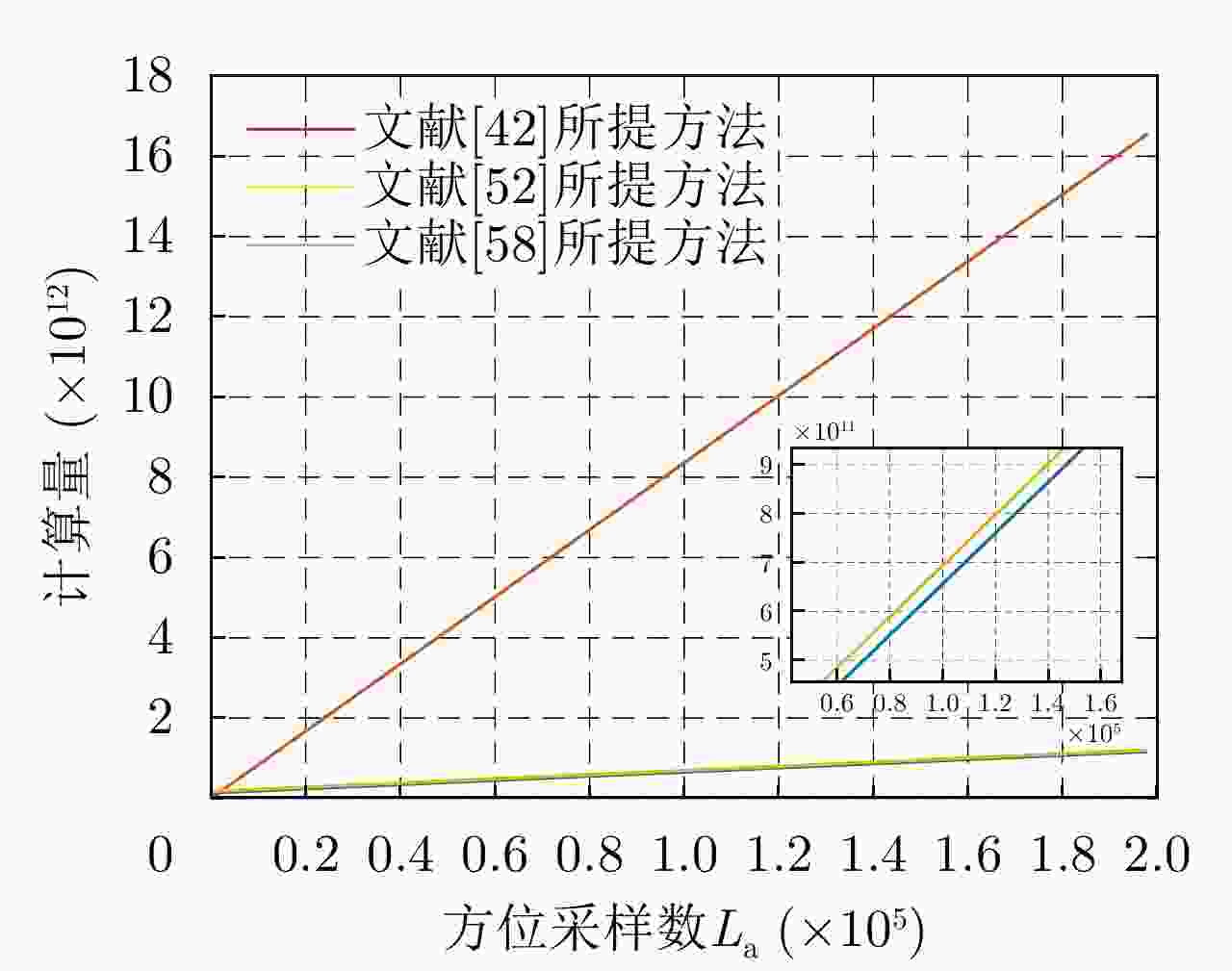
Table 4. Comparison of computational burden between algorithm proposed in Ref. [42], Ref. [52] and Ref. [58]
算法 计算量 文献[42]所提算法 $ \begin{aligned} & \frac{{16mD{N^2}{L_{\text{a}}}}}{{m + 1}}{{ + m{{D}}}}{N^2} + \rho mDN_{{\mathrm{DCT}}}^2 \\& + \rho \left( {2{D^2} + D + 27} \right){L_{\mathrm{a}}} \end{aligned} $ 文献[52]所提算法 $ \begin{aligned} & \frac{{16mD{N^2}{L_{\text{a}}}}}{{n\left( {m + 1} \right)}} + 64mD{N^2}{\log _2}n \\ & + 2mD{N^2}{\log _2}N + 4mD{N^2} \\ & + \left( {6{D^2} + 21D} \right){L_{\mathrm{a}}} \end{aligned} $ 文献[58]所提算法 $ \begin{aligned} & \frac{{16mD{N^2}{L_{\text{a}}}}}{{n\left( {m + 1} \right)}} + mD\left( {n + 4} \right){N^2}{\log _2}N \\ & - mD{N^2}{\log _2}\sqrt n + mD\left( {2n + 8} \right){N^2} \\& + m8N + \left( {6{D^2} + 21D} \right){L_{\mathrm{a}}} \end{aligned} $
下载: 导出CSV
-
[1] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005.BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005. [2] SOUMEKH M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms[M]. New York: Wiley, 1999. [3] CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data[M]. Boston: Artech House, 2005: 108–110. [4] MOREIRA A and HUANG Yonghong. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1029–1040. doi: 10.1109/36.312891 [5] RANEY R K, RUNGE H, BAMLER R, et al. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 786–799. doi: 10.1109/36.298008 [6] BAMLER R. A comparison of range-Doppler and wavenumber domain SAR focusing algorithms[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(4): 706–713. doi: 10.1109/36.158864 [7] LIN Yun, HONG Wen, TAN Weixian, et al. Extension of range migration algorithm to squint circular SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 651–655. doi: 10.1109/LGRS.2010.2098843 [8] VU V T, SJÖGREN T K, and PETTERSSON M I. SAR imaging in ground plane using fast backprojection for mono- and bistatic cases[C]. 2012 IEEE Radar Conference, Atlanta, GA, USA, 2012: 184–189. [9] 杨泽民. 快速时域SAR成像与三维SAR运动补偿方法研究[D]. [博士论文], 西安电子科技大学, 2016.YANG Zemin. Study on fast time domain SAR imaging and three dimensional SAR motion compensation methods[D]. [Ph.D. dissertation], Xidian University, 2016. [10] ANDERSSON L E. On the determination of a function from spherical averages[J]. SIAM Journal on Mathematical Analysis, 1988, 19(1): 214–232. doi: 10.1137/0519016 [11] FAWCETT J A. Inversion of N-dimensional spherical averages[J]. SIAM Journal on Applied Mathematics, 1985, 45(2): 336–341. doi: 10.1137/0145018 [12] ALBUQUERQUE M, PRATS P, and SCHEIBER R. Applications of time-domain back-projection SAR processing in the airborne case[C]. 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 1–4. [13] DURAND R, GINOLHAC G, THIRION-LEFEVRE L, et al. Back projection version of subspace detector SAR processors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1489–1497. doi: 10.1109/TAES.2011.5751274 [14] MUNSON D C, O’BRIEN J D, and JENKINS W K. A tomographic formulation of spotlight-mode synthetic aperture radar[J]. Proceedings of the IEEE, 1983, 71(8): 917–925. doi: 10.1109/PROC.1983.12698 [15] YEGULALP A F. Fast backprojection algorithm for synthetic aperture radar[C]. The 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No.99CH36249), Waltham, MA, USA, 1999: 60–65. [16] ULANDER L M H, HELLSTEN H, and STENSTROM G. Synthetic-aperture radar processing using fast factorized back-projection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 760–776. doi: 10.1109/TAES.2003.1238734 [17] 龙腾, 丁泽刚, 肖枫, 等. 星载高分辨频率步进SAR成像技术[J]. 雷达学报, 2019, 8(6): 782–792. doi: 10.12000/JR19076LONG Teng, DING Zegang, XIAO Feng, et al. Spaceborne high-resolution stepped-frequency SAR imaging technology[J]. Journal of Radars, 2019, 8(6): 782–792. doi: 10.12000/JR19076 [18] 丁赤飚, 仇晓兰, 徐丰, 等. 合成孔径雷达三维成像—从层析、阵列到微波视觉[J]. 雷达学报, 2019, 8(6): 693–709. doi: 10.12000/JR19090DING Chibiao, QIU Xiaolan, XU Feng, et al. Synthetic aperture radar three-dimensional imaging—from TomoSAR and array InSAR to microwave vision[J]. Journal of Radars, 2019, 8(6): 693–709. doi: 10.12000/JR19090 [19] CHEN Jianlai, SUN Guangcai, XING Mengdao, et al. A two-dimensional beam-steering method to simultaneously consider doppler centroid and ground observation in GEOSAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(1): 161–167. doi: 10.1109/JSTARS.2016.2544349 [20] 邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1–10. doi: 10.3724/SP.J.1300.2012.20015DENG Yunkai, ZHAO Fengjun, and WANG Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1–10. doi: 10.3724/SP.J.1300.2012.20015 [21] 李浩林. 机载SAR快速后向投影成像算法研究[D]. [博士论文], 西安电子科技大学, 2015.LI Haolin. Study on fast back-projection algorithms for airborne SAR image[D]. [Ph.D. dissertation], Xidian University, 2015. [22] 陈潇翔. 机载超高分辨SAR运动补偿成像技术研究[D]. [博士论文], 西安电子科技大学, 2021.CHEN Xiaoxiang. Study on motion compensation algorithm for ultra high resolution airborne SAR imaging[D]. [Ph.D. dissertation], Xidian University, 2021. [23] 杨泽民, 孙光才, 吴玉峰, 等. 一种新的基于极坐标格式的快速后向投影算法[J]. 电子与信息学报, 2014, 36(3): 537–544. doi: 10.3724/SP.J.1146.2013.00613YANG Zemin, SUN Guangcai, WU Yufeng, et al. A new fast back projection algorithm based on polar format algorithm[J]. Journal of Electronics & Information Technology, 2014, 36(3): 537–544. doi: 10.3724/SP.J.1146.2013.00613 [24] ZHANG Lei, LI Haolin, QIAO Zhijun, et al. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1460–1464. doi: 10.1109/LGRS.2013.2295326 [25] ZHANG Lei, LI Haolin, QIAO Zhijun, et al. Integrating autofocus techniques with fast factorized back-projection for high-resolution spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1394–1398. doi: 10.1109/LGRS.2013.2258886 [26] LIANG Yi, LI Guofei, WEN Jun, et al. A fast time-domain SAR imaging and corresponding autofocus method based on hybrid coordinate system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8627–8640. doi: 10.1109/TGRS.2019.2921917 [27] DONG Qi, YANG Zemin, SUN Guangcai, et al. Cartesian factorized backprojection algorithm for synthetic aperture radar[C]. 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 2016: 1074–1077. [28] FROLIND P O and ULANDER L M H. Evaluation of angular interpolation kernels in fast back-projection SAR processing[J]. IEE Proceedings-Radar, Sonar And Navigation, 2006, 153(3): 243–249. doi: 10.1049/ip-rsn:20045110 [29] YANG Zemin, SUN Guangcai, and XING Mengdao. A new fast back-projection algorithm using polar format algorithm[C]. 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 2013: 373–376. [30] YANG Zemin, DONG Qi, SUN Guangcai, et al. A fast implementation method for the FFBP algorithm[C]. 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 2015: 411–414. [31] YANG Lei, ZHOU Song, and BI Guoan. A modified fast factorized back-projection algorithm for squint UWB-SAR imaging[C]. 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 2015: 413–416. [32] WANG Yue, WU Junjie, ZHANG Shaoqing, et al. An accelerate FFBP algorithm of bistatic forward-looking SAR based on azimuth equidistant coordinates[C]. 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 2019: 1–5. [33] 邢孟道, 林浩, 陈溅来, 等. 多平台合成孔径雷达成像算法综述[J]. 雷达学报, 2019, 8(6): 732–757. doi: 10.12000/JR19102XING Mengdao, LIN Hao, CHEN Jianlai, et al. A review of imaging algorithms in multi-platform-borne synthetic aperture radar[J]. Journal of Radars, 2019, 8(6): 732–757. doi: 10.12000/JR19102 [34] 董祺, 杨泽民, 孙光才, 等. 子场景处理的弹载前斜视SAR时域成像算法[J]. 系统工程与电子技术, 2017, 39(5): 1013–1018. doi: 10.3969/j.issn.1001-506X.2017.05.10DONG Qi, YANG Zemin, SUN Guangcai, et al. Missile-borne forward squint SAR time-domain imaging algorithm based on sub-region processing[J]. Systems Engineering and Electronics, 2017, 39(5): 1013–1018. doi: 10.3969/j.issn.1001-506X.2017.05.10 [35] FENG Dong, AN Daoxiang, and HUANG Xiaotao. An extended fast factorized back projection algorithm for missile-borne bistatic forward-looking SAR imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(6): 2724–2734. doi: 10.1109/TAES.2018.2828238 [36] BIE Bowen, XING Mengdao, XIA Xianggen, et al. A frequency domain backprojection algorithm based on local cartesian coordinate and subregion range migration correction for high-squint sar mounted on maneuvering platforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(12): 7086–7101. doi: 10.1109/TGRS.2018.2848249 [37] CHEN Xiaoxiang, SUN Guangcai, XING Mengdao, et al. Ground cartesian back-projection algorithm for high squint diving TOPS SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(7): 5812–5827. doi: 10.1109/TGRS.2020.3011589 [38] HU Cheng, LIU Feifeng, YANG Wenfu, et al. Modification of slant range model and imaging processing in GEO SAR[C]. 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 2010: 4679–4682. [39] MONTI GUARNIERI A, LEANZA A, RECCHIA A, et al. Atmospheric phase screen in GEO-SAR: Estimation and compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1668–1679. doi: 10.1109/TGRS.2017.2766084 [40] ZENG Tao, LI Yinghe, DING Zegang, et al. Subaperture approach based on azimuth-dependent range cell migration correction and azimuth focusing parameter equalization for maneuvering high-squint-mode SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6718–6734. doi: 10.1109/TGRS.2015.2447393 [41] CHEN Quan, LIU Wenkang, SUN Guangcai, et al. A fast cartesian back-projection algorithm based on ground surface grid for GEO SAR focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5217114. doi: 10.1109/TGRS.2021.3125797 [42] RAN Lei, LIU Zheng, ZHANG Lei, et al. An autofocus algorithm for estimating residual trajectory deviations in synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3408–3425. doi: 10.1109/TGRS.2017.2670785 [43] WU Junjie, LI Yunli, PU Wei, et al. An effective autofocus method for fast factorized back-projection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 6145–6154. doi: 10.1109/TGRS.2019.2904608 [44] ZHANG Tao, LIAO Guisheng, LI Yachao, et al. A two-stage time-domain autofocus method based on generalized sharpness metrics and AFBP[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5205413. doi: 10.1109/TGRS.2021.3068789 [45] WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase gradient autofocus—a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827–835. doi: 10.1109/7.303752 [46] YE Wei, YEO T S, and BAO Zheng. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2487–2494. doi: 10.1109/36.789644 [47] SAMCZYNSKI P, PIETRZYK G, and KULPA K. Simple method for estimating along track acceleration using autofocus map drift algorithm[C]. Proceedings of International Radar Symposium, Berlin, Germany, 2005: 43–47. [48] SAMCZYNSKI P and KULPA K. Concept of the coherent autofocus map-drift technique[C]. 2006 International Radar Symposium, Krakow, Poland, 2006: 1–4. [49] SAMCZYNSKI P and KULPA K. Non iterative map-drift technique[C]. 2008 International Conference on Radar, Adelaide, SA, Australia, 2008: 76–81. [50] JAKOWATZ JR C V and WAHL D E. Considerations for autofocus of spotlight-mode SAR imagery created using a beamforming algorithm[C]. Algorithms for Synthetic Aperture Radar Imagery XVI, Orlando, FL, USA, 2009: 73370A. [51] ZHOU Song, YANG Lei, ZHAO Lifan, et al. Quasi-polar-based FFBP algorithm for miniature UAV SAR imaging without navigational data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7053–7065. doi: 10.1109/TGRS.2017.2739133 [52] DING Zegang, LI Linghao, WANG Yan, et al. An autofocus approach for UAV-based ultrawideband ultrawidebeam SAR data with frequency-dependent and 2-D space-variant motion errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5203518. doi: 10.1109/TGRS.2021.3062183 [53] RAN Lei, XIE Rong, LIU Zheng, et al. Simultaneous range and cross-range variant phase error estimation and compensation for highly squinted SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4448–4463. doi: 10.1109/TGRS.2018.2820102 [54] ASH J N. An autofocus method for backprojection imagery in synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 104–108. doi: 10.1109/LGRS.2011.2161456 [55] HU Kebin, ZHANG Xiaoling, HE Shufeng, et al. A less-memory and high-efficiency autofocus back projection algorithm for SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 890–894. doi: 10.1109/LGRS.2014.2365612 [56] CHEN Leping, AN Daoxiang, and HUANG Xiaotao. Extended autofocus backprojection algorithm for low-frequency SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1323–1327. doi: 10.1109/LGRS.2017.2711005 [57] LUO Yin, ZHAO Fengjun, LI Ning, et al. An autofocus cartesian factorized backprojection algorithm for spotlight synthetic aperture radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(8): 1244–1248. doi: 10.1109/LGRS.2018.2829483 [58] LOU Yishan, LIU Wenkang, XING Mengdao, et al. A novel motion compensation method applicable to ground cartesian back-projection algorithm for airborne circular SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5208917. doi: 10.1109/TGRS.2023.3276051 -
图(37) / 表(4)
计量
- 文章访问数: 2237
- HTML全文浏览量: 921
- PDF下载量: 670
- 被引次数: 0
