作者中心
专家审稿
责编办公
编辑办公
Joint Optimization of Transmit Power and Dwell Time for Asynchronous Multi-target Tracking in Heterogeneous Multiple Radar Networks with Imperfect Detection
-
摘要: 该文针对异步多目标跟踪场景，研究了非理想检测下的异构多雷达网络功率时间联合优化问题。首先，将各融合采样间隔内得到的来自不同雷达节点的所有异步量测信息融合为复合量测信息，结合该复合量测信息推导了非理想检测下包含雷达节点选择、辐射功率和驻留时间等参数的异步目标跟踪误差贝叶斯克拉美罗下界(BCRLB)解析表达式，并将其作为异步多目标跟踪精度的衡量指标。在此基础上，建立了非理想检测下面向异步多目标跟踪的异构多雷达网络功率时间联合优化模型，即以最小化异步多目标跟踪误差为优化目标，以满足给定的系统辐射资源限制为约束条件，对不同雷达网络中雷达节点的选择方式、辐射功率和驻留时间等发射参数进行自适应联合优化设计，从而提升异构多雷达网络的异步多目标跟踪精度。最后，针对上述优化问题，结合序列二次规划(SQP)算法和循环最小法，采用四步分解算法进行求解。仿真结果表明，与现有算法相比，所提算法能够有效提升异构多雷达网络的异步多目标跟踪精度。Abstract: The joint optimization problem of transmit power and dwell time of radar for asynchronous multi-target tracking in heterogeneous multiple radar networks with imperfect detection is investigated. Firstly, all the asynchronous measurements from different radar node in each fusion sampling interval are fused into composite measurement, thus the Bayesian Cramér-Rao Lower Bound (BCRLB) analytical expression of the asynchronous target tracking error with parameters such as radar node selection, transmit power and dwell time with imperfect detection is derived and used as the asynchronous target tracking accuracy measure. Based on this, a joint optimization model of transmit power and dwell time for asynchronous multi-target tracking in heterogeneous multiple radar networks with imperfect detection is established, with the optimization objective of minimizing the asynchronous multi-target tracking error and the constraints of given system transmit resource limitations, the parameters such as radar node selection, transmit power and dwell time in different radar networks are designed adaptively and optimally so as to improve the asynchronous multi-target tracking accuracy of the heterogeneous multiple radar networks system. Finally, a four-step decomposition algorithm combined with the Sequential Quadratic Programming (SQP) algorithm and cyclic minimization method is used to solve the optimization problem. Simulation results demonstrate that the asynchronous multi-target tracking accuracy of the heterogeneous multiple radar networks outperforms existing algorithms.
-
图 1 目标q在第k个融合采样间隔内的异步量测模型
Figure 1. Asynchronous measurement model of target q in the k-th fusion sampling interval
图 2 异构多雷达网络分布与目标运动轨迹
Figure 2. Deployment of heterogeneous multiple radar networks and trajectories of moving targets
图 3 目标1的雷达节点选择与功率时间优化结果
Figure 3. Radar node selection, power and dwell time optimization results of target 1
图 4 目标2的雷达节点选择与功率时间优化结果
Figure 4. Radar node selection, power and dwell time optimization results of target 2
图 5 不同检测概率下的各目标BCRLB
Figure 5. BCRLB of each target with different probabilities of detection
1 非理想检测下面向异步多目标跟踪的异构多雷达网络功率时间联合优化算法
1. Joint optimization of transmit power and dwell time for asynchronous multi-target tracking in heterogeneous multiple radar networks with imperfect detection
步骤1 根据功率和时间初始矩阵分配给各雷达节点相应的辐射
功率$ {\boldsymbol{\bar P}}_{{\text{t,}}k}^q $和驻留时间$ {\boldsymbol{\bar T}}_k^q $，松弛$ \mu _{n,m,k}^q $，采用SQP算法求
解式(21)，得到所有的雷达节点选择系数，降序排列后
依次选取$ {L_{\max }} $个雷达节点；步骤2 将优化模型式(22)分解为两个子优化问题，采用SQP算
法依次迭代求解式(23)和式(24)，得到辐射功率和驻留
时间优化分配结果$ {\boldsymbol{\hat P}}_{{\text{t,}}k}^q $和$ {\boldsymbol{\hat T}}_k^q $；步骤3 异构多雷达网络系统指定下一个目标进行相应的资源优
化分配，重复步骤1和步骤2，直到照射所有目标；步骤4 利用循环最小法得到最优雷达节点选择和功率时间分配
结果。
下载: 导出CSV
表 1 异构多雷达网络雷达节点发射参数设置
Table 1. Parameter settings of radar node in heterogeneous multiple radar networks
参数 数值 参数 数值 ${T_{{\text{fusion}}}}$ $6\;{\text{s} }$ ${ {\bar P_{\min } } }$ $100\;{\text{W}}$ ${ {\bar P_{ {} {\text{max} } } } }$ $1000\;{\text{ W} }$ $ {P_{{\text{PAR}}}} $ $300\;{\text{W}}$ $ {P_{{\text{MSR}}}} $ $300\;{\text{W} }$ ${ {\bar T_{\min } } }$ $0.003\;{\text{s}}$ ${ {\bar T_{\max } } }$ $0.03\;{\text{s} }$ $ {T_{{\text{CMIMO}}}} $ $0.006\;{\text{s}}$ $ {T_{{\text{MSR}}}} $ $0.006\;{\text{s}}$ $ \beta _k^q $ $1\;{\text{MHz}}$ $ P_{{\text{total}}}^q $ $1500\;{\text{W}}$ $ T_{{\text{total}}}^q $ $0.03\;{\text{s}}$
下载: 导出CSV
表 2 目标具体运动轨迹参数
Table 2. Specific trajectory parameters of targets
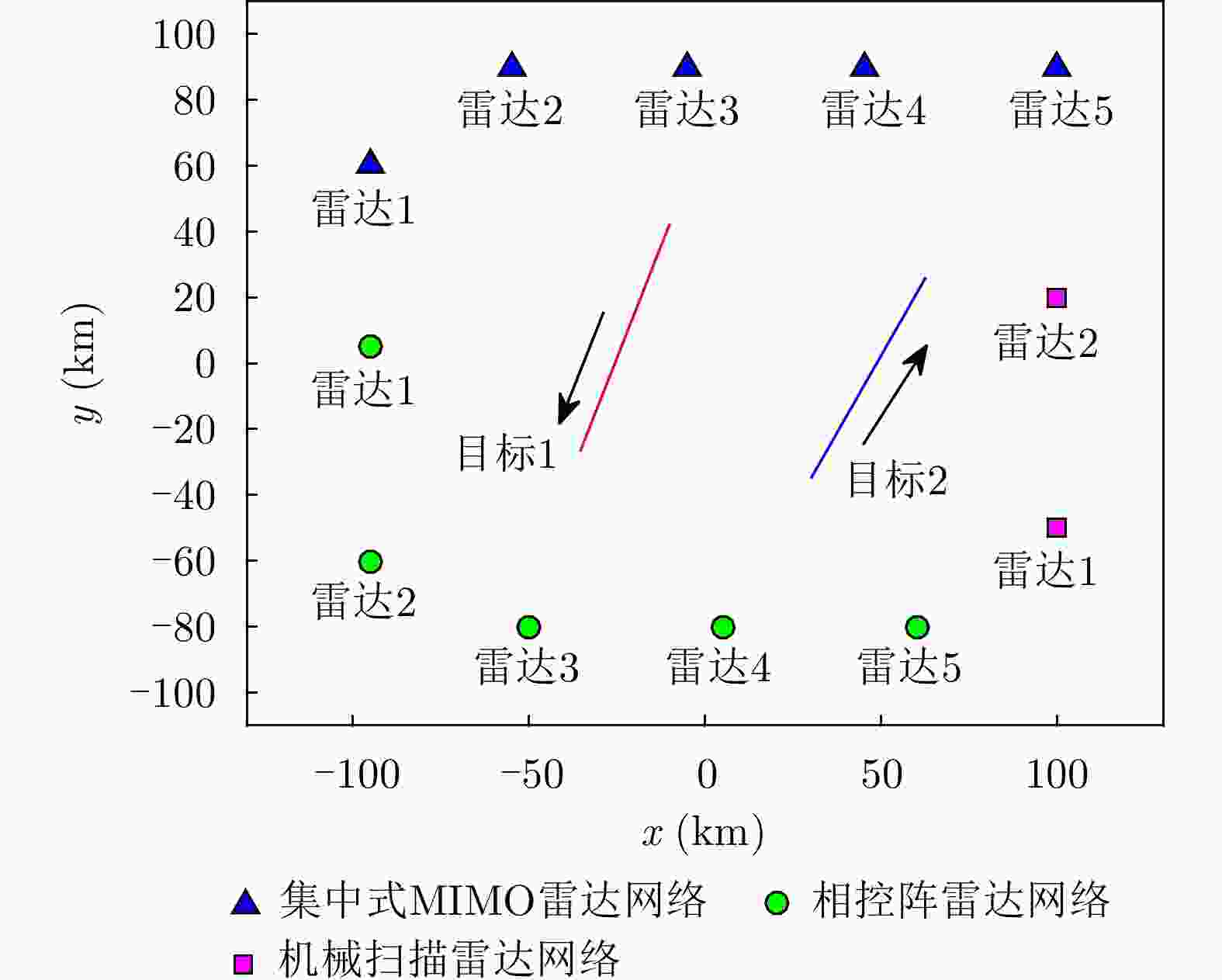
目标编号 初始位置($ {\text{km}} $) 运动速度($ {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}} $) 1 $ \left( { - 10,42.5} \right) $ $ \left( { - 125, - 340} \right) $ 2 $ \left( {30, - 35} \right) $ $ \left( {160,300} \right) $
下载: 导出CSV
表 3 各雷达节点的初始采样时间和采样间隔
Table 3. Initial sampling time and sampling interval of each radar node
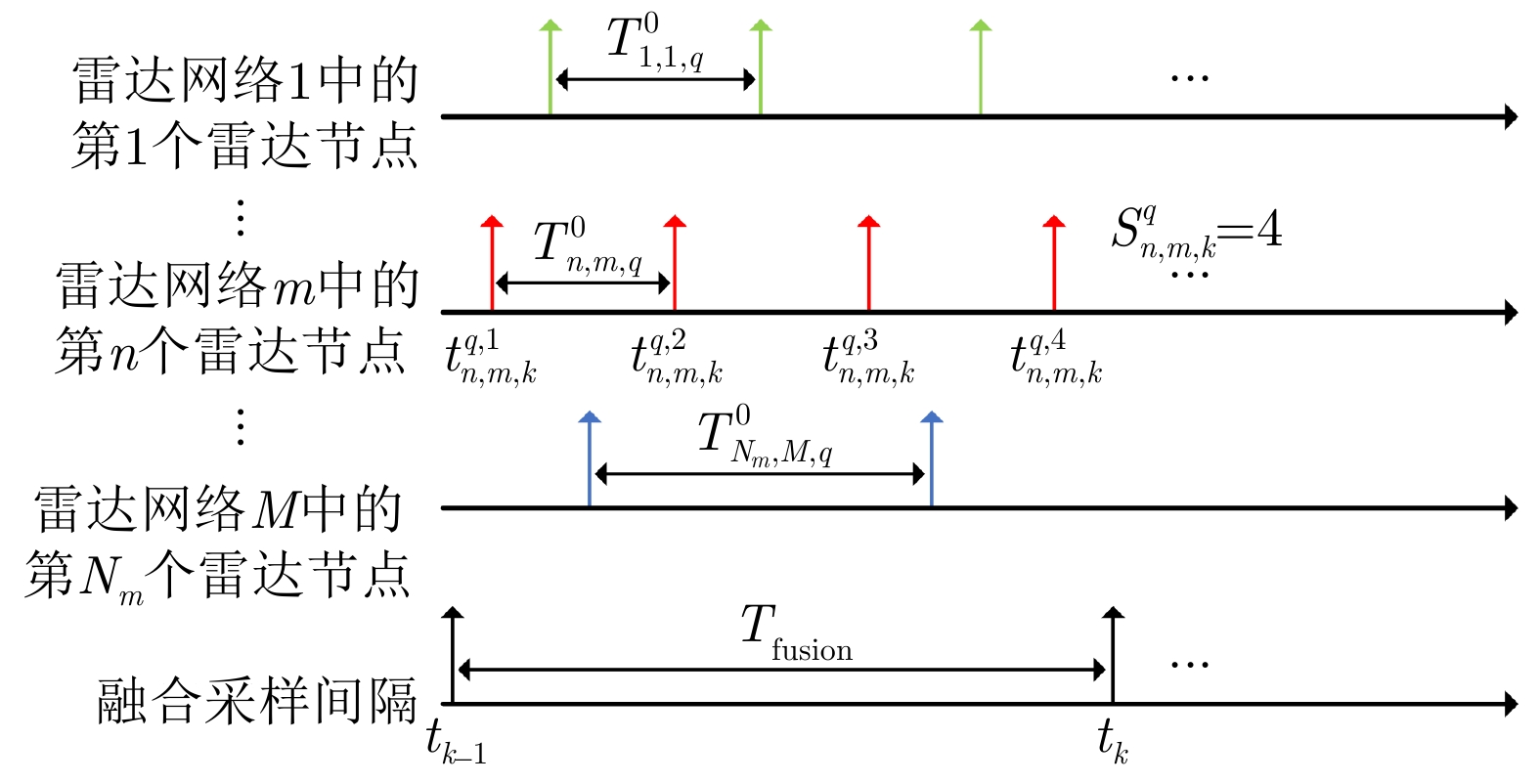
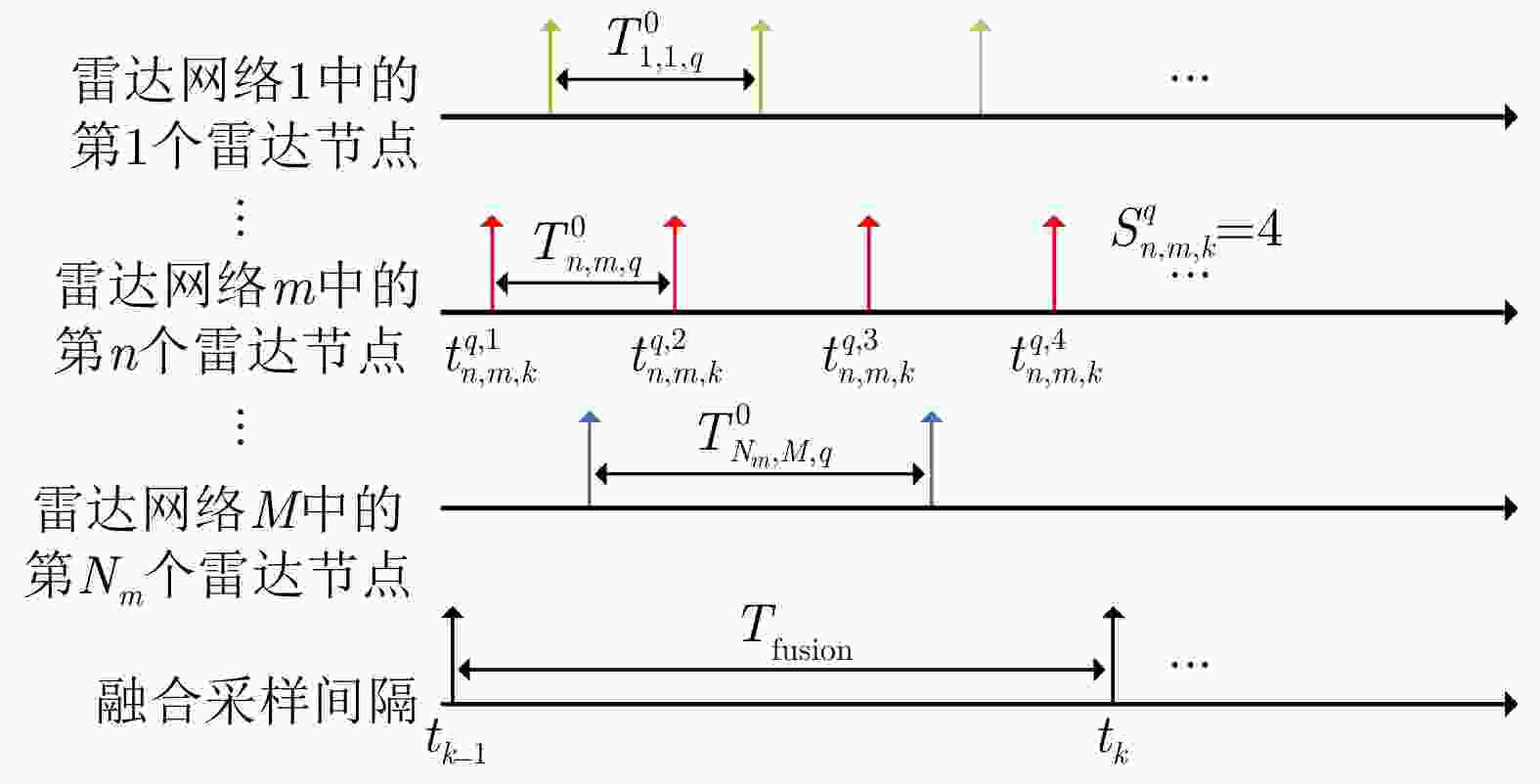
$ \left( {n,m} \right) $ $t_{n,m,q}^{{\text{ini} } }$ (s) $ T_{n,m,q}^0 $ (s) (1,1) 2 1 (2,1) 3 1 (3,1) 4 1 (4,1) 1 1 (5,1) 5 1 (1,2) 2 2 (2,2) 4 2 (3,2) 3 2 (4,2) 5 2 (5,2) 1 2 (1,3) 3 3 (2,3) 5 3
下载: 导出CSV
-
[1] 陈小龙, 黄勇, 金丹, 等, 译. 现代雷达系统导论(英文版)[M]. 北京: 电子工业出版社, 2021.CHEN Xiaolong, HUANG Yong, JIN Dan, et al, translation. Introduction to Modern Radar System[M]. Beijing: Publishing House of Electronics Industry, 2021. [2] 丁建江, 许红波, 周芬. 雷达组网技术[M]. 北京: 国防工业出版社, 2017.DING Jianjiang, XU Hongbo, and ZHOU Fen. The Technology of Netted Radar System[M]. Beijing: National Defense Industry Press, 2017. [3] ZHANG Haowei, LIU Weijian, ZHANG Zhaojian, et al. Joint target assignment and power allocation in multiple distributed MIMO radar networks[J]. IEEE Systems Journal, 2021, 15(1): 694–704. doi: 10.1109/JSYST.2020.2986020 [4] 刘宏伟, 严俊坤, 周生华. 网络化雷达协同探测技术[J]. 现代雷达, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002LIU Hongwei, YAN Junkun, and ZHOU Shenghua. Collaborative detection technology of netted radar[J]. Modern Radar, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002 [5] XIE Mingchi, YI Wei, KONG Lingjiang, et al. Receive-beam resource allocation for multiple target tracking with distributed MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2421–2436. doi: 10.1109/TAES.2018.2818579 [6] AJORLOO A, AMINI A, and BASTANI M H. A compressive sensing-based colocated MIMO radar power allocation and waveform design[J]. IEEE Sensors Journal, 2018, 18(22): 9420–9429. doi: 10.1109/JSEN.2018.2871214 [7] LU Yanxi, HE Zishu, CHENG Ziyang, et al. Adaptive resource allocation in decentralized colocated MIMO radar network for multiple targets tracking[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 152–157. [8] ZHANG Haowei, XIE Junwei, GE Jiaang, et al. Finite sensor selection algorithm in distributed MIMO radar for joint target tracking and detection[J]. Journal of Systems Engineering and Electronics, 2020, 31(2): 290–302. doi: 10.23919/JSEE.2020.000007 [9] 曾雅俊, 王俊, 魏少明, 等. 分布式多传感器多目标跟踪方法综述[J]. 雷达学报, 2023, 12(1): 197–213. doi: 10.12000/JR22111ZENG Yajun, WANG Jun, WEI Shaoming, et al. Review of the method for distributed multi-sensor multi-target tracking[J]. Journal of Radars, 2023, 12(1): 197–213. doi: 10.12000/JR22111 [10] YAN Junkun, PU Wenqiang, DAI Jinhui, et al. Resource allocation for search and track application in phased array radar based on Pareto bi-objective optimization[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3487–3499. doi: 10.1109/TVT.2019.2894960 [11] ZHANG Haowei, XIE Junwei, SHI Junpeng, et al. Sensor scheduling and resource allocation in distributed MIMO radar for joint target tracking and detection[J]. IEEE Access, 2019, 7: 62387–62400. doi: 10.1109/ACCESS.2019.2916334 [12] 靳标, 邝晓飞, 彭宇, 等. 基于合作博弈的组网雷达分布式功率分配方法[J]. 航空学报, 2022, 43(1): 324776. doi: 10.7527/S1000-6893.2020.24776JIN Biao, KUANG Xiaofei, PENG Yu, et al. Distributed power allocation method for netted radar based on cooperative game theory[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 324776. doi: 10.7527/S1000-6893.2020.24776 [13] ZHANG Haowei, LIU Weijian, XIE Junwei, et al. Joint subarray selection and power allocation for cognitive target tracking in large-scale MIMO radar networks[J]. IEEE Systems Journal, 2020, 14(2): 2569–2580. doi: 10.1109/JSYST.2019.2960401 [14] LU Yanxi, HE Zishu, LIU Shuangli, et al. Communication-awareness joint beams and power allocation scheme of radar network for manoeuvring targets tracking[J]. IET Radar, Sonar & Navigation, 2020, 14(2): 207–215. doi: 10.1049/iet-rsn.2019.0215 [15] SUN Hao, LI Ming, ZUO Lei, et al. Resource allocation for multitarget tracking and data reduction in radar network with sensor location uncertainty[J]. IEEE Transactions on Signal Processing, 2021, 69: 4843–4858. doi: 10.1109/TSP.2021.3101018 [16] SUN Hao, LI Ming, ZUO Lei, et al. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems[J]. IEEE Signal Processing Letters, 2021, 28: 1863–1867. doi: 10.1109/LSP.2021.3108675 [17] ZHANG Haowei, LIU Weijian, ZHANG Qiliang, et al. Joint resource optimization for a distributed MIMO radar when tracking multiple targets in the presence of deception jamming[J]. Signal Processing, 2022, 200: 108641. doi: 10.1016/j.sigpro.2022.108641 [18] SU Yang, CHENG Ting, HE Zishu, et al. Joint waveform control and resource optimization for maneuvering targets tracking in netted colocated MIMO radar systems[J]. IEEE Systems Journal, 2022, 16(3): 3960–3971. doi: 10.1109/JSYST.2021.3098622 [19] 杨琪. 异步多站雷达多目标融合跟踪方法研究[D]. [硕士论文], 电子科技大学, 2021.YANG Qi. A research of multi-target tracking method with asynchronous multi-station radar systems[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021. [20] YAN Junkun, LIU Hongwei, PU Wenqing, et al. Joint threshold adjustment and power allocation for cognitive target tracking in asynchronous radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3094–3106. doi: 10.1109/TSP.2017.2679693 [21] 严俊坤, 夏双志, 戴奉周, 等. 异步多基地雷达系统目标跟踪的功率分配算法[J]. 西安电子科技大学学报:自然科学版, 2013, 40(6): 32–38, 57. doi: 10.3969/j.issn.1001-2400.2013.06.006YAN Junkun, XIA Shuangzhi, DAI Fengzhou, et al. Power allocation strategy for target tracking in asynchronous multistatic radar systems[J]. Journal of Xidian University:Natural Science, 2013, 40(6): 32–38, 57. doi: 10.3969/j.issn.1001-2400.2013.06.006 [22] SUN Hao, LI Ming, ZUO Lei, et al. JPBA of ARN for target tracking in clutter[J]. IET Radar, Sonar & Navigation, 2019, 13(11): 2024–2033. doi: 10.1049/iet-rsn.2019.0038 [23] YAN Junkun, PU Wenqing, ZHOU Shenghua, et al. Optimal resource allocation for asynchronous multiple targets tracking in heterogeneous radar networks[J]. IEEE Transactions on Signal Processing, 2020, 68: 4055–4068. doi: 10.1109/TSP.2020.3007313 [24] FARINA A, RISTIC B, and TIMMONERI L. Cramer-Rao bound for nonlinear filtering with Pd<1 and its application to target tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(8): 1916–1924. doi: 10.1109/TSP.2002.800411 [25] ANASTASIO V, FARINA A, COLONE F, et al. Cramér-Rao bound with Pd<1 for target localisation accuracy in multistatic passive radar[J]. IET Radar, Sonar & Navigation, 2014, 8(7): 767–775. doi: 10.1049/iet-rsn.2013.0213 [26] SUN Jun, LU Xiujuan, YUAN Ye, et al. Resource allocation for multi-target tracking in multi-static radar systems with imperfect detection performance[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. [27] SUN Jun, YI Wei, VARSHNEY P K, et al. Resource scheduling for multi-target tracking in multi-radar systems with imperfect detection[J]. IEEE Transactions on Signal Processing, 2022, 70: 3878–3893. doi: 10.1109/TSP.2022.3191800 [28] 张永平. 基于全局多目标跟踪质量的雷达资源管理算法研究[D]. [硕士论文], 电子科技大学, 2022.ZHANG Yongping. Research on radar resource management algorithm based on overall multi-targets tracking quality[D]. [Master dissertation], University of Electronic Science and Technology of China, 2022. [29] 何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128 [30] TICHAVSKY P, MURAVCHIK C H, and NEHORAI A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1386–1396. doi: 10.1109/78.668800 [31] YAN Junkun, DAI Jinhui, PU Wenqiang, et al. Target capacity based resource optimization for multiple target tracking in radar network[J]. IEEE Transactions on Signal Processing, 2021, 69: 2410–2421. doi: 10.1109/TSP.2021.3071173 -
图(6) / 表(4)
计量
- 文章访问数: 665
- HTML全文浏览量: 367
- PDF下载量: 127
- 被引次数: 0
