作者中心
专家审稿
责编办公
编辑办公
基于任务效用最大化的多雷达协同任务规划算法
DOI: 10.12000/JR23013
-
1 1 若要消除该假设，可通过将一个待执行任务q拆分成在同一个位置的多个子任务。例如：可将某项任务\begin{document}${\boldsymbol{\nu}}_{{\rm{Prop}}}^q=\left\{\left(x^{q}, y^{q}\right), \rho^{q}, t^{q}\right\} $\end{document} \begin{document}${\boldsymbol{\nu}}_{{\rm{Sub}}{\text{-}}{\rm{Prop}}}^1,{\boldsymbol{\nu}}_{{\rm{Sub}}{\text{-}}{\rm{Prop}}}^2,\cdots, {\boldsymbol{\nu}}_{{\rm{Sub}}{\text{-}}{\rm{Prop}}}^k $\end{document} \begin{document}${\boldsymbol{\nu}}_{{\rm{Sub}}{\text{-}}{\rm{Prop}}}^k =\{(x^q,y^q),\rho^q,t^k\} $\end{document} \begin{document}$\sum t^k =t^q$\end{document}
作者简介:
袁 野，博士，主要研究方向为多雷达协同探测、目标跟踪、雷达资源管控技术等
杨 剑，博士，副教授，主要研究方向为雷达信号处理、阵列信号处理、精确制导与对抗技术等
刘辛雨，博士生，主要研究方向为雷达通信一体化信号设计、雷达对抗波形设计等
易 伟，博士，教授，主要研究方向为低可观测目标检测跟踪、多雷达协同探测等
孔令讲，博士，教授，主要研究方向为新体制雷达、统计信号处理、优化理论和算法、雷达信号处理、非合作信号处理技术和自适应阵列信号处理等
通讯作者:
-
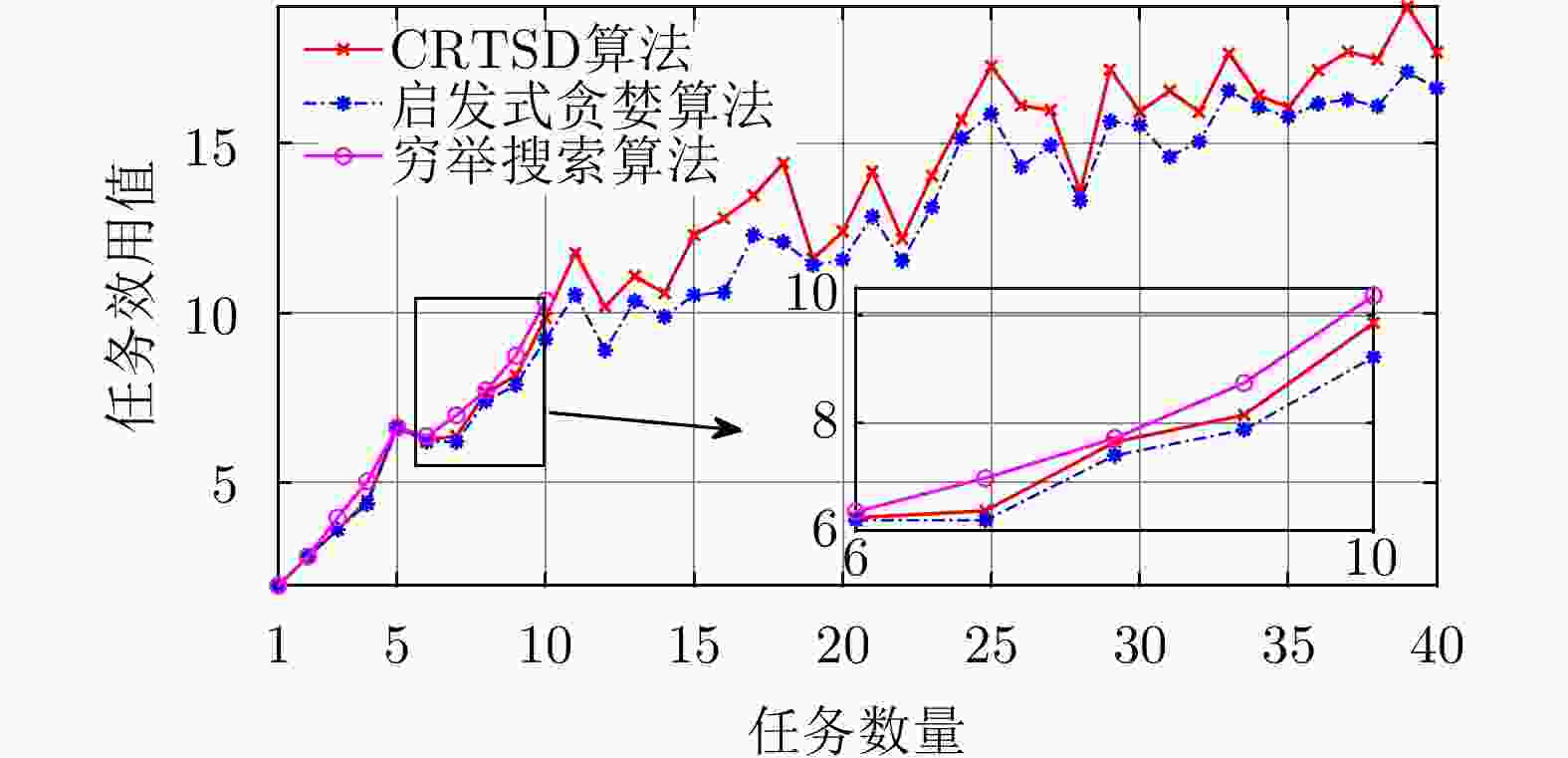
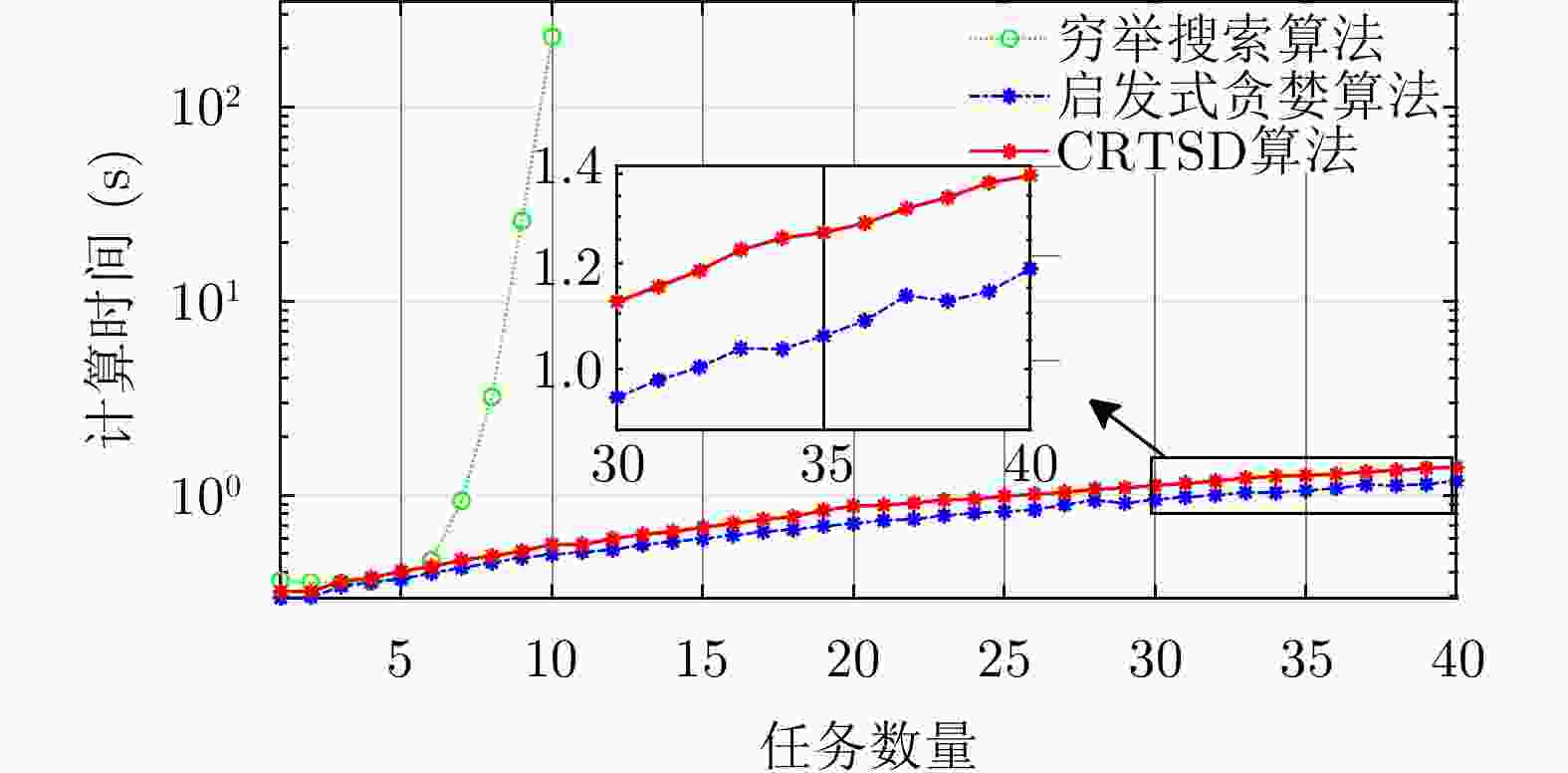
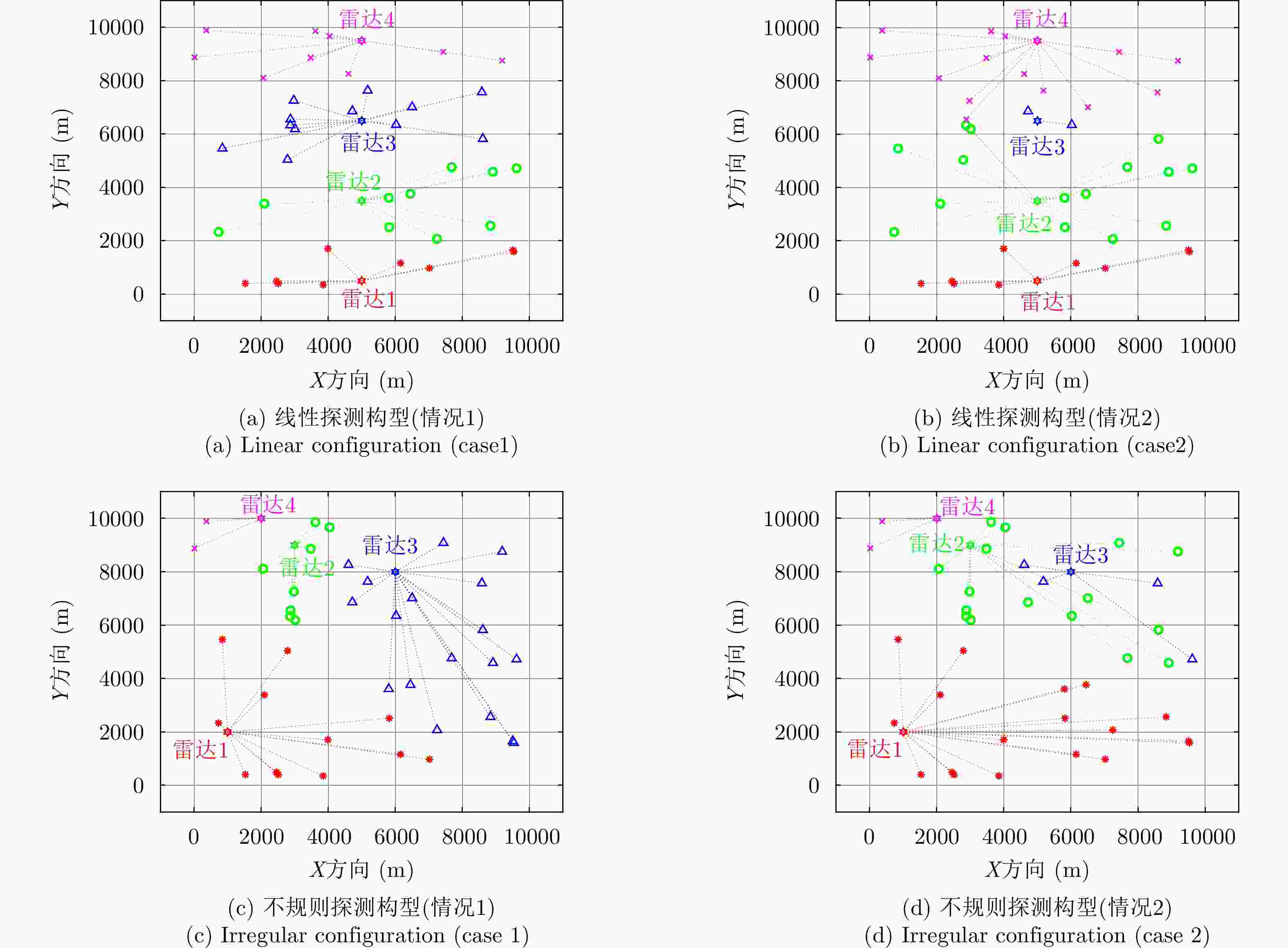
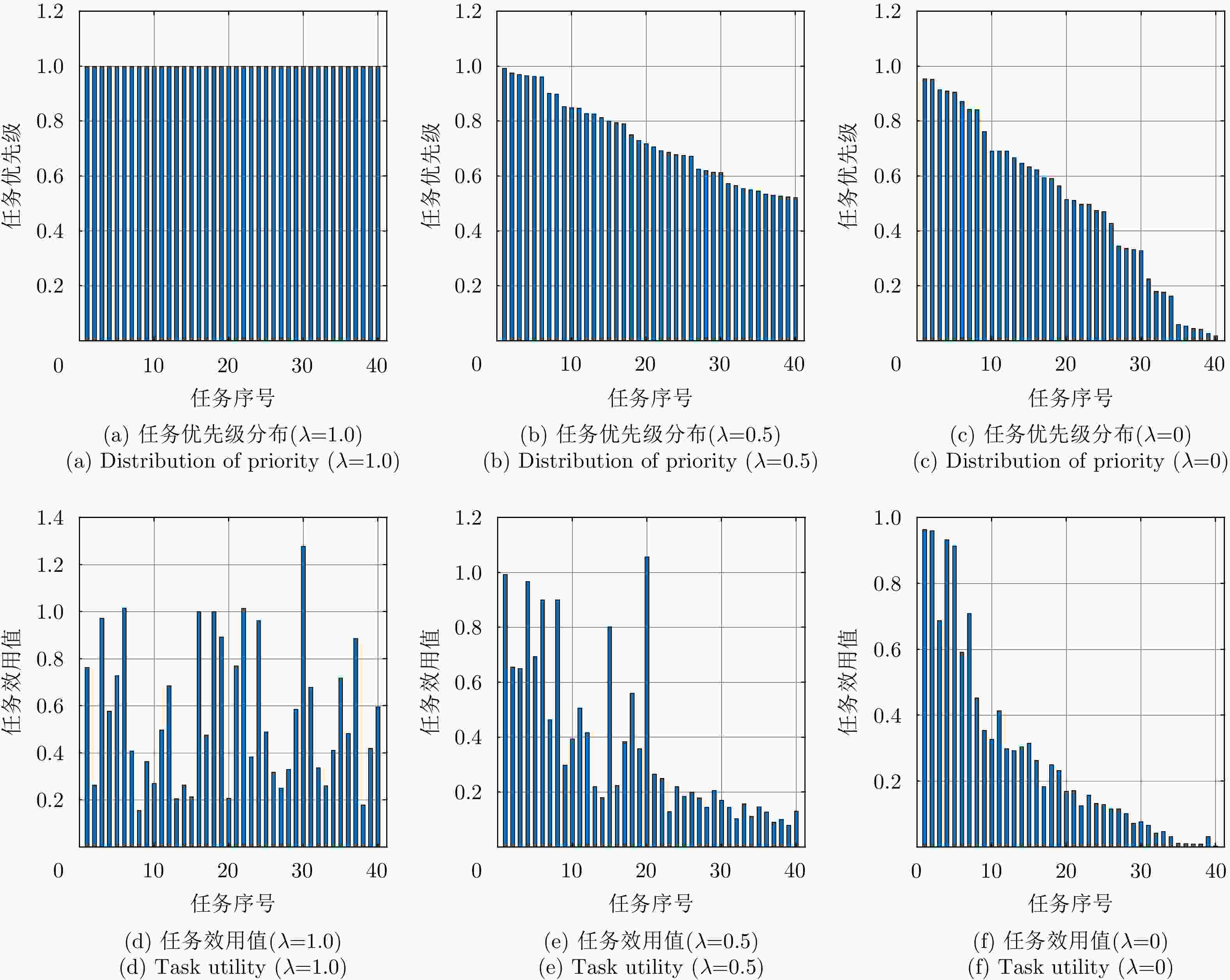
摘要: 该文针对多雷达协同场景下的多任务实时规划问题，提出了一种基于任务效用最大化的多雷达协同在线任务规划模型。该模型以任务效用函数最大化为目标将多雷达协同任务分配建模成一个基于整数规划的多变量混合优化问题；随后提出了启发式穷举搜索算法和基于凸松弛的两步解耦算法，可在多项式时间内完成了该NP难优化问题的求解，且分别在优化性能和计算效率方面有所侧重。仿真实验表明，相比于可找到最优解的穷举搜索算法，该文提出算法可有效降低任务规划问题复杂度，提升问题求解效率，以满足在线任务分配的实时性要求。Abstract: A utility maximization-based multiradar online task planning algorithm aiming at the real-time multitask planning problem is proposed in this paper. Using the maximization of the task utility function as the objective, multiradar task planning is formulated as an integer programming-based mixed multivariable optimization problem. Then, two algorithms, namely heuristic greedy search and convex relaxation-based two-step decoupling are proposed to solve the resulting NP-hard optimization problem in polynomial time, respectively. Simulation experiments demonstrate that compared with the optimal exhaustive search algorithm, the proposed algorithms can effectively reduce the computing time or improve solution efficiency such that the real-time requirement of online task planning can be satisfied.
-
图 1 任务排列与任务分配概念解释
Figure 1. An illustration of the concepts for task arrangement and task scheduling
图 2 任务规划示意图(
$ N=2,\;Q=8 $ )Figure 2. Schematic diagram of the task scheduling with
$N = 2,{\text{ }}Q = 8$ 
图 5 3种算法下的多雷达-多任务分配结果
Figure 5. Multiradar-multitask scheduling results of the three algorithms
图 6 3种算法下的各雷达分得的任务执行顺序排序结果
Figure 6. The task execution order of each radar under the three algorithms
图 7 不同任务数量Q下3种算法得到的任务效用值
Figure 7. Task utility values of the three algorithms with different number of tasks Q
图 8 不同任务数量Q下3种算法运行时间
Figure 8. Runtime of the three algorithms with different number of tasks Q
图 9 不同探测构型下CRTSD算法任务分配结果
Figure 9. Task scheduling results of CRTSD algorithm with different radar configurations
图 10 不同任务优先级设置下CRTSD算法得到的任务效用值
Figure 10. Task utility values of CRTSD algorithm with different task priorities
1 穷举搜索算法
1. Exhaustive search algorithm
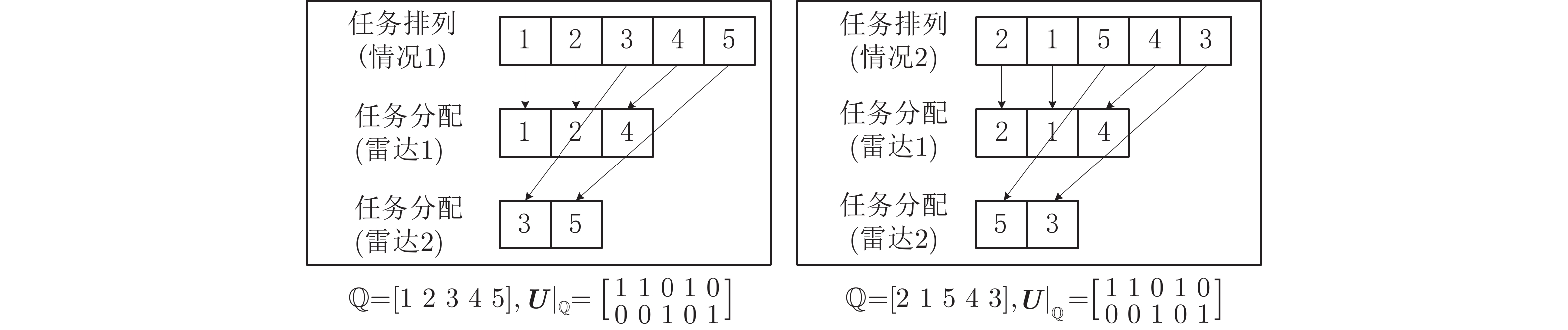
输入：雷达位置、雷达时间资源、任务位置、任务耗时 for ${\text{id}}{{\text{x}}_1} = 1:N$ for ${\text{id}}{{\text{x}}_2} = 1:N$ $ \ddots $ for ${\text{id}}{{\text{x}}_Q} = 1:N$ 完成任务-雷达节点分配：设置$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right.\left( {{\text{id}}{{\text{x}}_1},1} \right) = 1 $,
${\boldsymbol{U} }\left| {_\mathbb{Q} } \right.\left( { {\text{id} }{ {\text{x} }_2},2} \right) = 1,{\text{ } } \cdots$, ${\boldsymbol{U}}\left| {_\mathbb{Q}} \right.\left( {{\text{id}}{{\text{x}}_Q},Q} \right) = 1 $, $ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right. $其余
项为0；完成任务排序：根据上一步得到的$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right. $，对每个雷达分得
任务进行排列，并计算每次排列对应问题的目标函数值，选
出效用函数最大排列结果，记为$\phi \left( { {\text{id} }{ {\text{x} }_1},{\text{id} }{ {\text{x} }_2}, \cdots ,{\text{id} }{ {\text{x} }_Q} } \right)$；end ${\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}}$ end end 选出最大的$\phi \left( { {\text{id} }{ {\text{x} }_1}, {\text{id} }{ {\text{x} }_2}, \cdots ,{\text{id} }{ {\text{x} }_Q} } \right)$，其对应的任务分配方案即为
最优任务分配，记为：${\left\{ {\mathbb{Q},{\boldsymbol{U}}\left| {_\mathbb{Q}} \right.} \right\}^{{\text{OPT}}}}$；输出：任务分配方案${\left\{ {\mathbb{Q},{\boldsymbol{U}}\left| {_\mathbb{Q}} \right.} \right\}^{{\text{OPT}}}}$ 
下载: 导出CSV
2 离散化任务分配变量
2. Discretization of task scheduling variables
输入：问题求解得到的任务分配变量$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right. $ 初始化任务分配变量$ {{\boldsymbol{U}}^{{\text{opt}}}} $为$N \times Q$维零矩阵； for $i = 1:NQ$ 找出$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right. $中最大元素，记为$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right.\left( {q,n} \right) $； 判断若将$ {{\boldsymbol{U}}^{{\text{opt}}}}\left( {q,n} \right) $设置为1，并将$ {{\boldsymbol{U}}^{{\text{opt}}}} $代入式(15)后，是否
满足式(15)的所有约束；若满足，则设置$ {{\boldsymbol{U}}^{{\text{opt}}}}\left( {q,n} \right) = 1 $； 设置$ {\boldsymbol{U}}\left| {_\mathbb{Q}} \right.\left( {q,n} \right) = 0 $； end 输出：离散化的任务分配变量$ {{\boldsymbol{U}}^{{\text{opt}}}} $
下载: 导出CSV
3 启发式贪婪算法
3. Heuristic greedy search algorithm
输入：雷达位置、雷达时间资源、任务位置、任务耗时 设置$r_{\max }^q = 0{\text{ }}\left( {q = 1,2, \cdots ,Q} \right)$； for $q = 1:Q$ for $n = 1:N$ 计算任务q与雷达n的距离$r_n^q$； if $r_n^q > r_{\max }^q$ and $ {t_{n,\max }} > {t^q} $ 将任务q改为分配给节点n； 设置$ {t_{n,\max }} = {t_{n,\max }} - {t^q} $, $r_{\max }^q = r_n^q$； end end end for $n = 1:N$ 对雷达n分得的任务进行排序； end 输出：任务分配变量${ {\boldsymbol{U} }^{ {\text{opt} } } }$
下载: 导出CSV
-
[1] BAKER C J and HUME A L. Netted radar sensing[J]. IEEE Aerospace and Electronic Systems Magazine, 2003, 18(2): 3–6. doi: 10.1109/MAES.2003.1183861 [2] 马林, 周琳. 预警系统协同探测技术研究[J]. 现代雷达, 2020, 42(12): 1–6. doi: 10.16592/j.cnki.1004-7859.2020.12.001MA Lin and ZHOU Lin. A study on collaborative detection technology of early warning system[J]. Modern Radar, 2020, 42(12): 1–6. doi: 10.16592/j.cnki.1004-7859.2020.12.001 [3] 刘宏伟, 严峻坤, 周生华. 网络化雷达协同探测技术[J]. 现代雷达, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002LIU Hongwei, YAN Junkun, and ZHOU Shenghua. Collaborative detection technology of netted radar[J]. Modern Radar, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002 [4] 时晨光, 王奕杰, 代向荣, 等. 面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法[J]. 雷达学报, 2022, 11(5): 778–793. doi: 10.12000/JR22005SHI Chenguang, WANG Yijie, DAI Xiangrong, et al. Joint transmit resources and trajectory planning for target tracking in airborne radar networks[J]. Journal of Radars, 2022, 11(5): 778–793. doi: 10.12000/JR22005 [5] 余显祥, 路晴辉, 杨婧, 等. 短基线收发分置频域协同波形设计方法[J]. 雷达学报, 2022, 11(2): 227–239. doi: 10.12000/JR22014YU Xianxiang, LU Qinghui, YANG Jing, et al. Frequency domain cooperative waveform design method for short baseline transceiver[J]. Journal of Radars, 2022, 11(2): 227–239. doi: 10.12000/JR22014 [6] 杨晨阳, 毛士艺, 李少洪. 相控阵雷达中的TWS和TAS跟踪技术[J]. 电子学报, 1999, 27(6): 1–4, 8. doi: 10.3321/j.issn:0372-2112.1999.06.001YANG Chenyang, MAO Shiyi, and LI Shaohong. Track-While-Scan and Track-and Search tracking techniques in phased array radar[J]. Acta Electronica Sinica, 1999, 27(6): 1–4, 8. doi: 10.3321/j.issn:0372-2112.1999.06.001 [7] CHARLISH A, WOODBRIDGE K, and GRIFFITHS H. Phased array radar resource management using continuous double auction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2212–2224. doi: 10.1109/TAES.2015.130558 [8] DAI Jinhui, YAN Junkun, PU Wenqiang, et al. Adaptive channel assignment for maneuvering target tracking in multistatic passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, in press. [9] SUN Hao, LI Ming, ZUO Lei, et al. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems[J]. IEEE Signal Processing Letters, 2021, 28: 1863–1867. doi: 10.1109/LSP.2021.3108675 [10] 时晨光, 丁琳涛, 汪飞, 等. 面向射频隐身的组网雷达多目标跟踪下射频辐射资源优化分配算法[J]. 电子与信息学报, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636SHI Chenguang, DING Lintao, WANG Fei, et al. Radio frequency stealth-based optimal radio frequency resource allocation algorithm for multiple-target tracking in radar network[J]. Journal of Electronics &Information Technology, 2021, 43(3): 539–546. doi: 10.11999/JEIT200636 [11] 卢建斌, 肖慧, 胡卫东, 等. 基于非精确计算的空间探测相控阵雷达任务规划算法[J]. 飞行器测控学报, 2007, 26(3): 18–24.LU Jianbin, XIAO Hui, HU Weidong, et al. Mission planning algorithm based on imprecise computation for space detecting phased-array radars[J]. Journal of Spacecraft TT &C Technology, 2007, 26(3): 18–24. [12] 严俊坤, 白舸, 黄佳沁, 等. 多机雷达协同区域动态覆盖航迹优化方法[J]. 雷达学报, 2023, 12(3): 541–549. doi: 10.12000/JR22196YAN Junkun, BAI Ge, HUANG Jiaqin, et al. Flight path optimization method for dynamic area coverage based on multi-aircraft radars[J]. Journal of Radars, 2023, 12(3): 541–549. doi: 10.12000/JR22196 [13] YUAN Ye, YI Wei, KIRUBARAJAN T, et al. Scaled accuracy based power allocation for multi-target tracking with colocated MIMO radars[J]. Signal Processing, 2019, 158: 227–240. doi: 10.1016/j.sigpro.2019.01.014 [14] 张大琳, 易伟, 孔令讲. 面向组网雷达干扰任务的多干扰机资源联合优化分配方法[J]. 雷达学报, 2021, 10(4): 595–606. doi: 10.12000/JR21071ZHANG Dalin, YI Wei, and KONG Lingjiang. Optimal joint allocation of multijammer resources for jamming netted radar system[J]. Journal of Radars, 2021, 10(4): 595–606. doi: 10.12000/JR21071 [15] 李正杰, 谢军伟, 张浩为, 等. 一种低截获背景下的集中式MIMO雷达快速功率分配算法[J]. 雷达学报, 2023, 12(3): 602–615. doi: 10.12000/JR22203LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. A fast power allocation algorithm in a collocated MIMO radar under low interception backgrounds[J]. Journal of Radars, 2023, 12(3): 602–615. doi: 10.12000/JR22203 [16] ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227 [17] DING Lintao, SHI Chenguang, QIU Wei, et al. Joint dwell time and bandwidth optimization for multi-target tracking in radar network based on low probability of intercept[J]. Sensors, 2020, 20(5): 1269. doi: 10.3390/s20051269 [18] 程婷, 恒思宇, 李中柱. 基于脉冲交错的分布式雷达组网系统波束驻留调度[J]. 雷达学报, 2023, 12(3): 616–628. doi: 10.12000/JR22211CHENG Ting, HENG Siyu, and LI Zhongzhu. Real-time dwell scheduling algorithm for distributed phased array radar network based on pulse interleaving[J]. Journal of Radars, 2023, 12(3): 616–628. doi: 10.12000/JR22211 [19] CHENG Ting, LI Shuyi, and ZHANG Jie. Adaptive resource management in multiple targets tracking for co-located multiple input multiple output radar[J]. IET Radar, Sonar & Navigation, 2018, 12(9): 1038–1045. doi: 10.1049/iet-rsn.2018.5153 [20] 韦刚, 刘昌云, 郭相科. 基于多属性决策的相控阵雷达截获任务规划算法[J]. 现代雷达, 2016, 38(10): 42–46. doi: 10.16592/j.cnki.1004-7859.2016.10.011WEI Gang, LIU Changyun, and GUO Xiangke. Algorithms of search mission planning in phased array radar based on multi-attribute decision[J]. Modern Radar, 2016, 38(10): 42–46. doi: 10.16592/j.cnki.1004-7859.2016.10.011 [21] 朱希同, 杨瑞娟, 李晓柏, 等. 一种多功能天波超视距雷达任务规划调度方法[J]. 舰船电子工程, 2022, 42(2): 75–80. doi: 10.3969/j.issn.1672-9730.2022.02.016ZHU Xitong, YANG Ruijuan, LI Xiaobai, et al. A multifunctional sky-wave over-the-horizon radar task planning and scheduling method[J]. Ship Electronic Engineering, 2022, 42(2): 75–80. doi: 10.3969/j.issn.1672-9730.2022.02.016 [22] 赵宇, 李建勋, 曹兰英, 等. 基于二次规划的相控阵雷达任务自适应调度算法[J]. 系统工程与电子技术, 2012, 34(4): 698–703. doi: 10.3969/j.issn.1001-506X.2012.04.11ZHAO Yu, LI Jianxun, CAO Lanying, et al. Adaptive scheduling algorithm based on quadratic programming for multifunction phased array radars[J]. Systems Engineering and Electronics, 2012, 34(4): 698–703. doi: 10.3969/j.issn.1001-506X.2012.04.11 [23] 展红英. 相控阵雷达系统实时任务负载分配仿真研究[D]. [硕士论文], 电子科技大学, 2014.ZHAN Hongying. Research of real-time tasks load assignment simulation in phased array radar system[D]. [Master dissertation], University of Electronic Science and Technology of China, 2014. [24] 卢建斌, 肖慧, 席泽敏, 等. 相控阵雷达波束波形联合自适应调度算法[J]. 系统工程与电子技术, 2011, 33(1): 84–88. doi: 10.3969/j.issn.1001-506X.2011.01.17LU Jianbin, XIAO Hui, XI Zemin, et al. Joint adaptive scheduling algorithm of beam and waveform for phased array radars[J]. Systems Engineering and Electronics, 2011, 33(1): 84–88. doi: 10.3969/j.issn.1001-506X.2011.01.17 [25] IRCI A, SARANLI A, and BAYKAL B. Study on Q-RAM and feasible directions based methods for resource management in phased array radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1848–1864. doi: 10.1109/TAES.2010.5595599 [26] TICHAVSKY P, MURAVCHIK C H, and NEHORAI A. Posterior Cramér-Rao bounds for discrete-time nonlinear filtering[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1386–1396. doi: 10.1109/78.668800 [27] SKOLNIK M I. Theoretical accuracy of radar measurements[J]. IRE Transactions on Aeronautical and Navigational Electronics, 1960, ANE-7(4): 123–129. doi: 10.1109/TANE3.1960.4201757 [28] BOVET D P and CRESCENZI P. Introduction to the Theory of Complexity: Vol. 7[M]. New York: Prentice Hall, 1994. [29] GRANT M. CVX: MATLAB software for disciplined convex programming[EB/OL]. http://cvxr.com/cvx, 2008. -
图(10) / 表(3)
计量
- 文章访问数: 997
- HTML全文浏览量: 474
- PDF下载量: 244
- 被引次数: 0
