作者中心
专家审稿
责编办公
编辑办公
3D High-resolution Imaging Algorithm with Sparse Trajectory for Millimeter-wave Radar
-
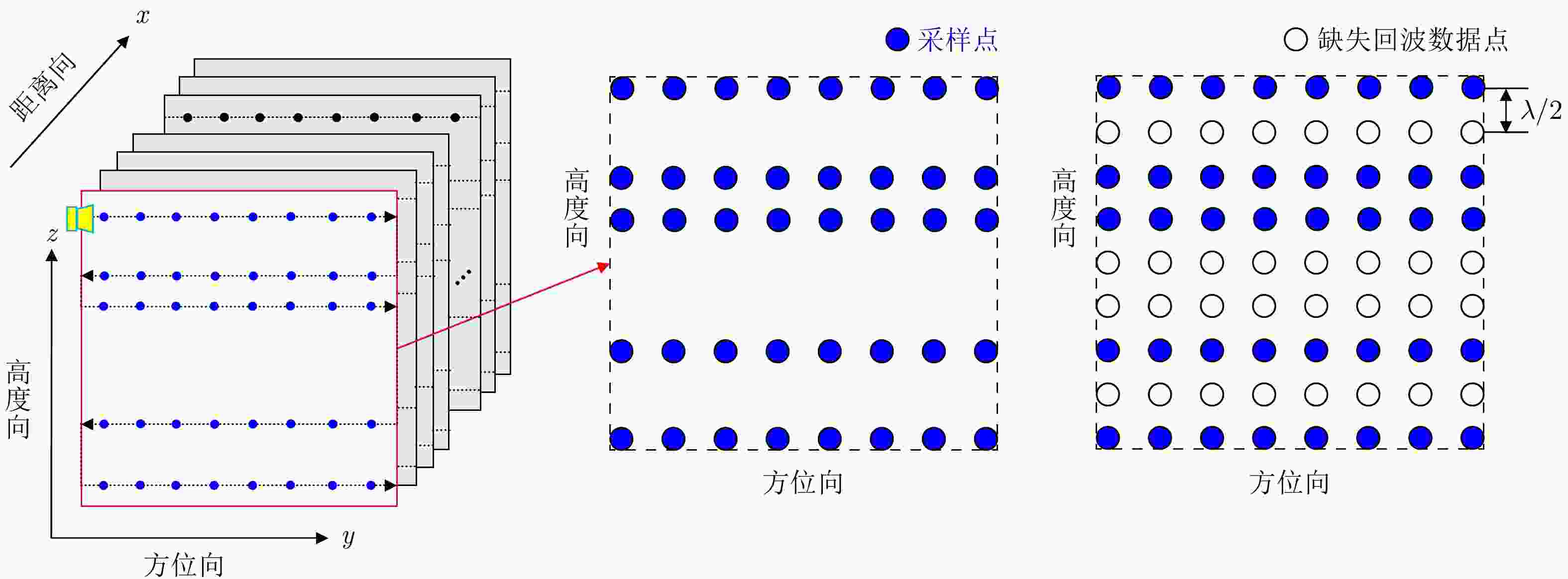
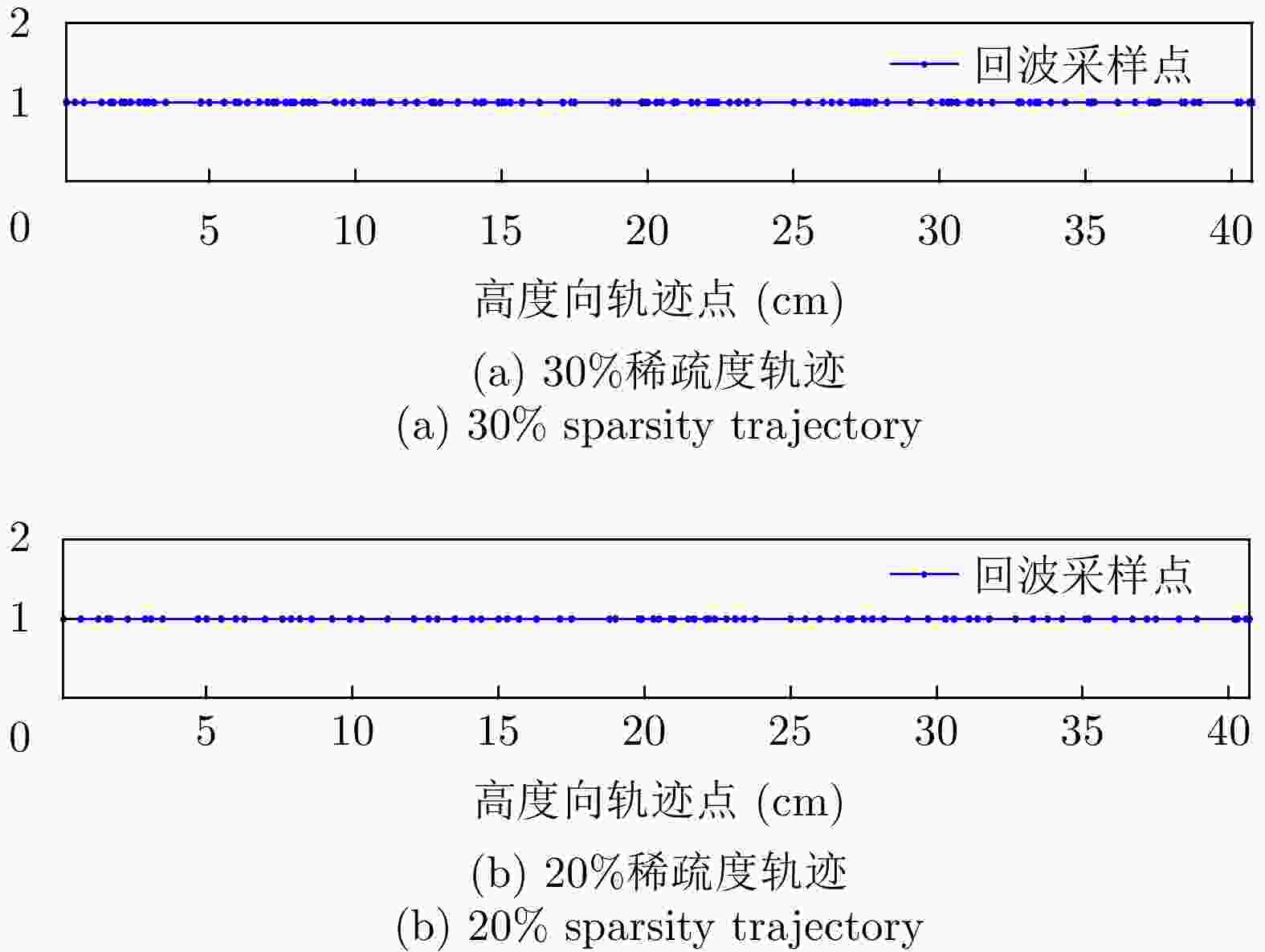
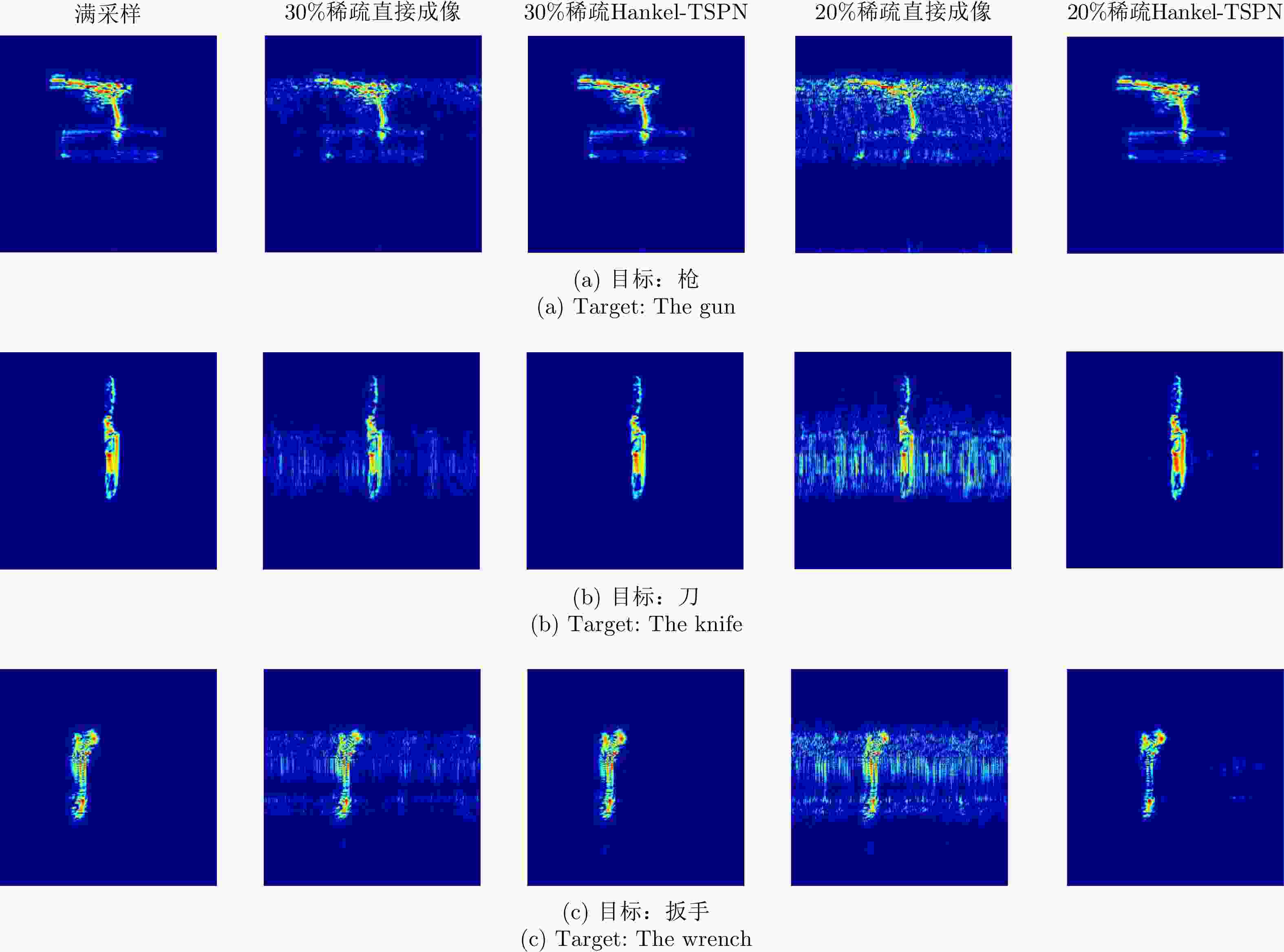
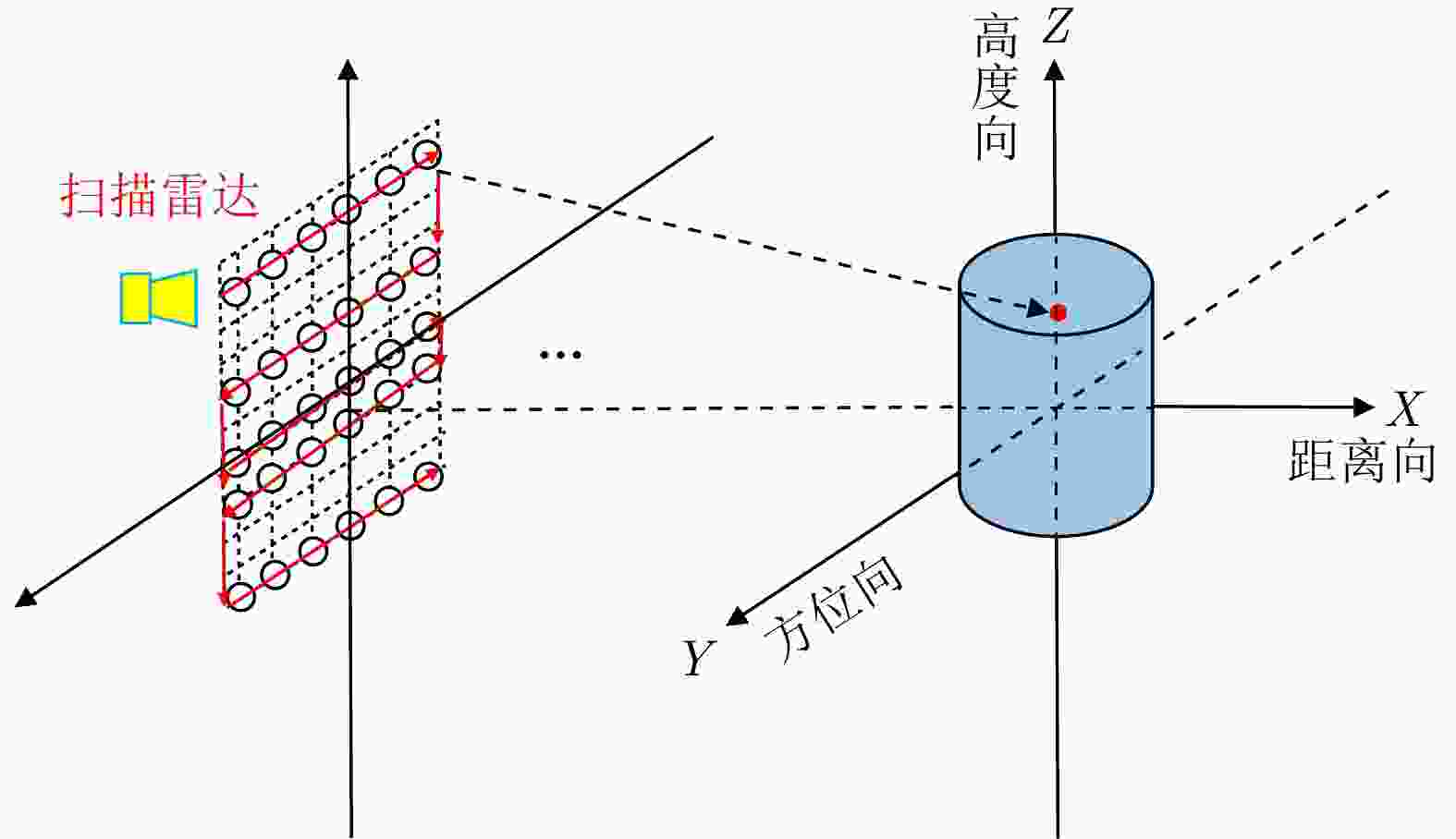
摘要: 近年来，由于毫米波雷达具有穿透能力强、体积小巧、探测精度高等特性，因此被广泛应用于安全检测、零件无损探测和医学诊断等领域。然而，由于硬件发射带宽的限制，如何实现超高二维分辨率成为毫米波雷达应用中的挑战之一。采用雷达平台扫描形成二维孔径的方式可以实现高度向和方位向的二维高分辨。然而，在扫描过程中，毫米波雷达在高度维会产生稀疏的轨迹，使得高度向回波采样稀疏，进而降低成像质量。为了解决这一问题，该文提出了一种基于Hankel变换矩阵填充的毫米波雷达高分辨三维成像算法。该方法采用了矩阵填充算法对稀疏采样回波进行了恢复，保证了毫米波雷达在扫描平面的成像精度。该文首先分析了毫米波雷达高度-距离切面的低秩先验特性，为了解决稀疏轨迹采样时，数据整行整列缺失的问题，对回波数据矩阵采用Hankel变换进行重新构造，使得待恢复数据矩阵满足矩阵填充算法应用条件。然后，提出了一种融合低秩与稀疏先验的基于截断的Schatten-p范数的矩阵填充算法，对采样数据矩阵进行恢复，以保证稀疏轨迹毫米波雷达的三维分辨率。最后，通过仿真和多组实测数据，证明了采用该文方法可以在仅使用20%~30%的高度向回波时仍实现目标高分辨三维成像。Abstract: In recent years, millimeter-wave radar has been widely used in safety detection, nondestructive detection of parts, and medical diagnosis because of its strong penetration ability, small size, and high detection accuracy. However, due to the limitation of hardware transmission bandwidth, achieving ultra-high two-dimensional resolution using millimeter-wave radar is challenging. Two-dimensional high-resolution imaging of altitude and azimuth can be realized using radar platform scanning to form a two-dimensional aperture. However, during the scanning process, the millimeter-wave radar produces sparse tracks in the height dimension, resulting in a sparse sampling of the altitude echo, thus reducing the imaging quality. In this paper, a high-resolution three-dimensional imaging algorithm for millimeter-wave radar based on Hankel transformation matrix filling is proposed to solve this problem. The matrix filling algorithm restores the sparse sampling echo, which guarantees the imaging accuracy of the millimeter-wave radar in the scanning plane. First, the low-rank prior characteristics of the millimeter-wave radar's elevation-range section were analyzed. To solve the problem of missing whole rows and columns of data during sparse trajectory sampling, the echo data matrix was reconstructed using the Hankel transform, and the sparse low-rank prior characteristics of the constructed matrix were analyzed. Furthermore, a matrix filling algorithm based on truncated Schatten-p norm combining low-rank and sparse priors was proposed to fill and reconstruct the echoes to ensure the three-dimensional resolution of the sparse trajectory millimeter-wave radar. Finally, using simulation and several sets of measured data, the proposed method was proved to achieve high-resolution three-dimensional imaging even when only 20%–30% of the height echo was used.
-
图 1 稀疏轨迹毫米波雷达几何构型
Figure 1. Geometric configuration of sparse trajectory millimeter wave radar
图 6 不同方法的高度-距离切面矩阵恢复图
Figure 6. Different methods of height-distance section matrix restoration
图 7 点目标不同稀疏度轨迹下成像结果
Figure 7. Imaging results of point targets with different sparsity trajectories
图 8 20%稀疏轨迹下中心点高度剖面对比图
Figure 8. Height profile comparison of center points under 20% sparse trajectory
图 10 稀疏度为20%的稀疏轨迹位置示意图
Figure 10. Location diagram of sparse trajectory with a sparsity of 20%
图 12 不同稀疏度的稀疏轨迹位置示意图
Figure 12. Location diagram of sparse trajectory with different sparsity
图 13 不同目标不同稀疏轨迹下成像结果图
Figure 13. Imaging results of different targets with different sparse trajectories
1 联合Hankel变换的TSPN矩阵填充算法(Hankel-TSPN)
1. TSPN matrix completion algorithm combined with Hankel transformation (Hankel-TSPN)
输入：获取第m个方位向的高度-距离切面${\boldsymbol{S} }' _{ {\text{H-R} } } \left( {t,{y_m},z} \right)$，
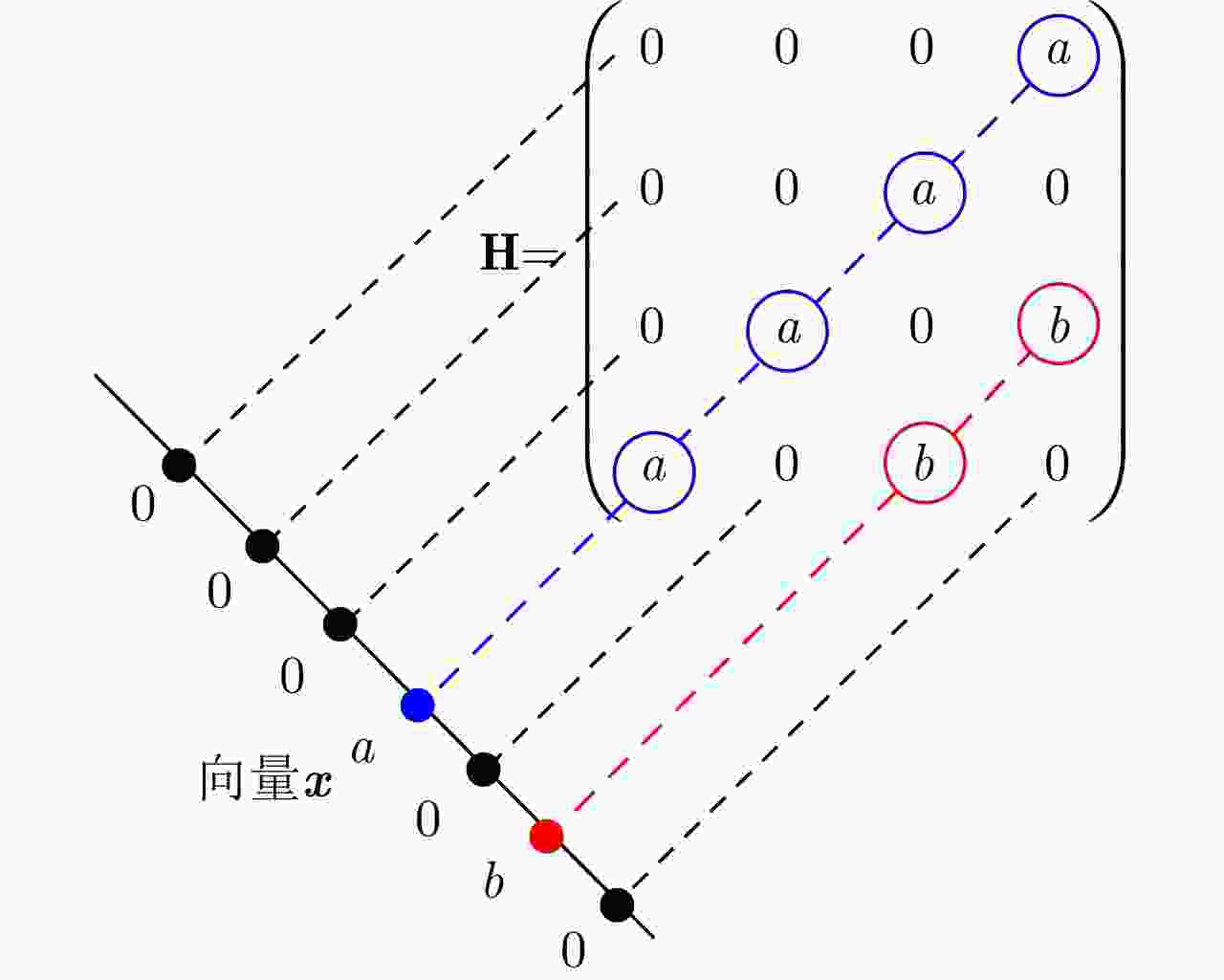
距离向长度K输出：第m个方位向的恢复高度-距离切面信号${ {\boldsymbol{S} }_{ {\rm{full} } } }\left( {t,{y_m},z} \right)$ 1. for kk=1 to K do 2. 对距离单元向量做Hankel变换：${ {\boldsymbol{H} }_{{1} } } = { {\bf{H} } }\left( { {\boldsymbol{S} }{'_{\bf{H} } }\left( { {t_{kk} },{y_m},z} \right)} \right)$ 3. TSPN矩阵填充 (a) 初始化：${{\boldsymbol{S}}_0} = {{\boldsymbol{D}}_0} = {{\boldsymbol{H}}_1}$, ${{\boldsymbol{Y}}}_{0},{{\boldsymbol{W}}}_{0},{{\boldsymbol{Z}}}_{0}$为零矩阵；迭代
次数MAX；惩罚参数${\beta _0}$；步长扩张算子$\rho $(b) for k=1 to ${\text{MAX}}$ do i. 更新S: ${{\boldsymbol{S}}^{k + 1}} = \arg \min \left\{ {L\left( {{\boldsymbol{S}},{{\boldsymbol{D}}^k},{{\boldsymbol{W}}^k},{{\boldsymbol{Y}}^k},{{\boldsymbol{Z}}^k}} \right)} \right\}$ ii. 更新W：
${{\boldsymbol{W}}^{k + 1}} = \arg \min \left\{ {L\left( {{{\boldsymbol{S}}^{k + 1}},{{\boldsymbol{D}}^k},{\boldsymbol{W}},{{\boldsymbol{Y}}^k},{{\boldsymbol{Z}}^k}} \right)} \right\}$iii. 更新D：
${{\boldsymbol{D}}^{k + 1}} = \arg \min \left\{ {L\left( {{{\boldsymbol{S}}^{k + 1}},{\boldsymbol{D}},{{\boldsymbol{W}}^{k + 1}},{{\boldsymbol{Y}}^k},{{\boldsymbol{Z}}^k}} \right)} \right\}$iv. 更新Y：${{\boldsymbol{Y}}^{k + 1}} = {{\boldsymbol{Y}}^k} + {\beta ^k}\left( {{{\boldsymbol{D}}^{k + 1}} - {{\boldsymbol{S}}^{k + 1}}} \right)$ v. 更新Z：${{\boldsymbol{Z}}^{k + 1}} = {{\boldsymbol{Z}}^k} + {\beta ^k} $$\left( {{{\boldsymbol{W}}^{k + 1}} - {\text{DCT}}\left( {{{\boldsymbol{S}}^{k + 1}}} \right)} \right)$ vi. 更新$\beta $：${\beta ^{k + 1}} = \rho {\beta ^k}$ (c) end 4. Hankel逆变换：${ {\boldsymbol{S} }_{ {\rm{full} } } }\left( { {t_{kk} },{y_m},z} \right) = { {{\boldsymbol{H}}}^{ { - 1} } }\left( { { {\boldsymbol{X} }^{ {\bf{MAX} } } } } \right)$ 5. end 
下载: 导出CSV
表 1 仿真参数
Table 1. Simulation parameter
参数名称 数值 载波频率${f_{\rm{c}}}$ 92.5 GHz 信号带宽${B_r}$ 5 GHz 方位孔径长度${L_{\rm{A} } }$ 0.16 m 方位采样点数 100 高度孔径长度${L_{\rm{H}}}$ 0.16 m 高度采样点数 100 等效面阵与目标距离${Z_0}$ 0.4 m
下载: 导出CSV
表 2 20%稀疏轨迹下高度剖面的峰值旁瓣比与积分旁瓣比(dB)
Table 2. Peak sidelobe ratio and integral sidelobe ratio of height profile at 20% sparse trajectory (dB)
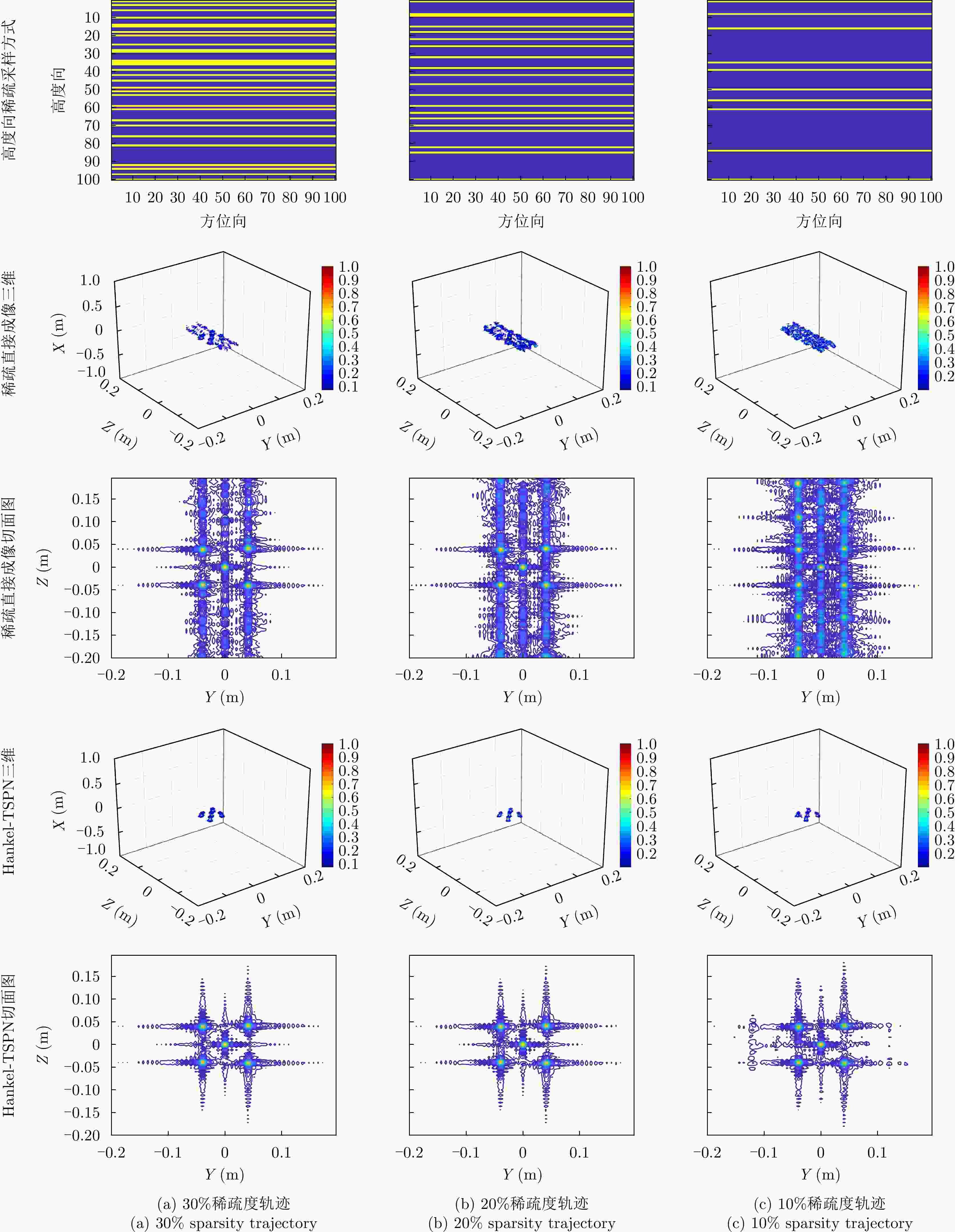
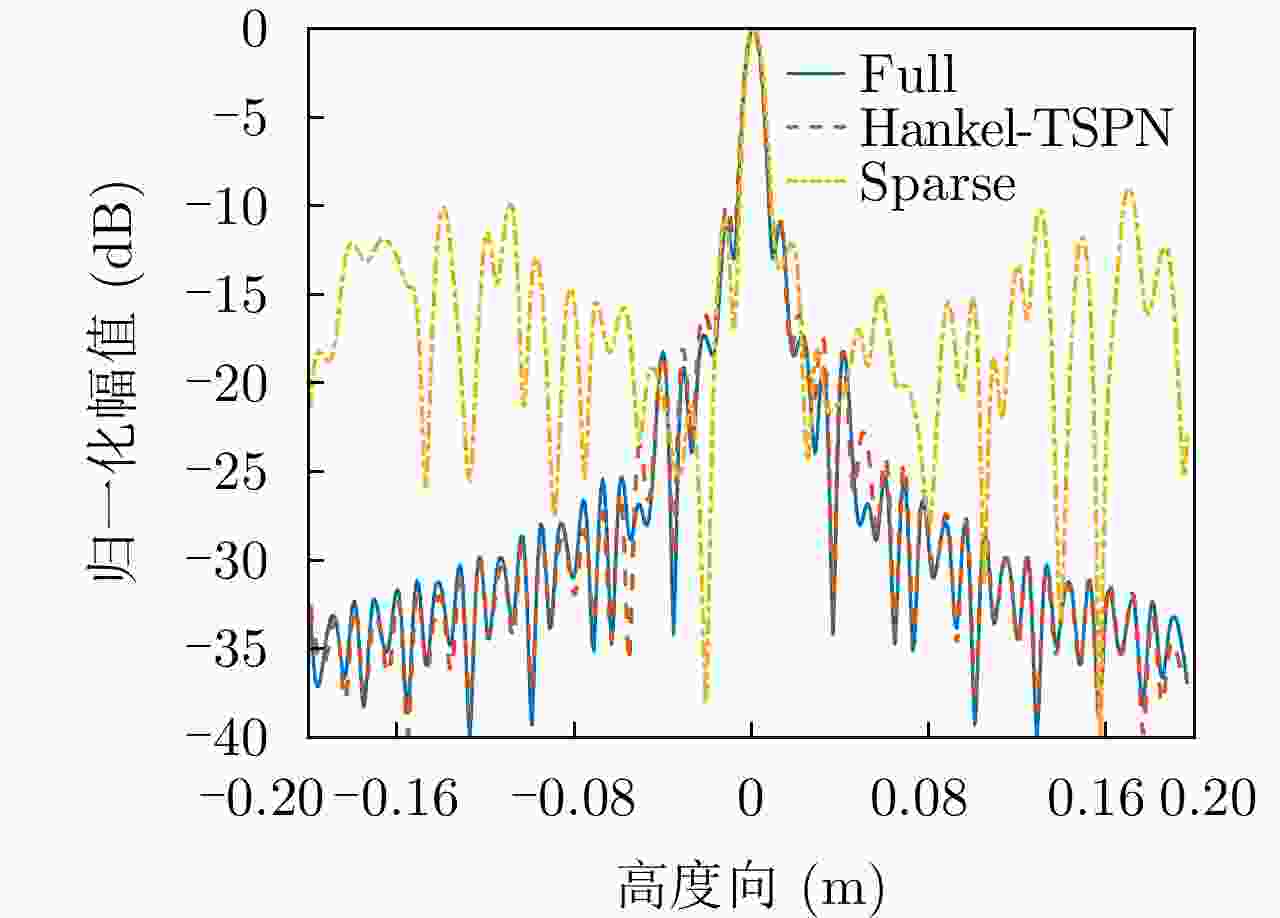
高度剖面指标 PSLR ISLR 满采 –11.0653 –7.6698 稀疏 –10.6606 –4.5651 TSPN –10.0541 –6.7948 Hankel-TSPN –10.6915 –6.9017
下载: 导出CSV
表 3 柠檬芯实测目标参数
Table 3. Lemon core measured target parameter
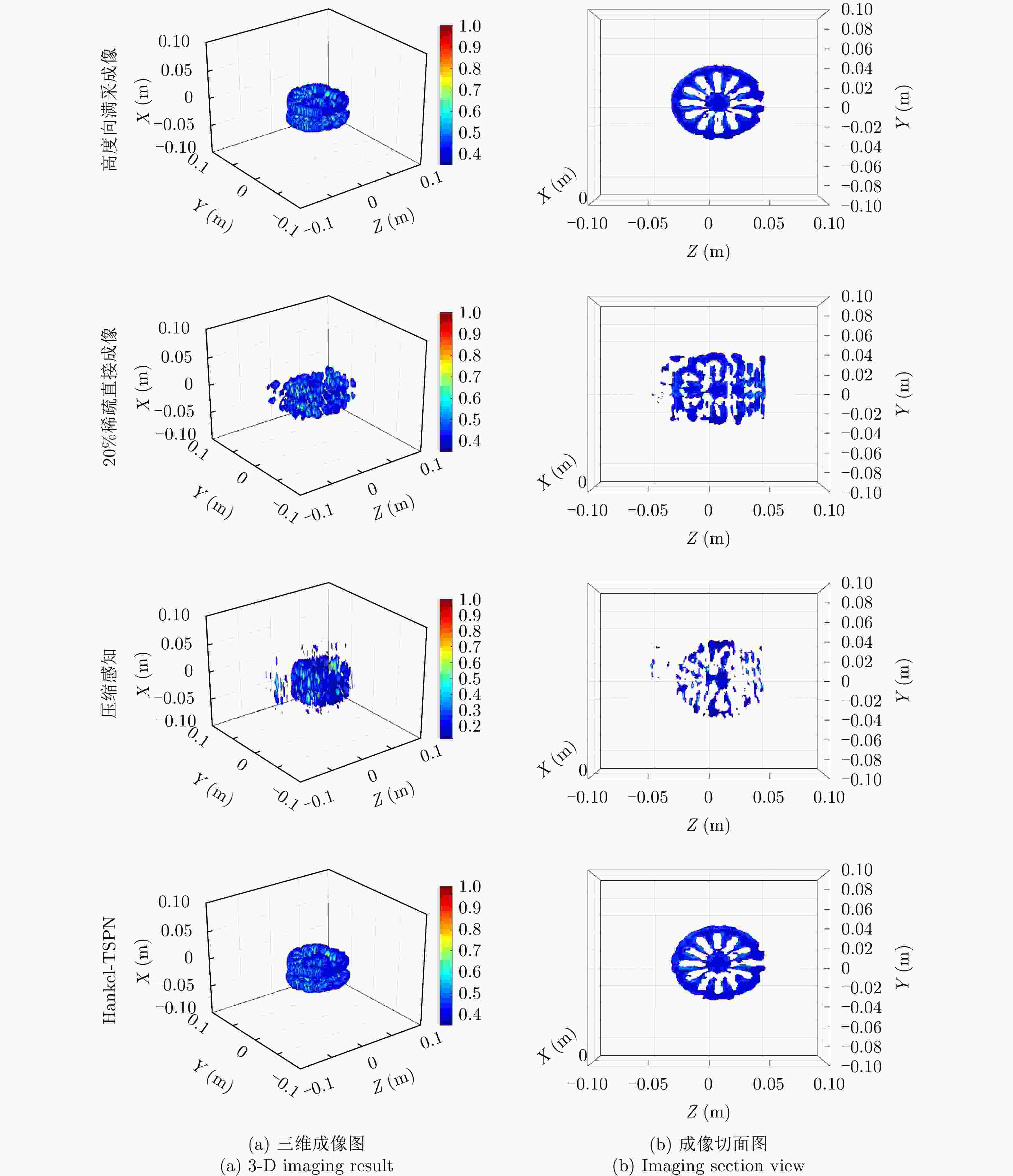
参数名称 参数值 载波频率${f_{\rm{c}}}$ 136 GHz 信号带宽${B_r}$ 8 GHz 方位孔径长度${L_{\rm{A}}}$ 0.11 m 方位采样点数 101 高度孔径长度${L_{\rm{H}}}$ 0.11 m 高度采样点数 101 等效面阵与目标距离${Z_0}$ 0.315 m 轨迹稀疏度I 20%
下载: 导出CSV
表 4 三维方位-高度切面图图像质量比较
Table 4. Comparison of image quality of 3D azimuth-height slice
成像指标 对比度 锐度 图像熵 图像相似度 满采 24.3884 1.63E+10 8.5221 1 Hankel-TSPN 20.2766 1.42E+10 8.3977 0.8855 压缩感知 15.4088 2.77E+08 7.9659 0.2723 稀疏 2.5119 5.42E+07 8.3259 0.1115
下载: 导出CSV
表 5 不同算法的计算复杂度
Table 5. Computational complexity of different algorithms
算法名称 计算复杂度 本文算法(Hankel-TSPN) O(MNKDxDyDz + MKiterN 3)，iter为TSPN循环次数 压缩感知(CS-SRBIM) $O\left( {{{\left( {MNK} \right)}^2}{D_x}{D_y}{D_z}} \right)$ 后向投影(BP) $O\left( {MNK{D_x}{D_y}{D_z}} \right)$
下载: 导出CSV
-
[1] 石星. 毫米波雷达的应用和发展[J]. 电讯技术, 2006, 46(1): 1–9. doi: 10.3969/j.issn.1001-893X.2006.01.001SHI Xing. Application and development of millimetre-wave radars[J]. Telecommunication Engineering, 2006, 46(1): 1–9. doi: 10.3969/j.issn.1001-893X.2006.01.001 [2] 黄昌霸. 车载毫米波雷达目标检测技术研究[D]. [硕士论文], 电子科技大学, 2020.HUANG Changba. Research of on-vehicle millimeter wave radar target detection technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2020. [3] ZHANG Weite, HEREDIA-JUESAS J, DIDDI M, et al. Experimental imaging results of a UAV-mounted downward-looking mm-wave radar[C]. 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, USA, 2019: 1639–1640. [4] 乞耀龙. 近景微波三维成像模型与方法研究[D]. [博士论文], 中国科学院大学, 2012.QI Yaolong. Study on the model and method of close-up microwave three-dimensional imaging[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2012. [5] ESSEN H, LORENZ F, HANTSCHER S, et al. Millimeterwave radar for runway debris detection[C]. 2011 Tyrrhenian International Workshop on Digital Communications - Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 2011: 65–68. [6] ROHMAN B P A, RUDRAPPA M T, SHARGORODSKYY M, et al. Moving human respiration sign detection using mm-wave radar via motion path reconstruction[C]. 2021 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications, Bandung, Indonesia, 2021: 196–200. [7] VERMA P, SHAKYA V S, SHARMA D, et al. MM-wave radar application for autonomous vehicles[C]. 2020 2nd International Conference on Advances in Computing, Communication Control and Networking, Greater Noida, India, 2020: 556–559. [8] 皮亦鸣, 杨建宇, 付毓生, 等. 合成孔径雷达成像原理[M]. 成都: 电子科技大学出版社, 2007: 49–50.PI Yiming, YANG Jianyu, FU Yusheng, et al. Synthetic Aperture Radar Imaging Technology[M]. Chengdu: University of Electronic Science and Technology of China Press, 2007: 49–50. [9] 陈文江, 陈麒安, 陈宏铭, 等. 5G毫米波天线阵列模组技术挑战与未来发展趋势[J]. 中国集成电路, 2021, 30(11): 40–45. doi: 10.3969/j.issn.1681-5289.2021.11.008CHEN Wenjiang, CHEN Qi’an, CHEN Hongming, et al. Technical challenges and development trend of 5G mm wave antenna array module[J]. China Integrated Circuit, 2021, 30(11): 40–45. doi: 10.3969/j.issn.1681-5289.2021.11.008 [10] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 [11] ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L1 -norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117 [12] OLIVERI G, ROCCA P, and MASSA A. A Bayesian-compressive-sampling-based inversion for imaging sparse scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3993–4006. doi: 10.1109/TGRS.2011.2128329 [13] CANDÈS E J and RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717–772. doi: 10.1007/s10208-009-9045-5 [14] CANDES E J and PLAN Y. Matrix completion with noise[J]. Proceedings of the IEEE, 2010, 98(6): 925–936. doi: 10.1109/JPROC.2009.2035722 [15] BI Dongjie, LI Xifeng, XIE Xuan, et al. Compressive sensing operator design and optimization for wideband 3-D millimeter-wave imaging[J]. IEEE Transactions on Microwave Theory and Techniques, 2022, 70(1): 542–555. doi: 10.1109/TMTT.2021.3100499 [16] WANG Mou, WEI Shunjun, SHI Jun, et al. CSR-Net: A novel complex-valued network for fast and precise 3-D microwave sparse reconstruction[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4476–4492. doi: 10.1109/JSTARS.2020.3014696 [17] HU Yue, LIU Xiaohan, and JACOB M. A generalized structured low-rank matrix completion algorithm for MR image recovery[J]. IEEE Transactions on Medical Imaging, 2019, 38(8): 1841–1851. doi: 10.1109/TMI.2018.2886290 [18] KHALIFA M O, ABDELHAFIZ A H, and ZERGUINE A. Sparse channel estimation using adaptive filtering and compressed sampling[C]. 2013 International Conference on Computing, Electrical and Electronic Engineering (ICCEEE), Khartoum, Sudan, 2013: 144–147. [19] WENG Zhiyuan and WANG Xin. Low-rank matrix completion for array signal processing[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 2012: 2697–2700. [20] ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Matrix completion for downward-looking 3-D SAR imaging with a random sparse linear array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1994–2006. doi: 10.1109/TGRS.2017.2771826 [21] MA Yuxin, HAI Yu, YANG Jianyu, et al. A near-field 3-D SAR imaging method with non-uniform sparse linear array based on matrix completion[C]. IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 2022: 1664–1667. [22] ZENG Xuan, MA Yuxin, LI Zhongyu, et al. A near-field fast time-frequency joint 3-D imaging algorithm based on aperture linearization[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021: 5163–5166, [23] YING Jiaxi, CAI Jianfeng, GUO Di, et al. Vandermonde factorization of hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5520–5533. doi: 10.1109/TSP.2018.2869122 [24] AHMED N, NATARAJAN T, and RAO K R. Discrete cosine transform[J]. IEEE Transactions on Computers, 1974, C-23(1): 90–93. doi: 10.1109/T-C.1974.223784 [25] 胡循勇, 杨晓梅, 李昊怡, 等. 融合低秩和稀疏先验的结构性缺失图像修复[J]. 北京航空航天大学学报, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663HU Xunyong, YANG Xiaomei, LI Haoyi, et al. Structural missing image inpainting based on low rank and sparse prior[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663 [26] BOYD S, PARIKH N, CHU E, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[M]. Hanover: Now Foundations and Trends, 2011: 13–23. doi: 10.1561/2200000016. [27] MERHAV N and KRESCH R. Approximate convolution using DCT coefficient multipliers[J]. IEEE Transactions on Circuits and Systems for Video Technology, 1998, 8(4): 378–385. doi: 10.1109/76.709404 [28] LI Oupeng, HE Jia, ZENG Kun, et al. Integrated sensing and communication in 6G a prototype of high resolution THz sensing on portable device[C]. 2021 Joint European Conference on Networks and Communications & 6G Summit, Porto, Portugal, 2021: 544–549. [29] 韦顺军. 线阵三维合成孔径雷达稀疏成像技术研究[D]. [博士论文], 电子科技大学, 2013.WEI Shunjun. Research on linear array three-dimensional synthetic aperture radar sparse imaging technology[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2013. [30] WEI Shunjun, ZHOU Zichen, WANG Mou, et al. 3DRIED: A high-resolution 3-D millimeter-wave radar dataset dedicated to imaging and evaluation[J]. Remote Sensing, 2021, 13(17): 3366. doi: 10.3390/rs13173366 -
计量
- 文章访问数: 1649
- HTML全文浏览量: 621
- PDF下载量: 435
- 被引次数: 0
