作者中心
专家审稿
责编办公
编辑办公
-
摘要: 相比于单部雷达系统，空间分置的网络化雷达由于空间分集、频率分集等优势，通常具备更优的探测性能。当前基于网络化雷达系统的融合检测方法大多仅依据目标回波幅度信息，未考虑相参雷达系统能够获取的多普勒信息对融合检测的增益。直观地，网络化雷达系统中不同雷达观测到目标的空间位置与径向速度应当满足一定的物理约束，利用该额外信息应当能够提升目标与虚警的可分性。基于此，该文提出了多普勒信息辅助的网络化雷达融合检测算法：首先利用多雷达站对同一目标角度与多普勒速度观测的耦合性构建观测间需要满足的约束不等式组，然后基于运筹学中两阶段法对该不等式组是否有可行解做出判断，进而对目标是否存在做出判决。仿真实验表明，所提算法能够有效提升网络化雷达系统的融合检测性能。同时，该文还针对所提算法分析了雷达布站位置及目标位置对融合检测性能的影响。Abstract: Compared with single-radar systems, spatially separated networked radar usually has better detection performance due to its advantages of spatial and frequency diversities. Most of the current fusion detection methods based on networked radar systems only rely on the echo amplitude information of the target without considering the Doppler information that a coherent radar system can obtain to assist detection of targets. Intuitively, the spatial position and radial velocity of a target observed by different radar devices in the networked radar systems should meet certain physical constraints under which the target and false target can be substantially distinguished. Based on this consideration, fusion detection for the networked radar aided by a Doppler information algorithm is proposed in this paper. First, a set of inequalities is constructed based on the coupling between the observation of the same target’s azimuth and Doppler velocity by multiple radar stations. Then, a two-phase method, an algorithm in operational research, is used to judge whether the inequalities have a feasible solution, based on which a judgment is made on whether the target exists. Finally, some simulations are conducted, which show that the proposed algorithm can effectively improve the detection performance of the networked radar system fusion detection. Additionally, the influence of radar station location and target position on the fusion detection performance of the proposed algorithm is analyzed.
-
Key words:
- Networked radar /
- Fusion detection /
- Doppler information /
- Two-phase method
-
图 2 单雷达站线性不等式组中直线位置关系
Figure 2. Position relation between lines in linear inequalities based on single radar station
图 3 单雷达站对应可行域
${R_i}$ Figure 3. Corresponding feasible region
${R_i}$ of single radar station
图 7 单雷达站对应可行域
${R_i}$ Figure 7. Corresponding feasible region
${R_i}$ of single radar station
图 11 各种传统融合检测器引入多普勒信息辅助检测前后的检测性能
Figure 11. Detection performance of various traditional fusion detectors before and after the introduction of Doppler information
图 15 不同雷达站个数下算法的检测性能曲线
Figure 15. Detection performance of different algorithms applied for scenes with different number of radar stations
图 16 3个雷达站顶角不同时对应的各雷达站位置
Figure 16. Locations of 3 radar stations with different top angles
图 17 不同雷达布站位置下
$\{ {R_i}\} _{i = 1}^3$ 的分布图Figure 17. Distribution of
$\{ {R_i}\} _{i = 1}^3$ based on radar systems with different locations of radars
图 18 不同雷达布站位置下检测性能曲线
Figure 18. Detection performance of algorithm applied in radar systems with different distributions of radars
图 20 不同目标位置下
$\{ {R_i}\} _{i = 1}^3$ 的分布图Figure 20. Distribution of
$\{ {R_i}\} _{i = 1}^3$ based on radar systems with different locations of the target
图 21 不同目标位置下检测性能曲线
Figure 21. Detection performance of algorithm applied in radar systems with different locations of targets
算法 1 多普勒信息辅助的融合检测算法 Alg. 1 Procedures of the proposed fusion detection method 步骤1 利用传统融合检测算法获得初次融合检测结果，若判决
结果为目标不存在则结束算法流程，返回该判决结果；若判决目
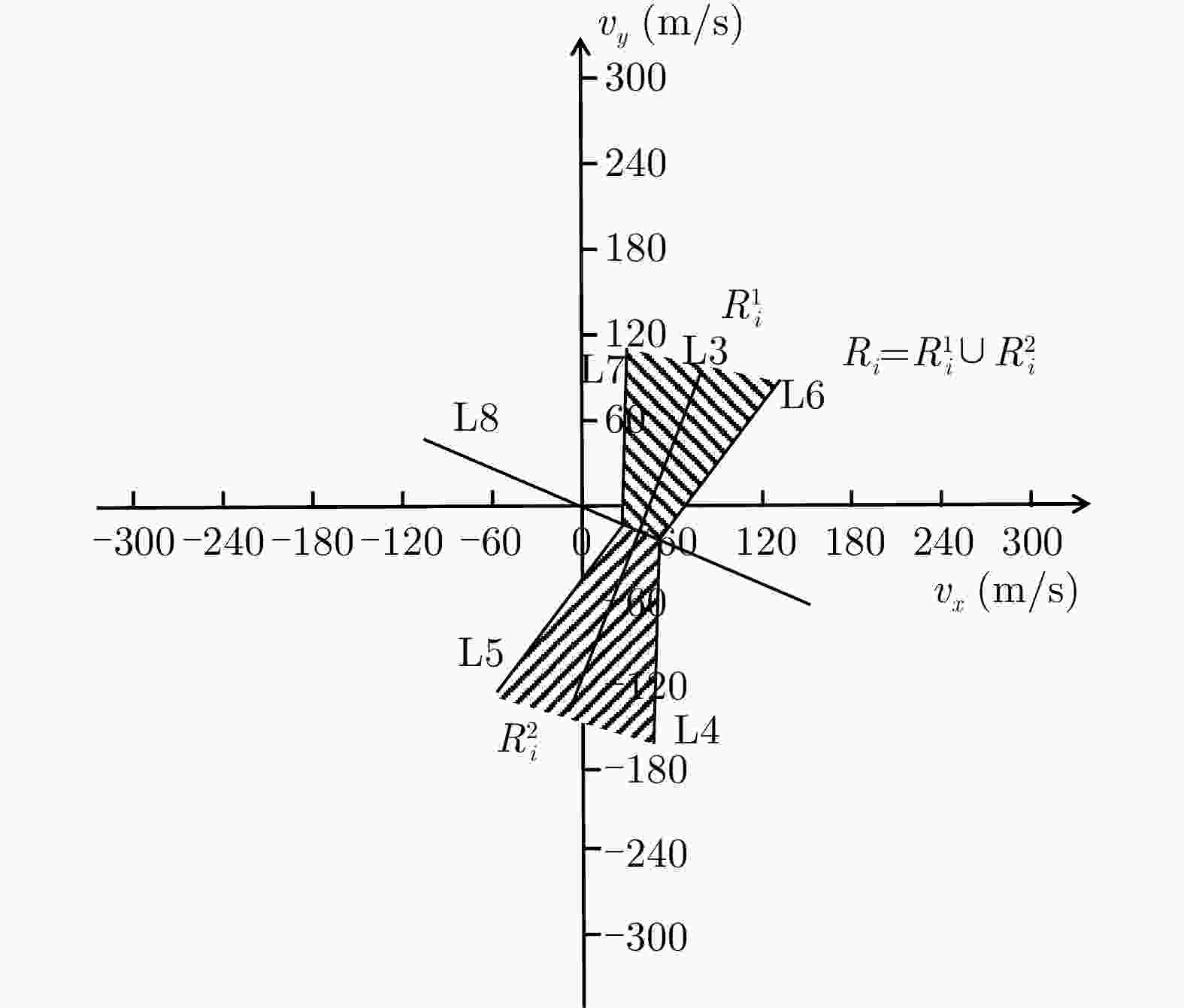
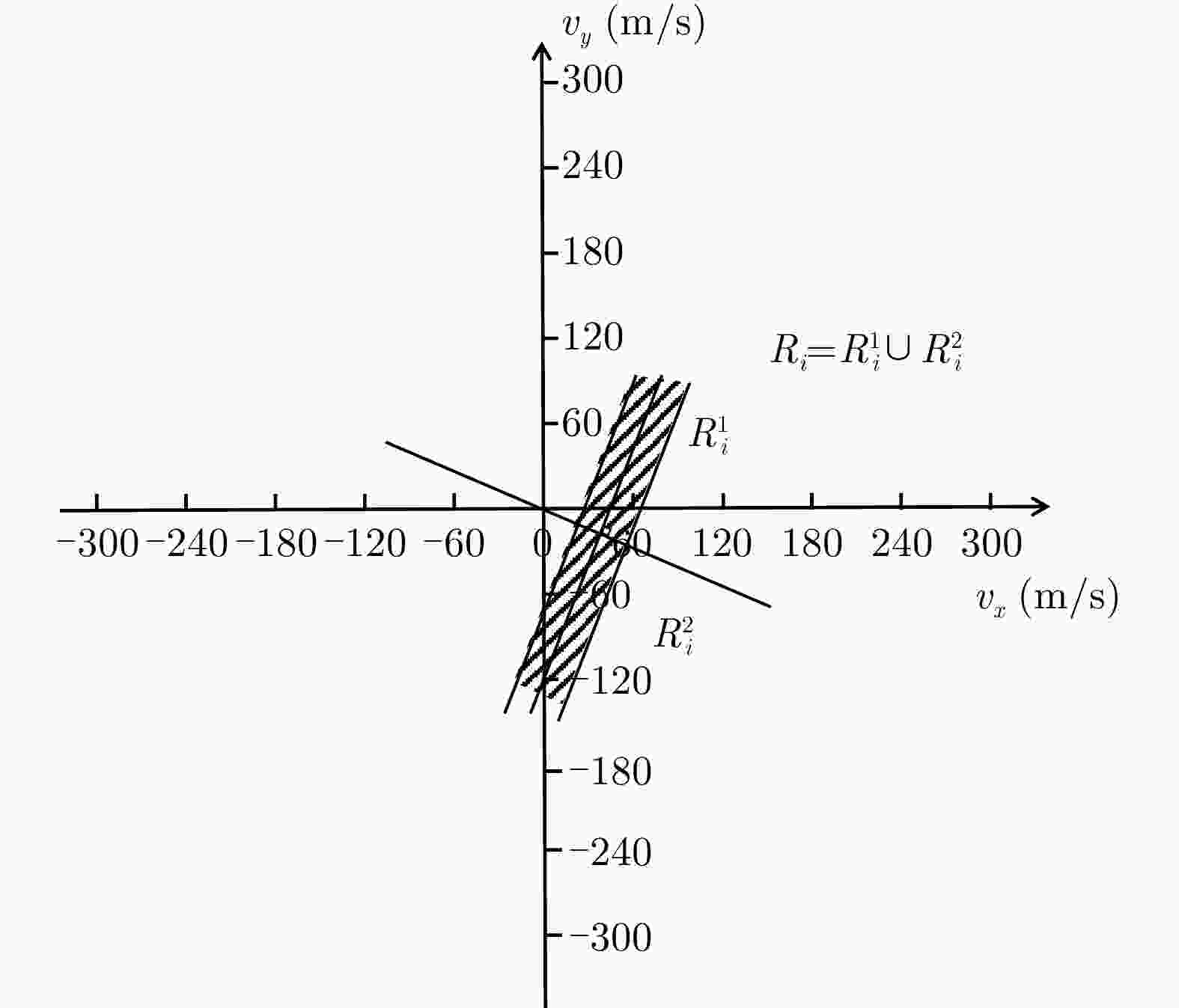
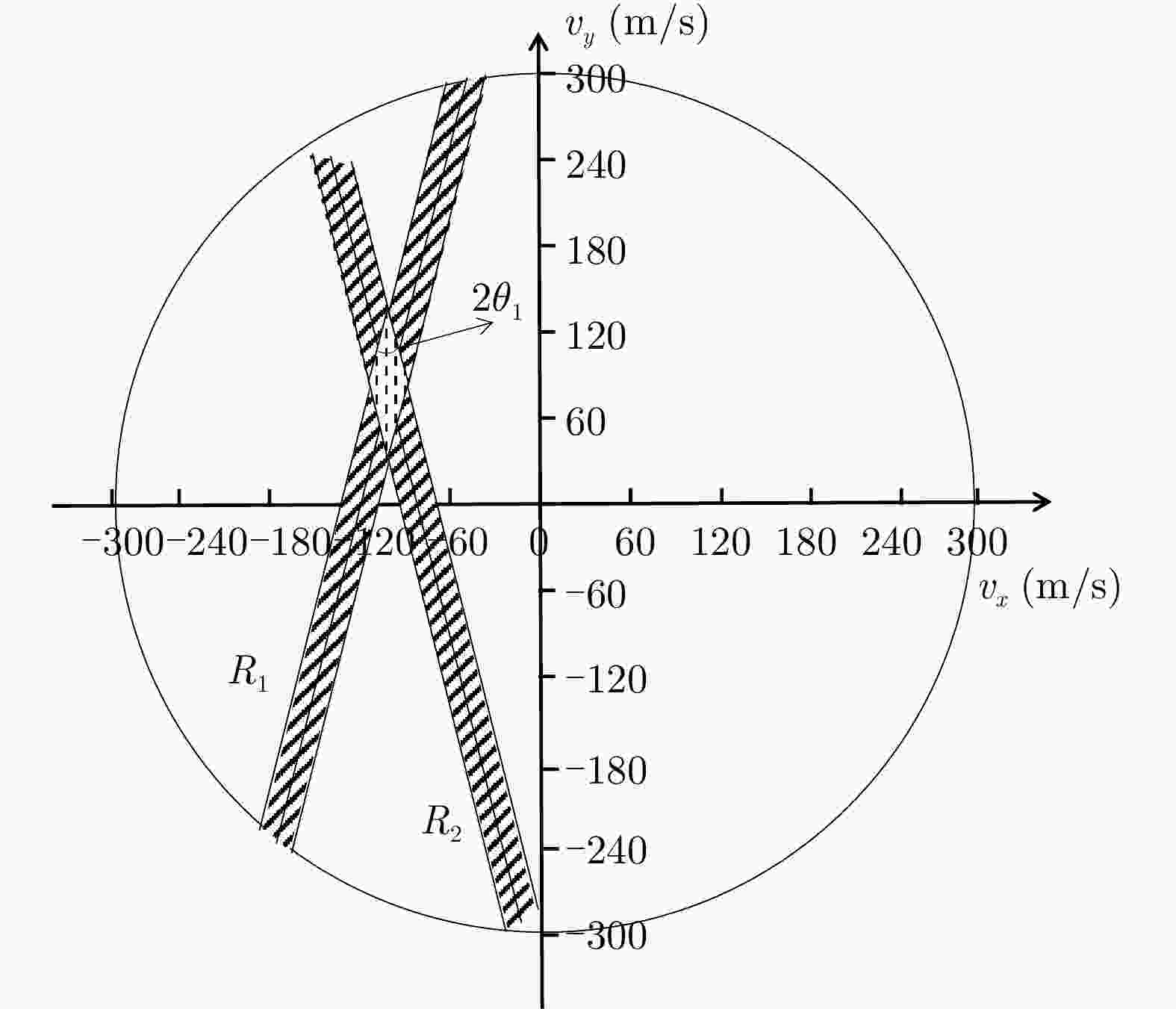
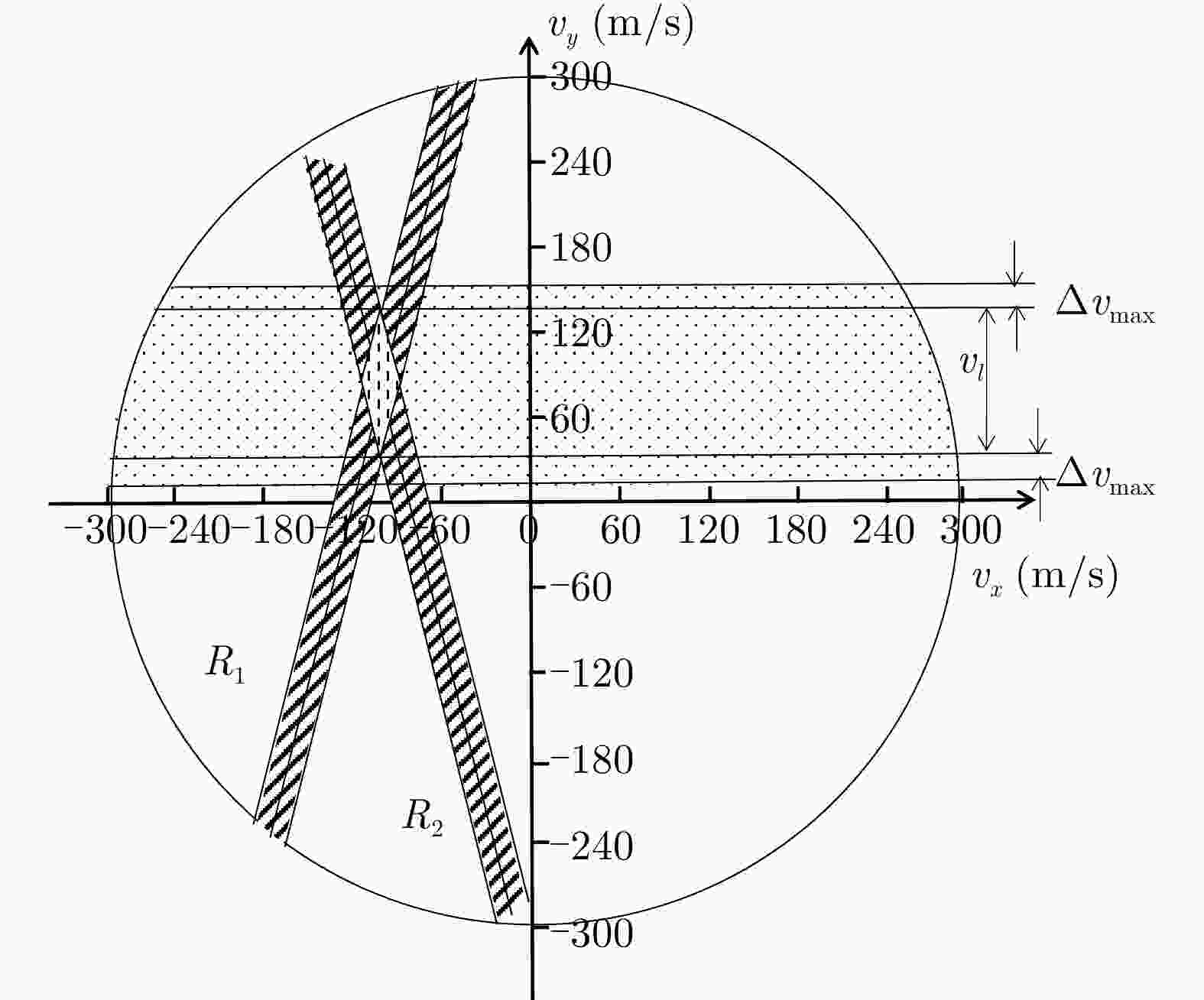
标存在则进入步骤2；步骤2 将各雷达站观测到目标的角度${\theta _{{\rm{O}}i} }$和径向多普勒速度${v_{{\rm{O}}i} }$
代入式(13)、式(14)中获得各雷达站对应的两个子线性不等式
组，之后依次选取每雷达站对应的其一子线性不等式组以及遍历
可能的速度模糊数构成一个新的线性不等式组
${\rm{LI} }({q_1},\:{q_2}, \cdots ,\:{q_N},\:{k_1},\:{k_2}, \cdots ,\:{k_N})$；步骤3 对构造的线性不等式组进行遍历，依次利用两阶段算法
对其进行有无可行解的判决，若某个线性不等式组存在可行域，
结束算法流程，返回目标存在的判决，否则转入步骤4；步骤4 对基于幅度信息初次融合检测结果进行修正，返回目标
不存在的判决，算法终止。
下载: 导出CSV
表 1 仿真实验雷达系统主要参数
Table 1. Main parameters of the radar systems in the simulation
参数 数值 载频${f_{\rm{c}}}$ 2 GHz 带宽B 2 MHz 脉冲重复频率${f_{\rm{r}}}$ 3 kHz 相参积累脉冲数${N_{\rm{c}}}$ $32$ 3 dB波束宽度${\theta _{3\;{\rm{dB}}} }$ 2°
下载: 导出CSV
-
[1] 何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理[M]. 2版. 北京: 清华大学出版社, 2011: 5–10.HE You, GUAN Jian, and MENG Xiangwei. Radar Target Detection and CFAR Processing[M]. 2nd ed. Beijing: Tsinghua University Press, 2011: 5–10. [2] RICHARD M A. Fundamentals of Radar Signal Processing[M]. 2nd ed. New York: McGraw-Hill Education, 2014. [3] SPAGNOLINI U and RAMPA V. Multitarget detection/tracking for monostatic ground penetrating radar: Application to pavement profiling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 383–394. doi: 10.1109/36.739074 [4] CHEN Xiaolong, SU Ningyuan, HUANG Yong, et al. False-alarm-controllable radar detection for marine target based on multi-features fusion via CNNs[J]. IEEE Sensors Journal, 2021, 21(7): 9099–9111. doi: 10.1109/jsen.2021.3054744 [5] 刘宏伟, 严峻坤, 周生华. 网络化雷达协同探测技术[J]. 现代雷达, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002LIU Hongwei, YAN Junkun, and ZHOU Shenghua. Collaborative detection technology of netted radar[J]. Modern Radar, 2020, 42(12): 7–12. doi: 10.16592/j.cnki.1004-7859.2020.12.002 [6] 周生华, 刘宏伟. MIMO雷达目标空间和频率散射多样性研究[J]. 电子与信息学报, 2010, 32(1): 38–42. doi: 10.3724/sp.j.1146.2008.01536ZHOU Shenghua and LIU Hongwei. Scattering properties of spatial and frequency diversity of MIMO radar targets[J]. Journal of Electronics &Information Technology, 2010, 32(1): 38–42. doi: 10.3724/sp.j.1146.2008.01536 [7] 王经鹤, 易伟, 孔令讲. 组网雷达多帧检测前跟踪算法研究[J]. 雷达学报, 2019, 8(4): 490–500. doi: 10.12000/JR18092WANG Jinghe, YI Wei, and KONG Lingjiang. Multi-frame track before detect method for the netted radar system[J]. Journal of Radars, 2019, 8(4): 490–500. doi: 10.12000/JR18092 [8] ZHANG Weiwei, SHI Chenguang, SALOUS S, et al. Convex optimization-based power allocation strategies for target localization in distributed hybrid non-coherent active-passive radar networks[J]. IEEE Transactions on Signal Processing, 2022, 70: 2476–2488. doi: 10.1109/tsp.2022.3173756 [9] 时晨光, 王奕杰, 代向荣, 等. 面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法[J]. 雷达学报, 2022, 11(5): 778–793. doi: 10.12000/JR22005SHI Chenguang, WANG Yijie, DAI Xiangrong, et al. Joint transmit resources and trajectory planning for target tracking in airborne radar networks[J]. Journal of Radars, 2022, 11(5): 778–793. doi: 10.12000/JR22005 [10] XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 729–743. doi: 10.1109/tsp.2017.2777394 [11] BARKAT M and VARSHNEY P K. Decentralized CFAR signal detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 141–149. doi: 10.1109/7.18676 [12] ELIAS-FUSTE A, BROQUETAS-IBARS A, ANTEQUERA J, et al. CFAR data fusion center with inhomogeneous receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 276–285. doi: 10.1109/7.135453 [13] CONTE E, D’ADDIO E, FARINA A, et al. Multistatic radar detection: Synthesis and comparison of optimum and suboptimum receivers[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1983, 130(6): 484–494. doi: 10.1049/ip-f-1.1983.0078 [14] D’ADDIO E and FARINA A. Overview of detection theory in multistatic radar[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1986, 133(7): 613–623. doi: 10.1049/ip-f-1.1986.0098 [15] THOMOPOULOS S C A, VISWANATHAN R, and BOUGOULIAS D C. Optimal decision fusion in multiple sensor systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(5): 644–653. doi: 10.1109/taes.1987.310858 [16] MATHUR A and WILLETT P. Local SNR considerations in decentralized CFAR detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 13–22. doi: 10.1109/7.640257 [17] GROSSI E, LOPS M, and VENTURINO L. A novel dynamic programming algorithm for track-before-detect in radar systems[J]. IEEE Transactions on Signal Processing, 2013, 61(10): 2608–2619. doi: 10.1109/tsp.2013.2251338 [18] GAO Chang, YAN Junkun, PENG Xiaojun, et al. Signal structure information-based target detection with a fully convolutional network[J]. Information Science, 2021, 576: 345–354. doi: 10.1016/j.ins.2021.06.066 [19] GAO Chang, YAN Junkun, PENG Xiaojun, et al. Intelligent multiframe detection aided by Doppler information and a deep neural network[J]. Information Science, 2022, 593: 432–448. [20] HU Zhijian, LEUNG H, and BLANCHETTE M. Statistical performance analysis of track initiation techniques[J]. IEEE Transactions on Signal Processing, 1997(2): 445–456. doi: 10.1109/78.554308 [21] 靳标, 李聪, 张贞凯. 回波幅度信息辅助的群目标航迹起始方法[J]. 雷达学报, 2020, 9(4): 723–729. doi: 10.12000/JR19088JIN Biao, LI Cong, and ZHANG Zhenkai. Group target track initiation method aided by echo amplitude information[J]. Journal of Radars, 2020, 9(4): 723–729. doi: 10.12000/JR19088 [22] SUNDARESAN A, VARSHNEY P K, and RAO N S V. Copula-based fusion of correlated decisions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 454–471. doi: 10.1109/taes.2011.5705686 [23] ZHANG Shan, KHANDURI P, and VARSHNEY P K. Distributed sequential detection: Dependent observations and imperfect communication[J]. IEEE Transactions on Signal Processing, 2020, 68: 830–842. doi: 10.1109/tsp.2019.2955830 [24] BREARLEY A L, MITRA G, and WILLIAMS H P. Analysis of mathematical programming problems prior to applying the simplex algorithm[J]. Mathematical Programming, 1975, 8(1): 54–83. doi: 10.1007/bf01580428 [25] ARSHAM H. Initialization of the simplex algorithm: An artificial-free approach[J]. SIAM Review, 1997, 39(4): 736–744. doi: 10.1137/s0036144596304722 [26] KALL P. Computational methods for solving two-stage stochastic linear programming problems[J]. Zeitschrift für angewandte Mathematik und Physik ZAMP, 1979, 30(2): 261–271. doi: 10.1007/bf01601939 [27] LUENBERGER D G and YE Y. Linear and Nonlinear Programming[M]. Springer, 2016. [28] WITTMANN-HOHLBEIN M and PISTIKOPOULOS E N. A two-stage method for the approximate solution of general multiparametric mixed-integer linear programming problems[J]. Industrial & Engineering Chemistry Research, 2012, 51(23): 8095–8107. doi: 10.1021/ie201408p [29] BORGWARDT K H. The average number of pivot steps required by the simplex-method is polynomial[J]. Zeitschrift für Operations Research, 1982, 26(1): 157–177. doi: 10.1007/bf01917108 [30] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 5版. 北京: 电子工业出版社, 2014: 20–23.DING Lufei, GENG Fulu, and CHEN Jianchun. Principle of Radar[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2014: 20–23. [31] HOBALLAH I Y and VARSHNEY P K. Distributed Bayesian signal detection[J]. IEEE Transactions on Information Theory, 1989, 35(5): 995–1000. doi: 10.1109/18.42208 -
计量
- 文章访问数: 1122
- HTML全文浏览量: 610
- PDF下载量: 309
- 被引次数: 0
