基于稀疏和低秩先验的雷达前视超分辨成像方法

唐军奎; 刘峥; 冉磊; 谢荣; 秦基凯

doi:10.12000/JR22199

基于稀疏和低秩先验的雷达前视超分辨成像方法

doi: 10.12000/JR22199

西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 国家自然科学基金(62001346)，CASC多传感器探测与识别技术研发中心种子基金(ZZJJ202102)

详细信息

作者简介:
唐军奎，博士生，主要研究方向为雷达前视成像、阵列信号处理

刘　峥，教授，主要研究方向为雷达信号处理的理论与系统设计、雷达精确制导技术、多传感器信息融合等

冉　磊，副教授，主要研究方向为无人机/弹载雷达成像技术、SAR图像目标检测与识别、雷达信号实时处理系统等

谢　荣，副教授，主要研究方向为雷达信号处理的理论与系统设计、雷达精确制导技术等

秦基凯，博士生，主要研究方向为雷达HRRP目标识别、SAR图像目标识别等

通讯作者:
刘峥 lz@xidian.edu.cn

冉磊 rl@xidian.edu.cn

责任主编：李悦丽 Corresponding Editor: LI Yueli
中图分类号: TN95
计量
- 文章访问数: 1324
- HTML全文浏览量: 889
- PDF下载量: 266
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-30
- 修回日期: 2022-12-24
- 网络出版日期: 2022-12-30
- 刊出日期: 2023-04-28

Radar Forward-looking Super-resolution Imaging Method Based on Sparse and Low-rank Priors

National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (62001346), Seed Funding Project of Multisensor Intelligent Detection and Recognition Technologies R&D Center of CASC (ZZJJ202102)

More Information

Corresponding author: LIU Zheng, lz@xidian.edu.cn; RAN Lei, rl@xidian.edu.cn

摘要

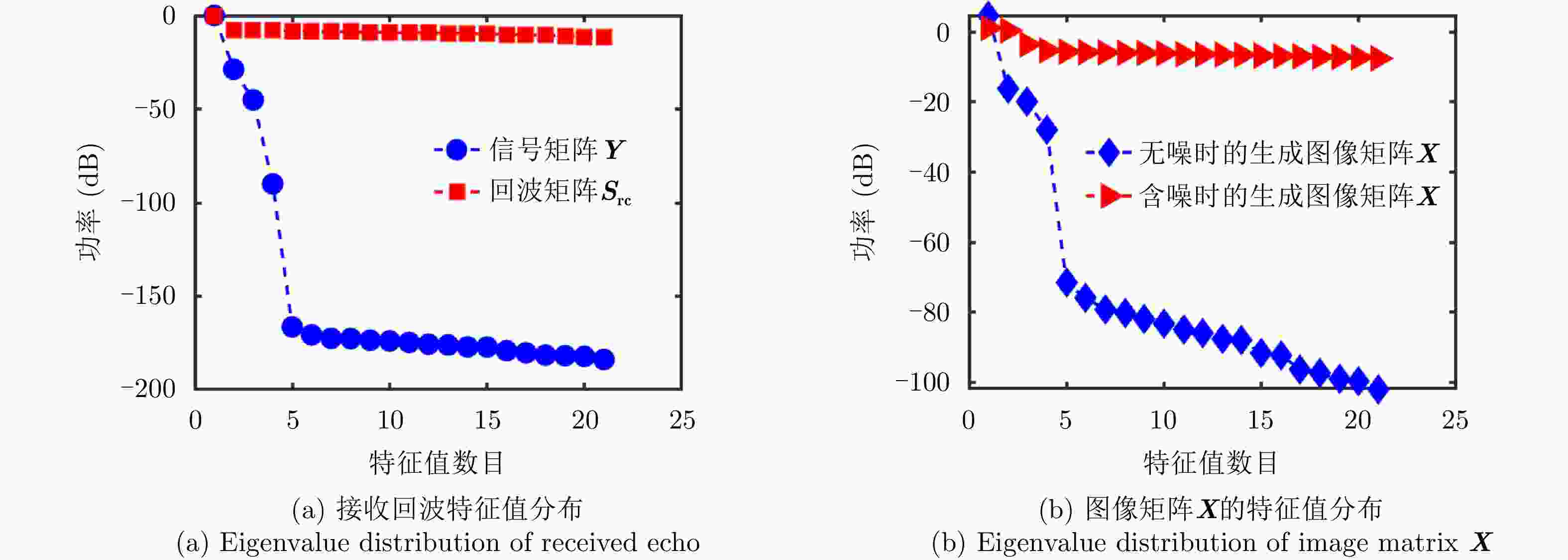
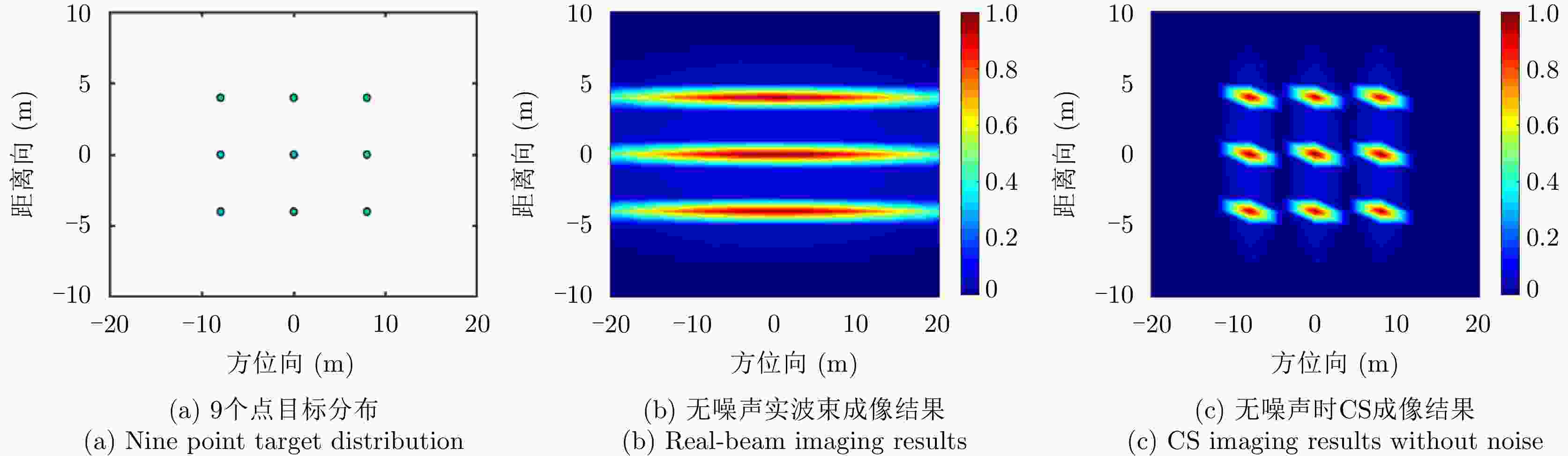
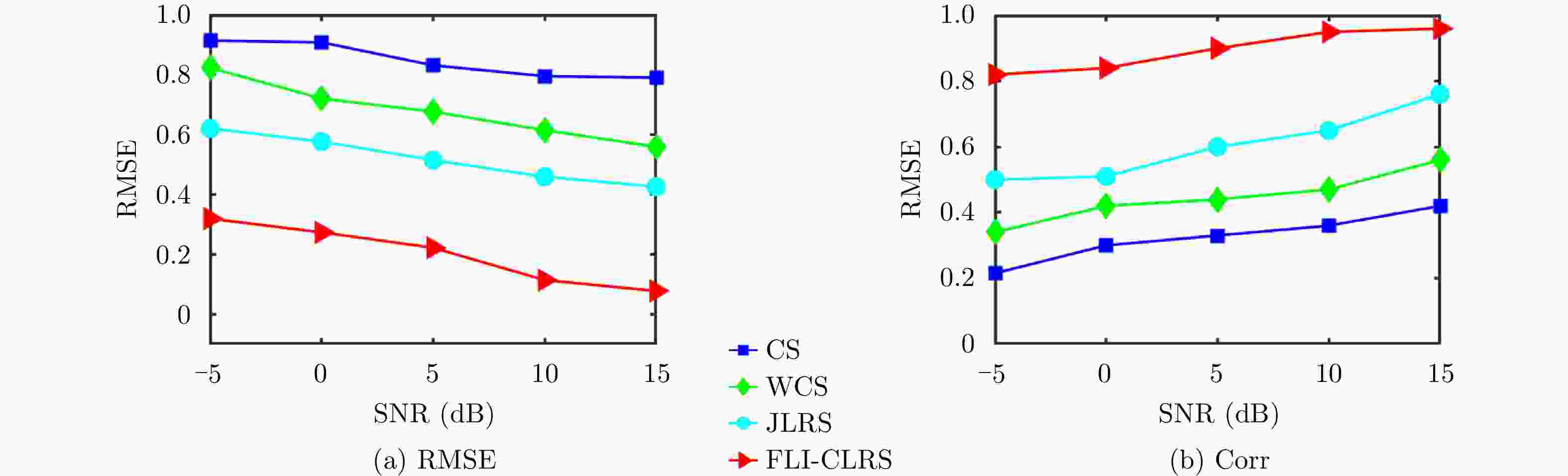
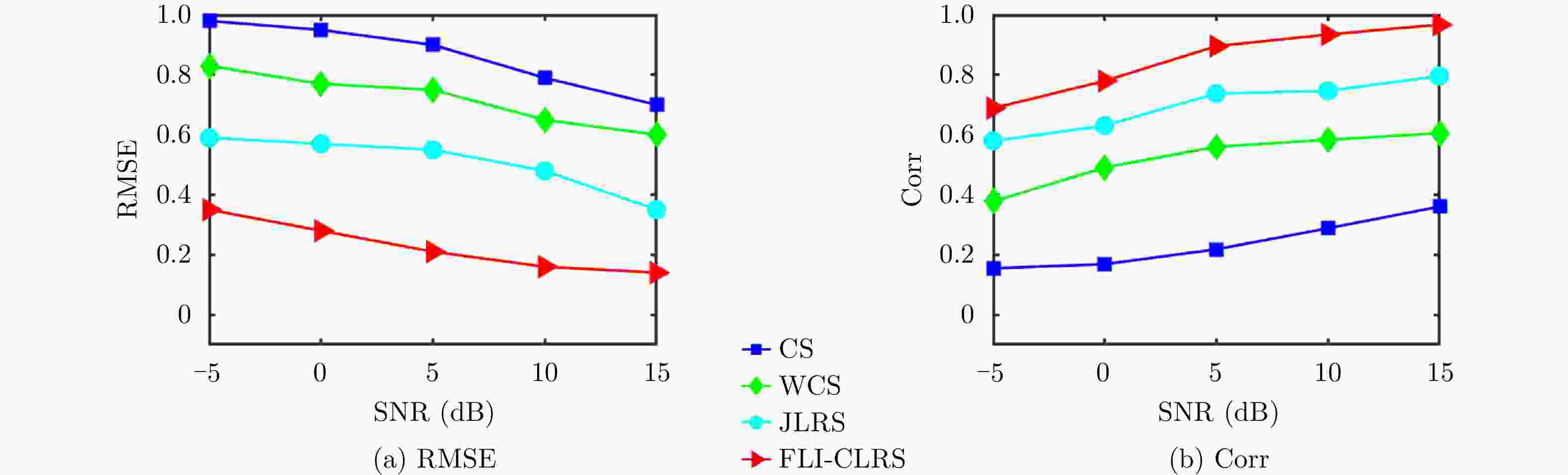
摘要: 在精确制导、自主着陆、地形测绘等多种领域，雷达前视成像至关重要。传统的基于实波束扫描的前视成像方法受到实际雷达孔径约束难以获得高分辨图像。与整个成像场景相比，感兴趣目标通常只占一小部分区域，这种稀疏性使得压缩感知(CS)可以应用于高分辨率前视图像重建。然而，雷达回波中的强噪声影响了基于CS方法生成图像质量。受到最终生成图像具有低秩特性的启发，该文建立了一种联合低秩和稀疏特性的前视超分辨成像模型。为了有效地解决所提模型中的双重约束优化问题，提出了一种在交替方向乘子法(ADMM)框架下基于增广拉格朗日乘子(ALM)的前视图像重构方法。仿真和实测数据实验结果表明，所提方法能够有效提高雷达前视成像的方位分辨率，并且具有较强噪声鲁棒性。
- 前视成像 /
- 超分辨成像 /
- 压缩感知(CS) /
- 低秩和稀疏特性 /
- 增广拉格朗日乘子(ALM) /
- 交替方向乘子法(ADMM)
Abstract: Radar forward-looking imaging is important in many fields, such as precision guidance, autonomous landing, and terrain mapping. Due to the constraints of actual radar aperture, obtaining high-resolution images using the traditional forward-looking imaging method based on real beam scanning is challenging. Compared with the entire imaging scene, the objects of interest usually occupy only a small part of the area. This sparsity enables the use of Compressed Sensing(CS) to reconstruct high-resolution forward-looking images. However, the high noise in the radar echo affects the quality of the image generated by the compressed sensing method. Inspired by the low-rank property of the final image, this paper proposes a forward-looking super-resolution imaging model that combines sparse and low-rank properties. To effectively solve the dual constraint optimization problem in the proposed model, a forward-looking image reconstruction method based on an Augmented Lagrange Multiplier(ALM) within the framework of the Alternating Direction Multiplier Method(ADMM) was proposed. Finally, the experimental results from simulation and real data show that the proposed method can effectively improve the azimuth resolution of radar forward-looking imaging while also being noise-robust.
- Forward-looking imaging /
- Super-resolution imaging /
- Compressed Sensing (CS) /
- Low rank and sparsity /
- Augmented Lagrange Multiplier (ALM) /
- Alternate Direction Multiplier Method (ADMM)

HTML全文

图 1 阵列雷达前视成像观测几何示意图

Figure 1. Array radar forward-looking imaging observation geometry schematic

下载: 全尺寸图片幻灯片

图 2 回波和生成的图像的特征值分布对比

Figure 2. Eigenvalue distribution comparison of echo and generated image

下载: 全尺寸图片幻灯片

图 3 点目标分布以及成像结果

Figure 3. Point target distribution and imaging results

下载: 全尺寸图片幻灯片

图 4 SNR=5 dB时仿真点目标不同方法成像结果对比

Figure 4. Comparison of imaging results of different methods for simulated point targets when SNR=5 dB

下载: 全尺寸图片幻灯片

图 5 仿真点目标的RMSE和Corr对比

Figure 5. RMSE and Corr comparison of simulation point targets

下载: 全尺寸图片幻灯片

图 6 实测数据实验场景及雷达平台

Figure 6. Experimental scenarios of measured data and radar platform

下载: 全尺寸图片幻灯片

图 7 实测数据成像结果

Figure 7. Measured data imaging results

下载: 全尺寸图片幻灯片

图 8 SNR=5 dB时实测数据不同方法成像结果对比

Figure 8. Comparison of imaging results of different methods for measurd data when SNR=5 dB

下载: 全尺寸图片幻灯片

图 9 实测数据的RMSE和Corr对比

Figure 9. RMSE and Corr comparison of measurd data

下载: 全尺寸图片幻灯片

表 1 式(14) ALM-ADMM求解流程

Table 1. ALM-ADMM solution flow of Eq. (14)

输入：字典矩阵A，观测数据${ {\boldsymbol{S} }_{ {\rm{rc} } } }$
初始化：迭代次数$k = 1$，拉格朗日乘子矩阵${\boldsymbol{Q}}_1^1 = {\boldsymbol{Q}}_2^1 = {\boldsymbol{Q}}_3^1 = {\boldsymbol{Q}}_4^1 = { {\boldsymbol{E} }^1} = { {\boldsymbol{Y} }^1} \in {0^{N \times M} }$，图像矩阵${ {\boldsymbol{Z} }^1} = { {\boldsymbol{J} }^1} = { {\boldsymbol{X} }^1} \in {0^{\bar N \times M} }$，正则化参数${\lambda _1},{\lambda _2} > 0$，惩罚项系数$u_1^1,u_2^1,u_3^1,u_4^1 > 0$，步长因子$\rho _1^{},\rho _2^{},\rho _3^{},\rho _4^{} > 1$。
更新迭代过程：
(1) 更新Z：　　$\left( { { {\boldsymbol{X} }^k} + {\boldsymbol{Q}}_1^k/\mu _1^k} \right) = {U^k}{\varSigma ^k}{\left( { {V^k} } \right)^{\rm{H} } }$; ${ {\boldsymbol{Z} }^{k + 1} } = {U^k}{\rm{soft} }\left( { {\varSigma ^k},\dfrac{1}{ {\mu_1^k} } } \right){\left( { {V^k} } \right)^{\rm{H} } }$
(2) 更新J：
${\boldsymbol{R} }_1^k = { {\boldsymbol{X} }^k} + \dfrac{ { {\boldsymbol{Q}}_4^k} }{ {u_4^k} } - \dfrac{ { {\lambda _1} } }{ { {\boldsymbol{Q}}_4^k} }$, ${\boldsymbol{R} }_2^k = { {\boldsymbol{X} }^k} + \dfrac{ { {\boldsymbol{Q} }_4^k} }{ {\mu _4^k} } + \dfrac{ { {\lambda _1} } }{ { {\boldsymbol{Q} }_4^k} }$; ${ {\boldsymbol{J} }^{k + 1} } = \max \left( {0,{\boldsymbol{R} }_1^k} \right) + \min \left( {0,{\boldsymbol{R} }_2^k} \right)$
(3) 更新X：
${ {\boldsymbol{X} }^{k + 1} } = \left( { { {\boldsymbol{A} }^{\rm{T} } }{\boldsymbol{A} } + 2{\boldsymbol{I} } } \right)/{\boldsymbol{I} } \cdot \left\{ { { {\boldsymbol{A} }^{\rm{T} } }\left[ { { {\boldsymbol{S} }_{ {\rm{rc} } } } - { {\boldsymbol{E} }^k} + { {\boldsymbol{Y} }^{k + 1} } - \left( {\dfrac{ { {\boldsymbol{Q} }_1^k} }{ {\mu _1^k} } + \dfrac{ { {\boldsymbol{Q} }_2^k} }{ {\mu _2^k} } } \right)} \right] - \dfrac{ { {\boldsymbol{Q} }_3^k} }{ {\mu _3^k} } - \dfrac{ { {\boldsymbol{Q} }_4^k} }{ {\mu _4^k} } + { {\boldsymbol{Z} }^{k + 1} } + { {\boldsymbol{J} }^{k + 1} } } \right\}$
(4) 更新E：　　${ {\boldsymbol{E} }^{k + 1} } = { {\mu _{\text{2} }^k\left( { { {\boldsymbol{S} }_{ {\rm{rc} } } } - {\boldsymbol{A} }{ {\boldsymbol{X} }^{k + 1} }{\text{ + } }\dfrac{ { {\boldsymbol{Q} }_2^k} }{ {\mu _{\text{2} }^k} } } \right)} \mathord{\left/ {\vphantom { {\mu _{\text{2} }^k\left( { {S_{rc} } - A{X^{k + 1} }{\text{ + } }\frac{ {Q_2^k} }{ {\mu _{\text{2} }^k} } } \right)} {\left( {\lambda _2^k + \mu _{\text{2} }^k} \right)} } } \right. } {\left( {\lambda _2^k + \mu _{\text{2} }^k} \right)} }$
(5) 更新$ {{\boldsymbol{Q}}_1} $, $ {{\boldsymbol{Q}}_2} $, $ {{\boldsymbol{Q}}_3} $, $ {{\boldsymbol{Q}}_4} $：
$\begin{aligned} & {\boldsymbol{Q} }_1^{k + 1} = {\boldsymbol{Q} }_1^k + \mu _1^k\left( { { {\boldsymbol{S} }_{ {\rm{rc} } } } - {\boldsymbol{A} }{ {\boldsymbol{X} }^{k + 1} } - { {\boldsymbol{E} }^{k + 1} } } \right),{\boldsymbol{Q} }_2^{k + 1} = {\boldsymbol{Q} }_2^k + \mu _2^k\left( { {\boldsymbol{Y} } - {\boldsymbol{A}}{ {\boldsymbol{X} }^{k + 1} } } \right) \\ & {\boldsymbol{Q} }_3^{k + 1} = {\boldsymbol{Q} }_3^k + \mu _3^k\left( { {\boldsymbol{X} } - { {\boldsymbol{Z} }^{k + 1} } } \right),{\boldsymbol{Q} }_4^{k + 1} = {\boldsymbol{Q} }_4^k + \mu _4^k\left( { {\boldsymbol{X} } - { {\boldsymbol{J} }^{k + 1} } } \right) \end{aligned}$
(6) 更新 $ {u_1},{u_2},{u_3},{u_4} $：
$ \mu _1^{k + 1} = {\rho _1}\mu _1^k,\mu _2^{k + 1} = {\rho _2}\mu _2^k,\mu _3^{k + 1} = {\rho _3}\mu _3^k,\mu _4^{k + 1} = {\rho _4}\mu _4^k $
输出：图像矩阵X

下载: 导出CSV

表 2 仿真实验雷达参数

Table 2. Radar parameters for simulation experiment

参数	数值
载频(GHz)	35
带宽(MHz)	150
脉冲重复间隔(μs)	250
平台运动速度(m/s)	150
天线长度(m)	0.4
天线阵元个数	94
工作距离(m)	3000

下载: 导出CSV

表 3 AWR2243 雷达关键参数

Table 3. Key parameters of AWR2243 radar

参数	数值
载频(GHz)	78.7
带宽(GHz)	2.5
天线长度(m)	0.16
雷达与目标距离(m)	9.5
天线阵元个数	86

下载: 导出CSV

参考文献(25)

[1]	MAO Deqing, ZHANG Yongchao, PEI Jifang, et al. Forward-looking geometric configuration optimization design for spaceborne-airborne multistatic synthetic aperture radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 8033–8047. doi: 10.1109/JSTARS.2021.3103802
[2]	陈洪猛, 李明, 王泽玉, 等. 基于多帧数据联合处理的机载单通道雷达贝叶斯前视成像[J]. 电子与信息学报, 2015, 37(10): 2328–2334. doi: 10.11999/JEIT150153 CHEN Hongmeng, LI Ming, WANG Zeyu, et al. Bayesian forward-looking imaging for airborne single-channel radar based on combined multiple frames data[J]. Journal of Electronics &Information Technology, 2015, 37(10): 2328–2334. doi: 10.11999/JEIT150153
[3]	RAN Lei, LIU Zheng, LI Tao, et al. An adaptive fast factorized back-projection algorithm with integrated target detection technique for high-resolution and high-squint spotlight SAR imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(1): 171–183. doi: 10.1109/JSTARS.2017.2771503
[4]	RAN Lei, LIU Zheng, ZHANG Lei, et al. An autofocus algorithm for estimating residual trajectory deviations in synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3408–3425. doi: 10.1109/TGRS.2017.2670785
[5]	梅海文, 孟自强, 李亚超, 等. 双基前视SAR几何定位及同步误差分析[J]. 电子与信息学报, 2018, 40(4): 882–889. doi: 10.11999/JEIT170677 MEI Haiwen, MENG Ziqiang, LI Yachao, et al. Bistatic forward-looking SAR geometrical positioning and analysis of synchronization error[J]. Journal of Electronics &Information Technology, 2018, 40(4): 882–889. doi: 10.11999/JEIT170677
[6]	LIU Zhutian, LI Zhongyu, YU Huaqin, et al. Bistatic forward-looking SAR moving target detection method based on joint clutter cancellation in echo-image domain with three receiving channels[J]. Sensors, 2018, 18(11): 3835. doi: 10.3390/s18113835
[7]	温晓杨, 匡纲要, 胡杰民, 等. 基于实波束扫描的相控阵雷达前视成像[J]. 航空学报, 2014, 35(7): 1977–1991. doi: 10.7527/S1000-6893.2013.0545 WEN Xiaoyang, KUANG Gangyao, HU Jiemin, et al. Forward-looking imaging based on real beam scanning phased array radars[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1977–1991. doi: 10.7527/S1000-6893.2013.0545
[8]	刘向阳, 杨君刚, 孟进, 等. 低信噪比下基于Hough变换的前视阵列SAR稀疏三维成像[J]. 雷达学报, 2017, 6(3): 316–323. doi: 10.12000/JR17011 LIU Xiangyang, YANG Jungang, MENG Jin, et al. Sparse three-dimensional imaging based on Hough transform for forward-looking array SAR in Low SNR[J]. Journal of Radars, 2017, 6(3): 316–323. doi: 10.12000/JR17011
[9]	HUANG Yulin, ZHA Yuebo, WANG Yue, et al. Forward looking radar imaging by truncated singular value decomposition and its application for adverse weather aircraft landing[J]. Sensors, 2015, 15(6): 14397–14414. doi: 10.3390/s150614397
[10]	XIA Jie, LU Xinfei, and CHEN Weidong. Multi-channel deconvolution for forward-looking phase array radar imaging[J]. Remote Sensing, 2017, 9(7): 703. doi: 10.3390/rs9070703
[11]	ZHA Yuebo, HUANG Yulin, SUN Zhichao, et al. Bayesian deconvolution for angular super-resolution in forward-looking scanning radar[J]. Sensors, 2015, 15(3): 6924–6946. doi: 10.3390/s150306924
[12]	李悦丽, 马萌恩, 赵崇辉, 等. 基于单脉冲雷达和差通道多普勒估计的前视成像[J]. 雷达学报, 2021, 10(1): 131–142. doi: 10.12000/JR20111 LI Yueli, MA Meng’en, ZHAO Chonghui, et al. Forward-looking imaging via Doppler estimates of sum-difference measurements in scanning monopulse radar[J]. Journal of Radars, 2021, 10(1): 131–142. doi: 10.12000/JR20111
[13]	GIUSTI E, CATALDO D, BACCI A, et al. ISAR image resolution enhancement: Compressive sensing versus state-of-the-art super-resolution techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 1983–1997. doi: 10.1109/taes.2018.2807283
[14]	ZHANG Shunsheng, ZHANG Wei, ZONG Zhulin, et al. High-resolution bistatic ISAR imaging based on two-dimensional compressed sensing[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(5): 2098–2111. doi: 10.1109/tap.2015.2408337
[15]	AO Dongyang, WANG Rui, HU Cheng, et al. A sparse SAR imaging method based on multiple measurement vectors model[J]. Remote Sensing, 2017, 9(3): 297. doi: 10.3390/rs9030297
[16]	QIU Wei, ZHOU Jianxiong, and FU Qiang. Jointly using low-rank and sparsity priors for sparse inverse synthetic aperture radar imaging[J]. IEEE Transactions on Image Processing, 2019, 29: 100–115. doi: 10.1109/tip.2019.2927458
[17]	ZHANG Xiaohua, BAI Ting, MENG Hongyun, et al. Compressive sensing-based ISAR imaging via the combination of the sparsity and nonlocal total variation[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 11(5): 990–994. doi: 10.1109/lgrs.2013.2284288
[18]	ZENG Chuangzhan, ZHU Weigang, JIA Xin, et al. Sparse aperture ISAR imaging method based on joint constraints of sparsity and low rank[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(1): 168–181. doi: 10.1109/tgrs.2020.2994179
[19]	ZHANG Lei, XING Mengdao, QIU Chengwei, et al. Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3824–3838. doi: 10.1109/tgrs.2010.2048575
[20]	LU Canyi, FENG Jiashi, YAN Shuicheng, et al. A unified alternating direction method of multipliers by majorization minimization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 527–541. doi: 10.1109/tpami.2017.2689021
[21]	WIPF D P and RAO B D. An empirical bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704–3716. doi: 10.1109/TSP.2007.894265
[22]	ZHANG Zhilin and RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912–926. doi: 10.1109/JSTSP.2011.2159773
[23]	COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477–2488. doi: 10.1109/TSP.2005.849172
[24]	WIPF D and NAGARAJAN S. Iterative reweighted ℓ₁ and ℓ₂ methods for finding sparse solutions[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 317–329. doi: 10.1109/JSTSP.2010.2042413
[25]	CAI Jianfeng, CANDÈS E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970