多扩展目标跟踪优化中基于威胁规避的无人机路径规划策略

陈辉; 魏凤旗; 韩崇昭

doi:10.12000/JR22116

多扩展目标跟踪优化中基于威胁规避的无人机路径规划策略

DOI: 10.12000/JR22116

1.
兰州理工大学电气工程与信息工程学院兰州 730050
2.
西安交通大学自动化科学与工程学院西安 710049

基金项目: 国家自然科学基金项目(62163023, 62173266, 62103318, 61873116)，甘肃省教育厅产业支撑计划项目(2021CYZC-02)

详细信息

作者简介:
陈　辉，博士，教授，博士生导师，主要研究方向为雷达目标跟踪、数据融合与电子对抗等

魏凤旗，硕士生，研究方向为数据融合与多目标跟踪技术

韩崇昭，教授，主要研究方向为多源信息融合、随机控制与自适应控制、非线性频谱分析等

通讯作者:
陈辉 huich78@hotmail.com

责任主编：易伟 Corresponding Editor: YI Wei
中图分类号: TP274
计量
- 文章访问数: 1272
- HTML全文浏览量: 490
- PDF下载量: 231
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-17
- 修回日期: 2022-07-22
- 网络出版日期: 2022-08-11
- 刊出日期: 2023-06-28

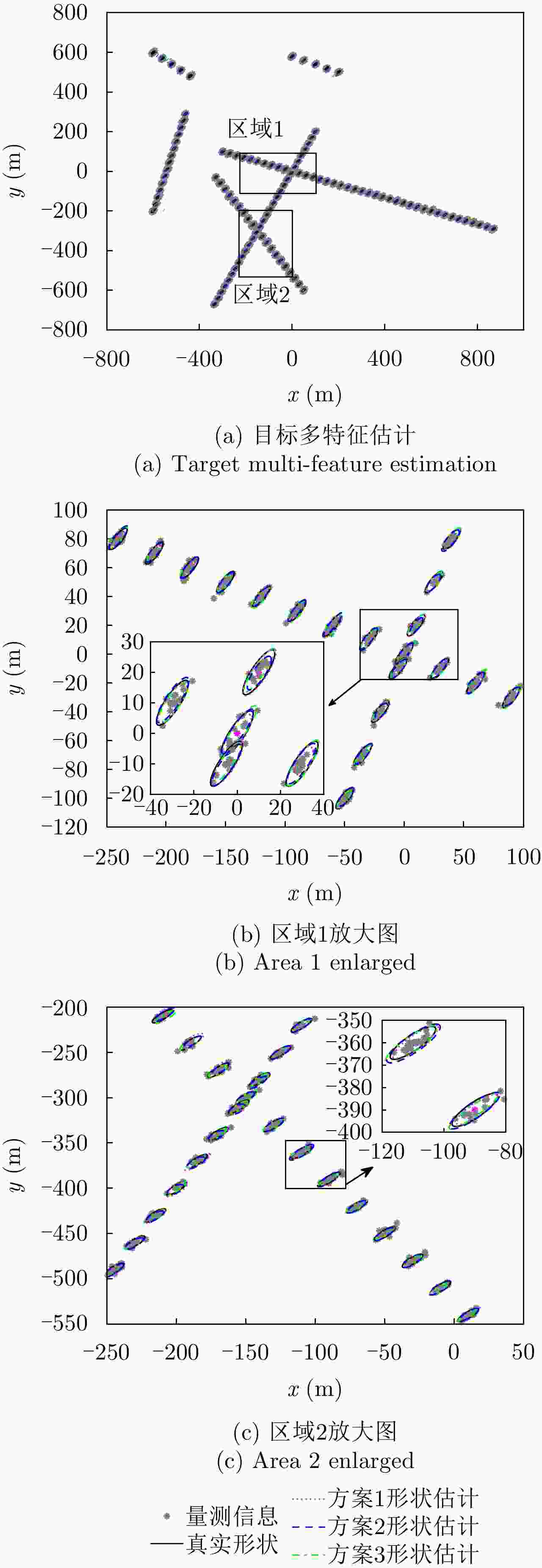
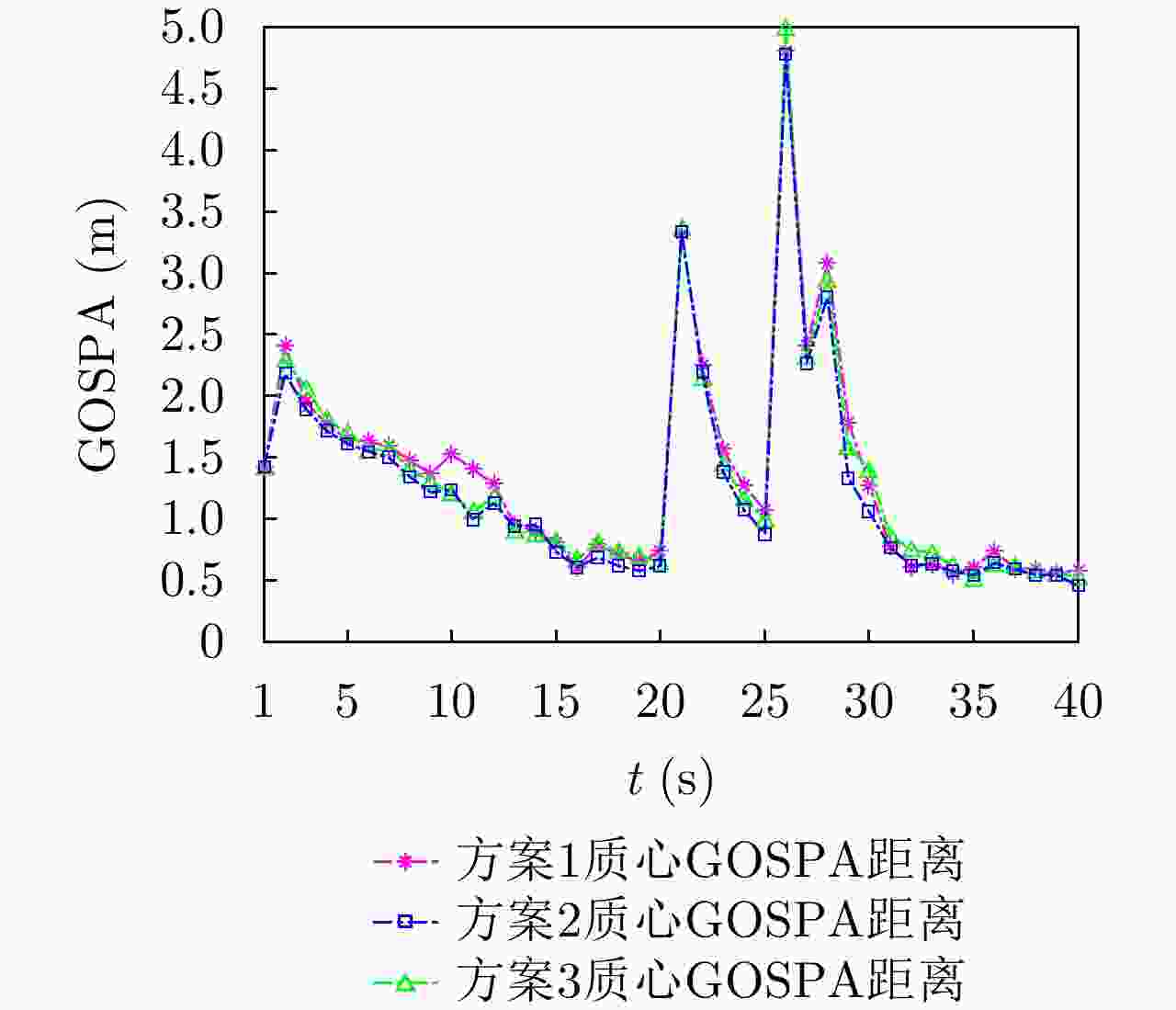
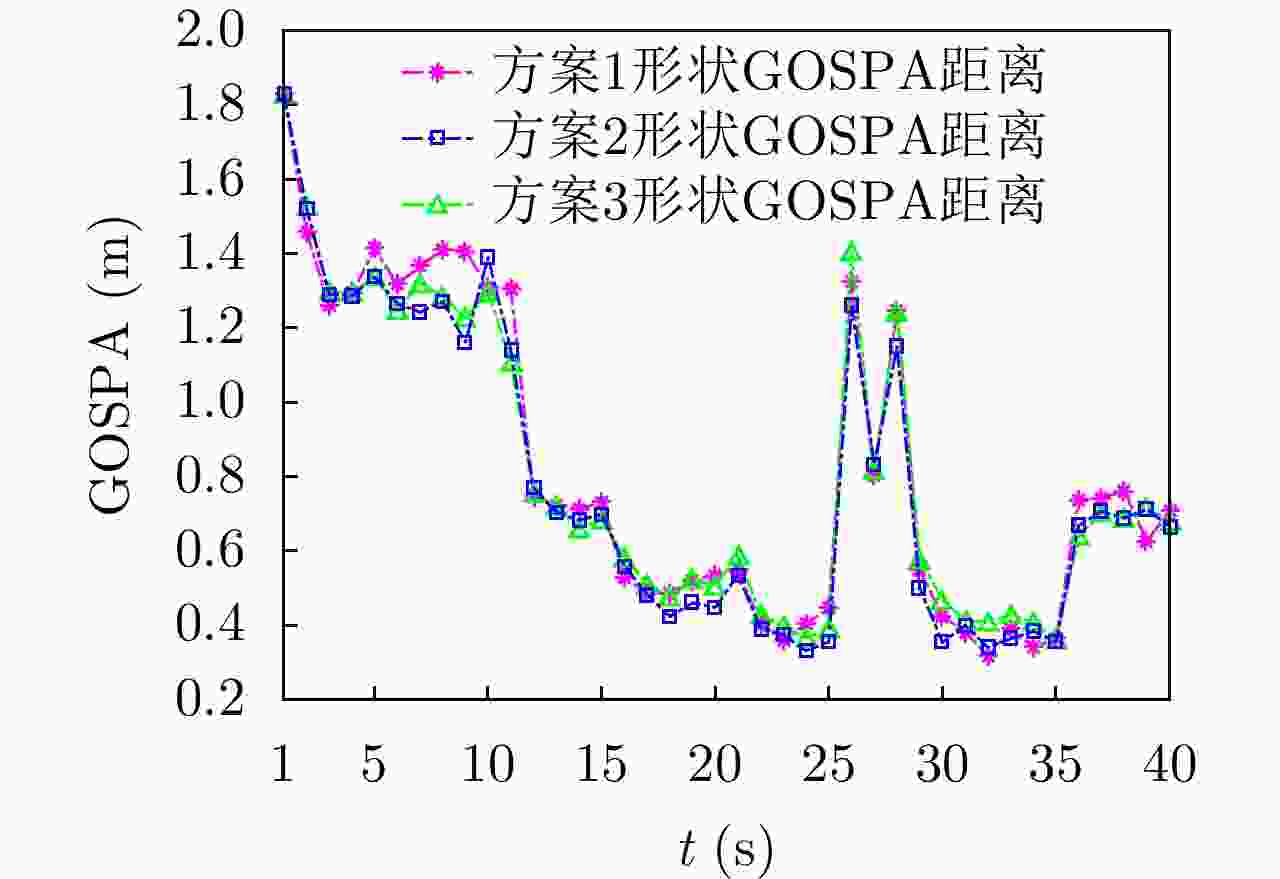
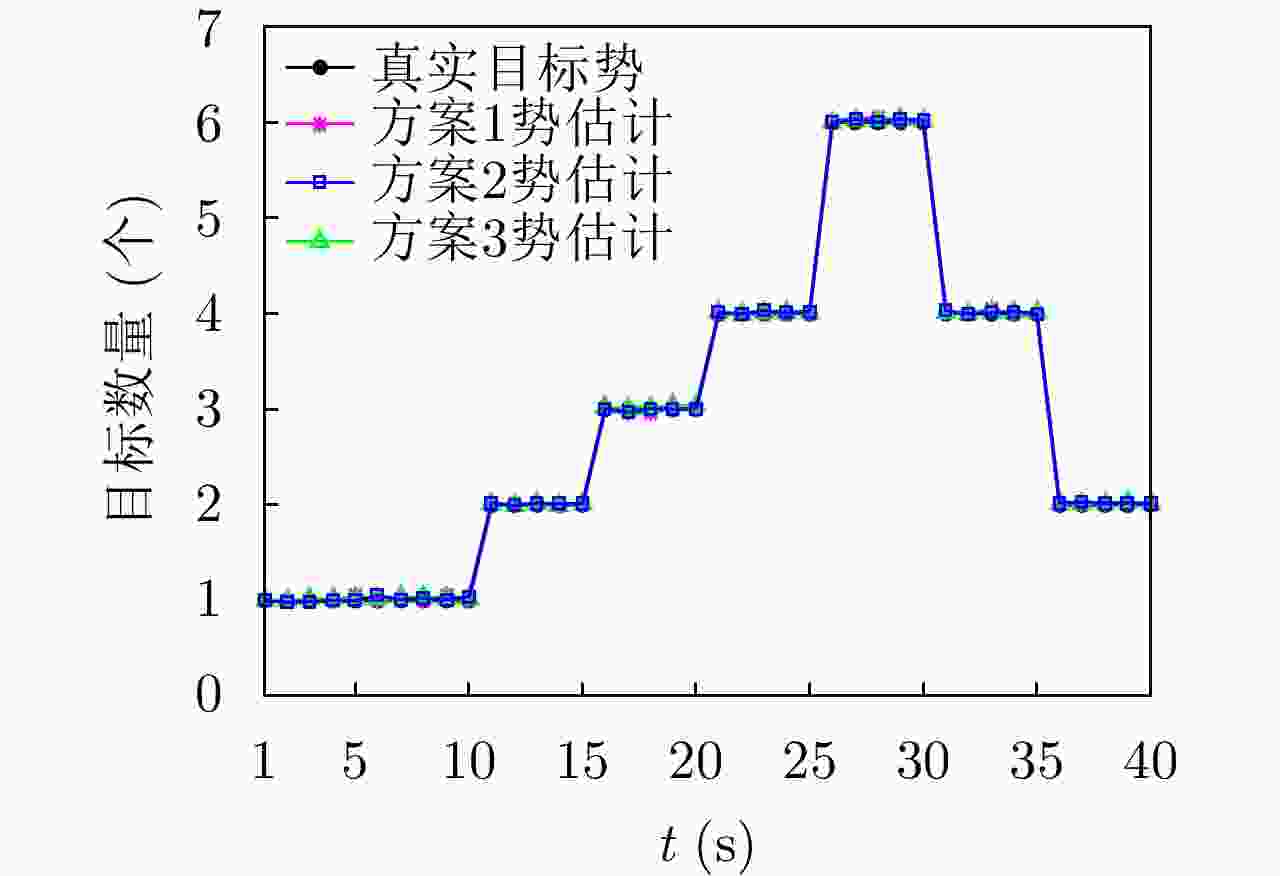
UAV Path Planning Strategy Based on Threat Avoidance in Multiple Extended Target Tracking Optimization

1.
College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
College of Automation Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China

Funds: The National Natural Science Foundation of China (62163023, 62173266, 62103318, 61873116), The Industrial Support Project of Education Department of Gansu Province (2021CYZC-02)

More Information

Corresponding author: CHEN Hui, huich78@hotmail.com

摘要

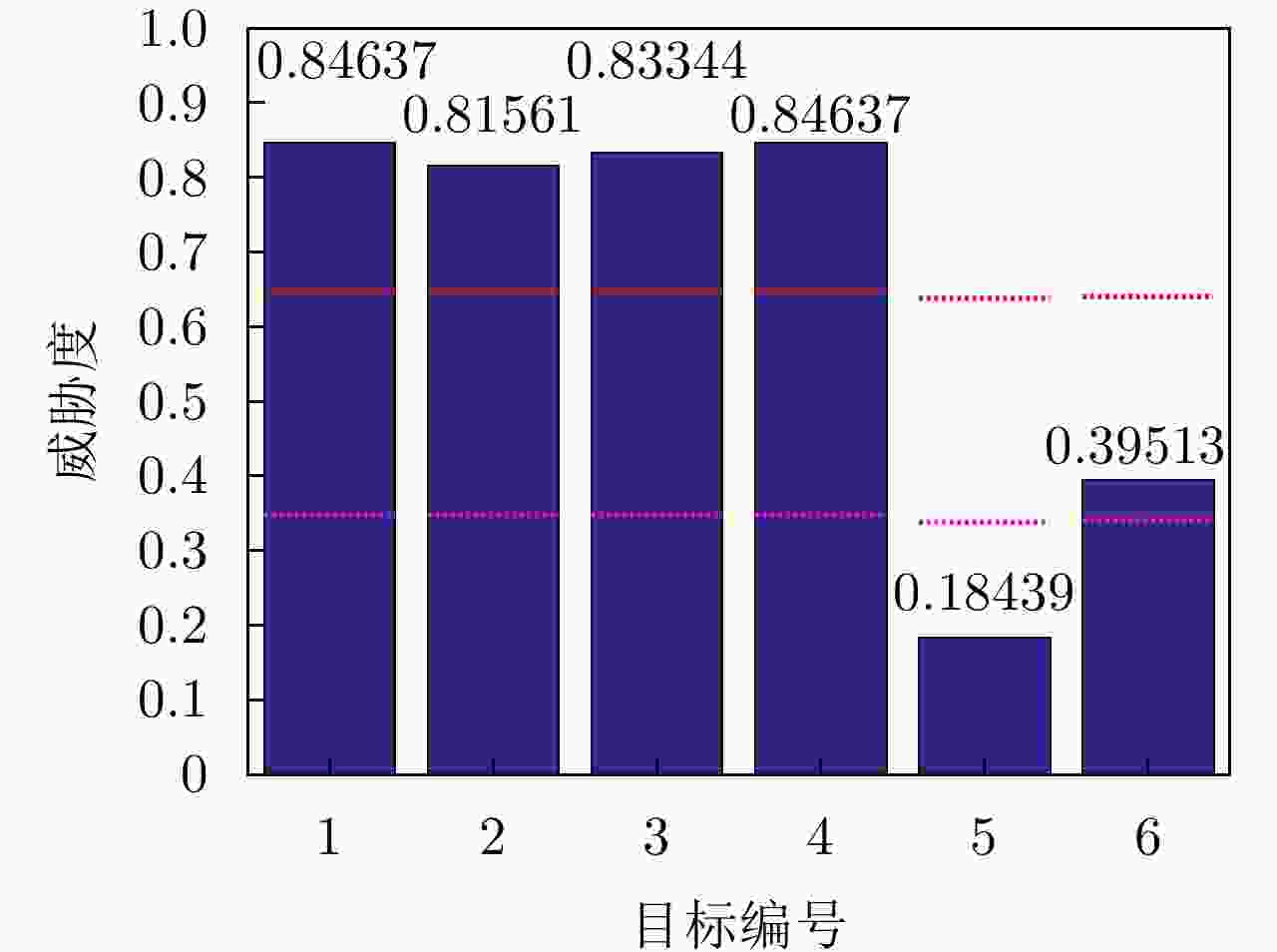
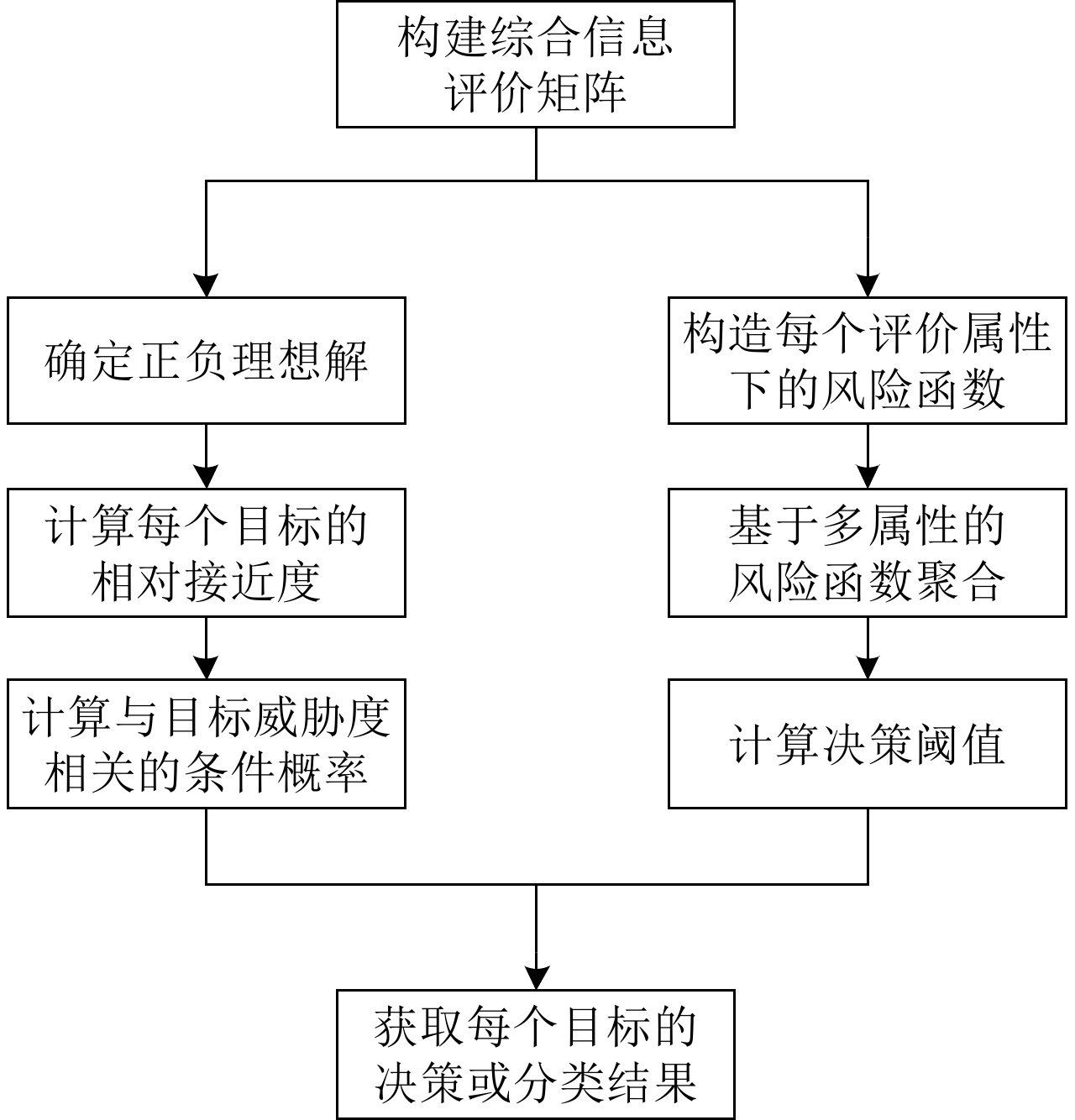
摘要: 为了降低无人机执行侦察任务时被摧毁的概率，该文提出一种有效减少威胁的路径规划算法。首先利用高分辨率机载雷达对多扩展目标进行稳健的跟踪估计，然后根据三向决策规则对各目标按威胁进行分类，并利用模糊理想解相似性排序技术(TOPSIS)的方法计算目标威胁度，综合多任务决策联合优化(联合评估目标威胁度和目标跟踪质量)作为评价准则对无人机进行路径规划。仿真实验表明，模糊威胁度评估方法在多扩展目标跟踪环境下是有效的，所提无人机路径规划算法是合理的，在不损失目标跟踪精度的条件下有效降低了目标威胁度。
- 路径规划 /
- 目标威胁度 /
- 三向决策规则 /
- 扩展目标跟踪
Abstract: To reduce the probability of UAV (Unmanned Aerial Vehicle) being destroyed during a reconnaissance mission, this study proposes an effective path planning algorithm to reduce the target threat. First, high-resolution airborne radar is used for robust tracking and estimation of multiple extended targets. Subsequently, the targets are classified based on the threat degree calculated via fuzzy TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution). Next, path planning of a UAV is performed considering joint optimization of multiple task decision-making (the joint evaluation of the target threat degree and target tracking performance) as an evaluation criterion. The simulation results indicate that the fuzzy threat assessment method is effective in multiple extended target tracking, and the proposed UAV path planning algorithm is reasonable. Thus the target threat is efficiently reduced without losing the tracking accuracy.
- Path planning /
- Target threat degree /
- Three-way decision rule /
- Extended target tracking

HTML全文

图 1 目标威胁评估过程

Figure 1. Target threat assessment process

下载: 全尺寸图片幻灯片

图 2 路径规划的基本原理图

Figure 2. Basic schematic diagram of path planning

下载: 全尺寸图片幻灯片

图 3 目标状态图示

Figure 3. Target status diagram

下载: 全尺寸图片幻灯片

图 4 目标威胁度评估

Figure 4. Target threat assessment

下载: 全尺寸图片幻灯片

图 5 目标实际轨迹与UAV原始轨迹

Figure 5. Actual target trajectory and UAV original trajectory

下载: 全尺寸图片幻灯片

图 6 穿越敌占区的UAV轨迹

Figure 6. UAV track crossing enemy occupied area

下载: 全尺寸图片幻灯片

图 7 完全自保的UAV轨迹

Figure 7. Fully self insured UAV trajectory

下载: 全尺寸图片幻灯片

图 8 MC实验中穿越敌占区的UAV轨迹分布

Figure 8. Trajectory distribution of UAV crossing enemy occupied area in MC experiment

下载: 全尺寸图片幻灯片

图 9 MC实验中完全自保的UAV轨迹分布

Figure 9. Trajectory distribution of fully self protected UAV in MC experiment

下载: 全尺寸图片幻灯片

图 10 目标威胁度评估统计均值

Figure 10. Statistical mean value of target threat assessment

下载: 全尺寸图片幻灯片

图 11 多扩展目标跟踪效果图

Figure 11. Multi-extended target tracking rendering

下载: 全尺寸图片幻灯片

图 12 目标质心位置GOSPA距离统计

Figure 12. GOSPA distance statistics of target centroid position

下载: 全尺寸图片幻灯片

图 13 目标形状(椭圆长短轴)估计GOSPA距离统计

Figure 13. Target shape (major and minor axes of ellipse) estimation GOSPA distance statistics

下载: 全尺寸图片幻灯片

图 14 多目标势估计

Figure 14. Multi-objective cardinality estimation

下载: 全尺寸图片幻灯片

表 1 分类风险函数

Table 1. Classification risk function

分类行为	$ A({\text{P}}) $	$ \neg A({\text{N}}) $
$ {a_{\text{P}}} $	$ {\lambda _{{\text{PP}}}} $	$ {\lambda _{{\text{PN}}}} $
$ {a_{\text{B}}} $	$ {\lambda _{{\text{BP}}}} $	$ {\lambda _{{\text{BN}}}} $
$ {a_{\text{N}}} $	$ {\lambda _{{\text{NP}}}} $	$ {\lambda _{{\text{NN}}}} $

下载: 导出CSV

表 2 GIW-MBer预测过程

Table 2. GIW-MBer prediction process

输入：${\boldsymbol{\zeta}} _{k - 1}^{\left( {i,j} \right)}$。
预测第j个GIW分量的参数：
${\boldsymbol{m}}_{k\|k - 1}^{\left( {i,j} \right)} = {\boldsymbol{F}}_{k\|k - 1}^i{\boldsymbol{m}}_{k - 1}^{\left( {i,j} \right)}$
${\boldsymbol{P}}_{k\|k - 1}^{\left( {i,j} \right)} = {\boldsymbol{F}}_{k\|k - 1}^i{\boldsymbol{P}}_{k - 1}^{\left( {i,j} \right)}{\left( {{\boldsymbol{F}}_{k\|k - 1}^i} \right)^{\rm T} } + {{\boldsymbol{Q}}_k}$
$v_{k\|k - 1}^{\left( {i,j} \right)} = {{\rm{e}}^{ - \frac{ { {T_s} } }{\tau } } }v_{k - 1}^{\left( {i,j} \right)}$，其中$ \tau $为时间衰减常数
${\boldsymbol{V} }_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {v_{k\|k - 1}^{\left( {i,j} \right)} - d - 1} }{ {v_{k - 1}^{\left( {i,j} \right)} - d - 1} }{\boldsymbol{V}}_{k - 1}^{\left( {i,j} \right)}$
${\boldsymbol{X}}_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {{\boldsymbol{V}}_{k\|k - 1}^{\left( {i,j} \right)} } }{ {v_{k\|k - 1}^{\left( {i,j} \right)} - 2d - 2} }$
输出：${\boldsymbol{\zeta}} _{k\|k - 1}^{\left( {i,j} \right)}$。

下载: 导出CSV

表 3 GIW-MBer更新过程

Table 3. GIW-MBer update process

输入：${\boldsymbol{\zeta}} _{k\|k - 1}^{\left( {i,j} \right)}$，量测集划分W。
更新第j个GIW分量的参数：　　　　$\bar {\boldsymbol{z} }_k^{\boldsymbol{W} } = \dfrac{1}{ {\left\| {\boldsymbol{W} } \right\|} }\displaystyle\sum\limits_{{\boldsymbol{z}}_k^{\left( i \right)} \in {\boldsymbol{W}}} { {\boldsymbol{z} }_k^{\left( i \right)} }$
${\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ { {\boldsymbol{V} }_{k\|k - 1}^{\left( {i,j} \right)} } }{ {v_{k\|k - 1}^{\left( {i,j} \right)} - 2d - 2} }$
${\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,W} \right)} = { {\boldsymbol{H} }_k}{\boldsymbol{P} }_{k\|k - 1}^{\left( {i,j} \right)}{\boldsymbol{H} }_k^{\text{T} } + \dfrac{ { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } }{ {\left\| {\boldsymbol{W} } \right\|} }$
${\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} = {\boldsymbol{P}}_{k\|k - 1}^{\left( {i,j} \right)}{\boldsymbol{H}}_k^{\text{T} }{\left( {{\boldsymbol{S}}_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} } \right)^{ - 1} }$
${\boldsymbol{\varepsilon} } _{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} = \bar {\boldsymbol{z} }_k^{\boldsymbol{W} } - { {\boldsymbol{H} }_k}{\boldsymbol{m} }_{k\|k - 1}^{\left( {i,j} \right)}$
${\boldsymbol{m}}_k^{\left( {i,j} \right)} = {\boldsymbol{m}}_{k\|k - 1}^{\left( {i,j} \right)} + {\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)}{\boldsymbol{\varepsilon}} _{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)}$
${\boldsymbol{P} }_k^{\left( {i,j} \right)} = {\boldsymbol{P} }_{k\|k - 1}^{\left( {i,j} \right)} - {\boldsymbol{K} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)}{\boldsymbol{S}}_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)}{\left( { {\boldsymbol{K} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} } \right)^{\text{T} } }$ 　　　　${\boldsymbol{Z} }_k^{\boldsymbol{W}} = \displaystyle\sum\limits_{ {\boldsymbol{z} }_k^{\left( i \right)} \in {\boldsymbol{W} } } {\left( { {\boldsymbol{z} }_k^{\left( i \right)} - \bar {\boldsymbol{z} }_k^{\boldsymbol{W}}} \right){ {\left( { {\boldsymbol{z} }_k^{\left( i \right)} - \bar {\boldsymbol{z} }_k^{\boldsymbol{W}}} \right)}^{\text{T} } } }$
$\begin{aligned} {\boldsymbol{N} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} =& {\left( { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } \right)^{\frac{1}{2} } }{\left( { {\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} } \right)^{ - \frac{1}{2} } }{\boldsymbol{\varepsilon} } _{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} \\ & \times {\left( { {\boldsymbol{\varepsilon} } _{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} } \right)^{\text{T} } }{\left( { {\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} } \right)^{ - \frac{ {\text{T} } }{2} } }{\left( { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } \right)^{\frac{ {\text{T} } }{2} } } \end{aligned}$
$v_k^{\left( {i,j,{\boldsymbol{W}}} \right)} = v_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} + \left\| {\boldsymbol{W} } \right\|$
${\boldsymbol{V} }_k^{\left( {i,j,{\boldsymbol{W} } } \right)} = {\boldsymbol{V} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W} } } \right)} + {\boldsymbol{N} }_{k\|k - 1}^{\left( {i,j,{\boldsymbol{W}}} \right)} + {\boldsymbol{Z} }_k^{\boldsymbol{W} }$
${\boldsymbol{X} }_k^{\left( {i,j,{\boldsymbol{W} } } \right)} = \dfrac{ { {\boldsymbol{V} }_k^{\left( {i,j,{\boldsymbol{W} } } \right)} } }{ {v_k^{\left( {i,j,{\boldsymbol{W} } } \right)} - 2d - 2} }$
输出：${\boldsymbol{\zeta}} _k^{\left( {i,j} \right)}$。

下载: 导出CSV

表 4 基于威胁规避的UAV路径规划算法

Table 4. UAV path planning algorithm for threat avoidance

输入：$ k - 1 $时刻多扩展目标多特征信息${{\boldsymbol{\zeta}} _{k - 1} }$与UAV坐标　　　${{\boldsymbol{x}}_{s,k - 1} }$，其中${{\boldsymbol{\zeta}} _{k - 1} } = \left\{ { { {\boldsymbol{m} }_{k - 1} },{ {\boldsymbol{P} }_{k - 1} },{v_{k - 1} },{ {\boldsymbol{V} }_{k - 1} } } \right\}$。
步骤1 多扩展目标跟踪的预测过程，得到$ {f_{k\|k - 1}}\left( { \cdot \| \cdot } \right) $。　步骤2 路径规划：
${\hat {\boldsymbol{\xi}} _{k\|k - 1} } = {\text{Sfun} }\left\{ { {f_{k\|k - 1} }\left( { \cdot \| \cdot } \right)} \right\}$，
确定所有可能的路径规划方案${{\boldsymbol{C}}_k}$。
${\text{for all } }c \in {{\boldsymbol{C}}_k}{\text{ do} }$
生成PIMS：${{\boldsymbol{Z}}_k}\left( u \right)$，
量测集划分：${\boldsymbol{\rho}} \angle {{\boldsymbol{Z}}_k}\left( u \right)$，
计算伪更新后验密度$ {f_{k,c}}\left( { \cdot \| \cdot } \right) $，
提取状态的统计平均：${\hat {\boldsymbol{\xi}} _{k,c} } \leftarrow {\text{Sfun} }\left\{ { {f_{k,c} }\left( { \cdot \| \cdot } \right)} \right\}$，
计算$\mathcal{D}\left( { {{\boldsymbol{\xi}} _{k,c} },{ {\bar {\boldsymbol{\xi}} }_{k,c} } } \right)$和$ \mathcal{V}\left( c \right) $。
$ {\text{end for}} $ 　　　　求解控制方案：${\hat c_k} = \mathop {\arg \min }\limits_{c \in {{\boldsymbol{C}}_k} } \{ {w_\mathcal{V} }\mathcal{V}\left( c \right)$ 　　　　$+ {w_\mathcal{D} }\mathcal{D}({{\boldsymbol{\xi}} _{k,c} },{\bar {\boldsymbol{\xi}} _{k,c} })\}$。
步骤3 多扩展目标跟踪的更新过程，得到$ {f_{k\|k}}\left( { \cdot \| \cdot } \right) $。
步骤4 提取多扩展目标状态信息${{\boldsymbol{\xi}} _k}$，计算目标势${N_k} = \left\| { {{\boldsymbol{\xi}} _k} } \right\|$。
输出：k时刻UAV坐标${{\boldsymbol{x}}_{s,k} }$，目标势$ {N_k} $，多扩展目标状态集${{\boldsymbol{\xi}} _k}$。

下载: 导出CSV

表 5 硬件配置

Table 5. Hardware configuration

参数	数值
CPU主频	3.1 GHz
最高睿频	5.2 GHz
内存类型	DDR4 3200 MHz
最大内存带宽	76.8 GB/s

下载: 导出CSV

表 6 目标状态

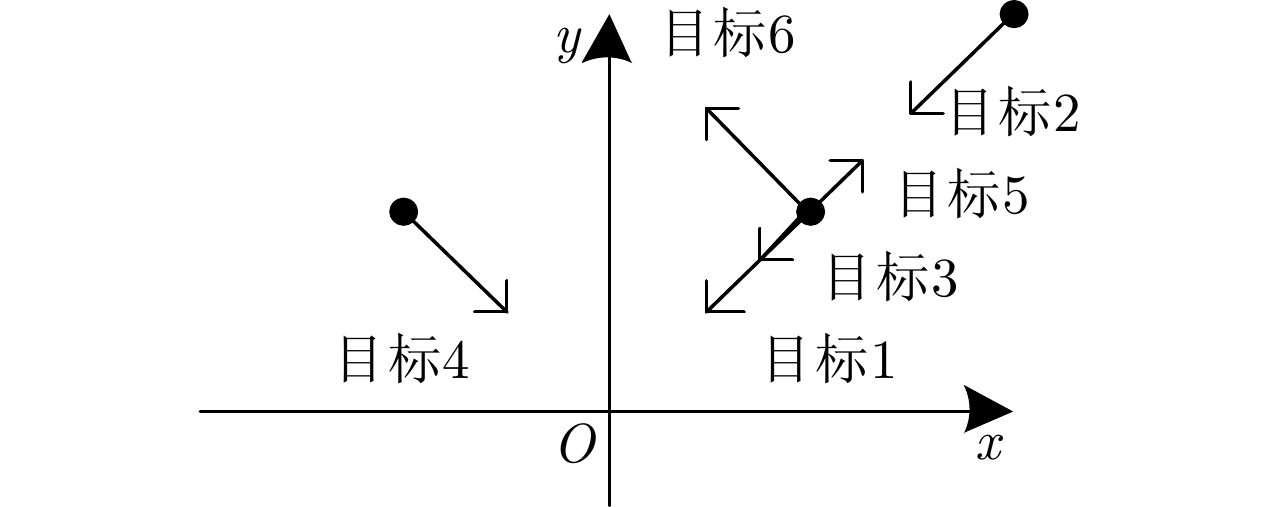
Table 6. Target status

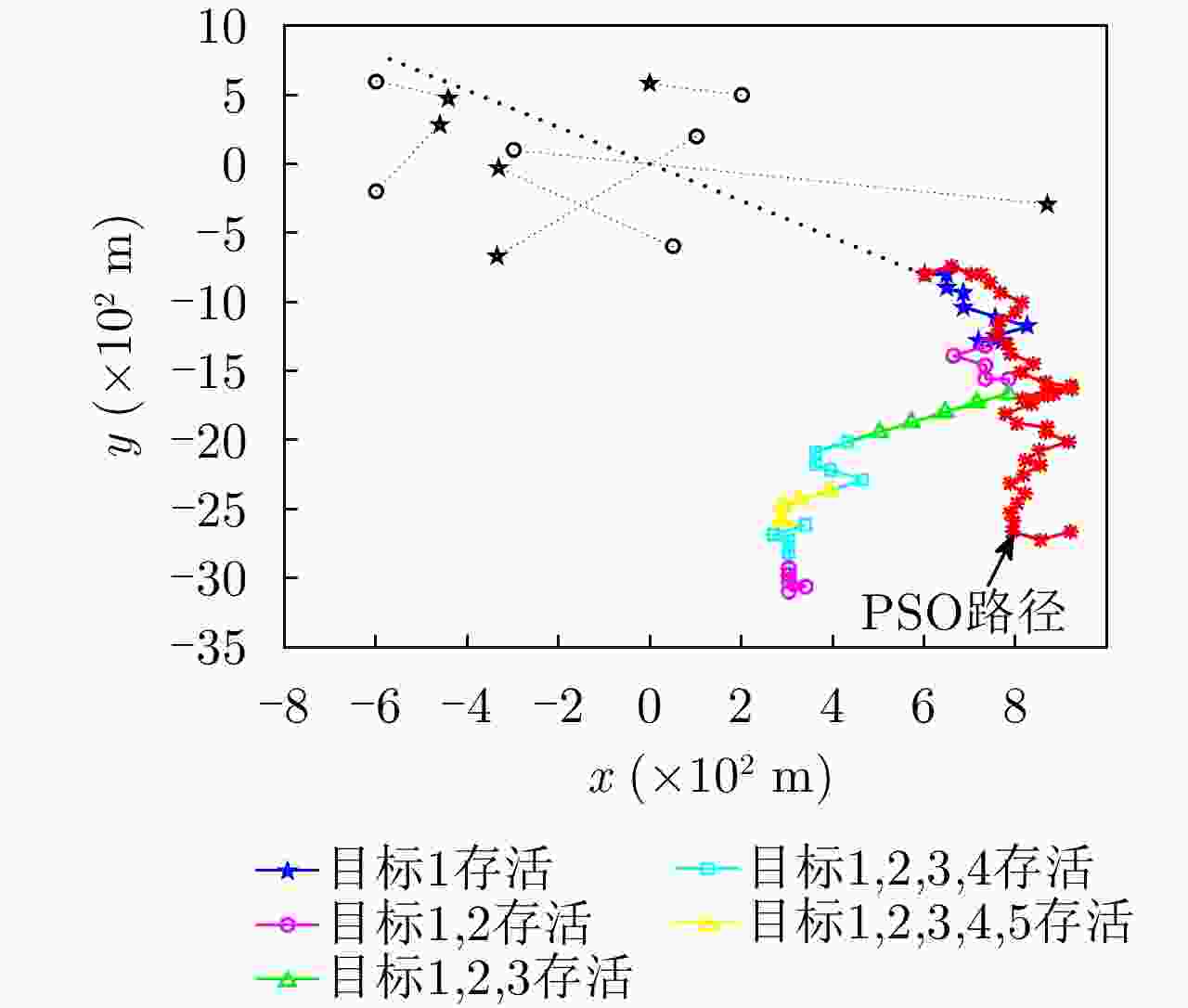
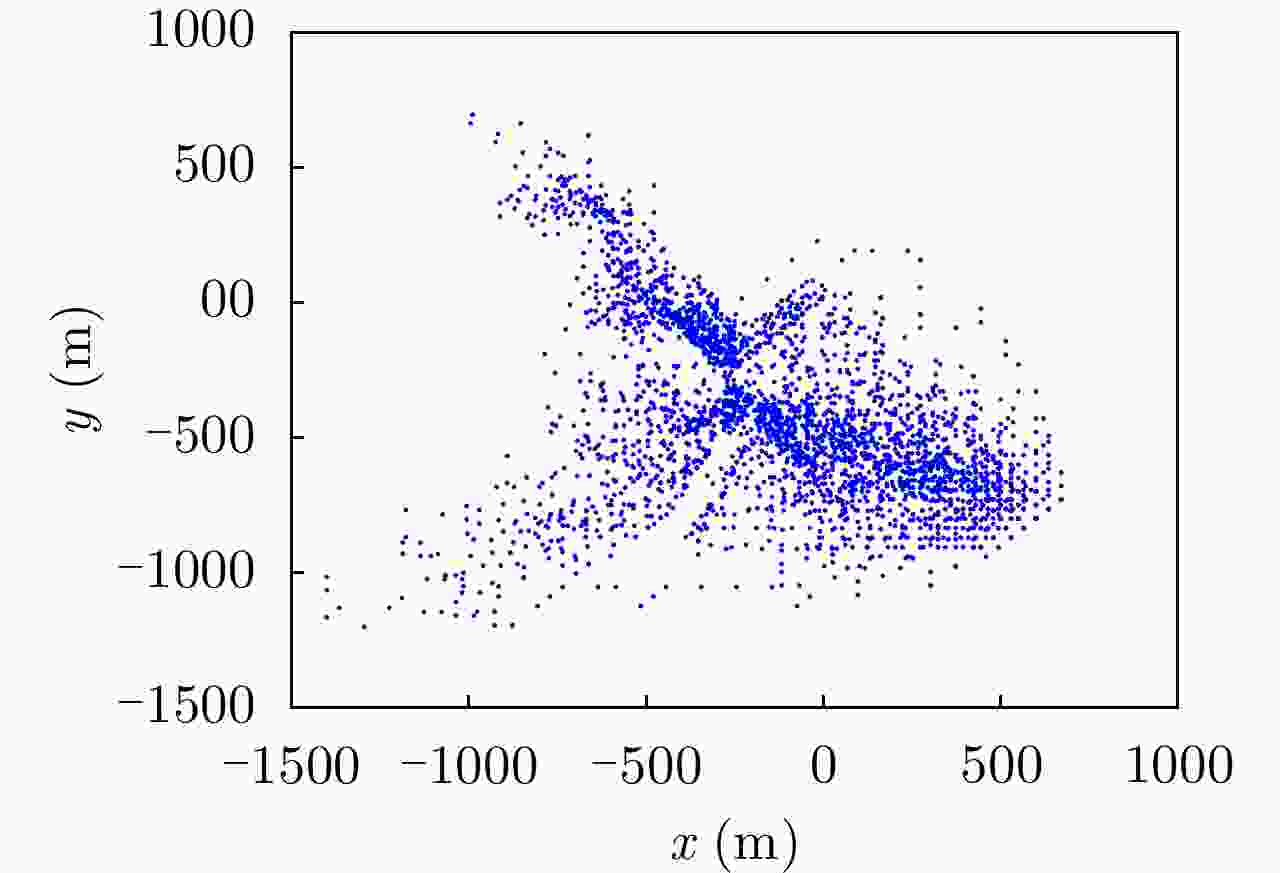
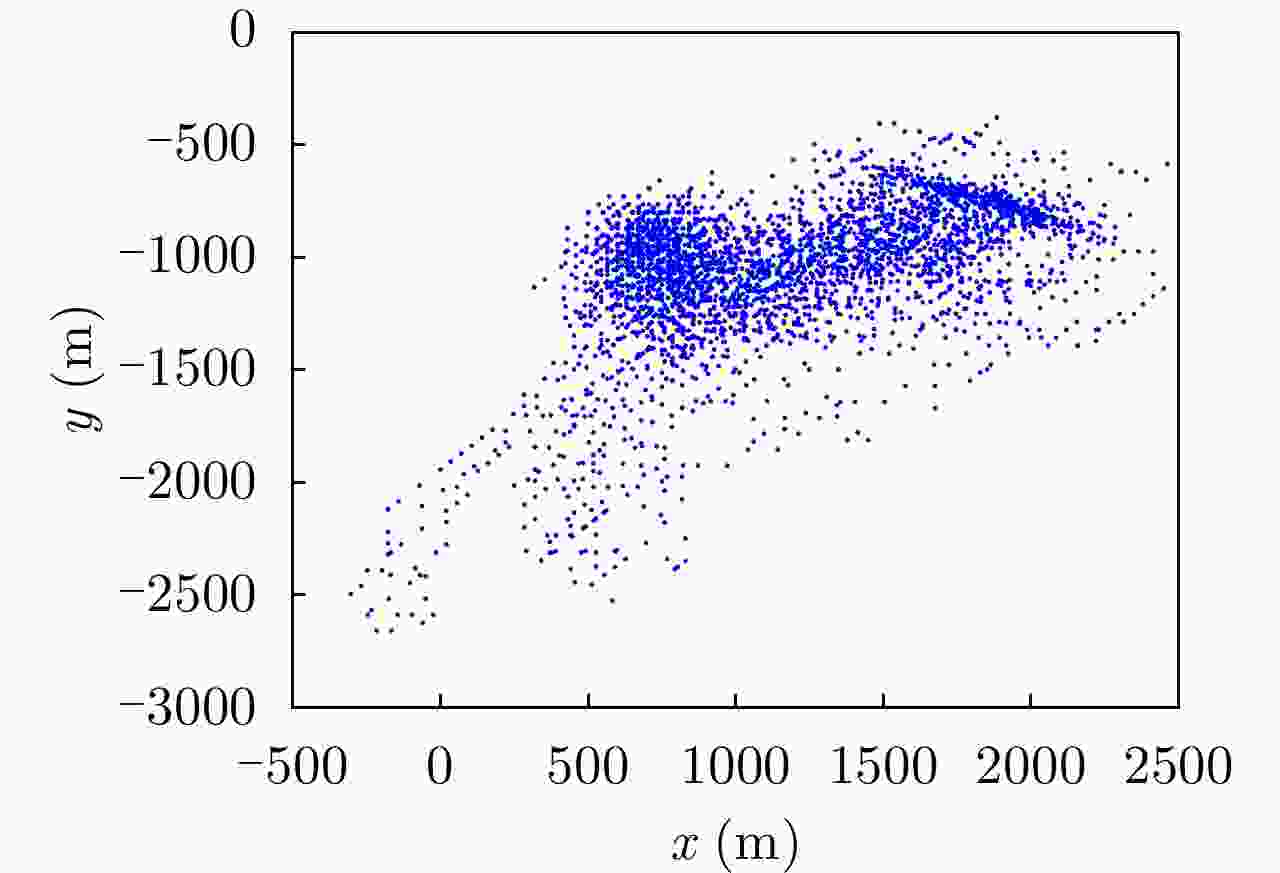
目标编号	位置(m; m)	速度(m/s; m/s)	运动方向(°)
1	[100; 100]	[–10; –10]	0
2	[200; 200]	[–10; –10]	0
3	[100; 100]	[–5; –5]	0
4	[–100; 100]	[10; –10]	0
5	[100; 100]	[5; 5]	180
6	[100; 100]	[–10; 10]	90

下载: 导出CSV

表 7 各运动体的初始状态

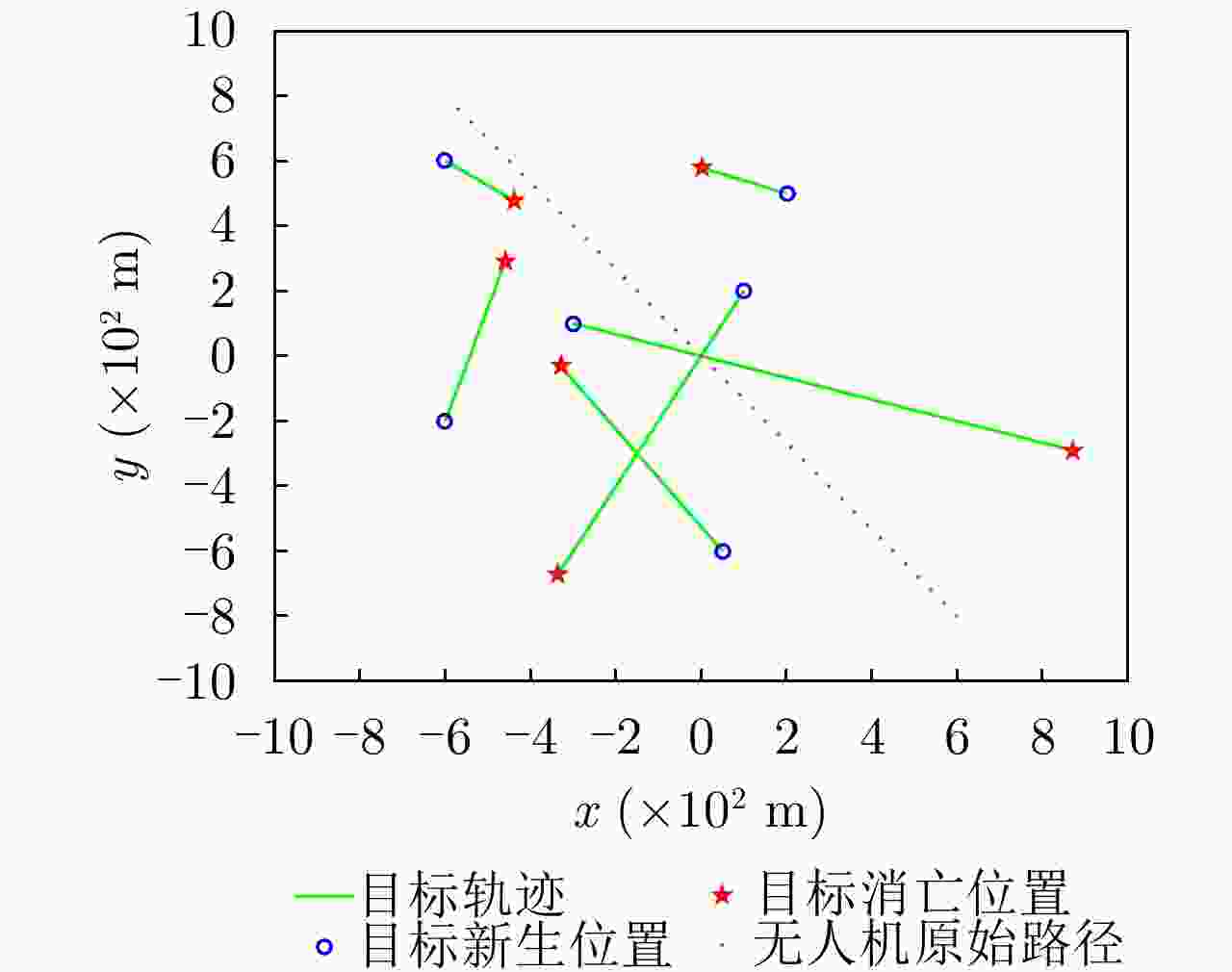
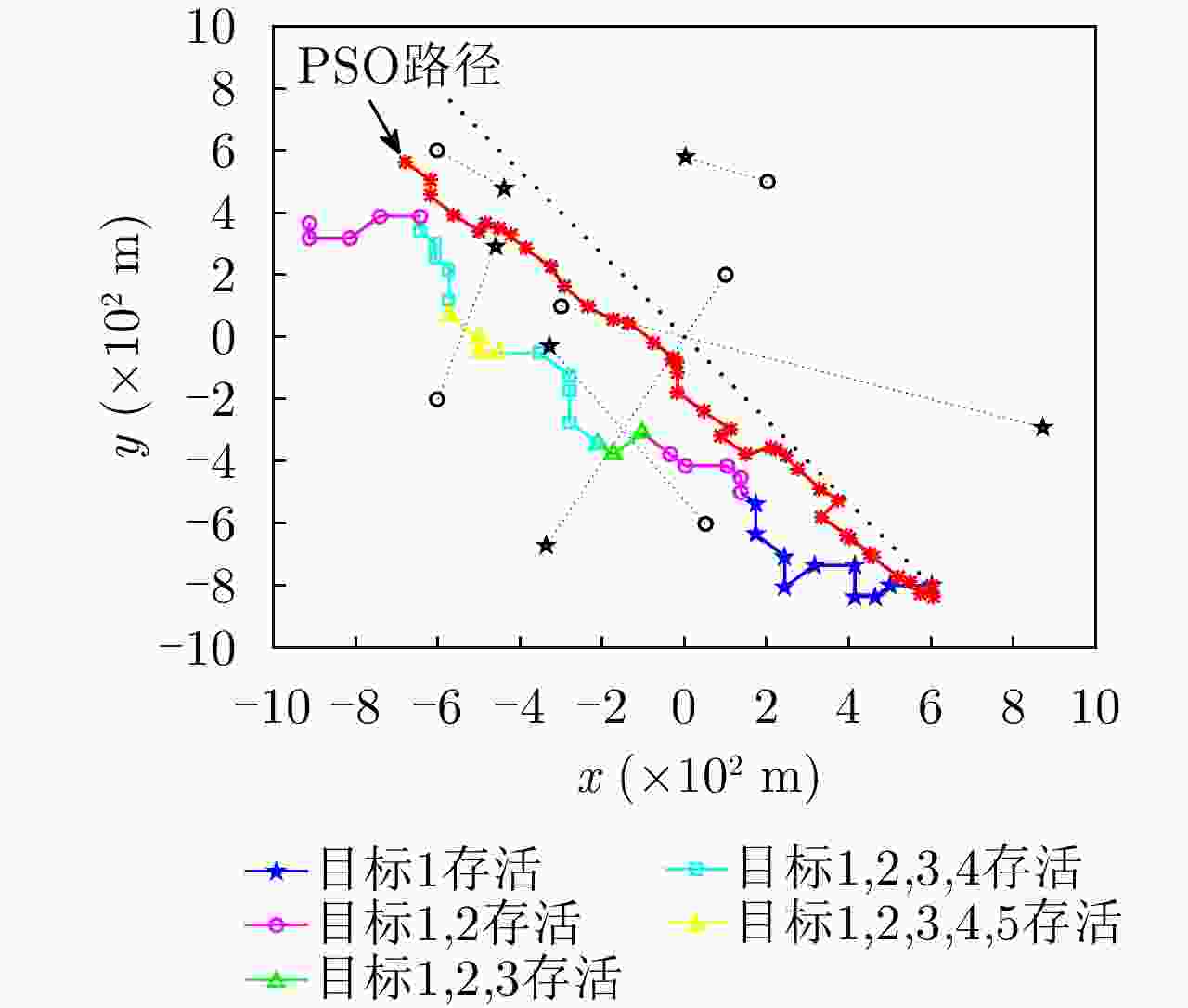
Table 7. Initial state of each moving object

目标	出生时刻 (s)	消亡时刻 (s)	初始状态 (m; m; m/s; m/s)
目标1	1	40	[–300; 100; 30; –10]
目标2	11	40	[100; 200; –15; –30]
目标3	16	35	[50; –600; –20; 30]
目标4	21	35	[–600; –200; 10; 35]
目标5	26	30	[200; 500; –50; 20]
目标6	26	30	[–600; 600; 40; –30]
UAV	/	/	[600; –800; –30; 40]

下载: 导出CSV

参考文献(43)

[1]	AGGARWAL S and KUMAR N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges[J]. Computer Communications, 2020, 149: 270–299. doi: 10.1016/j.comcom.2019.10.014
[2]	BAYERLEIN H, THEILE M, CACCAMO M, et al. Multi-UAV path planning for wireless data harvesting with deep reinforcement learning[J]. IEEE Open Journal of the Communications Society, 2021, 2: 1171–1187. doi: 10.1109/OJCOMS.2021.3081996
[3]	BOLOURIAN N and HAMMAD A. LiDAR-equipped UAV path planning considering potential locations of defects for bridge inspection[J]. Automation in Construction, 2020, 117: 103250. doi: 10.1016/j.autcon.2020.103250
[4]	BASIRI A, MARIANI V, SILANO G, et al. A survey on the application of path-planning algorithms for multi-rotor UAVs in precision agriculture[J]. Journal of Navigation, 2022, 75(2): 364–383. doi: 10.1017/S0373463321000825
[5]	KARUR K, SHARMA N, DHARMATTI C, et al. A survey of path planning algorithms for mobile robots[J]. Vehicles, 2021, 3(3): 448–468. doi: 10.3390/vehicles3030027
[6]	REN Tianzhu, ZHOU Rui, XIA Jie, et al. Three-dimensional path planning of UAV based on an improved A algorithm[C]. 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 2016: 140–145.
[7]	SARANYA C, UNNIKRISHNAN M, ALI S A, et al. Terrain based D* algorithm for path planning[J]. IFAC-PapersOnLine, 2016, 49(1): 178–182. doi: 10.1016/j.ifacol.2016.03.049
[8]	MAUROVIĆ I, SEDER M, LENAC K, et al. Path planning for active SLAM based on the D* algorithm with negative edge weights[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 48(8): 1321–1331. doi: 10.1109/TSMC.2017.2668603
[9]	RUZ J J, AREVALO O, DE LA CRUZ J M, et al. Using MILP for UAVs trajectory optimization under radar detection risk[C]. 2006 IEEE Conference on Emerging Technologies and Factory Automation, Prague, Czech Republic, 2006: 957–960.
[10]	PEHLIVANOGLU Y V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV[J]. Aerospace Science and Technology, 2012, 16(1): 47–55. doi: 10.1016/j.ast.2011.02.006
[11]	PHUNG M D and HA Q P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization[J]. Applied Soft Computing, 2021, 107: 107376. doi: 10.1016/j.asoc.2021.107376
[12]	KONATOWSKI S. Application of the ACO algorithm for UAV path planning[J]. Przeglad Elektrotechniczny, 2019, 1(7): 117–121. doi: 10.15199/48.2019.07.24
[13]	周彬, 郭艳, 李宁, 等. 基于导向强化Q学习的无人机路径规划[J]. 航空学报, 2021, 42(9): 325109. doi: 10.7527/S1000-6893.2021.25109 ZHOU Bin, GUO Yan, LI Ning, et al. Path planning of UAV using guided enhancement Q-learning algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(9): 325109. doi: 10.7527/S1000-6893.2021.25109
[14]	XU Liang and NIU Ruixin. Tracking visual object as an extended target[C]. 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, USA, 2021: 664–668.
[15]	陈辉, 杜金瑞, 韩崇昭. 基于星凸形随机超曲面模型多扩展目标多伯努利滤波器[J]. 自动化学报, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130 CHEN Hui, DU Jinrui, and HAN Chongzhao. A multiple extended target multi-bernouli filter based on star-convex random hypersurface model[J]. Acta Automatica Sinica, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130
[16]	KHALKHALI M B, VAHEDIAN A, and YAZDI H S. Multi-target state estimation using interactive Kalman filter for multi-vehicle tracking[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(3): 1131–1144. doi: 10.1109/TITS.2019.2902664
[17]	KIM D Y, VO B N, VO B T, et al. A labeled random finite set online multi-object tracker for video data[J]. Pattern Recognition, 2019, 90: 377–389. doi: 10.1016/j.patcog.2019.02.004
[18]	MAHLER R P S. Advances in Statistical Multisource-Multitarget Information Fusion[M]. Boston, USA: Artech House, 2014: 825–860.
[19]	MAHLER R P S. Statistical Multisource-Multitarget Information Fusion[M]. Boston, USA: Artech House, 2007: 655–667.
[20]	杨威, 付耀文, 龙建乾, 等. 基于有限集统计学理论的目标跟踪技术研究综述[J]. 电子学报, 2012, 40(7): 1440–1448. doi: 10.3969/j.issn.0372-2112.2012.07.025 YANG Wei, FU Yaowen, LONG Jianqian, et al. The FISST-based target tracking techniques: A survey[J]. Acta Electronica Sinica, 2012, 40(7): 1440–1448. doi: 10.3969/j.issn.0372-2112.2012.07.025
[21]	MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic systems, 2003, 39(4): 1152–1178. doi: 10.1109/TAES.2003.1261119
[22]	VO B N, SINGH S, and DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224–1245. doi: 10.1109/TAES.2005.1561884
[23]	VO B N and MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104. doi: 10.1109/TSP.2006.881190
[24]	VO B T, VO B N, and CANTONI A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409–423. doi: 10.1109/TSP.2008.2007924
[25]	VO B T and VO B N. Labeled random finite sets and multi-object conjugate priors[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3460–3475. doi: 10.1109/TSP.2013.2259822
[26]	VO B N, VO B T, and PHUNG D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6554–6567. doi: 10.1109/TSP.2014.2364014
[27]	REUTER S, VO B T, VO B N, et al. The labeled multi-Bernoulli filter[J]. IEEE Transactions on Signal Processing, 2014, 62(12): 3246–3260. doi: 10.1109/TSP.2014.2323064
[28]	BAUM M and HANEBECK U D. Random hypersurface models for extended object tracking[C]. 2009 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 2009: 178–183.
[29]	THORMANN K, BAUM M, and HONER J. Extended target tracking using Gaussian processes with high-resolution automotive radar[C]. 2018 21st International Conference on Information Fusion (FUSION), Cambridge, United Kingdom, 2018: 1764–1770.
[30]	KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042–1059. doi: 10.1109/TAES.2008.4655362
[31]	FELDMANN M, FRÄNKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409–1420. doi: 10.1109/TSP.2010.2101064
[32]	张银燕, 李弼程. 基于MIN-MAX云重心推理的目标威胁评估方法[J]. 系统仿真学报, 2014, 26(2): 411–418. doi: 10.16182/j.cnki.joss.2014.02.041 ZHANG Yinyan and LI Bicheng. Method of target threat assessment based on cloudy MIN-MAX center of gravity reasoning[J]. Journal of System Simulation, 2014, 26(2): 411–418. doi: 10.16182/j.cnki.joss.2014.02.041
[33]	李特, 冯琦, 张堃. 基于熵权灰色关联和D-S证据理论的威胁评估[J]. 计算机应用研究, 2013, 30(2): 380–382. doi: 10.3969/j.issn.1001-3695.2013.02.016 LI Te, FENG Qi, and ZHANG Kun. Threat assessment based on entropy weight grey incidence and D-S theory of evidence[J]. Application Research of Computers, 2013, 30(2): 380–382. doi: 10.3969/j.issn.1001-3695.2013.02.016
[34]	高晓光, 李青原, 邸若海. 基于DBN威胁评估的MPC无人机三维动态路径规划[J]. 系统工程与电子技术, 2014, 36(11): 2199–2205. doi: 10.3969/j.issn.1001-506X.2014.11.14 GAO Xiaoguang, LI Qingyuan, and DI Ruohai. MPC three-dimensional dynamic path planning for UAV based on DBN threat assessment[J]. Systems Engineering and Electronics, 2014, 36(11): 2199–2205. doi: 10.3969/j.issn.1001-506X.2014.11.14
[35]	张堃, 王雪, 张才坤, 等. 基于IFE动态直觉模糊法的空战目标威胁评估[J]. 系统工程与电子技术, 2014, 36(4): 697–701. doi: 10.3969/j.issn.1001-506X.2014.04.15 ZHANG Kun, WANG Xue, ZHANG Caikun, et al. Evaluating and sequencing of air target threat based on IFE and dynamic intuitionistic fuzzy sets[J]. Systems Engineering and Electronics, 2014, 36(4): 697–701. doi: 10.3969/j.issn.1001-506X.2014.04.15
[36]	GAO Yang, LI Dongsheng, and ZHONG Hua. A novel target threat assessment method based on three-way decisions under intuitionistic fuzzy multi-attribute decision making environment[J]. Engineering Applications of Artificial Intelligence, 2020, 87: 103276. doi: 10.1016/j.engappai.2019.103276
[37]	WANG Yi, LIU Sanyang, NIU Wei, et al. Threat assessment method based on intuitionistic fuzzy similarity measurement reasoning with orientation[J]. China Communications, 2014, 11(6): 119–128. doi: 10.1109/CC.2014.6879010
[38]	王小艺, 刘载文, 侯朝桢, 等. 基于模糊多属性决策的目标威胁估计方法[J]. 控制与决策, 2007, 22(8): 859–863. doi: 10.3321/j.issn:1001-0920.2007.08.004 WANG Xiaoyi, LIU Zaiwen, HOU Chaozhen, et al. Method of object threat assessment based on fuzzy MADM[J]. Control and Decision, 2007, 22(8): 859–863. doi: 10.3321/j.issn:1001-0920.2007.08.004
[39]	GRANSTRÖM K, FATEMI M, and SVENSSON L. Gamma Gaussian inverse-Wishart Poisson multi-Bernoulli filter for extended target tracking[C]. 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 2016: 893–900.
[40]	连峰, 马冬冬, 元向辉, 等. 扩展目标CBMeMBer滤波器及其高斯混合实现[J]. 控制与决策, 2015, 30(4): 611–616. doi: 10.13195/j.kzyjc.2014.0286 LIAN Feng, MA Dongdong, YUAN Xianghui, et al. CBMeMBer filter for extended targets and its Gaussian mixture implementations[J]. Control and Decision, 2015, 30(4): 611–616. doi: 10.13195/j.kzyjc.2014.0286
[41]	GOSTAR A K, HOSEINNEZHAD R, BAB-HADIASHAR A, et al. Sensor-management for multitarget filters via minimization of posterior dispersion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2877–2884. doi: 10.1109/TAES.2017.2718280
[42]	RAHMATHULLAH A S, GARCÍA-FERNÁNDEZ Á F, and SVENSSON L. Generalized optimal sub-pattern assignment metric[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–8.
[43]	LUNDQUIST C, GRANSTRÖM K, and ORGUNER U. An extended target CPHD filter and a gamma Gaussian inverse Wishart implementation[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 472–483. doi: 10.1109/JSTSP.2013.2245632