作者中心
专家审稿
责编办公
编辑办公
Modification and Compensation of the Line-of-Sight Motion Error for Multirotor UAV SAR
-
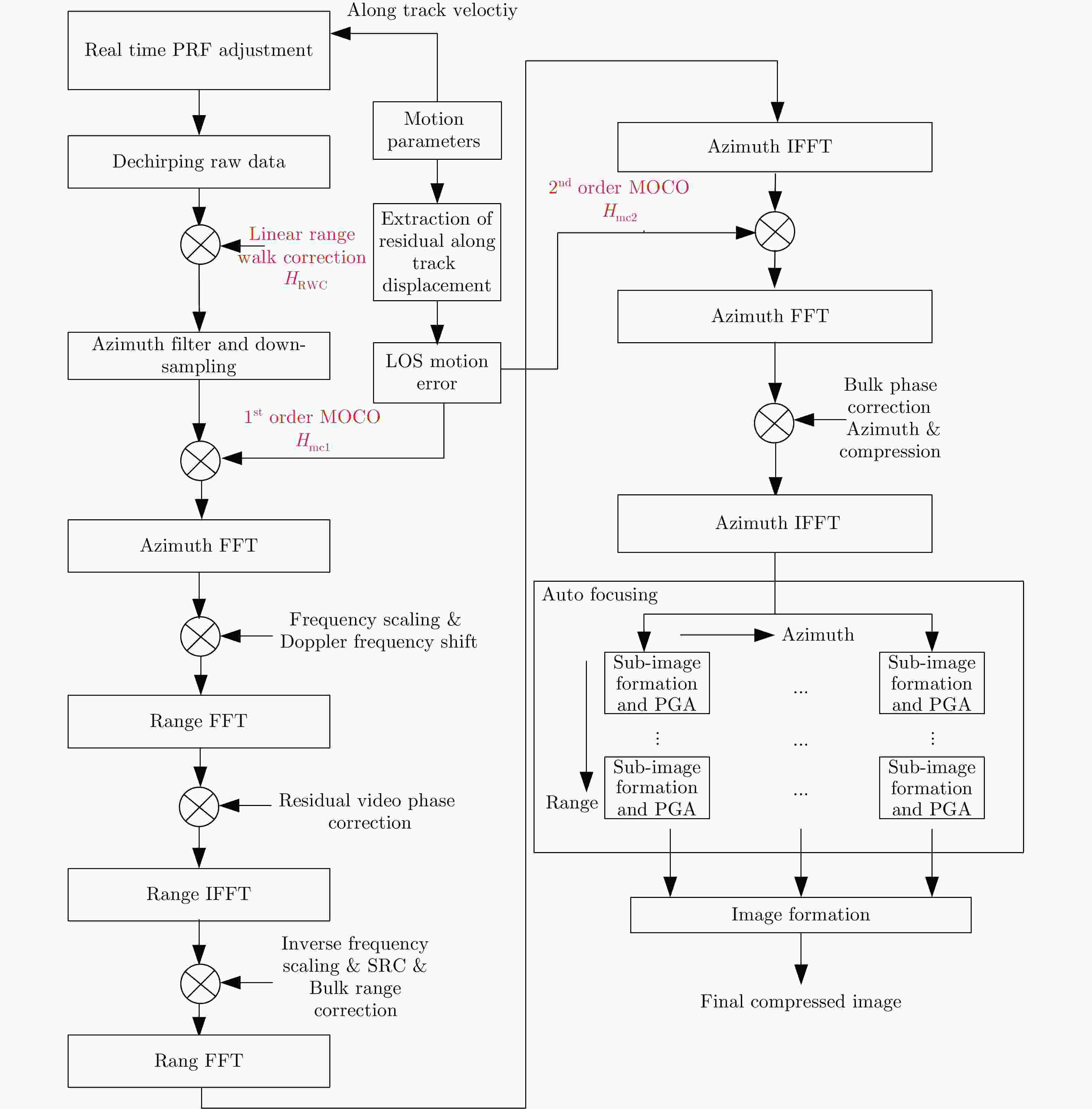
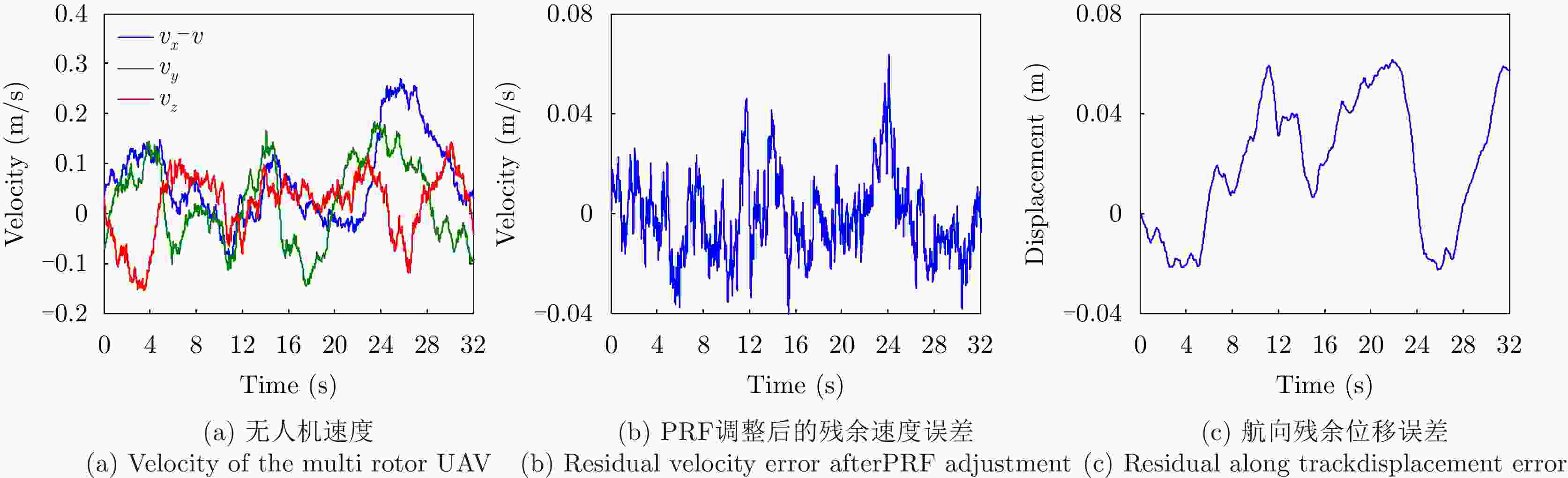
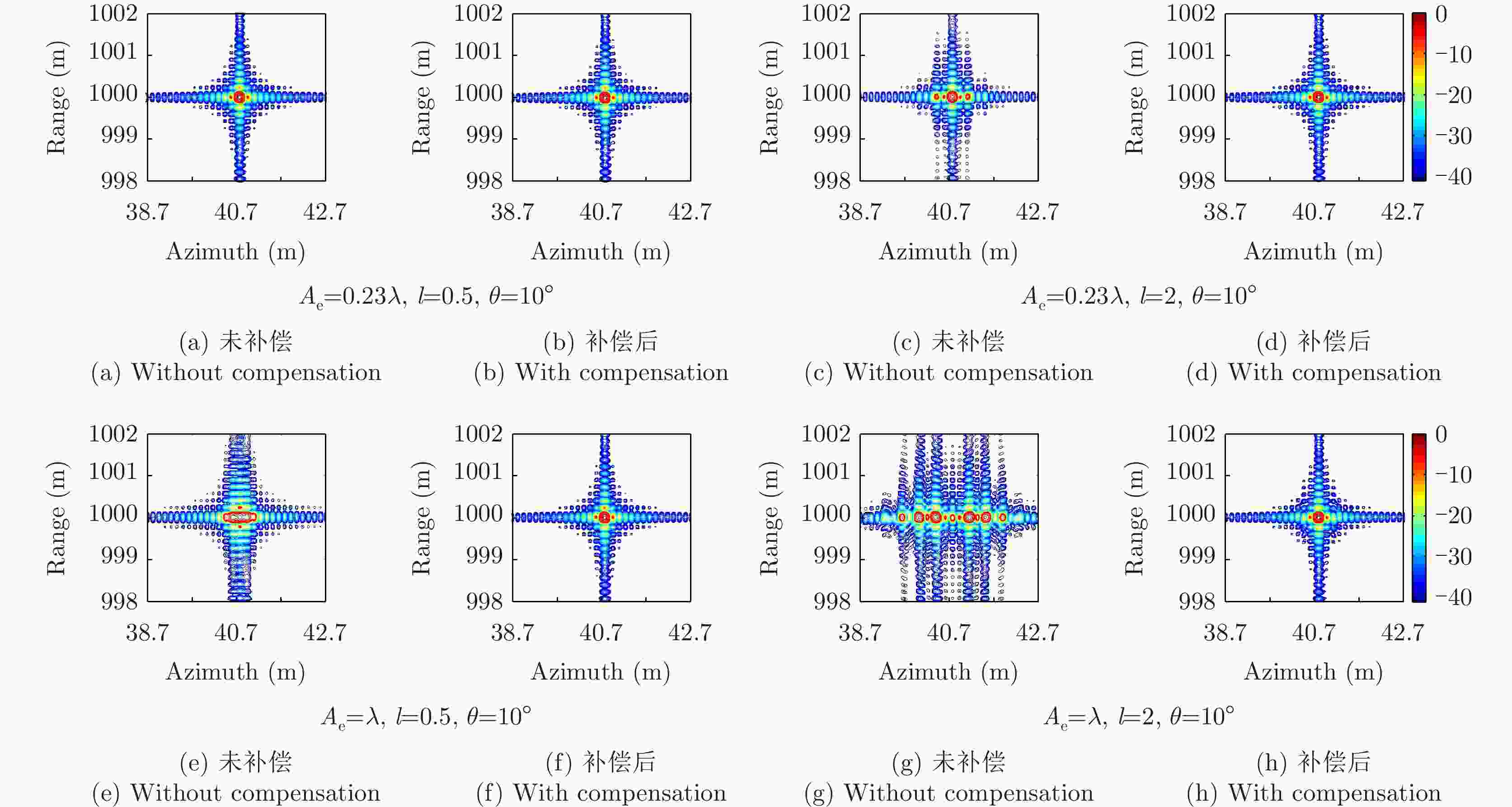
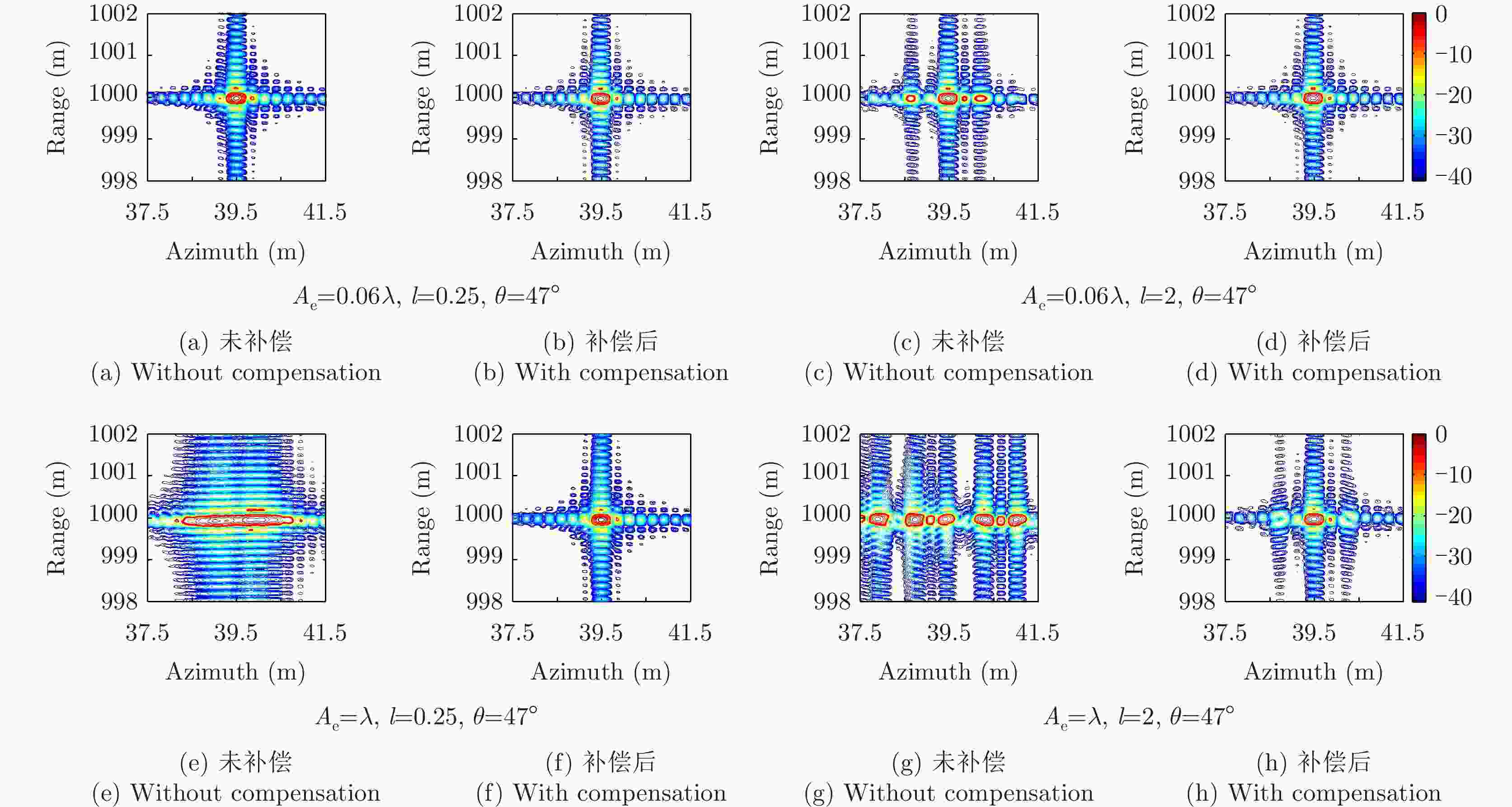
摘要: 多旋翼无人机体积小、重量轻、成本低，但由于飞行航迹极不稳定，成像信号处理难度很大。基于惯导数据实时调整脉冲重复频率(PRF)可预先补偿航向位移误差，但是，其残余误差在高波段合成孔径雷达(SAR)斜视成像时不能忽略。为此，利用位移实测值与理想值间的差异提取残余航向位移误差，修正了斜视成像几何下的视线运动误差，改进了传统的1阶、2阶视线误差补偿因子，并基于成对回波理论分析了旋翼无人机正弦位移误差的幅度和频率容限。仿真和实测数据验证了所提方法在大斜视成像时可减小视线运动误差约一个数量级，显著提高多旋翼无人机载SAR成像的性能。Abstract: The multirotor Unmanned Aerial Vehicle (UAV) has the advantages of small size, light weight, and low cost. However, imaging signal processing is complicated due to the extremely unstable flight path. Real-time adjustment of pulse repetition frequency based on inertial navigation data can compensate for the along-track displacement error in advance, but the residual error cannot be ignored for highly squinted high-band Synthetic Aperture Radar (SAR). Therefore, the residual along-track displacement error is extracted based on the difference between the measured displacement value and the ideal one, and then the Line-of-Sight (LOS) motion error of the squint imaging geometry is modified. The traditional first-order and second-order LOS error compensation factors are improved, and the tolerance of the amplitude and frequency of the sinusoidal displacement error of a multirotor UAV is analyzed based on paired echo theory. Simulation and flight experiments verify that the proposed method can reduce the LOS motion error by an order of magnitude in large squint imaging and significantly improve the imaging performance of the squinted SAR of a multirotor UAV.
-
1. 引言
信息化时代中对于深层次信息的需求日益迫切，目标识别就是根据某物体呈现的特征进行分析和判断，从而达到辨认和识别其身份和属性的目的。当这一过程不需要人工参与而只由机器自动完成时，就称该过程为自动目标识别(Automatic Target Recognition, ATR)。一旦将此项重要的任务交由机器来自主完成，应该如何评价ATR所取得的实际作用？
由于ATR技术与模式识别、人工智能等技术有着许多共同点，因此雷达、光学等信息处理研究领域中都包含ATR这一研究方向，许多学术机构及期刊会议也设有ATR专栏。IEEE很早就从图像处理角度定义过ATR：自动目标识别一般指通过计算机处理来自各种传感器的数据，实现自主或辅助目标的检测和识别[1]。
很多学者系统梳理过ATR的概念与技术发展。例如，文献[2]对雷达ATR技术现状与发展认识进行了总结，文献[3]从工程视角进一步对ATR技术发展进行了评述。ATR技术研究需要多个学科方向进行交叉融合[4]，而测试与评价对任何技术领域的发展都是非常重要的。随着ATR技术的快速发展，ATR评价方法的研究也逐步得到重视。例如，Ross等人[5–11]在历年SPIE会议上发表了一系列论文阐述SAR ATR评价的理念与方法，李彦鹏等人[12–14]对ATR效果评估进行了深入研究。但从总体来看，近年来通用性的评价方法研究较为少见。ATR评价方法研究经常被归属于某个相关技术领域，点缀在众多的图形图像[15,16]、信息处理[17,18]、系统工程[19,20]，乃至运筹管理[21,22]等领域的期刊或会议论文集中。
专门总结ATR评价方法的综述研究更为少见，更多的是在论文、专著中作为ATR技术发展的组成部分予以介绍。例如，文献[12,23–27]虽然都以ATR评价方法作为主题，但研究重点在于提出新的评价方法；文献[13]对ATR评价进行了介绍，但主要成果是为ATR系统的性能评价提供综合性分析工具。文献[28]是一篇有关ATR算法评价方法的综述文献，更多的是对上述学位论文及专著相关部分的总结。十多年来，ATR技术领域有了新的发展，同时给ATR评价带来了新的问题，但是该领域缺乏最新的综述文献对这些新进展进行归纳与总结。
本文面向通用的ATR算法与系统，不仅梳理和总结了ATR技术及其评价方法的发展，还对ATR评价方法研究背后的基础理论、方法模型等开展了分析讨论，并针对当前方法研究中存在的关键问题给出了自己的见解，旨在为科学、有效的ATR算法与系统评价提供方法借鉴和启发引导。
2. ATR技术发展回顾
2.1 统计模式识别应用
20世纪80～90年代的ATR研究基本可以看作统计模式识别理论在具体应用领域中的探索实践，处理方法上沿袭了传统的特征提取与选择、模板建库、分类器设计、匹配决策等经典模式识别环节。特征提取在统计模式识别中尤为关键，这也是早期ATR研究的重点内容。
以雷达对空中目标的识别为例，目标信号特征包括飞机的动力构件调制特征、目标谐振区极点特征、极化散射矩阵的不变量、微动特征，以及雷达成像时散射中心、结构特征等[29]。目标特征提取需要大量的实测数据，而当时的数据采集手段较为有限，造成用于匹配模板的标准状态与目标的实际状态之间存在较大差异，导致这一时期ATR系统的实用性较差。
2.2 基于模型或信息辅助的技术
当人们认识到模板匹配方法的局限性之后，开始尝试采用模型预测来应对实际情况中目标变化的多样性。基于模型的分类识别逐渐成为当时ATR研究的主流技术。其中，颇具代表性的当属美国国防部高级研究计划局(Defense Advanced Research Projects Agency, DARPA)和美国空军实验室(Air Force Research Laboratory, AFRL)联合开展的MSTAR (Moving and Stationary Target Acquisition and Recognition)计划[30]，研制出较为成熟的基于模型SAR ATR系统。
针对传统ATR系统难以引入外部信息、缺少对目标相关知识利用等问题，文献[31]建议采用知识推理辅助的目标识别方法。这类方法中，基于上下文知识的目标识别技术首先得到了关注和深入研究[32]。随后，本体论[33]、可视化[34]、数据融合[35]等方法被陆续引入。ATR研究的范围逐步提升到更广泛的全局信息利用层面。
2.3 深度学习方法
早期基于神经网络的ATR技术大多采用小规模的网络分类器[36–39]。随着深度学习研究兴起，深度学习方法已成为当前ATR技术的一个研究热点[40–42]。深度卷积神经网络(Convolutional Neural Networks, CNN)的成功[43]同样在声呐图像、雷达图像的识别应用中得到了验证[44–46]。深度学习方法在信息处理过程中不再严格区分“特征提取”与“分类识别”，而是直接完成目标识别的全过程[47]。
目前，CNN已被广泛应用于一维距离像识别[48–50]、SAR图像识别[51–55]和红外图像识别[56–58]等场景，并且被证明在提升泛化性能方面有不错的表现[59]，但有些场景中也容易受到噪声干扰[60,61]和欺骗[62]等因素影响。另外，虽然迁移学习[63]在SAR图像ATR的应用中取得了一定成功[64–66]，但人们还是对深度学习ATR方法的可解释性存在着一定的疑惑[67]。
2.4 困难与制约
从20世纪50年代雷达目标识别领域研究[68]开始，ATR技术已经取得了长足的进步。然而，要真正解决目标识别问题，ATR技术仍面临许多困难与挑战。除了目标识别问题本身的复杂性之外，ATR领域缺乏系统、科学的性能测试与评价方法也是制约其技术发展的瓶颈问题之一。
ATR评价方法研究正是要致力于改变这一现状，对ATR算法或系统进行性能评价与预测，使得ATR研究具备成为真正科学领域的基本要素[4]。文献[69]是有关ATR发展的较早评述，其中对于ATR评价重要性和发展的预测已被实践所证明。为构建实用化的ATR系统，必须先建立起有效的ATR评价方法及性能测试系统[70]。
3. ATR评价方法研究成果
ATR评价实际上贯穿于整个ATR研制过程。以研制一个ATR算法为例，图1[71]给出了ATR评价在各个阶段的不同内容。
无论处于哪个阶段，ATR算法的评价都离不开性能指标定义、测试条件构建和推断与决策等环节。本节分别归纳总结这几方面的研究成果。
3.1 性能指标定义
识别性能对于ATR算法来说无疑非常重要，许多文献中提到的ATR性能指标就是指衡量其识别能力的指标。至于泛化能力等其他方面的能力，通常采用分析某个关键识别指标(如识别率)随测试条件变化的下降程度来度量。故本文重点阐述ATR识别性能指标。
混淆矩阵(Confusion Matrix)从模式分类研究时期起就被广泛使用，通常记录成一张由行和列构成的二维表格。单元格用下标(i,j )定位，记录目标i被自动判别为目标j的次数或比率。配合彩色或灰度幅度值，混淆矩阵能够更加直观地展示目标识别的结果，如图2[72]所示。
对于m类目标的情况，混淆矩阵至少包含了m2个单元格，详细记录了ATR算法对于每一类目标正确识别及混淆判别的结果。当目标类型数据较多时，混淆矩阵难以直观展示测试结果。对此，可以利用混淆矩阵推算出另一类被经常使用的评价指标—概率型指标，反映ATR过程中对某个目标类别的正确/错误判别概率，如检测概率(Probability of Detection, PD)、虚警概率(Probability of False Alarm, PFA)、识别率等。
如果说概率型指标是以数的形式对混淆矩阵进行简化，那么ROC (Receiver Operating Characteristic)曲线就是用图的形式对PD和PFA之间存在的约束关系进行描述。ROC曲线最早应用于雷达检测领域，如图3[73]所示。
图3给出了存在高斯白噪声(非目标)n情况下，对同样服从正态分布的信号(目标)sn依据检测门限x0得到的ROC曲线。显然，越大的曲线下面积(Area Under the Curve, AUC)意味着ATR系统在保持低虚警概率P(S/n)的同时，具有更高的检测概率P(S/sn)。AUC因而成为评价“目标-非目标”这种二分类ATR算法性能的最常见评价指标，并逐步从雷达ATR领域扩展到其他领域，如医学病理图像ATR诊断性能评价[74,75]。文献[76]对一些基于ROC曲线的ATR算法性能评价方法进行了较为系统的总结。
采用深度学习方法的ATR算法，更倾向于采用由精确率(Precision)和召回率(Recall)所构成的P-R曲线[77]。为避免P-R曲线因为样本的排序而出现摇摆，一般还要对其进行平滑处理，如图4所示。
与AUC类似，平均精度(Average Precision, AP)由P-R曲线所衍生，表示不同召回率下精确率的平均值。至于如何对P-R曲线做离散化取值，如何计算平滑后的P-R曲线下面积，都有一系列相应的规范要求，具体方法可以参考文献[78,79]。此外，P-R曲线虽然同样是针对某类目标而言的，但可以通过对各类目标的AP值再取平均值(mean AP, mAP)来实现多分类的ATR算法性能评价。因此，AUC也可以说是mAP的特例。
综上所述，ATR算法识别性能的评价指标主要包括：以表格形式记录的混淆矩阵，根据目标识别阶段定义的概率型指标，以及ROC曲线、P-R曲线等图形及衍生指标。表1总结了常见的ATR识别性能指标。
表 1 常见ATR识别性能指标Table 1. Common ATR performance measures形式 典型代表 使用要点 适用范围 优/缺点 表格 混淆矩阵 每行数据记录一类目标被正确识别或错误混淆的情况 任意m类目标的分类性能评价 优点：记录所有目标类型之间的相互区分结果
缺点：目标类型数m较大时展示效果不直观概率 检测概率PD
虚警概率PFA
种类识别概率PCC
类型识别概率PID逐级识别过程中特定事件的发生概率 目标识别过程中某个决策任务结果的不确定性度量 优点：内涵清晰，指标点估计值计算简单
缺点：需要根据多次目标识别试验进行统计推断曲线 ROC曲线
P-R曲线转换为AUC, AP采用下面积、曲线积分的形式度量 相互制约的两方面
性能综合刻画优点：综合评价阈值变化对两个相互制约指标的影响
缺点：需调整阈值进行量化，精度受阈值离散取值的影响3.2 测试条件构建
ATR技术最终将应用于真实环境，需要将ATR算法加载到实际系统中进行检验。MSTAR计划将SAR ATR系统所处的条件分为4类[9]：ATR系统面临的真实环境称为工作条件(Operation Conditions, OC)，性能评价时所构建的测试条件(Test Condtions)只是OC的子集。用于算法训练的数据样本代表了ATR系统的训练条件(Training Condtions)。此外，对于模型驱动的ATR系统还可以定义其建模条件(Modeled Condtions)。上述4类条件之间的关系如图5(a)所示；而ATR系统评价其实只能考察ATR系统的准确性(Accuracy)、稳健性(Robustness)和扩展性(Extensibility)，三者共同反映了部分的有效性(Utility)，如图5(b)所示。
为了更好地评价ATR系统的扩展性，AFRL进一步将OC划分为标准工作条件(Standard Operation Condition, SOC)和扩展工作条件(Extended Operation Condition, EOC)[80]，根据ATR任务的具体需求设置具有代表性的EOC，并在目标类型、地面背景、传感器姿态等因素维度上构建差异化的测试条件。测试条件构建最后体现为不同的数据集：一般来说，SOC采集的一部分数据构成训练数据集，主要被用作ATR算法训练开发和自检；EOC的数据相对于研制方保密，形成测试数据集并用于ATR系统性能评价。
在SAR ATR技术领域中，MSTAR数据集被广泛使用。MSTAR数据集包含X波段0.25 m×0.25 m分辨率的全方位SAR图像序列，方位角间隔1°，图像分辨率128×128像素，所含目标多为车辆[81]。其中，常见的几类地面目标如图6所示[82]。
公开发布的数据中提供设置的因素包括外形差异和俯仰角差异[82]。通常一类(Class)目标中包括若干不同的类型(Type)，用于评价ATR算法在目标外形差异条件下的扩展性；部分目标还具有多个差异较大俯仰角的观测图像，用于评价ATR算法在不同成像视角条件下的扩展性。文献[83]总结了如何正确使用MSTAR数据开展SAR ATR评价工作。文献[84]对MSTAR数据所发挥的作用进行了分析，总结了1995—2020年使用该数据论文的引用次数，如图7所示。
在光学图像ATR技术领域，包含海量图像的数据集为ATR系统提供了比较接近真实环境的测试条件，从而极大地促进了数据驱动的ATR技术飞速发展。其中，颇具代表性的图像数据集有PASCAL VOC[85,86], ImageNet[87], MS COCO[88]和Open Images[89]等。这些数据集经常被作为目标检测、模式识别等领域中ATR算法性能测试的基准条件。
3.3 推断与决策
分析表1不难发现，混淆矩阵由于其记录结果难以直观比较，需要转换为反映特定性能的概率型指标；而体现“检测-虚警”“精确率-召回率”等概率型指标之间相互约束关系的ROC曲线、P-R曲线等，也是以概率指标作为基础。由于实际测试次数的限制，基于概率型指标的性能评价通常被归结为统计推断问题，下面结合实例进行详细介绍。
以识别率指标为例，在统计学中可抽象为Bernoulli试验的成败概率。记n个测试样本中正确识别的次数为X，则X为服从二项分布的随机变量。X=k (k=0, 1, 2, ···, n)的概率为
P{X=k}=(nk)pk(1−p)n−k (1) 当n较大时(至少要求n≥30)，识别率指标的测试结果
ˆp=X/n 可以用正态分布近似，在置信度1–α下识别率指标的区间估计结果为[ˆp−zα/2√ˆp(1−ˆp)n,ˆp+zα/2√ˆp(1−ˆp)n] (2) 其中，zα/2表示标准正态分布N(0,1)的α/2分位数。
对ATR算法性能评价中特别关心的识别率达标问题，可以通过构建检验统计量进行假设检验予以判断。例如，合同对ATR算法的识别率指标要求为p0，可以构建如下的原假设H0和备选假设H1来判断识别率精确率是否达标[73]：
H0:p≥p0H1:p<p0z0=ˆp−p0√ˆp(1−ˆp)n～N(0,1) (3) 其中的检验统计量z0由测试结果
ˆp 、合同要求值p0和样本容量n共同计算。若该假设检验的显著性水平取α，则当z0>–zα时，判定识别率指标达到规定值。文献[90]在上述正态近似假设前提下，对等价误识率的估计精度、区分度等问题进行了详细讨论，其研究结果表明需要大量的测试样本才能保证推断结果具有统计意义。对任意测试样本容量的一般情况，文献[91]提出了一种基于特定事件贝叶斯后验概率的评价方法，有效解决了根据概率型指标进行ATR算法考核检验、比较排序等评价问题。
上述评价方法都只是根据某个关键的概率型指标进行评价，但实际中的ATR系统具有多方面属性，需要构建合适的评价指标体系才能开展全面评价。ATR系统评价所面临的多指标综合评价问题，在决策分析领域中被称为多属性决策(Multi-Attribute Decision-Making, MADM)问题，一般可采用分值模型或关系模型进行多指标聚合。
顾名思义，分值模型通过获取综合评分来实现多指标综合评价，类似于雷达等技术领域中广泛使用质量因数(Figure of Metric, FoM)[92]对系统的整体性能进行综合描述。FoM的通式可概括为
FoM=n∑i=1aiwi (4) 其中，ai表示第i个指标的评分值，wi表示该项指标的权重。
为得到ATR系统的综合评分值，Klimack等人[93]将决策分析(Decision Analysis, DA)理论引入ATR系统评价，以价值函数和效用函数作为获取指标评分值的量化工具，然后再用一种混合价值/效用(Hybrid Value-Utility)[94]的分值模型聚合多个指标的评分值。文献[95]结合某ATR系统评价给出了详细的指标分解、赋权和评分过程，并且归纳出一个通用的评分决策模型，如图8[95]所示。图8中底层的红色曲线表示各指标值的概率分布，倒数第二级的绿色曲线表示每个指标对应的价值函数或效用函数，需要根据具体的应用场景进行构建。
除分值模型之外，关系模型是另一类常见的评价决策模型。关系模型从形式上可以概况为[96]：称(U,R)为评价关系模型，其中U={x1, x2, ···, xn}为评价对象集，R为评价对象之间的关系集
R=[R(x1,x1)R(x1,x2)⋯R(x1,xn)R(x2,x1)R(x2,x2)⋯R(x2,xn)⋮⋮⋱⋮R(xn,x1)R(xn,x2)⋯R(xn,xn)] (5) 其中，R(xi,xj)表示评价对象xi与xj之间的某种优劣关系。
不同于分值模型，关系模型避开了不同数据类型指标的评分要求，不需要为每个评价指标构造价值函数或效用函数。例如，对ATR系统评价中最为常见的实数型、风险型和区间型指标，文献[97]通过建立基于标准优劣差异x的偏好映射实现对式(5)中矩阵元素的赋值，从而完成了混合3种数据类型的多指标ATR系统综合评价。
4. ATR评价研究最新进展
第3节分别对ATR评价方法研究中的性能指标定义、测试条件构建、推断与决策等方面的成果进行了归纳总结，本节继续对一些最新的研究进展进行分析与评述。
性能指标定义方面，消除评价指标不确定性的归一化方法研究已经开始引起关注。例如，对于识别率等具有不确定性的概率型指标，文献[98]提出一种前景函数构建方法，将识别率的增量转变成前景价值，其所设计的前景价值函数不仅具有边际递减效应，而且不敏感于测试样本容量的变化。另外，随着深度学习方法在ATR技术领域的广泛应用，对于ATR算法可解释性[99,100]的要求日益强烈，成为这类ATR算法评价的研究热点。可解释性研究的重点在于提出可量化的指标，但是当前常见的一些方法(如LIME[101], Grad-CAM[102]等)尚缺乏被一致认可的量化指标。
测试条件构建方面，随着国内学界对数据的逐渐重视，国内多个研究机构陆续发布了可用于ATR算法研究与系统测评的数据资源，包括雷达[103–105]、红外[106,107]等多种传感器采集的数据。代表测试条件的数据集质量问题，也开始引起人们的广泛关注。例如，文献[108]分别针对图像数据集和文本数据集，提出了面向任务的数据集质量评价和数据选择方法，实现了任务相关性和内容多样性的量化度量。当实测数据不能完全满足工作条件的多样性需求时，人工合成及仿真计算等方法也逐步成为一种有益的补充手段[109–112]。通过不断提高所构建测试条件与实际工作条件的逼真度，ATR系统的有效性可以用在测试数据集上的扩展性来等效近似。
推断与决策方面，适用于ATR评价的混合型多属性决策问题已引起国内外的普遍关注，陆续提出了多种混合型多属性决策方法[113,114]。国内学者对区间数[115,116]、模糊型[117,118]和语言变量[119]等类型的多数属性决策问题抱有较浓厚的研究兴趣。文献[120]总结了各类不确定性和混合型多属性决策方法，给出了一些新的决策方法与应用实例。ATR系统评价方法研究中，借鉴这些最新决策理论成果的报道较为少见。文献[121]针对制导装置提出了基于区间直觉模糊集的性能评价方法，但是评价方法的合理性仍有待实际应用检验。
5. 结语
ATR评价方法的研究伴随着ATR技术发展，陆续取得了不少研究成果。理论上，测评方法分为理论分析和实验测量两种技术途径，本文只涉及基于测试的评价方法。这是由于ATR技术与实际应用结合紧密，大部分的ATR算法和ATR系统的性能指标需要根据实际测试结果计算，因而制约了理论分析方法的发展。对基于测试的ATR评价方法，获取识别率等关键指标的边界值是一个难点问题。作者认为，如果将ATR算法作为结构未知的“黑箱”进行测试，始终难以从根本上解决ATR算法的可信应用问题。基于理论分析的方法研究，则有可能从对ATR算法内部认知的角度突破该难题。
下面根据当前的研究现状，提出两个值得深入思考和持续研究的方向。
(1) 借鉴多属性决策理论，进行综合评价方法创新。
现阶段对于不确定性多属性决策方法、不确定信息下的案例推理决策方法等方面的研究成果颇为丰富，但对ATR系统评价而言，最为关键的问题是根据评价指标自身的定义与内涵，谨慎选择合适的不确定信息类型予以描述和度量，然后再从众多的已有方法成果中挑选合适的决策模型(亦称为集结算子)来融合决策者的主观偏好。这些研究工作貌似只是对现有理论方法的修改，却灵活解决了ATR评价工作所要面临的各种实际问题，也是构建ATR评价指标体系的理论依据所在。因此，有必要针对ATR评价问题中特有的混合型多属性决策问题，研究相应的决策模型及综合评价方法，解决多指标的ATR综合评价问题。
(2) 持续数据工程建设，提升测试样本数据质量。
ATR算法技术主流从最初的模板匹配到后面的模型驱动，再到现在的以深度学习为代表的数据驱动，对于训练数据和测试数据的需求都在不断增加。ATR评价主要关心如何适当减少测试数据，同时又能够保证测试样本涵盖实际工作条件的各类场景，实际上提出了数据使用规范与数据集质量评价这两个方面的需求。因此，还需进一步加强测试流程的规范化研究，重点分析测试样本的数据质量，构建合理的质量指标体系对测试数据集进行量化考核，保证测试结果反映ATR系统的真实性能表现。
ATR评价方法的研究已取得一定成果，但仍然跟不上ATR技术的发展需求。随着相关学科领域的发展及ATR技术自身的持续深入研究，建议在ATR技术领域中将ATR评价设立为一个独立的研究方向，为模式分类、目标检测、敌我识别、无人作战等高新技术应用提供科学的检验标准与决策依据。
-
图 1 存在运动误差时雷达斜视成像的几何关系图
Figure 1. Geometry for highly squinted SAR imaging with motion error
图 2 旋翼无人机FMCW SAR斜视成像处理流程
Figure 2. Flow chart of squint FMCW SAR imaging for multirotor UAV
图 3 旋翼无人机的速度特点以及PRF调整后的航向位移误差
Figure 3. Velocity characteristics of multirotor UAV and along track displacement error after PRF adjustment
图 4 点目标的方位压缩结果(
θ0=10∘ )Figure 4. Azimuthal compression results for point targets (
θ0=10∘ )
图 5 点目标的方位压缩结果(
θ0=47∘ )Figure 5. Azimuthal compression results for point targets (
θ0=47∘ )
图 6 本文算法误差容限下的点目标方位压缩结果(
θ0=47∘ )Figure 6. Azimuthal compression results for point targets under error limit of our proposed algorithm (
θ0=47∘ )
图 7 无人机载SAR及采用式(5)—式(7)分别提取的视线误差曲线
Figure 7. Multirotor UAV SAR and the LOS displacement curves extracted using Eqs. (5)—(7)
图 8 完成视线运动补偿的距离包络曲线对比
Figure 8. Comparison of range envelopes after LOS motion compensation
图 9 视线运动误差补偿后的成像结果对比(斜视角47°)
Figure 9. Comparison of image results after LOS motion error compensation (Squinted angle: 47°)
图 10 视线运动误差修正前后点目标的成像结果对比
Figure 10. Comparison of image results before and after modification of LOS motion error
图 11 视线运动误差修正前后点目标的剖面图对比
Figure 11. Comparison of profiles of a point target before and after modification of LOS motion error
图 12 视线运动误差修正前后近距离目标图像对比
Figure 12. Comparison of near-range target image before and after modification of LOS motion error
图 13 视线运动误差修正前后远距离目标图像对比
Figure 13. Comparison of far-range target image before and after modification of LOS motion error
图 14 视线运动误差修正前后田野场景成像对比
Figure 14. Comparison of images of a field scene before and after modification of LOS motion error
表 1 雷达系统仿真实验参数
Table 1. Experimental parameters of radar systems
参数 数值 参数 数值 信号带宽 900 MHz 平台飞行速度 10 m/s 雷达中心频率 15 GHz 距离向采样率 10 MHz 信号时宽 400 μs 场景中心斜距 1 km 去调频参考斜距 1 km 成像斜视角 10°/47° 参考脉冲重复频率PRF 2 kHz 方位向点数(抽样后) 2048 距离向点数 4096 平台飞行高度 200 m 
下载: 导出CSV
表 2 图11中点目标成像性能指标对比
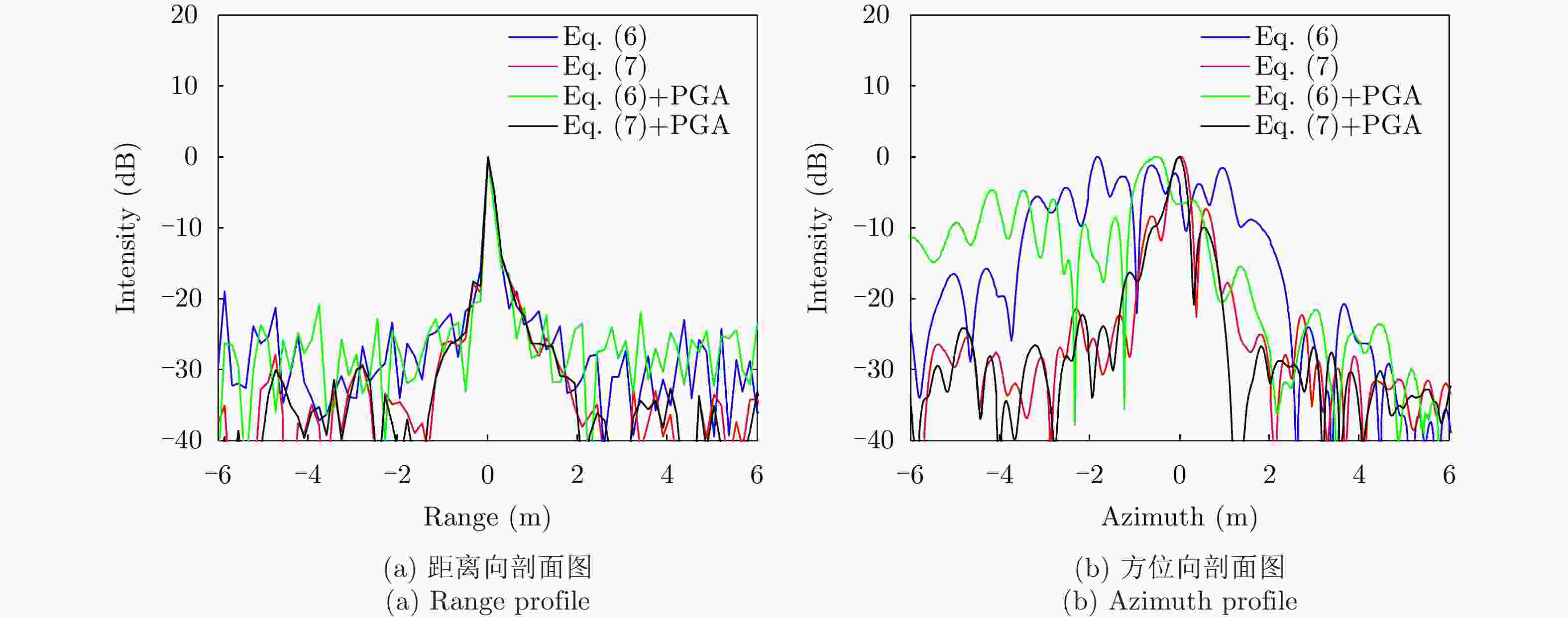
Table 2. Comparison of image performance of the point target in Fig. 11
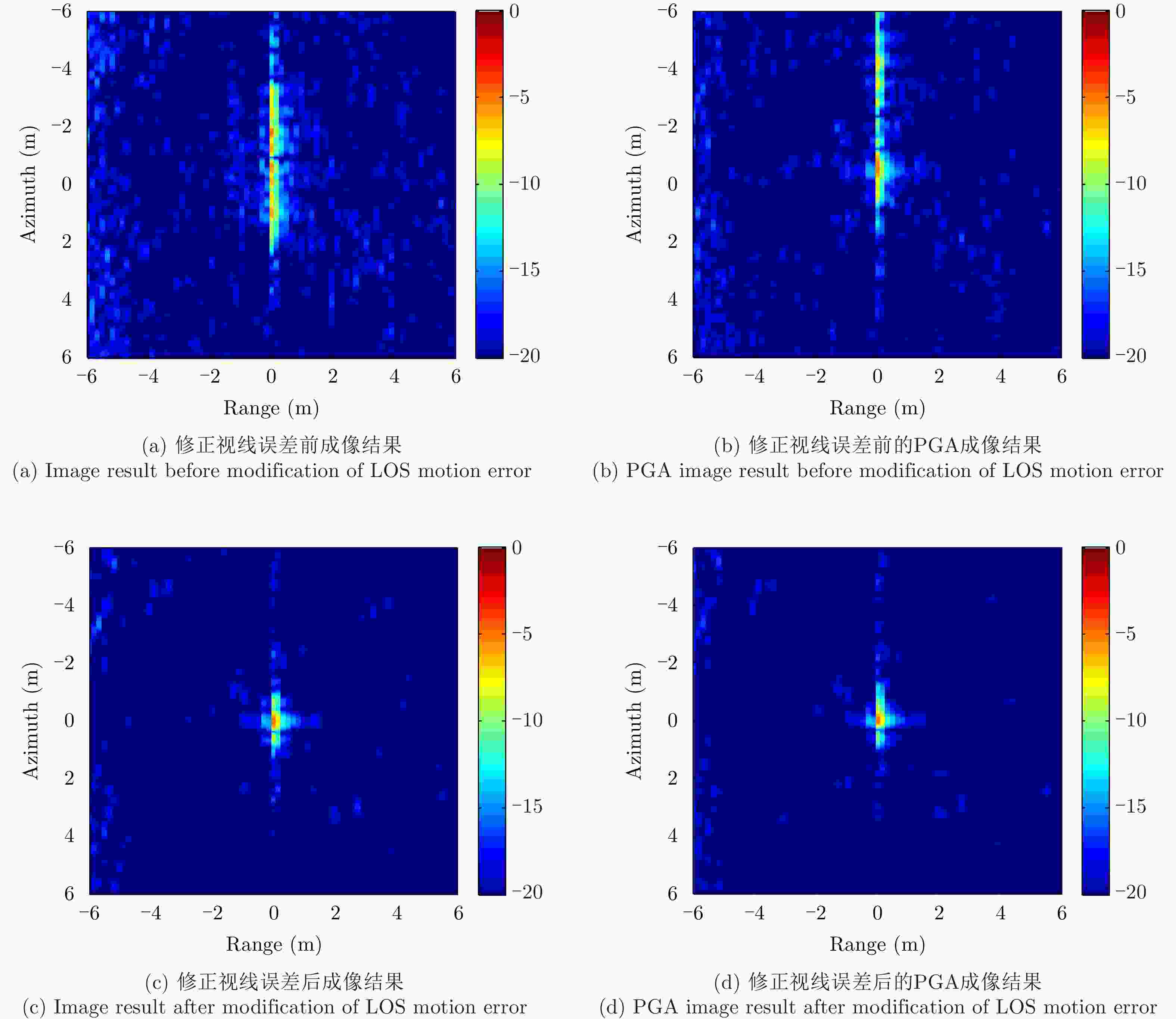
运动误差补偿方法 距离分辨率(m) 方位分辨率(m) 距离向PSLR(dB) 方位向PSLR(dB) 距离向ISLR(dB) 方位向ISLR(dB) 视线误差修正前 0.2151 0.8976 –18.8341 –2.5750 –11.9464 4.6462 视线误差修正前+PGA 0.2140 0.6586 –21.2475 –6.2690 –12.7365 1.3083 视线误差修正后 0.2151 0.3409 –17.9402 –7.0802 –14.0103 –2.6761 视线误差修正+PGA 0.2182 0.3276 –17.6637 –10.0202 –14.2019 –3.1933
下载: 导出CSV
-
[1] ZHOU Song, YANG Lei, ZHAO Lifan, et al. Quasi-polar-based FFBP algorithm for miniature UAV SAR imaging without navigational data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7053–7065. doi: 10.1109/tgrs.2017.2739133 [2] HU Xianyang, MA Changzheng, HU Ruizhi, et al. Imaging for small UAV-borne FMCW SAR[J]. Sensors, 2018, 19(1): 87. doi: 10.3390/s19010087 [3] YI Tianzhu, HE Zhihua, HE Feng, et al. Generalized nonlinear chirp scaling algorithm for high-resolution highly squint SAR imaging[J]. Sensors, 2017, 17(11): 2568. doi: 10.3390/s17112568 [4] 邢孟道, 林浩, 陈溅来, 等. 多平台合成孔径雷达成像算法综述[J]. 雷达学报, 2019, 8(6): 732–757. doi: 10.12000/JR19102XING Mengdao, LIN Hao, CHEN Jianlai, et al. A review of imaging algorithms in multi-platform-borne synthetic aperture radar[J]. Journal of Radars, 2019, 8(6): 732–757. doi: 10.12000/JR19102 [5] BERIZZI F, MARTORELLA M, CACCIAMANO A, et al. A contrast-based algorithm for synthetic range-profile motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3053–3062. doi: 10.1109/TGRS.2008.2002576 [6] MANCILL C E and SWIGER J M. A map drift autofocus technique for correcting higher order SAR phase error[C]. 27th Annual Tri-Service Radar Symposium Record, Monterey, USA, 1981: 391–400. [7] HUANG Yan, LIU Feiyang, CHEN Zhanye, et al. An improved map-drift algorithm for unmanned aerial vehicle SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(11): 1–5. doi: 10.1109/LGRS.2020.3011973 [8] XING Mengdao, JIANG Xiuwei, WU Renbiao, et al. Motion compensation for UAV SAR based on raw radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2870–2883. doi: 10.1109/TGRS.2009.2015657 [9] DE MACEDO K A C, SCHEIBER R, and MOREIRA A. An autofocus approach for residual motion errors with application to airborne repeat-pass SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3151–3162. doi: 10.1109/TGRS.2008.924004 [10] ZHANG Lei, SHENG Jialian, XING Mengdao, et al. Wavenumber-domain autofocusing for highly squinted UAV SAR imagery[J]. IEEE Sensors Journal, 2012, 12(5): 1574–1588. doi: 10.1109/JSEN.2011.2175216 [11] ZHANG Lei, QIAO Zhijun, XING Mengdao, et al. A robust motion compensation approach for UAV SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3202–3218. doi: 10.1109/TGRS.2011.2180392 [12] XIONG Tao, XING Mengdao, WANG Yong, et al. Minimum-entropy-based autofocus algorithm for SAR data using chebyshev approximation and method of series reversion, and its implementation in a data processor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1719–1728. doi: 10.1109/tgrs.2013.2253781 [13] SU Y A, LIU Weixian, FENG Hongchuan, et al. Study of multi-rotor UAV SAR processing[C]. 2017 IEEE Radar Conference (RadarConf), Seattle, USA, 2017: 226–232. [14] 邢涛, 胡庆荣, 李军, 等. 机载毫米波SAR垂直航向运动补偿分析与比较[J]. 火控雷达技术, 2016, 45(1): 13–22. doi: 10.3969/j.issn.1008-8652.2016.01.003XING Tao, HU Qingrong, LI Jun, et al. Analysis and comparison of airborne MMW SAR vertical course motion compensation[J]. Fire Control Radar Technology, 2016, 45(1): 13–22. doi: 10.3969/j.issn.1008-8652.2016.01.003 [15] 黎涛, 付耀文, 张健丰, 等. 多旋翼无人机载SAR视线向运动误差补偿方法[J]. 信号处理, 2022, 38(3): 491–501. doi: 10.16798/j.issn.1003-0530.2022.03.006LI Tao, FU Yaowen, ZHANG Jianfeng, et al. A method of line-of-sight motion error compensation for multi-rotor UAV SAR[J]. Journal of Signal Processing, 2022, 38(3): 491–501. doi: 10.16798/j.issn.1003-0530.2022.03.006 [16] 邢涛, 李军, 胡庆荣, 等. 毫米波小斜视SAR垂直航向运动分析与补偿[J]. 西安电子科技大学学报, 2016, 43(1): 127–132. doi: 10.3969/j.issn.1001-2400.2016.01.023XING Tao, LI Jun, HU Qingrong, et al. Cross-track motion analysis and compensation of millimeter wave small squint SAR[J]. Journal of Xidian University, 2016, 43(1): 127–132. doi: 10.3969/j.issn.1001-2400.2016.01.023 [17] SU Hao, WEI Shunjun, ZHANG Xiaoling, et al. Efficient autofocus of small multi-rotor UAV SAR by minimum entropy BP algorithm[J]. The Journal of Engineering, 2019, 2019(21): 7356–7359. doi: 10.1049/joe.2019.0625 [18] BEZVESILNIY O O, GOROVYI I M, and VAVRIV D M. Autofocusing SAR images via local estimates of flight trajectory[J]. International Journal of Microwave and Wireless Technologies, 2016, 8(6): 881–889. doi: 10.1017/S1759078716000180 [19] SHEN Wei, HE Xueli, MAO Xinhua, et al. An autofocus algorithm for multi-rotor UAV SAR[C]. International Symposium on Antennas and Propagation (ISAP), Phuket, Thailand, 2017: 1–2. [20] FORNARO G. Trajectory deviations in airborne SAR: Analysis and compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 997–1009. doi: 10.1109/7.784069 [21] GU Chengfei, CHANG Wenge, LI Xiangyang, et al. A new distortion correction method for FMCW SAR real-time imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(3): 429–433. doi: 10.1109/LGRS.2017.2647962 [22] 曾朝阳, 王辉. W波段UAV MISAR实时成像运动补偿方法[J]. 上海航天(中英文), 2020, 37(1): 63–69, 100. doi: 10.19328/j.cnki.1006-1630.2020.01.009ZENG Zhaoyang and WANG Hui. The motion compensation method for W-band UAV MISAR real-time imaging[J]. Aerospace Shanghai (Chinese &English) , 2020, 37(1): 63–69, 100. doi: 10.19328/j.cnki.1006-1630.2020.01.009 [23] 贾高伟, 常文革. 高分辨率UAV SAR的三维运动误差分离与补偿[J]. 国防科技大学学报, 2014, 36(4): 71–76. doi: 10.11887/j.cn.201404013JIA Gaowei and CHANG Wenge. Three-dimensional motion error correction for unmanned aerial vehicle synthetic aperture radar[J]. Journal of National University of Defense Technology, 2014, 36(4): 71–76. doi: 10.11887/j.cn.201404013 [24] CARIS M, STANKO S, PALM S, et al. Synthetic aperture radar at millimeter wavelength for UAV surveillance applications[C]. 2015 IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a better tomorrow (RTSI), Turin, Italy, 2015: 349–352. [25] STANKO S, JOHANNES W, SOMMER R, et al. Millimeterwave radar for SAR on UAVs with real-time image display[C]. 2011 12th International Radar Symposium (IRS), Leipzig, Germany, 2011: 507–511. [26] SUN B M, KENNEY R H, YEARY M B, et al. An up-sampled particle filter fusion technique and its application in synthetic aperture radar imaging[J]. IEEE Journal of Microwaves, 2022, 2(1): 108–122. doi: 10.1109/JMW.2021.3123531 [27] 张雨轮, 张涛, 李涛, 等. 基于惯导的机载斜视SAR运动补偿研究[J]. 火控雷达技术, 2014, 43(1): 18–21, 41. doi: 10.19472/j.cnki.1008-8652.2014.01.005ZHANG Yulun, ZHANG Tao, LI Tao, et al. Study on IMU based motion compensation for airborne squint SAR[J]. Fire Control Radar Technology, 2014, 43(1): 18–21, 41. doi: 10.19472/j.cnki.1008-8652.2014.01.005 [28] LIANG Yujie, LIANG Yi, ZHANG Gang, et al. A modified design method of pulse repetition frequency for synthetic aperture radar system based on the single point equivalent squint model[J]. IET Radar, Sonar & Navigation, 2021, 15(7): 748–759. doi: 10.1049/rsn2.12081 [29] TSUNODA S I, PACE F, STENCE J, et al. Lynx: A high-resolution synthetic aperture radar[C]. Proceedings of SPIE 3704, Radar Sensor Technology IV, Orlando, USA, 1999: 20–27. [30] 李建阳, 常文革, 李悦丽. UWB SAR实时PRF调整[J]. 现代雷达, 2009, 31(4): 34–37. doi: 10.16592/j.cnki.1004-7859.2009.04.008LI Jianyang, CHANG Wenge, and LI Yueli. Real time adjustment of PRF in UWB SAR[J]. Modern Radar, 2009, 31(4): 34–37. doi: 10.16592/j.cnki.1004-7859.2009.04.008 [31] LIANG Yi, LI Guofei, ZHANG Gang, et al. A nonparametric paired echo suppression method for helicopter-borne SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2080–2084. doi: 10.1109/LGRS.2019.2962175 [32] KLAUDER J R, PRICE A C, DARLINGTON S, et al. The theory and design of chirp radars[J]. The Bell System Technical Journal, 1960, 39(4): 745–808. doi: 10.1002/j.1538-7305.1960.tb03942.x [33] 张澄波. 合孔径雷达: 原理、系统分析与应用[M]. 北京: 科学出版社, 1989: 140–152.ZHANG Chengbo. Synthetic Aperture Radar: Principles, System Analyses, Applications[M]. Beijing: Science Press, 1989: 140–152. [34] 沈永欢, 梁在中, 许履瑚, 等. 实用数学手册[M]. 北京: 科学出版社, 1992: 668–672.SHEN Yonghuan, LIANG Zaizhong, XU Lvhu, et al. Handbook of Practical Mathematics[M]. Beijing: Science Press, 1992: 668–672. [35] CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood: Artech House, 2005: 60. -
下载:
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
