作者中心
专家审稿
责编办公
编辑办公
Coprime Array Based Direct Position Determination of Signals with Single Moving Observation
-
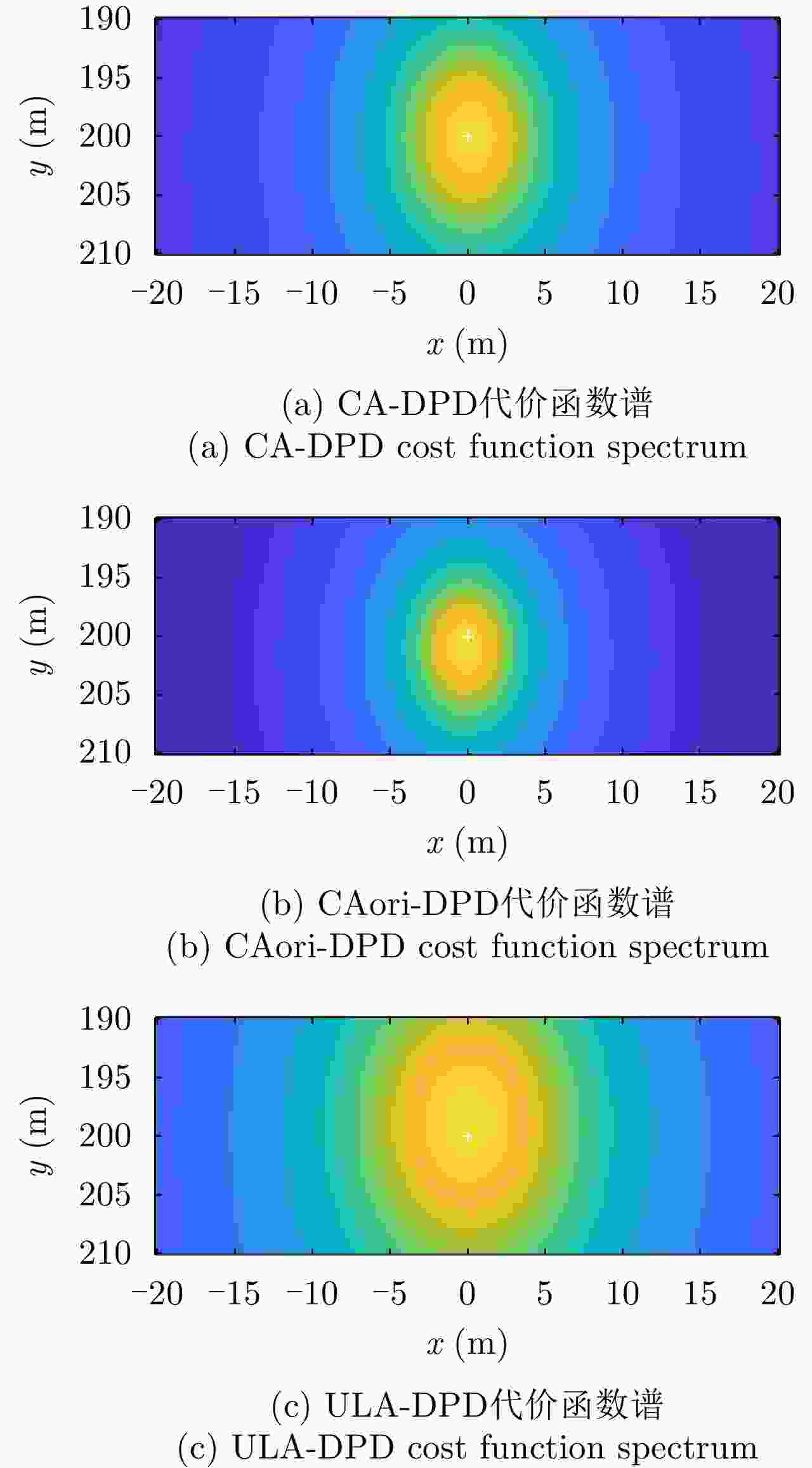
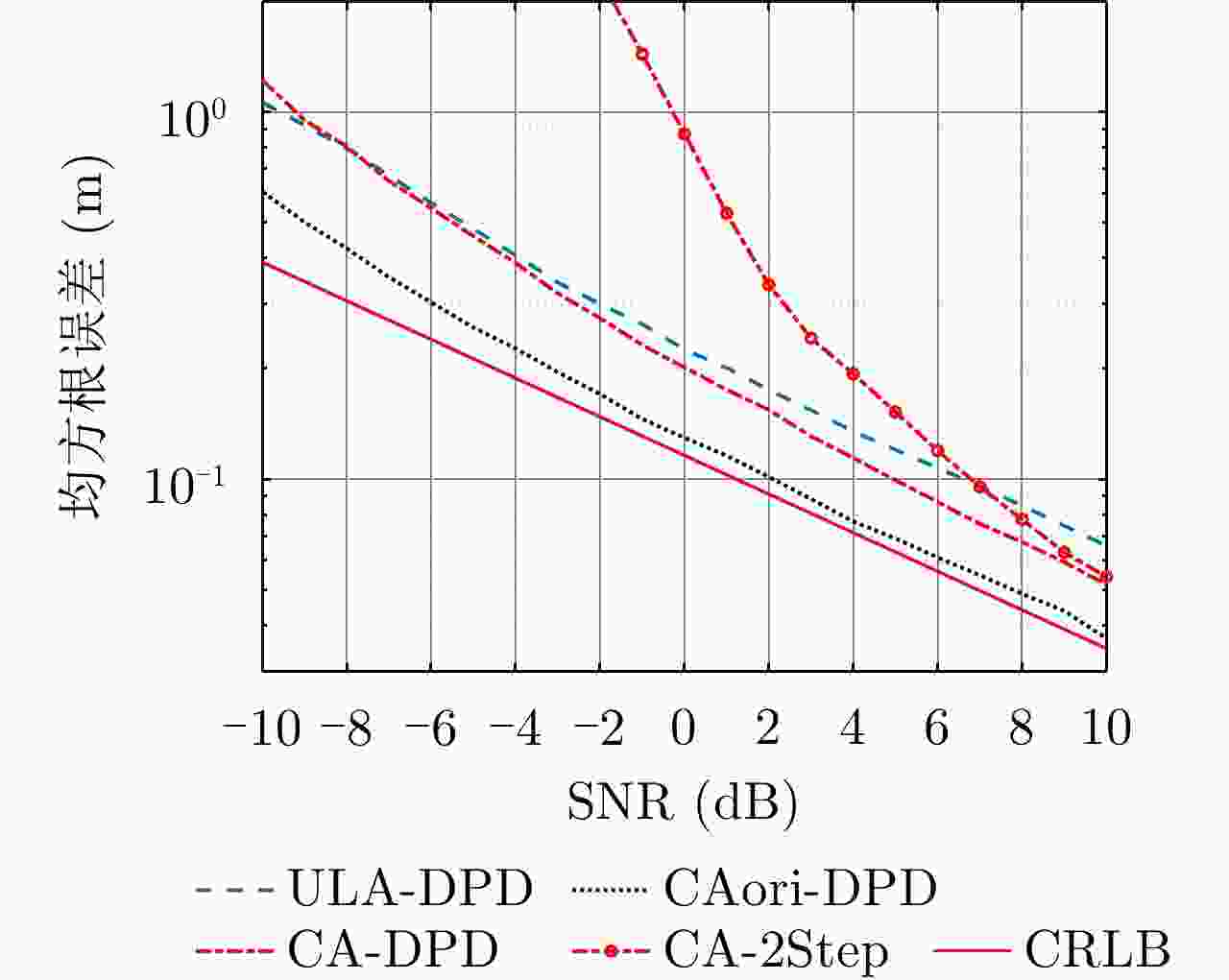
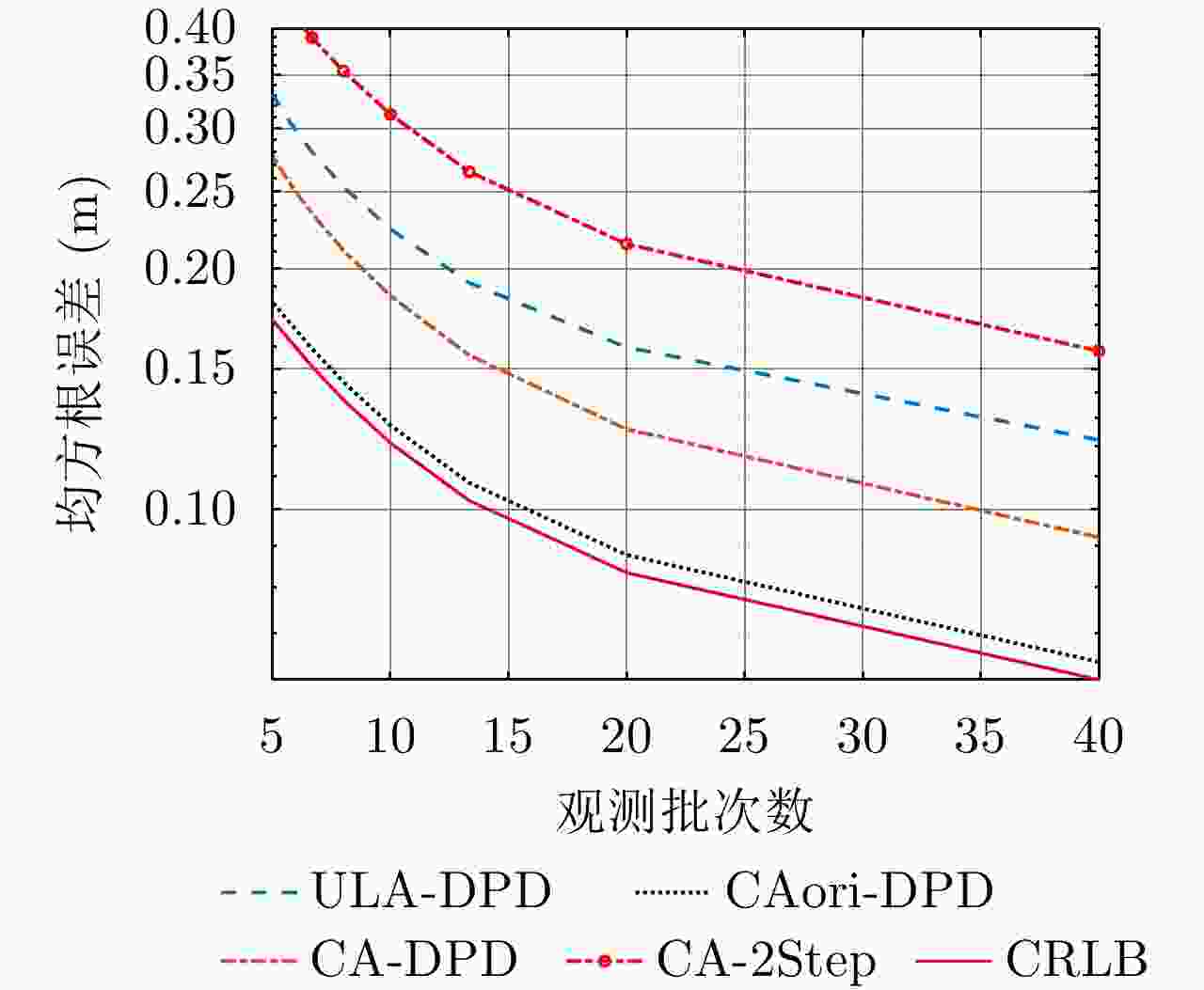
摘要: 信号直接定位方法是一种新型无源定位体制，具有适应低信噪比、无需参数关联等优势。为适应复杂电磁环境，该文提出了一种基于互质阵列的运动单站信号直接定位方法。以典型窄带信号为例，该文首先构建了互质阵列截获信号模型，然后推导了其差分共性阵对应的等效信号数学模型，最后使用空间谱技术构建了直接定位代价函数，实现了定位。经仿真分析验证，采用相同互质阵列时，该方法在分辨率和精度稍有损失的情况下可大幅提升传统直接定位方法的自由度，且与基于均匀线阵的直接定位方法相比，该方法在自由度、分辨率和定位精度等方面都具有优势。Abstract: Signal Direct Position Determination (DPD) is a novel passive localization technology, which shows superior performance in terms of low signal noise rate adaptability and no parameter association necessity. To adapt to the complex electromagnetic environment, this study proposes a coprime array-based DPD method with single moving observation. Considering narrowband signals as an example, this study first formulates the intercepted signal model, then derives its equivalent model related to the corresponding difference co-array, and finally builds the DPD cost function via spatial spectrum technology. Simulation results show that the proposed method can greatly improve the degree of freedom compared to the traditional DPD with a minor loss of resolution and accuracy when an identical coprime array is used. Meanwhile, compared to the uniform linear array-based DPD, the proposed method shows superior performance in terms of the degree of freedom, resolution, and accuracy of localization.
-
1. 引言
作为信息的载体，电磁波可由多个维度调制信息，如幅度、相位、频率和极化等[1]。根据经典电动力学理论，Maxwell方程所描述的电磁波包含线动量和角动量[2]，而角动量又包括自旋角动量(Spin Angular Momentum, SAM)和轨道角动量(Orbital Angular Momentum, OAM)[3]。理论上，携带轨道角动量的电磁波束具有无穷多种模态且各模态间相互正交，因此可实现模分复用从而提高频谱效率及信道容量以解决探测系统探测效率低的问题[4,5]。各模态的OAM波束的相位呈差异性分布，基于OAM波束的探测成像系统可从回波信号中获取更多的目标信息以实现高分辨率成像，因此，OAM波束在雷达探测领域也有着巨大的应用前景[6-10]。
针对OAM在雷达探测中的应用，相关学者进行了大量研究，主要包括基于OAM的目标重构及OAM波束的传播特性两个方面。针对基于OAM的目标重构，2013年，郭桂蓉团队[1]构建了基于OAM波束的成像模型，利用傅里叶变换的方法对回波信号进行处理，验证了OAM波束在雷达目标成像领域存在巨大的应用潜力。2017年，袁铁柱[6]分析了基于傅里叶变换电磁涡旋波成像方法，验证了目标处于小俯仰角条件下成像的可行性。2019年，Wang等人[7]提出一种涡流SAR(Synthetic Aperture Radar)成像方法，将OAM波束和条带SAR技术相结合，通过改进的距离多普勒(Range-Doppler, RD)算法来获取目标的二维图像。由仿真结果可知，该涡旋SAR成像方法的方位分辨率比常规SAR提高近8倍。2020年，Liu等人[8] 研究了双耦合OAM波束的电磁涡流成像，采用傅里叶变换的方法对目标进行重建，有效缩短了传统成像所需要的时间，大大提高了雷达成像效率。2020年，杜永兴等人[9]建立了多收多发电磁涡旋SAR成像模型，极大提高了方位向分辨率。2021年，Liu等人[10]提出一种基于分数阶OAM波束的电磁涡流增强成像方法，有效缓解了噪声对成像性能的影响。但上述研究均未考虑不同模态OAM波束的主瓣指向差异对成像系统性能的影响，本文对同主瓣指向的多模态OAM波束在目标特征识别的应用进行理论分析和仿真，进一步挖掘OAM波束在雷达探测中的潜力。针对OAM波束的传播特性，2017年，Yu等人[11]研究了远场目标对高阶贝塞尔涡旋波束的散射。2019年，相关学者将OAM波束进行分解，通过理论分析及数值仿真，归纳了OAM波束在两介质交界面及绝缘平板上的反射及折射规律[12]。2020年，Liu等人[13]研究了OAM波束与电大尺寸标准物体的相互作用，分析了金属球体和锥体的后向散射特性。为进一步分析多模OAM波束在目标探测及识别中的应用潜能，基于上述研究，本文设置多种观测场景及反射场景，通过理论分析及数值仿真对各场景下OAM波束呈现的传播特性及反射特性进行归纳总结并对同主瓣指向的多模态OAM波束在目标探测及识别方面的应用进行研究。
目标识别的主要流程包括：(1)从目标散射回波中提取目标特征；(2)由(1)获得的目标特征建立特征数据库；(3)获取待识别目标的特征数据；(4)将待识别目标的特征数据与数据库对比并输出判决。可知目标识别的关键是目标特征的提取，而卷积神经网络(Convolutional Neural Network, CNN)作为一种经典的深度学习算法是深度学习技术中特征提取的有效方法之一[14]。于1988年提出的LeNet-5被视为第1个真正意义上的卷积神经网络，因此也成为推动卷积神经网络发展的基石[15]。2012年，AlexNet[16]在ImageNet大规模视觉识别挑战赛上成功夺冠使得卷积神经网络再次引起相关学者的注意。随着对卷积神经网络研究的不断深入，VGGNet, GoogleNet, ResNet等网络被相继提出[17-19]。本文通过卷积神经网络建立目标反射信息与目标特征识别的关联，从而实现目标特征的智能识别。鉴于本实验的输入为数值矩阵且数据量较小，采用上述网络反而易引起过拟合、计算复杂度提高及梯度弥散等问题，因此本文基于LeNet-5网络搭建了一个3层的网络结构(其中卷积层和池化层作为一个layer)进行实验。
本文各章节内容介绍如下：第2节通过理论分析详细介绍了OAM波束特征的影响因素，并通过数值仿真获得在不同场景下OAM波束的传播及反射特性。第3节搭建卷积神经网络对第2节中各反射场景获得的回波信号进行训练，实现对未知场景的判断及场景内目标位置的识别。第4节对全文内容进行总结。
2. OAM波束的产生及特性分析
2.1 基于均匀圆形阵列的OAM波束产生方法
OAM波束的产生方式包括螺旋相位板、旋转抛物面、均匀圆形阵列及超表面等[20,21]。其他产生方式通过圆形阵列等效可以较容易地实现对OAM波束的幅相特性分析，本文以圆形阵列为基础，采用不同半径的多环结构产生发散角相同的多模态OAM，假设其阵元数目为
N ，半径为R ，阵元的长度为d ，第n 个阵元的矢量位置为rn=R(xcosφn+ ysinφn) ，电流分布Jn=Wexp(jlφn) ，其中，W 为电流密度，φn=2πn/N 为该阵元的初始相位，l 表示待合成OAM波束的模态。那么空间中某点P(r,θ,φ) 处的电场分布为El(r,θ,φ)=−jωμN∑n=1∫Jnexp(−jk|r−rn|)4π|r−rn|dVn=−ωμWdNexp(jkr)j−l+14πr⋅exp(jlφ)Jl(kRsinθ) (1) 由式(1)不难发现，区别于传统电磁波束，OAM波束的幅度特征与贝塞尔函数保持一致，沿传播轴的电场幅度为0，且其相位与方位角呈线性关系，绕传播轴一周其相位变化
2πl 。圆环半径与OAM波束发散角之间的关系[8]可表示为θ0=argmax{J2l(kRsinθ)} (2) 对于图1所示的实验场景，获得2, 3模态OAM波束的幅度和相位分布如图2所示，随模态的增大波束发散角增大。由式(2)可知通过调整圆环的半径可以改变波束的发散角，在发散角为
θ=12.5∘ 的情况下，各圆环半径与模态数的对应值见表1。
图 1 均匀圆形阵列产生OAM波束的示意图Figure 1. Structure diagram of OAM beam generated by uniform circular array
图 2 2模态和3模态OAM波束的幅相分布Figure 2. Amplitude and phase distribution of OAM beams with 2-mode and 3-mode表 1 阵列的半径Table 1. Radius of array模态l 阵列半径R (m) 1 0.0450 2 0.0747 3 0.1026 4 0.1302 5 0.1569 6 0.1836 7 0.2097 8 0.2361 9 0.2619 2.2 OAM波束的传播特性及反射特性分析
本文以3种观测面为例，分析OAM波束在传播过程中的幅度及相位分布，如图3所示观测面1位于发射阵列的左上方且垂直于OAM波束的主瓣指向，观测面2位于发射阵列的正上方且垂直于
z 轴，观测面3位于OAM波束的主瓣辐射区域且平行于xoy 平面。为便于在较小的观测面内观测较全面的幅相信息，设置均匀圆形阵列的半径为15λ ，产生2模态的OAM波束，此时OAM波束的主瓣指向为θ=1.949∘ ，3种观测面中心的位置坐标分别为(0,25m, 1000m) ,(0,0,1000m) ,(0,25m,1000m) ，则OAM波束传播到3种观测面时的幅相分布如图4所示。由图4可知，与观测面2的电场分布相比，观测面1与观测面3均无法展现OAM波束的幅相特性。同时对比图4(b)、图4(d)、图4(f)可以发现3种观测面的相位分布存在一个共性，如图5所示，沿红色箭头所指方向，相位变化速度越来越快。
为进一步验证图5所示规律，提取式(1)中的相位项
−((π/2)l+π/2+lφ+kr) ，取φ=π/2 对应区域(即平行于y 轴的径向区域)的相位进行分析，该区域y 轴射线上的相位表达式为p(y)=−(π2+kr)=−(π2+k√y2+z2) (3) 其中，
p(y) 为相位函数，z 为观测面的高度。以y>0 为例，验证图5所示现象只需证明p(y) 的变化速率随y 的增大而增大即可，也即p(y) 的变化速率|p′(y)| 的1阶导数恒大于0。由式(3)可求得|p′(y)| 如式(4)，进而推导出|p′(y)| 的1阶导数如式(5)。由式(5)可知|p′(y)|′>0 恒成立，可知|p′(y)|′ 随y 的增大而增大，即在观测面内随观测点与观测面中心距离的增大，相位变化速度加快。|p′(y)|=ky√y2+z2 (4) |p′(y)|′=kz2(y2+z2)3/2 (5) 以上分析了OAM波束传播到不同观测面的幅度和相位分布。下面将分析OAM波束经上述3种反射面获得的反射回波的幅度特征，为观察OAM波束与传统电磁波束反射特性的差异，本文以
l=0 和l=2 的OAM波束为例进行分析，该仿真实验采用半径为2.5λ 的发射阵列，此时OAM波束的主瓣指向为θ=11.259∘ ，反射面的中心位置与xoy 面的距离仍为1000 m，反射面的尺寸均为10λ×10λ 。由于反射实验所选取的反射面尺寸较小，入射到反射面的电磁波并非完整OAM波束，鉴于OAM波束可以分解为无数个传播方向不同的平面波[12]，因此采用传统电磁波反射特性的分析方法对所设置的3种反射场景的发射回波进行分析。如图6，将反射平面划分成M×N 个小反射单元，其中M=N ，则第m 行n 列的反射单元位置可表示为(rmn,θmn,φmn) ，由式(1)可知OAM波束传播到该位置处的电场为−ωμWdNexp(jkrmn)j−l+14πrmnexp(jlφmn)Jl(kRsinθmn) 假设入射波经反射面被全反射，结合惠更斯原理[22]则空间中某点
R(r,θ,φ) 处的电场分布可视为OAM波束经各反射单元的反射波在该点处的叠加，各反射单元可视为独立的阵元，以第m 行n 列的发射阵元为例，其初始幅相特性为−ωμWdNexp(jkrmn)j−l+14πrmnexp(jlφmn)Jl(kRsinθmn) 基于阵列合成的方法，可获得
R(r,θ,φ) 处的电场分布为Er,l(r,θ,φ)=−jωμM∑m=1N∑n=1∫−ωμWdNexp(jkrmn)j−l+14πrmn⋅exp(jlφmn)Jl(kRsinθmn)⋅exp(−jk|r−rn|)4π|r−rn|dVmn (6) 由于贝塞尔函数为特殊函数，难以将式(6)进一步简化为一个闭式表达式，因此只能通过仿真观察不同反射面对应的反射波特征，最终，获得OAM波束经3种反射面的反射回波如图7所示。由图7(a)和图7(b)不难看出，传统电磁波与2模态OAM波束经反射面2获得的反射幅度方向图有明显差异；而其余2种反射面对应的反射幅度方向图难以看出幅度差异。传统电磁波和OAM波束经反射面1和反射面3对应的反射波束差异甚微主要因为反射平面尺寸较小且距
z 轴较远，传统电磁波和OAM波束在反射面上的相位分布梯度差异较小；对于反射面2，虽然反射面尺寸小但相位分布梯度较大，因此可以明显展示出两种波束经相同反射目标呈现的反射角差异。理论上，不同模态的OAM波束的相位分布存在空间差异，对于固定的反射面，其反射方向图的主瓣指向也应有所不同，传统电磁波的反射定律对于OAM波束不再适用。为验证上述结论，以反射面1为例，对不同模态的OAM波束经反射面1反射的场景进行数值仿真。为便于比较，采用同心圆环阵列产生不同模态的OAM波束以保证各模态的OAM波束的主瓣指向一致。入射波的俯仰角为OAM波束的主瓣指向θ0=11.259∘ ，方位角为φ0=90∘ ，波束的反射角由θ ,φ 表示。最终，获得不同模态OAM波束的反射角如表2所示。
图 7 传统波束与OAM波束经不同反射面的回波方向图Figure 7. Echo pattern of traditional beam and OAM beam through different reflector表 2 OAM波束经反射面1的反射角Table 2. Reflection angle of OAM beam passing through reflector 1l θ (°) φ (°) 1 11.2523 89.9940 2 11.2523 89.9819 3 11.2523 89.9819 4 11.2523 89.9699 5 11.2523 89.9579 6 11.2523 89.9579 7 11.2523 89.9458 8 11.2523 89.9458 由表2不难看出，模态不同，主瓣指向相同的OAM波束经相同的反射平面获得的俯仰向反射角
θ 均相同且与设定的主瓣指向基本一致；方位向反射角φ 虽与入射波的方位角φ0 近似，但是随模态的增加方位向反射角φ 与方位向入射角的差异逐渐增大。上述现象即验证了各模态的相位分布差异导致波束反射角差异。2.3 OAM波束在不同反射场景下的反射数据分析
本节设置3种反射场景，不同场景中的反射目标呈某一趋势动态变化，通过分析对应场景的反射回波讨论多模态OAM波束用于未知场景的判断及场景内目标位置识别的可行性，3种场景如图8所示。
场景1内的反射面初始位置与
xoy 面的夹角为θ0 ，即垂直于OAM波束的主瓣指向，待分析数据为反射平面与xoy 面的夹角为(θ0−α/2)∼(θ0+α/2) 时观测点处收集到的反射回波的幅相信息；场景2的反射面初始位置位于发射阵列的正上方，待分析数据为反射面沿y 轴每平移10 m观测点处采集的回波信息；场景3内反射面初始位置位于发射阵列上方且偏离z 轴100 m处，待分析数据为反射面绕z 轴等夹角旋转时观测点处采集的回波信息。3种实验场景的观测点位置均为(1000m,168.83∘, 270.14∘) ，获得3种反射场景的回波信息分别如图9—图11所示。
图 9 反射场景1中观测点处反射信息Figure 9. Reflection information at observation point in reflection scene 1
图 10 反射场景2中观测点处反射信息Figure 10. Reflection information at observation point in reflection scene 2
图 11 反射场景3中观测点处反射信息Figure 11. Reflection information at observation point in reflection scene 3为便于分析，本文将采集的回波幅度信息进行归一化。由图9可知，在反射场景1中，反射面处于不同位置时观测点处观测到不同模态OAM波束对应的反射波幅度变化规律基本保持一致；各模态OAM波束对应的反射波的相位变化趋势相同但奇数模态与偶数模态OAM波束对应的反射波束存在一定的相位差；对于场景2，随反射平面的位置变化，不同模态OAM波束对应的反射波束的幅度变化趋势存在明显差异且相位变化也存在差异，如图10所示；对于场景3，虽然不同模态OAM波束对应的回波信号的幅度保持一致，但相位具有明显差异。综合可知，3种场景间的回波信号特征各异，且各场景内不同位置反射目标的回波也存着幅度或相位的差异，因此对于多模OAM波束的探测系统可通过场景间的信息差异判断反射场景类别，通过提取场景内不同位置的差异信息识别场景内目标。
3. 基于卷积神经网络的目标场景及位置识别
第2节介绍了基于圆形阵列的OAM波束产生方法，并通过仿真实验对OAM波束的传播特性及不同场景下的反射特性进行了深入研究。本节搭建卷积神经网络，将2.3节中的3种场景反射数据进行训练从而实现未知场景的判断，随后对3种反射场景的反射目标位置进行识别。
3.1 网络的搭建与训练
3.1.1 网络结构
实验开始前先对原始数据进行预处理，将其转化为数值矩阵形式，而灰度图像也是一个数值矩阵，因此本网络的输入可视为单通道的灰度图像，且灰度图像的尺寸较小。因此，本文所研究的问题仅需一个结构简单的网络即可解决。本文所用网络由2个卷积层、2个池化层和1个全连接层构成，其中输入数据为28×28的实数矩阵，卷积核的尺寸为5×5，数目为6，池化窗口的尺寸为2×2，如图12所示。
3.1.2 网络训练流程
(1) 参数初始化
训练开始前，首先采用随机数初始化各个参数权值。为避免网络因权值过大而进入饱和状态，一般选取较小的随机数作为初始值赋给各参数，且各权值的初始值应各不相同，否则网络丧失学习能力。本文采用的初始化方法为Xavier初始化，其思想是使前向传播和反向传播的输出与输入具有相似的分布，以便其方差保持一致，一定程度上可避免网络训练时的梯度发散问题[23]。Xavier初始化方法的表达式为
w=rand(−1,1)×√6m+n (7) 其中，
m 为该层输入神经元的数目，n 为该层输出神经元的数目。各个输出特征矩阵的偏置均初始化为0。(2) 前向传播
将训练数据进入网络经卷积层conv1、池化层pooling1、卷积层conv2、池化层pooling2及全连接层获得输出向量。
(3) 反向传播
反向传播算法是基于梯度下降算法建立的，根据目标的负梯度方向调整参数，本文采用均方误差函数作为损失函数对结果进行优化，如式(8)所示。首先设定学习率，并计算出前向传播输出结果与目标的误差；然后，分别计算出输出层和前面隐层神经元的梯度项；最后，根据每一层的误差梯度更新各层权值及偏置。经多次迭代，损失函数逐渐减小从而提升网络训练效果。
Loss=N∑i=1(ei)22N (8) 其中，
e=F(x)−Y 为一维向量表示网络输出与标签的绝对误差，x为测试数据集，F(x)为网络输出，Y为网络的测试标签，N表示测试数据集总数目。3.2 反射场景判断及抗噪性能分析
2.3节分析了不同模态OAM波束在3种反射场景的反射特征，本节对3种反射场景中指定观测点处获得的反射数据进行训练从而实现未知场景的判断。已知2.3节采集的反射数据为复数形式，而所搭建网络的输入为
28×28 的实数矩阵，因此在训练之前应对原始数据进行预处理。因本文采用14种模态的OAM波束进行实验，对同一观测点经过28次探测后，获得的数据尺寸为28×14 ，为将原始数据转化成28×28 的实数矩阵，将其模值和相位分别提取出来并将两组数据拼接起来，此时28×14 的复数矩阵将转化成28×28 的实数向量。为获得较理想的实验结果，本文对发射阵列及所搭建的卷积神经网络进行优化，最终获得实验场景的具体参数如表3所示。表 3 发射阵列及卷积神经网络的相关参数Table 3. Parameters of transmit array and convolutional neural network实验参数 参数值 频率 (GHz) 10 阵元数目 (个) 40 反射面尺寸 10λ 迭代次数 100 反向传播学习率 1 各场景选取的训练数据数目和测试数据数目分别为300和40。对于场景1，反射平面的旋转范围
α 为60∘ ，反射面每旋转0.2∘ ，在观测点处采集1次数据即可获得该场景下所需的训练数据；在场景2中，反射面沿y 轴每移动1 m，在观测点处收集1次数据；场景3中的反射面中心距z 轴100 m，每绕z 轴旋转1.2°，在观测点处记录一次数据，旋转一周即可获得300组训练数据。数据采集完成后，需对每个输入数据添加相应的标签。对于本实验，需添加3种标签，3种场景依次对应(1,0,0)T ,(0,1,0)T ,(0,0,1)T 。完成上述操作后，即可进行训练与测试。本文通过场景识别准确率来衡量系统性能的优劣，如式(9)所示P=(1−mN)×100% (9) 其中，m表示错误识别数目，N表示测试数据集的总数目。
由实验结果可知，所搭建网络对于3种反射场景的场景判断准确率为
97.5% ，即对于给定反射数据可准确判断场景类别。随训练迭代次数的增加，损失函数的变化情况如图13所示。为进一步观测该网络的泛化能力，本文对样本数据进行调整，此时3种场景的观测范围同上，但所采集的样本数据的数目调整为340，其中每种场景的前300个样本数据作为训练数据，后40个样本数据作为测试数据，也即测试数据与训练数据的交集为空。此时经24次仿真实验，网络对3种反射场景的场景判断准确率保持在86.904% 附近。通过与原始仿真场景对比可知，当测试数据与训练数据无交集时，网络对反射场景判断的准确率有所降低，但仍保持在80% 以上。基于3.1节的实验场景，本节将对卷积神经网络用于场景判断的抗噪性能进行分析，以引入加性高斯白噪声为例，首先观察噪声引入后对OAM波束的影响，图14为信噪比为10 dB时2模态OAM波束的幅相特征，对比图4(a)和图4(b)可以看出，引入噪声后OAM波束的幅度及相位均发生一定畸变。
图 14 信噪比为10 dB时，2模态OAM波束的幅相特性Figure 14. Amplitude and phase characteristics of 2-mode OAM beam when SNR is 10 dB为分析网络抗噪性能，在上节仿真场景的基础上引入噪声。网络的训练数据为未被噪声污染的反射数据。测试数据采用120组引入噪声的反射数据，获得网络对场景的判断准确率与信噪比的关系如图15所示。其中，3种场景的准确判断个数随信噪比的关系如图16所示。
由图15可知，随着信噪比的增大所搭建的卷积神经网络的场景判断准确率增高。对120组测试数据的判断结果进行统计，如图15所示，随信噪比的改变，场景2和场景3的准确判断数目相对稳定，而场景1的判断准确率随信噪比的降低急速下降。造成这种现象的原因可由2.3节中3种反射场景回波的幅相特性进行解释，对于场景1，由图9可知随反射面的变化仅奇数模态OAM波束和偶数模态OAM波束对应反射波存在固定相位差，其余信息均相同，因此对于反射场景1的回波所携带的信息量较少使得其特征不具代表性，当噪声引入时很容易淹没其特征信息从而不易对该场景做出准确判断；反射场景2中，各模态的OAM波束对应的反射波束的幅度及相位均存在差异，因此其携带的特征信息更多，自身特征更加明显从而抗噪声干扰的能力更强，因此低信噪比条件下也能被准确判断；同理，对于场景3，虽然各模态OAM波束对应的反射波束的幅度变化规律相同，但其相位分布存在明显差异，因此，相比反射场景1，反射场景3获得的反射数据携带的信息更多，受噪声的影响更小。
3.3 场景内目标位置识别及抗噪性能分析
本节将基于上节的卷积网络对某一反射场景中各位置的反射数据进行训练从而对场景间目标位置的识别进行讨论。以第2种应用场景为例对参数设置及数据选取进行说明，对于场景2，反射平面沿
y 轴移动1 m在观测点处采集一次数据，共采集1000次。将1000个样本数据根据位置进行分组并添加标签，如分析目标间距为100 m时的识别准确率，将样本数据等分为11组，在每组的起始位置设置相应的标签，数据采集及标签设置示意图如图17所示。反射场景1与反射场景3数据处理方法与反射场景2相同，其中反射场景1的训练数据为800个，测试数据为80个，反射场景3的训练数据为900个，测试数据为80个，3种场景内的目标识别准确率如图18。由图18可知，随着目标相对间隔的增大，所搭建的卷积神经网络对目标位置识别的准确率越高，同时当目标间隔小于一个临界值时，网络的识别准确率急速下降。以场景3为例，相邻反射面方位夹角为10∘ 网络识别准确率为90% ，但方位夹角为5∘ 网络识别准确率仅为26.2% 。
图 17 样本数据获取及标签设置示意图Figure 17. Schematic diagram of sample data acquisition and label setting
图 18 目标间隔对场景内目标位置识别准确率的影响Figure 18. Influence of target interval on accuracy of target location recognition in scene最后，对所搭建网络用于场景内目标识别的抗噪性能进行分析，3种反射场景的可识别间隔分别设置为
25∘ ,100m 和30∘ 。噪声条件下，所搭建网络对3种场景内目标识别的准确率，如图19所示。可知噪声的引入均会对3种场景的目标识别准确率产生一定影响，当SNR<20dB 时，3种场景内的目标识别准确率均大幅降低。
图 19 信噪比对场景内目标位置识别准确率的影响Figure 19. Influence of SNR on the accuracy of target position recognition in scene4. 总结
为实现高效目标探测，本文将基于多模OAM波束的目标探测方法与卷积神经网络相结合实现对目标特征的智能识别。首先，本文对OAM的传输特性进行了理论分析，给出了满足多模OAM波束特征；在此基础上，对不同模态OAM波束在不同反射场景下的回波信号进行了研究，并采用卷积神经网络提取各应用场景的反射数据特征，从而实现未知场景的判断及场景内目标的识别，同时对整体系统进行了抗噪性能分析。实验结果表明，无噪条件下，目标场景判断的准确率可达
97.5% ；但当SNR<20dB 时，3种场景内的目标识别准确率均明显降低，对环境的依赖性较高。 -
图 4 运动单观测站对6个辐射源进行定位场景示意图
Figure 4. The scene of 6 radiation sources localized by single moving observation
图 11 定位均方根误差与快拍数关系图
Figure 11. Relation between the number of sampling points in each observation interval and localization RMSE
图 12 定位均方根误差与观测批次数关系图
Figure 12. Relation between the number of observation interval and localization RMSE
表 1 算法耗时
Table 1. Elapsed time of algorithms
算法 耗时(ms) ULA-DPD 1192.0 CA-DPD 1337.1 CAori-DPD 1197.3 CA-2Step 276.9 
下载: 导出CSV
-
[1] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [2] MCCLOUD M L and SCHARF L L. A new subspace identification algorithm for high-resolution DOA estimation[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(10): 1382–1390. doi: 10.1109/TAP.2002.805244 [3] RAJ A G and MCCLELLAN J H. Single snapshot super-resolution DOA Estimation for arbitrary array geometries[J]. IEEE Signal Processing Letters, 2019, 26(1): 119–123. doi: 10.1109/LSP.2018.2881927 [4] SELVA J. Efficient wideband DOA estimation through function evaluation techniques[J]. IEEE Transactions on Signal Processing, 2018, 66(12): 3112–3123. doi: 10.1109/TSP.2018.2824256 [5] YANG J R. Measurement of amplitude and phase differences between two RF signals by using signal power detection[J]. IEEE Microwave and Wireless Components Letters, 2014, 24(3): 206–208. doi: 10.1109/LMWC.2013.2293665 [6] BALLAL T and BLEAKLEY C J. Phase-difference ambiguity resolution for a single-frequency signal in the near-field using a receiver triplet[J]. IEEE Transactions on Signal Processing, 2010, 58(11): 5920–5926. doi: 10.1109/TSP.2010.2062180 [7] BALLAL T and BLEAKLEY C J. Phase-difference ambiguity resolution for a single-frequency signal[J]. IEEE Signal Processing Letters, 2008, 15: 853–856. doi: 10.1109/LSP.2008.2005439 [8] CARTER G C. Coherence and Time Delay Estimation[M]. Piscataway: IEEE Press, 1993. [9] CHAN Y T and HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905–1915. doi: 10.1109/78.301830 [10] HO K C. Bias reduction for an explicit solution of source localization using TDOA[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2101–2114. doi: 10.1109/TSP.2012.2187283 [11] HO K C and CHAN Y T. Solution and performance analysis of geolocation by TDOA[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(4): 1311–1322. doi: 10.1109/7.259534 [12] ULMAN R and GERANIOTIS E. Wideband TDOA/FDOA processing using summation of short-time CAF’s[J]. IEEE Transactions on Signal Processing, 1999, 47(12): 3193–3200. doi: 10.1109/78.806065 [13] HO K C, LU Xiaoning, and KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684–696. doi: 10.1109/TSP.2006.885744 [14] BELLO P. Joint estimation of delay, Doppler, and Doppler rate[J]. IEEE Transactions on Information Theory, 1960, 6(3): 330–341. doi: 10.1109/TIT.1960.1057562 [15] ABATZOGLOU T. Fast maximum likelihood joint estimation of frequency and frequency rate[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Tokyo, Japan, 1986: 4019–4012. doi: 10.1109/ICASSP.1986.1168717. [16] ZHANG Shuangri and XING Mengdao. A novel Doppler chirp rate and baseline estimation approach in the time domain based on weighted local Maximum-Likelihood for an MCHRWS SAR system[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(3): 299–303. [17] ZHANG Weiqiang. Fast Doppler rate estimation based on fourth-order moment spectrum[J]. Electronics Letters, 2015, 51(23): 1926–1928. doi: 10.1049/el.2015.2182 [18] TRINH-HOANG M, VIBERG M, and PESAVENTO M. Partial relaxation approach: An eigenvalue-based DOA estimator framework[J]. IEEE Transactions on Signal Processing, 2018, 66(23): 6190–6203. doi: 10.1109/TSP.2018.2875853 [19] WU Xiaohuan, ZHU Weiping, and YAN Jun. A high-resolution DOA estimation method with a family of nonconvex penalties[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 4925–4938. doi: 10.1109/TVT.2018.2817638 [20] XU Xu, YE Zhongfu, and ZHANG Yufeng. DOA estimation for mixed signals in the presence of mutual coupling[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3523–3532. doi: 10.1109/TSP.2009.2021919 [21] CATOVIC A and SAHINOGLU Z. The Cramer-Rao bounds of hybrid TOA/RSS and TDOA/RSS location estimation schemes[J]. IEEE Communications Letters, 2004, 8(10): 626–628. doi: 10.1109/LCOMM.2004.835319 [22] LI Xinrong. RSS-based location estimation with unknown pathloss model[J]. IEEE Transactions on Wireless Communications, 2006, 5(12): 3626–3633. doi: 10.1109/TWC.2006.256985 [23] PATWARI N, HERO A O, PERKINS M, et al. Relative location estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2137–2148. doi: 10.1109/TSP.2003.814469 [24] WANG Gang and YANG Kehu. A new approach to sensor node localization using RSS measurements in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(5): 1389–1395. doi: 10.1109/TWC.2011.031611.101585 [25] WEISS A J. On the accuracy of a cellular location system based on RSS measurements[J]. IEEE Transactions on Vehicular Technology, 2003, 52(6): 1508–1518. doi: 10.1109/TVT.2003.819613 [26] 郭福成, 樊昀, 周一宇, 等. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012: 44–47.GUO Fucheng, FAN Yun, ZHOU Yiyu, et al. Localization Principles in Space Electronic Reconnaissance[M]. Beijing: National Defense Industry Press, 2012: 44–47. [27] 宋科康, 冯文涛. 采用Direct算法的外辐射源雷达高效直接定位方法[J]. 信号处理, 2020, 36(1): 149–154. doi: 10.16798/j.issn.1003-0530.2020.01.018SONG Kefeng and FENG Wentao. An efficient method of direct position determination of passive radar with direct algorithm[J]. Journal of Signal Processing, 2020, 36(1): 149–154. doi: 10.16798/j.issn.1003-0530.2020.01.018 [28] 余婉婷, 于宏毅, 杜剑平, 等. 辐射源信号波形已知的超视距目标直接定位方法[J]. 电子学报, 2019, 47(11): 2368–2377. doi: 10.3969/j.issn.0372-2112.2019.11.019YU Wanting, YU Hongyi, DU Jianping, et al. A direct position determination method for over-the-horizon target on known radiation source waveforms[J]. Acta Electronica Sinica, 2019, 47(11): 2368–2377. doi: 10.3969/j.issn.0372-2112.2019.11.019 [29] ZHAO Hanying, ZHANG Ning, and SHEN Yuan. Beamspace direct localization for large-scale antenna array systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 3529–3544. doi: 10.1109/TSP.2020.2996155 [30] AMAR A and WEISS A J. Advances in direct position determination[C]. Processing Workshop Proceedings, 2004 Sensor Array and Multichannel Signal, Barcelona, Spain, 2004: 584–588. [31] AMAR A and WEISS A J. Direct position determination in the presence of model errors—known waveforms[J]. Digital Signal Processing, 2006, 16(1): 52–83. doi: 10.1016/j.dsp.2005.03.003 [32] AMAR A and WEISS A J. Analysis of direct position determination approach in the presence of model errors[C]. IEEE/SP 13th Workshop on Statistical Signal Processing, 2005, Bordeaux, France, 2005: 521–524. [33] WANG Ding and WU Ying. Statistical performance analysis of direct position determination method based on Doppler shifts in presence of model errors[J]. Multidimensional Systems and Signal Processing, 2017, 28(1): 149–182. doi: 10.1007/s11045-015-0338-3 [34] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513–516. doi: 10.1109/LSP.2004.826501 [35] AMAR A and WEISS A J. Direct position determination (DPD) of multiple known and unknown radio-frequency signals[C]. 2004 12th European Signal Processing Conference, Vienna, Austria, 2004: 1115–1118. [36] WEISS A J and AMAR A. Direct position determination of multiple radio signals[J]. EURASIP Journal on Advances in Signal Processing, 2005, 2005(1): 653549. doi: 10.1155/ASP.2005.37 [37] LU Zhiyu, BA Bin, WANG Jianhui, et al. A direct position determination method with combined TDOA and FDOA based on particle filter[J]. Chinese Journal of Aeronautics, 2018, 31(1): 161–168. doi: 10.1016/j.cja.2017.11.007 [38] ZHOU Longjian, ZHU Weiqiang, LUO Jingqing, et al. Direct positioning maximum likelihood estimator using TDOA and FDOA for coherent short-pulse radar[J]. IET Radar, Sonar & Navigation, 2017, 11(10): 1505–1511. doi: 10.1049/iet-rsn.2016.0437 [39] 王云龙, 吴瑛. 联合时延与多普勒频率的直接定位改进算法[J]. 西安交通大学学报, 2015, 49(4): 123–129. doi: 10.7652/xjtuxb201504020WANG Yunlong and WU Ying. An improved direct position determination algorithm with combined time delay and Doppler[J]. Journal of Xi’an Jiaotong University, 2015, 49(4): 123–129. doi: 10.7652/xjtuxb201504020 [40] TIRER T and WEISS A J. High resolution localization of narrowband radio emitters based on doppler frequency shifts[J]. Signal Processing, 2017, 141: 288–298. doi: 10.1016/j.sigpro.2017.06.019 [41] TIRER T and WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2): 192–196. doi: 10.1109/LSP.2015.2503921 [42] WU Guizhu, ZHANG Ming, and GUO Fucheng. High-resolution direct position determination based on eigenspace using a single moving ULA[J]. Signal, Image and Video Processing, 2019, 13(5): 887–894. doi: 10.1007/s11760-019-01425-4 [43] OISPUU M and NICKEL U. 3D passive source localization by a multi-array network: Noncoherent vs. coherent processing[C]. 2010 International ITG Workshop on Smart Antennas (WSA), Bremem, Germany, 2010: 300–305. [44] WU Guizhou, ZHANG Min, HE Chaoxin, et al. Direct position determination using single moving rotating linear array: Noncoherent and coherent processing[J]. Chinese Journal of Aeronautics, 2020, 33(2): 688–700. doi: 10.1016/j.cja.2019.07.027 [45] VAIDYANATHAN P P and PAL P. Sparse sensing with Co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682 [46] PAL P and VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167–4181. doi: 10.1109/TSP.2010.2049264 [47] QIN Si, ZHANG Y D, and AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377–1390. doi: 10.1109/TSP.2015.2393838 [48] LIU Chunlin and VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997–4012. doi: 10.1109/TSP.2016.2558159 [49] LIU Jianyan, ZHANG Yanmei, LU Yilong, et al. Augmented nested arrays with enhanced DOF and reduced mutual coupling[J]. IEEE Transactions on Signal Processing, 2017, 65(21): 5549–5563. doi: 10.1109/TSP.2017.2736493 [50] ZHANG Yankui, BA Bin, WANG Daming, et al. Direct position determination of multiple non-circular sources with a moving coprime array[J]. Sensors, 2018, 18(5): 1479. doi: 10.3390/s18051479 [51] KUMAR G, PONNUSAMY P, and AMIRI I S. Direct localization of multiple noncircular sources with a moving nested array[J]. IEEE Access, 2019, 7: 101106–101116. doi: 10.1109/ACCESS.2019.2929805 [52] CZARNECKI S V, JOHNSON J A, GRAY C M, et al. Self-resolving LBI triangulation[P/OL]. US, 5835060A, 1998. http://fx.gfkd.chaoxing.com/detail_38502727e7500f26da641ed9afec03488195a6654876bab11921b0a3ea25510133e7f87ae1903bd666c0a358461822c556999c638672b0c5948ab7aaa01c6a6c8cfe3d4a29101f7e57ea89991e2828e1? [53] QIAN Yang, YANG Zhongtian, and ZENG Haowei. Direct position determination for augmented coprime arrays via weighted subspace data fusion method[J]. Mathematical Problems in Engineering, 2021, 2021: 2825025. doi: 10.1155/2021/2825025 [54] TORRIERI D J. Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, 20(2): 182–98. doi: 10.1109/TAES.1984.310439 期刊类型引用(7)
1. 梁梦薇，何劲，舒汀，郁文贤. 阵元位置互质的线性阵列：阵列校正和波束形成. 电子与信息学报. 2024(01): 240-248 . 
百度学术2. 郑航，周成伟，王勇，史治国. EMVS互质面阵张量波束成形. 信号处理. 2024(02): 250-262 . 百度学术3. 张苗，高宏亮，邓志安. 基于虚拟阵列孔洞插值的互质阵列直接定位方法. 舰船电子工程. 2024(02): 70-75 . 百度学术4. 罗军，张顺生. 联合自适应LASSO与块稀疏贝叶斯直接定位方法. 雷达科学与技术. 2024(03): 265-274 . 百度学术5. 招乾民，张顺生. 改进实值空时子空间数据融合的单星直接定位方法. 信号处理. 2024(06): 1111-1121 . 百度学术6. 陈梁栋，黄知涛，王翔，吴癸周. 基于角速度信息先验的固定无源单站直接定位方法. 电子学报. 2024(07): 2190-2200 . 百度学术7. 李建峰，朱珂慧，江航，张小飞，吴启晖. 基于多频率聚焦与融合的相干辐射源时差直接定位方法. 电子学报. 2023(08): 2110-2117 . 百度学术其他类型引用(4)
-
下载:
百度学术
计量
- 文章访问数: 1015
- HTML全文浏览量: 522
- PDF下载量: 151
- 被引次数: 11
