Three-dimensional Imaging Using the Electromagnetic Vortex Synthetic Aperture Radar
-
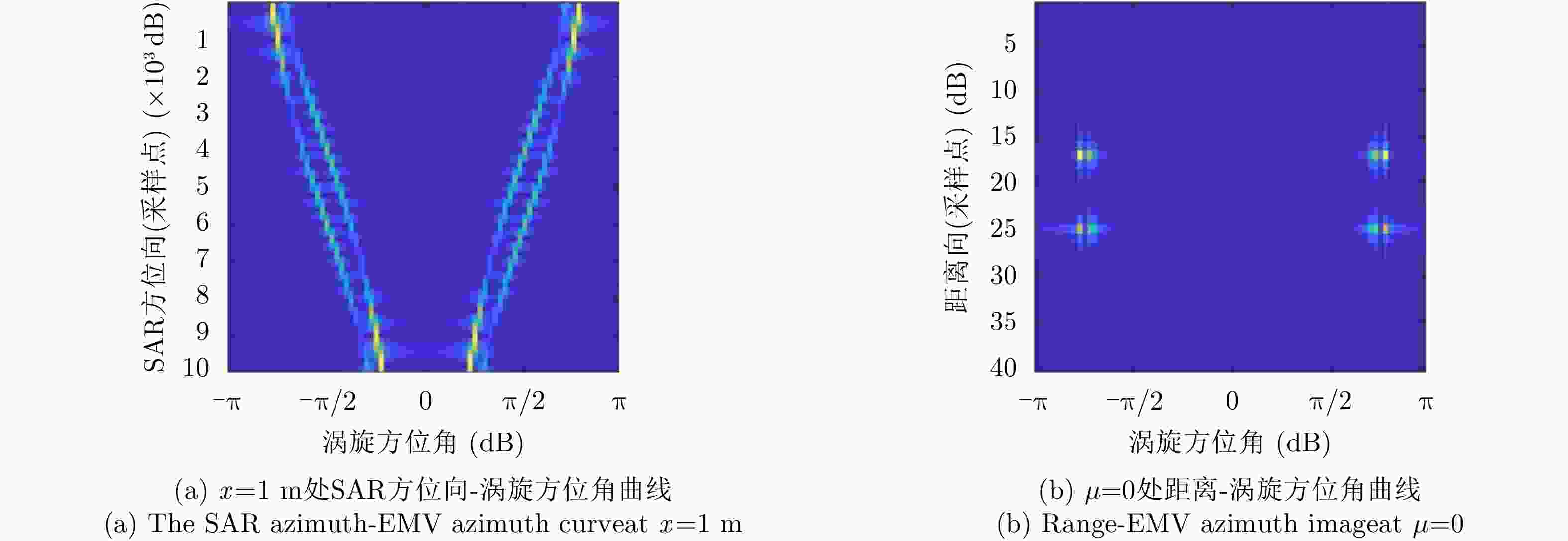
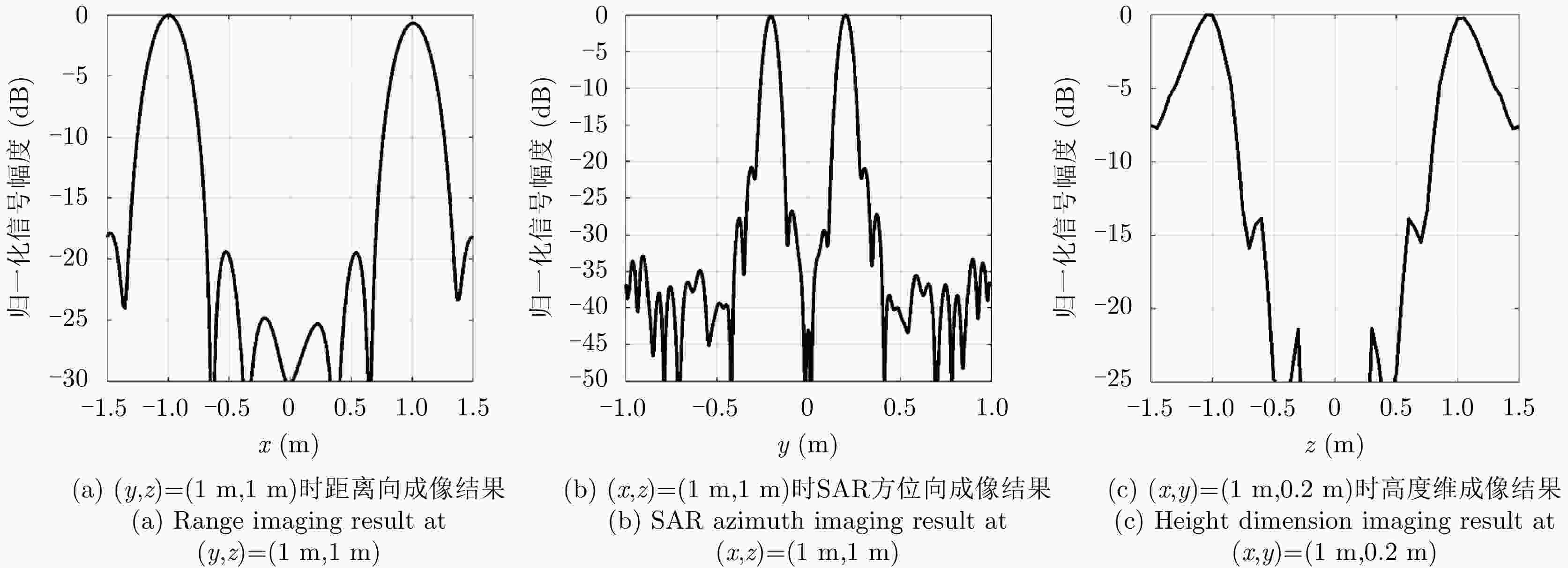
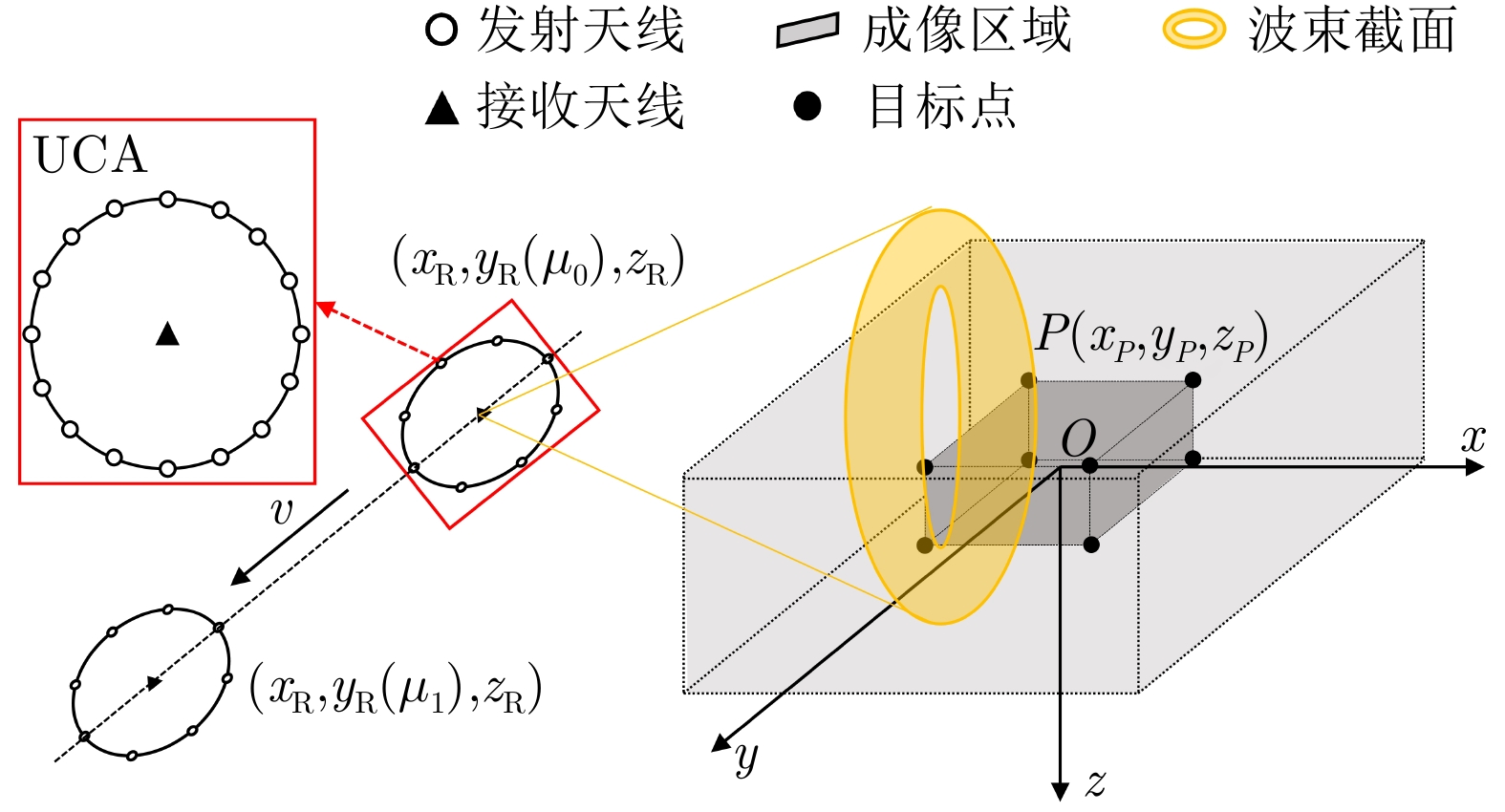
摘要: 涡旋电磁波得名于其传播时围绕行进轴的旋转现象,该电磁属性被称为轨道角动量。基于其在方位角上的目标分辨能力,该文将涡旋电磁波引入传统的合成孔径成像中,提出了一种新的三维成像方案。在结合轨道角动量模态域之后,将合成孔径雷达二维回波扩展到三维。首先,基于波形分集理论,获取同时多模态回波数据,并利用傅里叶变换(FT)变换到方位角维,形成距离-合成孔径方位-方位角三维数据。然后,基于Radon-FT,提出了一种联合二维方位压缩算法来生成三维目标成像。仿真结果验证了系统和算法的性能,证明了涡旋电磁三维合成孔径成像雷达系统的优越性。Abstract: The ElectroMagnetic Vortex (EMV) wave is named after the rotation around the wave propagation axis. This electromagnetic characteristic is called the Orbital Angular Momentum (OAM). Considering its azimuth angular resolution, this paper introduces the EMV wave into traditional Synthetic Aperture Radar (SAR) imaging and proposes a novel Three-Dimensional (3D) imaging scheme called EMV-SAR. In EMV-SAR, the echo is extended into 3D after involving the OAM mode domain. Based on the waveform diversity technology, the multiOAM-mode echo is obtained and simultaneously transformed into azimuthal angular signals via Fourier Transform (FT) to form the 3D data of range-azimuth-angular. In this study, we propose a joint two-dimensional azimuthal compression algorithm to generate 3D target imaging based on Radon FT. The simulation results validate the performance of the proposed system and algorithms and demonstrate the superiority of EMV-SAR in 3D imaging.
-
表 1 仿真涉及雷达参数
Table 1. Simulation Radar parameters
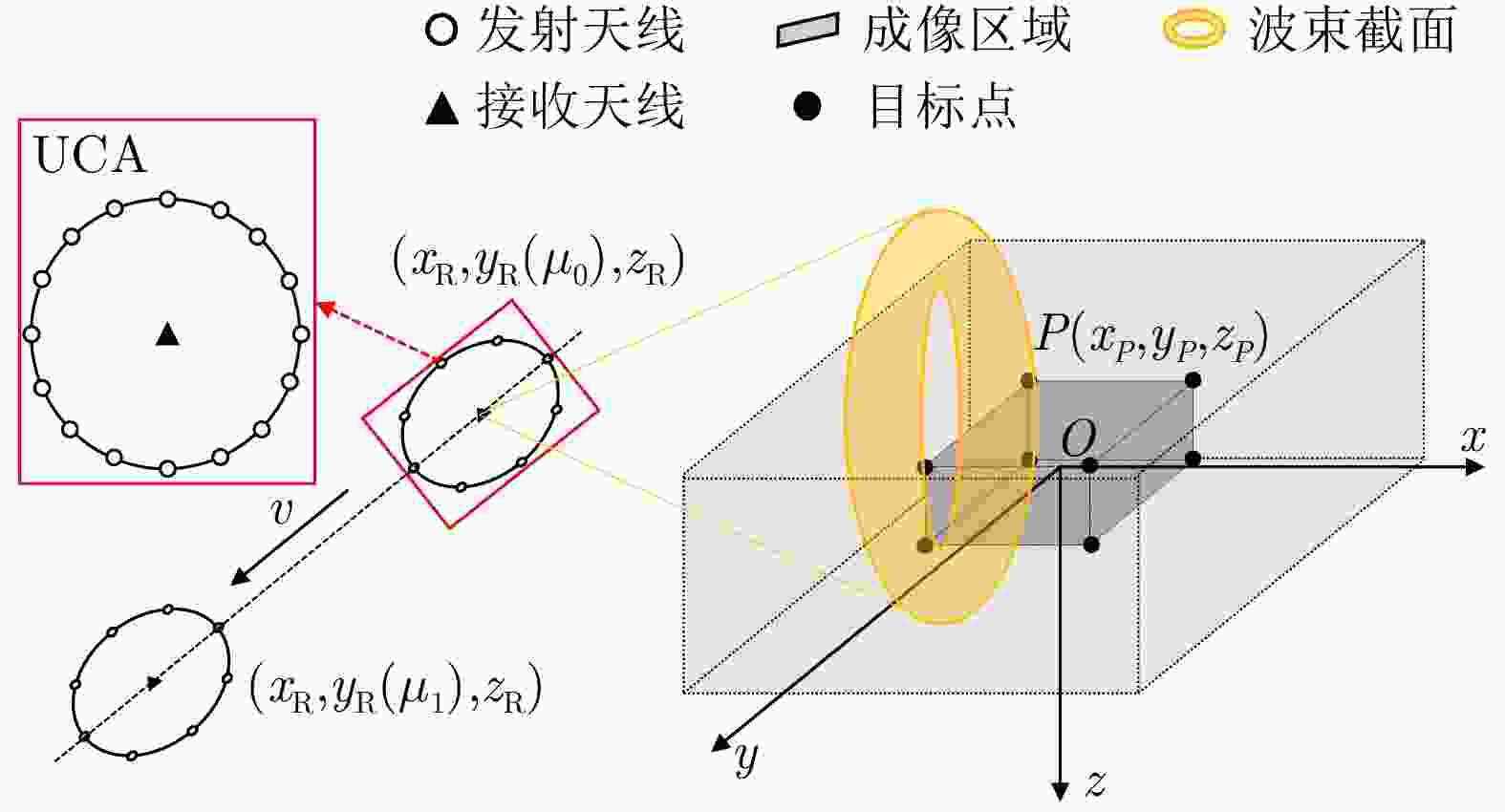
参数 值 雷达坐标 (m) (–20, [–1, 1], 0) 成像区域 (m) ([–5,5], [–1,1], [–1.5,1.5]) OAM模态 [–40,40] 雷达高度 (m) 300 雷达速度 (m/s) 20 载频 (GHz) 35 脉冲重复频率 (Hz) 2000 信号带宽 (GHz) 1 UCA半径 ($\lambda $) 40 UCA阵元个数 50 表 2 点目标理论坐标与仿真坐标
Table 2. Theoretical coordinates and simulation coordinates of point targets
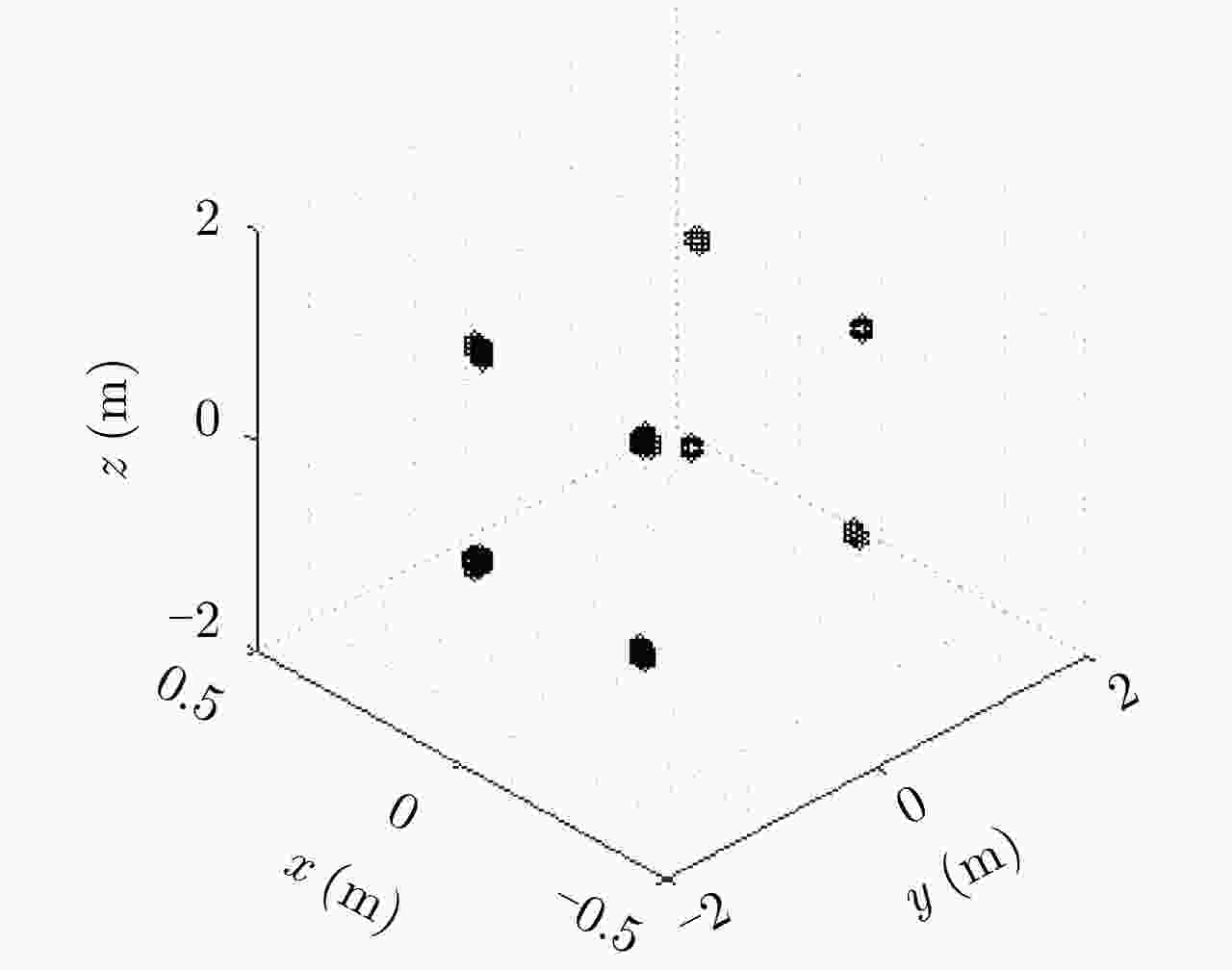
参数 初始坐标 (m) 重构结果 (m) 点目标1 (1, 0.2, 1) (0.99, 0.19, 0.95) 点目标2 (1, 0.2, –1) (0.99, 0.21, –1.00) 点目标3 (1, –0.2, 1) (1.00, –0.21, 1.05) 点目标4 (1, –0.2, –1) (1.00, –0.19, –1.00) 点目标5 (–1, 0.2, 1) (–1.05, 0.20, 0.95) 点目标6 (–1, 0.2, –1) (–1.05, 0.21, –1.05) 点目标7 (–1, –0.2, 1) (–1.05, –0.22, 1.05) 点目标8 (–1, –0.2, –1) (–1.05, –0.20, –1.00) -
[1] GISIN N. Quantum Science and Technology[M]. Springer International Publishing AG, 2017. [2] MOHAMMADI S M, DALDORFF L K S, BERGMAN J E S, et al. Orbital angular momentum in radio—A system study[J]. IEEE transactions on Antennas and Propagation, 2010, 58(2): 565–572. doi: 10.1109/TAP.2009.2037701 [3] TAMBURINI F, MARI E, SPONSELLI A, et al. Encoding many channels on the same frequency through radio vorticity: first experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. doi: 10.1088/1367-2630/14/3/033001 [4] EDFORS O and JOHANSSON A J. Is orbital angular momentum (OAM) based radio communication an unexploited area?[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 1126–1131. doi: 10.1109/TAP.2011.2173142 [5] TAMBURINI F, THIDÉ B, MARI E, et al. Reply to comment on ‘Encoding many channels on the same frequency through radio vorticity: First experimental test’[J]. New Journal of Physics, 2012, 14(11): 118002. doi: 10.1088/1367-2630/14/11/118002 [6] TAMBURINI F, THIDÉ B, BOAGA V, et al. Experimental demonstration of free-space information transfer using phase modulated orbital angular momentum radio[J]. arXiv: 1302.2990, 2013. [7] YAN Yan, XIE Guodong, LAVERY M P J, et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing[J]. Nature Communications, 2014, 5(1): 4876. doi: 10.1038/ncomms5876 [8] 李蹊, 冯志勇, 冯建元, 等. 电磁涡旋及其在无线通信中的应用[J]. 电讯技术, 2015, 55(10): 1067–1073. doi: 10.3969/j.issn.1001-893x.2015.10.001LI Xi, FENG Zhiyong, FENG Jianyuan, et al. Electromagnetic vortex and its application in wireless communication[J]. Telecommunication Engineering, 2015, 55(10): 1067–1073. doi: 10.3969/j.issn.1001-893x.2015.10.001 [9] CURLANDER J C and MCDONOUGH R N. Synthetic Aperture Radar[M]. New York: Wiley-Interscience, 1991. [10] CHENG Q, ALOMAINY A, and HAO Y. Compressive millimeter-wave phased array imaging[J]. IEEE Access, 2016, 4: 9580–9588. doi: 10.1109/ACCESS.2016.2635118 [11] LIU Kang, CHENG Yongqiang, YANG Zhaocheng, et al. Orbital-angular-momentum-based electromagnetic vortex imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 711–714. doi: 10.1109/LAWP.2014.2376970 [12] BU Xiangxi, ZHANG Zhuo, CHEN Longyong, et al. Implementation of vortex electromagnetic waves high-resolution synthetic aperture radar imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(5): 764–767. doi: 10.1109/LAWP.2018.2814980 [13] 洪文, 王彦平, 林赟, 等. 新体制SAR三维成像技术研究进展[J]. 雷达学报, 2018, 7(6): 633–654. doi: 10.12000/JR18109HONG Wen, WANG Yanping, LIN Yun, et al. Research progress on three-dimensional SAR imaging techniques[J]. Journal of Radars, 2018, 7(6): 633–654. doi: 10.12000/JR18109 [14] 杜永兴, 仝宗俊, 秦岭, 等. 基于改进BP算法的电磁涡旋成像方法[J]. 雷达科学与技术, 2020, 18(5): 539–545. doi: 10.3969/j.issn.1672-2337.2020.05.012DU Yongxing, TONG Zongjun, QIN Ling, et al. Electromagnetic vortex imaging method based on improved BP algorithm[J]. Radar Science and Technology, 2020, 18(5): 539–545. doi: 10.3969/j.issn.1672-2337.2020.05.012 [15] SHU Gaofeng, WANG Nan, WANG Wentao, et al. A novel vortex synthetic aperture radar imaging system: decreasing the pulse repetition frequency without increasing the antenna aperture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, in press. doi: 10.1109/TGRS.2021.3053650 [16] WANG Jianqiu, LIU Kang, CHENG Yongqiang, et al. Three-dimensional target imaging based on vortex stripmap SAR[J]. IEEE Sensors Journal, 2019, 19(4): 1338–1345. doi: 10.1109/JSEN.2018.2879814 [17] BU Xiangxi, ZHANG Zhuo, CHEN Longyong, et al. Synthetic aperture radar interferometry based on vortex electromagnetic waves[J]. IEEE Access, 2019, 7: 82693–82700. doi: 10.1109/ACCESS.2019.2908209 [18] MA Hui and LIU Hongwei. Waveform diversity-based generation of convergent beam carrying orbital angular momentum[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(7): 5487–5495. doi: 10.1109/TAP.2020.2981724 -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: