作者中心
专家审稿
责编办公
编辑办公
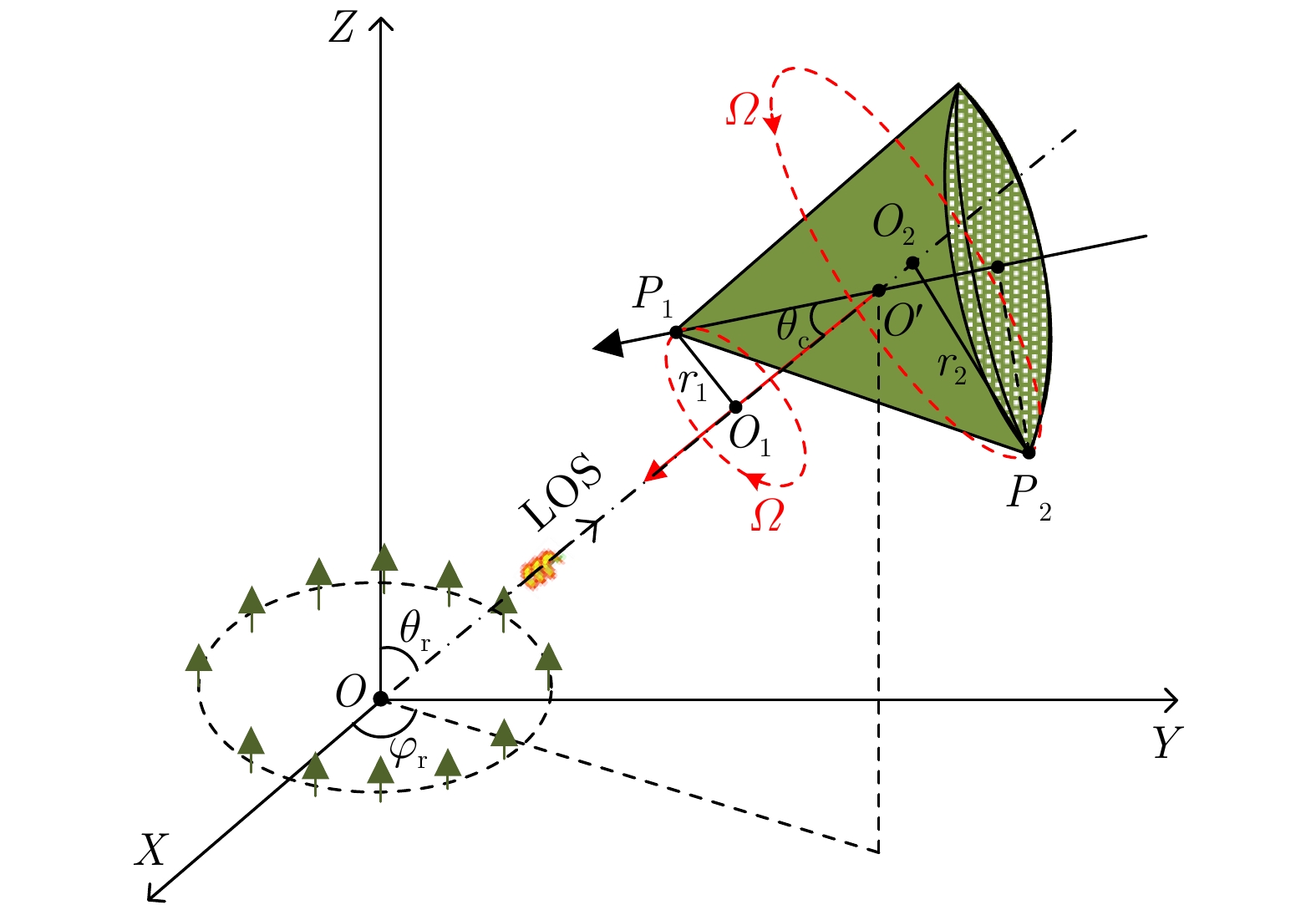
Rotational Doppler Detection of a Cone-shaped Target under the Illumination of a Vortex Electromagnetic Wave
-
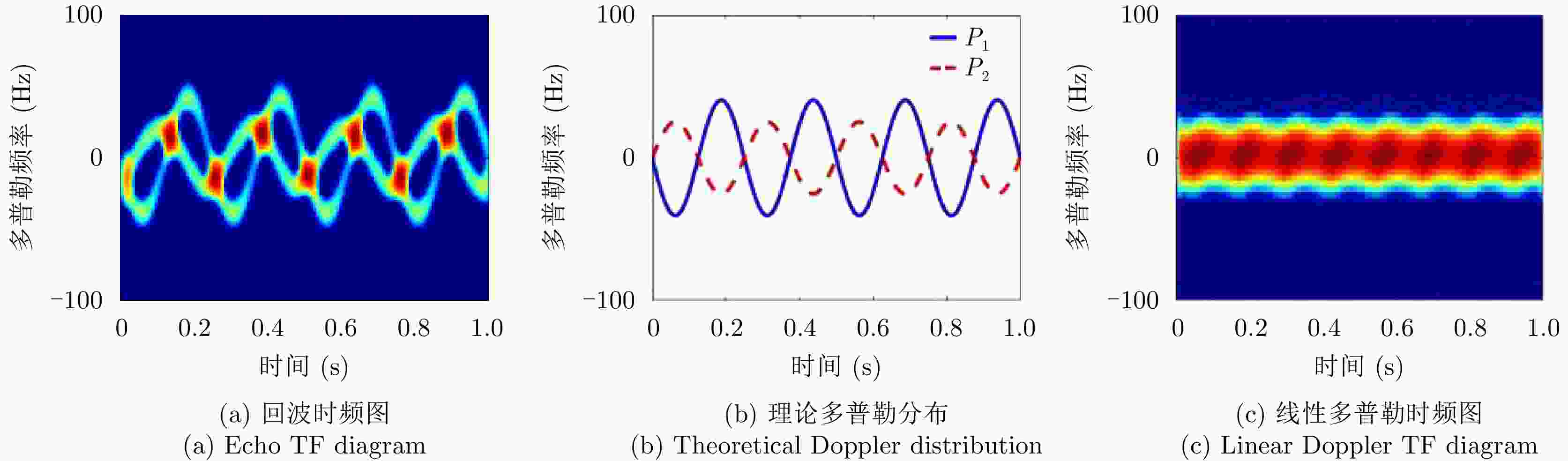
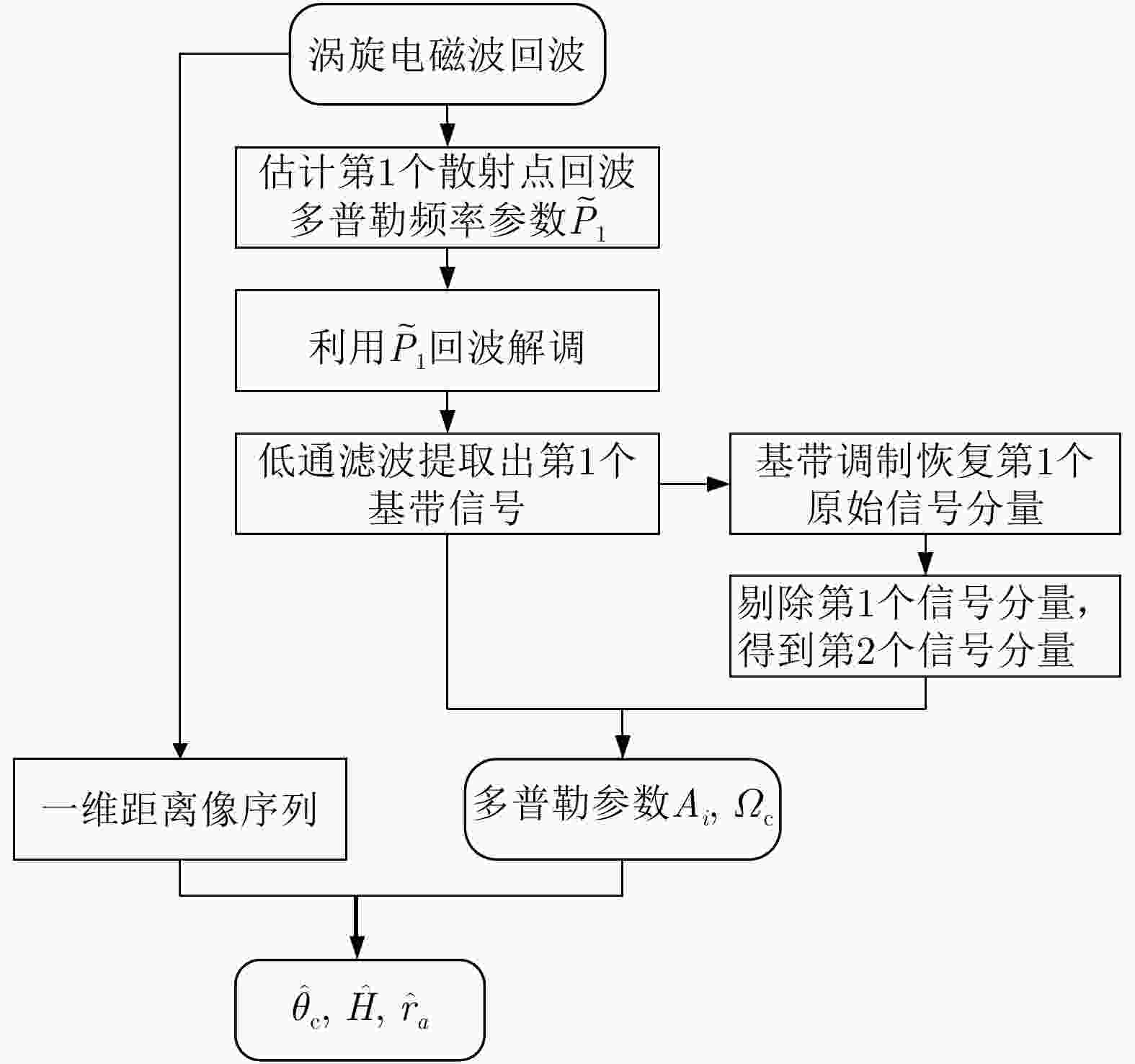
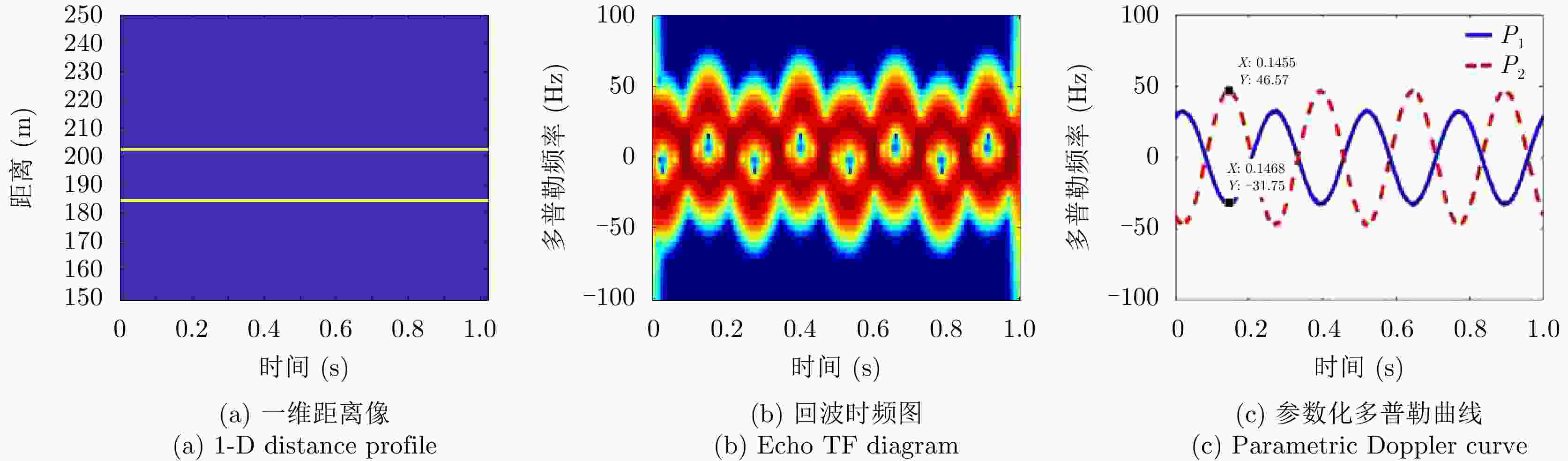
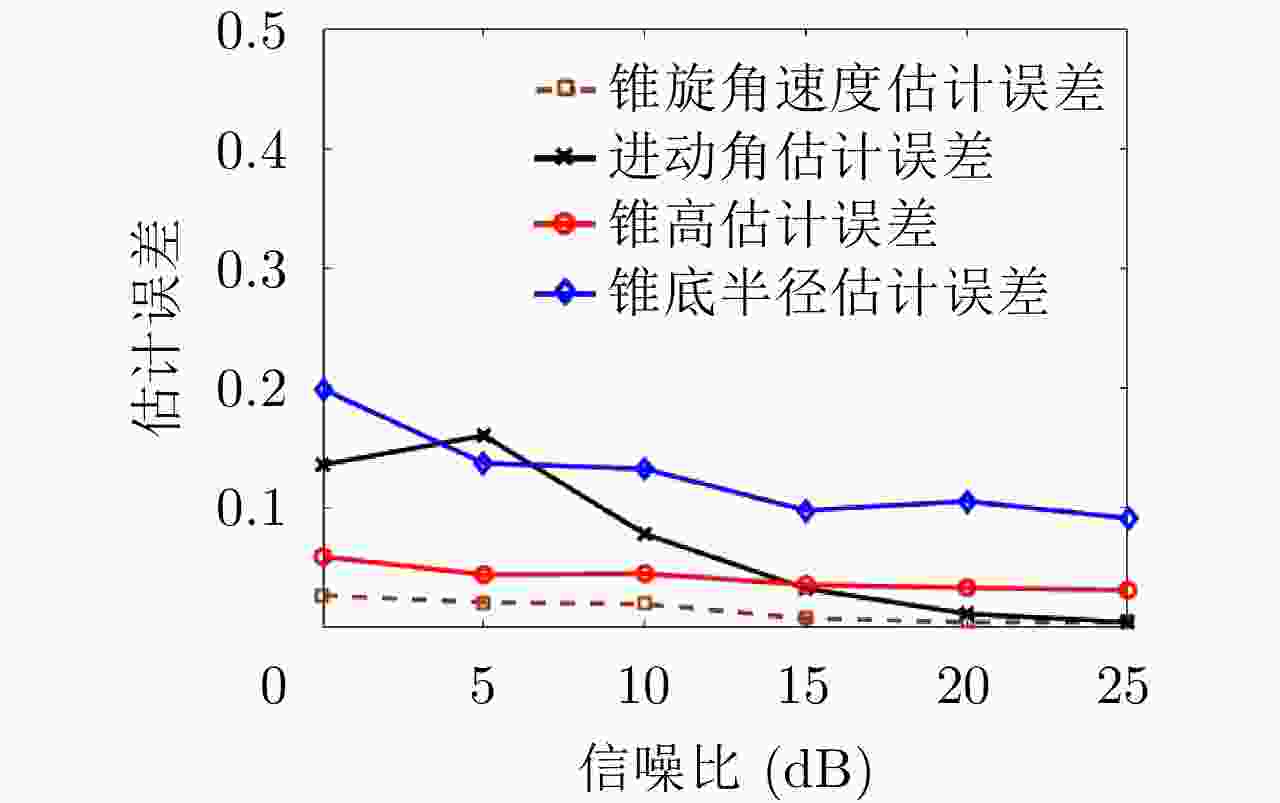
摘要: 涡旋电磁波具有独特螺旋状波前结构，其受目标横向微动调制产生的旋转多普勒效应，有望为雷达目标探测技术的发展提供一个新途径。在涡旋电磁波照射下，利用锥体微动对回波瞬时频率的周期性调制特性，可以有效反演出锥体目标的微动参数和几何特征。该文重点研究了雷达前视条件下的锥体目标参数估计。首先，基于涡旋电磁波雷达目标旋转多普勒探测原理，推导了涡旋电磁波锥体目标回波数学方程，建立了锥体目标回波旋转多普勒模型。其次，提出了前视条件下的锥体目标参数估计方法，利用锥顶散射点和锥底散射点两维的旋转多普勒信息，可以对锥体目标微动参数和几何特征参数进行有效估计，仿真结果验证了该文所提方法的有效性及抗噪声鲁棒性。Abstract: The vortex ElectroMagnetic (EM) wave has a unique spiral phase wavefront. The rotational Doppler effect, induced by the lateral micromotion of a target is expected to provide a new mode of radar target detection. Under the illumination of vortex EM waves, the micromotion of a cone-shaped target periodically modulates the instantaneous frequency of the radar echo; this can effectively reflect the geometric characteristics and micromotion parameters of a cone-shaped target. This paper focuses on the estimation of cone-shaped target parameters under forward-looking radar conditions. First, based on the principle of vortex EM wave target rotational Doppler detection, a mathematical equation describing the vortex EM wave of a cone-shaped target echo is derived, and an echo rotational Doppler model is established. Second, a method for cone-shaped target parameter estimation under forward-looking conditions is proposed. Using the two-dimensional rotational Doppler information of the scattering points at the top and bottom of a cone-shaped target, the micromotion and geometric parameters of the target can be effectively estimated. The simulation results verify the effectiveness and robustness of the method proposed in this paper.
-
图 1 涡旋电磁波雷达锥体目标探测示意图
Figure 1. Diagram of the vortex electromagnetic radar cone-shaped target detection
图 3 回波时频分布与多普勒模型对比
Figure 3. Comparison of echo time-frequency distribution and Doppler model
图 4 信号分离及参数估计方法流程
Figure 4. Flowchart of the signal separation and parameter estimation method
表 1 参数估计结果
Table 1. Parameter estimation result
参数 真实值 估计值 估计误差 (%) θc 15° 14.5758° 2.83 Ωc 8π rad/s 7.8821π rad/s 1.47 H 2 m 2.0105 m 0.52 ra 0.5 m 0.5426 m 8.52 
下载: 导出CSV
-
[1] TAMBURINI F, MARI E, SPONSELLI A, et al. Encoding many channels on the same frequency through radio vorticity: First experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. doi: 10.1088/1367-2630/14/3/033001 [2] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185–8189. doi: 10.1103/PhysRevA.45.8185 [3] LIU Kang, CHENG Yongqiang, LI Xiang, et al. Microwave-sensing technology using orbital angular momentum: Overview of its advantages[J]. IEEE Vehicular Technology Magazine, 2019, 14(2): 112–118. doi: 10.1109/MVT.2018.2890673 [4] WANG Jianqiu, LIU Kang, CHENG Yongqiang, et al. Vortex SAR imaging method based on OAM beams design[J]. IEEE Sensors Journal, 2019, 19(24): 11873–11879. doi: 10.1109/JSEN.2019.2937976 [5] ZHENG Jiayu, ZHENG Shilie, SHAO Zhenlei, et al. Analysis of rotational Doppler effect based on radio waves carrying orbital angular momentum[J]. Journal of Applied Physics, 2018, 124(16): 164907. doi: 10.1063/1.5050448 [6] ZHAO Mingyang, GAO Xinlu, XIE Mutong, et al. Measurement of the rotational Doppler frequency shift of a spinning object using a radio frequency orbital angular momentum beam[J]. Optics Letters, 2016, 41(11): 2549–2552. doi: 10.1364/OL.41.002549 [7] NIENHUIS G. Doppler effect induced by rotating lenses[J]. Optics Communications, 1996, 132(1/2): 8–14. [8] COURTIAL J, DHOLAKIA K, ROBERTSON D A, et al. Measurement of the rotational frequency shift imparted to a rotating light beam possessing orbital angular momentum[J]. Physical Review Letters, 1998, 80(15): 3217–3219. doi: 10.1103/PhysRevLett.80.3217 [9] COURTIAL J, ROBERTSON D A, DHOLAKIA K, et al. Rotational frequency shift of a light beam[J]. Physical Review Letters, 1998, 81(22): 4828–4830. doi: 10.1103/PhysRevLett.81.4828 [10] LAVERY M P J, SPEIRITS F C, BARNETT S M, et al. Detection of a spinning object using light’s orbital angular momentum[J]. Science, 2013, 341(6145): 537–540. doi: 10.1126/science.1239936 [11] CVIJETIC N, MILIONE G, IP E, et al. Detecting lateral motion using light’s orbital angular momentum[J]. Scientific Reports, 2015, 5(1): 15422. doi: 10.1038/srep15422 [12] ZHENG Jiayu, ZHENG S, SHAO Zhenlei, et al. Rotational Doppler effect based on the radio orbital angular momentum wave[C]. 2017 Asia Pacific Microwave Conference, Malaysia, 2017. [13] 傅子玲, 王智, 崔粲, 等. 利用涡旋光束的旋转多普勒效应测量角速度[J]. 激光与光电子学进展, 2019, 56(18): 180501. doi: 10.3788/LOP56.180501FU Ziling, WANG Zhi, CUI Can, et al. Angular velocity measurement based on rotational Doppler effect of vortex beam[J]. Laser &Optoelectronics Progress, 2019, 56(18): 180501. doi: 10.3788/LOP56.180501 [14] 陈行勇, 黎湘, 郭桂蓉, 等. 微进动弹道导弹目标雷达特征提取[J]. 电子与信息学报, 2006,, 28(4): 643–646.CHEN Xingyong, LI Xiang, GUO Guirong, et al. Radar feature extraction of micri-precession ballistic missile warhead[J]. Journal of Electronics &Information Technology, 2006,, 28(4): 643–646. [15] LEI PENG, SUN Jinping, WANG Jun, et al. Micromotion parameter estimation of free rigid targets based on radar micro-Doppler[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3776–3786. doi: 10.1109/TGRS.2012.2185244 [16] 雷腾, 刘进忙, 杨少春, 等. 基于三站一维距离像融合的弹道目标特征提取方法研究[J]. 宇航学报, 2012, 33(2): 228–234. doi: 10.3873/j.issn.1000-1328.2012.02.012LEI Teng, LIU Jinmang, YANG Shaochun, et al. Study on feature extraction method of ballistic target based on three-station range profiles[J]. Journal of Astronautics, 2012, 33(2): 228–234. doi: 10.3873/j.issn.1000-1328.2012.02.012 [17] 徐昕, 赵安军, 吉莎杉. 基于RCS的空间目标识别研究[J]. 火力与指挥控制, 2010, 35(10): 134–136. doi: 10.3969/j.issn.1002-0640.2010.10.037XU Xin, ZHAO Anjun, and JI Shashan. Recognition techniques for space targets based on RCS[J]. Fire Control & Command Control, 2010, 35(10): 134–136. doi: 10.3969/j.issn.1002-0640.2010.10.037 [18] 庄钊文, 肖顺平, 王雪松. 雷达极化信息处理及其应用[M]. 北京: 国防工业出版社, 1999ZHUANG Zhaowen, XIAO Shunping, and WANG Xuesong. Radar Polarization Information Processing and Application[M]. Beijing: National Defense Industry Press, 1999. [19] 马君国, 赵宏钟, 李保国. 基于结构特征的空间目标识别算法[J]. 现代雷达, 2006, 27(7): 67–70. doi: 10.3969/j.issn.1004-7859.2006.07.020MA Junguo, ZHAO Hongzhong, and LI Baoguo. Space target recognition algorithm based on structure feature[J]. Modern Radar, 2006, 27(7): 67–70. doi: 10.3969/j.issn.1004-7859.2006.07.020 [20] 潘勉. 雷达高分辨距离像目标识别技术研究[D], 西安电子科技大学, 2013PAN Mian. Study of radar target recognition technology based on high range resolution profile[D]. [Ph.D. dissertation], Xidian University, 2013. [21] HU Yuankui and YANG Yiming. Automatic target recognition of ISAR images based on Hausdorff distance[C]. The 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 477–479. [22] LIU Yongxiang, LI Xiang, ZHUANG Zhaowen, et al. Estimation of micro-motion parameters based on micro-Doppler[J]. IET Signal Processing, 2010, 4(3): 213–217. doi: 10.1049/iet-spr.2009.0042 [23] CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: Phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2–21. [24] RENHORN I G E, KARLSSON C, LETALICK D, et al. Coherent laser radar for vibrometry: Robust design and adaptive signal processing[C]. The SPIE 2472, Applied Laser Radar Technology II, Orlando, USA, 1995. [25] 王兆云, 张兴敢, 柏业超. 基于微多普勒的锥体目标进动和结构参数估计[J]. 南京大学学报: 自然科学, 2014, 50(2): 148–153.WANG Zhaoyun, ZHANG Xinggan, and BAI Yechao. Precession and structural parameter estimation of cone-shaped target based on the micro-Doppler[J]. Journal of Nanjing University:Natural Sciences, 2014, 50(2): 148–153. [26] 韩勋, 杜兰, 刘宏伟. 基于窄带微多普勒调制的锥体目标参数估计[J]. 电子与信息学报, 2015, 37(4): 961–968. doi: 10.11999/JEIT140814HAN Xun, DU Lan, and LIU Hongwei. Parameter estimation of cone-shaped target based on narrowband micro-Doppler modulation[J]. Journal of Electronics &Information Technology, 2015, 37(4): 961–968. doi: 10.11999/JEIT140814 [27] LIU Baiyang, CHU Hongchen, GIDDENS H, et al. Experimental observation of linear and rotational Doppler shifts from several designer surfaces[J]. Scientific Reports, 2019, 9(1): 8971. doi: 10.1038/s41598-019-45516-1 [28] 陈是扦, 彭志科, 邢冠培. 基于参数化解调的旋转目标微多普勒频率提取方法[J]. 上海航天, 2018, 35(5): 39–44. doi: 10.19328/j.cnki.1006-1630.2018.05.006CHEN Shiqian, PENG Zhike, and XING Guanpei. Micro-Doppler frequency extraction for rotating targets based on parameterized demodulation[J]. Aerospace Shanghai, 2018, 35(5): 39–44. doi: 10.19328/j.cnki.1006-1630.2018.05.006 -
图(6) / 表(1)
计量
- 文章访问数: 1805
- HTML全文浏览量: 1283
- PDF下载量: 222
- 被引次数: 0
