作者中心
专家审稿
责编办公
编辑办公
SAR Target Physics Interpretable Recognition Method Based on Three Dimensional Parametric Electromagnetic Part Model
-
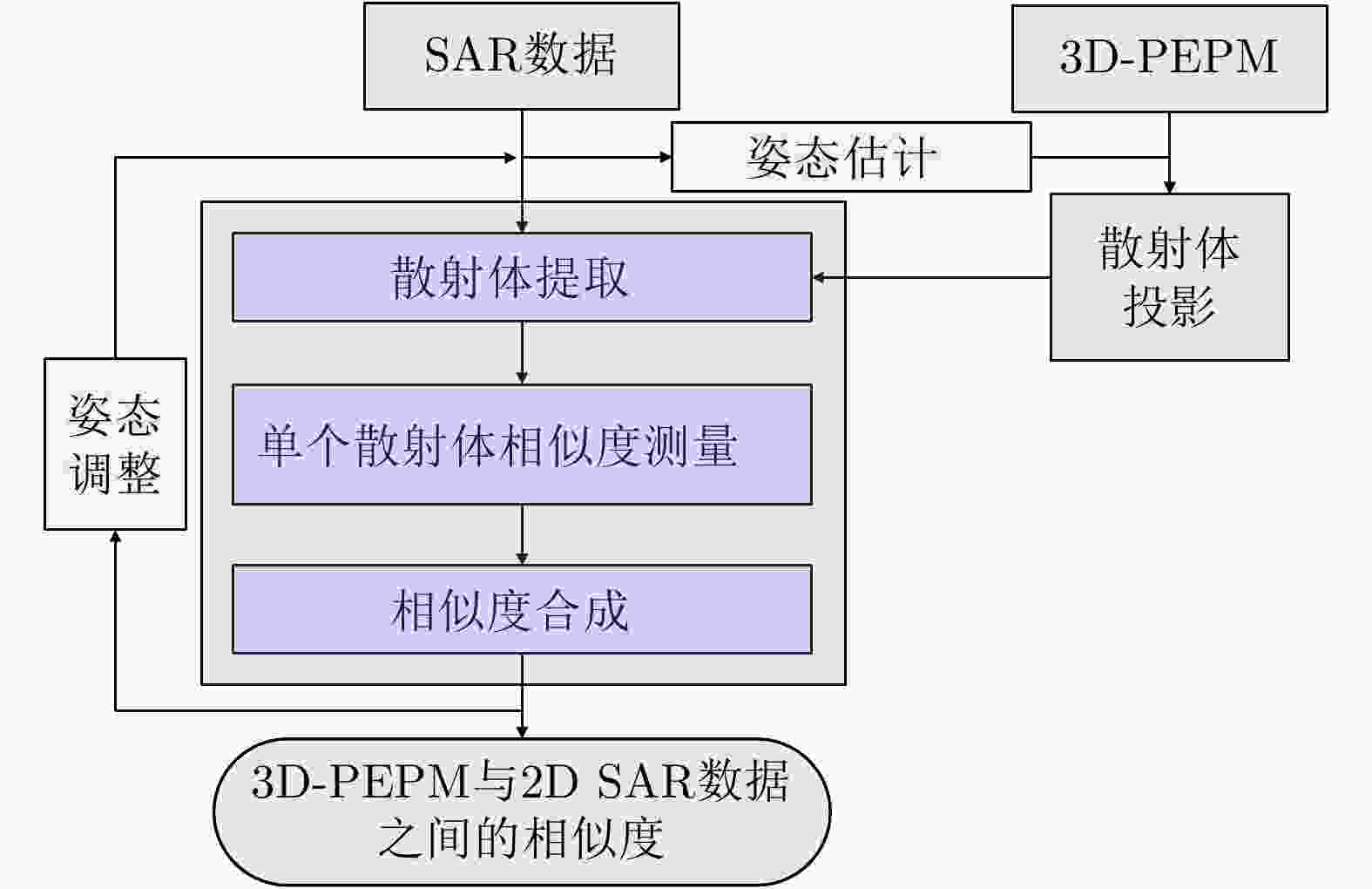
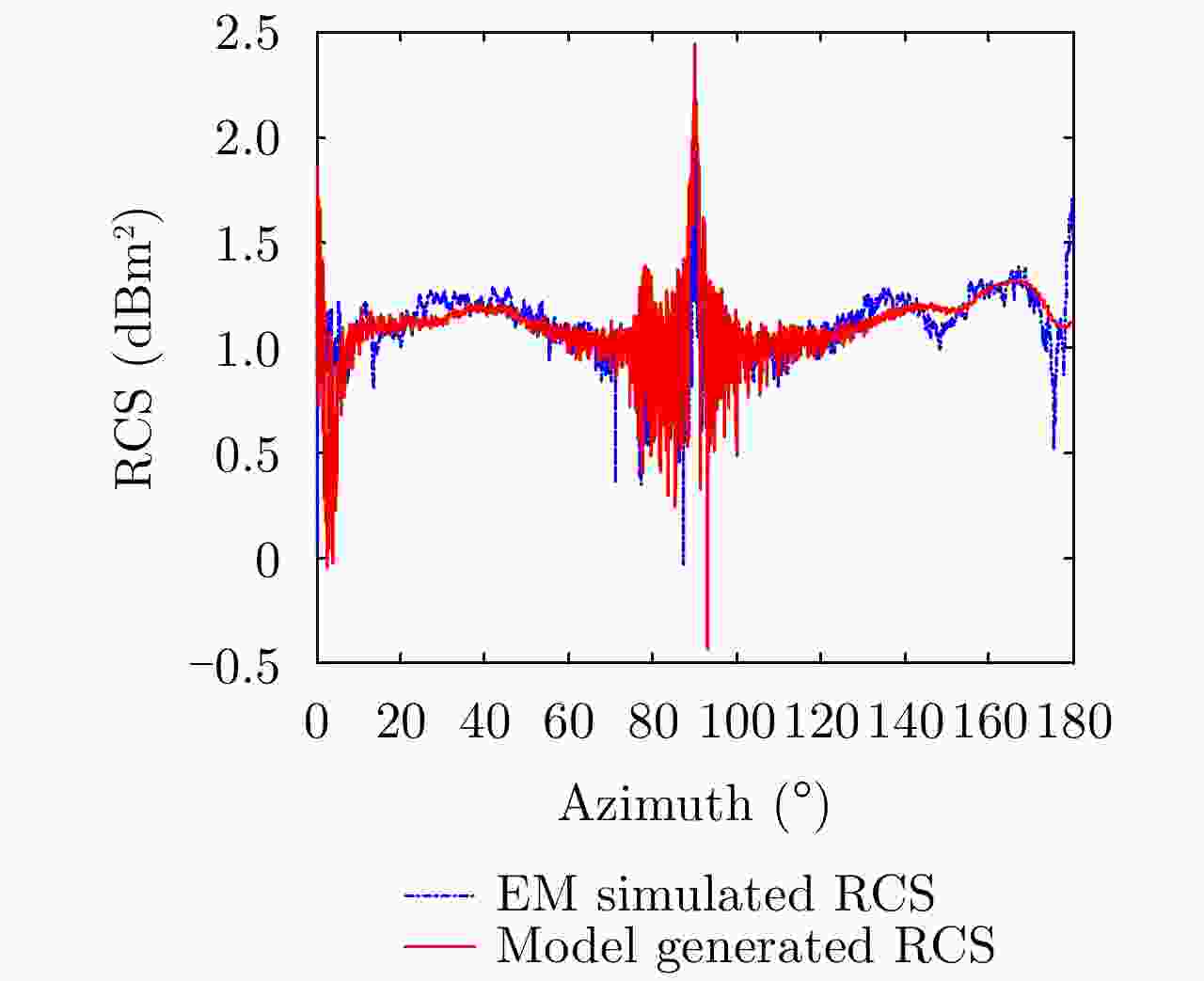
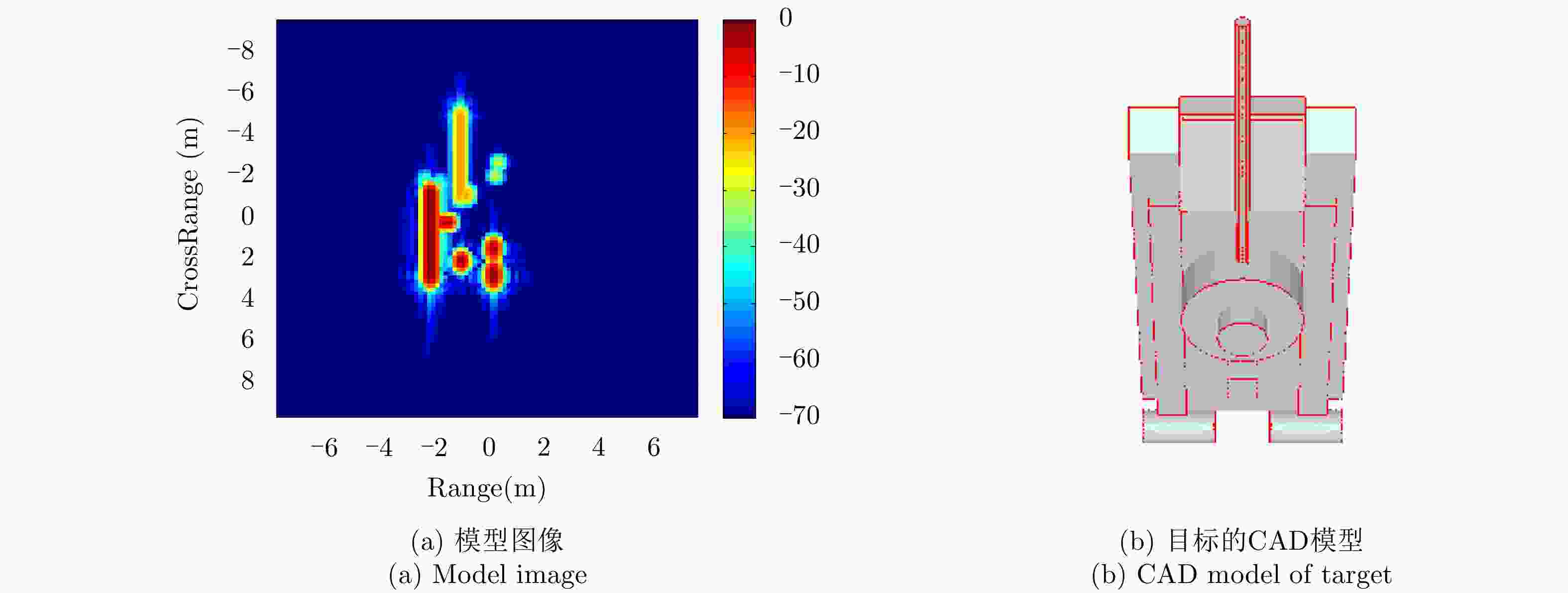
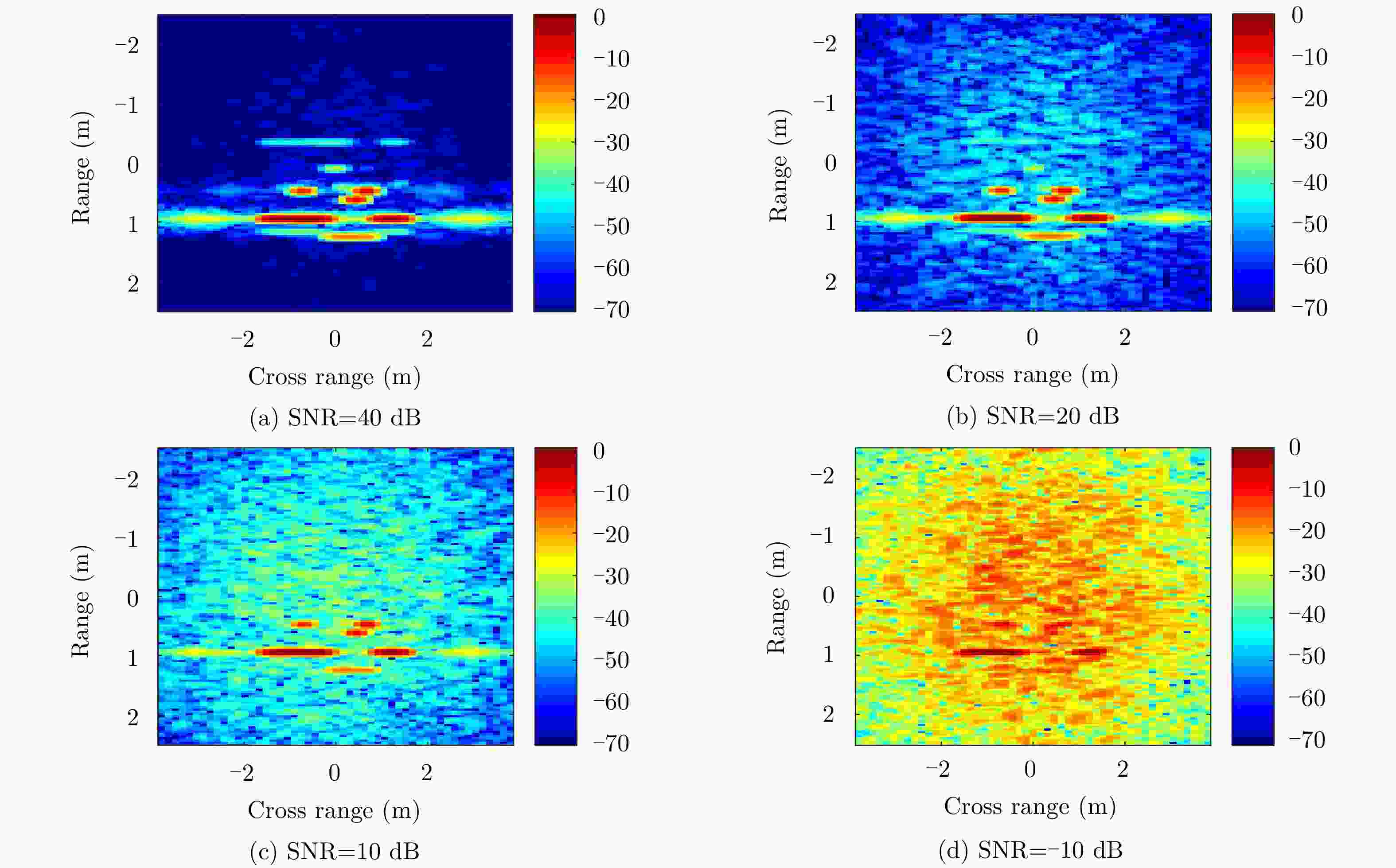
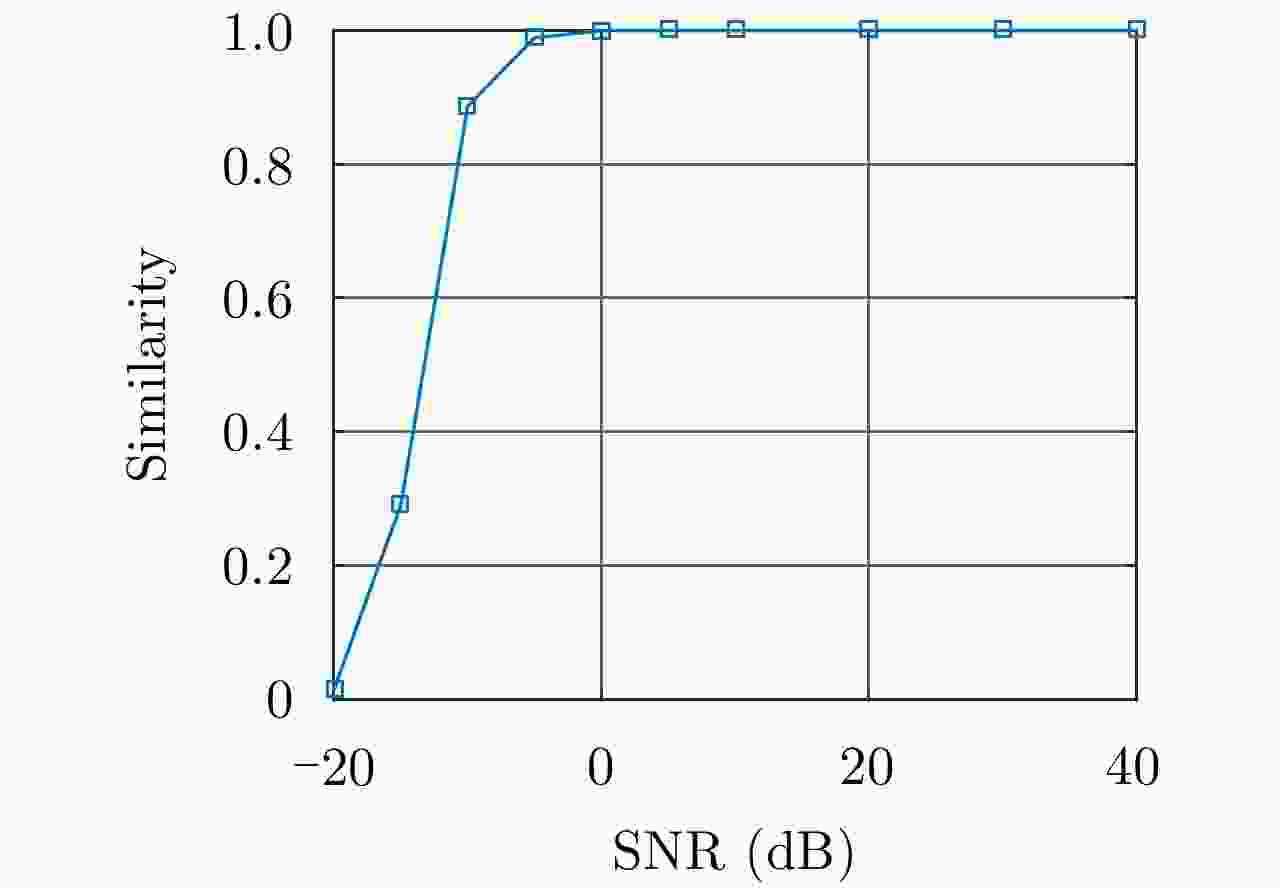
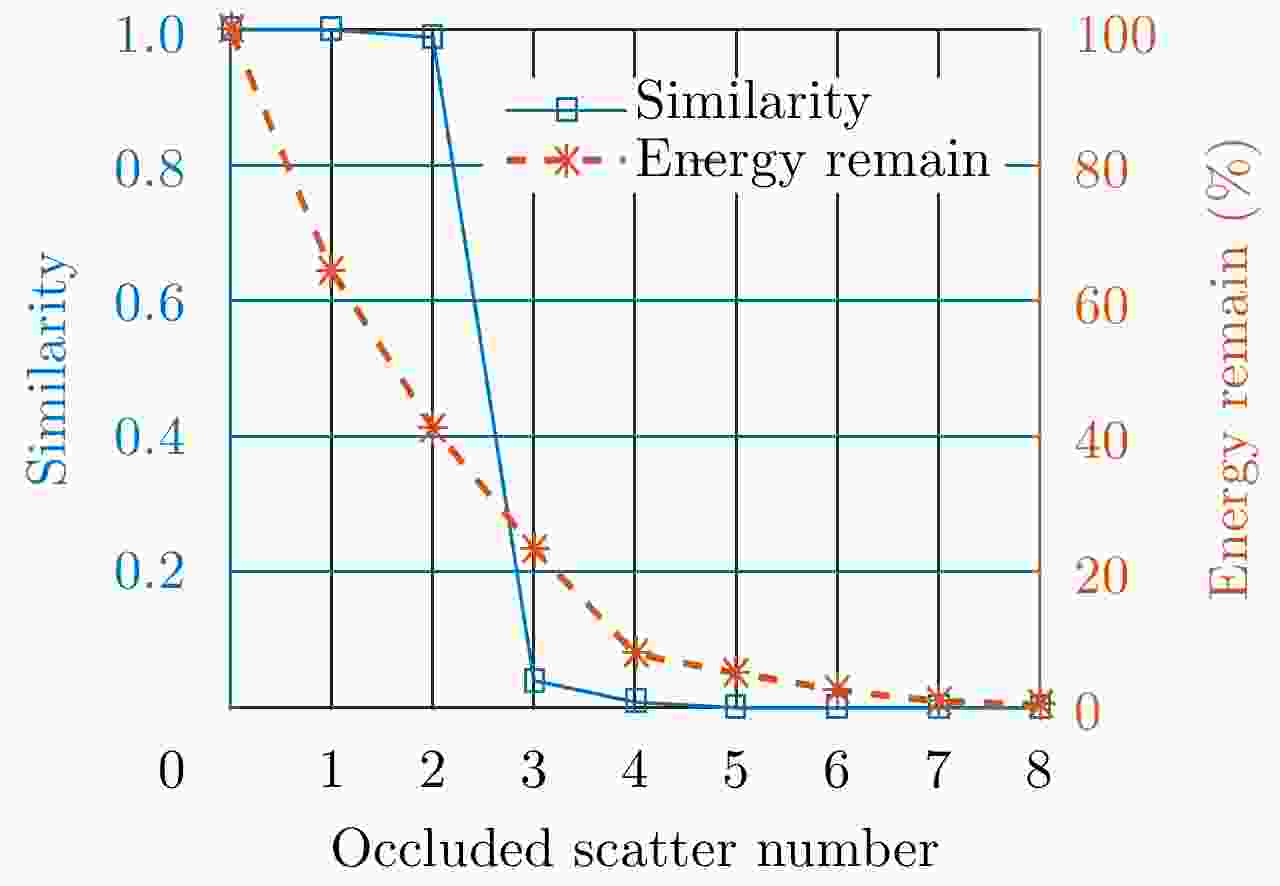
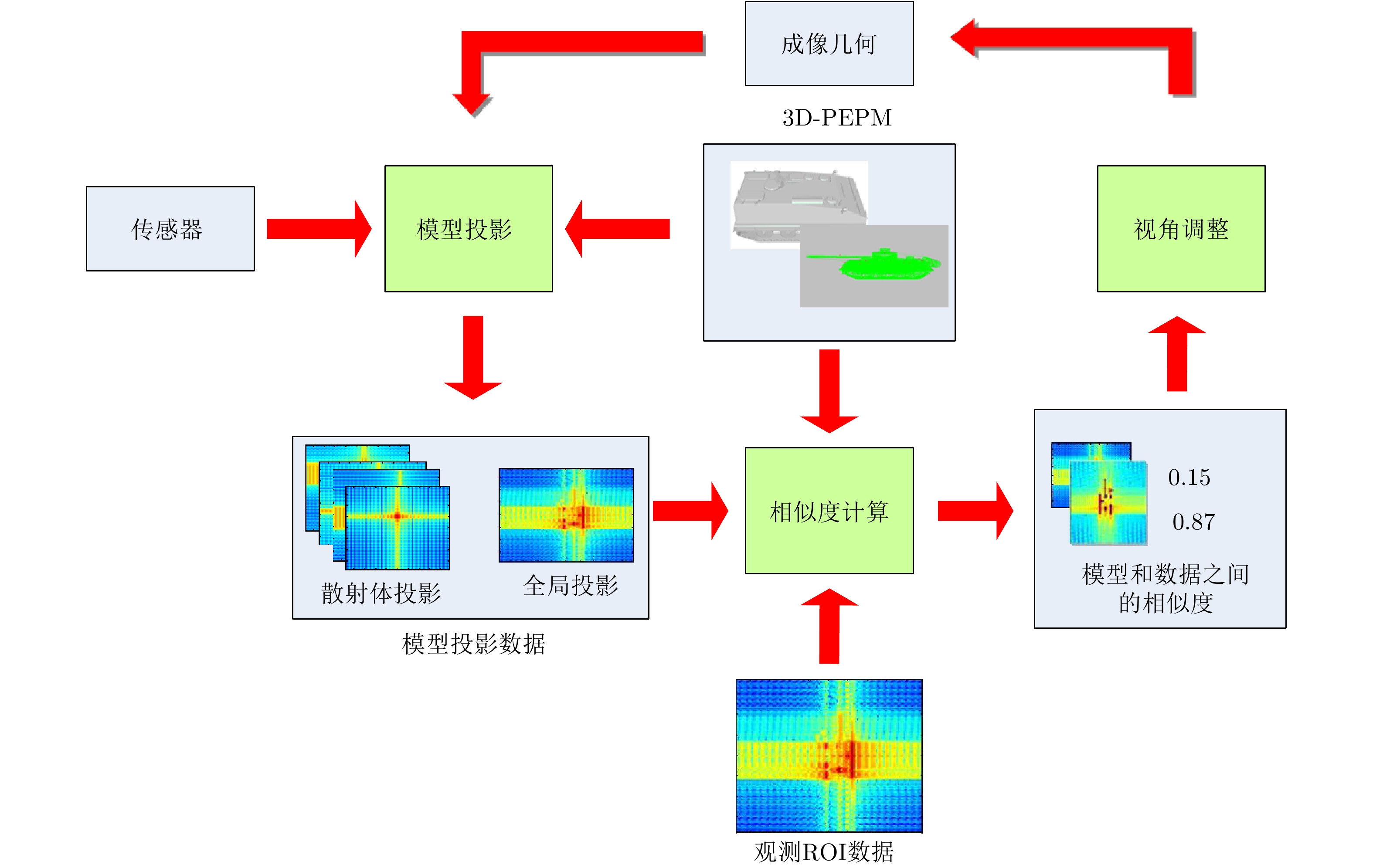
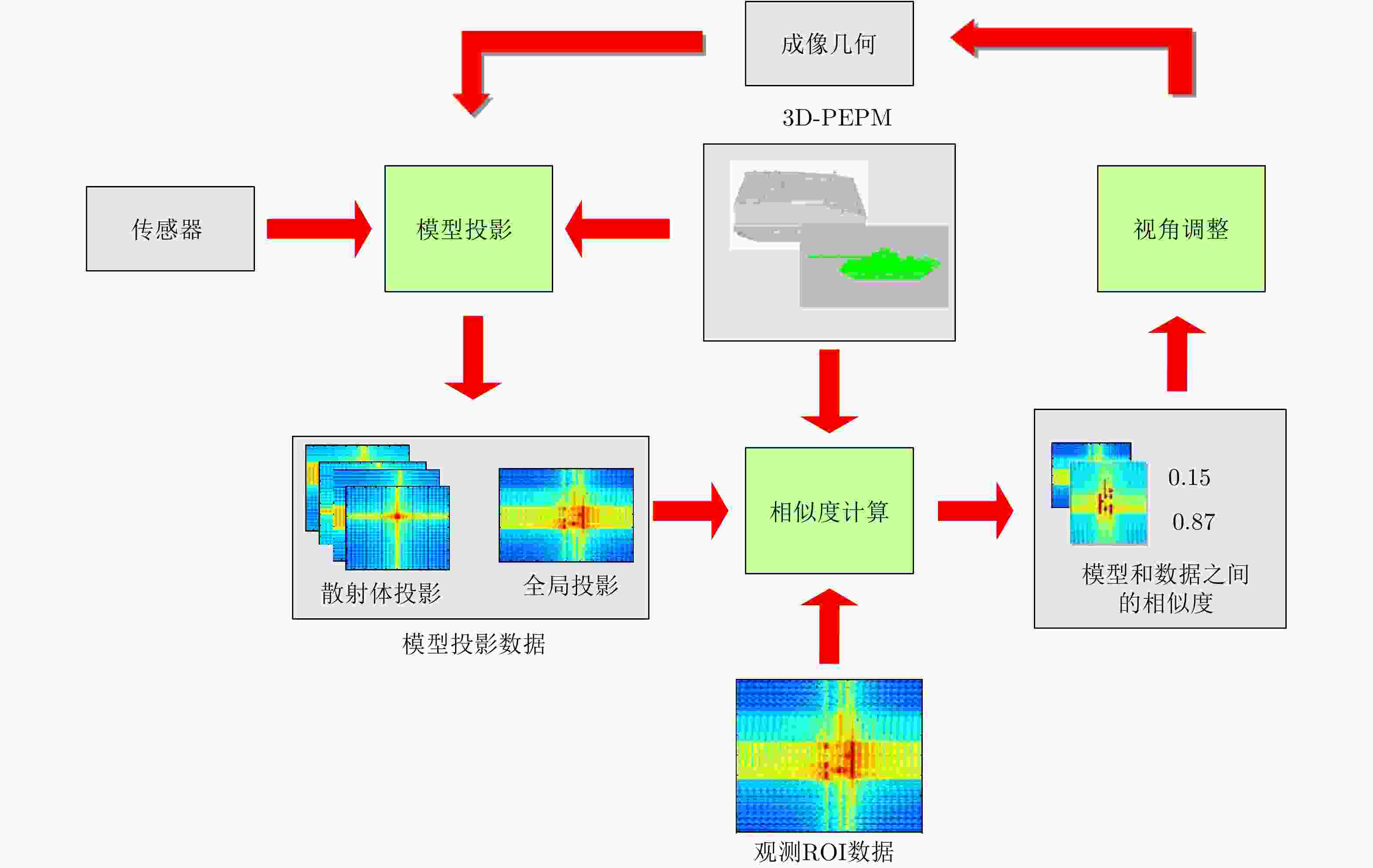
摘要: 该文通过部件级三维参数化电磁模型(3D-PEPM)描述了复杂目标的电磁散射现象，并基于此模型提出了一种新的合成孔径雷达(SAR)目标识别方法。该方法首先根据雷达参数将3D-PEPM中各个散射体的散射响应投影到二维图像平面，预测每个散射体的位置和形状，然后根据3D-PEPM提供的先验信息评估3D-PEPM与SAR数据之间的相似程度，最后利用一种视角调整方法对整个过程进行优化，产生3D-PEPM和SAR数据之间的最终匹配分数，并根据该匹配分数完成识别决策。这种识别方法明确标识了SAR数据和3D-PEPM散射体之间的对应关系，具有清晰的物理可解释性，能够有效处理各种扩展条件下的SAR目标识别问题，仿真实验验证了该方法的有效性。Abstract: In this paper, a target’s electromagnetic scattering phenomenon is characterized by the Three Dimensional Parametric Electromagnetic Part Model (3D-PEPM) and a novel Synthetic Aperture Radar (SAR) target recognition method is proposed based on the model. The proposed method projects the individual scatterers in the 3D-PEPM to the 2D image plane to predict the location and appearance for each scatterer according to the radar parameters firstly. Then based on the prior information provided by the 3D-PEPM, the similarities between the 3D-PEPM and SAR data are evaluated. Finally, a view angle adjusting method is utilized to optimize the whole process to produce the final match score between the model and SAR data, and the recognition decision is made according to the match score. The proposed recognition method identifies clearly the correspondences of the scatterers between SAR data and 3D-PEPM and enjoys the explicit physical interpretability, so it can deal with SAR recognition problems under various extended operating conditions. Experiments on simulated data reveal the effectiveness of the proposed method.
-
图 7 模型和EM仿真软件产生的目标RCS对比
Figure 7. Comparison of target RCS generated by 3D-PEPM and EM simulation software
图 8 不同视角下基于3D-PEPM生成的图像
Figure 8. Images generated from different perspectives based on 3D-PEPM
图 9 相同视角下3个模型的观测图像
Figure 9. Observation images of three models in the same perspective
图 10 模型图像和3D-PEPM物理相关的散射体
Figure 10. Model image and 3D-PEPM physically related scatterers
图 11 模型图像和3D-PEPM物理相关的散射体
Figure 11. Model image and 3D-PEPM physically related scatterers
图 12 相同视角下3个模型的观测图像
Figure 12. Observation images of three models in the same perspective
图 13 Slicy目标在不同信噪比下的仿真图像
Figure 13. The simulated images of the slicy target under different SNR
图 15 散射体遮挡下的相似度测量性能
Figure 15. Performance of similarity measurement under scatterer occlusion
表 1 参数的统计模型
Table 1. Statistical model of parameters
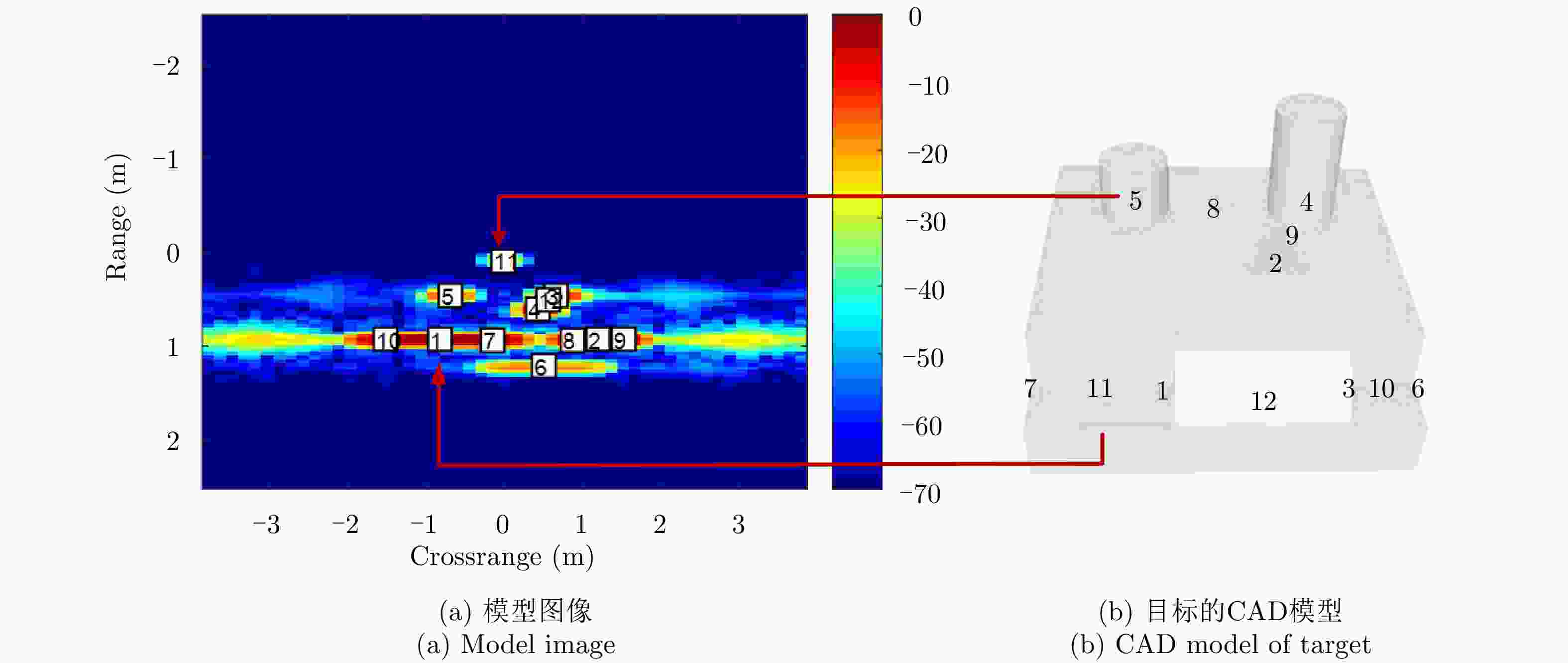
特征属性 均值 方差 距离向位置 $x$ ${x_0}$ ${\sigma^2 _x} = {f^2_{ {\rm{Downrange} } } }$ 方位向位置 $y$ ${y_0}$ ${\sigma^2 _y} = {f^2_{ {\rm{Crossrange} } } }$ 幅度 $\log 10(\left| A \right|)$ $\lg ({\left| A \right|_0})$ ${\sigma^2 _A} = 0.5$ 长度 $L$ ${L_0}$ ${\sigma^2 _L} = {(2{f_{ {\rm{Crossrange} } } })^2}$ 
下载: 导出CSV
表 2 模型投影和从数据估计得到的散射体参数的对比
Table 2. Comparison between model projection and scatterer parameters estimated from data
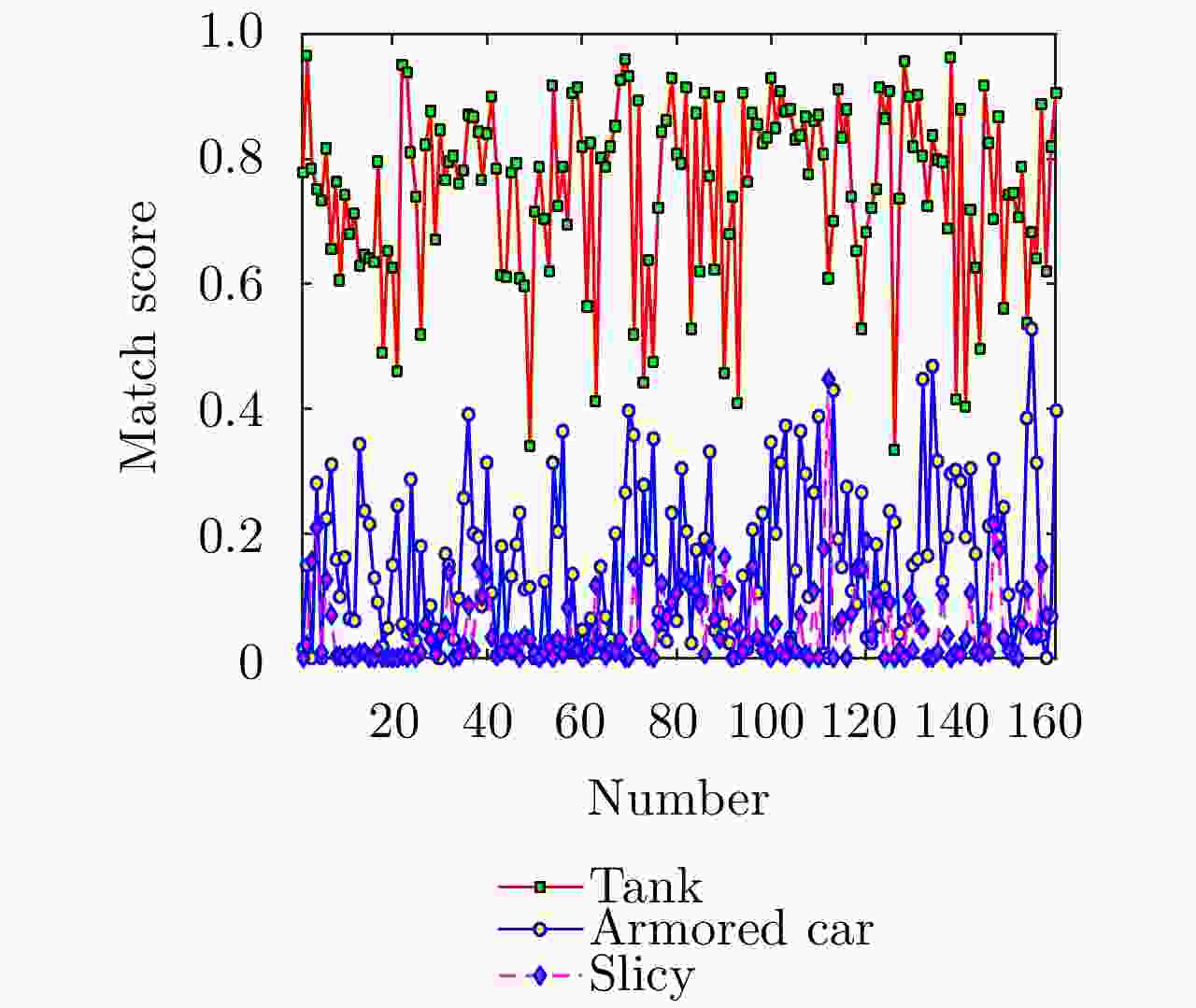
序号 模型投影得到的散射体参数 从数据估计得到的散射体参数 相似度 X(m) Y(m) L(m) A X(m) Y(m) L(m) A 1 –1.932 0.567 4.416 1.000 –1.932 0.487 4.265 1.000 0.643 2 –0.901 1.772 0.649 0.532 –0.900 1.780 0 0.193 0.254 3 0.181 1.212 0.708 0.458 0.182 1.210 0.695 0.095 0.902 4 0.181 2.400 1.057 0.328 0.183 2.394 0.868 0.114 0.705 5 0.181 –1.126 0.668 0.091 0.178 –1.168 0.633 0.048 0.841 6 –1.601 0 0 0.067 –1.730 –0.001 0 0.076 0.664 7 –1.068 –3.031 4.377 0.052 –0.929 –2.879 4.276 0.044 0.351 8 –0.772 –1.264 0.647 0.010 –0.770 –1.262 0.697 0.018 0.922 9 –1.431 0 0 0.008 –1.548 –0.002 0 0.045 0.689 10 0.338 –2.598 0.325 0.006 0.340 –2.324 0 0.001 0.227
下载: 导出CSV
-
[1] EL-DARYMLI K, GILL E W, MCGUIRE P, et al. Automatic target recognition in synthetic aperture radar imagery: A state-of-the-art review[J]. IEEE Access, 2016, 4: 6014–6058. doi: 10.1109/ACCESS.2016.2611492 [2] NOVAK L M, OWIRKA G J, BROWER W S, et al. The automatic target-recognition system in SAIP[J]. The Lincoln Laboratory Journal, 1997, 10(2): 187–202. [3] PARK J I, PARK S H, and KIM K T. New discrimination features for SAR automatic target recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 476–480. doi: 10.1109/LGRS.2012.2210385 [4] NICOLI L P and ANAGNOSTOPOULOS G C. Shape-based recognition of targets in synthetic aperture radar images using elliptical Fourier descriptors[C]. SPIE 6967, Automatic Target Recognition XVIII, Orlando, USA, 2008. [5] MISHRA A K. Validation of PCA and LDA for SAR ATR[C]. The TENCON 2008 - 2008 IEEE Region 10 Conference, Hyderabad, India, 2008: 1–6. [6] 宦若虹, 杨汝良. 基于小波域NMF特征提取的SAR图像目标识别方法[J]. 电子与信息学报, 2009, 31(3): 588–591. doi: 10.3724/SP.J.1146.2007.01808HUAN Ruohong and YANG Ruliang. Synthetic aperture radar images target recognition based on wavelet domain NMF feature extraction[J]. Journal of Electronics &Information Technology, 2009, 31(3): 588–591. doi: 10.3724/SP.J.1146.2007.01808 [7] DONG Ganggang and KUANG Gangyao. Classification on the monogenic scale space: Application to target recognition in SAR image[J]. IEEE Transactions on Image Processing, 2015, 24(8): 2527–2539. doi: 10.1109/TIP.2015.2421440 [8] POTTER L C and MOSES R L. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79–91. doi: 10.1109/83.552098 [9] MOSES P L, POTTER L C, and GUPTA I J. Feature extraction using attributed scattering center models for model-based automatic target recognition (ATR)[R]. AFRL-SN-WP-TR-2006-1004, 2005. [10] LIU Xian, HUANG Yulin, PEI Jifang, et al. Sample discriminant analysis for SAR ATR[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(12): 2120–2124. doi: 10.1109/LGRS.2014.2321164 [11] HUANG Yulin, PEI Jifang, YANG Jianyu, et al. Neighborhood geometric center scaling embedding for SAR ATR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 180–192. doi: 10.1109/TAES.2013.110769 [12] DING Jun, CHEN Bo, LIU Hongwei, et al. Convolutional neural network with data augmentation for SAR target recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 364–368. [13] CHEN Sizhe, WANG Haipeng, XU Feng, et al. Target classification using the deep convolutional networks for SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4806–4817. doi: 10.1109/TGRS.2016.2551720 [14] ROSS T D, BRADLEY J J, HUDSON L J, et al. SAR ATR: So what’s the problem? An MSTAR perspective[C]. SPIE 3721, Algorithms for Synthetic Aperture Radar Imagery VI, Orlando, USA, 1999: 606–610. [15] KEYDEL E R, LEE S W, and MOORE J T. MSTAR extended operating conditions: A tutorial[C]. SPIE 2757, Algorithms for Synthetic Aperture Radar Imagery III, Orlando, USA, 1996: 228–242. [16] JONES III G and BHANU B. Recognition of articulated and occluded objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(7): 603–613. doi: 10.1109/34.777371 [17] DIEMUNSCH J R and WISSINGER J. Moving and stationary target acquisition and recognition (MSTAR) model-based automatic target recognition: Search technology for a robust ATR[C]. SPIE 3370, Algorithms for Synthetic Aperture Radar Imagery V, Orlando, USA, 1998: 481–492. [18] HUANG Peikang, YIN Hongcheng, and XU Xiaojian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2006. [19] CHIANG H C, MOSES R L, and POTTER L C. Model-based Bayesian feature matching with application to synthetic aperture radar target recognition[J]. Pattern Recognition, 2001, 34(8): 1539–1553. doi: 10.1016/S0031-3203(00)00089-3 [20] ZHOU Jianxiong, SHI Zhiguang, XIAO Cheng, et al. Automatic target recognition of SAR images based on global scattering center model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3713–3729. doi: 10.1109/TGRS.2011.2162526 [21] JACKSON J A. Three-dimensional feature models for synthetic aperture radar and experiments in feature extraction[D]. [Ph. D. dissertation], Ohio State University, 2009. [22] 文贡坚, 朱国强, 殷红成, 等. 基于三维电磁散射参数化模型的SAR目标识别方法[J]. 雷达学报, 2017, 6(2): 115–135. doi: 10.12000/JR17034WEN Gongjian, ZHU Guoqiang, YIN Hongcheng, et al. SAR ATR based on 3D parametric electromagnetic scattering model[J]. Journal of Radars, 2017, 6(2): 115–135. doi: 10.12000/JR17034 [23] GIUSTI E, MARTORELLA M, and CAPRIA A. Polarimetrically-persistent-scatterer-based automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4588–4599. doi: 10.1109/TGRS.2011.2164804 [24] TANG Tao and SU Yi. Object recognition based on feature matching of scattering centers in SAR imagery[C]. The 5th International Congress on Image and Signal Processing, Chongqing, China, 2012: 1073–1076. [25] MARTORELLA M, GIUSTI E, DEMI L, et al. Target recognition by means of polarimetric ISAR images[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 225–239. doi: 10.1109/TAES.2011.5705672 [26] SAVILLE M A, SAINI D K, and SMITH J. Commercial vehicle classification from spectrum parted linked image test-attributed synthetic aperture radar imagery[J]. IET Radar, Sonar & Navigation, 2016, 10(3): 569–576. [27] RICHARDS J A. Target model generation from multiple synthetic aperture radar image[D]. [Ph. D. dissertation], 1996, MIT. [28] HE Yang, HE Siyuan, ZHANG Yunhua, et al. A forward approach to establish parametric scattering center models for known complex radar targets applied to SAR ATR[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6192–6205. doi: 10.1109/TAP.2014.2360700 [29] ZHOU Jianxiong, SHI Zhiguang, and FU Qiang. Three-dimensional scattering center extraction based on wide aperture data at a single elevation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1638–1655. doi: 10.1109/TGRS.2014.2346509 [30] VOICU L I, PATTON R, and MYLER H R. Multicriterion vehicle pose estimation for SAR ATR[C]. SPIE 3721, Algorithms for Synthetic Aperture Radar Imagery VI, Orlando, USA, 1999: 3721. [31] CUI Xunxue, ZHANG Jichun, and ZHOU Pucheng. Hypothesis testing for target detection model in sensor networks[C]. The 7th International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, China, 2010. [32] BOSE R. Lean CLEAN: Deconvolution algorithm for radar imaging of contiguous targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 2190–2199. doi: 10.1109/TAES.2011.5937291 [33] SHAFER G. A Mathematical Theory of Evidence[M]. Princeton: Princeton University Press, 1976. [34] FELZENSZWALB P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part-based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627–1645. doi: 10.1109/TPAMI.2009.167 -
计量
- 文章访问数: 2688
- HTML全文浏览量: 1169
- PDF下载量: 219
- 被引次数: 0
