-
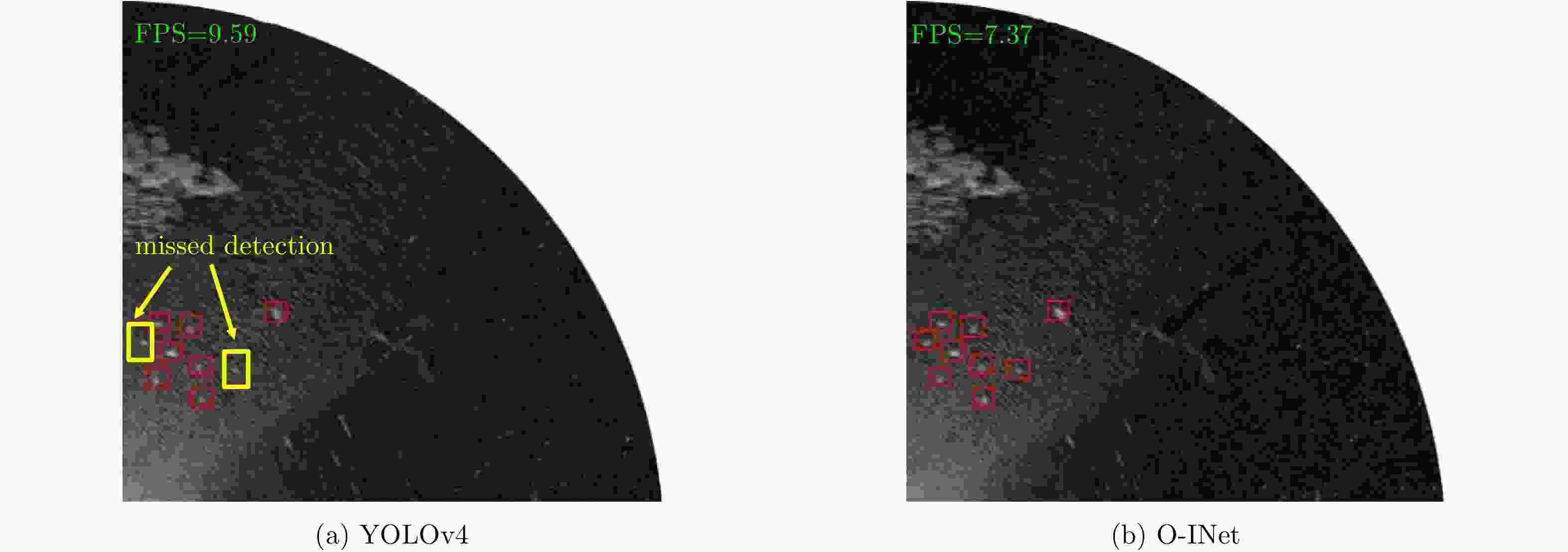
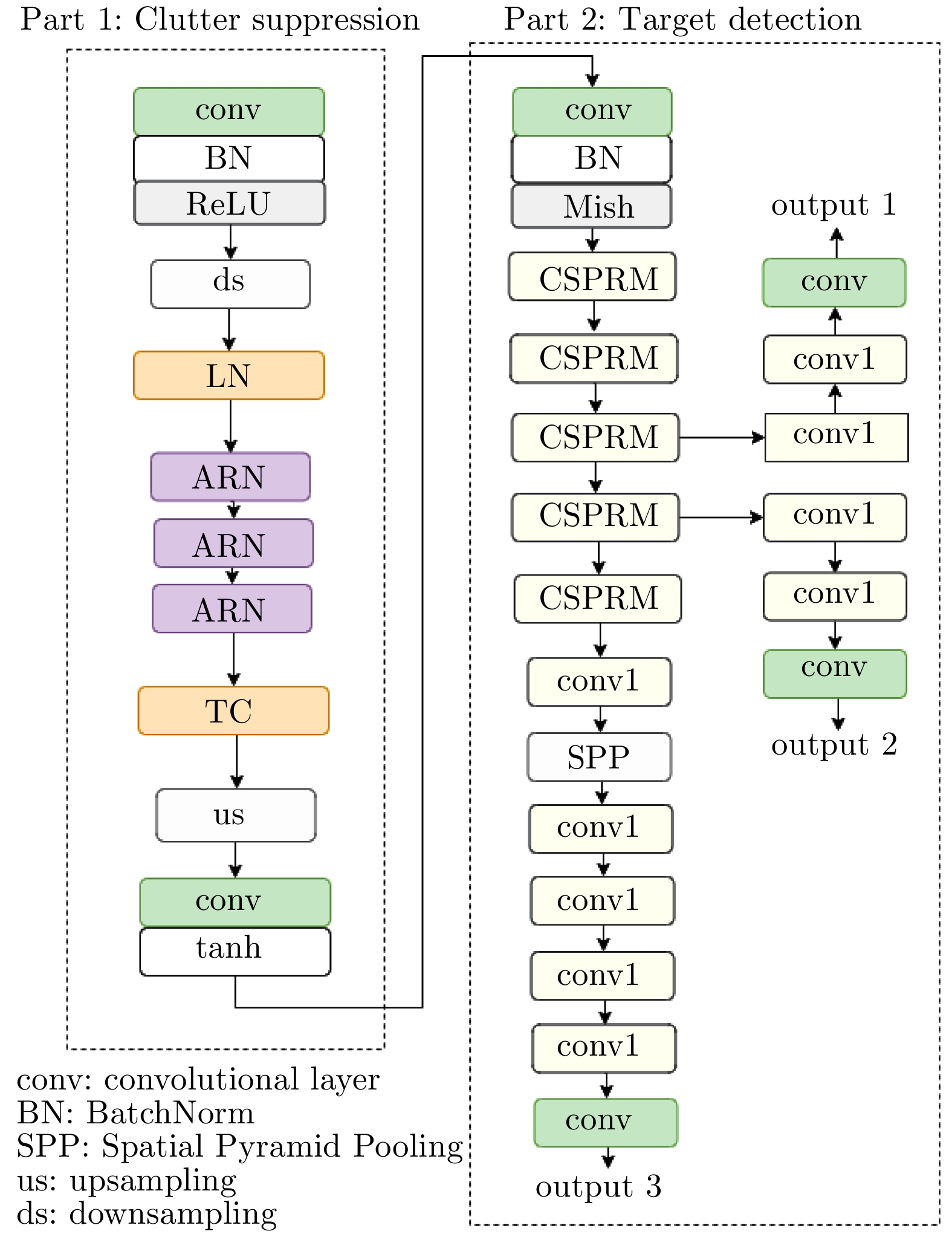
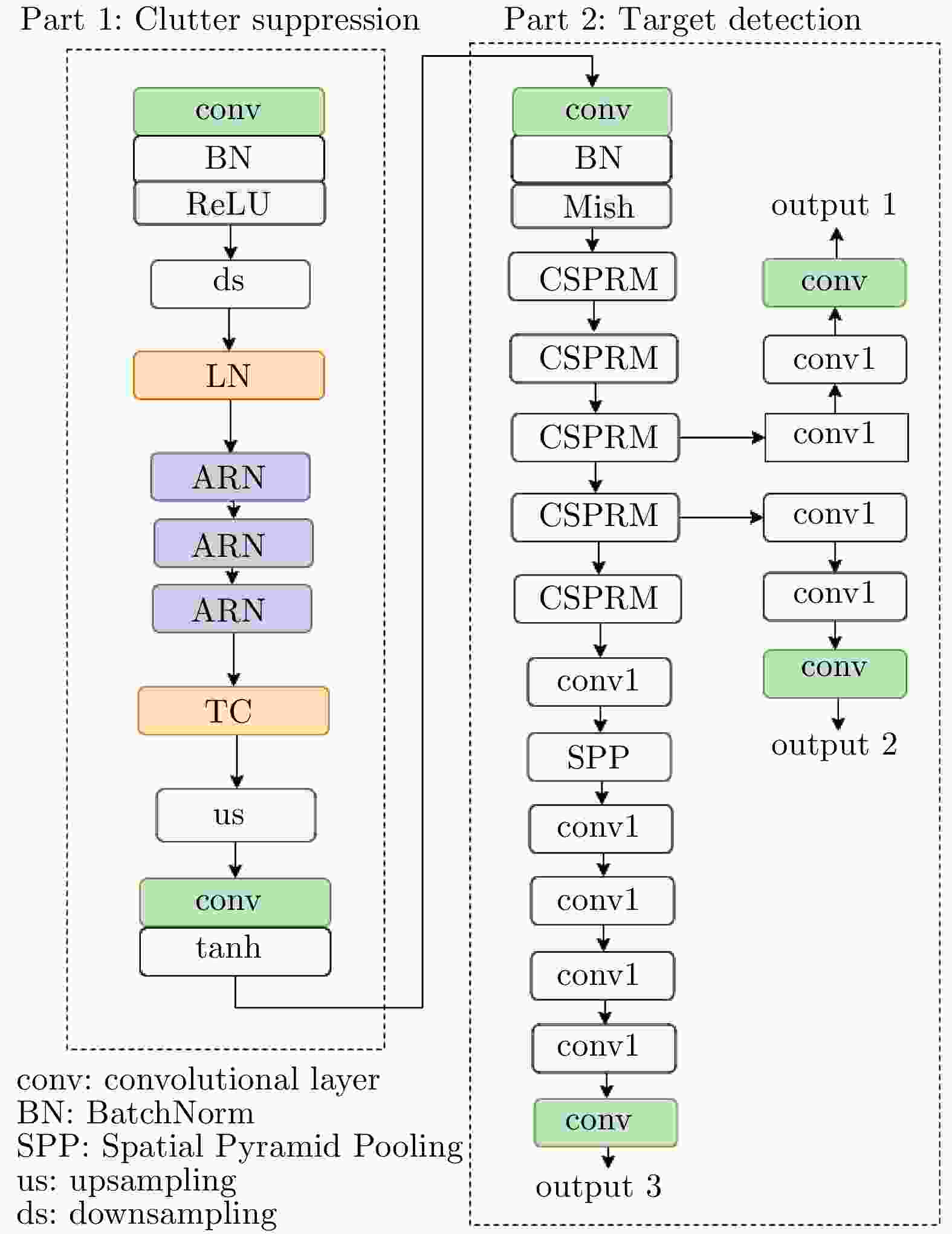
摘要: 强海杂波与海面目标的复杂特性使得海面目标回波微弱,有效的海杂波抑制和稳健快速的目标检测是雷达对海上目标探测需考虑的重要因素。然而,现有的海面目标检测算法对于复杂环境下的目标检测性能有限,环境和目标特性适应性差。该文设计了一种杂波抑制和目标检测融合网络(INet),通过层归一化-传递和连接方法提取关键目标特征,采用注意力网络抑制杂波和增强目标,构建跨阶段局部残差网络保证检测网络的轻量化和准确性。基于导航雷达在多种观测条件下采集的回波数据,构建了海面目标雷达图像数据集;通过模型的预训练和平面位置显示器(PPI)图像的帧间积累对INet进行了优化,得到了Optimized INet(O-INet)模型。经过多种天气条件下实测数据测试和验证,并与YOLOv3, YOLOv4,双参数CFAR和二维CA-CFAR对比后证明,所提方法在提高检测概率、降低虚警率和复杂条件下的强泛化能力有显著优势。Abstract: A marine radar device is a major navigation tool for boaters and ships. The images produced by marine radars detect not only hard targets such as ships and coastlines, but also reflections from the sea surface, known as sea clutter. The strong sea clutter and the complex characteristics of marine targets result in transmission of weak echo signals of the images to the radar, which makes difficult for radars to distinguish and analyze. So, effective sea clutter suppression and robust, fast target detection mechanisms are needed for radar to detect marine targets efficiently. However, the existing marine target detection algorithms have limited performance for target detection under complex environments, and have poor adaptability to environment and target characteristics. In this paper, an Integrated Network (INet) for clutter suppression and target detection algorithm is proposed and designed to optimize the signals received from the targets. The layer normalization algorithm integrated with transfer function is used to extract key target features, and the spatial attention network is used to suppress the clutter and to enhance the target signals, and a local cross-scale residual network is built to ensure the weightlessness of the system and accuracy of the detection network. Based on the echo data collected by the navigation radar under various observation conditions, radar images with marine target dataset were constructed. INet was optimized through pre-training of the model and inter-frame accumulation of Plan Position Indicator (PPI) images to obtain the Optimized INet (O-INet). The measured data were verified, tested, and compared with data obtained through various algorithms such as YOLOv3, YOLOv4, two-parameter CFAR, and two-dimensional CA-CFAR. The results obtained prove that the proposed method has superior advantages over other methods in improving detection probability, reducing false alarm rate, and strong generalization ability under complex conditions.
-
表 1 实时验证数据集参数
Table 1. Parameters of real-time verification dataset
数据编号 目标数量 目标尺度 目标速度 海况 背景 PPI视频帧数 Data_01# 3 中型船 中速 2级 海杂波较弱 150 Data_02# 2 中、小型船 低速 2级 地杂波较弱 150 Data_03# 9 中、小型船 低速 4级 海杂波较强 50 Data_04# 5 中、小型船 低速 4级 大雪 50 Data_05# 2 中、小型船 低速 4级 中雨 50 表 2 测试结果
Table 2. Test result
算法 Recall FA 速度 INet 91.12% 1.30% 9.12 FPS 表 3 INet模型优化结果对比
Table 3. Comparison of optimization results
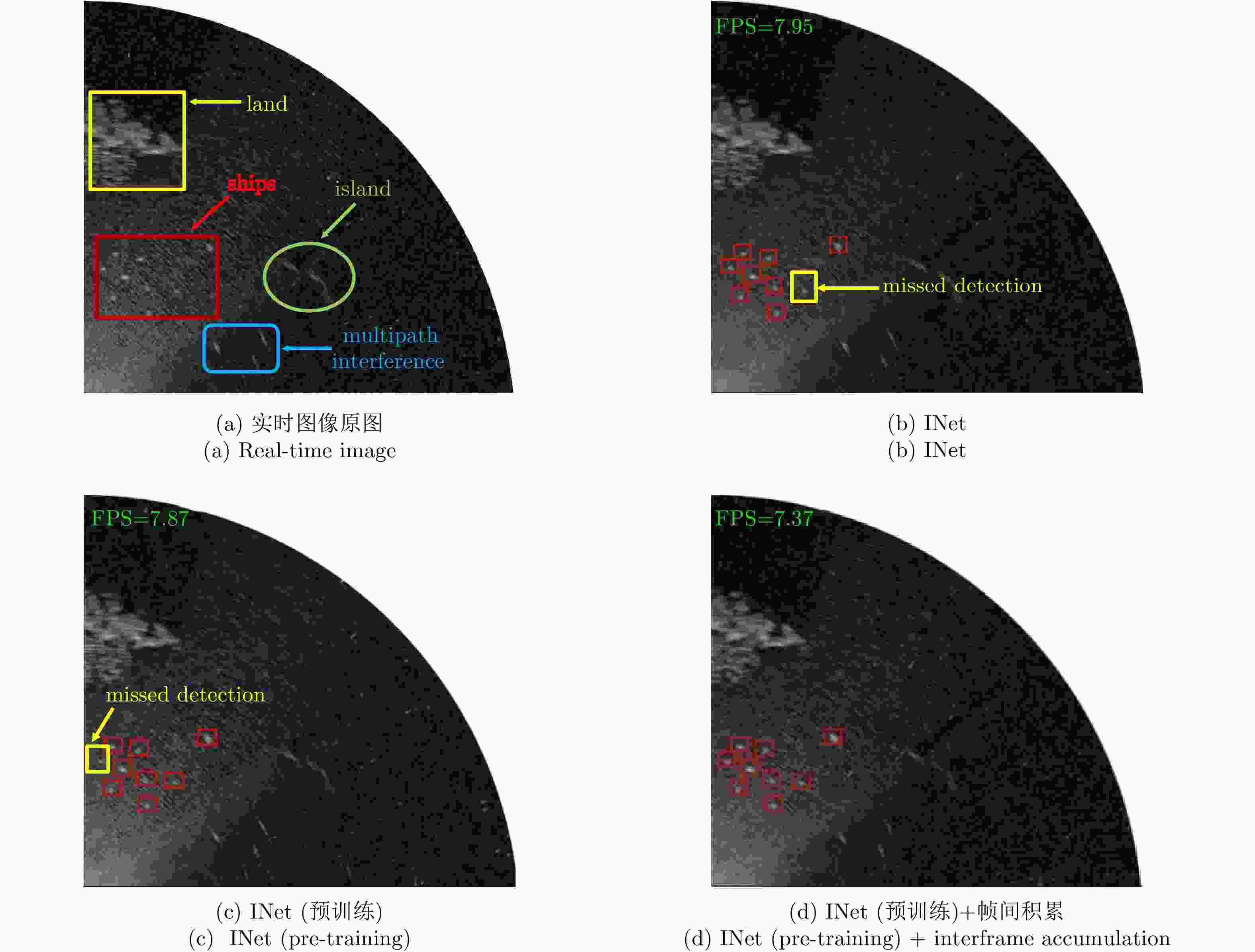
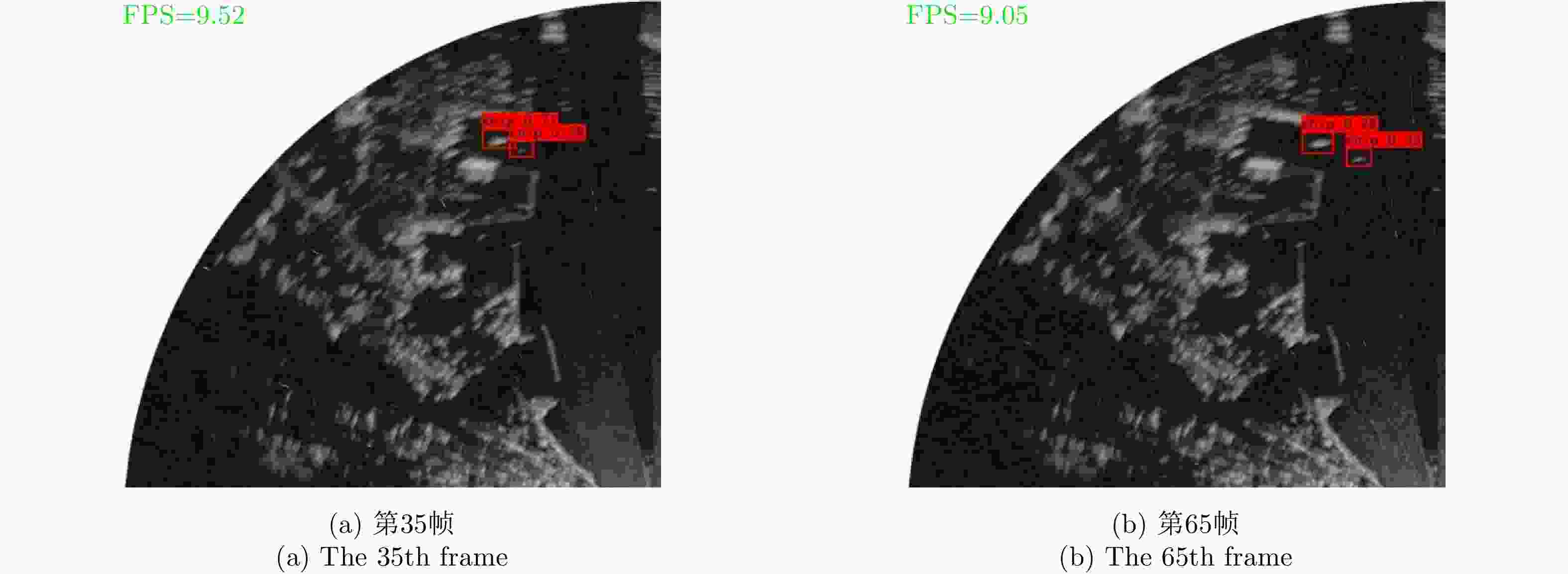
算法 简称 Recall (%) FA (%) 平均速度(FPS) INet INet 91.12 1.12 9.12 INet(预训练) \ 92.27 0.37 9.04 INet +帧间积累 \ 91.55 0.59 9.03 INet (预训练)
+帧间积累O-INet 92.73 0.33 8.79 表 4 各类算法的实验结果对比
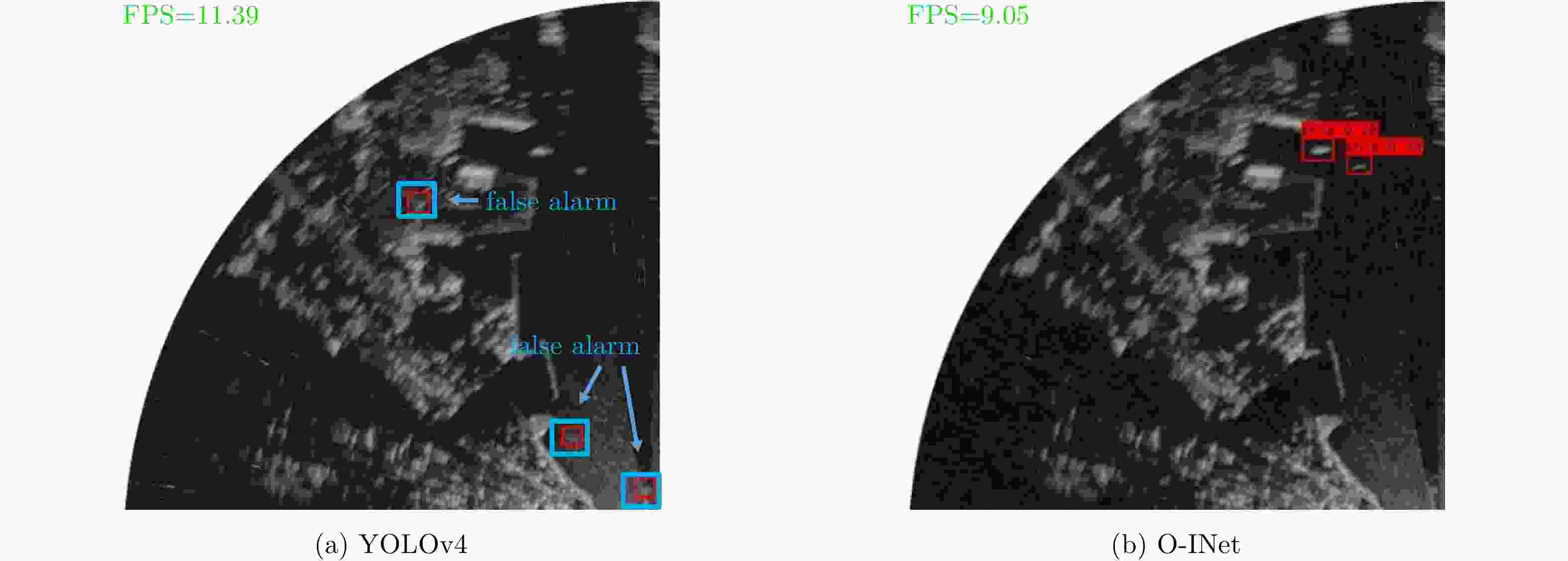
Table 4. Comparison of experimental results on different algorithms
表 5 对测试集的检测结果(%)
Table 5. Test results about the test dataset (%)
方法 Pfa=10–4 Pfa=10–3 Pfa=10–2 非相参积累+双参数CFAR 16.94 42.52 57.71 非相参积累+二维 CA-CFAR 18.25 37.76 54.29 O-INet 80.98 91.04 93.65 -
[1] 何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理[M]. 2版. 北京: 清华大学出版社, 2011: 1–15.HE You, GUAN Jian, and MENG Xiangwei. Radar Target Detection and CFAR Processing[M]. 2nd ed. Beijing: Tsinghua University Press, 2011: 1–15. [2] 黄勇, 陈小龙, 关键. 实测海尖峰特性分析及抑制方法[J]. 雷达学报, 2015, 4(3): 334–342. doi: 10.12000/JR14108HUANG Yong, CHEN Xiaolong, and GUAN Jian. Property analysis and suppression method of real measured sea spikes[J]. Journal of Radars, 2015, 4(3): 334–342. doi: 10.12000/JR14108 [3] TRUNK G V and GEORGE S F. Detection of targets in non-Gaussian sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, AES-6(5): 620–628. doi: 10.1109/TAES.1970.310062 [4] 刘宁波, 董云龙, 王国庆, 等. X波段雷达对海探测试验与数据获取[J]. 雷达学报, 2019, 8(5): 656–667. doi: 10.12000/JR19089LIU Ningbo, DONG Yunlong, WANG Guoqing, et al. Sea-detecting X-band radar and data acquisition program[J]. Journal of Radars, 2019, 8(5): 656–667. doi: 10.12000/JR19089 [5] YU Xiaohan, CHEN Xiaolong, HUANG Yong, et al. Fast detection method for low-observable maneuvering target via robust sparse fractional Fourier transform[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 978–982. doi: 10.1109/LGRS.2019.2939264 [6] 许述文, 石星宇, 水鹏朗. 复合高斯杂波下抑制失配信号的自适应检测器[J]. 雷达学报, 2019, 8(3): 326–334. doi: 10.12000/JR19030XU Shuwen, SHI Xingyu, and SHUI Penglang. An adaptive detector with mismatched signals rejection in compound Gaussian clutter[J]. Journal of Radars, 2019, 8(3): 326–334. doi: 10.12000/JR19030 [7] LIU Yi, ZHANG Shufang, SUO Jidong, et al. Research on a new Comprehensive CFAR (Comp-CFAR) processing method[J]. IEEE Access, 2019, 7: 19401–19413. doi: 10.1109/ACCESS.2019.2897358 [8] WANG H and CAI L. A localized adaptive MTD processor[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(3): 532–539. doi: 10.1109/7.81435 [9] CHEN Xiaolong, GUAN Jian, WANG Guoqing, et al. Fast and refined processing of radar maneuvering target based on hierarchical detection via sparse fractional representation[J]. IEEE Access, 2019, 7: 149878–149889. doi: 10.1109/ACCESS.2019.2947169 [10] CHEN Xiaolong, YU Xiaohan, HUANG Yong, et al. Adaptive clutter suppression and detection algorithm for radar maneuvering target with high-order motions via sparse fractional ambiguity function[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 1515–1526. doi: 10.1109/JSTARS.2020.2981046 [11] 王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040 [12] 牟效乾, 陈小龙, 苏宁远, 等. 基于时频图深度学习的雷达动目标检测与分类[J]. 太赫兹科学与电子信息学报, 2019, 17(1): 105–111. doi: 10.11805/TKYDA201901.0105MOU Xiaoqian, CHEN Xiaolong, SU Ningyuan, et al. Radar detection and classification of moving target using deep convolutional neural networks on time-frequency graphs[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(1): 105–111. doi: 10.11805/TKYDA201901.0105 [13] REN Shaoqing, HE Kaiming, GIRSHICK R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(6): 1137–1149. doi: 10.1109/TPAMI.2016.2577031 [14] REDMON J and FARHADI A. YOLOv3: An incremental improvement[EB/OL]. https://arxiv.org/abs/1804.02767, 2018. [15] BOCHKOVSKIY A, WANG C Y, and LIAO H Y M. YOLOv4: Optimal speed and accuracy of object detection[EB/OL]. https://arxiv.org/abs/2004.10934,2020. [16] 杜兰, 王兆成, 王燕, 等. 复杂场景下单通道SAR目标检测及鉴别研究进展综述[J]. 雷达学报, 2020, 9(1): 34–54. doi: 10.12000/JR19104DU Lan, WANG Zhaocheng, WANG Yan, et al. Survey of research progress on target detection and discrimination of single-channel SAR images for complex scenes[J]. Journal of Radars, 2020, 9(1): 34–54. doi: 10.12000/JR19104 [17] 苏宁远, 陈小龙, 陈宝欣, 等. 雷达海上目标双通道卷积神经网络特征融合智能检测方法[J]. 现代雷达, 2019, 41(10): 47–52, 57. doi: 10.16592/j.cnki.1004-7859.2019.10.009SU Ningyuan, CHEN Xiaolong, CHEN Baoxin, et al. Dual-channel convolutional neural networks feature fusion method for radar maritime target intelligent detection[J]. Modern Radar, 2019, 41(10): 47–52, 57. doi: 10.16592/j.cnki.1004-7859.2019.10.009 [18] 苏宁远, 陈小龙, 关键, 等. 基于卷积神经网络的海上微动目标检测与分类方法[J]. 雷达学报, 2018, 7(5): 565–574. doi: 10.12000/JR18077SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Detection and classification of maritime target with micro-motion based on CNNs[J]. Journal of Radars, 2018, 7(5): 565–574. doi: 10.12000/JR18077 [19] CHEN Chen, HE Chuan, HU Changhua, et al. MSARN: A deep neural network based on an adaptive recalibration mechanism for multiscale and arbitrary-oriented SAR ship detection[J]. IEEE Access, 2019, 7: 159262–159283. doi: 10.1109/ACCESS.2019.2951030 [20] 黄洁, 姜志国, 张浩鹏, 等. 基于卷积神经网络的遥感图像舰船目标检测[J]. 北京航空航天大学学报, 2017, 43(9): 1841–1848. doi: 10.13700/j.bh.1001-5965.2016.0755HUANG Jie, JIANG Zhiguo, ZHANG Haopeng, et al. Ship object detection in remote sensing images using convolutional neural networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1841–1848. doi: 10.13700/j.bh.1001-5965.2016.0755 [21] WEI Xiukun, WEI Dehua, SUO Da, et al. Multi-target defect identification for railway track line based on image processing and improved YOLOv3 model[J]. IEEE Access, 2020, 8: 61973–61988. doi: 10.1109/ACCESS.2020.2984264 [22] XIAO Dong, SHAN Feng, LI Ze, et al. A target detection model based on improved Tiny-Yolov3 under the environment of mining truck[J]. IEEE Access, 2019, 7: 123757–123764. doi: 10.1109/ACCESS.2019.2928603 [23] ZHANG Huibing, QIN Longfei, LI Jun, et al. Real-time detection method for small traffic signs based on Yolov3[J]. IEEE Access, 2020, 8: 64145–64156. doi: 10.1109/ACCESS.2020.2984554 [24] BA J L, KIROS J R, and HINTON G E. Layer normalization[EB/OL]. https://arxiv.org/abs/1607.06450, 2016. [25] WANG C Y, LIAO H Y M, YEH I H, et al. CSPNet: A new backbone that can enhance learning capability of CNN[EB/OL]. https://arxiv.org/abs/1911.11929,2019. [26] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [27] AI Jiaqiu, YANG Xuezhi, DONG Zhangyu, et al. A new two parameter CFAR ship detector in Log-Normal clutter[C]. 2017 IEEE Radar Conference (RadarConf), Seattle, USA, 2017: 195–199. doi: 10.1109/RADAR.2017.7944196. [28] YANG Jianyu, LU Chao, and LI Liangchao. Target detection in passive millimeter wave image based on two-dimensional cell-weighted average CFAR[C]. The IEEE 11th International Conference on Signal Processing, Beijing, China, 2012: 917–921. doi: 10.1109/ICoSP.2012.6491729. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: