近场非圆信号参数快速估计算法

宋嘉奇; 陶海红

doi:10.12000/JR20053

近场非圆信号参数快速估计算法

DOI: 10.12000/JR20053

宋嘉奇,
陶海红^,

西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 国家自然科学基金(61971355)，国家部委基金

详细信息

作者简介:
宋嘉奇(1992–)，2013年于西安电子科技大学获工学学士学位，现为西安电子科技大学雷达信号处理国家重点实验室博士研究生，主要研究方向为阵列信号处理。E-mail: theo_song@163.com

陶海红(1976–)，女，西安电子科技大学教授，博士生导师，主要研究领域为雷达信号处理与检测、高速实时信号处理、阵列信号处理。E-mail: hhtao@xidian.edu.cn

通讯作者:
陶海红 hhtao@xidian.edu.cn

责任主编：魏玺章 Corresponding Editor: WEI Xizhang
中图分类号: TN911.7
计量
- 文章访问数: 1669
- HTML全文浏览量: 623
- PDF下载量: 122
- 被引次数: 10
出版历程
- 收稿日期: 2020-05-02
- 修回日期: 2020-07-17
- 网络出版日期: 2020-08-28

A Fast Parameter Estimation Algorithm for Near-field Non-circular Signals

SONG Jiaqi,
TAO Haihong^,

National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (61971355), The National Ministries Foundation

More Information

Corresponding author: TAO Haihong, hhtao@xidian.edu.cn

摘要

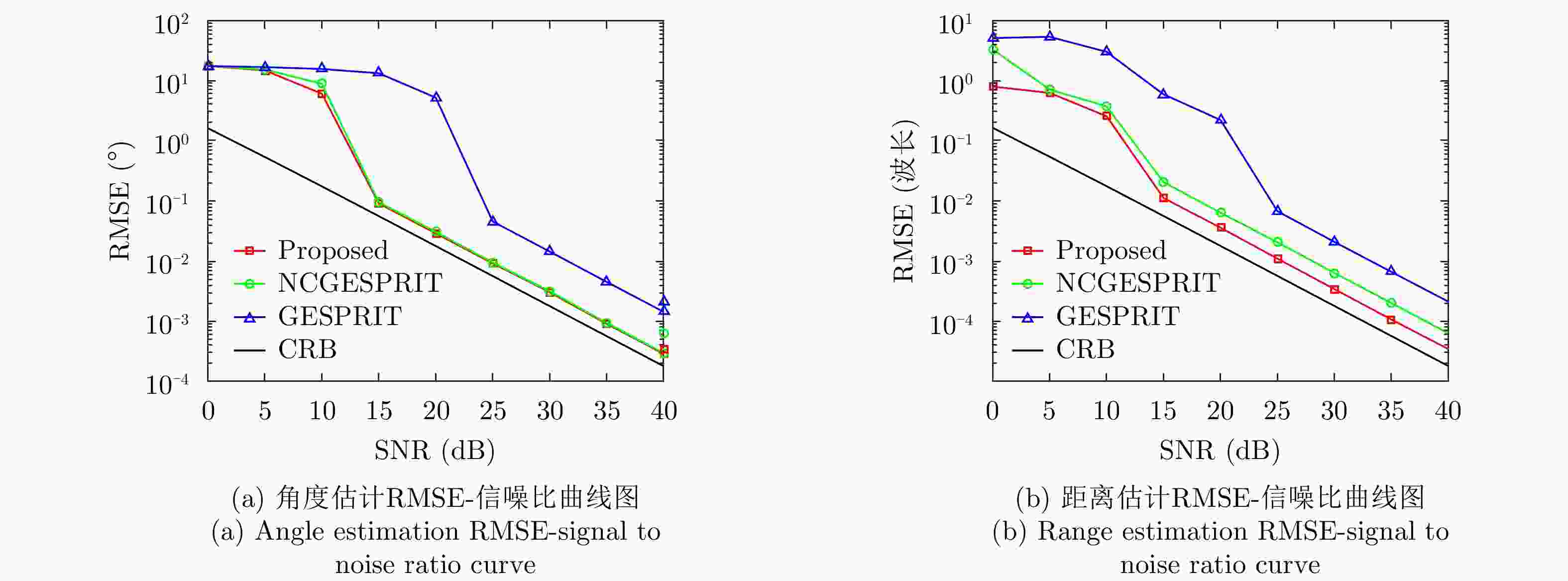
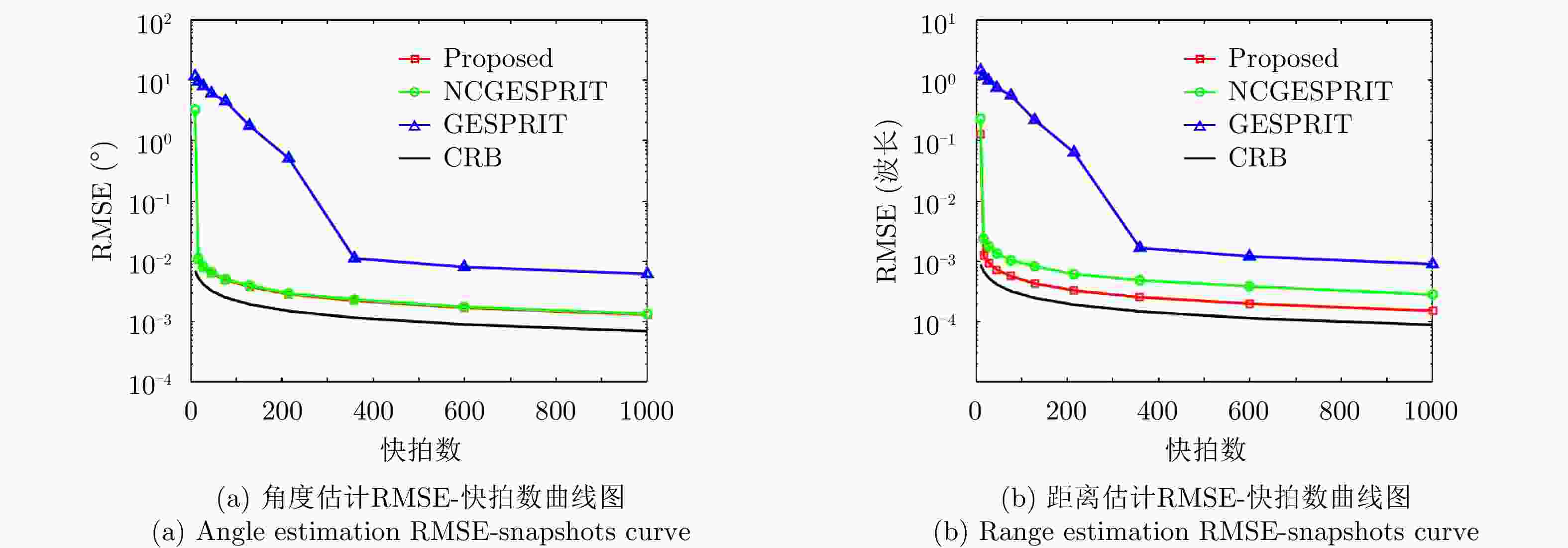
摘要: 该文基于对称的均匀线阵提出了一种近场非圆信号参数的快速估计算法，算法基于信号的非圆特性以及阵列的对称性对近场导向矢量进行解耦，并利用多项式求根取代传统的谱峰搜索对近场源的角度及距离参数进行快速估计。基于给定的阵列结构，建立非圆信号参数估计的多项式数学模型，然后对其进行求根即可获得近场信号源位置参数。所提算法采用多项式求根的方法有效地降低了运算复杂度，同时利用信号的非圆特性提高了参数估计的自由度(DOF)。通过性能分析和计算机仿真实验可以看出该算法能够分辨更多的近场非圆信号，并且参数估计性能有所提升，更接近于近场源参数估计的克拉美罗界(CRB)。
- 近场参数估计 /
- 非圆信号 /
- 降秩定理 /
- 多项式求根 /
- 克拉美罗界
Abstract: In this paper, a fast parameter estimation algorithm for near-field non-circular signals is proposed, which is based on symmetric, uniform, and linear array, that decouple the near-field steering vector via non-circularity and symmetry. Then, the position parameters are estimated based upon polynomial rooting technique instead of traditional spectral search. After fixing the array structure, the parameters for estimation equation are ascertained. Then the values of position parameters are obtained by solving the polynomial equations; consequently, computational difficulty is alleviated effectively. In addition, the Degree-Of-Freedom (DOF) is increased by utilizing the non-circularity characteristics of the impinging sources. It can be seen from the performance analysis and computer simulation experiments that the proposed algorithm can resolve more near-field non-circular signals and can improve parameter estimation performance, which is closer to the Cramer–Rao Bound (CRB) estimation.
- Near-field parameter estimation /
- Non-circular signal /
- Rank reduction theory /
- Polynomial rooting technique /
- Cramer-Rao Bound (CRB)

HTML全文

图 1 近场参数估计示意图

Figure 1. Schematic diagram of near-field parameter estimation

下载: 全尺寸图片幻灯片

图 2 RMSE-信噪比曲线图

Figure 2. RMSE-signal to noise ratio curve

下载: 全尺寸图片幻灯片

图 3 RMSE-快拍数曲线图

Figure 3. RMSE-snapshots curve

下载: 全尺寸图片幻灯片

图 4 三种算法的运算时间比较

Figure 4. Comparison of operation time of three algorithms

下载: 全尺寸图片幻灯片

表 1 矩阵M中的元素

Table 1. Elements of matrix M

元素位置	表达式	元素位置	表达式
${m_{11}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{L} }({ {{u} }_i},{ {{u} }_j}){z^{ { {{u} }_i} - { {{u} }_j} } } } }$	${m_{12}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{L} }({ {{u} }_i},{ {{v} }_j}){z^{ { {{u} }_i} - { {{v} }_j} } } } }$
${m_{13}}(z)$	$\displaystyle\sum \nolimits_i { {{S} }({ {{u} }_i},{ {{u} }_i}){z^{2{ {{u} }_i} - 4} } + } \underbrace {\displaystyle\sum \nolimits\nolimits_i {\displaystyle\sum \nolimits\nolimits_j { {{S} }({ {{u} }_i},{ {{u} }_j})} } }_{i \ne j}$	${m_{14}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{S} }({ {{u} }_i},{ {{v} }_j})} } {z^{ { {{u} }_i} - { {{v} }_j} } }$
${m_{21}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{L} }({ {{v} }_i},{ {{u} }_j}){z^{ { {{v} }_i} - { {{u} }_j} } } } }$	${m_{22}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{L} }({ {{v} }_i},{ {{v} }_j}){z^{ { {{v} }_i} - { {{v} }_j} } } } }$
${m_{23}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{S} }({ {{v} }_i},{ {{u} }_j}){z^{ - { {{v} }_i} + { {{u} }_j} } } } }$	${m_{24}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{S} }({ {{v} }_i},{ {{v} }_j}){z^{ { {{v} }_i} - { {{v} }_j} } } } }$
${m_{31}}(z)$	$\displaystyle\sum \nolimits_i { {{Y} }({ {{u} }_i},{ {{u} }_i}){z^{ - 2{ {{u} }_i} + 4} } + } \underbrace {\displaystyle\sum \nolimits\nolimits_i {\displaystyle\sum \nolimits\nolimits_j { {{Y} }({ {{u} }_i},{ {{u} }_j})} } }_{i \ne j}$	${m_{32}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{Y} }({ {{u} }_i},{ {{v} }_j}){z^{ - { {{u} }_i} + { {{v} }_j} } } } }$
${m_{33}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{W} }({ {{u} }_i},{ {{u} }_j}){z^{ - { {{u} }_i} + { {{u} }_j} } } } }$	${m_{34}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{W} }({ {{u} }_i},{ {{v} }_j}){z^{ - { {{u} }_i} + { {{v} }_j} } } } }$
${m_{41}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{Y} }({ {{v} }_i},{ {{u} }_j})} } {z^{ { {{v} }_i} - { {{u} }_j} } }$	${m_{42}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{Y} }({ {{v} }_i},{ {{v} }_j}){z^{ { {{v} }_i} - { {{v} }_j} } } } }$
${m_{43}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{W} }({ {{v} }_i},{ {{u} }_j}){z^{ - { {{v} }_i} + { {{u} }_j} } } } }$	${m_{44}}(z)$	$\displaystyle\sum \nolimits_i {\displaystyle\sum \nolimits_j { {{W} }({ {{v} }_i},{ {{v} }_j}){z^{ { {{v} }_i} - { {{v} }_j} } } } }$

下载: 导出CSV

表 2 算法运算复杂度比较

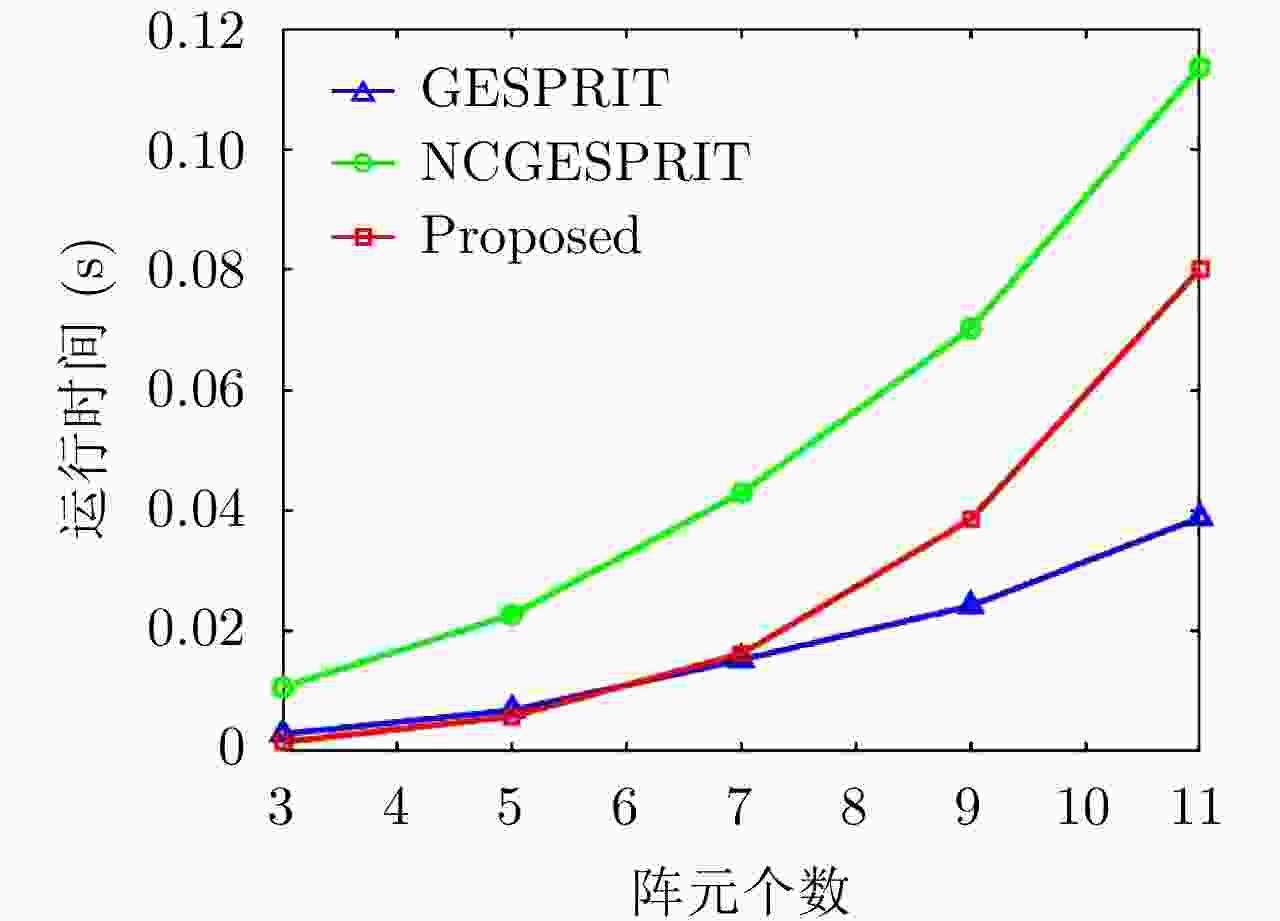
Table 2. Algorithm complexity comparison

算法	统计量矩阵	特征值分解	谱峰搜索
GESPRIT	$O(2{N^2}/L)$	$8{N^3}/3$	$K{N^2}/{\Delta _r}({R_{\max } } - {R_{\min } }) + 360{N^2}/{\Delta _\theta }$
NCGESPRIT	$O(4{N^2}/L)$	$32{N^3}/3$	$4K{N^2}/{\Delta _r}({R_{\max } } - {R_{\min } }) + 720{N^2}/{\Delta _\theta }$
本文算法	$O(4{N^2}/L)$	$32{N^3}/3$

下载: 导出CSV

参考文献(15)

[1]	JOHNSON R C. Antenna Engineering Handbook[M]. 3rd ed. New York, USA: McGraw-Hill, 1993: 36–39.
[2]	HUANG Y D and BARKAT M. Near-field multiple source localization by passive sensor array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(7): 968–975. doi: 10.1109/8.86917
[3]	CHALLA R N and SHAMSUNDER S. High-order subspace-based algorithms for passive localization of near-field sources[C]. The 29th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1995: 777–781. doi: 10.1109/ACSSC.1995.540806.
[4]	ZHI Wanjun and CHIA M Y W. Near-field source localization via symmetric subarrays[J]. IEEE Signal Processing Letters, 2007, 14(6): 409–412. doi: 10.1109/LSP.2006.888390
[5]	XIE Jian, TAO Haihong, RAO Xuan, et al. Comments on “near-field source localization via symmetric subarrays”[J]. IEEE Signal Processing Letters, 2015, 22(5): 643–644. doi: 10.1109/LSP.2014.2364174
[6]	CHARGÉ P, WANG Yide, and SAILLARD J. A non-circular sources direction finding method using polynomial rooting[J]. Signal Processing, 2001, 81(8): 1765–1770. doi: 10.1016/S0165-1684(01)00071-8
[7]	SHEN Lei, LIU Zhiwen, and XU Yougen. Parameter estimation of rectilinear signals using multiple noncollocated and diversely polarized antennas[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–5. doi: 10.1109/RADAR.2016.8059546.
[8]	XIE Jian, TAO Haihong, RAO Xuan, et al. Real-valued localisation algorithm for near-field non-circular sources[J]. Electronics Letters, 2015, 51(17): 1330–1331. doi: 10.1049/el.2015.0454
[9]	XIE Jian, TAO Haihong, RAO Xuan, et al. Passive localization of noncircular sources in the near-field[C]. 2015 16th International Radar Symposium (IRS), Dresden, Germany, 2015: 493–498. doi: 10.1109/IRS.2015.7226309.
[10]	XIE Jian, TAO Haihong, RAO Xuan, et al. Efficient method of passive localization for near-field noncircular sources[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 1223–1226. doi: 10.1109/LAWP.2015.2399534
[11]	KUANG Meidong, WANG Ling, XIE Jian, et al. Real-valued near-field localization of partially polarized noncircular sources with a cross-dipole array[J]. IEEE Access, 2019, 7: 36623–36632. doi: 10.1109/ACCESS.2019.2904837
[12]	CHEN Hua, LI Youming, ZHU Weiping, et al. Joint DOA and range estimation for mixed near-field and far-field strictly noncircular sources[C]. 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 2018: 1–5. doi: 10.1109/ICDSP.2018.8631547.
[13]	CHEN Hua, LIU Wei, ZHU Weiping, et al. Noncircularity-based localization for mixed near-field and far-field sources with unknown mutual coupling[C]. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, 2018: 3236–3240. doi: 10.1109/ICASSP.2018.8462266.
[14]	FERREOL A, BOYER E, and LARZABAL P. Low-cost algorithm for some bearing estimation methods in presence of separable nuisance parameters[J]. Electronics Letters, 2004, 40(15): 966–967. doi: 10.1049/el:20040537
[15]	STOICA P, LARSSON E G, and GERSHMAN A B. The stochastic CRB for array processing: A textbook derivation[J]. IEEE Signal Processing Letters, 2001, 8(5): 148–150. doi: 10.1109/97.917699

施引文献

期刊类型引用(5)

1.	张顺生，李鑫，黄栎冰，王文钦. 距离角度失配条件下的FDA-MIMO雷达运动目标检测算法. 信号处理. 2024(01): 197-206 . 百度学术
2.	丁俊淞，张顺生，王文钦. 基于多普勒偏移补偿的非线性FDA-MIMO雷达运动目标检测算法. 信号处理. 2024(02): 272-279 . 百度学术
3.	陈雨馨，彭意群，柳润金，丁一鹏. 基于CK-Hough联合算法的人体微多普勒频率估计. 中南大学学报(自然科学版). 2024(09): 3329-3341 . 百度学术
4.	刘德顺，夏德平，陈露，马艳峰. 基于神经网络的FDA-MIMO低截获发射波形和接收波束形成联合设计. 雷达学报. 2024(06): 1239-1251 . 本站查看
5.	施兴相，廖可非. 频率分集阵列的ISAR成像技术. 国外电子测量技术. 2023(03): 8-13 . 百度学术