基于地基雷达图像的无监督变化检测

黄平平; 任慧芳; 谭维贤; 段盈宏; 徐伟; 刘方

doi:10.12000/JR20004

基于地基雷达图像的无监督变化检测

doi: 10.12000/JR20004

内蒙古工业大学信息工程学院呼和浩特 010051
内蒙古自治区雷达技术与应用重点实验室呼和浩特 010051

基金项目: 国家自然科学基金重点项目(61631011)，内蒙古自治区财政厅创新引导项目(KCBJ2017, KCBJ2018014)，内蒙古自治区科技重大专项和科技计划项目，装备预研领域基金一般领域基金(JZX7Y20190253040901, JZX7Y20190253041401)

详细信息

作者简介:
黄平平(1978–)，男，山东海阳人，博士，教授，2010年获中国科学院电子学研究所博士学位，现任内蒙古工业大学信息工程学院副院长，自治区雷达技术与应用重点实验室主任，“草原英才”创新团队负责人，全国“工人先锋号”负责人。兼任中央军委装备发展部某专家组成员、中国电子学会信号处理分会委员、中国电子教育学会研究生教育分会理事。获自治区优秀共产党员、自治区五一劳动奖章、自治区青年科技奖、自治区自然科学一等奖、自治区科技进步一等奖等荣誉与奖励。入选国家“百千万人才工程”、自治区突出贡献专家、自治区“草原英才”、自治区自然科学杰出青年、高等学校青年科技英才等人才工程。近几年，共主持国家级项目8项，其他各类科研项目20余项，获得授权国家发明专利30余项，发表学术论文130余篇。主要从事结合国家重大需求及内蒙古自治区经济发展需求，新体制雷达系统设计、雷达信号处理和微波遥感应用等方面的研究。E-mail: hpp@imut.edu.cn

任慧芳(1992–)，女，内蒙古呼和浩特人，现于内蒙古工业大学信息工程学院雷达技术与应用重点实验室攻读硕士学位，主要研究方向为微变监测雷达和遥感图像变化检测。E-mail: Rhf_412922@163.com

谭维贤(1981–)，男，湖北恩施人，博士，教授，硕士生导师，2009年获中国科学院电子学研究所工学博士学位，2015年至今，内蒙古工业大学雷达技术研究所、内蒙古自治区雷达技术与应用重点实验室任教。入选内蒙古自治区“草原英才”工程，主要从事结合国家重大需求及内蒙古自治区经济发展需求，雷达系统技术、微变监测雷达、雷达信号处理和微波遥感等方面的研究。E-mail: wxtan@imut.edu.cn

通讯作者:
黄平平 hpp@imut.edu.cn

责任主编：王彦平 Corresponding Editor: WANG Yanping
中图分类号: TP753
计量
- 文章访问数: 3287
- HTML全文浏览量: 1181
- PDF下载量: 238
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-11
- 修回日期: 2020-03-22
- 网络出版日期: 2020-06-01

Unsupervised Change Detection Using Ground-based Radar Image

College of Information Engineering, Inner Mongolia University of Technology, Hohhot 010051, China
Inner Mongolia Key Laboratory of Radar Technology and Application, Hohhot 010051, China

Funds: The Key Projects of National Natural Science Foundation of China (61631011), The Innovation Guidance Project of Finance Department of Inner Mongolia Autonomous Region (KCBJ2017, KCBJ2018014), The Major Science and Technology Projects and Science and Technology Programs of Inner Mongolia Autonomous Region, Equipment Pre-research Field Fund General Field Fund (JZX7Y20190253040901, JZX7Y20190253041401)

More Information

Corresponding author: HUANG Pingping, hpp@imut.edu.cn

摘要

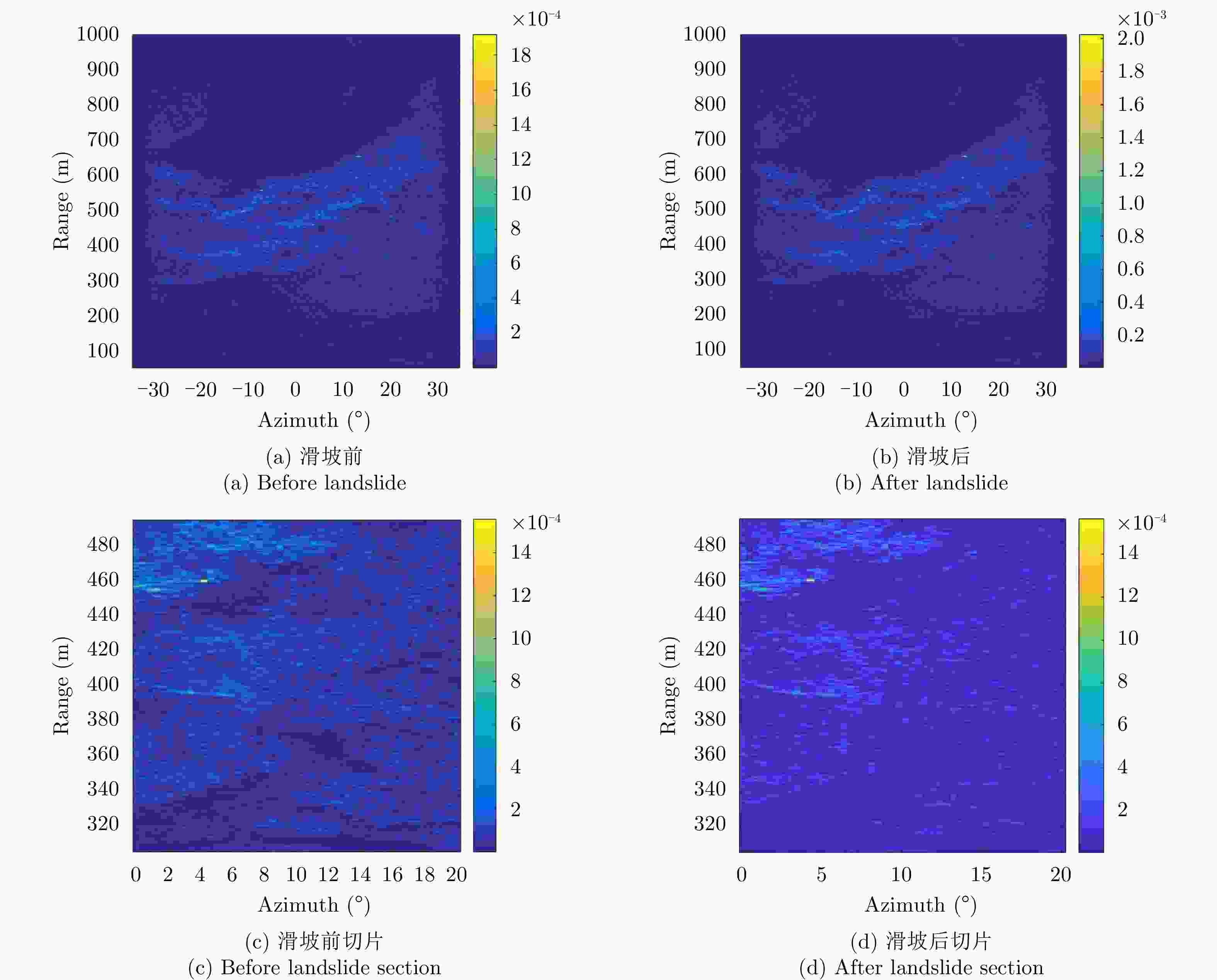
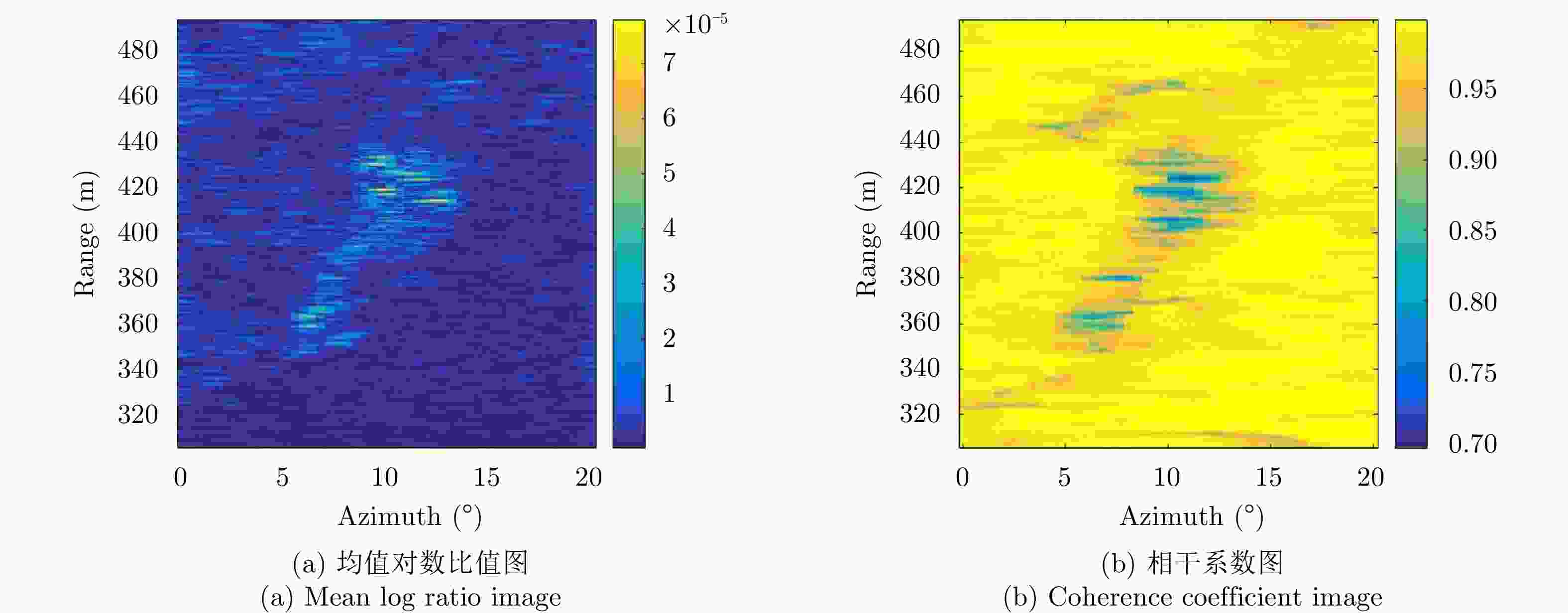
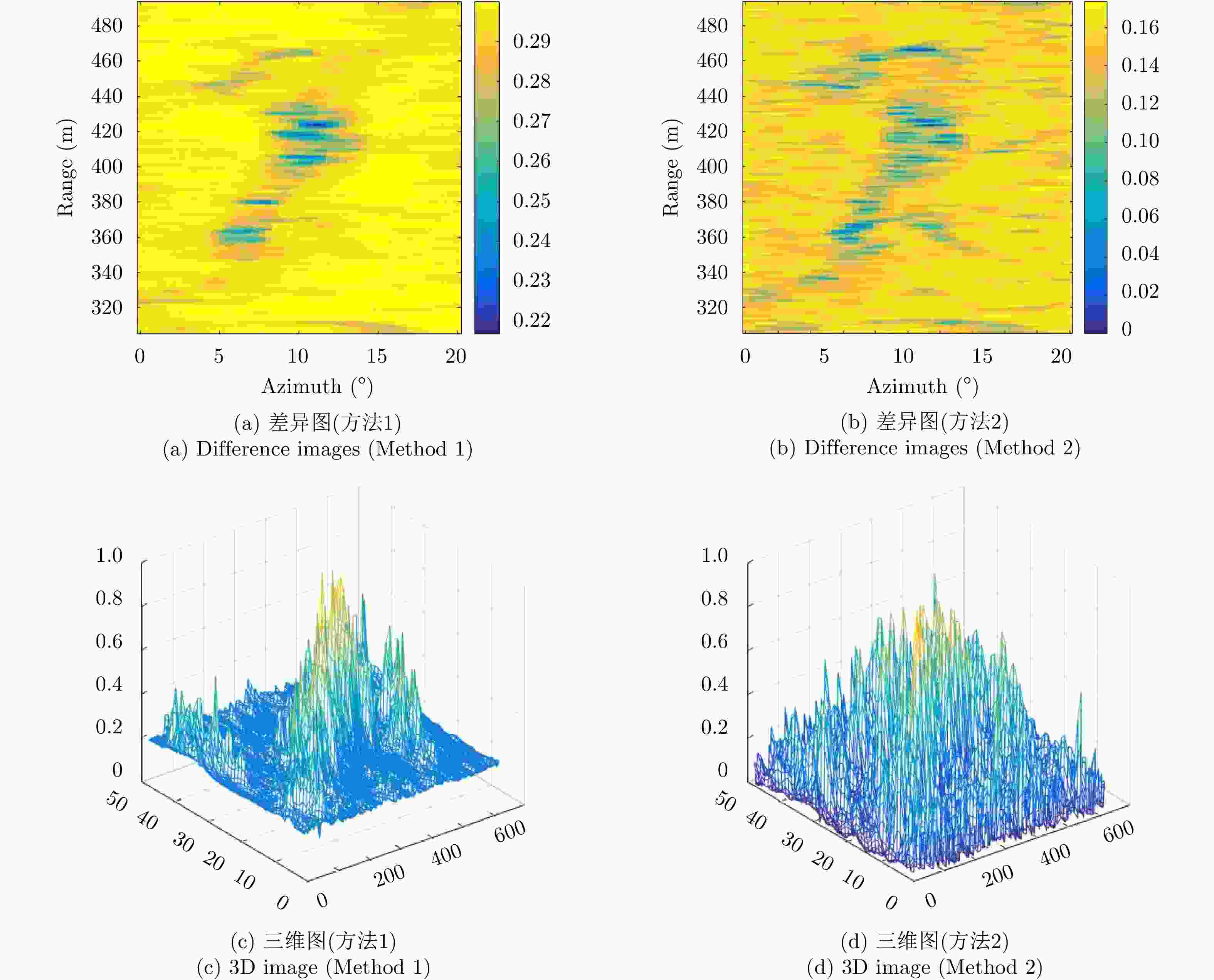
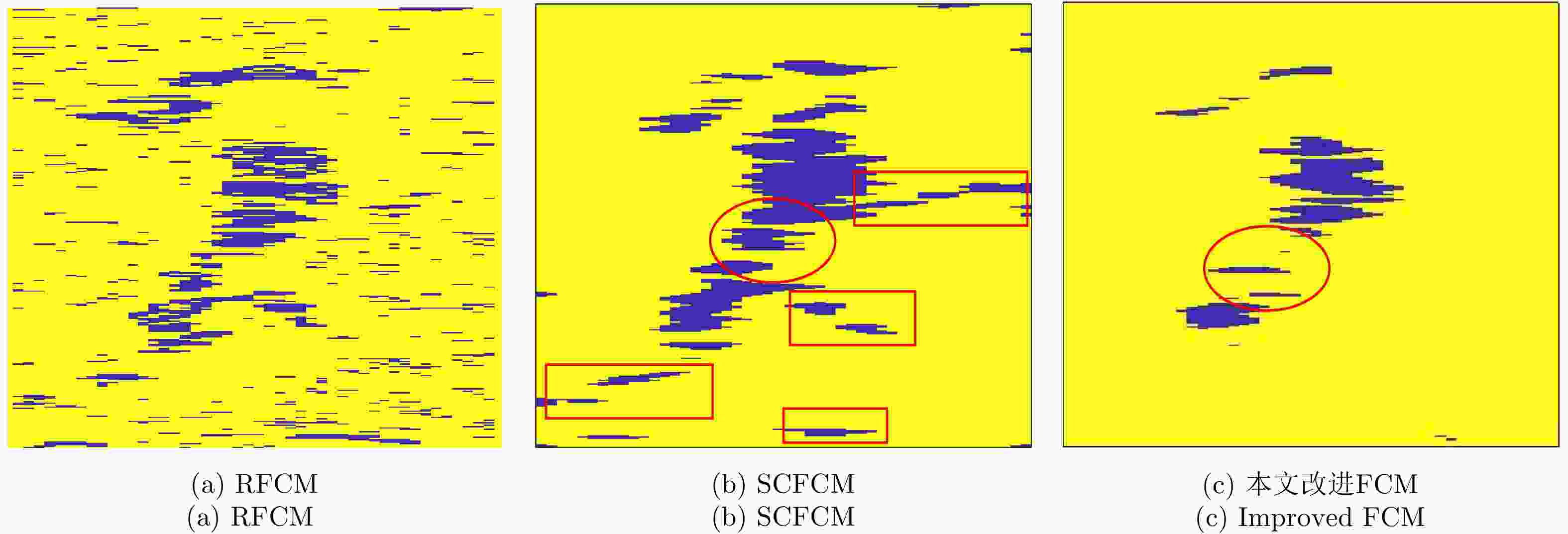
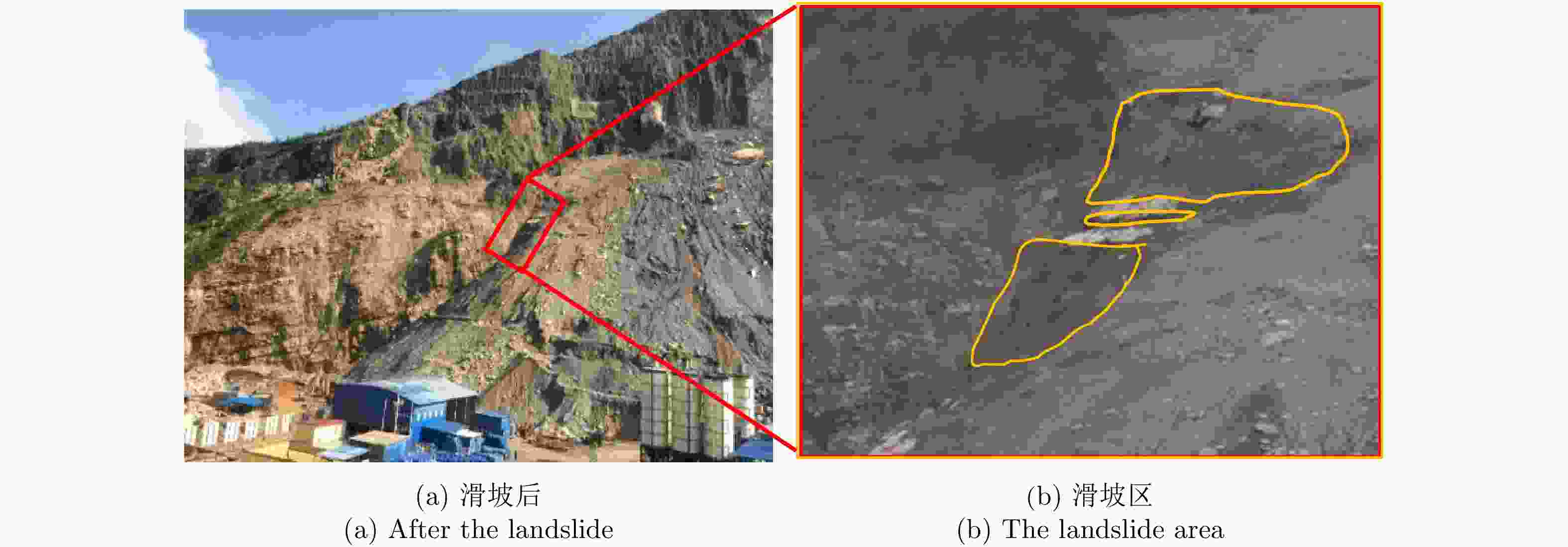
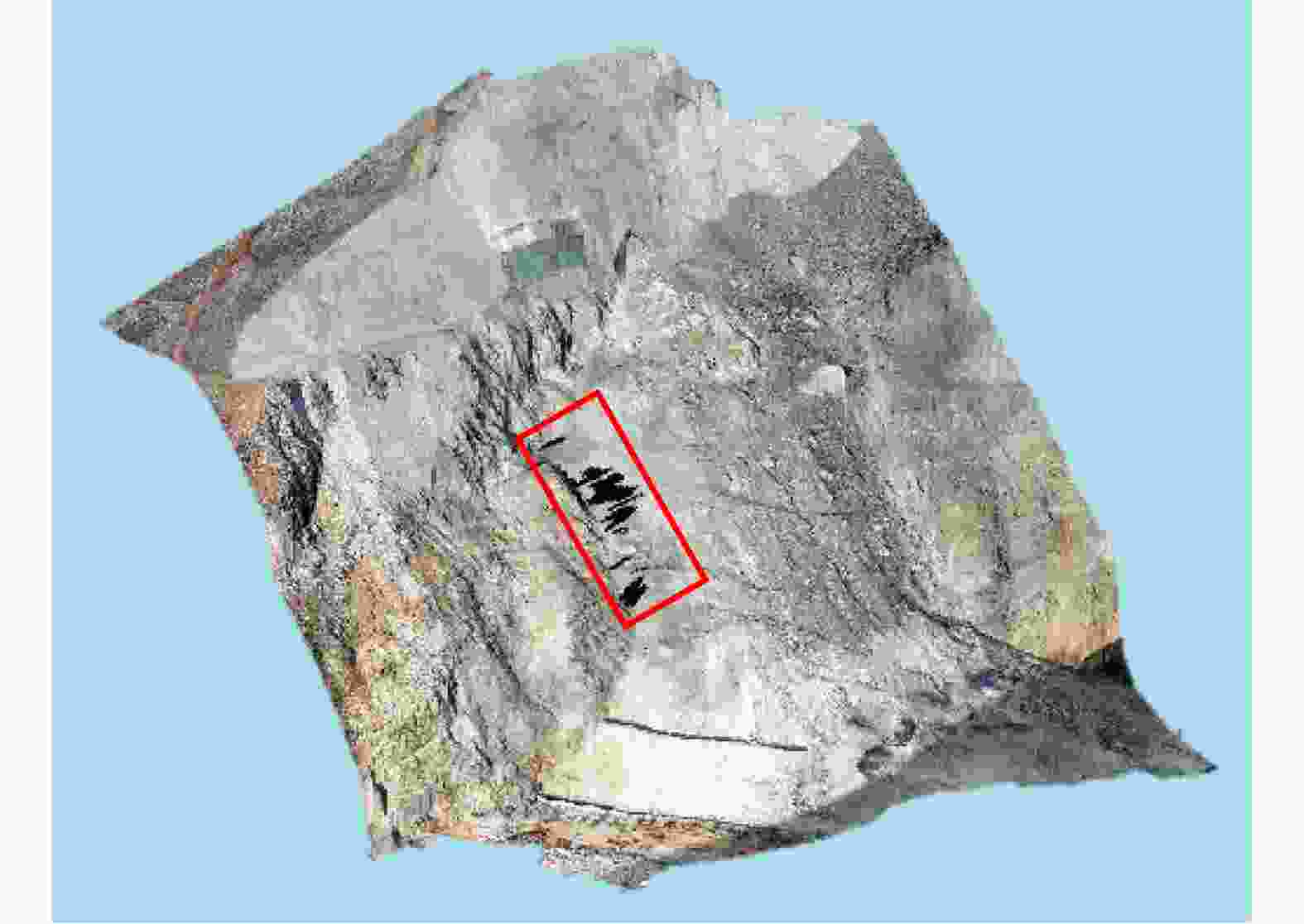
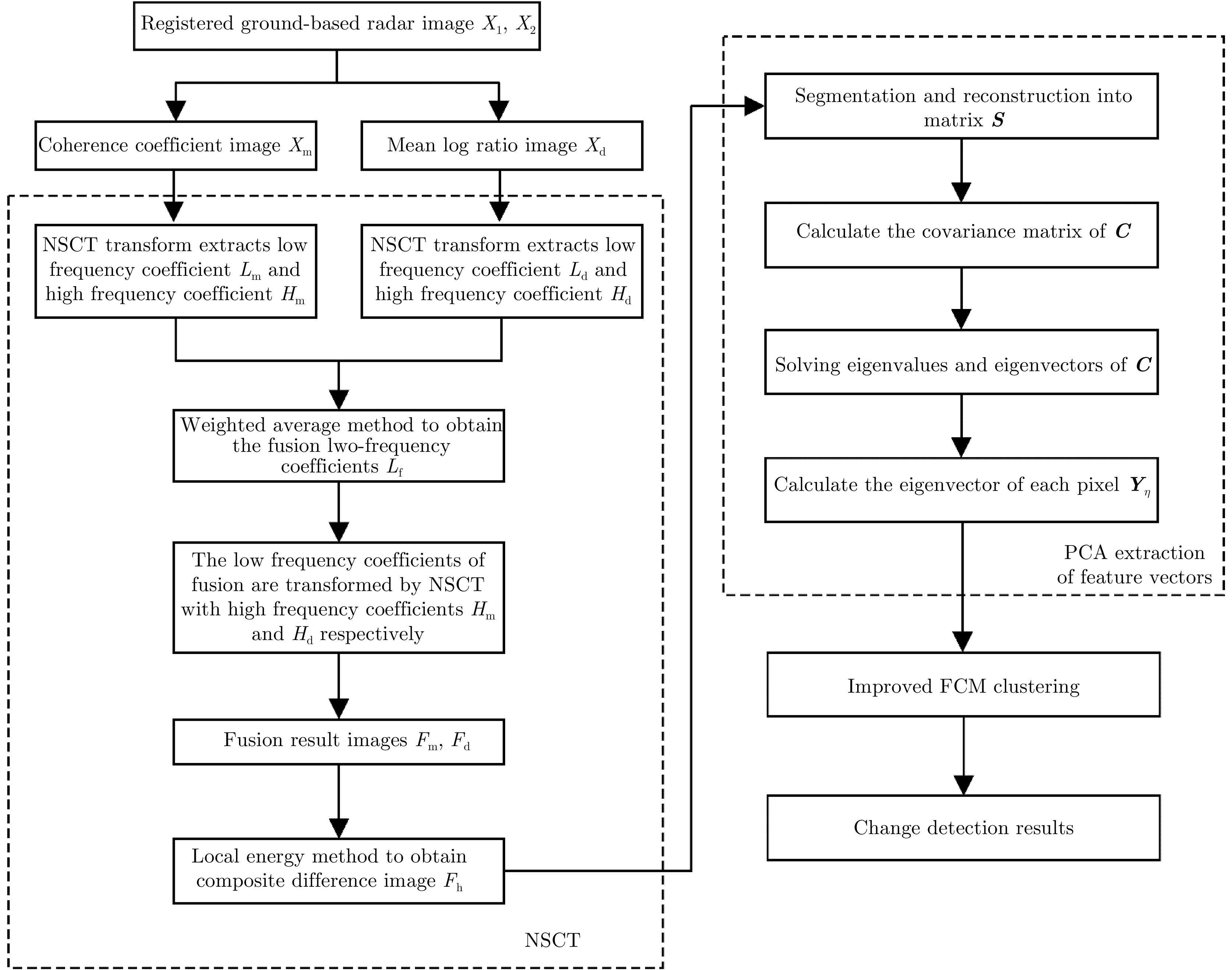
摘要: 地基雷达是近20几年逐渐发展成熟的微波遥感成像技术，目前已广泛应用于滑坡、崩塌等地质灾害的监测中。地基雷达通过干涉测量原理可以监测到目标区域发生的微小形变，然而受人为因素、地质因素、气象因素等影响，导致雷达图像失相干严重，给长期定量化监测带来较大的难度。因此，迫切需要在定量监测的基础上，进一步开展变化检测方面的应用，为长期全面了解监测区域的动态变化提供有效信息。针对上述问题，该文提出了一种基于改进的模糊C均值聚类(FCM)算法对地基雷达图像进行无监督变化检测，该方法首次利用相干系数图和均值对数比值图进行非下采样轮廓波变换(NSCT)和局部能量法得到合成差异图，然后利用主成分分析(PCA)提取合成差异图中每个像素的特征向量，根据地基雷达图像特点对FCM进行改进，通过改进的FCM对每个像素的特征向量进行聚类得到最终的变化检测结果。利用地基雷达LSA对中国西南某省出现的堰塞体的治理过程进行监测，获取监测区域的地基雷达图像，监测过程中受降水等影响监测体出现滑坡，使用该文方法对其进行变化检测，结果表明该文方法更容易进行聚类分割，变化检测结果在保留变化区域的同时噪声点明显减少。
- 地基雷达图像 /
- 变化检测 /
- 无监督 /
- 相干系数 /
- 改进的模糊C均值聚类
Abstract: Ground-based radar is a microwave remote sensing imaging technology that has been gradually developed throughout the past 20 years so that it has become mature. At present, it has been widely used in monitoring geological disasters such as landslides and collapses. Ground-based radars can detect micro-variations in target areas through the principle of interferometry. However, due to human factors, geological factors, and meteorological factors, the radar image of the monitored area is incoherent, which makes long-term quantitative monitoring difficult. Therefore, further developing the application of change detection while considering quantitative monitoring is urgent, to provide effective information on long-term changes and comprehensively understand the dynamic changes in the monitored area. To solve the above problems, an unsupervised change detection method using ground-based radar images and based on an improved Fuzzy C-Means clustering (FCM) algorithm is proposed in this paper. In this method, for the first time, the Nonsubsampled Contourlet Transform (NSCT) is performed on the coherence coefficient map and the mean log ratio map to obtain the fusion difference map. Then, principal component analysis is used to extract the feature vectors of each pixel in the fusion difference image. The FCM is improved according to the characteristics of the ground-based radar images. The improved FCM is used to cluster the feature vectors of each pixel to obtain the change detection result. A ground-based radar LSA was used to monitor the treatment process of a dam in southwest China. During the monitoring process, landslides occurred in the monitored area affected by precipitation and other factors. This method is used to detect the change of the radar image before and after the landslide. The results show that the proposed method allows for easier clustering and segmenting, and the change detection results can significantly reduce the noise points while retaining the change area.
- Ground-based radar image /
- Change detection /
- Unsupervised /
- Coherence coefficient /
- Improved Fuzzy C-Means (FCM)

HTML全文

图 1 地基雷达图像无监督变化检测流程图

Figure 1. Flow chart for unsupervised change detection based on ground-based radar image

下载: 全尺寸图片幻灯片

图 2 监测现场图

Figure 2. Monitoring site images

下载: 全尺寸图片幻灯片

图 3 实验数据

Figure 3. Experimental data

下载: 全尺寸图片幻灯片

图 4 初始差异图

Figure 4. Initial difference images

下载: 全尺寸图片幻灯片

图 5 差异图对比

Figure 5. Difference images comparison

下载: 全尺寸图片幻灯片

图 6 聚类结果对比

Figure 6. Clustering result comparison

下载: 全尺寸图片幻灯片

图 7 监测现场光学图

Figure 7. Optical image of monitoring site

下载: 全尺寸图片幻灯片

图 8 变化检测结果与地形3维数据融合图

Figure 8. Effect of fusion of change detection results and UAV tilt photography

下载: 全尺寸图片幻灯片

表 1 改进的FCM算法计算步骤

Table 1. Improved FCM algorithm calculation steps

　算法：改进的FCM算法计算步骤

　输入：融合差异图每个像素的特征向量${{ Y}_\eta }$

　(1) 初始化隶属度$u$，满足式(10)；

　(2) 通过式(12)计算聚类中${C_i}$；

　(3) 根据式(17)计算目标函数$J$；

　(4) 迭代计算：当迭代次数$ \le q$时，

　　　　根据式(18)更新隶属度矩阵，返回步骤(2)继续执行

　　　　当迭代次数$ > q$时，

　　　　停止迭代；

　输出：隶属度矩阵${{ u}_{\eta 1} }$和${{ u}_{\eta 2} }$

下载: 导出CSV

表 2 地基雷达LSA系统参数

Table 2. Ground-based radar LSA system parameters

参数	数值	参数	数值
频率范围	16.5～17.5 GHz	监测范围(方位向)	60°× 30°
形变监测精度	0.1 mm	脉冲重复频率	优于500 Hz
作用距离	5 km	位移观测周期	240～600 s
图像分辨率	0.3 m × 0.0054 rad	供电电源	AC 220 V/DC 24 V
设备总重	$ \le 150\;{\rm{kg} }$	工作温度	–30～ 50 ℃

下载: 导出CSV

参考文献(21)

[1]	WANG Yan, DU Lan, and DAI Hui. Unsupervised SAR image change detection based on SIFT keypoints and region information[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 931–935. doi: 10.1109/LGRS.2016.2554606
[2]	GONG Maoguo, SU Linzhi, JIA Meng, et al. Fuzzy clustering with a modified MRF energy function for change detection in synthetic aperture radar images[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 98–109. doi: 10.1109/TFUZZ.2013.2249072
[3]	GAO Feng, DONG Junyu, LI Bo, et al. Automatic change detection in synthetic aperture radar images based on PCANet[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1792–1796. doi: 10.1109/LGRS.2016.2611001
[4]	GONG Maoguo, CAO Yu, and WU Qiaodi. A neighborhood-based ratio approach for change detection in SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 307–311. doi: 10.1109/LGRS.2011.2167211
[5]	GONG Maoguo, ZHOU Zhiqiang, and MA Jingjing. Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering[J]. IEEE Transactions on Image Processing, 2012, 21(4): 2141–2151. doi: 10.1109/TIP.2011.2170702
[6]	SUMAIYA M N and KUMARI R S S. Logarithmic mean-based thresholding for SAR image change detection[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(11): 1726–1728. doi: 10.1109/LGRS.2016.2606119
[7]	杨祥立, 徐德伟, 黄平平, 等. 融合相干/非相干信息的高分辨率SAR图像变化检测[J]. 雷达学报, 2015, 4(5): 582–590. doi: 10.12000/JR15073 YANG Xiangli, XU Dewei, HUANG Pingping, et al. Change detection of high resolution SAR images by the fusion of coherent/incoherent information[J]. Journal of Radars, 2015, 4(5): 582–590. doi: 10.12000/JR15073
[8]	ELGUEBALY T and BOUGUILA N. A Bayesian approach for SAR images segmentation and changes detection[C]. The 25th Biennial Symposium on Communications, Kingston, Canada, 2010: 24–27. doi: 10.1109/BSC.2010.5473011.
[9]	邵宁远, 邹焕新, 陈诚, 等. 面向变化检测的SAR图像超像素协同分割算法[J]. 系统工程与电子技术, 2019, 41(7): 1496–1503. doi: 10.3969/j.issn.1001-506X.2019.07.09 SHAO Ningyuan, ZOU Huanxin, CHEN Cheng, et al. Change detection oriented superpixel cosegmentation algorithm for SAR images[J]. Systems Engineering and Electronics, 2019, 41(7): 1496–1503. doi: 10.3969/j.issn.1001-506X.2019.07.09
[10]	CARINCOTTE C, DERRODE S, and BOURENNANE S. Unsupervised change detection on SAR images using fuzzy hidden Markov chains[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2): 432–441. doi: 10.1109/TGRS.2005.861007
[11]	BEZDEK J C, EHRLICH R, and FULL W. FCM: The fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191–203. doi: 10.1016/0098-3004(84)90020-7
[12]	PHAM D L. Spatial models for fuzzy clustering[J]. Computer Vision and Image Understanding, 2001, 84(2): 285–297. doi: 10.1006/cviu.2001.0951
[13]	TRAN T N, WEHRENS R, and BUYDENS L M C. Clustering multispectral images: A tutorial[J]. Chemometrics and Intelligent Laboratory Systems, 2005, 77(1/2): 3–17. doi: 10.1016/j.chemolab.2004.07.011
[14]	LI Zhenfang, BAO Zheng, LI Hai, et al. Image autocoregistration and InSAR interferogram estimation using joint subspace projection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2): 288–297. doi: 10.1109/TGRS.2005.860984
[15]	HYDE P, DUBAYAH R, WALKER W, et al. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) synergy[J]. Remote Sensing of Environment, 2006, 102(1/2): 63–73. doi: 10.1016/j.rse.2006.01.021
[16]	ADU J, GAN Jianhong, WANG Yan, et al. Image fusion based on nonsubsampled contourlet transform for infrared and visible light image[J]. Infrared Physics & Technology, 2013, 61: 94–100. doi: 10.1016/j.infrared.2013.07.010
[17]	WU Chao and WU Yiquan. Multitemporal images change detection using nonsubsampled contourlet transform and kernel fuzzy C-means clustering[C]. The 2nd International Symposium on Intelligence Information Processing and Trusted Computing, Wuhan, China, 2011: 22–23. doi: 10.1109/IPTC.2011.31.
[18]	李青松, 覃锡忠, 贾振红, 等. 非下采样Contourlet域融合和参数化内核图割的SAR图像无监督水灾变化检测[J]. 中国图象图形学报, 2014, 19(6): 971–978. doi: 10.11834/jig.20140619 LI Qingsong, QIN Xizhong, JIA Zhenhong, et al. Unsupervised detection of flood changes with SAR images combining nonsubsampled Contourlet domain fusion and parametric kernel graph cuts[J]. Journal of Image and Graphics, 2014, 19(6): 971–978. doi: 10.11834/jig.20140619
[19]	刘陆洋, 贾振红, 杨杰, 等. 利用双差异图和PCA的SAR图像变化检测[J]. 计算机工程与设计, 2019, 40(7): 2002–2006. LIU Luyang, JIA Zhenhong, YANG Jie, et al. SAR image chang detective using double difference images and PCA algorithm[J]. Computer Engineering and Design, 2019, 40(7): 2002–2006.
[20]	慕彩红, 霍利利, 刘逸, 等. 基于小波融合和PCA-核模糊聚类的遥感图像变化检测[J]. 电子学报, 2015, 43(7): 1375–1381. doi: 10.3969/j.issn.0372-2112.2015.07.019 MU Caihong, HUO Lili, LIU Yi, et al. Change detection for remote sensing images based on wavelet fusion and PCA-Kernel fuzzy clustering[J]. Acta Electronica Sinica, 2015, 43(7): 1375–1381. doi: 10.3969/j.issn.0372-2112.2015.07.019
[21]	EL-DAWLATLY S, OSMAN H, and SHAHEIN H I. New spatial FCM approach with application to SAR target clustering[C]. The 8th International Conference on Signal Processing, Beijing, China, 2006. doi: 10.1109/ICOSP.2006.345896.