基于多输入多输出合成孔径雷达的二维混合基线抗欺骗干扰方法

曾铮; 张福博; 陈龙永; 卜祥玺; 周思言

doi:10.12000/JR18118

基于多输入多输出合成孔径雷达的二维混合基线抗欺骗干扰方法

DOI: 10.12000/JR18118

曾铮^1,2,,
张福博^1,,
陈龙永^1,2, ,,
卜祥玺^1,2,,
周思言^1,2,

①.
中国科学院电子学研究所微波成像技术重点实验室北京 100190
②.
中国科学院大学北京 100049

基金项目: 国家部委基金(41874059)

详细信息

作者简介:
曾铮：曾铮(1994–)，男，江西人，北京理工大学学士，中国科学院电子学研究所硕士研究生，主要研究方向为雷达信号处理、合成孔径雷达电子对抗。E-mail: zengzheng16@mails.ucas.ac.cn

张福博(1988–)，男，河北人，博士，中国科学院电子学研究所副研究员，研究方向为多通道SAR 3维重建、新体制雷达、阵列雷达信号处理。E-mail: zhangfubo8866@126.com

陈龙永(1979–)，男，研究员，博士生导师，现任中国科学院电子学研究所微波成像技术重点实验室常务副主任，主要研究方向为高分辨率合成孔径雷达系统、干涉合成孔径雷达系统、微波成像新概念、新体制和新技术等。E-mail: lychen@mail.ie.ac.cn

卜祥玺(1991–)，男，山东人，吉林大学学士，中国科学院电子学研究所博士研究生，主要研究方向为涡旋电磁波的应用、雷达系统设计和雷达成像新技术。E-mail: buxiangxi14@mails.ucas.ac.cn

周思言(1995–)，女，重庆人，中国科学技术大学学士，中国科学院电子学研究所硕士研究生，主要研究方向为雷达信号处理、雷达点云重建。E-mail: zhousiyan17@mails.ucas.ac.cn

通讯作者:
陈龙永 lychen@mail.ie.ac.cn

中图分类号: TN958
计量
- 文章访问数: 2877
- HTML全文浏览量: 943
- PDF下载量: 173
- 被引次数: 0
出版历程
- 收稿日期: 2018-12-21
- 修回日期: 2019-02-22
- 网络出版日期: 2019-02-28

A Two-dimensional Mixed Baseline Method Based on MIMO-SAR for Countering Deceptive Jamming

ZENG Zheng^{1,2
,},
ZHANG Fubo^1
,,
CHEN Longyong^{1,2
, ,},
BU Xiangxi^{1,2
,},
ZHOU Siyan^{1,2
,}

①.
Science and Technology on Microwave Imaging Laboratory, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
②.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Ministries Foundation (41874059)

More Information

Corresponding author: CHEN Longyong, lychen@mail.ie.ac.cn

摘要

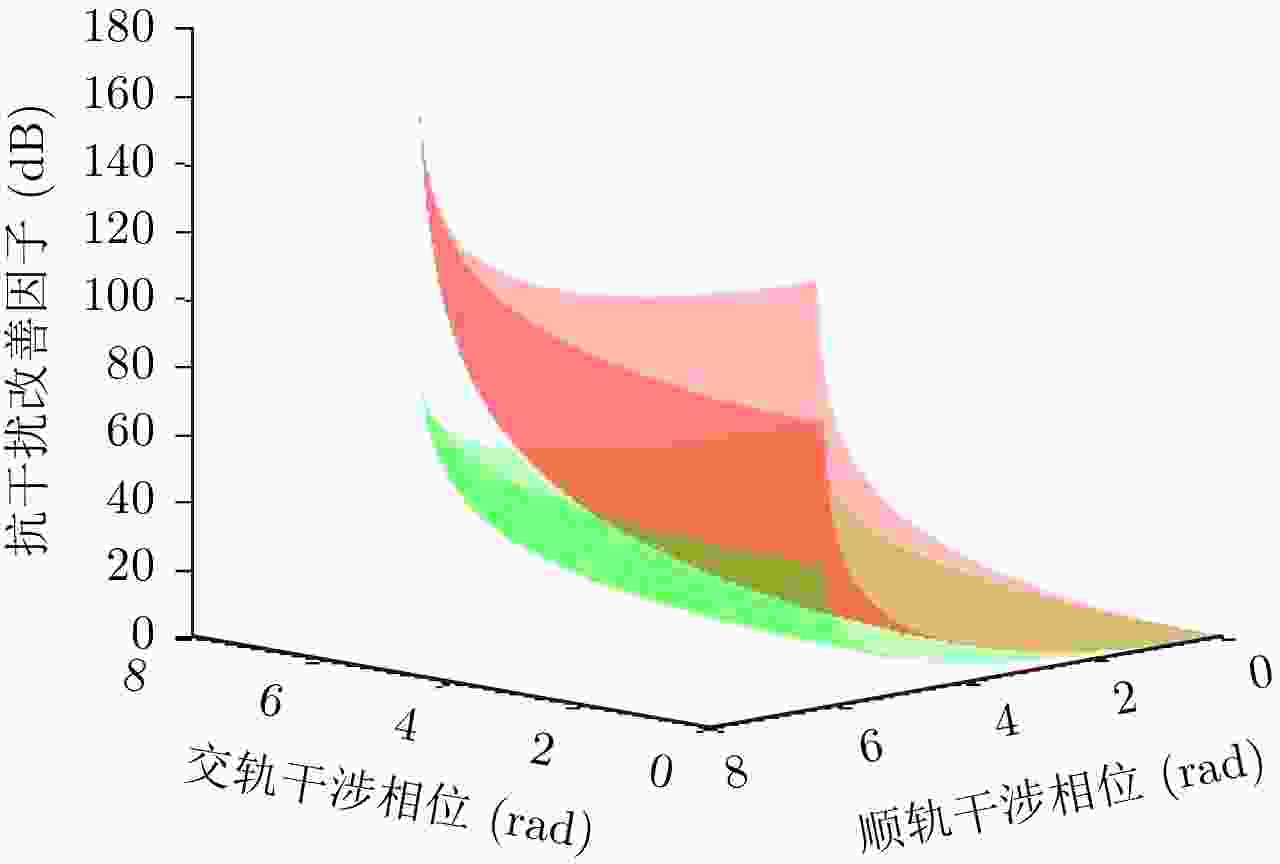
摘要: 针对距离延时和方位多普勒频率调制两类合成孔径雷达(SAR)欺骗干扰问题，该文提出一种基于多输入多输出合成孔径雷达(MIMO-SAR)的2维混合基线抗欺骗干扰方法。该方法采用基于MIMO-SAR的相位编码方案，使得多通道信号正交，利用多维相位信息识别欺骗干扰，通过相位补偿抑制干扰目标，从而提升雷达抗欺骗干扰能力。该文采用雷达抗干扰改善因子进行定量效果评估，在平台空间受限的条件下，该文方法比传统单发多收系统的雷达抗干扰改善因子提升3倍。仿真实验结果证明了该方法的有效性与正确性。
- 抗欺骗干扰 /
- 多输入多输出合成孔径雷达 /
- 相位补偿 /
- 雷达抗干扰改善因子
Abstract: A novel approach using two-dimensional mixed baseline based on Multi-Input Multi-Output Synthetic Aperture Radar (MIMO-SAR) has been proposed for range delay and azimuth Doppler frequency modulation used in deceptive jamming. Based on MIMO-SAR phase coding method, which makes the multi-channel signal orthogonal, we propose the detection of deceptive jamming phenomenon by employing multi-dimensional phase information, and suppress the jamming targets via phase compensation to improve the ability of countering deceptive jamming. Moreover, we utilize radar anti-jamming improvement factor as a quantitative evaluating index. In the limited platform space, the radar anti-jamming improvement factor of the proposed method is three times greater than that of conventional single-input multi-output systems. Experimental results demonstrate the validity of our method.
- Deceptive jamming countering /
- Multi-Input Multi-Output Synthetic Aperture Radar (MIMO-SAR) /
- Phase compensation /
- The radar anti-jamming improvement factor

HTML全文

图 1 多普勒频谱示意图

Figure 1. Diagrammatic sketch of Doppler spectrum

下载: 全尺寸图片幻灯片

图 2 距离向抗欺骗干扰几何模型

Figure 2. Geometric model of range anti-deception jamming

下载: 全尺寸图片幻灯片

图 3 方位向抗欺骗干扰几何模型

Figure 3. Geometric model of azimuth anti-deception jamming

下载: 全尺寸图片幻灯片

图 4 2维抗欺骗干扰几何模型

Figure 4. Geometric model for two-dimensional anti-deception jamming

下载: 全尺寸图片幻灯片

图 5 方法流程

Figure 5. Method flow

下载: 全尺寸图片幻灯片

图 6 4发4收与单发4收对比

Figure 6. Comparison of 4-in-4-out and 4-in-1-out

下载: 全尺寸图片幻灯片

图 7 点目标成像

Figure 7. Point target imaging

下载: 全尺寸图片幻灯片

图 8 真实目标干涉相位

Figure 8. Interferometric phase of real target

下载: 全尺寸图片幻灯片

图 9 干扰目标干涉相位

Figure 9. Interferometric phase of jamming target

下载: 全尺寸图片幻灯片

图 10 点目标成像

Figure 10. Point target imaging

下载: 全尺寸图片幻灯片

图 11 真实目标干涉相位

Figure 11. Interferometric phase of real target

下载: 全尺寸图片幻灯片

图 12 干扰目标干涉相位

Figure 12. Interferometric phase of jamming target

下载: 全尺寸图片幻灯片

图 13 干扰目标成像

Figure 13. Jamming target imaging

下载: 全尺寸图片幻灯片

图 14 抗干扰后目标成像

Figure 14. Target imaging after anti-jamming

下载: 全尺寸图片幻灯片

表 1 仿真参数

Table 1. Simulation parameters

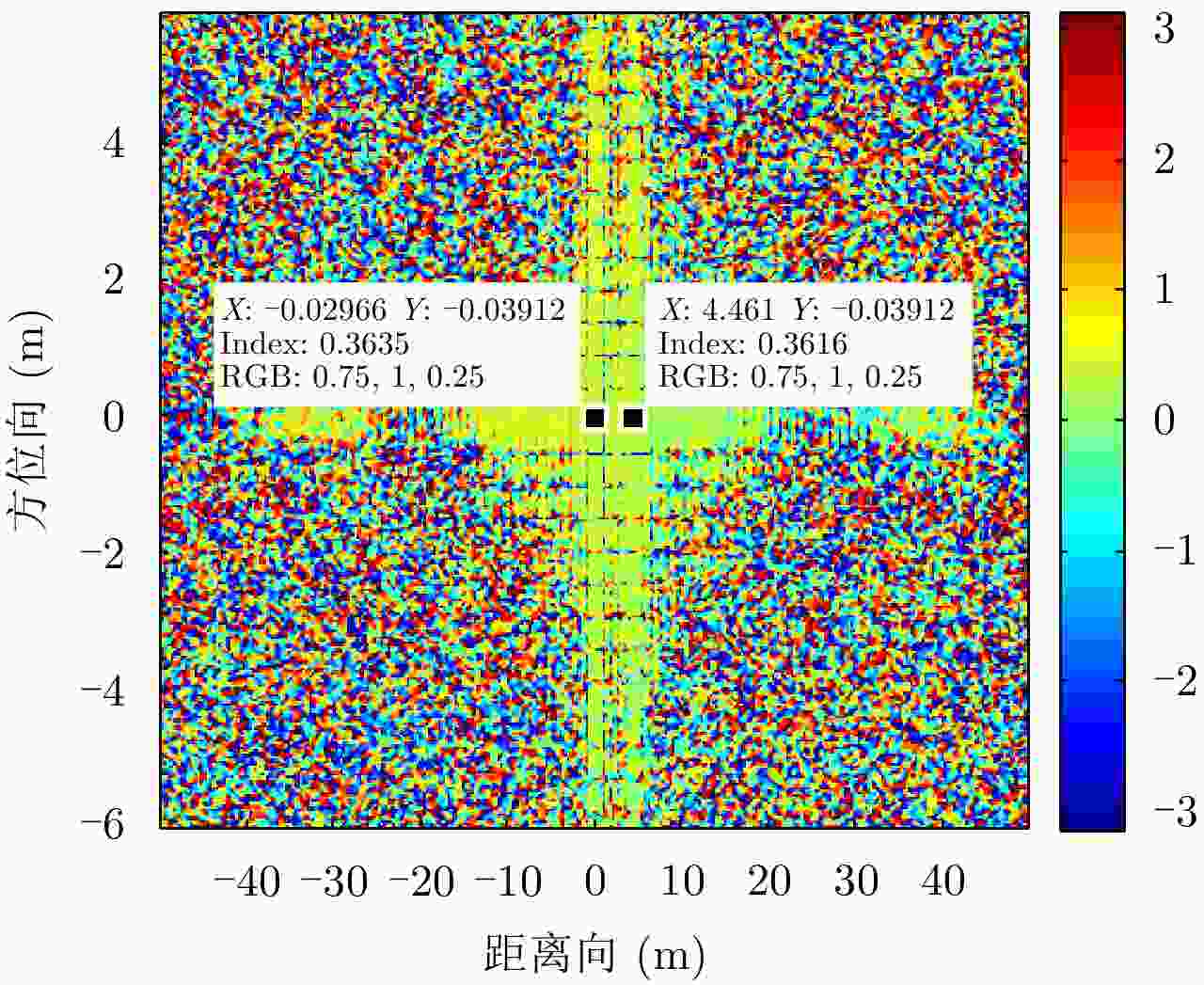
参数	数值
景中心斜距(km)	1.414
雷达有效速度(m/s)	150
发射脉冲时宽(μs)	2.5
距离调频率(Hz/s)	20 × 10¹²
雷达工作频率(GHz)	5.3
多普勒带宽(Hz)	80
距离采样率(MHz)	60
方位采样率(Hz)	400
回波信噪比(dB)	10
距离基线长度(m)	4
方位基线长度(m)	2

下载: 导出CSV

表 2 9点目标交轨干涉相位

Table 2. Cross-track interference phase of nine-point target

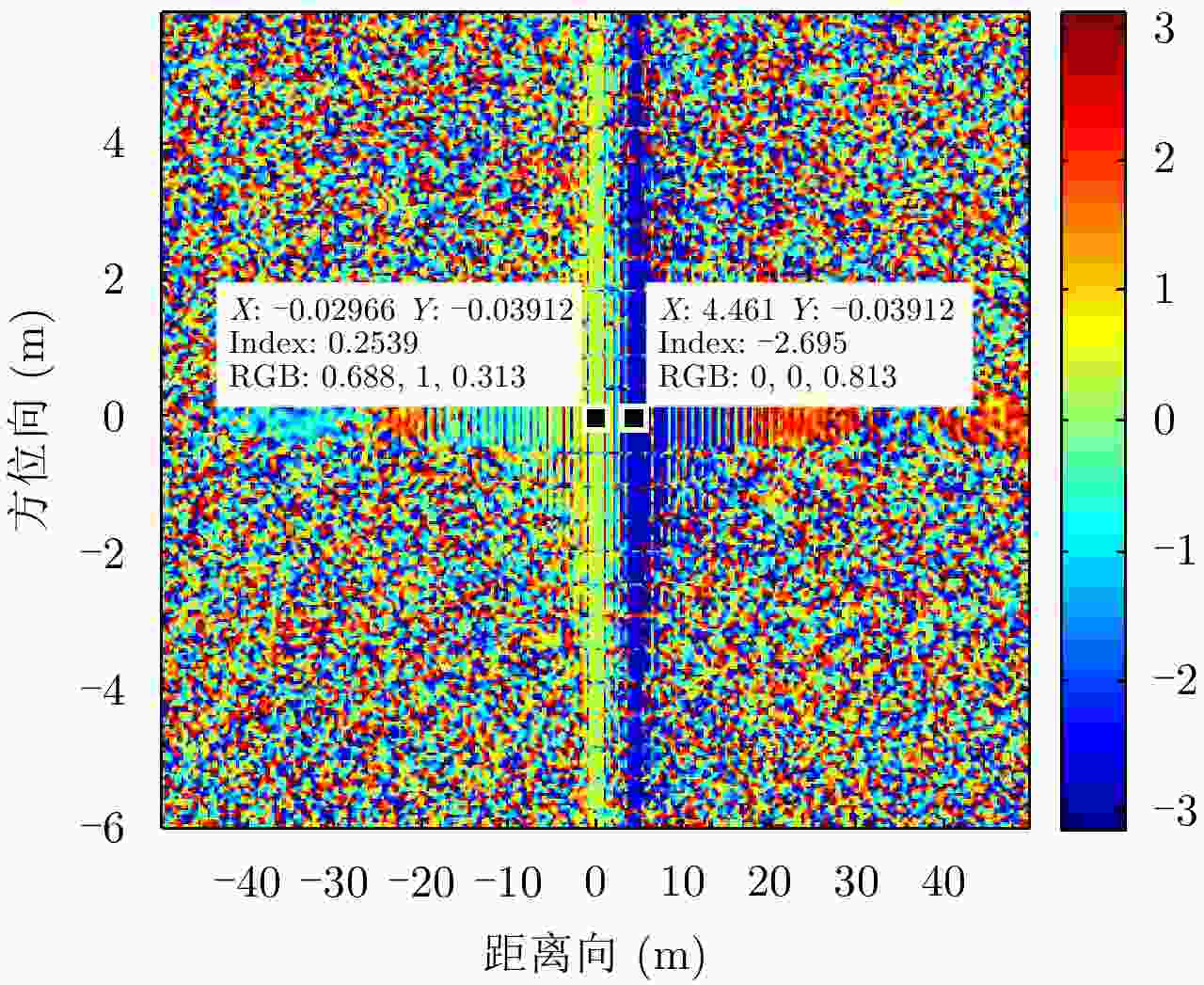
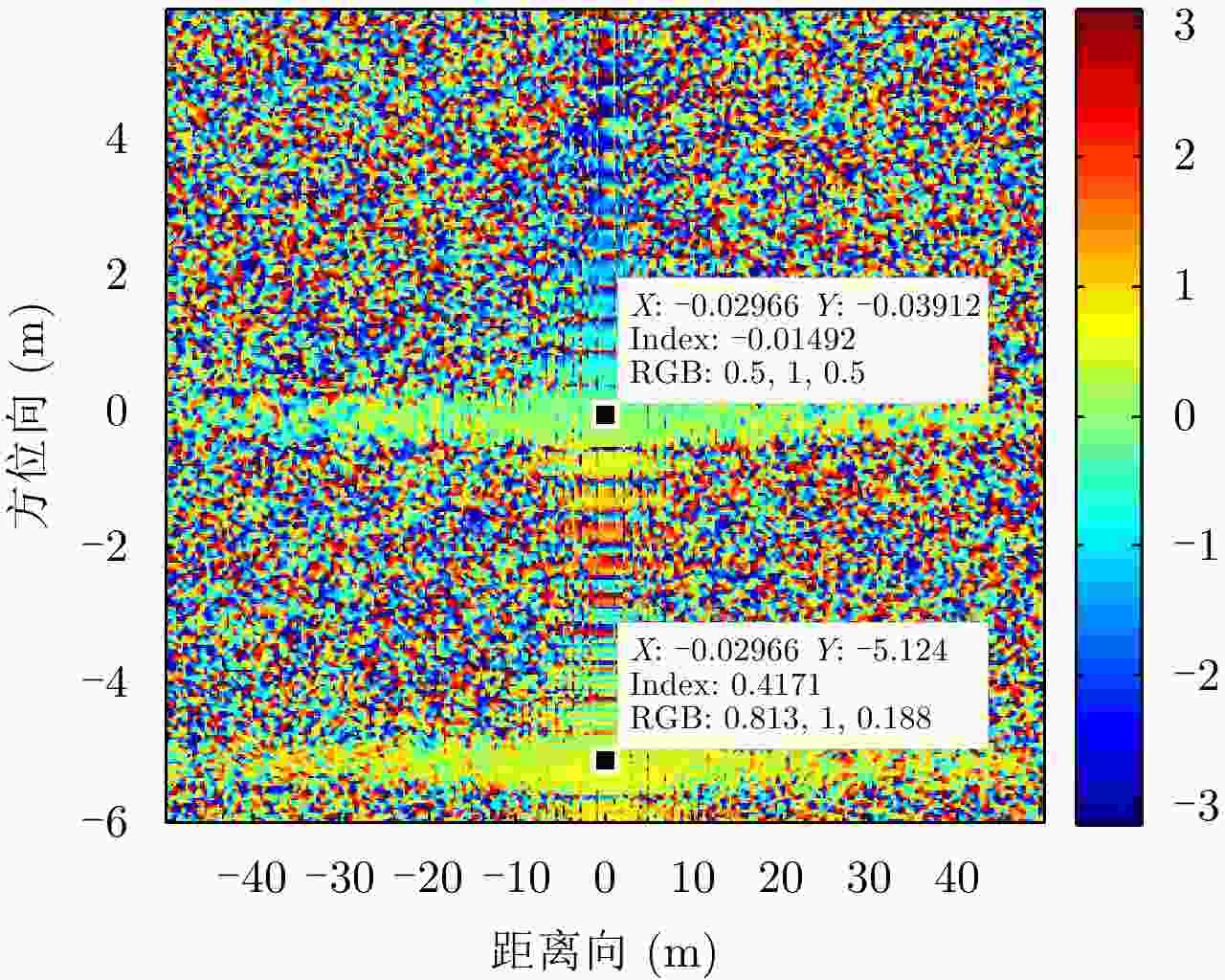
相位(rad)	第1列	第2列	第3列
第1行	0.1348	0.1370	0.1423
第2行	0.1360	0.1390	0.1407
第3行	0.1379	0.1370	0.1425

下载: 导出CSV

表 3 9点目标顺轨干涉相位

Table 3. Along-track interference phase of nine-point target

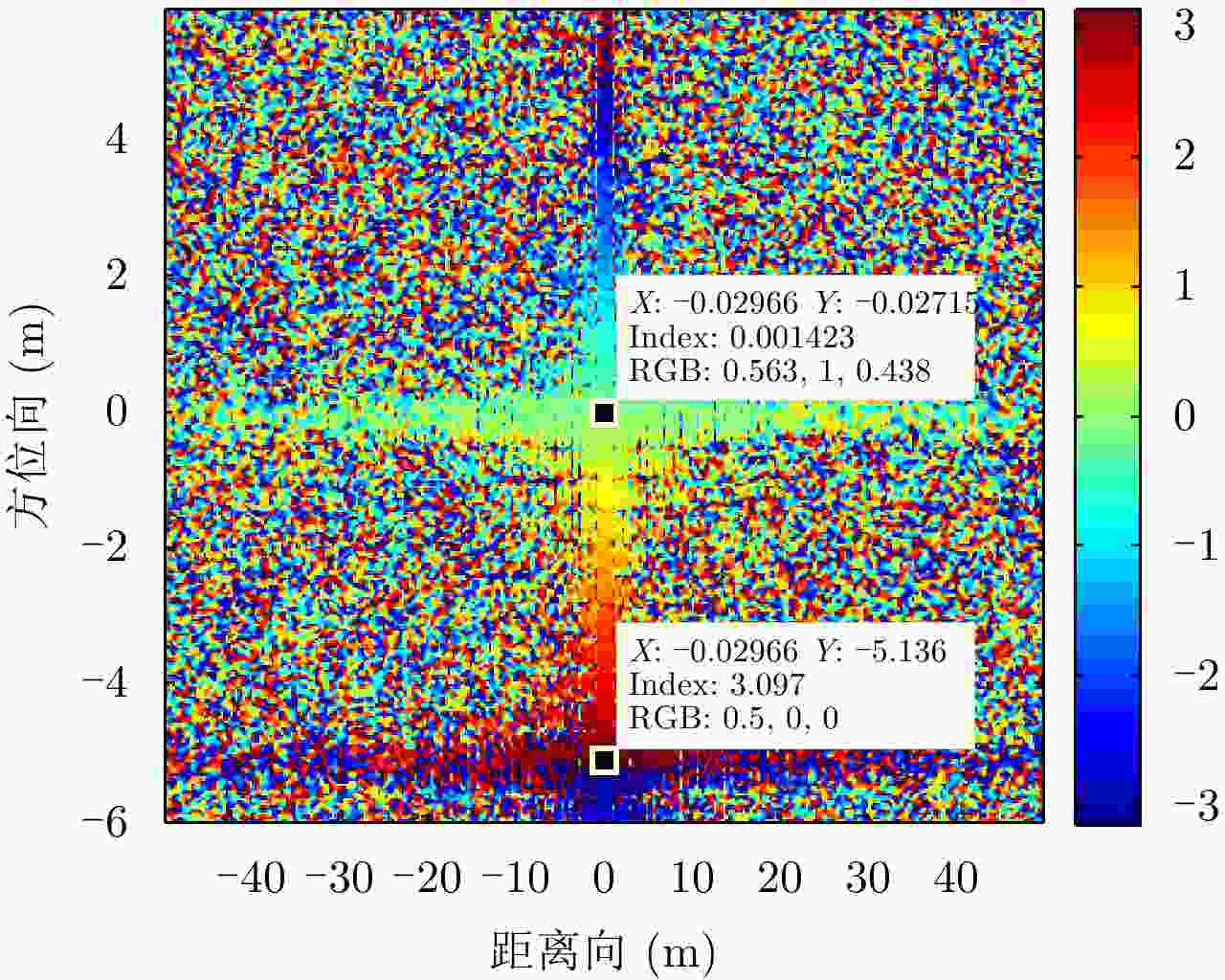
相位(rad)	第1列	第2列	第3列
第1行	3.085	3.085	3.085
第2行	0	0	0
第3行	–3.085	–3.086	–3.086

下载: 导出CSV

参考文献(19)

[1]	朱守保, 罗强, 童创明. SAR图像欺骗干扰方法研究[J]. 电光与控制, 2012, 19(4): 39–42. doi: 10.3969/j.issn.1671-637X.2012.04.010 ZHU Shoubao, LUO Qiang, and TONG Chuangming. Methods of deceptive jamming to SAR image[J]. Electronics Optics &Control, 2012, 19(4): 39–42. doi: 10.3969/j.issn.1671-637X.2012.04.010
[2]	ZHANG Jindong, ZHU Daiyin, and ZHANG Gong. New antivelocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290–1300. doi: 10.1109/TAES.2013.6494414
[3]	孙光才, 周峰, 邢孟道, 等. 虚假场景SAR欺骗式干扰技术及实时性分析[J]. 西安电子科技大学学报(自然科学版), 2009, 36(5): 813–818, 866. SUN Guangcai, ZHOU Feng, XING Mengdao, et al. Deception-jamming technology against the SAR based on the deceptive scene and real-time analyses[J]. Journal of Xidian University, 2009, 36(5): 813–818, 866.
[4]	马晓岩, 秦江敏, 贺照辉, 等. 抑制SAR压制性干扰的三通道对消方法[J]. 电子学报, 2007, 35(6): 1015–1020. doi: 10.3321/j.issn:0372-2112.2007.06.002 MA Xiaoyan, QIN Jiangmin, HE Zhaohui, et al. Three-channel cancellation of SAR blanketing jamming suppression[J]. Acta Electronica Sinica, 2007, 35(6): 1015–1020. doi: 10.3321/j.issn:0372-2112.2007.06.002
[5]	ZHOU F, SUN G, BAI X, et al. A novel method for adaptive SAR barrage jamming suppression[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 292–296. doi: 10.1109/LGRS.2011.2166753
[6]	王晓东, 马泉成. 基于FMCW合成孔径雷达抗欺骗干扰方法研究[J]. 计算机仿真, 2013, 30(7): 5–10. doi: 10.3969/j.issn.1006-9348.2013.07.002 WANG Xiaodong and MA Quancheng. Anti-deception jamming method for frequency modulated continuous wave synthetic aperture radar[J]. Computer Simulation, 2013, 30(7): 5–10. doi: 10.3969/j.issn.1006-9348.2013.07.002
[7]	彭发祥, 李宏伟, 蔡斌, 等. 星载多发多收SAR成像和抗欺骗干扰研究[J]. 现代防御技术, 2012, 40(2): 143–149, 154. doi: 10.3969/j.issn.1009-086x.2012.02.028 PENG Faxiang, LI Hongwei, CAI Bin, et al. Research on spaceborne MIMO-SAR imaging and anti-deceptive jamming[J]. Modern Defence Technology, 2012, 40(2): 143–149, 154. doi: 10.3969/j.issn.1009-086x.2012.02.028
[8]	齐维孔, 禹卫东. 距离向DBF-SAR系统抗欺骗干扰研究[J]. 电子与信息学报, 2010, 32(12): 2830–2835. doi: 10.3724/SP.J.1146.2010.00074 QI Weikong and YU Weidong. Research on countering deceptive jamming with range DBF-SAR system[J]. Journal of Electronics &Information Technology, 2010, 32(12): 2830–2835. doi: 10.3724/SP.J.1146.2010.00074
[9]	SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 191–205. doi: 10.1109/TAES.2006.1603414
[10]	Emmanuel Arturo Solis Nepote. Chaotic and chaotic based frequency modulated signals for radar imaging[D]. [Master dissertation], University of Manitoba, 2003.
[11]	LI Chen and ZHU Daiyin. The detection of deception jamming against SAR based on dual-aperture antenna cross-track interferometry[C]. 2006 CIE International Conference on Radar, Shanghai, China, 2006: 1–4. doi: 10.1009/ICR.2006.343274.
[12]	QIN Jiangmin, YANG Jun, HE Zhaohui, et al. Analysis of target loss due to suppressing SAR jamming using dual-channel cancellation[C]. 2006 CIE International Conference on Radar, Shanghai, China, 2006: 1–4. doi: 10.1109/ICR.2006.343324.
[13]	SUN Bingzhang and LI Jingwen. A new interference elimination method for multi-satellite SAR system[C]. IGARSS 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 2008, 4: IV-1316–IV-1319. doi: 10.1109/IGARSS.2008.4779973
[14]	ZHAO Bo, HUANG Lei, LI Jian, et al. Target reconstruction from deceptively jammed single-channel SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 152–167. doi: 10.1109/TGRS.2017.2744178
[15]	王杰, 丁赤飚, 梁兴东, 等. 机载同时同频MIMO-SAR系统研究概述[J]. 雷达学报, 2018, 7(2): 220–234. doi: 10.12000/JR17046 WANG Jie, DING Chibiao, LIANG Xingdong, et al. Research outline of airborne MIMO-SAR system with same time-frequency coverage[J]. Journal of Radars, 2018, 7(2): 220–234. doi: 10.12000/JR17046
[16]	黄洪旭, 黄知涛, 周一宇. 对合成孔径雷达的移频干扰研究[J]. 宇航学报, 2006, 27(3): 463–468. doi: 10.3321/j.issn:1000-1328.2006.03.027 HUANG Hongxu, HUANG Zhitao, and ZHOU Yiyu. A study on the shift-frequency jamming to SAR[J]. Journal of Astronautics, 2006, 27(3): 463–468. doi: 10.3321/j.issn:1000-1328.2006.03.027
[17]	HE Xiaodong, WANG Zhen, and TANG Bin. Two-dimensional frequency modulation jamming to SAR based on ship-borne jammer[J]. International Journal of Electronics Letters, 2016, 4(2): 141–157. doi: 10.1080/00207217.2014.966782
[18]	许宝民, 郑光勇, 李宏. 合成孔径雷达有源欺骗干扰仿真分析[J]. 飞行器测控学报, 2010, 29(3): 84–87. XU Baomin, ZHENG Guangyong, and LI Hong. Simulation research on active deceptive jamming to SAR[J]. Journal of Spacecraft TT &C Technology, 2010, 29(3): 84–87.
[19]	刘永才, 王伟, 潘小义, 等. 基于延迟-移频的SAR有源欺骗干扰有效区域研究[J]. 雷达学报, 2013, 2(1): 46–53. doi: 10.3724/SP.J.1300.2012.13001 LIU Yongcai, WANG Wei, PAN Xiaoyi, et al. Effective region of active decoy jamming to SAR based on time-delay doppler-shift method[J]. Journal of Radars, 2013, 2(1): 46–53. doi: 10.3724/SP.J.1300.2012.13001