基于参数估计的下视稀疏阵列三维SAR运动误差补偿和成像处理方法

刘奇勇; 张群; 洪文; 苏令华; 梁佳

doi:10.12000/JR18107

基于参数估计的下视稀疏阵列三维SAR运动误差补偿和成像处理方法

DOI: 10.12000/JR18107

刘奇勇¹,
张群^2,3,4, ,,
洪文^5,6,
苏令华^2,3,
梁佳^2,3

①.
空军工程大学研究生院西安 710077
②.
空军工程大学信息与导航学院西安 710077
③.
信息感知技术协同创新中心西安 710077
④.
复旦大学电磁波信息科学教育部重点实验室上海 200433
⑤.
微波成像技术国家重点实验室北京 100190
⑥.
中国科学院电子学研究所北京 100190

基金项目: 国家自然科学基金(61471386, 61871396)，陕西省自然科学基础研究计划(2016JM4008)

详细信息

作者简介:
刘奇勇(1990–)，男，湖南邵阳人，空军工程大学博士生，主要研究方向为SAR成像、线阵SAR 3维成像

张　群(1964–)，男，陕西合阳人，空军工程大学信息与导航学院教授，博士生导师，主要研究方向为雷达成像与目标识别。E-mail: zhangqunnus@gmail.com

洪　文(1968–)，女，上海人，中国科学院电子学研究所研究员，博士生导师，主要研究方向为极化/极化干涉SAR处理及应用、3维SAR信号处理、圆迹SAR信号处理以及稀疏微波成像技术

苏令华(1979–)，男，山东枣庄人，空军工程大学信息与导航学院讲师，主要研究方向为遥感图像处理、雷达信号处理、DSP算法设计

梁　佳(1985–)，男，陕西西安人，空军工程大学信息与导航学院讲师，主要研究方向为雷达成像

通讯作者:
张群 zhangqunnus@gmail.com

中图分类号: TN957
计量
- 文章访问数: 3291
- HTML全文浏览量: 702
- PDF下载量: 179
- 被引次数: 0
出版历程
- 收稿日期: 2018-12-03
- 修回日期: 2018-12-27
- 网络出版日期: 2018-12-28

DLSLA 3D SAR Motion Error Compensation and Imaging Method Based on Parameter Estimation

Liu Qiyong¹,
Zhang Qun^{2,3,4
, ,},
Hong Wen^5,6,
Su Linghua^2,3,
Liang Jia^2,3

①.
Air Force Engineering University Graduate College, Xi’an 710077, China
②.
College of Information and Navigation, Air Force Engineering University, Xi’an 710077, China
③.
Collaborative Innovation Center of Information Sensing and Understanding, Xi’an 710077, China
④.
The Key Laboratory for Information Science of Electromagnetic Waves (Ministry of Education), Fudan University, Shanghai 200433, China
⑤.
National Key Laboratory of Microwave Imaging Technology, Beijing 100190, China
⑥.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China

Funds: The National Natural Science Foundation of China (61471386, 61871396), The Natural Science Foundation Research Program of Shaanxi Province (2016JM4008)

摘要

摘要: 当载机存在偏航角速度时，载机航线会偏离理想航线，对稀疏阵列下视3维合成孔径雷达(DLSLA 3D SAR)成像产生影响。该文建立了载机在飞行过程中存在偏航角速度下的DLSLA 3D SAR成像模型，通过理论推导得到了信号的多普勒调频率表达式，多普勒调频率与目标被调制后的跨航向坐标有关，而与被调制后的方位向坐标无关。进一步，完成跨航向信号处理之后，在平台的速度和偏航角速度不准的情况下，利用参数化稀疏表征方法实现了平台的速度和偏航角速度的估计，并完成了方位向稀疏场景的重构，最后提出了一种形变校正方法。仿真实验验证了该算法的有效性。
- 稀疏阵列下视3维合成孔径雷达 /
- 运动误差 /
- 多普勒调频率 /
- 参数化稀疏表征
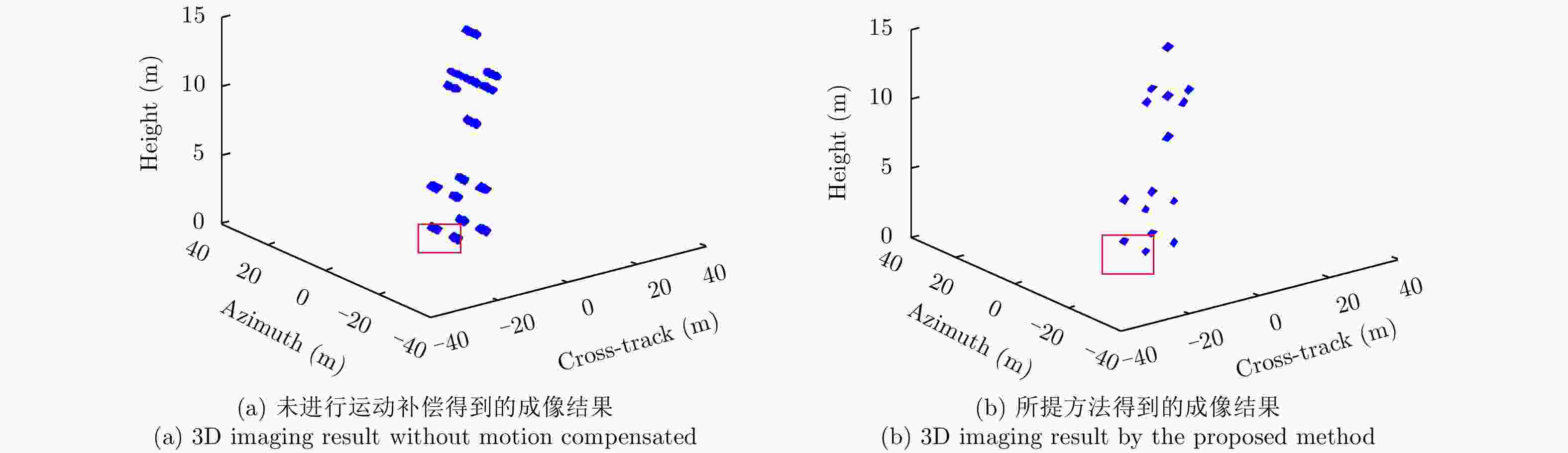
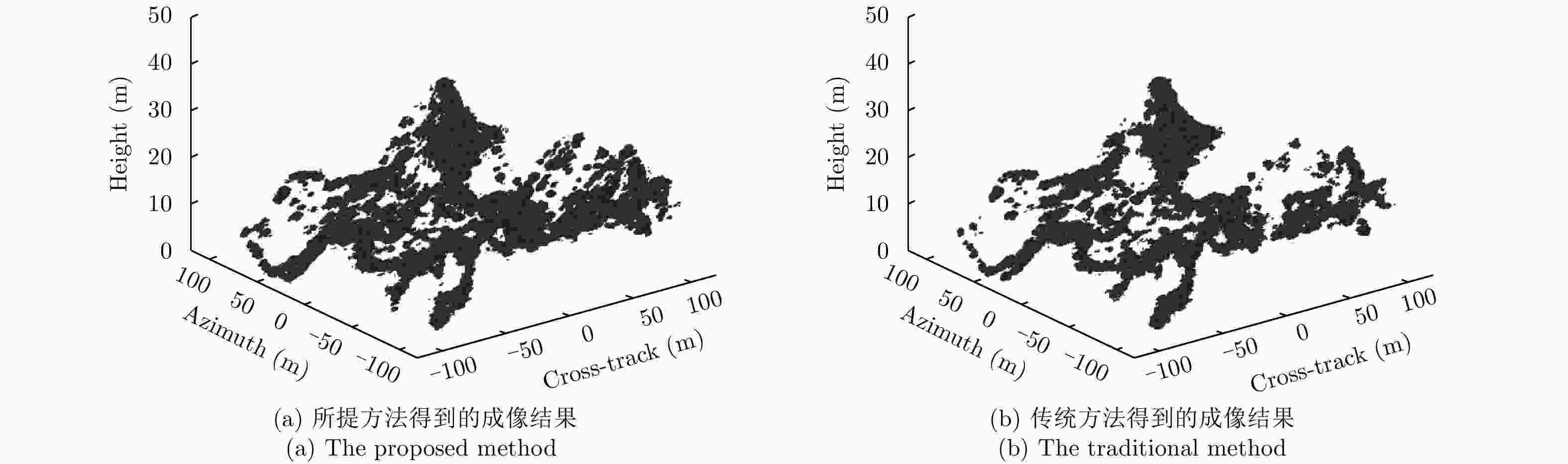
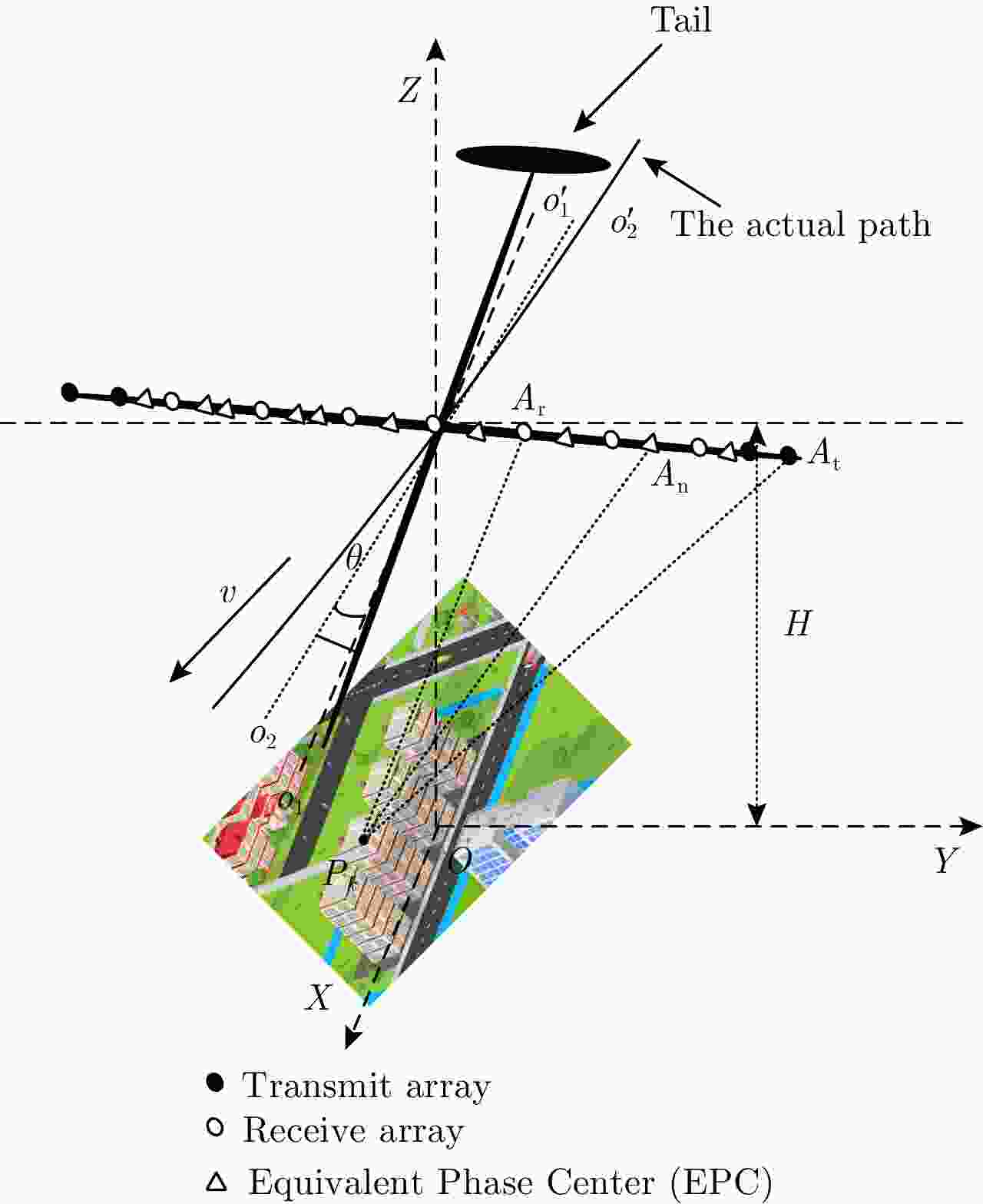
Abstract: In the presence of yaw angular velocity, a body will deviate from its ideal flight path, which will affect imaging of Downward-Looking Sparse Linear Array 3D Synthetic Aperture Radar (DLSLA 3D SAR). In this paper, an imaging model including yaw rate is established. Furthermore, Doppler frequency modulation, which is related to cross-track coordinates and not azimuth coordinates, was theoretically calculated. Thus, a cross-track signal could be reconstructed to obtain the cross-track coordinates before azimuth signal compression. Based on the parametric sparse representation, the velocity and yaw rate of the platform were estimated, and the azimuth signal was compressed. Moreover, a deformation correction method is proposed to correct image deformation. The simulation results demonstrate the validity of the proposed method.
- Downward-Looking Sparse Linear Array 3D Synthetic Aperture Radar (DLSLA 3D SAR) /
- Motion error /
- Doppler frequency rate /
- Parametric sparse representation

HTML全文

图 1 DLSLA 3D SAR成像几何模型

Figure 1. DLSLA 3D SAR imaging geometry model

下载: 全尺寸图片幻灯片

图 2 所提方法流程图

Figure 2. The flow chart of the proposed method

下载: 全尺寸图片幻灯片

图 3 3维孤立点目标模型

Figure 3. 3D isolated targets model

下载: 全尺寸图片幻灯片

图 4 成像结果

Figure 4. Imaging result

下载: 全尺寸图片幻灯片

图 5 方位向截面图

Figure 5. The azimuth sectional image

下载: 全尺寸图片幻灯片

图 6 方位向-跨航向平面投影图

Figure 6. 2D projection onto azimuth and cross-track plane

下载: 全尺寸图片幻灯片

图 7 成像场景示意图

Figure 7. The ideal scene

下载: 全尺寸图片幻灯片

图 8 分布式场景DLSLA 3D SAR成像结果

Figure 8. 3D imaging result of scene

下载: 全尺寸图片幻灯片

图 9 方位向-跨航向平面投影图

Figure 9. 2D projection onto azimuth and cross-track plane

下载: 全尺寸图片幻灯片

图 10 形变校正后的方位向-跨航向平面投影图

Figure 10. 2D projection onto azimuth and cross-track plane after deformation correction.

下载: 全尺寸图片幻灯片

表 1 平台和天线的参数

Table 1. Parameters of platform and antenna

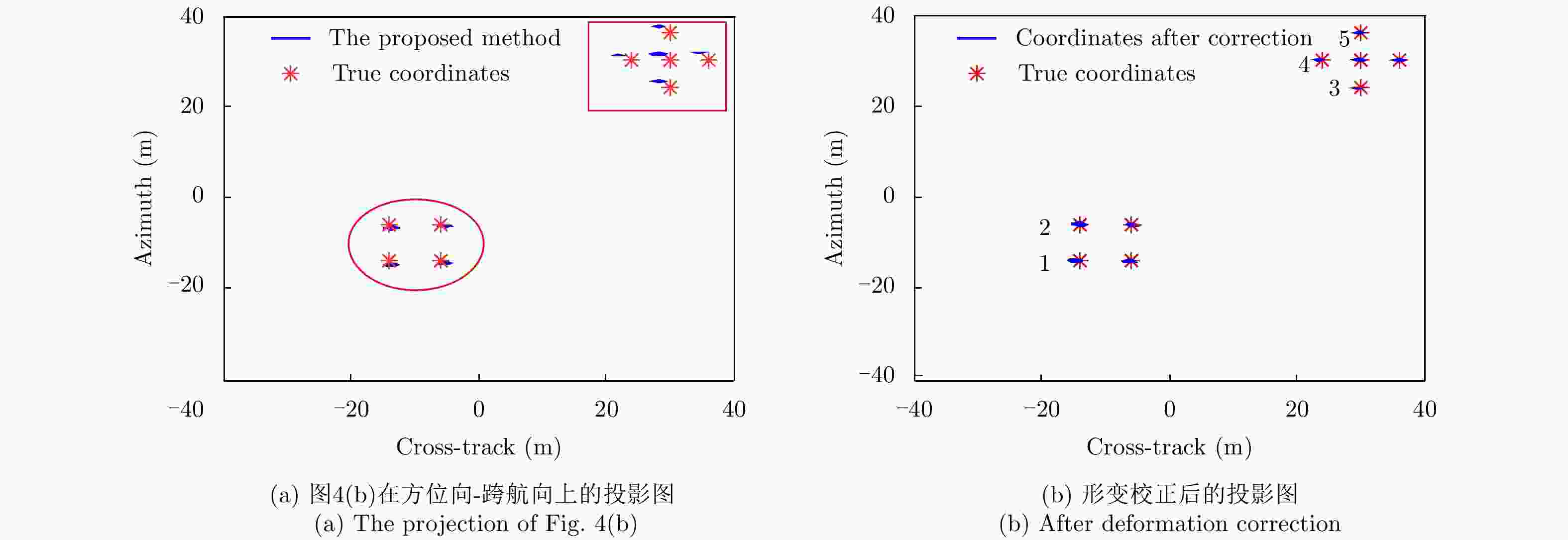
参数	值	参数	值
载频f_c (GHz)	17	脉冲重复频率PRF (Hz)	5000
带宽B_r (MHz)	200	发射天线数量N_t	16
平台高度H (m)	1300	接收天线数量N_r	15
平台速度v (m/s)	60	跨航向分辨率(m)	5.42
脉冲持续时间T_r (μs)	0.1	方位向分辨率(m)	0.5
偏航角速度(°/s)	2	初始偏航角(°)	3

下载: 导出CSV

表 2 图5中两种结果对应3 dB宽度

Table 2. The 3 dB width of the two methods in Fig. 5

目标	直接法	参数化稀疏表征法	提升倍数
1	2.26 m	0.41 m	5.51
2	2.51 m	0.36 m	6.97

下载: 导出CSV

表 3 形变校正前后的方位向、跨航向坐标

Table 3. The azimuth and cross-track coordinates before and after deformation correction

目标	实际坐标(m)	校正前的坐标(m)	校正后的坐标(m)	提升倍数
1	(–14, –14)	(–14.92, –13.13)	(–13.95, –14.49)	(18.40, 1.77)
2	(–6, –14)	(–6.64, –13.60)	(–6.09, –14.02)	(7.10, 20.00)
3	(24, 30)	(25.45, 28.26)	(24.01, 29.49)	(145.00, 3.41)
4	(30, 24)	(30.96, 21.98)	(29.89, 23.41)	(8.72, 3.42)
5	(36, 30)	(37.48, 28.26)	(36.19, 29.89)	(7.79, 15.81)

下载: 导出CSV

表 4 形变校正前后的方位向、跨航向坐标

Table 4. The azimuth and cross-track coordinates before and after deformation correction

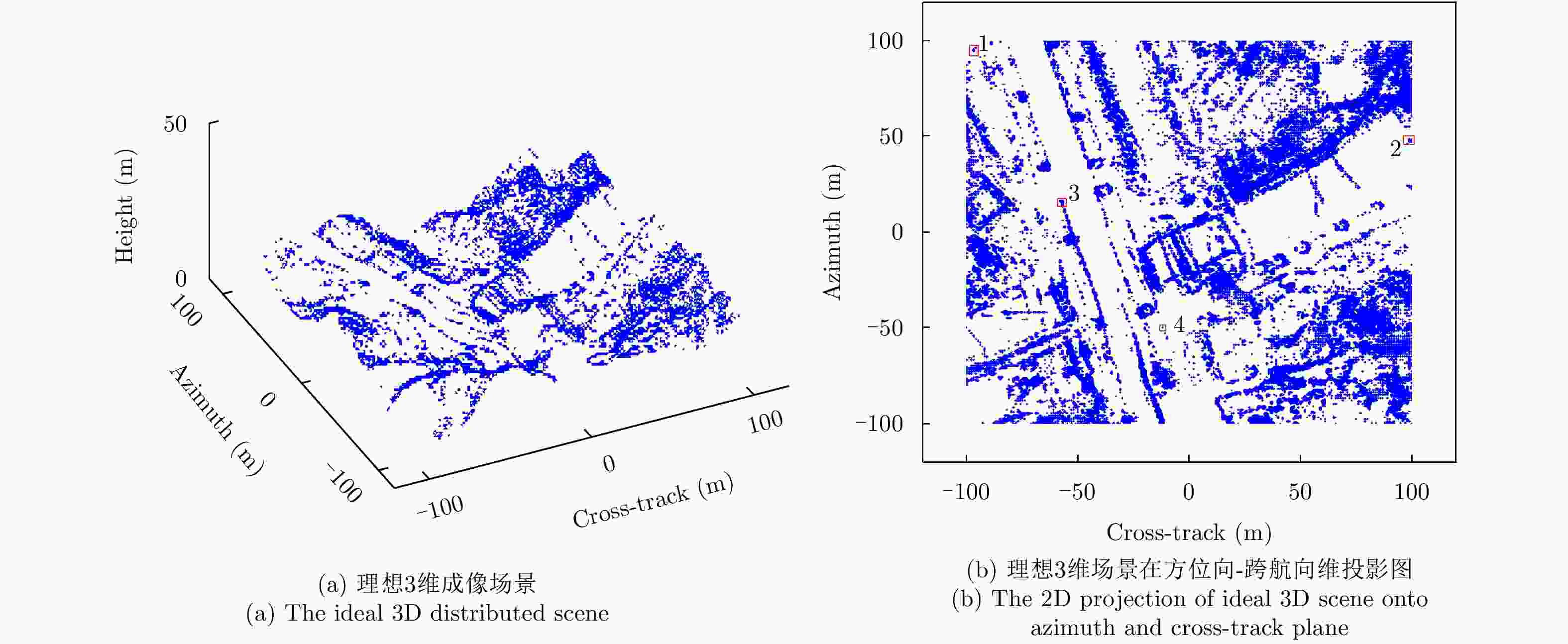
目标	实际坐标(m)	校正前的坐标(m)	校正后的坐标(m)	提升倍数
1	(95, –97)	(81.72, –105.10)	(95.32, –99.31)	(41.50, 3.50)
2	(48, 100)	(60.12, 97.15)	(48.23, 100.92)	(52.69, 3.09)
3	(16, –57)	(12.68, –59.62)	(16.30, –58.53)	(11.06, 1.71)
4	(–50, –12)	(–49.32, –11.56)	(–49.91, –11.58)	(7.55, 1.04)

下载: 导出CSV

参考文献(17)

[1]	Budillon A, Evangelista A, and Schirinzi G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488–499. DOI: 10.1109/TGRS.2010.2054099
[2]	Zhu X X and Bamler R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. DOI: 10.1109/TGRS.2010.2050487
[3]	Peng X M, Tan W X, Hong W, et al. Airborne DLSLA 3-D SAR image reconstruction by combination of polar formatting and L1 regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 213–226. DOI: 10.1109/TGRS.2015.2453202
[4]	徐宗本, 吴一戎, 张冰尘, 等. 基于L_1/2正则化理论的稀疏雷达成像[J]. 科学通报, 2018, 63(14): 1306–1319. DOI: 10.1360/N972018-00372 Xu Zong-ben, Wu Yi-rong, Zhang Bing-chen, et al. Sparse radar imaging based on L_1/2 regularization theory[J]. Chinese Science Bulletin, 2018, 63(14): 1306–1319. DOI: 10.1360/N972018-00372
[5]	毕辉, 张冰尘, 洪文. 基于RIPless理论的层析SAR成像航迹分布优化方法[J]. 航空学报, 2016, 37(2): 680–687. DOI: 10.7527/S1000-6893.2015.0131 Bi Hui, Zhang Bingchen, and Hong Wen. Track distribution optimization method based on TomoSAR via RIPless theory[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 680–687. DOI: 10.7527/S1000-6893.2015.0131
[6]	侯丽英, 林赟, 洪文. 干涉圆迹SAR的目标三维重建方法研究[J]. 雷达学报, 2016, 5(5): 538–547. DOI: 10.12000/JR16009 Hou Li-ying, Lin Yun, and Hong Wen. Three-dimensional reconstruction method study based on interferometric circular SAR[J]. Journal of Radars, 2016, 5(5): 538–547. DOI: 10.12000/JR16009
[7]	李烈辰, 李道京, 张清娟. 基于压缩感知的三孔径毫米波合成孔径雷达侧视三维成像[J]. 电子与信息学报, 2013, 35(3): 552–558. DOI: 10.3724/SP.J.1146.2012.01016 Li Lie-chen, Li Dao-jing, and Zhang Qing-juan. Three-aperture millimeter-wave SAR side-looking three-dimensional imaging based on compressed sensing[J]. Journal of Electronics&Information Technology, 2013, 35(3): 552–558. DOI: 10.3724/SP.J.1146.2012.01016
[8]	张清娟, 李道京, 李烈辰. 连续场景的稀疏阵列SAR侧视三维成像研究[J]. 电子与信息学报, 2013, 35(5): 1097–1102. DOI: 10.3724/SP.J.1146.2012.01136 Zhang Qing-juan, Li Dao-jing, and Li Lie-chen. Research on continuous scene side-looking 3D imaging based on sparse array[J]. Journal of Electronics&Information Technology, 2013, 35(5): 1097–1102. DOI: 10.3724/SP.J.1146.2012.01136
[9]	田鹤, 李道京, 潘洁, 等. 基于修正均匀冗余阵列正反编码的稀疏阵列SAR下视三维成像处理[J]. 电子与信息学报, 2017, 39(9): 2203–2211. DOI: 10.11999/JEIT161209 Tian He, Li Dao-jing, Pan Jie, et al. Downward-looking 3D imaging processing of sparse array SAR based on modified uniformly redundant arrays positive and negative coding[J]. Journal of Electronics&Information Technology, 2017, 39(9): 2203–2211. DOI: 10.11999/JEIT161209
[10]	李道京, 侯颖妮, 滕秀敏, 等. 稀疏阵列天线雷达技术及其应用[M]. 北京: 科学出版社, 2014. Li Dao-jing, Hou Ying-ni, Teng Xiu-min, et al.. Sparse Array Antenna Radar Imaging Technology and Application[M]. Beijing: Science Press, 2014.
[11]	Bao Q, Han K Y, Peng X M, et al. DLSLA 3-D SAR imaging algorithm for off-grid targets based on pseudo-polar formatting and atomic norm minimization[J]. Science China Information Sciences, 2016, 59(6): 062310. DOI: 10.1007/s11432-015-5477-5
[12]	Liu Q Y, Zhang Q, Luo Y, et al. Fast algorithm for sparse signal reconstruction based on off-grid model[J]. IET Radar,Sonar&Navigation, 2018, 12(4): 390–397. DOI: 10.1049/iet-rsn.2017.0319
[13]	丁振宇, 谭维贤, 王彦平, 等. 基于波数域子孔径的机载三维SAR偏航角运动误差补偿[J]. 雷达学报, 2015, 4(4): 467–473. DOI: 10.12000/JR15016 Ding Zhen-yu, Tan Wei-xian, Wang Yan-ping, et al. Yaw angle error compensation for airborne 3-D SAR based on wavenumber-domain subblock[J]. Journal of Radars, 2015, 4(4): 467–473. DOI: 10.12000/JR15016
[14]	杨泽民, 孙光才, 邢孟道, 等. 基于多通道联合自聚焦技术的机载三维SAR运动补偿[J]. 电子与信息学报, 2012, 34(7): 1581–1588. DOI: 10.3724/SP.J.1146.2011.01365 Yang Ze-min, Sun Guang-cai, Xing Meng-dao, et al. Motion compensation for airborne 3-D SAR based on joint multi-channel auto-focusing technology[J]. Journal of Electronics&Information Technology, 2012, 34(7): 1581–1588. DOI: 10.3724/SP.J.1146.2011.01365
[15]	Chen Y C, Li G, Zhang Q, et al. Motion compensation for airborne SAR via parametric sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 551–562. DOI: 10.1109/TGRS.2016.2611522
[16]	刘云龙, 李焱磊, 周良将, 等. 一种机载SAR快速几何精校正算法[J]. 雷达学报, 2016, 5(4): 419–424. DOI: 10.12000/JR16064 Liu Yun-long, Li Yan-lei, Zhou Liang-jiang, et al. A fast precise geometric calibration method for airborne SAR[J]. Journal of Radars, 2016, 5(4): 419–424. DOI: 10.12000/JR16064
[17]	王力宝, 许稼, 皇甫堪, 等. MIMO-SAR等效相位中心误差分析与补偿[J]. 电子学报, 2009, 37(12): 2688–2693. DOI: 10.3321/j.issn:0372-2112.2009.12.015 Wang Li-bao, Xu Jia, Huangfu Kan, et al. Analysis and compensation of equivalent phase center error in MIMO-SAR[J]. Acta Electronica Sinica, 2009, 37(12): 2688–2693. DOI: 10.3321/j.issn:0372-2112.2009.12.015