基于方位相位编码的脉内聚束SAR成像方法

吴玉峰; 叶少华; 冯大政

doi:10.12000/JR17114

基于方位相位编码的脉内聚束SAR成像方法

DOI: 10.12000/JR17114

①.
中国航空工业集团公司雷华电子技术研究所无锡 214063
②.
西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 航空基金（2015ZC07005）

详细信息

作者简介:
吴玉峰(1985–)，男，浙江衢州人，博士，工程师。现为中国航空工业集团公司雷华电子技术研究所系统工程师，主要研究方向为SAR系统设计、SAR成像算法。E-mail: wyf1176@163.com

叶少华(1966–)，男，江苏江阴人，研究员，副总工程师。现为中国航空工业集团公司雷华电子技术研究所副总工程师，主要研究方向为雷达系统设计、雷达信号处理。E-mail: ye_shaohua@sina.com

冯大政(1959–)，男，陕西安康人，教授，博士生导师。现为西安电子科技大学电子工程学院二级教授，主要研究方向为雷达信号处理、类脑神经网络和图像处理等。E-mail: dzfeng@xidian.edu.cn

通讯作者:
吴玉峰 wyf1176@163.com

计量
- 文章访问数: 2492
- HTML全文浏览量: 603
- PDF下载量: 357
- 被引次数: 0
出版历程
- 收稿日期: 2017-11-28
- 修回日期: 2018-02-07
- 网络出版日期: 2018-08-28

Intra-pulse Spotlight SAR Imaging Method Based on Azimuth Phase Coding

Wu Yufeng^{1
, ,},
Ye Shaohua^1
,,
Feng Dazheng^2
,

①.
AVIC Leihua Electronic Technology Research Institute, Wuxi 214063, China
②.
National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The Aeronautical Foundation of China (2015ZC07005)

摘要

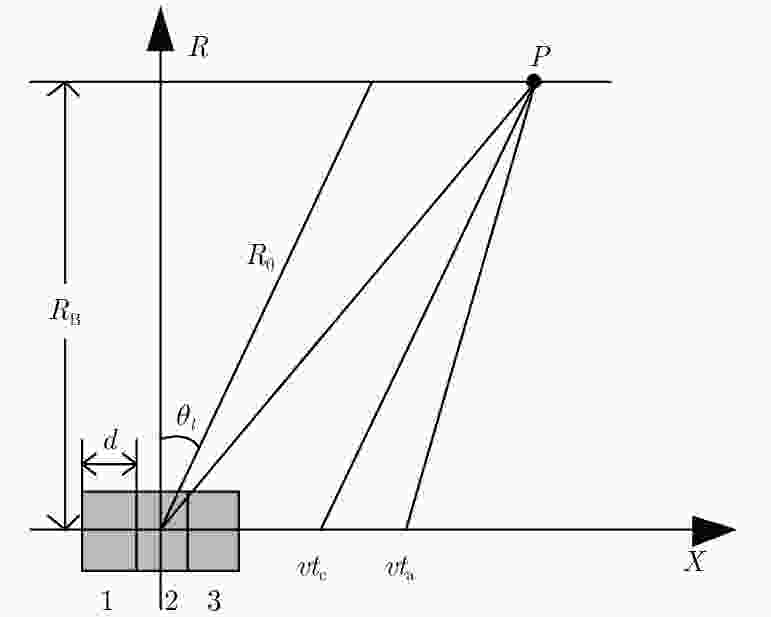
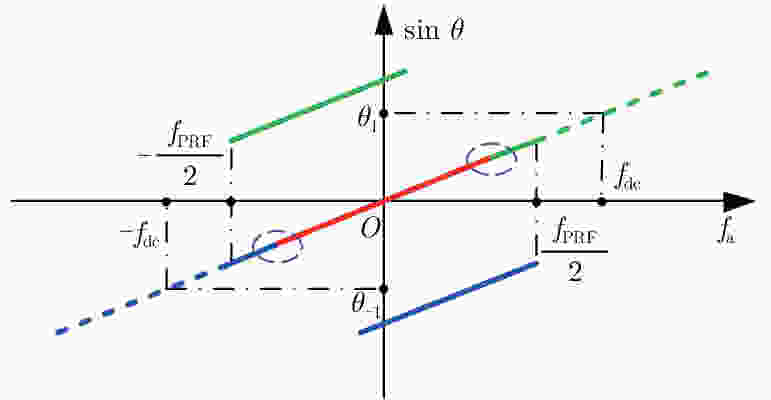
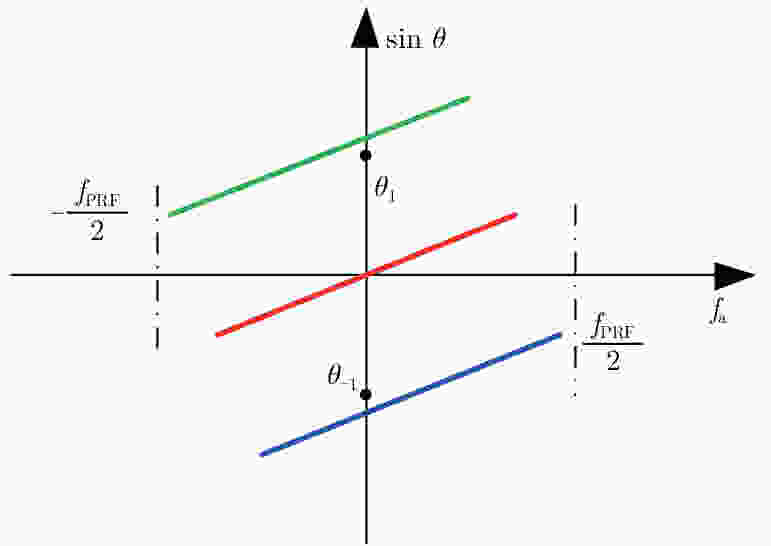
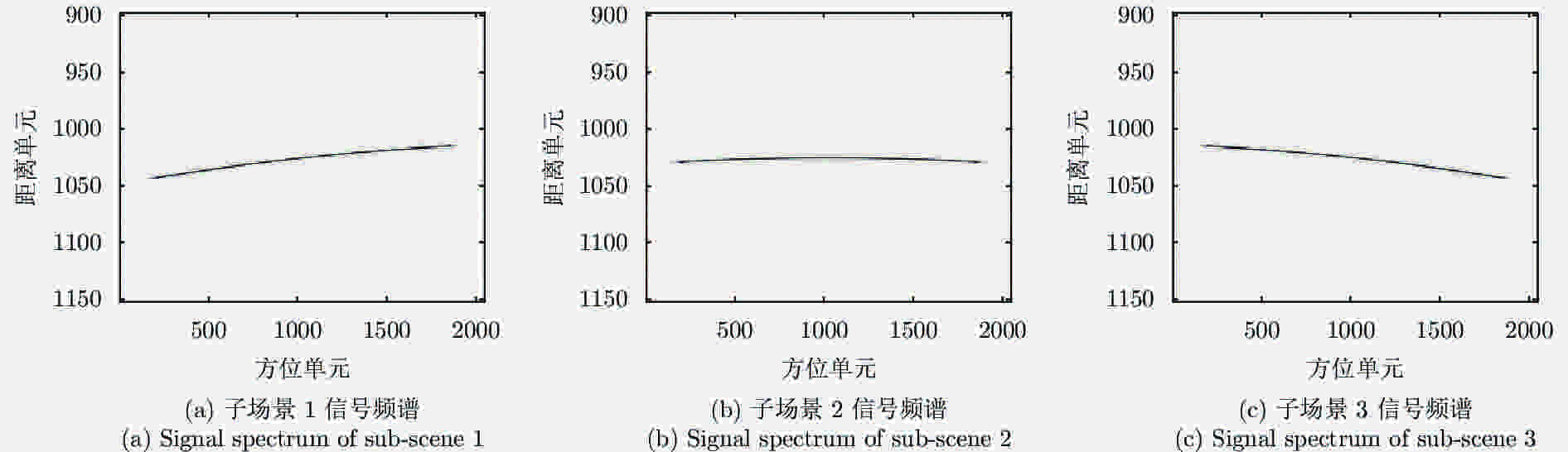
摘要: 脉内聚束模式有效克服了星载合成孔径雷达(Synthetic Aperture Radar, SAR)高分辨率与宽测绘带之间的矛盾，同时可以兼顾回波的信噪比。然而距离维空域滤波的信号分离方法容易受地形起伏的影响，甚至失效。针对此，该文提出了一种结合方位相位编码(Azimuth Phase Coding, APC)的脉内聚束SAR成像方法，利用APC技术使不同子脉冲回波的方位频谱处在不同的脉冲重复频率(Pulse Repetition Frequencies, PRF)范围，然后利用方位自适应波束形成技术来分离回波信号。文中对信号分离方法以及频移因子的选择进行了详细的讨论。最后仿真实验结果验证了所提方法的有效性。
- 合成孔径雷达 /
- 脉内聚束模式 /
- 方位相位编码 /
- 方位多通道 /
- 信号分离
Abstract: The intra-pulse spotlight imaging mode can effectively overcome the contradiction between high resolution and wide swath in spaceborne Synthetic Aperture Radar (SAR), and considers the echo’s signal-to-noise ratio. However, signal division by spatial filtering along the range direction may be impacted by fluctuating terrain. To solve this problem, a novel intra-pulse spotlight imaging method based on Azimuth Phase Coding (APC) is proposed in this paper. Using APC, the azimuth spectrum of echo data from different sub-pulses will locate in different Pulse Repetition Frequencies (PRF). As such, the signal can be divided using an azimuth adaptive beamforming technique. The signal separation method and selection of the shift factor are discussed in detail. Finally, simulation results demonstrate the effectiveness of the proposed method.
- Synthetic Aperture Radar (SAR) /
- Intra-pulse spotlight mode /
- Azimuth Phase Coding (APC) /
- Azimuth multi-channel /
- Signal division

HTML全文

图 1 方位多通道脉内聚束SAR收发信号模型

Figure 1. Transmitting and receiving signal modes of azimuth multi-channel intra-pulse spotlight SAR

下载: 全尺寸图片幻灯片

图 2 斜距平面成像几何

Figure 2. Imaging geometry in the slant-range plane

下载: 全尺寸图片幻灯片

图 3 不同方位子场景回波信号的时频关系

Figure 3. Time-frequency relation of different azimuth sub-scene echo signal

下载: 全尺寸图片幻灯片

图 4 引入APC技术后的时频关系

Figure 4. Time-frequency relation after adopting the APC technique

下载: 全尺寸图片幻灯片

图 5 某一通道的回波信号及其频谱

Figure 5. Echo signal and spectrum of one channel

下载: 全尺寸图片幻灯片

图 6 文献[13]方法信号分离结果

Figure 6. Signal division results by the method in Ref. [13]

下载: 全尺寸图片幻灯片

图 7 本文方法信号分离结果

Figure 7. Signal division results by the method in the paper

下载: 全尺寸图片幻灯片

图 8 完整的多普勒频谱以及成像结果

Figure 8. Imaging result of the combined complete Doppler spectrum

下载: 全尺寸图片幻灯片

图 9 面目标仿真结果

Figure 9. Simulation results of area target

下载: 全尺寸图片幻灯片

表 1 仿真参数

Table 1. Simulation parameters

参数	值	参数	值
雷达载频(GHz)	9.65	方位孔径(m)	4.8
脉冲总时宽(μs)	30	脉冲重复频率(Hz)	3600
子脉冲信号带宽(MHz)	150	场景中心距离(km)	596
采样频率(MHz)	180	子脉冲个数	3
平台速度(m/s)	7200	方位通道数	3

下载: 导出CSV

表 2 成像性能参数统计

Table 2. Parameters of the focused targets

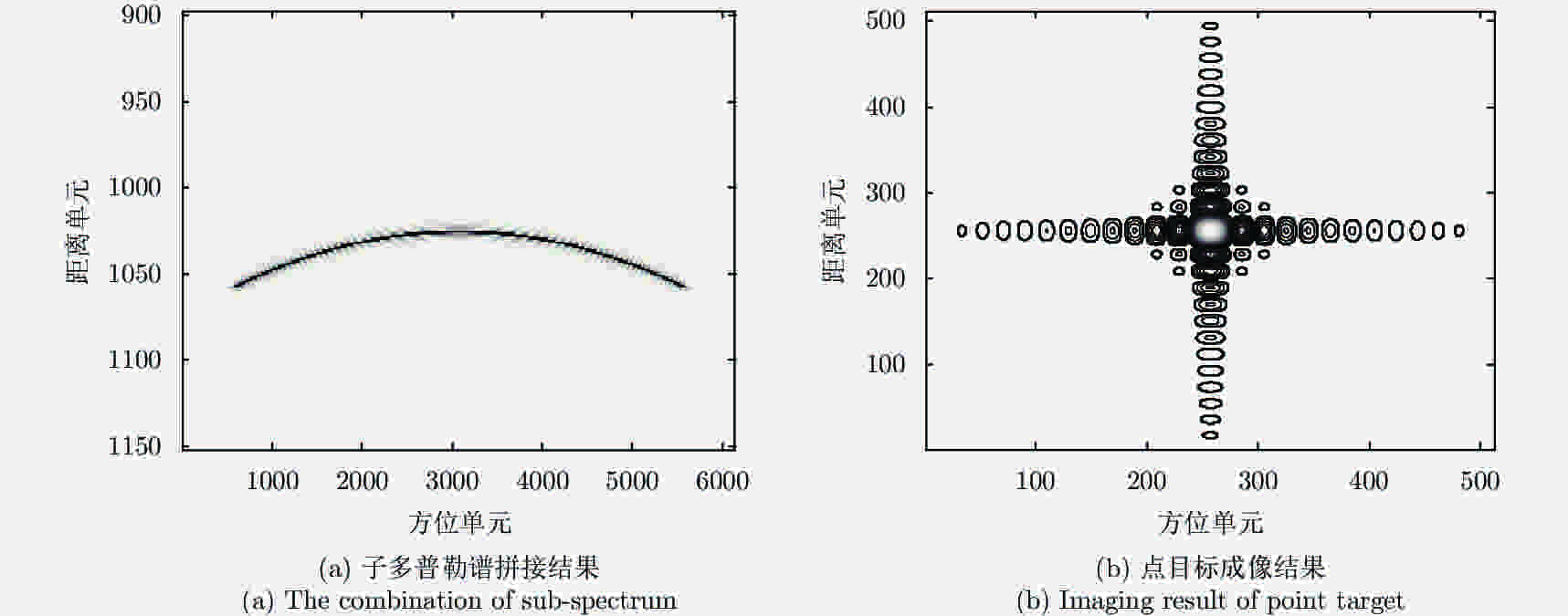
距离向		方位向
PSLR (dB)	–13.28	PSLR (dB)	–13.28
ISLR (dB)	–9.67	ISLR (dB)	–9.81
分辨率 (m)	1.0087	分辨率 (m)	0.8157

下载: 导出CSV

参考文献(18)

[1]	Freeman A, Johnson W T K, Huneycutt B, et al. The " Myth” of the minimum SAR antenna area constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 320–324. DOI: 10.1109/36.823926
[2]	Fan B, Qin Y L, You P, et al. An improved PFA with aperture accommodation for widefield spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 3–7. DOI: 10.1109/LGRS.2014.2322858
[3]	Wu Y, Sun G C, Yang C, et al. Processing of very high resolution spaceborne sliding spotlight SAR data using velocity scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1505–1518. DOI: 10.1109/TGRS.2015.2481923
[4]	Li N, Wang R, Deng Y K, et al. Improved full-aperture ScanSAR imaging algorithm based on aperture interpolation[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 1101–1105. DOI: 10.1109/LGRS.2014.2384594
[5]	Meta A, Mittermayer J, Prats P, et al. TOPS imaging with TerraSAR-X: Mode design and performance analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 759–769. DOI: 10.1109/TGRS.2009.2026743
[6]	Callaghan G D and Longstaff I D. Wide-swath space-borne SAR and range ambiguity[C]. Radar 97, Edinburgh, UK, 1997: 248–252
[7]	李杨, 黄杰文, 禹卫东. 高分辨率宽测绘带星载SAR距离向DBF处理[J]. 电子与信息学报, 2011, 33(6): 1510–1514. DOI: 10.3724/SP.J.1146.2010.01157 Li Yang, Huang Jie-wen, and Yu Wei-dong. Range DBF processing for high-resolution wide-swath spaceborne SAR[J]. Journal of Electronics&Information Technology, 2011, 33(6): 1510–1514. DOI: 10.3724/SP.J.1146.2010.01157
[8]	Wang W, Wang R, Deng Y K, et al. Improved digital beam-forming approach with scaling function for range multi-channel synthetic aperture radar system[J]. IET Radar,Sonar&Navigation, 2016, 10(2): 379–385.
[9]	Currie A and Brown M A. Wide-swath SAR[J]. IEE Proceedings F-Radar and Signal Processing, 1992, 139(2): 122–135. DOI: 10.1049/ip-f-2.1992.0016
[10]	Liu B C and He Y J. Improved DBF algorithm for multichannel high-resolution wide-swath SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1209–1225. DOI: 10.1109/TGRS.2015.2476496
[11]	Li X S, Xing M D, Xia X G, et al. Simultaneous stationary scene imaging and ground moving target indication for high-resolution wide-swath SAR system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4224–4239. DOI: 10.1109/TGRS.2016.2538564
[12]	Krieger G, Gebert N, and Moreira A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 31–46. DOI: 10.1109/TGRS.2007.905974
[13]	武其松, 邢孟道, 刘保昌, 等. 脉内聚束SAR方位高分辨率宽测绘带成像[J]. 西安电子科技大学学报(自然科学版), 2010, 37(4): 676–682, 699. DOI: 10.3969/j.issn.1001-2400.2010.04.017 Wu Qi-song, Xing Meng-dao, Liu Bao-chang, et al. High azimuth resolution wide swath imaging based on the intrapulse spotlight SAR[J]. Journal of Xidian University, 2010, 37(4): 676–682, 699. DOI: 10.3969/j.issn.1001-2400.2010.04.017
[14]	Dall J and Kusk A. Azimuth phase coding for range ambiguity suppression in SAR[C]. International Geoscience and Remote Sensing Symposium, Anchorage, USA, 2004, 3: 1734–1737
[15]	郭磊, 王宇, 邓云凯, 等. 基于方位向相位编码技术的方位向多通道SAR距离模糊抑制方法[J]. 电子与信息学报, 2015, 37(3): 601–606. DOI: 10.11999/JEIT140707 Guo Lei, Wang Yu, Deng Yun-kai, et al. Range ambiguity suppression for multi-channel SAR system using azimuth phase coding technique[J]. Journal of Electronics&Information Technology, 2015, 37(3): 601–606. DOI: 10.11999/JEIT140707
[16]	邢孟道, 李真芳, 保铮, 等. 分布式小卫星雷达空时频成像方法研究[J]. 宇航学报, 2005, 26(S1): 70–76, 82. DOI: 10.3321/j.issn:1000-1328.2005.z1.014 Xing Meng-dao, Li Zhen-fang, Bao Zheng, et al. Study of distributed microsatellites radar space-time-frequency imaging method[J]. Journal of Astronautics, 2005, 26(S1): 70–76, 82. DOI: 10.3321/j.issn:1000-1328.2005.z1.014
[17]	Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood, MA, USA: Artech House, 2005
[18]	Zhang S X, Xing M D, Xia X G, et al. Multichannel HRWS SAR imaging based on range-variant channel calibration and multi-Doppler-direction restriction ambiguity suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4306–4327. DOI: 10.1109/TGRS.2013.2281329