基于方位相位编码的脉内聚束SAR成像方法

吴玉峰; 叶少华; 冯大政

doi:10.12000/JR17114

基于方位相位编码的脉内聚束SAR成像方法

DOI: 10.12000/JR17114

①.
中国航空工业集团公司雷华电子技术研究所无锡 214063
②.
西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 航空基金（2015ZC07005）

详细信息

作者简介:
吴玉峰(1985–)，男，浙江衢州人，博士，工程师。现为中国航空工业集团公司雷华电子技术研究所系统工程师，主要研究方向为SAR系统设计、SAR成像算法。E-mail: wyf1176@163.com

叶少华(1966–)，男，江苏江阴人，研究员，副总工程师。现为中国航空工业集团公司雷华电子技术研究所副总工程师，主要研究方向为雷达系统设计、雷达信号处理。E-mail: ye_shaohua@sina.com

冯大政(1959–)，男，陕西安康人，教授，博士生导师。现为西安电子科技大学电子工程学院二级教授，主要研究方向为雷达信号处理、类脑神经网络和图像处理等。E-mail: dzfeng@xidian.edu.cn

通讯作者:
吴玉峰 wyf1176@163.com

计量
- 文章访问数: 2466
- HTML全文浏览量: 574
- PDF下载量: 362
- 被引次数: 10
出版历程
- 收稿日期: 2017-11-28
- 修回日期: 2018-02-07
- 网络出版日期: 2018-08-28

Intra-pulse Spotlight SAR Imaging Method Based on Azimuth Phase Coding

Wu Yufeng^{1
, ,},
Ye Shaohua^1
,,
Feng Dazheng^2
,

①.
AVIC Leihua Electronic Technology Research Institute, Wuxi 214063, China
②.
National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The Aeronautical Foundation of China (2015ZC07005)

摘要

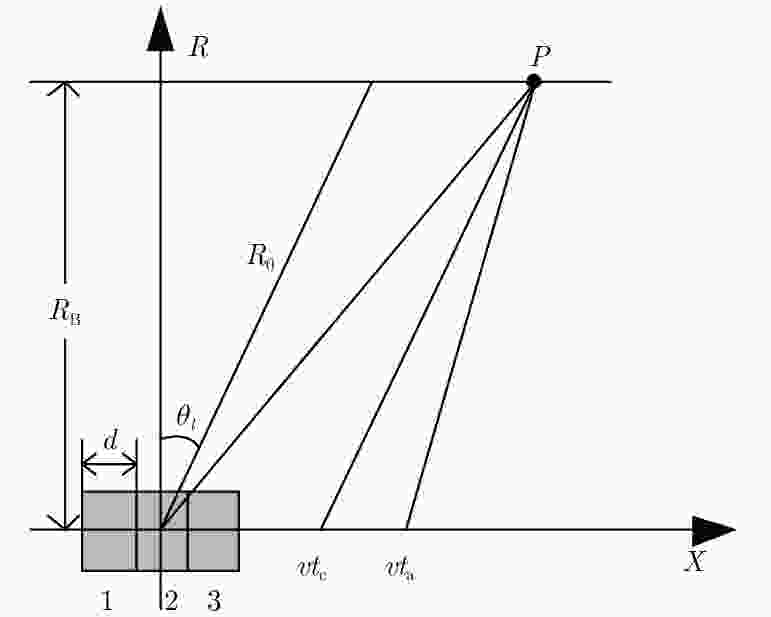
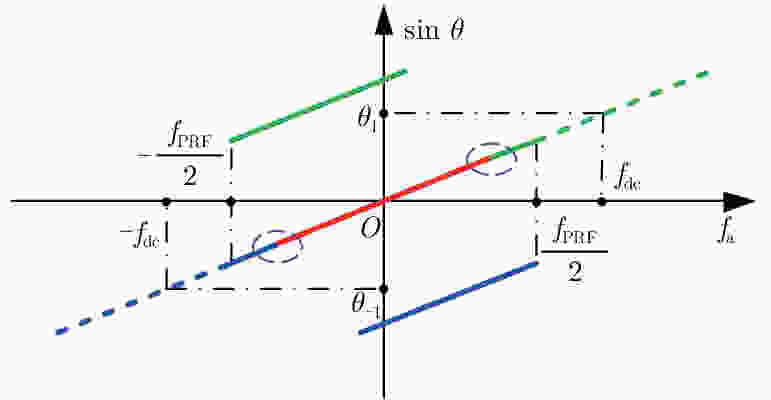
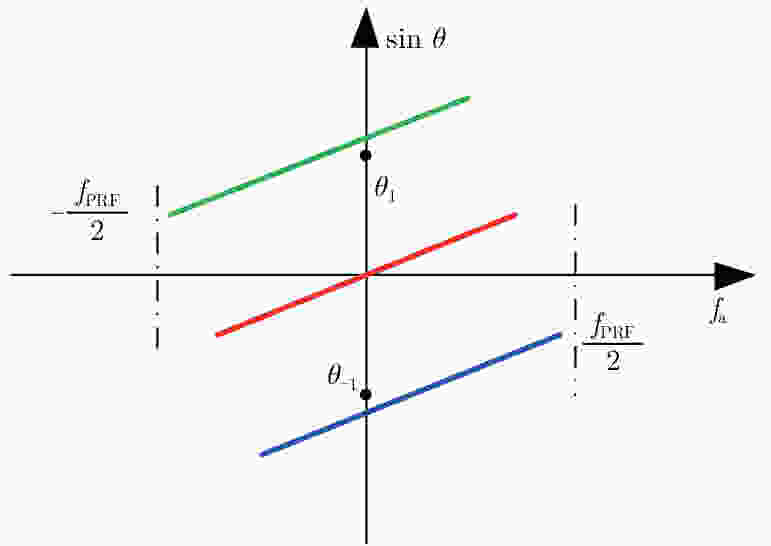
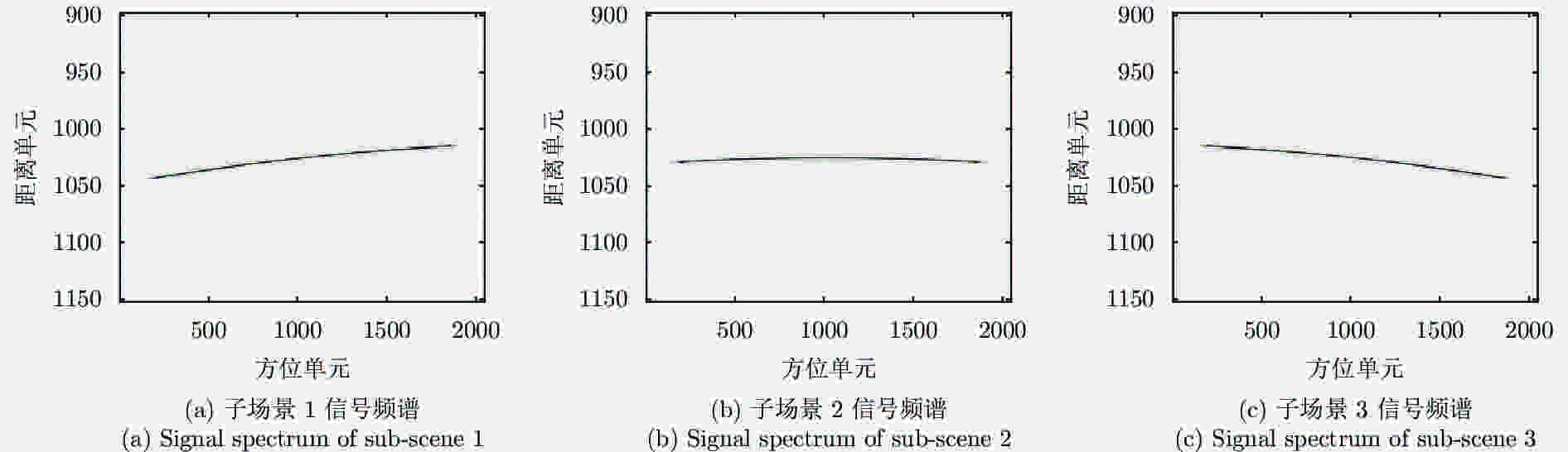
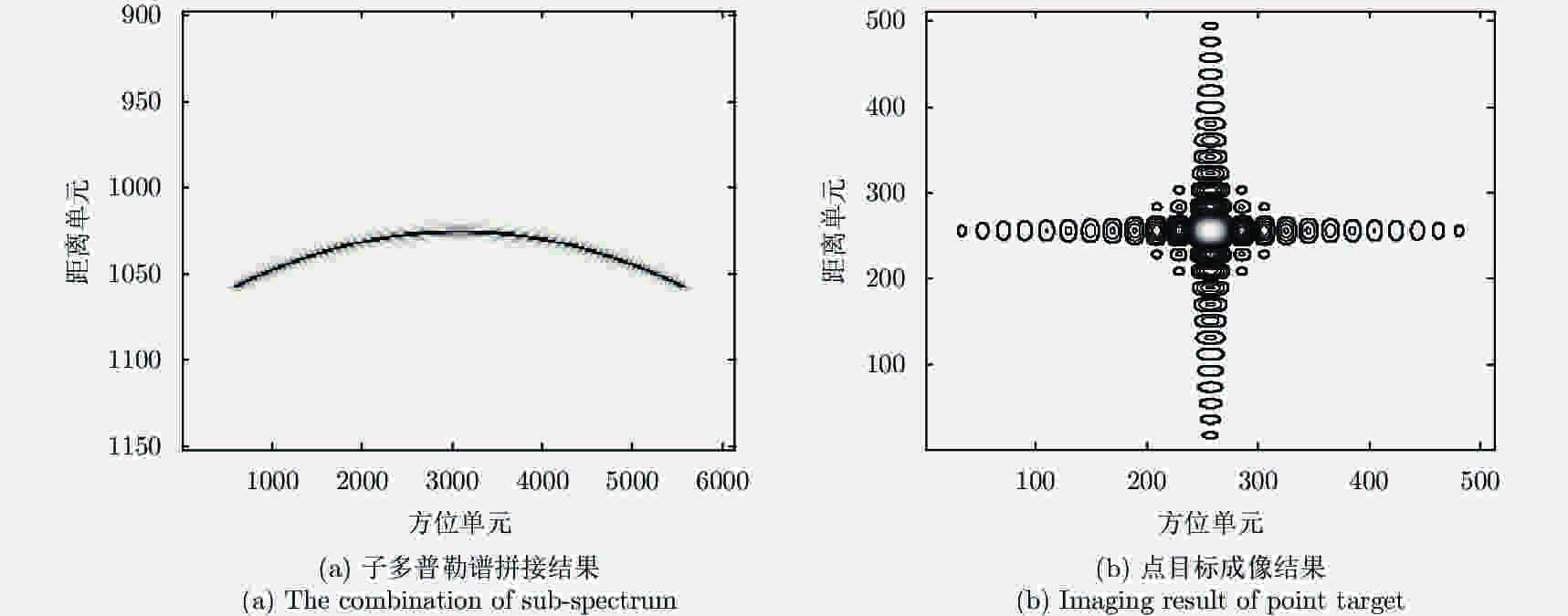
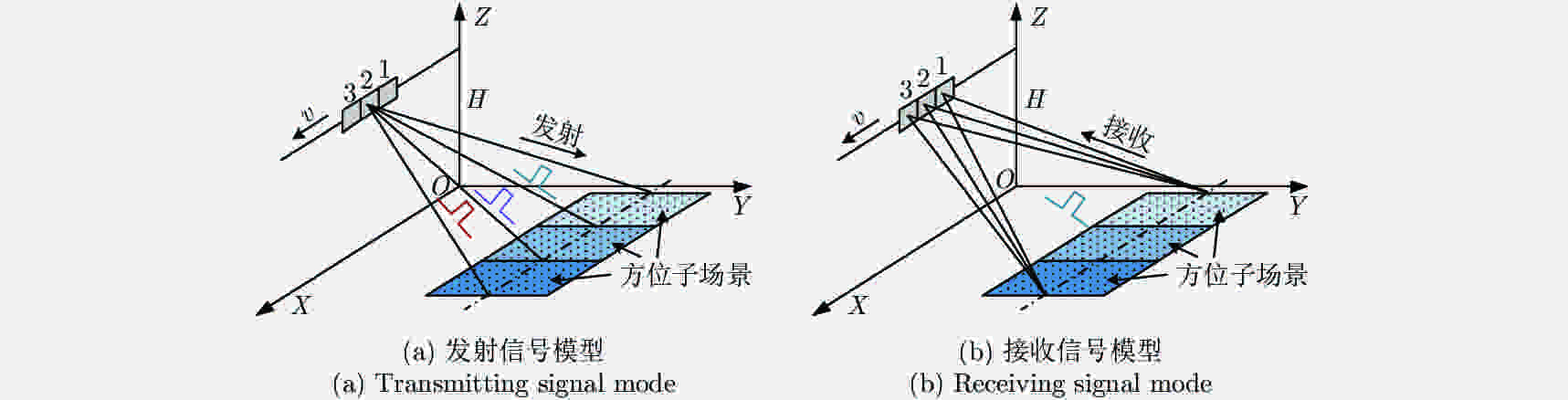
摘要: 脉内聚束模式有效克服了星载合成孔径雷达(Synthetic Aperture Radar, SAR)高分辨率与宽测绘带之间的矛盾，同时可以兼顾回波的信噪比。然而距离维空域滤波的信号分离方法容易受地形起伏的影响，甚至失效。针对此，该文提出了一种结合方位相位编码(Azimuth Phase Coding, APC)的脉内聚束SAR成像方法，利用APC技术使不同子脉冲回波的方位频谱处在不同的脉冲重复频率(Pulse Repetition Frequencies, PRF)范围，然后利用方位自适应波束形成技术来分离回波信号。文中对信号分离方法以及频移因子的选择进行了详细的讨论。最后仿真实验结果验证了所提方法的有效性。
- 合成孔径雷达 /
- 脉内聚束模式 /
- 方位相位编码 /
- 方位多通道 /
- 信号分离
Abstract: The intra-pulse spotlight imaging mode can effectively overcome the contradiction between high resolution and wide swath in spaceborne Synthetic Aperture Radar (SAR), and considers the echo’s signal-to-noise ratio. However, signal division by spatial filtering along the range direction may be impacted by fluctuating terrain. To solve this problem, a novel intra-pulse spotlight imaging method based on Azimuth Phase Coding (APC) is proposed in this paper. Using APC, the azimuth spectrum of echo data from different sub-pulses will locate in different Pulse Repetition Frequencies (PRF). As such, the signal can be divided using an azimuth adaptive beamforming technique. The signal separation method and selection of the shift factor are discussed in detail. Finally, simulation results demonstrate the effectiveness of the proposed method.
- Synthetic Aperture Radar (SAR) /
- Intra-pulse spotlight mode /
- Azimuth Phase Coding (APC) /
- Azimuth multi-channel /
- Signal division

HTML全文

1. Introduction

In recent years, Frequency Diverse Array (FDA) radar has received much attention due to its range-angle-time-dependent beampattern^[1,2]. Combining the advantages of FDA and traditional phased array Multiple-Input Multiple-Output (MIMO) radar in the degree of freedom, the FDA Multiple-Input Multiple Output (FDA-MIMO) radar was proposed in Ref. [3] and applied in many fields^[4-9]. For parameter estimation algorithm, the authors first proposed a FDA-MIMO target localization algorithm based on sparse reconstruction theory^[10], and an unbiased joint range and angle estimation method was proposed in Ref. [11]. The work of Ref. [12] further proved that the FDA-MIMO is superior to traditional MIMO radar in range and angle estimation performance, and the authors of Ref. [13] introduced a super-resolution MUSIC algorithm for target location, and analyzed its resolution threshold. Meanwhile, high-resolution Doppler processing is utilized for moving target parameter estimation^[14]. The Estimation of Signal Parameters via Rotational Invariance Technique (ESPRIT) and PARAllel FACtor (PARAFAC) was proposed in Ref. [15], which is a search-free algorithm for FDA-MIMO.

Moreover, the research of conformal array has received more and more attention. Conformal array is a non-planar array that can be completely attached to the surface of the carrier^[16]. It has significant advantages such as reducing the aerodynamic impact on the carrier and smaller radar cross section^[17]. In addition, conformal array can achieve wide-angle scanning with a lower SideLobe Level (SLL)^[18]. Different from traditional arrays, the element beampattern of conformal array needs to be modeled separately in the parameter estimation due to the difference of carrier curvature^[19-21].

As far as we know, most of the existing researches on FDA-MIMO are based on linear array, while there is little research on the combination of FDA-MIMO and conformal array^[22]. In this paper, we replace the receiving array in the traditional FDA-MIMO with conformal array. Compared with conventional FDA-MIMO, conformal FDA-MIMO inherits the merits of conformal array and FDA-MIMO, which can effectively improve the stealth and anti-stealth performance of the carrier, and reduce the volume and the air resistance of the carrier. For conformal FDA-MIMO, we further study the parameters estimation algorithm. The major contributions of this paper are summarized as follows:

(1) A conformal FDA-MIMO radar model is first formulated.

(2) The parameter estimation Cramér-Rao Lower Bound (CRLB) for conformal FDA-MIMO radar is derived.

(3) Inspired by the existing work of Refs. [23,24], a Reduced-Dimension MUSIC (RD-MUSIC) algorithm for conformal FDA-MIMO radar is correspondingly proposed to reduce the complexity.

The rest of the paper consists of four parts. Section 2 formulates the conformal FDA-MIMO radar model, and Section 3 derives a RD-MUSIC algorithm for conformal FDA-MIMO radar. Simulation results for conformal FDA-MIMO radar with semi conical conformal receiving array are provided in Section 4. Finally, conclusions are drawn in Section 5.

2. Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

For the convenience of analysis, we consider a monostatic conformal FDA-MIMO radar which is composed by a $M$ -element linear FDA transmitting array and a $N$ -element conformal receiving array, as shown in Fig. 1. d denotes the inter-element spacing, the carrier frequency at the mth transmitting element is ${f_m} = {f_1} + \Delta f(m - 1)$ , $m = 1,2, \cdots ,M$ where ${f_1}$ is the transmission frequency of the first antenna element, which is called as reference frequency, and $\Delta f$ is the frequency offset between the adjacent array elements.

Figure 1. Conformal FDA-MIMO radar

DownLoad: Full-Size Img PowerPoint

The complex envelope of the transmitted signal of the mth transmitting element is denoted as ${{\varphi _m}} (t)$ , assume the transmitting waveforms have orthogonality,

$\int_{{T_p}} {{\varphi _m}} (t)\varphi _{{m_1}}^*(t - \tau ){\rm{d}}t = 0,\quad {m_1} \ne m$

(1)

where $\tau$ denotes the time delay, ${T_p}$ denotes the pulse duration, and ${\left( \cdot \right)^ * }$ is conjugate operator. The signal transmitted from the mth element can be expressed as

${s_m}(t) = {a_m}(t,\theta ,\phi ,r){\varphi _m}(t),\quad 0 \le t \le {T_p}$

(2)

where

$\begin{split} & {a_m}(t,\theta ,\phi ,r) \hfill \\ & =\exp \left\{ { - {\rm{j}}2\pi \left( \begin{gathered} \frac{{(m - 1)\Delta fr}}{{\rm{c}}} - \frac{{{f_1}(m - 1){{d}}\sin \alpha }}{{\rm{c}}} \hfill \\ - (m - 1)\Delta ft \hfill \\ \end{gathered} \right)} \right\} \end{split}$

(3)

is the mth element of the transmitting steering vector according to the phase difference between adjacent elements, the angle between far-field target and transmitting array is denoted as $\alpha = \arcsin (\sin \theta \cos \phi )$ , where $\arcsin ( \cdot )$ denotes arcsine operator, $\alpha$ can be calculated by using the inner product between the target vector and unit vector along the $X$ -axis. $\theta ,\phi ,r$ are the elevation, azimuth and range between the target and the origin point, respectively. The phase difference between adjacent elements is

$\Delta {\psi _{t0}} = 2\pi \left( {\frac{{\Delta fr}}{{\rm{c}}} - \frac{{{f_1}d\sin \alpha }}{{\rm{c}}} - \Delta ft} \right)$

(4)

where ${\rm{c}}$ is light speed. For far-field target ${P}\left( {r,\theta ,\phi } \right)$ , the transmitting steering vector is

$\begin{split} {{\boldsymbol{a}}_0}\left( {t,\theta ,\phi ,r} \right) =& \left[ {1,\exp \left\{ { - {\rm{j}}\Delta {\psi _{t0}}} \right\}, \cdots ,} \right. \\ &{\left. {\exp \left\{ { - {\rm{j}}(M - 1)\Delta {\psi _{t0}}} \right\}} \right]^{\rm{T}}} \end{split}$

(5)

For the conformal receiving array, as shown in Fig. 1(b), the time delay between target ${P}\left( {r,\theta ,\phi } \right)$ and the nth receiving array element is

${\tau _n} = {r_n}/{\rm{c}}$

(6)

where ${r_n}$ is the range between target and the nth receiving array element. For far-field assumption, the ${r_n}$ can be approximated as

${r_n} \approx r - {\vec {\boldsymbol{p}}_n} \cdot \vec {\boldsymbol{r}}$

(7)

where r denotes the range between the target and the origin point, ${\vec {\boldsymbol{p}}_n} = {x_n}{{\boldsymbol{e}}_x} + {y_n}{{\boldsymbol{e}}_y} + {z_n}{{\boldsymbol{e}}_z}$ denotes the position vector from the nth element to origin point, and $\vec {\boldsymbol{r}} = \sin \theta \cos \phi {{\boldsymbol{e}}_x} + \sin \theta \sin \phi {{\boldsymbol{e}}_y} + \cos\theta {{\boldsymbol{e}}_z}$ is the unit vector in target orientation, where ${{\boldsymbol{e}}_x},{{\boldsymbol{e}}_y}$ and ${{\boldsymbol{e}}_z}$ are the unit vectors along the X- , Y- , and $Z$ -axis, respectively. $({x_n},{y_n},{z_n})$ are the coordinates of the nth element in the Cartesian coordinate system. For simplicity, we let $u = \sin \theta \cos \phi$ , $v = \sin \theta \cos \phi$ , so the time delay ${\tau _n} =$ $(r - (u{x_n} + v{y_n} + \cos \theta {z_n}))/{\rm{c}}$ . The time delay between the first element and the nth element at the receiving array is expressed as

$\begin{split} \Delta {\tau _{{r_n}}} =& {\tau _1} - {\tau _n} \\ =& \frac{{u({x_n} - {x_1}) + v({y_n} - {y_1}) + \cos \theta ({z_n} - {z_1})}}{{\rm{c}}} \\ \end{split}$

(8)

And the corresponding phase difference between the first element and the nth element is

$\Delta {\psi _{{R_n}}} = 2\pi {f_1}\Delta {\tau _{{r_n}}}$

(9)

Consequently, the receiving steering vector is

$\begin{split} {\boldsymbol{b}}\left( {\theta ,\phi } \right) =& \left[ {{r_1}(\theta ,\phi ),{r_2}(\theta ,\phi )\exp (j\Delta {\psi _{{r_2}}}), \cdots ,} \right. \\ &{\left. {{r_N}(\theta ,\phi )\exp({\rm{j}}\Delta {\psi _{{r_N}}})} \right]^{\rm{T}}} \\ \end{split}$

(10)

where ${r_n}(\theta ,\phi )$ is the nth conformal receiving array element beampattern which should be designed in its own local Cartesian coordinate system. In this paper, we utilize Euler rotation method to establish transformation frame between local coordinate system and global coordinate system^[25,26].

Then the total phase difference between adjacent transmitting array elements can be rewritten as

$\Delta {\psi _t} = 2\pi \left( {\frac{{\Delta f2r}}{{\rm{c}}} - \frac{{{f_1}d\sin \alpha }}{{\rm{c}}} - \Delta ft} \right)$

(11)

where the factor $2r$ in the first term represents the two-way transmission and reception, and the correspondingly transmitting steering vector is written as

$\begin{split} {\boldsymbol{a}}\left( {t,\theta ,\phi ,r} \right) =& \left[ {1,\exp \left\{ { - {\rm{j}}\Delta {\psi _t}} \right\}, \cdots ,} \right. \\ & {\left. {\exp \left\{ { - {\rm{j}}(M - 1)\Delta {\psi _t}} \right\}} \right]^{\rm{T}}} \end{split}$

(12)

Assuming L far-field targets are located at $\left( {{\theta _i},{\phi _i},{R_i}} \right)$ , $i = 1,2,\cdots,L$ and snapshot number is $K$ . After matched filtering, the received signal can be formulated as following matrix (13,14)

${\boldsymbol{X = AS + N}}$

(13)

where the array manifold ${\boldsymbol{A}}$ is expressed as

$\begin{split} {\boldsymbol{A}} = &\left[ {{{\boldsymbol{a}}_{t,r}}\left( {{\theta _1},{\phi _1},{r_1}} \right), \cdots ,{{\boldsymbol{a}}_{t,r}}\left( {{\theta _L},{\phi _L},{r_L}} \right)} \right] \hfill \\ =& \left[ {\boldsymbol{b}}\left( {{\theta _1},{\phi _1}} \right) \otimes {\boldsymbol{a}}\left( {{\theta _1},{\phi _1},{r_1}} \right), \cdots ,{\boldsymbol{b}}\left( {{\theta _L},{\phi _L}} \right) \right.\\ & \left.\otimes {\boldsymbol{a}}\left( {{\theta _L},{\phi _L},{r_L}} \right) \right] \end{split}$

(14)

where ${{\boldsymbol{a}}_{t,r}}\left( {\theta ,\phi ,r} \right)$ is the joint transmitting-receiving steering vector, ${\boldsymbol{S}} = \left[ {s({t_1}),s({t_2}), \cdots ,s({t_K})} \right] \in {\mathbb{C}^{L \times K}}$ and ${\boldsymbol{N}} \in {\mathbb{C}^{MN \times K}}$ denote the signal matrix and noise matrix, respectively, where noise follows the independent identical distribution, and $\otimes$ denotes Kronecker product.

$\begin{split} {\boldsymbol{a}}\left( {\theta ,\phi ,r} \right) =& \left[ 1\; {\exp \left\{ { - {\rm{j}}2\pi \left( {\dfrac{{2\Delta fr}}{{\rm{c}}} - \dfrac{{{f_1}d\sin \alpha }}{{\rm{c}}}} \right)} \right\}} \right. \hfill \\ &\left. \cdots {\exp \left\{ { - {\rm{j}}2\pi (M - 1)\left( {\dfrac{{2\Delta fr}}{{\rm{c}}} - \dfrac{{{f_1}d\sin \alpha }}{{\rm{c}}}} \right)} \right\}} \right] \end{split}$

(15)

which can be expressed as

${\boldsymbol{a}}\left( {\theta ,\phi ,r} \right) = {\boldsymbol{a}}\left( {\theta ,\phi } \right) \odot {\boldsymbol{a}}\left( r \right)$

(16)

where

$\begin{split} {\boldsymbol{a}}(r) =& \left[ {1,\exp \left( - {\rm{j}}2\pi \frac{{2\Delta fr}}{{\rm{c}}}\right), \cdots ,} \right. \\ & {\left. {\exp\left( { - {\rm{j}}2\pi (M - 1)\frac{{2\Delta fr}}{{\rm{c}}}} \right)} \right]^{\rm{T}}}\qquad \end{split}$

(17)

$\begin{split} {\boldsymbol{a}}(\theta ,\phi ) =& \left[ {1,\exp \left({\rm{j}}2\pi \frac{{{f_1}d\sin \alpha }}{{\rm{c}}}\right),} \cdots ,\right. \hfill \\ &{\left. { \exp \left[{\rm{j}}2\pi (M - 1)\frac{{{f_1}d\sin \alpha }}{{\rm{c}}}\right]} \right]^{\rm{T}}} \end{split}$

(18)

and $\odot$ represents Hadamard product operator.

2.2 CRLB of conformal FDA-MIMO

The CRLB can be obtained from the inverse of Fisher information matrix^[27,28], which establishes a lower bound for the variance of any unbiased estimator. We employ the CRLB for conformal FDA-MIMO parameter estimation to evaluate the performance of some parameter estimation algorithms.

The discrete signal model is

${\boldsymbol{x}}[k] = {{\boldsymbol{a}}_{t,r}}(\theta ,\phi ,r)s[k] + {\boldsymbol{N}}[k],\quad k = 1,2, \cdots ,K$

(19)

For the sake of simplification, we take ${{\boldsymbol{a}}_{t,r}}$ as the abbreviation of ${{\boldsymbol{a}}_{t,r}}(\theta ,\phi ,r)$ .

The Probability Distribution Function (PDF) of the signal model with $K$ snapshots is

$\begin{split} p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.) =& \frac{1}{{{{(2\pi \sigma _n^2)}^{\textstyle\frac{K}{2}}}}} \\ & \cdot \exp \left( - \frac{1}{{\sigma _n^2}}{({\boldsymbol{x}} - {{\boldsymbol{a}}_{t,r}}{\boldsymbol{s}})^{\rm{H}}}({\boldsymbol{x}} - {{\boldsymbol{a}}_{t,r}}{\boldsymbol{s}})\right) \\ \end{split}$

(20)

where ${\boldsymbol{x}} = [{\boldsymbol{x}}(1),{\boldsymbol{x}}(2),\cdots,{\boldsymbol{x}}(K)]$ and ${\boldsymbol{s}} = [s(1),$ $s(2), \cdots,s(K)]$ .

The CRLB matrix form of elevation angle, azimuth angle and range is given by Eq. (21), diagonal elements $\left\{ {{C_{\theta \theta }},{C_{\phi\phi} } ,{C_{rr}}} \right\}$ represent CRLB of estimating elevation angle, azimuth angle and range, respectively.

$\begin{split} {\rm{CRLB}} = &\left[ {\begin{array}{*{20}{c}} {{C_{\theta \theta }}}&{{C_{\theta \phi }}}&{{C_{\theta r}}} \\ {{C_{\phi \theta }}}&{{C_{\phi\phi} } }&{{C_{\phi r}}} \\ {{C_{r\theta }}}&{{C_{r\phi }}}&{{C_{rr}}} \end{array}} \right] \\ =& {{\rm{FIM}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{F_{11}}}&{{F_{12}}}&{{F_{13}}} \\ {{F_{21}}}&{{F_{22}}}&{{F_{23}}} \\ {{F_{31}}}&{{F_{32}}}&{{F_{33}}} \end{array}} \right] \end{split}$

(21)

The elements of Fisher matrix can be expressed as

${F_{ij}} = - E\left[ {\dfrac{{{\partial ^2}\ln (p(x\mid \theta ,\phi ,r))}}{{\partial {x_i}\partial {x_j}}}} \right],\quad i,j = 1,2,3$

(22)

In the case of $K$ snapshots, PDF can be rewritten as

$\begin{split} p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.) =& C\exp \left\{ { - \frac{1}{{\sigma _n^2}}} \right.\sum\limits_{n = 1}^K {{{\bigr({\boldsymbol{x}}[k] - {{\boldsymbol{a}}_{t,r}}s[k]\bigr)}^{\rm{H}}}} \\ & { \cdot \bigr({\boldsymbol{x}}[k] - {{\boldsymbol{a}}_{t,r}}s[k]\bigr)} \} \\[-18pt] \end{split}$

(23)

where $C$ is a constant, natural logarithm of Eq. (23) is

$\begin{split} \ln (p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.)) =& \ln (C) - \frac{1}{{\sigma _n^2}}\sum\limits_{k = 1}^K {{{\bigr({\boldsymbol{x}}[k] - {{\boldsymbol{a}}_{t,r}}s[k]\bigr)}^{\rm{H}}}} \\ & \cdot \bigr({\boldsymbol{x}}[k] - {{\boldsymbol{a}}_{t,r}}s[k]\bigr) \\[-10pt] \end{split}$

(24)

where $\ln ( \cdot )$ represents the logarithm operator. The first entry of Fisher matrix can be expressed as

${F_{11}} = - E\left[ {\frac{{{\partial ^2}\ln (p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.))}}{{\partial {\theta ^2}}}} \right]$

(25)

Correspondingly, the first derivative of natural logarithm is given by

$\begin{split} \frac{{\partial \ln (p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.))}}{{\partial \theta }} =& - \frac{1}{{\sigma _n^2}}\sum\limits_{k = {\text{1}}}^K {\left( { - {{\boldsymbol{x}}^{\rm{H}}}\left[ k \right]\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}s\left[ k \right]} \right.} \hfill \\ & - \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}s\left[ k \right]{\boldsymbol{x}}\left[ k \right] + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}{{\boldsymbol{a}}_{t,r}}{s^2}\left[ n \right]{\boldsymbol{a}} \hfill \\ &\left. { + {\boldsymbol{a}}_{t,r}^{\rm{H}}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}{s^2}\left[ n \right]} \right) \\[-20pt] \end{split}$

(26)

Then we can obtain the second derivative of

$\begin{split} & \frac{{{\partial ^2}\ln (p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.))}}{{\partial {\theta ^2}}} \hfill \\ & \quad= - \frac{1}{{\sigma _n^2}}\sum\limits_{k = {\text{1}}}^K {\left( { - {\boldsymbol{x}}{{\left[ k \right]}^{\rm{H}}}\frac{{{\partial ^2}{{\boldsymbol{a}}_{t,r}}}}{{\partial {\theta ^2}}}s\left[ k \right]} \right.} \hfill \\ & \qquad - \frac{{{\partial ^2}{\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial {\theta ^2}}}s\left( k \right){\boldsymbol{x}}\left[ k \right] \hfill + \frac{{{\partial ^2}{\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial {\theta ^2}}}{{\boldsymbol{a}}_{t,r}}s{\left[ k \right]^2} \\ & \qquad+ \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}s{\left[ k \right]^2} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}s{{\left[ k \right]}^2} \\ & \qquad \left.+ {\boldsymbol{a}}_{t,r}^{\rm{H}}\frac{{{\partial ^2}{{\boldsymbol{a}}_{t,r}}}}{{\partial {\theta ^2}}}s{{\left[ k \right]}^2} \right) \end{split}$

(27)

And then we have

$\begin{split} \sum\limits_{k = 1}^K {\boldsymbol{x}} [k] =& \sum\limits_{k = 1}^K {{{\boldsymbol{a}}_{t,r}}s[k] + {\boldsymbol{N}}[k]} \\ =& {{\boldsymbol{a}}_{t,r}}(\theta ,\phi ,r)\sum\limits_{k = 1}^K s [k] \end{split}$

(28)

and

$\sum\limits_{k = 1}^K {{s^2}} [k] = K{{\rm{var}}} (s[k]) = K\sigma _s^2$

(29)

where ${{\rm{var}}} ( \cdot )$ is a symbol of variance. Therefore, the PDF after quadratic derivation can be written as

$\begin{split} &E\left[ {\frac{{{\partial ^2}\ln (p({\boldsymbol{x}}\left| {\theta ,\phi ,r} \right.))}}{{\partial {\theta ^2}}}} \right] \hfill \\ & \quad=- \frac{{K\sigma _s^2}}{{\sigma _n^2}}\left( {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}} \right) \\ & \quad= - \frac{{2K\sigma _s^2}}{{\sigma _n^2}}{\left\| {\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}} \right\|^2} \end{split}$

(30)

where $\left\| \cdot \right\|$ denotes 2-norm. Similarly, the other elements of the Fisher matrix can also be derived in the similar way, so the Fisher matrix can be expressed as

$\begin{split} {{\rm{CRLB}}^{ - 1}} = & {\rm{FIM}} = \frac{{2K\sigma _s^2}}{{\sigma _n^2}} \\ & \cdot \left[ {\begin{array}{*{20}{c}} {{{\left\| {\dfrac{{\partial {\boldsymbol{a}}}}{{\partial \theta }}} \right\|}^2}}&{{{\rm{FIM}}_{12}}}&{{{\rm{FIM}}_{13}}} \\ {{{\rm{FIM}}_{21}}}&{{{\left\| {\dfrac{{\partial {\boldsymbol{a}}}}{{\partial \phi }}} \right\|}^2}}&{{{\rm{FIM}}_{23}}} \\ {{{\rm{FIM}}_{31}}}&{{{\rm{FIM}}_{32}}}&{{{\left\| {\dfrac{{\partial {\boldsymbol{a}}}}{{\partial r}}} \right\|}^2}} \end{array}} \right] \end{split}$

(31)

where

${{\rm{FIM}}_{12}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \phi }} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \phi }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}} \right],$

${{\rm{FIM}}_{13}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial r}} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial r}}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }}} \right],$

${{\rm{FIM}}_{21}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \phi }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \phi }}} \right],$

${{\rm{FIM}}_{23}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \phi }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial r}} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial r}}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \phi }}} \right],$

${{\rm{FIM}}_{31}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial r}}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \theta }} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \theta }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial r}}} \right],$

${{\rm{FIM}}_{32}} = \frac{1}{2}\left[ {\frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial r}}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial \phi }} + \frac{{\partial {\boldsymbol{a}}_{t,r}^{\rm{H}}}}{{\partial \phi }}\frac{{\partial {{\boldsymbol{a}}_{t,r}}}}{{\partial r}}} \right],$

$\quad \frac{{\sigma _s^2}}{{\sigma _n^2}} = {\rm{SNR}}$

Finally, the CRLB of conformal FDA-MIMO can be calculated by the inverse of Fisher matrix.

3. Reduced-Dimension Target Parameter Estimation Algorithm

The covariance matrix of the conformal FDA-MIMO receiving signal can be written as

${{\boldsymbol{R}}_{\boldsymbol{X}}} = {\boldsymbol{A}}{{\boldsymbol{R}}_s}{{\boldsymbol{A}}^{\rm{H}}} + {\sigma ^2}{{\boldsymbol{I}}_{MN}}$

(32)

where ${{\boldsymbol{R}}_s}$ represents the covariance matrix of transmitting signal, ${{\boldsymbol{I}}_{MN}}$ denotes $MN$ dimensional identity matrix. For independent target signal and noise, ${{\boldsymbol{R}}_{\boldsymbol{X}}}$ can be decomposed as

${{\boldsymbol{R}}_{\boldsymbol{X}}} = {{\boldsymbol{U}}_{\boldsymbol{S}}}{{\boldsymbol{\varLambda }}_{\boldsymbol{S}}}{\boldsymbol{U}}_{\boldsymbol{S}}^{\rm{H}}{\boldsymbol{ + }}{{\boldsymbol{U}}_n}{{\boldsymbol{\varLambda }}_n}{\boldsymbol{U}}_n^{\rm{H}}$

(33)

The traditional MUSIC algorithm is utilized to estimate the three-dimensional parameters $\left\{ {\theta ,\phi ,r} \right\}$ , MUSIC spectrum can be expressed as

${P_{{\rm{MUSIC}}}}(\theta ,\phi ,r) = \frac{1}{{{\boldsymbol{a}}_{t,r}^{\rm{H}}(\theta ,\phi ,r){{\boldsymbol{U}}_n}{\boldsymbol{U}}_n^{\rm{H}}{{\boldsymbol{a}}_{t,r}}(\theta ,\phi ,r)}}$

(34)

The target location can be obtained by mapping the peak indexes of MUSIC spectrum.

Traditional MUSIC parameter estimation algorithm is realized by 3D parameter search, which has good performance at the cost of high computational complexity. When the angular scan interval is less than 0.1°, the running time of single Monte-Carlo simulation is in hours, which is unpracticable for us to analysis conformal FDA-MIMO estimation performance by hundreds of simulations.

In order to reduce the computation complexity of the parameter estimation algorithm for conformal FDA-MIMO, we propose a RD-MUSIC algorithm, which has a significant increase in computing speed at the cost of little estimation performance loss.

At first, we define

$\begin{split} V(\theta ,\phi ,r) =& {\boldsymbol{a}}_{t,r}^{\rm{H}}{(\theta ,\phi ,r)^{\rm{H}}}{{\boldsymbol{U}}_n}{\boldsymbol{U}}_n^{\rm{H}}{{\boldsymbol{a}}_{t,r}}(\theta ,\phi ,r) \\ = &{\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {\boldsymbol{a}}(\theta ,\phi ,r)} \right]^{\rm{H}}}{{\boldsymbol{U}}_n} \\ &\cdot{\boldsymbol{U}}_n^{\rm{H}}\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {\boldsymbol{a}}(\theta ,\phi ,r)} \right] \end{split}$

(35)

Eq. (35) can be further calculated by

$\begin{split} V(\theta ,\phi ,r) =& {{\boldsymbol{a}}^{\rm{H}}}(\theta ,\phi ,r){\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {I_M}} \right]^{\rm{H}}} \\ & \times{{\boldsymbol{U}}_n}{\boldsymbol{U}}_n^{\rm{H}}\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {I_M}} \right]{\boldsymbol{a}}(\theta ,\phi ,r) \\ =& {{\boldsymbol{a}}^{\rm{H}}}(\theta ,\phi ,r){\boldsymbol{Q}}(\theta ,\phi ){\boldsymbol{a}}(\theta ,\phi ,r) \end{split}$

(36)

where ${\boldsymbol{Q}}(\theta ,\phi ) = {\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {I_M}} \right]^{\rm{H}}}{{\boldsymbol{U}}_n}{\boldsymbol{U}}_n^{\rm{H}}\left[ {{\boldsymbol{b}}(\theta ,\phi ) \otimes {I_M}} \right]$ ,

Eq. (36) can be transformed into a quadratic programming problem. To avoid ${\boldsymbol{a}}(\theta ,\phi ,r) = {{{\bf{0}}}_M}$ , we add a constraint ${\boldsymbol{e}}_1^{\rm{H}}{\boldsymbol{a}}(\theta ,\phi ,r) = 1$ , where ${\boldsymbol{e}}_1^{}$ denotes unit vector. As a result, the quadratic programming problem can be redefined as

$\left\{ \begin{aligned} & {\mathop {\min }\limits_{\theta ,\phi ,r} {\text{ }}{{\boldsymbol{a}}^{\rm{H}}}(\theta ,\phi ,r){\boldsymbol{Q}}(\theta ,\phi ){\boldsymbol{a}}(\theta ,\phi ,r)} \\ & {{\rm{s.t.}}{\text{ }}{\boldsymbol{e}}_1^{\text{H}}{\boldsymbol{a}}(\theta ,\phi ,r) = 1{\text{ }}} \end{aligned} \right.$

(37)

The penalty function can be constructed as

$\begin{split} L(\theta ,\phi ,r) =& {{\boldsymbol{a}}^{\rm{H}}}(\theta ,\phi ,r){\boldsymbol{Q}}(\theta ,\phi ){\boldsymbol{a}}(\theta ,\phi ,r) \\ & - \mu \left({\boldsymbol{e}}_1^{\text{H}}{\boldsymbol{a}}(\theta ,\phi ,r) - 1\right) \\ \end{split}$

(38)

where $\mu$ is a constant, because ${\boldsymbol{a}}\left( {\theta ,\phi ,r} \right) = {\boldsymbol{a}}\left( {\theta ,\phi } \right) \odot$ ${\boldsymbol{a}}\left( r \right)$ , so we can obtain

$\begin{split} \frac{{\partial L(\theta ,\phi ,r)}}{{\partial {\boldsymbol{a}}(r)}} =& 2{\rm{diag}}\left\{ {{\boldsymbol{a}}(\theta ,\phi )} \right\}{\boldsymbol{Q}}(\theta ,\phi ){\boldsymbol{a}}(\theta ,\phi ,r) \\ & - \mu {\rm{diag}}\left\{ {{\boldsymbol{a}}(\theta ,\phi )} \right\}{\boldsymbol{e}}_{\boldsymbol{1}}^{} \end{split}$

(39)

where ${\rm{diag}}( \cdot )$ denotes diagonalization.

And then let $\dfrac{{\partial L(\theta ,\phi ,r)}}{{\partial {\boldsymbol{a}}(r)}} = 0$ , we can get

${\boldsymbol{a}}\left( r \right) = \varsigma {{\boldsymbol{Q}}^{ - 1}}(\theta ,\phi ){\boldsymbol{e}}_1^{}./{\boldsymbol{a}}(\theta ,\phi )$

(40)

where $\varsigma$ is a constant, $./$ denotes the division of the corresponding elements, which is opposite of Hadamard product. Substituting the constraint ${\boldsymbol{e}}_1^{\rm{H}}{\boldsymbol{a}}(\theta ,\phi ,r) = 1$ into ${\boldsymbol{a}}\left( r \right)$ , we can obtain $\varsigma = 1/({\boldsymbol{e}}_1^{\rm{H}}{{\boldsymbol{Q}}^{ - 1}}$ $\cdot(\theta ,\phi ){\boldsymbol{e}}_1 )$ , then ${\boldsymbol{a}}\left( r \right)$ can be expressed as

${\boldsymbol{a}}\left( r \right) = \frac{{{{\boldsymbol{Q}}^{ - 1}}\left( {\theta ,\phi } \right){{\boldsymbol{e}}_1}}}{{{\boldsymbol{e}}_1^{\rm{H}}{{\boldsymbol{Q}}^{ - 1}}\left( {\theta ,\phi } \right){{\boldsymbol{e}}_1}}}./{\boldsymbol{a}}\left( {\theta ,\phi } \right)$

(41)

Substituting ${\boldsymbol{a}}\left( r \right)$ into Eq. (37), the target azimuths and elevations can be estimated by searching two-dimensional azimuth-elevation spectrum,

$\begin{split} \hfill \lt \hat \theta ,\hat \phi \gt =& {\text{arg}}\mathop {\min }\limits_{\theta ,\phi } \frac{1}{{{\boldsymbol{e}}_1^{\text{H}}{{\boldsymbol{Q}}^{ - 1}}(\theta ,\phi ){{\boldsymbol{e}}_{\boldsymbol{1}}}}} \\ =& {\text{arg}}\mathop {\max }\limits_{\theta ,\phi } {\boldsymbol{e}}_1^{\text{H}}{{\boldsymbol{Q}}^{ - 1}}(\theta ,\phi ){{\boldsymbol{e}}_{\boldsymbol{1}}} \end{split}$

(42)

Given azimuth-elevation estimations obtained by mapping the $L$ peak points, the range information can be obtained by searching range-dimensional spectrum,

$P\left({\hat \theta _i},{\hat \phi _i},r\right){\text{ }} = \frac{1}{{{\boldsymbol{a}}_{t,r}^{\rm{H}}\left({{\hat \theta }_i},{{\hat \phi }_i},r\right){{\boldsymbol{U}}_n}{\boldsymbol{U}}_n^{\rm{H}}{{\boldsymbol{a}}_{t,r}}\left({{\hat \theta }_i},{{\hat \phi }_i},r\right)}}$

(43)

4. Simulation Results

For conformal array, different array layouts produce different element patterns. We select the semi conical conformal array which is shown in Fig. 2 as the receiving array for the following simulation.

Figure 2. Conformal FDA-MIMO semi conical receiving array

DownLoad: Full-Size Img PowerPoint

The simulation parameters are provided as follows: $M = 10,N = 7,{f_1} = 10\;{\rm{GHz}},\Delta f = 3\;{\rm{kHz}},$ $d = \lambda /2 = c/2{f_1}$ and $c = 3 \times {10^8}\;{\rm{m}}/{\rm{s}}$ .

4.1 Analysis of computational complexity

We first analyze the computational complexity of the algorithms in respect of the calculation of covariance matrix, the eigenvalue decomposition of the matrix and the spectral search. The main complexity of the MUISC algorithm and our proposed RD-MUISC algorithm are respectively as

$O\left(KL{({MN})^2} + 4/3{({MN})^{\text{3}}}{{ + L}}{\eta _1}{\eta _2}{\eta _3}{({MN})^2} \right)$

(44)

$O\left(KL{({MN})^2} + 4/3{({MN})^{\text{3}}}{{ + L}}{\eta _1}{\eta _2}{({MN})^2} + L{\eta _3}{({MN})^2}\right)$

(45)

Where $K$ and $L$ denote snapshot number and signal sources number, ${\eta _1},{\eta _2}$ and ${\eta _3}$ represent search number in three-dimensional parameter $\theta ,\phi ,r$ , respectively.

From Eq. (44) and Eq. (45), we can see that the main complexity reduction of the RD-MUSIC algorithm lies in the calculation of the spectral search function. With the increase of the search accuracy, the complexity reduction is more significant.

The computational complexity of algorithms is compared in Fig. 3. It can be seen from Fig. 3 that the difference of computational complexity between the two algorithms gradually increases with the increase of search accuracy. In the case of high accuracy, the computational efficiency of RD-MUSIC algorithm can reach more than ${10^3}$ times of the traditional MUSIC algorithm. The simulation results show that RD-MUSIC algorithm has advantage in computing efficiency for conformal FDA-MIMO.

Figure 3. Comparison of computational complexity under different scan spacing

DownLoad: Full-Size Img PowerPoint

4.2 Single target parameter estimation

In order to illustrate the effectiveness of the RD-MUSIC algorithm for a single target which is located at $({30^\circ },{20^\circ },10\;{\rm{km}})$ , we first give the parameter estimation probability of success with 1000 times Monte Carlo simulation, as shown in Fig. 4, the criterion of successful estimation is defined as the absolute difference between the estimation value and the actual value is less than a designed threshold $\varGamma$ . More specifically, the criterion is $\left| {\hat \theta - \theta } \right| < {\varGamma _\theta },\left| {\hat \phi - \phi } \right| < {\varGamma _\phi },\left| {\hat r - r} \right| < {\varGamma _r}$ , and suppose ${\varGamma _\theta } = \varGamma \times {1^\circ },{\varGamma _\phi } = \varGamma \times {1^\circ },{\varGamma _r} = \varGamma \times 100\;{\rm{m}},$ in the simulation, as well as the search paces are set as $\left[ {{{0.05}^\circ },{{0.05}^\circ },0.05\;{\rm{km}}} \right]$ , respectively. From Fig. 4, we can see that the probability of success gets higher as $\varGamma$ gets bigger, which is consistent with expected.

Figure 4. The parameter estimation probability of RD-MUSIC algorithm with different thresholds

DownLoad: Full-Size Img PowerPoint

Then, we consider the single target parameter estimation performance, Fig. 5 shows the RMSE of different algorithms with the increase of SNR under 200 snapshots condition, and Fig. 6 demonstrates the RMSE of different algorithms with the increase of snapshot number when SNR=0 dB. As shown in Fig. 5 and Fig. 6, the RMSEs of conformal FDA-MIMO gradually descend with the increasing of SNRs and snapshots, respectively. At the same time, the performance of traditional algorithm is slightly higher than RD-MUSIC algorithm. When the number of snapshots is more than 200, the difference of RMSEs is less than ${10^{ - 1}}$ . Therefore, the performance loss of RD-MUSIC algorithm is acceptable compared with the improved computational speed. Note that, here we set 100 times Monte Carlo simulation to avoid running too long.

Figure 5. The RMSE versus snapshot for single target case

DownLoad: Full-Size Img PowerPoint

Figure 6. The RMSE versus SNR for two targets case

DownLoad: Full-Size Img PowerPoint

4.3 Multiple targets parameter estimation

Without loss of generality, we finally consider two targets which are located at $({30^\circ },{20^\circ },$ $10\;{\rm{km}})$ and $({30^\circ },{20^\circ },12\;{\rm{km}})$ , respectively, the remaining parameters are the same as single target case. Fig. 7 and Fig. 8 respectively show the RMSE of different algorithms with the increase of SNR and snapshot number in the case of two targets.

Figure 7. The RMSE versus snapshot for two targets case

DownLoad: Full-Size Img PowerPoint

Figure 8. The RMSE versus snapshot for two targets case

DownLoad: Full-Size Img PowerPoint

It can be seen from Fig. 7 that the RMSE curve trend of angle estimation is consistent with that of single target case. The performance of traditional MUSIC algorithm is slightly better than that of RD-MUSIC algorithm. In the range dimension, the performance of traditional algorithm hardly changes with SNR, and RD-MUSIC algorithm is obviously better than traditional MUSIC algorithm. The proposed RD-MUSIC algorithm first estimates the angles, and then estimates the multiple peaks from range-dimensional spectrum, which avoids the ambiguity in the three-dimensional spectral search. Therefore, the RD-MUSIC algorithm has better range resolution for multiple targets estimation.

5. Conclusion

In this paper, a conformal FDA-MIMO radar is first established, and the corresponding signal receiving mathematical model is formulated. In order to avoid the computational complexity caused by three-dimensional parameter search of MUSIC algorithm, we propose a RD-MUSIC algorithm by solving a quadratic programming problem. Simulation results show that the RD-MUSIC algorithm has comparative angle estimation performance with that of traditional MUSIC algorithm while greatly reducing the computation time. And the RD-MUSIC algorithm has better range estimation performance for multiple targets.

图 1 方位多通道脉内聚束SAR收发信号模型

Figure 1. Transmitting and receiving signal modes of azimuth multi-channel intra-pulse spotlight SAR

下载: 全尺寸图片幻灯片

图 2 斜距平面成像几何

Figure 2. Imaging geometry in the slant-range plane

下载: 全尺寸图片幻灯片

图 3 不同方位子场景回波信号的时频关系

Figure 3. Time-frequency relation of different azimuth sub-scene echo signal

下载: 全尺寸图片幻灯片

图 4 引入APC技术后的时频关系

Figure 4. Time-frequency relation after adopting the APC technique

下载: 全尺寸图片幻灯片

图 5 某一通道的回波信号及其频谱

Figure 5. Echo signal and spectrum of one channel

下载: 全尺寸图片幻灯片

图 6 文献[13]方法信号分离结果

Figure 6. Signal division results by the method in Ref. [13]

下载: 全尺寸图片幻灯片

图 7 本文方法信号分离结果

Figure 7. Signal division results by the method in the paper

下载: 全尺寸图片幻灯片

图 8 完整的多普勒频谱以及成像结果

Figure 8. Imaging result of the combined complete Doppler spectrum

下载: 全尺寸图片幻灯片

图 9 面目标仿真结果

Figure 9. Simulation results of area target

下载: 全尺寸图片幻灯片

表 1 仿真参数

Table 1. Simulation parameters

参数	值	参数	值
雷达载频(GHz)	9.65	方位孔径(m)	4.8
脉冲总时宽(μs)	30	脉冲重复频率(Hz)	3600
子脉冲信号带宽(MHz)	150	场景中心距离(km)	596
采样频率(MHz)	180	子脉冲个数	3
平台速度(m/s)	7200	方位通道数	3

下载: 导出CSV

表 2 成像性能参数统计

Table 2. Parameters of the focused targets

距离向		方位向
PSLR (dB)	–13.28	PSLR (dB)	–13.28
ISLR (dB)	–9.67	ISLR (dB)	–9.81
分辨率 (m)	1.0087	分辨率 (m)	0.8157

下载: 导出CSV

参考文献(18)

[1]	Freeman A, Johnson W T K, Huneycutt B, et al. The " Myth” of the minimum SAR antenna area constraint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 320–324. DOI: 10.1109/36.823926
[2]	Fan B, Qin Y L, You P, et al. An improved PFA with aperture accommodation for widefield spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 3–7. DOI: 10.1109/LGRS.2014.2322858
[3]	Wu Y, Sun G C, Yang C, et al. Processing of very high resolution spaceborne sliding spotlight SAR data using velocity scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1505–1518. DOI: 10.1109/TGRS.2015.2481923
[4]	Li N, Wang R, Deng Y K, et al. Improved full-aperture ScanSAR imaging algorithm based on aperture interpolation[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 1101–1105. DOI: 10.1109/LGRS.2014.2384594
[5]	Meta A, Mittermayer J, Prats P, et al. TOPS imaging with TerraSAR-X: Mode design and performance analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 759–769. DOI: 10.1109/TGRS.2009.2026743
[6]	Callaghan G D and Longstaff I D. Wide-swath space-borne SAR and range ambiguity[C]. Radar 97, Edinburgh, UK, 1997: 248–252
[7]	李杨, 黄杰文, 禹卫东. 高分辨率宽测绘带星载SAR距离向DBF处理[J]. 电子与信息学报, 2011, 33(6): 1510–1514. DOI: 10.3724/SP.J.1146.2010.01157 Li Yang, Huang Jie-wen, and Yu Wei-dong. Range DBF processing for high-resolution wide-swath spaceborne SAR[J]. Journal of Electronics&Information Technology, 2011, 33(6): 1510–1514. DOI: 10.3724/SP.J.1146.2010.01157
[8]	Wang W, Wang R, Deng Y K, et al. Improved digital beam-forming approach with scaling function for range multi-channel synthetic aperture radar system[J]. IET Radar,Sonar&Navigation, 2016, 10(2): 379–385.
[9]	Currie A and Brown M A. Wide-swath SAR[J]. IEE Proceedings F-Radar and Signal Processing, 1992, 139(2): 122–135. DOI: 10.1049/ip-f-2.1992.0016
[10]	Liu B C and He Y J. Improved DBF algorithm for multichannel high-resolution wide-swath SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1209–1225. DOI: 10.1109/TGRS.2015.2476496
[11]	Li X S, Xing M D, Xia X G, et al. Simultaneous stationary scene imaging and ground moving target indication for high-resolution wide-swath SAR system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4224–4239. DOI: 10.1109/TGRS.2016.2538564
[12]	Krieger G, Gebert N, and Moreira A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 31–46. DOI: 10.1109/TGRS.2007.905974
[13]	武其松, 邢孟道, 刘保昌, 等. 脉内聚束SAR方位高分辨率宽测绘带成像[J]. 西安电子科技大学学报(自然科学版), 2010, 37(4): 676–682, 699. DOI: 10.3969/j.issn.1001-2400.2010.04.017 Wu Qi-song, Xing Meng-dao, Liu Bao-chang, et al. High azimuth resolution wide swath imaging based on the intrapulse spotlight SAR[J]. Journal of Xidian University, 2010, 37(4): 676–682, 699. DOI: 10.3969/j.issn.1001-2400.2010.04.017
[14]	Dall J and Kusk A. Azimuth phase coding for range ambiguity suppression in SAR[C]. International Geoscience and Remote Sensing Symposium, Anchorage, USA, 2004, 3: 1734–1737
[15]	郭磊, 王宇, 邓云凯, 等. 基于方位向相位编码技术的方位向多通道SAR距离模糊抑制方法[J]. 电子与信息学报, 2015, 37(3): 601–606. DOI: 10.11999/JEIT140707 Guo Lei, Wang Yu, Deng Yun-kai, et al. Range ambiguity suppression for multi-channel SAR system using azimuth phase coding technique[J]. Journal of Electronics&Information Technology, 2015, 37(3): 601–606. DOI: 10.11999/JEIT140707
[16]	邢孟道, 李真芳, 保铮, 等. 分布式小卫星雷达空时频成像方法研究[J]. 宇航学报, 2005, 26(S1): 70–76, 82. DOI: 10.3321/j.issn:1000-1328.2005.z1.014 Xing Meng-dao, Li Zhen-fang, Bao Zheng, et al. Study of distributed microsatellites radar space-time-frequency imaging method[J]. Journal of Astronautics, 2005, 26(S1): 70–76, 82. DOI: 10.3321/j.issn:1000-1328.2005.z1.014
[17]	Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood, MA, USA: Artech House, 2005
[18]	Zhang S X, Xing M D, Xia X G, et al. Multichannel HRWS SAR imaging based on range-variant channel calibration and multi-Doppler-direction restriction ambiguity suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4306–4327. DOI: 10.1109/TGRS.2013.2281329

施引文献

期刊类型引用(4)

1.	葛津津，周浩，凌天庆. 一种应用于脉冲探地雷达前端的探测子系统. 电子测量技术. 2022(04): 27-32 . 百度学术
2.	尹诗，郭伟. 用于探地雷达的超宽带天线设计与仿真. 电子设计工程. 2018(03): 98-102 . 百度学术
3.	宋立伟，张超，洪涛. 冲击波载荷对平面阵列天线电性能的影响. 电子机械工程. 2017(04): 1-5+58 . 百度学术
4.	尹德，叶盛波，刘晋伟，纪奕才，刘小军，方广有. 一种用于高速公路探地雷达的新型时域超宽带TEM喇叭天线. 雷达学报. 2017(06): 611-618 . 本站查看

其他类型引用(6)

资源附件(0)

访问统计

图(9) / 表(2)

计量

文章访问数: 2466
HTML全文浏览量: 574
PDF下载量: 362
被引次数: 10

1. Introduction
2. Conformal FDA-MIMO Radar
2.1 General conformal FDA-MIMO signal model
2.2 CRLB of conformal FDA-MIMO
3. Reduced-Dimension Target Parameter Estimation Algorithm
4. Simulation Results
4.1 Analysis of computational complexity
4.2 Single target parameter estimation
4.3 Multiple targets parameter estimation
5. Conclusion

1. Introduction
2. Conformal FDA-MIMO Radar
2.1 General conformal FDA-MIMO signal model
2.2 CRLB of conformal FDA-MIMO
3. Reduced-Dimension Target Parameter Estimation Algorithm
4. Simulation Results
4.1 Analysis of computational complexity
4.2 Single target parameter estimation
4.3 Multiple targets parameter estimation
5. Conclusion

参考文献(18)

施引文献

资源附件(0)

访问统计

基于方位相位编码的脉内聚束SAR成像方法

DOI: 10.12000/JR17114

通讯作者:
吴玉峰 wyf1176@163.com

计量

Intra-pulse Spotlight SAR Imaging Method Based on Azimuth Phase Coding

1. Introduction

2. Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

2.2 CRLB of conformal FDA-MIMO

3. Reduced-Dimension Target Parameter Estimation Algorithm

4. Simulation Results

4.1 Analysis of computational complexity

4.2 Single target parameter estimation

4.3 Multiple targets parameter estimation

5. Conclusion

期刊类型引用(4)

其他类型引用(6)

计量

目录

1. Introduction

2. Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

2.2 CRLB of conformal FDA-MIMO

3. Reduced-Dimension Target Parameter Estimation Algorithm

4. Simulation Results

4.1 Analysis of computational complexity

4.2 Single target parameter estimation

4.3 Multiple targets parameter estimation

5. Conclusion

期刊介绍

联系我们

基于方位相位编码的脉内聚束SAR成像方法

DOI: 10.12000/JR17114

通讯作者: 吴玉峰 wyf1176@163.com

计量

出版历程

Intra-pulse Spotlight SAR Imaging Method Based on Azimuth Phase Coding

1. Introduction

2. Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

2.2 CRLB of conformal FDA-MIMO

3. Reduced-Dimension Target Parameter Estimation Algorithm

4. Simulation Results

4.1 Analysis of computational complexity

4.2 Single target parameter estimation

4.3 Multiple targets parameter estimation

5. Conclusion

期刊类型引用(4)

其他类型引用(6)

计量

出版历程

目录

1. Introduction

2. Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

2.2 CRLB of conformal FDA-MIMO

3. Reduced-Dimension Target Parameter Estimation Algorithm

4. Simulation Results

4.1 Analysis of computational complexity

4.2 Single target parameter estimation

4.3 Multiple targets parameter estimation

5. Conclusion

期刊介绍

联系我们

通讯作者:
吴玉峰 wyf1176@163.com