作者中心
专家审稿
责编办公
编辑办公
Channel Phase Mismatch Calibration for Multichannel in Azimuth SAR Imaging Based on Eigen-structure Method
-
摘要: 作为实现高分辨率宽幅成像的重要技术手段之一，方位多通道合成孔径雷达(Synthetic Aperture Radar, SAR)近年来得到了广泛的研究与发展。在进行多通道数据重建之前，通道之间的传输特性必须校正一致，以避免图像中出现严重的虚假目标。在多通道SAR数据处理中，精确的基带多普勒中心估计对系统的通道失配校正和高分辨率成像具有非常重要的意义。但是单一通道数据的多普勒频谱混叠制约了传统基带多普勒中心估计算法在方位多通道SAR系统中的应用。基于特征分解处理，该文提出一种新的基带多普勒中心估计方法。该方法在推导过程中考虑了波束指向存在斜视的影响，能够实现方位多通道SAR系统基带多普勒中心和通道间相位误差的鲁棒估计。仿真实验和C波段方位向四通道机载SAR实验数据处理分析验证了算法的有效性。Abstract: As one of the most important means to achieve a High-Resolution and Wide-Swath (HRWS) imaging of the earth, multichannel in azimuth Synthetic Aperture Radar (SAR) have attracted considerable attention in recent years. However, prior to the unambiguous reconstruction of the multichannel SAR signal, each channel needs to be well calibrated, otherwise the performance of the reconstruction processor may degrade or even lose its effectiveness. Accurate baseband Doppler centroid estimation are critical for channel mismatch calibration and high-resolution imaging in the multichannel SAR systems. However, in the multichannel HRWS SAR system, the signal acquired by each channel is under-sampled that renders the traditional Doppler centroid estimation methods obsolete. In this paper, an eigen-structure method has been used to achieve a robust estimation of the baseband Doppler centroid and the phase mismatch in the multichannel SAR system. Processing with simulated and experimental C-band, four-channel airborne SAR data validates the effectiveness of this method.
-
图 4 数据重采样过程(红色实心圆点表示原始多通道数据，黑色实心圆点表示重采样之后的多通道数据)
Figure 4. Process of resampling original experimental data (red solid dots represent original experimental data, and black solid dots represent resampled data)
图 6 C波段四通道机载SAR实验数据成像结果
Figure 6. Imaging results of the C-band four channel airborne SAR experimental data
表 1 星载仿真实验参数
Table 1. System parameters of simulated spaceborne experiment
系统参数 数值 通道数目 4 信噪比(dB) 40 轨道高度(km) 630 平台速度(m/s) 7545 载频(GHz) 5.4 发射信号带宽(MHz) 80 脉冲重复频率(Hz) 1257.5 多普勒带宽(Hz) 2515 
下载: 导出CSV
表 2 仿真实验相位误差设置
Table 2. Phase mismatch set in simulated experiment
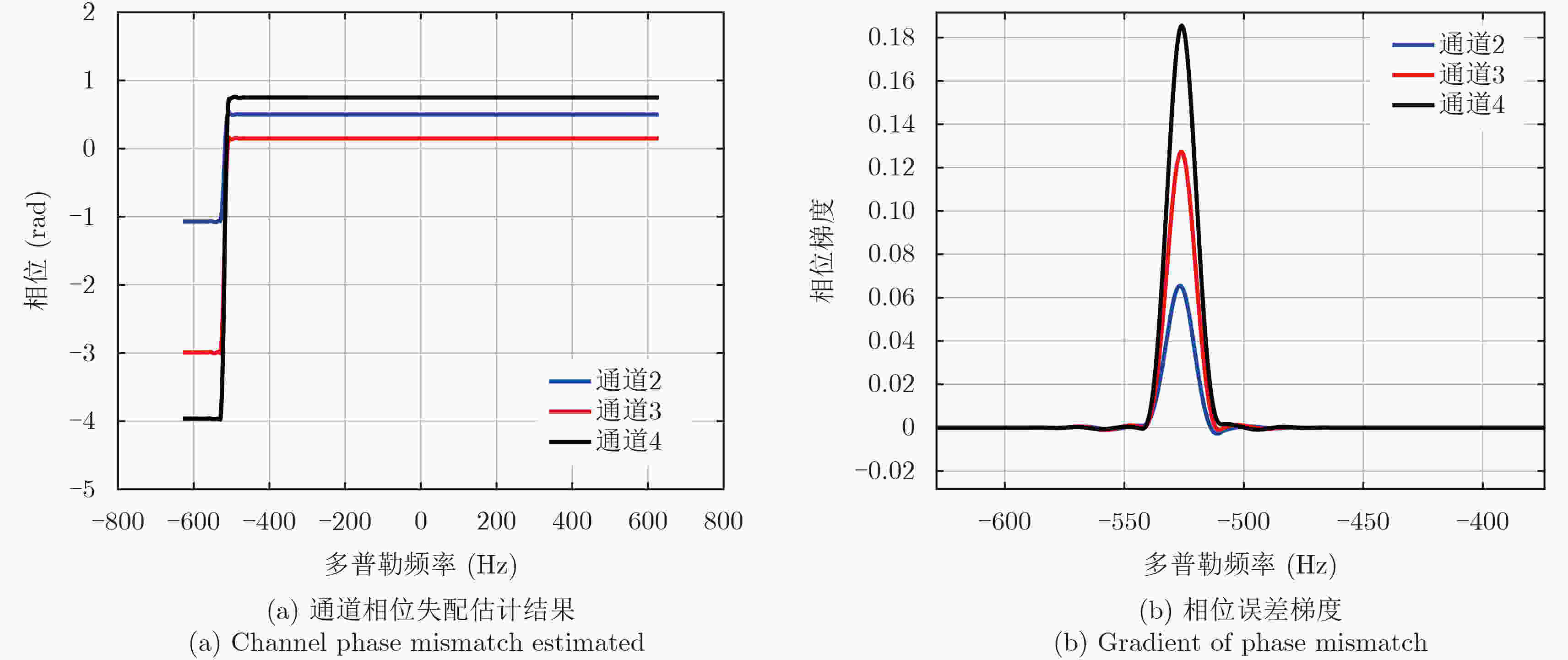
通道 相位误差(rad) 通道1 – 通道2 0.5 通道3 0.15 通道4 0.75
下载: 导出CSV
表 3 仿真实验相位误差和基带多普勒中心估计结果
Table 3. Estimation of phase mismatch and baseband Doppler centroid in simulated experiment
通道 相位失配(rad) 基带多普勒中心估计(Hz) 预设 估计 预设 估计 通道1 – – – – 通道2 0.50 0.4999 100 100.85 通道3 0.15 0.1496 100 100.64 通道4 0.75 0.7495 100 100.25
下载: 导出CSV
表 4 C波段方位向四通道机载SAR实验参数
Table 4. Experimental parameters of C-band azimuth four channel airborne SAR system
系统参数 数值 通道数目 4 平台高度(m) 8600 平台速度(m/s) 129.64 载频(GHz) 5.4 发射信号带宽(MHz) 210 方位向天线尺寸(m) 0.624 脉冲重复频率(Hz) 137.19
下载: 导出CSV
表 5 C波段四通道机载SAR实验数据处理结果
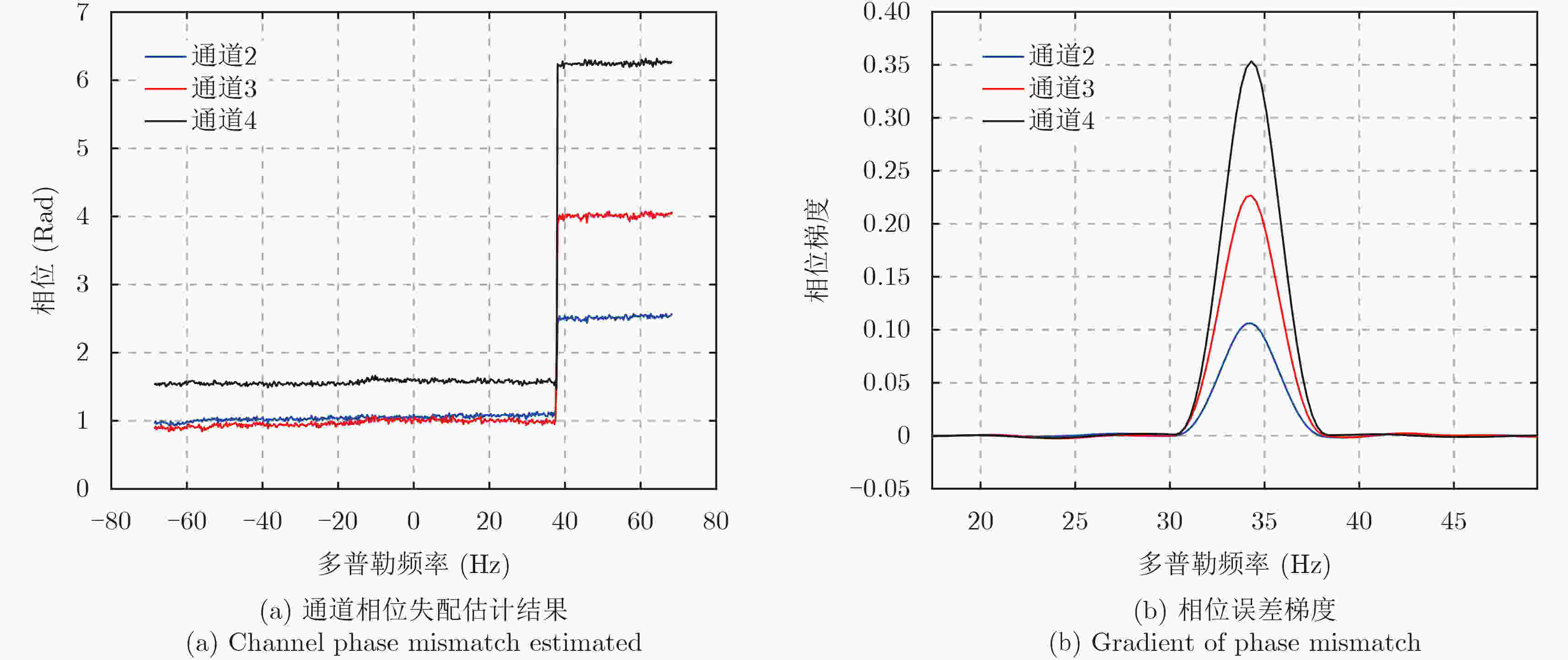
Table 5. Experimental results of C-band four channel airborne SAR system
通道 相位失配(rad) 系统多普勒中心(Hz) 通道1 – – 通道2 1.058 –34.57 通道3 0.994 –34.18 通道4 1.577 –34.29
下载: 导出CSV
-
[1] Gebert N, Krieger G, and Moreira A. High resolution wide swath SAR imaging with digital beamforming-performance analysis, optimization, system design[C]. Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, July 2006: 341–344. [2] Gebert N, de Almeida F, and Krieger G. Airborne demonstration of multichannel SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 963–967. DOI: 10.1109/LGRS.2011.2144563 [3] Kim J H, Younis M, Prats-Iraola P, et al. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 579–590. DOI: 10.1109/TGRS.2012.2201947 [4] Li Zhenfang, Bao Zheng, Wang Hongyang, et al. Performance improvement for constellation SAR using signal processing techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 436–452. DOI: 10.1109/TAES.2006.1642562 [5] Zhang Lei, Xing Mengdao, Qiu Chengwei, et al. Adaptive two-step calibration for high resolution and wide-swath SAR imaging[J]. IET Radar,Sonar&Navigation, 2010, 4(4): 548–559. [6] Zhang Shuangxi, Xing Mengdao, Xia Xianggen, et al. Multichannel HRWS SAR imaging based on range-variant channel calibration and multi-Doppler-direction restriction ambiguity suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4306–4327. DOI: 10.1109/TGRS.2013.2281329 [7] 张磊, 全英汇, 邢孟道, 等. 一种子空间投影的高分辨宽测绘带SAR成像通道均衡方法[J]. 电子与信息学报, 2010, 32(1): 1–6. DOI: 10.3724/SP.J.1146.2008.01821Zhang Lei, Quan Yinghui, Xing Mengdao, et al. An SSP based channel calibration for high-resolution and wide-swath SAR imagery[J]. Journal of Electronics&Information Technology, 2010, 32(1): 1–6. DOI: 10.3724/SP.J.1146.2008.01821 [8] Feng Jin, Gao Canguan, Zhang Yi, et al. Phase mismatch calibration of the multichannel SAR based on azimuth cross correlation[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 903–907. DOI: 10.1109/LGRS.2012.2227107 [9] Liu Yanyang, Li Zhenfang, Wang Zhibin, et al. On the baseband Doppler centroid estimation for multichannel HRWS SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(12): 2050–2054. DOI: 10.1109/LGRS.2014.2318511 [10] Li Jianbin, Li Xiaoping, Lin Mingfu, et al. Maximum-likelihood-based Doppler centroid estimation algorithm for MC-HRWS SAR system[J]. Electronics Letters, 2014, 50(22): 1630–1631. DOI: 10.1049/el.2014.2723 [11] 刘艳阳, 李真芳, 杨桃丽, 等. 一种单星方位多通道高分辨率宽测绘带SAR系统通道相位偏差时域估计新方法[J]. 电子与信息学报, 2012, 34(12): 2913–2919. DOI: 10.3724/SP.J.1146.2012.00562Liu Yanyang, Li Zhenfang, Yang Taoli, et al. A novel channel phase bias estimation method for spaceborne along-track multi-channel HRWS SAR in time-domain[J]. Journal of Electronics&Information Technology, 2012, 34(12): 2913–2919. DOI: 10.3724/SP.J.1146.2012.00562 [12] 王志斌, 刘艳阳, 李真芳, 等. 基于多普勒谱优化的HRWS SAR系统通道相位偏差估计算法[J]. 电子与信息学报, 2016, 38(12): 3026–3033. DOI: 10.11999/JEIT161038Wang Zhibin, Liu Yanyang, Li Zhenfang, et al. Phase bias estimation algorithm for HRWS SAR system in azimuth based on Doppler spectrum optimization[J]. Journal of Electronics&Information Technology, 2016, 38(12): 3026–3033. DOI: 10.11999/JEIT161038 [13] Gebert N. Multi-channel azimuth processing for high-resolution wide-swath SAR imaging[D]. [Ph.D. dissertation], German Aerospace Center, 2009: 20, 22. [14] Krieger G, Gebert N, and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260–264. DOI: 10.1109/LGRS.2004.832700 [15] Friedlander B and Weiss A J. Eigenstructure methods for direction finding with sensor gain and phase uncertainties[C]. Proceedings of International Conference on Acoustics, Speech, and Signal Processing, California, USA, April 1988: 2681–2684. [16] Guo Xiaojiang, Gao Yesheng, Wang Kaizhi, et al. Improved channel error calibration algorithm for azimuth multichannel SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 1022–1026. DOI: 10.1109/LGRS.2016.2561961 [17] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood: Artech House, 2005: 194–200. [18] Lanari R, Zoffoli S, Sansosti E, et al. New approach for hybrid strip-map/spotlight SAR data focusing[J]. IEE Proceedings-Radar,Sonar and Navigation, 2001, 148(6): 363–372. DOI: 10.1049/ip-rsn:20010662 [19] Baumgartner S V and Krieger G. Simultaneous high-resolution wide-swath SAR imaging and ground moving target indication: Processing approaches and system concepts[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5015–5029. DOI: 10.1109/JSTARS.2015.2450019 -
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 0
