Robust Design of Constant Modulus Sequence and Receiver Filter in the Presence of Signal-dependent Clutter
-
摘要: 该文针对信号相关杂波环境下的运动目标检测问题,研究一种稳健的慢时间发射波形和接收滤波器设计方法。首先,基于杂波2阶统计特性不确定时的最坏SINR (the Worst-case SINR, W-SINR),建立非凸恒模约束下高维的发射-接收联合优化模型;然后,提出一种基于序列迭代的优化算法(Iterative Sequential Optimization, ISO)。每步迭代中,该算法将一个高维优化问题转化为多个1维分式规划问题,并通过丁克尔巴赫(Dinkelbach)方法进行求解。最后,仿真实验证明,ISO具有对抗不确定杂波信息的能力,使系统具有更好的适应能力;此外,相比半正定松弛(Semi-Definite Relaxation, SDR)与随机化方法,提出的算法在W-SINR优化值与计算复杂度上均具有明显的优势。
-
关键词:
- 稳健设计 /
- 信干噪比(SINR) /
- 恒模序列 /
- 迭代序列优化
Abstract: In this paper, we focus on the detection of a moving point-like target embedded in uncertain signal-dependent clutter and develop robust transmit-code and receive-filter designs in slow-time. First, based on the Worst-case Signal-to-Interference-plus-Noise Ratio (W-SINR) when the second-order clutter statistics are uncertain, we establish a high-dimensional transmit-receive optimization model that considers the constant modulus constraint with non-convexity. Next, we propose an Iterative Sequential Optimization (ISO) algorithm. At each iteration, it converts a high-dimensional optimization into multiple one-dimensional fractional programming problems that can be efficiently solved using Dinkelbach’s method. Finally, we use numerical examples to confirm that the ISO can resist the uncertain knowledge of signal-dependent clutter, which enables the radar system to adapt to complicated environments. Moreover, compared to Semi-Definite Relaxation (SDR)-related and randomization methods, the proposed algorithm is superior with respect to both optimized W-SINR and computational time. -
表 1 稳健的发射-接收联合设计算法
Table 1. Algorithm for the robust transmit-receive design
输入: ${{{s}}_0},\xi ,\sigma _{\left( {k,l} \right)}^2,{f_{\left( {k,l} \right)}},{\varepsilon _{\left( {k,l} \right)}},{\delta _{\left( {k,l} \right)}},k = 1,2, ·\!·\!· ,N,l = 1,2, ·\!·\!· ,L$ 输出:P1的最优解 $\left( {{{{s}}_{{\rm{opt}}}},{{{w}}_{{\rm{opt}}}}} \right)$ (1) 由式(11)得到 ${{{M}}_{{\rm{opt}}\left( {k,l} \right)}}$然后根据式(13)计算 $ \widehat{ {Σ} _{\rm{c}}}\left( {{s}} \right)$; (2) 对于 $n = 0,i = 0$然后初始化序列 ${{{s}}^{\left( 0 \right)}} = {{{s}}_0}$; (3) 由式(17)计算 ${{{w}}^{\left( 0 \right)}}$,根据式(14)计算 ${\stackrel \frown {\rho}} _0{\rm{ = }}\mathord{\stackrel \frown {\rho}} \left( {{{{s}}^{\left( 0 \right)}},{{{w}}^{\left( 0 \right)}}} \right)$; (4) n=n+1; (5) 根据式(19)和式(22)分别计算矩阵 ${{Σ}_{\rm{t}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$和 ${Θ}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$; (6) i=i+1; (7) 根据式(26)和式(27)分别计算 ${a_{r,i}},{b_{r,i}}\left( {r = 0,1,2} \right)$; (8) 在可行域内随机产生初始码字 ${s_{i,0}}$; (9) 解式(28)并得到最优解 ${s_{{\rm{opti}}}}$; (10) 如果i=N,输出 ${{{s}}^{\left( n \right)}} = {\left[ {{s_{{\rm{opt1}}}}\;{s_{{\rm{opt}}2}}\; ·\!·\!· {\rm{ }}{s_{{\rm{opt}}N}}} \right]^{\rm{T}}}$,否则返回步骤(6); (11) 由式(17)计算 ${{{w}}^{\left( n \right)}}$,根据式(14)计算 ${\mathord{\stackrel \frown {\rho}} _n}{\rm{ = }}\mathord{\stackrel \frown {\rho}} \left( {{{{s}}^{\left( n \right)}},{{{w}}^{\left( n \right)}}} \right)$; (12) 如果 $\left| {{{\mathord{\stackrel \frown {\rho}} }_n} - {{\mathord{\stackrel \frown {\rho}} }_{n - 1}}} \right| \le \xi $ ( $\xi $是一个用来控制收敛的自定义参数), 输出 ${{{s}}_{{\rm{opt}}}}{\rm{ = }}{{{s}}^{\left( n \right)}},{{{w}}_{{\rm{opt}}}}{\rm{ = }}{{{w}}^{\left( n \right)}}$;否则返回步骤(4),直到收敛。 表 2 收敛条件 $\left| {{{\mathord{\stackrel \frown {ρ} } }_{n}} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \!\!\le\!\! {10^{ - 3}}$下3种算法的迭代次数和计算时间
Table 2. Iteration number and computation time (in seconds) of all the three algorithms with the exit condition $\left| {{{\mathord{\stackrel \frown{{ρ}}} }_n} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \le {{10}^{ - 3}}$
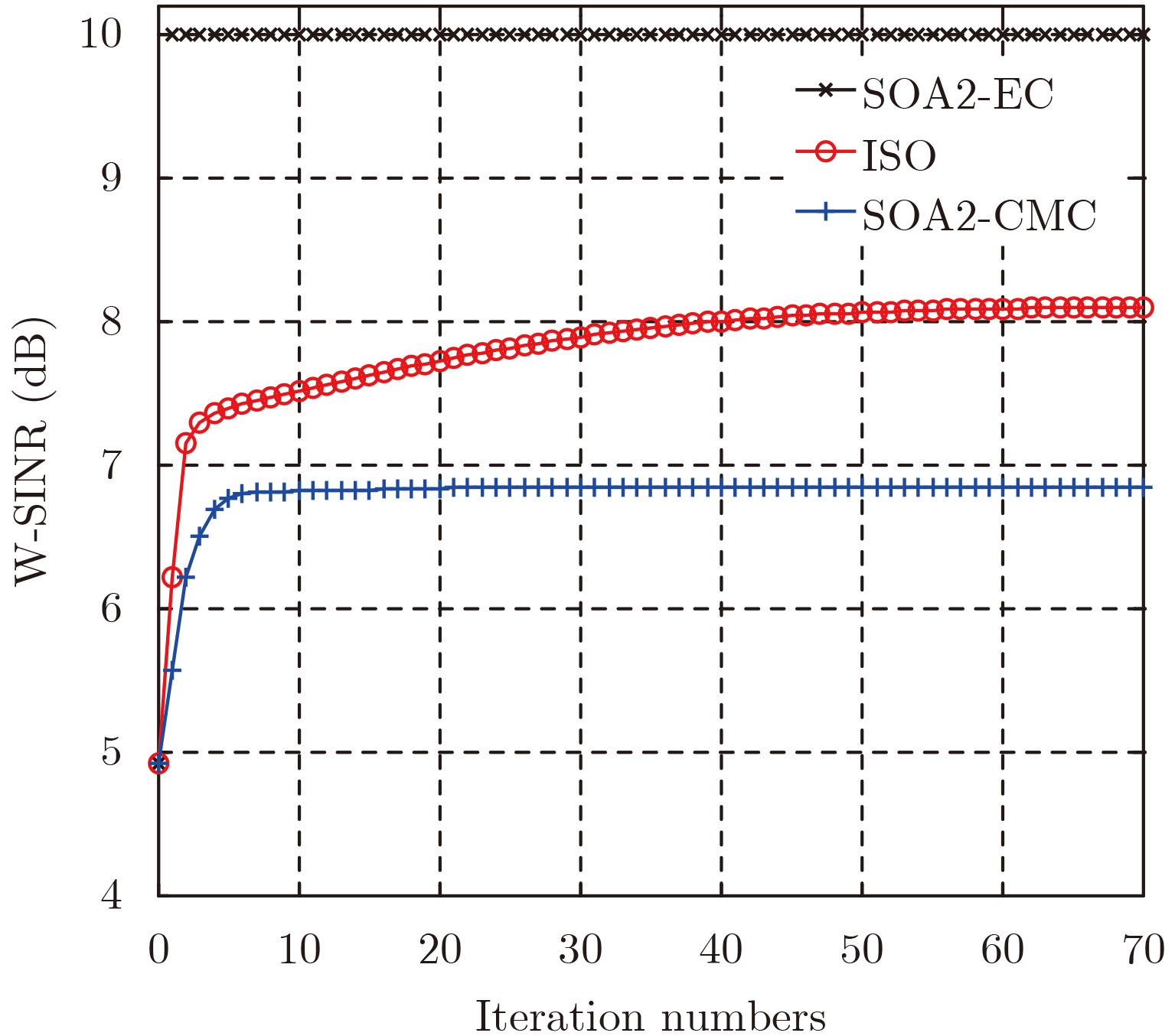
算法 迭代次数 计算时间(s) SOA2-EC 4 0.005 ISO 73 0.220 SOA2-CMC 45 23.920 -
[1] Haykin S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30–40. doi: 10.1109/MSP.2006.1593335 [2] Guerci J R. Cognitive Radar: The Knowledge-aided Fully Adaptive Approach[M]. London: Artech House, 2010: 20–30. [3] 黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J]. 电子学报, 2012, 40(9): 1863–1870. http://www.cnki.com.cn/Article/CJFDTOTAL-DZZZ201315020.htmLi Xiang and Fan Mei-mei. Research advance on cognitive radar and its key technology[J]. Acta Electronica Sinica, 2012, 40(9): 1863–1870. http://www.cnki.com.cn/Article/CJFDTOTAL-DZZZ201315020.htm [4] 范梅梅. 认知雷达目标识别自适应波形设计技术研究[D]. [硕士论文], 国防科学技术大学, 2012: 1–6.Fan Mei-mei. Adaptive waveform design for target recognition in cognitive radar[D]. [Master dissertation], National University of Defense Technology, 2012: 1–6. [5] Stoica P, Li Jian, and Xue Ming. Transmit codes and receive filters for radar[J]. IEEE Signal Processing Magazine, 2008, 25(6): 94–109. doi: 10.1109/MSP.2008.929231 [6] Aubry A, De Maio A, Piezzo M, et al.. Cognitive design of the receive filter and transmitted phase code in reverberating environment[J]. IET Radar, Sonar & Navigation, 2012, 6(9): 822–833. [7] 王璐璐, 王宏强, 王满喜, 等. 雷达目标检测的最优波形设计综述[J]. 雷达学报, 2016, 5(5): 487–498. http://radars.ie.ac.cn/CN/abstract/abstract378.shtmlWang Lu-lu, Wang Hong-qiang, Wang Man-xi, et al.. An overview of radar waveform optimization for target detection[J]. Journal of Radars, 2016, 5(5): 487–498. http://radars.ie.ac.cn/CN/abstract/abstract378.shtml [8] Cui Guo-long, Li Hong-bin, and Rangaswamy M. MIMO radar waveform design with constant modulus and similarity constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343–353. doi: 10.1109/TSP.2013.2288086 [9] Stoica P, He Hao, and Li Jian. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1730–1740. doi: 10.1109/TSP.2011.2179652 [10] 纠博, 刘宏伟, 李丽亚, 等. 雷达波形优化的特征互信息方法[J]. 西安电子科技大学学报(自然科学版), 2009, 36(1): 139–144. http://www.cnki.com.cn/Article/CJFDTOTAL-XDKD200901027.htmJiu Bo, Liu Hong-wei, Li Li-ya, et al.. Feature mutual information method for radar waveform optimization[J]. Journal of Xidian University, 2009, 36(1): 139–144. http://www.cnki.com.cn/Article/CJFDTOTAL-XDKD200901027.htm [11] Naghsh M M, Soltanalian M, Stoica P, et al.. A Doppler robust design of transmit sequence and receive filter in the presence of signal-dependent interference[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 772–785. doi: 10.1109/TSP.2013.2288082 [12] Karbasi S M, Aubry A, Carotenuto V, et al.. Knowledge-based design of space-time transmit code and receive filter for a multiple-input-multiple-output radar in signal-dependent interference[J]. IET Radar, Sonar & Navigation, 2015, 9(8): 1124–1135. [13] Aubry A, De Maio A, and Naghsh M N. Optimizing radar waveform and Doppler filter bank via generalized fractional programming[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1387–1399. doi: 10.1109/JSTSP.2015.2469259 [14] Zhu Wei and Tang Jun. Robust design of transmit waveform and receive filter for colocated MIMO radar[J]. IEEE Signal Processing Letters, 2015, 22(11): 2112–2116. doi: 10.1109/LSP.2015.2461460 [15] Aubry A, Demaio A, Farina A, et al.. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace & Electronic Systems, 2013, 49(1): 93–117. [16] He Hao, Li Jian, and Stoica P. Waveform Design for Active Sensing Systems—A Computational Approach[M]. Cambridge, U. K., Cambridge University Press, 2012: 2–6. [17] 倪国熙. 常用的矩阵理论和方法[M]. 上海: 上海科学技术出版社, 1984: 18–22.Ni Guo-xi. Common Matrix Theory and Method[M]. Shanghai: Shanghai Science and Technology Press, 1984: 18–22. [18] 何子述, 夏威, 等. 现代数字信号处理及其应用[M]. 北京: 清华大学出版社, 2009: 100–106.He Zi-shu, Xia Wei, et al.. Advanced Digital Signal Processing and Application[M]. Beijing: Tsinghua University Press, 2009: 100–106. [19] Yu Xian-xiang, Cui Guo-long, Kong Ling-jiang, et al.. Space-time transmit code and receive filter design for colocated MIMO radar[C]. IEEE Radar Conference, Philadelphia, PA, 2016: 1–6. [20] Golub G H and Van Loan C F. Matrix computations[J]. The Mathematical Gazette, 1990, 74(469): 324–325. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公

 下载:
下载: