1.   引言

随着电子信息技术的不断发展，传统的有源雷达系统不仅面临着隐身飞机、反辐射导弹等先进军事设备带来的重大威胁，还需要面对超低空突防、综合电子干扰等高超作战手段的严峻挑战。外辐射源雷达系统是指本身不发射能量，而是被动地接收目标反射的空间电磁环境中已经存在的外部辐射源发射的电磁信号来进行目标检测与跟踪的雷达系统。外辐射源雷达系统没有大功率的发射源，隐蔽性好，具有强大的生存能力和潜在的反隐身、低空探测功能，具有传统有源雷达系统无法比拟的优点，在国防领域的发展前景十分广阔，是世界各国的学者研究的热点^[1-3]。

在雷达目标检测中，最常用的算法是恒虚警(Constant False Alarm Rate, CFAR)检测算法^[4]。这是一种跟踪前检测(Detect-Before-Track, DBT)算法，根据奈曼-皮尔逊(Neyman-Pearson, NP)准则计算出阈值，对单帧雷达回波信号进行阈值判决。然而不同于传统的有源雷达系统，外辐射源雷达系统的发射功率和发射波形不可控，目标回波的信噪比(Signal-to-Noise Ratio, SNR)通常比较低，过高的阈值会导致信噪比较低的目标无法被检测，若降低阈值，则会产生过多的虚假点迹，降低算法的实时性。

为了有效地对低信噪比的弱目标进行检测，形成了一类检测前跟踪(Track-Before-Detect, TBD)算法。这类算法并不直接对单帧数据进行阈值判决形成点迹，而是利用目标的运动特征沿着可能的运动轨迹进行多帧回波信号的能量积累，在此基础上实现微弱目标的检测和跟踪。传统的TBD算法主要包括霍夫变换、动态规划和粒子滤波等方法。基于霍夫变换^[5]的弱目标检测算法能实现简单的直线运动轨迹的弱目标检测，但对于机动目标的检测性能较差。基于动态规划^[6,7]的弱目标算法将多帧目标轨迹估计问题转化为单帧的最优状态估计问题，能对机动目标进行轨迹估计，但对状态空间中的每一个状态进行遍历操作导致动态规划算法计算复杂度高，运行时间长。而且，基于动态规划和基于霍夫变换的弱目标检测算法都是批处理算法，需要等待多帧观测数据才能开始处理，实时性较差。

TBD算法的另一种重要实现方式是递归实现，无需等待多帧观测数据。递归算法^[8-12]以贝叶斯滤波为代表。然而除了某些特殊情形，贝叶斯滤波难以在连续的状态空间中得到精确的解析解。一种解决方式是将连续状态空间进行离散格点化，递推计算后验概率密度函数在离散目标状态格点上的取值^[13]。离散格点贝叶斯滤波的方法实现简单，在进行目标检测时，通常将目标不存在作为一种特殊的状态添加到状态空间中，需要建立目标存在和目标不存在两种状态之间的转移概率模型，而转移概率模型的好坏直接影响着目标检测性能。贝叶斯滤波另一种常用的逼近实现形式是粒子滤波^[14]。粒子滤波算法通过寻找一组在状态空间传播的随机样本来逼近后验概率密度函数，按时间递推地更新随机样本和相应的权值，进而可以递推地通过近似的后验概率密度函数对目标的状态进行估计，从而实现弱目标的检测和跟踪。粒子滤波能够有效地解决观测非线性问题，但需要大量的粒子来保证其滤波性能，导致算法的计算复杂度较高，运行时间较长，难以保证外辐射源雷达系统中目标检测较高的实时性需求。

外辐射源雷达系统利用各种民用或者商用信号作为辐射源，通常工作在较低的频段，波长较长。基于外辐射源雷达系统的目标检测特点，针对上述问题的不足，为了提高目标检测算法的实时性，同时保证算法的检测性能，本文对目标状态空间进行离散网格化处理，结合经典的递推贝叶斯滤波的思想在多帧观测数据之间进行信息的传递和积累，提出了一种实现简单、计算复杂度低、可并行度高的基于信息积累的外辐射源目标检测方法。该算法引入了信息论中常用的信息熵对目标状态的不确定度进行度量，并利用信息熵作为目标是否存在的判决条件，避免了对目标存在和目标不存在两种状态之间转移概率的先验建模，减少了算法的超参数。最后通过仿真实验和对实测数据的处理验证了算法的有效性和实时性。

本文中，${( \cdot )^{\rm{T}}}$和 ${( \cdot )^{\rm{*}}}$分别表示向量或矩阵的转置和共轭操作。本文内容安排如下：第2节对外辐射源雷达系统进行建模，第3节介绍基于信息积累的目标检测算法，第4节给出实验结果，第5节进行总结。

2.   外辐射源系统模型

外辐射源雷达工作场景示意图如图1所示。分别用${{{x}}_{\rm{e}}}, {{{x}}_{\rm{r}}},{{ x}}{\rm{(}}t{\rm{)}}$表示辐射源、雷达接收机和目标所在位置的三维笛卡尔空间坐标；${{v}}{\rm{(}}t{\rm{)}}$表示目标的运动速度矢量；$s(t)$表示辐射源连续发射的复基带信号。

图  1  外辐射源雷达工作场景示意图

Figure  1.  Working principle for passive radar

下载: 全尺寸图片 幻灯片

为简单起见，假设参考通道接收到的直达波信号经过处理后能够恢复出发射信号$s(t)$，回波通道接收信号经过处理后所包含的直达波和其他杂波被成功滤除，则回波信号可以建模为^[2]

其中，$A(t),\phi (t),\tau (t),{f_{\rm{d}}}(t)$分别代表幅度、相位、延时和多普勒频移；$w(t)$是均值为0，方差为${\sigma ^2}$的加性复高斯白噪声。延时和多普勒频移可以通过式(3)和式(4)来计算^[2]

其中，$\rm c$为光速，${f_{\rm{c}}}$为载波频率。

定义模糊函数

将回波信号与参考信号进行相参积累处理，结果如式(6)所示。

对式(6)进行采样，

其中，

f_s为信号的采样频率。

对$y_k^{i,j}$取模，得到

令$A_k^{i,j} = A{{\rm{e}}^{ - {\rm{j}}2\pi \left( {{f_j} - {f_{\rm d}}} \right)\left( {{t_i} + kT} \right)}}{\chi _k}\left( {{t_i} - \tau ,{f_j} - {f_{\rm d}}} \right)$，则式(10)简化为

定义${{ z}_k} = \left\{ {z_k^{i,j}} \right\}(i = 0,1, ··· ,I - 1,j = 0,\,1,\, ··· , J - 1)$表示k 时刻的观测结果矩阵。过去1到k时刻的所有观测结果用${{ z}_{1:k}} = \left( {{{ z}_1},{{ z}_2}, ··· ,{{ z}_k}} \right)$表示，后续将基于此观测结果进行目标检测。

3.   基于信息积累的目标检测算法

经典的递推贝叶斯滤波过程分为两步：预测步和更新步^[13]。假设已知k–1时刻的概率密度函数$p\left( {{{{x}}_{k - 1}}|{{ z}_{1:k - 1}}} \right)$，k时刻得到新的观测值${{ z}_k}$，预测过程利用过去的观测结果${{ z}_{1:k - 1}}$对目标状态${{{x}}_k}$进行预测得到概率密度函数$p\left( {{{{x}}_k}|{{ z}_{1:k - 1}}} \right)$，更新过程利用新的观测值${{ z}_k}$去更新概率密度函数$p\left( {{{{x}}_k}|{{ z}_{1:k}}} \right)$。

基于信息积累的目标检测算法利用经典的递推贝叶斯滤波的思想，首先将目标状态空间离散化，与式(11)中的观测结果相对应，目标状态在式(12)所示的笛卡尔积中取值。

定义符号${x^{i,j}} \triangleq (i,j)$，当目标状态取值${{{x}}_k} = {x^{i,j}}$时，对应的延时为${t_i}$，多普勒频移为${f_j}$。因此概率密度函数$p\left( {{{{x}}_{k - 1}}|{{{z}}_{1:k - 1}}} \right)$可以用式(13)来表示。

其中，$\delta$函数的定义如式(14)所示

$w_{k{\rm{ - }}1|k - 1}^{i,j}$的取值满足

预测过程，假设目标状态${{{x}}_k}$按照1阶马尔科夫过程变化，${{T}}_{k - 1}^{(m,n) \to (i,j)}$表示目标k–1时刻处于${x^{m,n}}$状态，k 时刻转移到${x^{i,j}}$状态的概率，满足式(16)

若目标匀速运动，则目标信息传递矩阵T与时刻k无关，具有齐次性；若目标非匀速运动，则目标状态变化为非齐次1阶马尔科夫过程，目标信息传递矩阵T_k随时刻k变化，反映目标运动的机动性。获取目标信息传递矩阵T_k有多种灵活的方式，可以根据已知目标的先验信息预先存储，或者按照目标状态空间划分的网格设置多个通道，也可以利用跟踪的信息反馈进行实时更新。

预测过程得到概率密度函数$p\left( {{{{x}}_k}|{{{z}}_{1:k - 1}}} \right)$如式(17)所示。

更新过程，k时刻得到新的观测值${{{z}}_k}$，其中的分量${z^{i,j}}$是相互独立的。若k时刻不存在目标，则$z_k^{i,j}$服从式(19)所示的瑞利分布^[15]。其中${\alpha ^2}$为噪声的方差。

若k时刻存在目标，则$z_k^{i,j}$服从如式(20)所示的莱斯分布^[15]，$A_k^{i,j}({{{x}}_k})$是与目标状态${{{x}}_k}$相关的第$(i,j)$格点的目标幅度。

定义式(21)所示的似然函数

由于每个分量$z_k^{i,j}$是相互独立的，因此观测值${{{z}}_k}$对应的似然函数可以写成式(22)的形式。

根据更新过程的表达式

得到最终的概率密度函数$p\left( {{{{x}}_k}|{{{z}}_{1:k}}} \right)$如式(24)所示。

至此得到了状态变量${{{x}}_k}$的离散概率分布，式(26)所示的信息熵反映了目标状态在$k$时刻的不确定度。

假设初始时刻${{{x}}_0}$为均匀分布，无任何观测数据时目标状态的不确定性最大；随着观测数据的增加，获取到更多关于目标状态的信息，目标状态的不确定性下降，熵值下降。当目标状态的确定度达到一定水平，即熵值下降到一定门限的时候，判定当前时刻存在目标。假设判决门限为${H_{{\rm{thr}}}}$，如果${H_k} < {H_{{\rm{thr}}}}$，判定目标存在；如果${H_k} \ge {H_{{\rm{thr}}}}$，判定目标不存在。

基于信息积累的目标检测方法总结如表1所示。

表  1  基于信息积累的目标检测方法

Table  1.  The method of target detection based on information accumulation

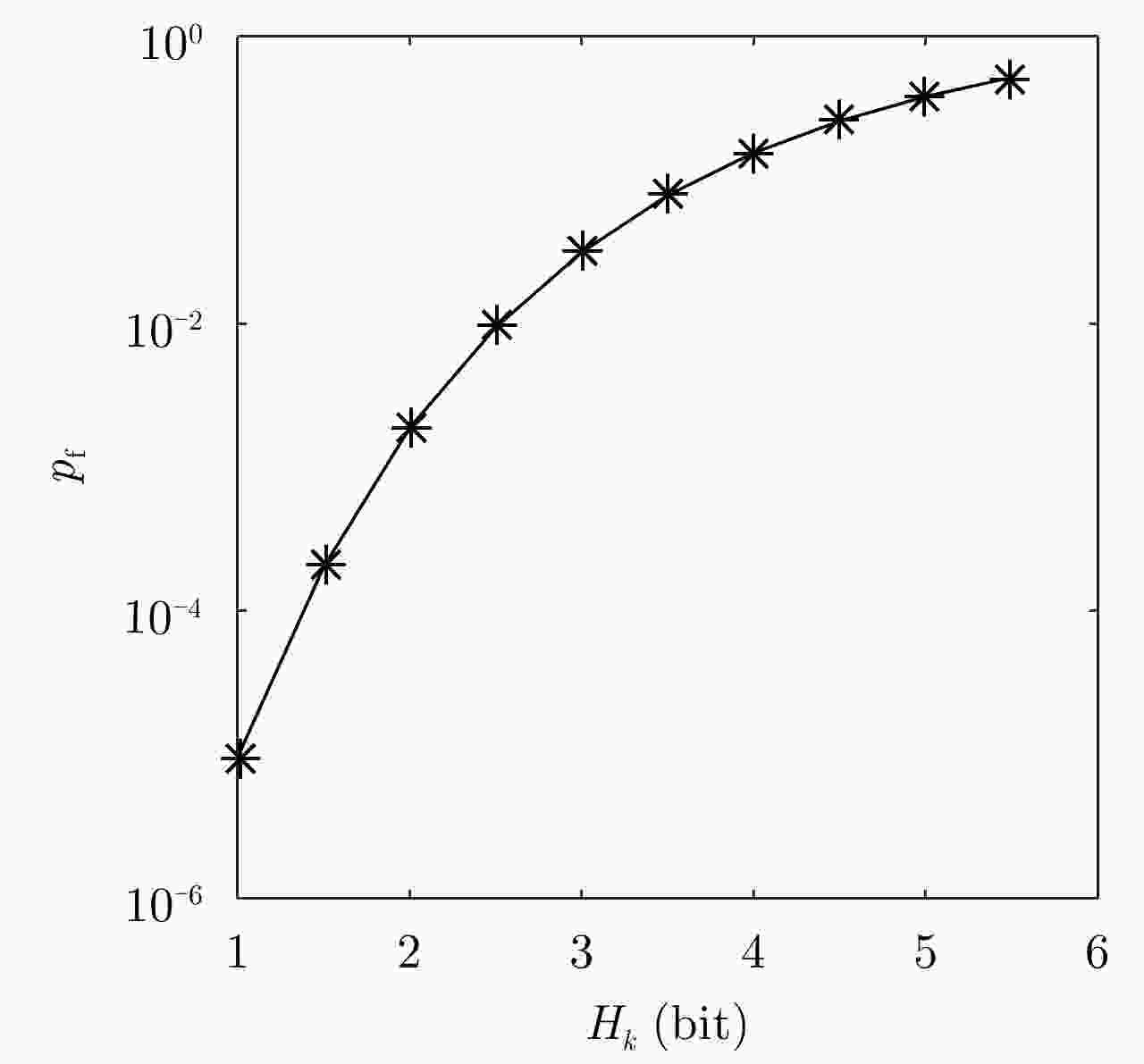
初始化： 　　 $p\left( { { {{x} }_0} } \right) = \displaystyle\sum\limits_{i = 0}^{I - 1} {\displaystyle\sum\limits_{j = 0}^{J - 1} {\frac{1}{ {IJ} } } } \delta \left( { { {{x} }_0} - {x^{i,j} } } \right) \qquad$ 　　${H_0} = - \displaystyle\sum\limits_{i = 0}^{I - 1} {\displaystyle\sum\limits_{j = 0}^{J - 1} {w_{0|0}^{i,j} } } {\log _2}\left( {w_{0|0}^{i,j} } \right) = {\log _2}(IJ)$

对于时刻$k = 1,2,3, ··· ,K$：

获得观测值${ {{z} }_k}$，信息传递矩阵${{ T}_k}$，似然函数$\mathcal{L}\left( {{{{z}}_k}|{{{x}}_k}} \right)$。

预测步，根据式(17)、式(18)预测概率密度函数$p\left( { { {{x} }_k}|{ {{z} }_{1:k - 1} } } \right)$。

更新步，根据式(24)、式(25)更新概率密度函数$p\left( {{{{x}}_k}|{{{z}}_{1:k}}} \right)$。

根据式(26)计算信息熵${H_k}$。

根据${H_k}$进行目标检测，如果${H_k} < {H_{{\rm{thr}}}}$，判定目标存在，目标 　　状态${{{x}}_k} = \arg {\max _{(i,j)}}w_{k|k}^{i,j}$；

如果${H_k} \ge {H_{ {\rm{thr} } } }$，判定目标不存在。

下载: 导出CSV 

| 显示表格

4.   实验结果

4.1   仿真实验

本节实验仿真选择调频广播信号作为外辐射源，利用软件无线电平台接收北京地区载波频率为97.4 MHz的一段调频广播信号，经过解调后得到的基带复信号作为发射信号$s(t)$，采样频率${f_{\rm{s}}} = 200$ kHz。调频广播信号的模糊函数如图2所示，接近于理想的“图钉型”函数，适用于作为目标检测的外辐射源。

图  2  调频广播信号模糊函数

Figure  2.  The ambiguity function of FM broadcast signal

下载: 全尺寸图片 幻灯片

外辐射源的位置${{{x}}_{\rm{e}}} = {({\rm{0, - 75e3,300}})^{\rm{T}}}$m，雷达接收机的位置${{{x}}_{\rm{r}}} = {({\rm{0,0,70}})^{\rm{T}}}$m。

相参积累的时间$T = 0.5$ s，即每一帧对应的时间间隔为0.5 s。将每一帧划分为500个子段，每一个子段对应的时间间隔为1 ms。按照这种处理方式，可以计算出延时单元的个数$I = 200$, ${t_0} = 0$ s。多普勒频移单元的个数$J = 500,$ ${f_0} = - 500$ Hz，对应的频率区间为$[ - 500,500)$ Hz。

(1) 仿真场景1

本场景主要研究虚警概率与信息熵判决门限的关系。总共观测2000帧数据，数据中不包含目标，只包含背景噪声。调整信息熵的判决门限，统计其虚警概率，虚警概率的计算方式为判决目标存在的帧数占总的观测帧数的比例。对每个判决门限都进行200次蒙特卡罗仿真实验，得到的虚警概率${p_{\rm{f}}}$随信息熵判决门限${H_k}$的变化曲线如图3所示。

图  3  虚警概率随判决门限变化曲线

Figure  3.  Relationship of the probability of false alarm and threshold

下载: 全尺寸图片 幻灯片

(2) 仿真场景2

本场景主要对比分析不同算法的运行时间和检测性能。考虑的是单目标直线运动的场景，总共观测50帧数据，目标第1帧开始出现，一直持续到第50帧。目标初始位置位于${(50{\rm{,60,1}})^{\rm{T}}}$ km，保持匀速直线运动，运动速度${{v}} = {( - 180{\rm{, - 120, - 2}})^{\rm{T}}}$ m/s。目标散射截面积按照Swerling I型起伏，均值为10 ${{\rm{m}}^2}$。噪声设置为零均值加性复高斯噪声，调整噪声功率，使得所对应的观测数据的平均信噪比随之变化。

为了对比不同算法的性能，选择文献[10]中介绍的粒子滤波算法，新生粒子数设置为 2000，存活粒子数设置为 2000。除此之外，文献[16]中介绍的动态规划算法以及离散格点贝叶斯滤波算法也用于对比，目标新生概率设置为0.9，目标消亡概率设置为0.1。而作为对比的经典DBT检测算法选择单元平均恒虚警算法(Cell Averaging Constant False-Alarm Rate, CA-CFAR)，参考单元设置为16，保护单元设置为2。

选择各个算法的参数，使得各个算法在不含目标的背景噪声下的虚警概率保持一致，设置为1E-5。然后针对每个信噪比的数据，独立地进行 200 次蒙特卡罗仿真实验，统计各个算法在不同信噪比下的检测概率，检测概率的计算方式为目标被成功检测的帧数占总观测帧数的比例，得到的目标检测概率${p_{\rm{d}}}$随信噪比变化曲线如图4所示。

图  4  目标检测概率随信噪比的变化曲线

Figure  4.  Relationship of the probability of target detection and SNR

下载: 全尺寸图片 幻灯片

平均单帧检测的运行时间对比如表2所示，处理器平台为Intel®Core^TM i7-8750H 型号的12核CPU，主频为2.20 GHz；软件平台为Matlab R2018b。

表  2  多种目标检测算法的运行时间对比

Table  2.  Comparison of running time among multiple target detection algorithms

算法	本文算法	离散格点贝叶斯滤波	动态规划	粒子滤波	CA-CFAR
单帧运行时间(s)	0.016	0.018	1.200	1.102	0.003

下载: 导出CSV 

| 显示表格

由于只对判决为目标存在的帧进行状态估计，因此在对比不同算法的目标位置的估计精度时，只考虑判决为目标存在的所有帧的集合K，而不考虑其他判决为目标不存在的帧。按式(27)统计目标位置估计的均方根误差 (Root Mean Square Error, RMSE)。其中，N为集合K 中元素的个数，${\hat r_k}$为第k帧目标位置的估计值，${r_{k,0}}$为第k帧目标的真实位置。目标位置估计的均方根误差随信噪比的变化曲线如图5所示。

图  5  目标位置估计的均方根误差随信噪比的变化曲线

Figure  5.  Relationship of the RMSE and SNR

下载: 全尺寸图片 幻灯片

对比不同算法的检测结果和运行时间可以看出，传统的跟踪前检测算法运行时间较快，但由于没有信息的积累，只有在单帧的观测信号的信噪比足够高时才能把目标检测出来；相比于跟踪前检测算法，检测前跟踪算法的检测性能得到了一定程度的提升。其中，动态规划算法的检测概率较高，但在低信噪比下的估计精度欠佳；动态规划算法需要对状态空间进行遍历，运行时间比较长，而且批处理的方法会造成检测的滞后；粒子滤波算法的检测和估计性能都比较好，但需要大量的粒子来保证其滤波性能，计算复杂度高，运行时间也比较长；本文所提的基于信息积累的目标检测算法与离散格点贝叶斯滤波算法的检测和估计性能接近，在估计精度和计算效率之间进行了折中，两种算法的估计精度都略差于粒子滤波算法，但同时算法的计算复杂度和运行时间也低于粒子滤波算法，保证了目标检测算法的实时性需求。而另一方面，相比于离散格点贝叶斯滤波算法，本文所提的基于信息积累的目标检测算法避免了对目标存在和目标不存在两种状态之间转移概率的先验建模，实现更为简单。

(3) 仿真场景3

式(20)的计算需要首先估计噪声，然后根据预设目标的信噪比通道去计算目标幅度。本小节考虑预设目标的信噪比通道与实际目标信噪比不匹配的场景，仿真目标的运动参数与仿真场景2一致。匹配情形将信噪比通道预设为仿真目标的信噪比，失配情形将信噪比通道预设为固定值10 dB。选择算法参数使得两种情形下的虚警概率相同，并比较其检测概率和估计精度。检测概率随信噪比的变化曲线如图6所示，目标位置估计精度随信噪比的变化曲线如图7所示。可以看出，当预设的信噪比通道与真实目标的信噪比高6～7 dB时，目标的检测概率与估计精度有略微的下降；而当预设的信噪比通道与真实目标的信噪比的差异在3 dB以内时，失配对目标的检测概率与估计精度几乎不造成影响，说明算法具有一定的鲁棒性。

图  6  目标检测概率随信噪比的变化曲线

Figure  6.  Relationship of the probability of target detection and SNR

下载: 全尺寸图片 幻灯片

图  7  目标位置估计的均方根误差随信噪比的变化曲线

Figure  7.  Relationship of the RMSE and SNR

下载: 全尺寸图片 幻灯片

4.2   实测数据处理

本小节通过对实测数据的处理验证基于信息积累的目标检测算法的有效性，所选用的实测数据来自于实际的基于调频广播信号的外辐射源雷达系统的接收数据。调频广播信号的带宽为80 kHz，系统采样频率f_s = 200 kHz。相干积累的时间T = 1 s，即每一帧对应的时间间隔为1 s；将每一帧划分为1000 个子段，每一个子段对应的时间间隔为1 ms。截取目标附近的距离多普勒结果进行处理，包括100个距离单元，200个多普勒单元，目标的平均信噪比为6 dB，总共观测25 帧数据。

信息熵随时间k变化曲线如图8所示，可以看出目标经过一定时间的信息积累后被成功检测出来。目标的距离和多普勒频移的估计结果分别如图9和图10所示。从目标状态的估计结果可以看出本文所提方法能有效地检测出实测数据中的目标。

图  8  信息熵随时间变化曲线

Figure  8.  Relationship of the information entropy and time

下载: 全尺寸图片 幻灯片

图  9  目标距离的估计结果

Figure  9.  The results of the estimated target range

下载: 全尺寸图片 幻灯片

图  10  目标多普勒频移的估计结果

Figure  10.  The results of the estimated target Doppler frequency

下载: 全尺寸图片 幻灯片

5.   结束语

针对外辐射源雷达系统目标检测的问题，为了简化检测算法的复杂度，提升检测算法的实时性能，本文首先对外辐射源雷达系统的目标状态和观测数据进行了建模分析，然后把目标状态空间离散网格化，在此基础上结合贝叶斯滤波的思想在多帧观测数据之间进行信息的传递和积累，提出基于信息积累的外辐射源目标检测算法，并引入信息熵作为目标是否存在的判决依据，最后通过仿真实验和实测数据处理验证了算法的有效性和高效性。

为简化分析，本文仅仿真了复高斯噪声的情形，未来的工作将针对更复杂的背景杂波下的检测性能作进一步的分析，并将算法扩展到多目标的情形。