基于自适应高程约束的TomoSAR三维成像

任子帅; 张照; 高雨欣; 郭睿

doi:10.12000/JR23111

基于自适应高程约束的TomoSAR三维成像

DOI: 10.12000/JR23111 CSTR: 32380.14.JR23111

任子帅¹,
张照¹,
高雨欣²,
郭睿^1, ,

1.
西北工业大学自动化学院西安 710129
2.
西北工业大学电子信息学院西安 710129

基金项目: 国家自然基金(42104039, 61971326)，陕西省自然科学基础计划项目(2023-JC-QN-0370)

详细信息

作者简介:
任子帅，硕士生，主要研究方向为层析合成孔径雷达三维成像及点云处理

张　照，硕士，主要研究方向为合成孔径雷达干涉测量及层析成像

高雨欣，硕士生，主要研究方向为合成孔径雷达三维成像及雷达定标

郭　睿，博士，副教授，主要研究方向为雷达遥感技术及应用、激光探测技术等

通讯作者:
郭睿 gr2003@nwpu.edu.cn

责任主编：廖明生 Corresponding Editor: LIAO Mingsheng
中图分类号: TN95
计量
- 文章访问数: 788
- HTML全文浏览量: 238
- PDF下载量: 239
- 被引次数: 13
出版历程
- 收稿日期: 2023-06-21
- 修回日期: 2023-08-03
- 网络出版日期: 2023-09-01
- 刊出日期: 2023-10-28

Three-dimensional Imaging of Tomographic SAR Based on Adaptive Elevation Constraint

1.
School of Automation, Northwestern Polytechnical University, Xi’an 710129, China
2.
School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China

Funds: The National Natural Science Foundation of China (42104039, 61971326), Natural Science Basic Research Program of Shaanxi (2023-JC-QN-0370)

More Information

Corresponding author: GUO Rui, gr2003@nwpu.edu.cn

摘要

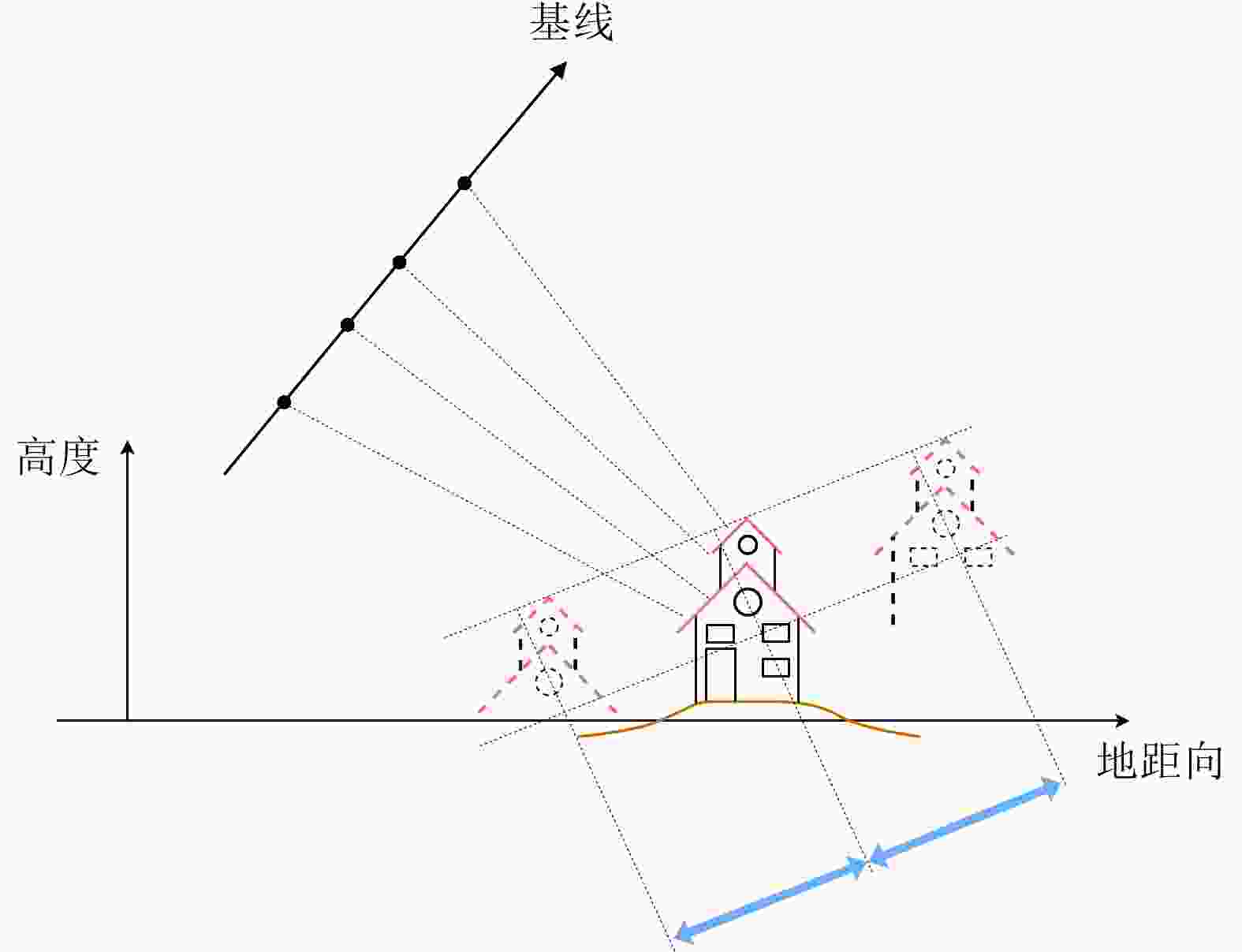
摘要: 层析合成孔径雷达成像(TomoSAR)是2010年以来SAR成像领域尤其是城市三维成像的热门研究方向。但在TomoSAR三维重建中，相位缠绕会引起高程散射剖面的周期性谱峰，并导致散射体高程向位置的错误估计和三维成像结果中建筑点云的分层，即高程模糊。该文针对这一现象，提出一种自适应调整高程搜索范围的方法，以提升散射体高程估计的准确度，并改善高程模糊。该方法首先进行场景的高度预估计，然后根据高度预估计构建高程采样中心线性函数并计算搜索半径，从而确定并更新各像素的高程搜索范围，保留真实谱峰并隔离模糊峰值。机载和星载的实测数据实验表明所提方法明显改善了高程模糊和伪影问题，提高了三维点云的空间集中度和连续性。
- 层析合成孔径雷达成像(TomoSAR) /
- 相位缠绕 /
- 高程模糊 /
- 散射体 /
- 高程搜索范围
Abstract: Synthetic Aperture Radar Tomography (TomoSAR) has emerged as a hot research topic in the field of SAR imaging, particularly for three-dimensional (3D) urban imaging in recent years. However, in TomoSAR 3D reconstruction, due to the phase unwrapping difficulty, periodic spectral peaks appear in the reconstruction results of the reflectivity profile along the elevation. This results in errors in estimating the elevation locations of the scatterers and causing layering effects in 3D imaging results, which is the elevation ambiguity. In light of this phenomenon observed in TomoSAR, a method for the adaptive adjustment of the elevation search range is proposed to improve the accuracy of the elevation estimation and reduce elevation ambiguity. In this method, the height of the scene is first estimated, the linear function of the elevation sampling center is subsequently constructed based on the height pre-estimations, and the search radius is finally calculated. Thereafter, the elevation search range of each pixel in the SAR image is determined and updated, preserving the true spectral peaks while isolating the ambiguity peaks. The experimental results for airborne and spaceborne measured data demonstrate that the proposed method significantly improves elevation ambiguity and artifacts-related issues while also improving the spatial concentration and continuity of 3D point clouds.
- TomoSAR /
- Phase unwrapping /
- Elevation ambiguity /
- Scatterers /
- Elevation sample range

HTML全文

1. 引言

在传统跟踪方法中，目标假设为点目标，只占据一个分辨单元，但随着传感器分辨率的提高，目标将占据多个分辨单元，称该类目标为扩展目标。检测前跟踪算法是低信杂噪比(Signal To Clutter Noise Ratio, SCNR)下对目标进行处理的一种多帧信号积累方法，它使用传感器原始量测数据，并通过多次扫描量测数据的积累来提高信噪比，而粒子滤波(Particle Filter, PF)方法非常适合处理这类问题。Salmond^[1]在2001年第1次明确提出PF-TBD的概念，并将该方法应用于凝视型光电传感器的单目标检测与跟踪处理中。2005年，Rutten^[2]提出了一种针对观测噪声为Rayleigh情形下的PF-TBD算法。TSOU Haiping^[3]提出了基于极大似然估计的扩展目标跟踪算法，研究了目标发生旋转时的跟踪问题。Gilholm K^[4]利用多假设Kalman滤波来实现扩展目标跟踪，并分析了扩展目标中具有空间分布的散射点。Franken D^[5]提出扩展目标模型为对称正定随机矩阵，并用Bayes方法分析和解决该问题。Ling Fan^[6]建立椭圆模型，并在状态向量中加入目标存在变量和目标形状参数。针对雷达扩展目标，吴兆平^[7]利用传感器获得的数据，确立更接近于实际的线性扩展模型，并推导出了扩展模型的似然比函数，同时，对原始的粒子滤波算法进行了优化。为实现隐身扩展目标的检测与跟踪，于洪波^[8,9]将目标强度和空间长度引入状态向量，利用粒子滤波实现目标的跟踪和目标长度的估计。

上述问题只考虑Gaussian噪声下的微弱目标检测问题，没有考虑有杂波的情况。例如，当雷达工作于下视状态时，经过空时自适应(Space-Time Adaptive Processing, STAP)技术抑制杂波后的量测数据除了受噪声影响外还受剩余杂波的影响，使得传统基于噪声假设的量测模型不准确。同时，随着雷达性能的改善，研究者发现地(海)杂波出现了很长的波动，其杂波的统计特性明显偏离高斯分布。当高分辨雷达处于低视角观测时，通过考察地(海)杂波发现^[10–12]，Weibull分布能较好地刻画实际环境中的杂波统计特性。

针对杂波环境下微弱扩展目标的检测与跟踪问题，本文以杆状物体作为研究对象，对距离和方位进行划分，并给出不同区域上含有Weibull杂波的传感器量测模型。利用扩散函数，在点目标的基础上，推导了扩展目标的似然函数以及粒子权重的计算。在状态向量中加入目标存在状态以及目标形状参数，利用粒子滤波算法分别实现扩展目标状态和形状参数的检测和估计。仿真实验表明，杂波环境下基于粒子滤波的微弱扩展目标检测前跟踪算法具有较好的稳定性。

2. 系统模型

2.1 目标状态模型

考虑x-y平面内运动的杆状目标，目标状态转移具有如下形式：

${x_{k + 1}} = f({x_k}) + {v_k}$

(1)

其中，目标的状态 ${x_k} = {\left[ {\begin{array}{*{20}{c}}{{x_k}}&{{{\dot x}_k}}&{{y_k}}&{{{\dot y}_k}}&{{I_k}}&{{l_k}}\end{array}} \right]^{\rm T}}$ , (x_k, y_k), $\left( {{{\dot x}_k},{{\dot y}_k}} \right)$ 分别表示目标中心的位置、速度，I_k, l_k分别表示扩散目标的强度和空间长度，v_k为过程噪声。用E_k对目标存在状态建模，且描述为2态Markov链，定义目标“新生”概率P_b $\buildrel \Delta \over =$ P $\left\{ {{E_k}\!=\! 1|{E_{k - 1}} \!=\! 0} \right\}$ 和“死亡”概率P_d $\buildrel \Delta \over =$ P{E_k=0|E_k–1=1}，其中，E_k=0表示目标不存在，E_k=1表示目标存在，则Markov转换概率矩阵为：

$\phi =\left[ \begin{matrix} 1-{{P}_{b}} &{{P}_{b}} \\ {{P}_{d}} &1-{{P}_{d}} \\ \end{matrix} \right]$

(2)

2.2 量测模型

考虑经过脉冲压缩处理后的雷达距离-多普勒量测数据。假设距离和方位分别包含N_r和N_a个单元，距离和方位的分辨率分别为D_r和D_a，用 $\varOmega$ $\ \ \buildrel \Delta \over = \ \$ $\left\{ {1,2, \cdots ,{N_{\rm r}}} \right\}$ 和K $\buildrel \Delta \over =$ $\left\{ {1,2, \cdots ,{N_{\rm a}}} \right\}$ 来表示距离和方位上的分辨单元集合。对于距离向^[13]，由于目标的扩展，目标回波所占距离单元表示如下：

$\begin{aligned}{\varOmega _{\rm T}} = & \left\{ {\left\lceil {\frac{{{r_k} - L\left( {{x_k}} \right)/2}}{{{\varDelta _{\rm{r}}}}}} \right\rceil , \cdots ,\left\lceil {\frac{{{r_k}}}{{{\varDelta _{\rm{r}}}}}} \right\rceil , \cdots ,} \right.\\& \left. {\left\lceil {\frac{{{r_k} + L\left( {{x_k}} \right)/2}}{{{\varDelta _{\rm{r}}}}}} \right\rceil } \right\}\end{aligned}$

(3)

其中， $\left\lceil X \right\rceil$ 表示向上求整， ${r_k} = \sqrt {x_k^2 + y_k^2}$ , $L\left( {{x_k}} \right)$ 表示目标距离向长度。

对于方位向，目标回波所占的方位单元表示如下：

$\begin{aligned}{K_T} = & \left\{ {\left\lceil {\frac{{{a_k} - V\left( {{x_k}} \right)/2}}{{{\varDelta _{\rm{r}}}}}} \right\rceil , \cdots ,\left\lceil {\frac{{{a_k}}}{{{\varDelta _{\rm{a}}}}}} \right\rceil , \cdots ,} \right.\\& \left. {\left\lceil {\frac{{{a_k} + V\left( {{x_k}} \right)/2}}{{{\varDelta _{\rm{a}}}}}} \right\rceil } \right\}\end{aligned}$

(4)

其中， ${a_k} = \arctan\left( {{y_k}/{x_k}} \right)$ , V(x_k)表示目标方位向长度。

假设雷达在相同扫描区域已经产生多帧距离-多普勒图像，z_k(i, j)表示k时刻量测数据，具体形式为：

${{z}_{k}}\left( i,j \right)=\left\{ \begin{array}{*{35}{l}} \begin{array}{*{35}{l}} {{v}_{k}}\left( i,j \right)+{{n}_{k}}\left( i,j \right),i\in \Omega ,j\in K, \\ {{E}_{k}}=0 \\ \end{array} \\ \begin{array}{*{35}{l}} {{h}_{k}}\left( i,j \right)+{{v}_{k}}\left( i,j \right)+{{n}_{k}}\left( i,j \right),i\in {{\Omega }_{T}},j\in {{K}_{T}}, \\ {{E}_{k}}=1 \\ \end{array} \\ \begin{array}{*{35}{l}} {{v}_{k}}\left( i,j \right)+{{n}_{k}}\left( i,j \right),i\in \Omega \backslash {{\Omega }_{T}},j\in K\backslash {{K}_{T}}, \\ {{E}_{k}}=1 \\ \end{array} \\ \end{array} \right.$

(6)

式中， $i = 1,2, \cdots ,{N_{\rm r}},j = 1,2, \cdots ,{N_{\rm a}}$ , h_k(i, j)为目标在分辨单元(i, j)处的信号，n_k(i, j)表示在(i, j)处的杂波，v_k(i, j)为量测噪声，假设为零均值、方差为 $2{\sigma ^2}$ 的复高斯噪声。h_k(i, j)表示散射点对分辨单元(i, j)的强度影响，一般情况下h_k(i, j)可近似为2维高斯分布形式^[14,15]，则散射点在传感器分辨单元(i, j)的强度影响为^[7]：

$\begin{aligned}{h_k}\left( {i,j} \right) \approx & \frac{{{\varDelta _{\rm r}}{\varDelta _{\rm a}}{I_k}}}{{2 {π} {{{Σ} \;\!}^2}}}\\& \cdot \exp \left\{ { - \frac{{{{\left( {i{\varDelta _{\rm r}} - {x_k}} \right)}^2} + {{\left( {j{\varDelta _{\rm a}} - {y_k}} \right)}^2}}}{{2{{{Σ} \;\!}^2}}}} \right\}\end{aligned}$

(6)

其中 ${Σ}$ 为已知参数，表示传感器模糊斑点数量。k时刻的量测数据可表示为 ${z_k} = \{ {z_k}(i,j),i = 1, ·\!·\!· ,$ ${N_{\rm r}},j = 1, ·\!·\!· ,{N_{\rm a}}\}$ ，直到k时刻的完整量测数据集合表示为 ${Z_k} = \left\{ {{z_i},i = 1, ·\!·\!· ,k} \right\}$ 。

在实际雷达环境中，存在许多地物、海和云雨等各种杂波，经研究表明^[12]，Weibull分布在一定程度内可以与实际杂波吻合。因此，设 $\left| {n_k^{\left( {i,j} \right)}} \right|$ 符合以下Weibull分布，即

$\begin{aligned}p\left( x \right) = & \frac{p}{q}{\left( {\frac{x}{q}} \right)^{p - 1}}\exp \left[ { - {{\left( {\frac{x}{q}} \right)}^p}} \right],\\& x \ge 0,\ p > 0,\ q > 0\end{aligned}$

(7)

其中，p为形状参数，q为尺度参数。

3. 杂波环境下扩展目标的PF-TBD算法

设 ${z'\!\!_k}\left( {i,j} \right) = \left| {{h_k}\left( {i,j} \right) + {v_k}\left( {i,j} \right)} \right|$ 表示信号加噪声幅度，对于分辨单元(i, j)，当E_k=1时， ${z'\!\!_k}\left( {i,j} \right)$ 近似服从非中心的2阶卡方分布，即

$\begin{aligned} & \!\!\!\!\!\!\!\!\!\!\!\!\!\! p\left( {{{z'}\!\!_k}\left( {i,j} \right)|{x_k},{E_k} = 1} \right)\\ = & \frac{1}{{{\sigma ^2}}}\exp \left( { - \frac{{{{z'}\!\!_k}\left( {i,j} \right) + {h_k}\left( {i,j} \right)}}{{{\sigma ^2}}}} \right)\\& \cdot {I_0}\left( {\frac{{2\sqrt {{{z'}\!\!_k}\left( {i,j} \right){h_k}\left( {i,j} \right)} }}{{{\sigma ^2}}}} \right)\end{aligned}$

(8)

当E_k=0时，分辨单元(i, j)内信号的幅度近似服从瑞利分布^[13]，即

$p\left( {z}'{{}_{k}}\left( i,j \right)|{{E}_{k}}=0 \right)=\frac{\left| {z}'{{}_{k}}\left( i,j \right) \right|}{{{\sigma }^{2}}}\exp \left( -\frac{{{\left| {z}'{{}_{k}}\left( i,j \right) \right|}^{2}}}{2{{\sigma }^{2}}} \right)$

(9)

在目标存在时，考虑Weibull杂波因子，量测值z_k(i, j)的幅度服从非中心卡方分布与Weibull的混合分布，借用文献[16]的思想，根据混合概率密度公式

$f\left( y \right) = \rho {f_0}\left( {y,{\lambda _0}} \right) + \left( {1 - \rho } \right){f_1}\left( {y,\theta } \right),\ y > 0$

(10)

得到似然函数：

$\begin{aligned}& \!\!\!\!\!\!\!\!\!\!\!\! p\left( {\left| {{z_k}\left( {i,j} \right)} \right|\left| {{x_k},{E_k} = 1} \right.} \right)\\ = & \rho \frac{1}{{{\sigma ^2}}}\exp \left( { - \frac{{\left| {{z_k}\left( {i,j} \right)} \right| + {h_k}\left( {i,j} \right)}}{{{\sigma ^2}}}} \right)\\& \cdot {I_0}\left( {\frac{{2\sqrt {\left| {{z_k}\left( {i,j} \right)} \right|{h_k}\left( {i,j} \right)} }}{{{\sigma ^2}}}} \right)\\ & + \left( {1 - \rho } \right)\frac{p}{q}{\left( {\frac{{\left| {{z_k}\left( {i,j} \right)} \right|}}{q}} \right)^{{{p - 1}}}}\\ & \cdot \exp \left[ { - {{\left( {\frac{{\left| {{z_k}\left( {i,j} \right)} \right|}}{q}} \right)}^p}} \right]\end{aligned}$

(11)

同上，当E_k=0时，量测值z_k(i, j)的幅度服从瑞利分布与Weibull分布的混合分布，则相应的似然函数为：

$\begin{aligned}& \!\!\!\!\!\!\!\!\!\!\!\!\! p\left( {\left| {{z_k}\left( {i,j} \right)} \right|\left| {{E_k} = 0} \right.} \right)\\ = & \kappa \frac{{\left| {{z_k}\left( {i,j} \right)} \right|}}{{{\sigma ^2}}}\exp \left( { - \frac{{{{\left| {{z_k}\left( {i,j} \right)} \right|}^2}}}{{2{\sigma ^2}}}} \right)\\ & + \left( {1 - \varepsilon } \right)\frac{p}{q}{\left( {\frac{{\left| {{z_k}\left( {i,j} \right)} \right|}}{q}} \right)^{{{p - 1}}}}\\& \cdot \exp \left[ { - {{\left( {\frac{{\left| {{z_k}\left( {i,j} \right)} \right|}}{q}} \right)}^p}} \right]\end{aligned}$

(12)

式中， $\rho$ 和 $\varepsilon$ 为比例系数( $\rho \in \left[ {0,1} \right],\varepsilon \in \left[ {0,1} \right]$ )。

随着雷达分辨率的提高，目标的物理尺寸大于距离分辨率，这样就会引起目标在距离和方位上的线性扩展，则扩展目标的似然函数为^[17]：

$p\left( {{z_k}|{x_k},{E_k} = 1} \right) = \int {p\left( {{z_k}|\hat x,{E_k} = 1} \right)p\left( {{{\hat x}_k}|{x_k}} \right){\rm{d}}{{\hat x}_k}}$

(13)

其中，x_k为中心点， ${\hat x_k}$ 为扩展点； $p\left( {{{\hat x}_k}|{x_k}} \right)$ 表示从点x_k扩展到 ${\hat x_k}$ 的概率密度函数。

目标在距离和方位角发生2维线性扩展。设线性扩展目标长度为N_z，扩展目标的方向与观察者视线方向的夹角为 $\theta$ ，则目标扩展后的坐标范围^[7]为：

$\begin{aligned}& \left( {\left[ {{l_k} - 0.5{N_z}\tan \theta ,{l_k} + 0.5{N_z}\tan \theta } \right],} \right.\\& \quad\quad\ \left. {\left[ {{d_k} - 0.5{N_z}\cos \theta ,{d_k} + 0.5{N_z}\cos \theta } \right]} \right)\end{aligned}$

(14)

其中，(l_k, d_k)表示扩展目标的中心位置。根据以上条件，则其似然函数为：

$\begin{align} & p\left( {{z}_{k}}|{{x}_{k}},{{E}_{k}}=1 \right)=\int_{-{{n}_{z}}/2}^{{{n}_{z}}/2}{p\left( {{z}_{k}}|{{x}_{k}},{{E}_{k}}=1 \right)p\left( {{{\hat{x}}}_{k}}|{{x}_{k}} \right)\text{d}{{{\hat{x}}}_{k}}} \\ & =\frac{1}{{{n}_{z}}}\int_{-{{n}_{z}}/2}^{{{n}_{z}}/2}{\left( \rho \frac{1}{{{\sigma }^{2}}}\exp \left( -\frac{{{z}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right)+{{h}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right)}{{{\sigma }^{2}}} \right) \right.} \\ & \cdot {{I}_{0}}\left( \frac{2\sqrt{{{z}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right){{h}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right)}}{{{\sigma }^{2}}} \right) \\ & +\left( 1-\rho \right)\frac{p}{q}{{\left( \frac{{{z}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right)}{q} \right)}^{p-1}} \\ & \left. \cdot \exp \left[ -{{\left( \frac{{{z}_{k}}\left( i-u\tan \theta ,j-u\cos \theta \right)}{q} \right)}^{p}} \right] \right)\text{d}u \\ \end{align}$

假设各个(i, j)内的z_k^{(i, j)}是独立的，似然函数可表示为：

$\begin{aligned} & \!\!\!\!\!\!\!\!\!\!\!\! p\left( {\left| {{z_k}} \right||{x_k},{E_k} = 1} \right)\\ \approx & \prod\limits_{i \in {C_i}\left( {{{x}_k}} \right)} {\prod\limits_{j \in {C_{j}}\left( {{x_k}} \right)} p } \left( {\left| {{z_k}\left( {i,j} \right)} \right|{x_k},{E_k} = 1} \right)\\& {\; \cdot \prod\limits_{i \notin {C_{i}}\left( {{{x}_k}} \right)} {\prod\limits_{j \notin {C_{j}}\left( {{x_k}} \right)} p } \left( {\left| {{z_k}\left( {i,j} \right)} \right|{x_k},{E_k} = 0} \right)}\end{aligned}$

(16)

$p\left( {\left| {{z_k}} \right||{E_k} = 0} \right) = \mathop \prod \limits_{i = 1}^{{N_\rm{r}}} \mathop \prod \limits_{j = 1}^{{N_{\rm a}}} p\left( {\left| {{z_k}\left( {i,j} \right)} \right||{E_k} = 0} \right)$

(17)

式中，C_i(x_k)和C_j(x_k)表示(i, j)内受回波影响的集合。

假设该模型中扩展目标每一时刻仅有限个回波(散射点)时^[18]，设散射点个数为M时，则有：

$p\left( {{z_k}|{x_k},{E_k} = 1} \right) \approx \frac{1}{M}\sum\limits_{i = 1}^M {p\left( {{z_k}|x_k^{\left( {i} \right)}} \right)}$

(18)

其中，x_k⁽ⁱ⁾表示在某一时间k相互独立的散射点。

$\begin{aligned}& \!\!\!\!\!\!\!\!\!\!\!\!\! p\left( {{z_k}|{x_k},{E_k} = 1} \right)\\ = & \sum\limits_{r = 0}^{n - 1} {\left( {\rho \frac{1}{{{\sigma ^2}}}\exp \left( { - \frac{{{z_k}\left( {i - {t_{r}}\tan \theta ,j - {t_{r}}\cos \theta } \right) + {h_k}\left( {i - {t_{r}}\tan \theta ,j - {t_r}\cos \theta } \right)}}{{{\sigma ^2}}}} \right)} \right.} \\& \cdot {I_{\rm{0}}}\left( {\frac{{2\sqrt {{z_k}\left( {i - {t_r}\tan \theta ,j - {t_r}\cos \theta } \right){h_k}\left( {i - {t_r}\tan \theta ,j - {t_{\mathop{ r}\nolimits} }\cos \theta } \right)} }}{{{\sigma ^2}}}} \right)\\& + \left( {1 - \rho } \right)\frac{p}{q}{\left( {\frac{{{z_k}\left( {i - {t_{r}}\tan \theta ,j - {t_{r}}\cos \theta } \right)}}{q}} \right)^{p - 1}}\\& \left. { \cdot \exp \left[ { - {{\left( {\frac{{{z_k}\left( {i - {t_{r}}\tan \theta ,j - {t_{r}}\cos \theta } \right)}}{q}} \right)}^p}} \right]} \right)\left( {{x_{{r} + 1}} - {x_{r}}} \right)\end{aligned}$

(19)

定义似然比为：

$L\left( {\left| {{z_k}} \right||x_k^{n},{E_k} = 1} \right) = \frac{{p\left( {\left| {{z_k}} \right||x_k^n,{E_k} = 1} \right)}}{{p\left( {\left| {{z_{k}}} \right||{E_{k}} = 0} \right)}}$

(20)

$\!\!\!\!\!\! L\left( {\left| {{z_k}} \right||{E_k} = 0} \right) = \frac{{p\left( {\left| {{z_k}} \right||{E_k} = 0} \right)}}{{p\left( {\left| {{z_k}} \right||{E_k} = 0} \right)}} = 1$

(21)

因此，对状态为 $x_k^n$ 的目标，将式(8)、式(19)代入式(20)、式(21)中，可以计算出未归一化权重 $\tilde \omega _k^{n}$ 。

下面给出PF-TBD算法^[19]。首先，引入混合状态向量 ${y_k} = {\left[ {x_k^{\rm T} {E_k}} \right]^{\rm{T}}}$ 。设在k–1时刻的联合PDF为 $p\left( {{y_{k - 1}}|{Z_{k - 1}}} \right)$ 可由粒子集 $\left\{ {y_{k - 1}^n,\omega _{k - 1}^n} \right\}_{n = 1}^N$ 来描述，N为粒子数量。则该算法运算步骤如下所示：

$\left[ {\left\{ {y_k^n} \right\}_{n\rm{ = 1}}^N} \right] = {\rm PF} - {\rm TBD}\left[ {\left\{ {y_{k\rm{ - 1}}^n} \right\}_{n\rm{ = 1}}^N,{z_k}} \right]$

(22)

步骤1 计算目标的存在变量 $\left[ {\left\{ {E_k^n} \right\}_{n\rm{ = 1}}^N} \right]$ 目标存在变量转移 $\left[ {\left\{ {E_{{k - 1}}^{n}} \right\}_{n\rm{ = 1}}^N,\varPhi } \right]$ ；

步骤2 从X_kⁿ中抽取M个散射点：

$\left\{ {\chi _{k}^{{n,m}}} \right\}_{m\rm{ = 1}}^M \sim \psi \left( {{\chi _{k}}|X_k^n} \right)$

(23)

步骤3 FOR n=1:N

(1) 对“新生”(即 $E_{{k - 1}}^n = 0,E_k^n = 1$ )粒子采样 $x_k^n \sim {p_\rm{b}}\left( {{x_k}|{z_k}} \right)$ ；

(2) 对“存活”(即 $E_{k\rm{ - 1}}^n = 1,E_k^n = 1$ )粒子采样 $x_k^n \sim p\left( {{x_k}|x_{k\rm{ - 1}}^n} \right)$ ；

(3) 计算权重 $\tilde \omega _k^n$ ；

步骤4 用 $x_k^n \sim {p_\rm{b}}\left( {{x_k}{|}{z_k}} \right)$ 替换权重比较低的 $x_k^n \sim p\left( {{x_k}|x_{k\rm{ - 1}}^n} \right)$ ，并计算相应的权重；

步骤5 归一化粒子权重， $\left\{ \omega _{k}^{n}=\tilde{\omega }_{k}^{n}/\sum\limits_{n=1}^{N}{\tilde{\omega }_{k}^{n}} \right\}_{n=1}^{N}\text{ }$ ；

步骤6 粒子重采样， $\left[ {\left\{ {y_k^n,1/N} \right\}_{n\rm{ = 1}}^N} \right]$ =重采样 $\left[ {\left\{ {y_k^n,\omega _k^n} \right\}_{n\rm{ = 1}}^N} \right]$ 。

目标在k时刻后验PDF为P_k $\buildrel \wedge \over =$ P{E_k=1|Z_k}，因此

${\hat P_k} = \sum\limits_{n = 1}^N {{{E_k^n} / {N, \ \ 0 \le }}} \hat P \le 1$

(24)

估计目标状态为：

${\hat x_k} = \sum\limits_{n = 1}^N {\left( {x_k^nE_k^n} \right) \biggr/ \sum\limits_{n = 1}^N {E_k^n} }$

(25)

4. 仿真实验

本节将通过仿真实验来说明在杂波环境下基于粒子滤波的雷达扩展目标TBD算法的有效性。假设目标的运动方程为：

${{x}_k} = {F}{{x}_{k - 1}} + {{w}}_{k - 1}$

(26)

其中，

${F} = \left[ {\begin{array}{*{20}{c}}1&1&0&0&0&0\\0&1&0&0&0&0\\0&0&1&1&0&0\\0&0&0&1&0&0\\0&0&0&0&1&0\\0&0&0&0&0&1\end{array}} \right]$

(27)

目标在x-y平面内做匀速直线运动，w_k–1为零均值Gaussian噪声，其协方差Q为：

${Q} = \left[ {\begin{array}{*{20}{c}}{\frac{{{q_1}}}{3}{T^\rm{3}}}&{\frac{{{q_1}}}{2}{T^2}}&0&0&0&0\\{\frac{{{q_1}}}{2}{T^2}}&{{q_1}T}&0&0&0&0\\0&0&{\frac{{{q_1}}}{3}{T^3}}&{\frac{{{q_1}}}{2}{T^2}}&0&0\\0&0&{\frac{{{q_1}}}{2}{T^2}}&{{q_1}T}&0&0\\0&0&0&0&{{q_2}T}&0\\0&0&0&0&0&{{q_3}T}\end{array}} \right]$

(28)

其中，q₁和q₂分别表示运动和强度的过程噪声方差。设置q₁=0.001, q₂=0.01, q₃=0.01设置T为1 s。其他相关参数设置为D_x=D_y=1, ${\Large\varSigma} = 0.9$ , ${N_\rm{r}} = {N_\rm{a}} = 20$ , ${\alpha _{m}} = 0.3$ ，观测噪声方差为 ${\sigma ^2} = 1$ 。取 ${{x}_\rm{1}} = {\left[ {\begin{array}{*{20}{c}}0&1&2&0&I\end{array}} \right]^\rm{T}}$ ，在整个跟踪过程中，共有32帧。其中，第7到25帧时E_k=1，共19帧，而杂波和噪声从第1帧到第32帧一直存在。信杂噪比计算公式为：

${\rm SCNR} = \frac{S}{{V + C}}$

(29)

其中，S为信号功率，C为杂波功率，V为噪声功率。

图1模拟了散射点模型。根据散射点状态可知，从状态点到扩散点满足均匀分布。在图中，为了清楚地体现扩散效果，围绕着中心点取了8个扩散点。

图 1 目标散射点

Figure 1. Target scatter point

下载: 全尺寸图片幻灯片

图2给出了扩展目标在x-y平面上的运动轨迹，其中x轴、y轴只是相对值。在整个过程中，目标做匀速直线运动。目标的初始位置为(10, 2)，设设杆长l为2，即占据2个分辨率单元。

图 2 扩展目标真实航迹图

Figure 2. Real track of extended target

下载: 全尺寸图片幻灯片

滤波参数设置为：目标的p_b和p_d都取为0.1，初始存在概率 ${\mu _1}$ =0.05，信号强度门限 $\gamma$ =0.5, v_max=1, I_min=5, I_max=50, p=2。

图3是不同SCNR下扩展目标的平均存在概率图，设置门限为0.5，即目标的平均概率超过0.5，认为能够检测到目标，否则相反。从整体上来看，SCNR=3 dB, 6 dB, 9 dB和12 dB均能够检测到目标存在。SCNR=12 dB能够准确检测出目标出现时刻和消失时刻。SCNR=9 dB在目标出现时有2个时刻延迟，但能够准确检测到目标消失时刻。SCNR=3 dB, 6 dB时在目标出现时有2个时刻延迟，而目标消失时刻则有1个延时。

图 3 目标的平均存在概率

Figure 3. Average existence probability of target

下载: 全尺寸图片幻灯片

从图4可以看出，在目标开始出现时，不同SCNR下，误差都比较大，但经过几个时刻后，误差趋于稳定，但仍有一些波动。比较这4种不同情况，SCNR=3 dB的误差最大，这是比较符合实际情况。

图 4 目标位置的RMSE

Figure 4. RMSE of target position

下载: 全尺寸图片幻灯片

图5是目标长度的随时间变化的RMSE，从图中可以看出，目标刚出现时，误差比较大，随着时间的积累，误差逐渐减少。比较不同SCNR下的误差值，可以得出，SCNR=12 dB时，误差最小，也比较平缓，SCNR=3 dB估计值不太理想，误差一直居高不小。SCNR=6 dB和SCNR=9 dB时，误差均可以接受。

图 5 目标长度的RMSE

Figure 5. RMSE of target length

下载: 全尺寸图片幻灯片

5. 总结

针对杂波环境下的雷达扩展目标检测前跟踪问题，采用了含有Weibull杂波分布的杆状量测模型，运用散射点函数，推导出扩展目标的似然函数和粒子权重。基于粒子滤波，抽样得到散射点集合。实验结果表明，Weibull杂波环境下PF-TBD算法具有较好的稳定性。

图 1 TomoSAR三维成像几何模型

Figure 1. TomoSAR 3D geometric model

下载: 全尺寸图片幻灯片

图 2 高程向的伪目标示意图

Figure 2. Pseudo target in the elevation

下载: 全尺寸图片幻灯片

图 3 仿真数据1的高程散射剖面反演结果

Figure 3. Reconstruction results of elevation reflectivity profile of the first simulation data

下载: 全尺寸图片幻灯片

图 4 仿真数据2的高程散射剖面反演结果

Figure 4. Reconstruction results of elevation reflectivity profile of the second simulation data

下载: 全尺寸图片幻灯片

图 5 自适应高程搜索范围方法流程图

Figure 5. The flowchart of adaptive elevation search range method (blue: The boundary before constraints; red: Boundaries after constraints; yellow: Elevation sampling center)

下载: 全尺寸图片幻灯片

图 6 峨眉区域的Google Earth光学图和SAR幅度图

Figure 6. Google Earth optical map and SAR amplitude map of Emei area

下载: 全尺寸图片幻灯片

图 7 峨眉数据的三维重建结果

Figure 7. 3D reconstruction results of Emei data

下载: 全尺寸图片幻灯片

图 8 峨眉数据的散射剖面反演结果

Figure 8. Inversion results of scattering profile from Emei data

下载: 全尺寸图片幻灯片

图 9 不同高度估计下的平均邻域高度差和散射体完整度

Figure 9. $\Delta {h_{\text{E}}}$ and C at different height estimation

下载: 全尺寸图片幻灯片

图 10 巴塞罗那区域的Google Earth光学图和SAR幅度图

Figure 10. Google Earth optical map and SAR amplitude map of Barcelona area

下载: 全尺寸图片幻灯片

图 11 巴塞罗那数据的三维重建结果

Figure 11. 3D reconstruction results of Barcelona data

下载: 全尺寸图片幻灯片

图 12 所选像素的CS高程稀疏反演

Figure 12. Sparse inversion on elevation by CS of the selected pixel

下载: 全尺寸图片幻灯片

表 1 仿真实验1参数

Table 1. Experimental parameters for the first simulation data

参数	数值	参数	数值
通道数	11	波长	0.02 m
基线跨度	1 m	下视角	45°
最小基线间隔	0.1 m	高程模糊间隔	100 m
斜距	1000 m	高程瑞利分辨率	10 m

下载: 导出CSV

表 2 仿真实验2参数

Table 2. Experimental parameters for the second simulation data

参数	数值	参数	数值
航过数	11	波长	0.03 m
基线跨度	450 m	下视角	45°
最小基线间隔	21 m	最大不模糊高程	428.6 m
斜距	600 km	高程瑞利分辨率	20 m

下载: 导出CSV

表 3 峨眉数据参数

Table 3. Parameters of Emei data

参数	数值
载波频率	14.5 GHz
最小基线间隔	0.1115 m
最大基线长度	1.1274 m
载机航线海拔	2157 m
场景海拔	420 m
中心斜距	2040.1 m
中心下视角	31.6°
距离向像素尺寸	0.1362 m
方位向像素尺寸	0.1051 m

下载: 导出CSV

表 4 峨眉数据的平均邻域高度差(m)

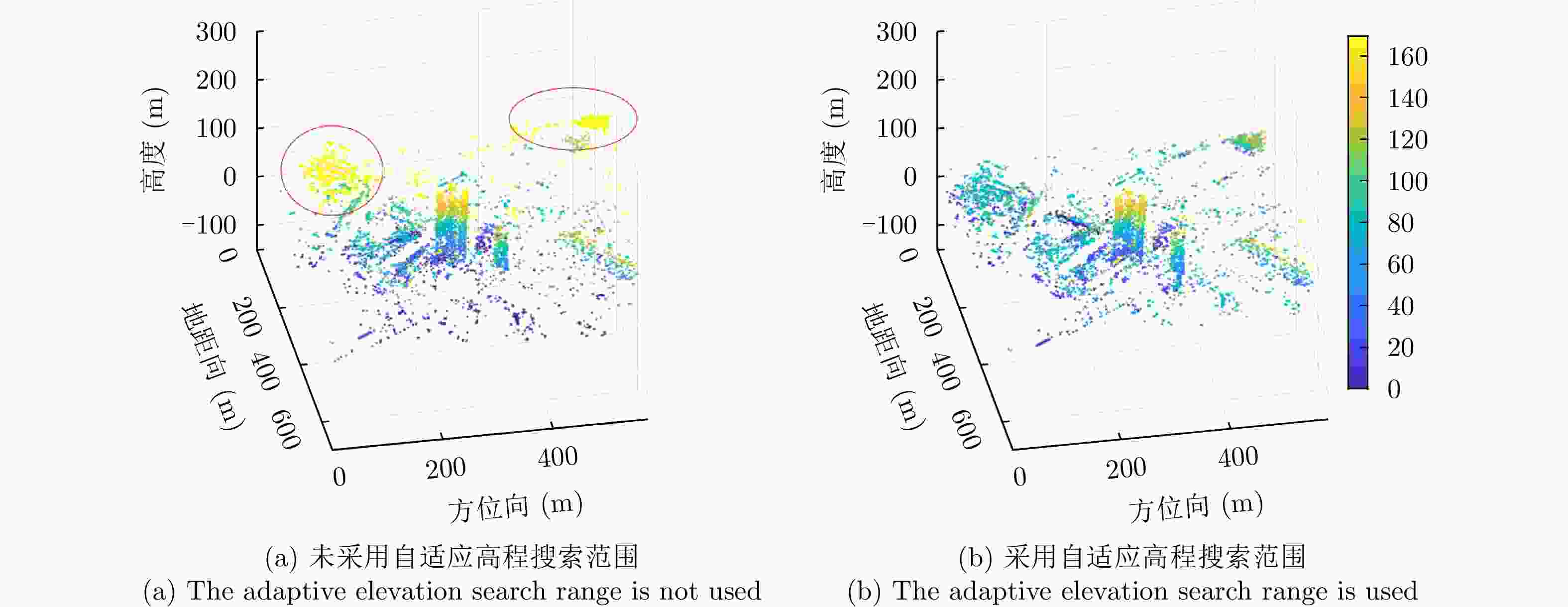
Table 4. $\Delta {{\boldsymbol{h}}_{\bf{E}}}$ of Emei data (m)

未采用自适应高程搜索范围 $\Delta {h_{\text{E}}}$	采用自适应高程搜索范围 $\Delta {h_{\text{E}}}$
12.6512	7.5453

下载: 导出CSV

表 5 巴塞罗那数据参数

Table 5. Parameters of Barcelona data

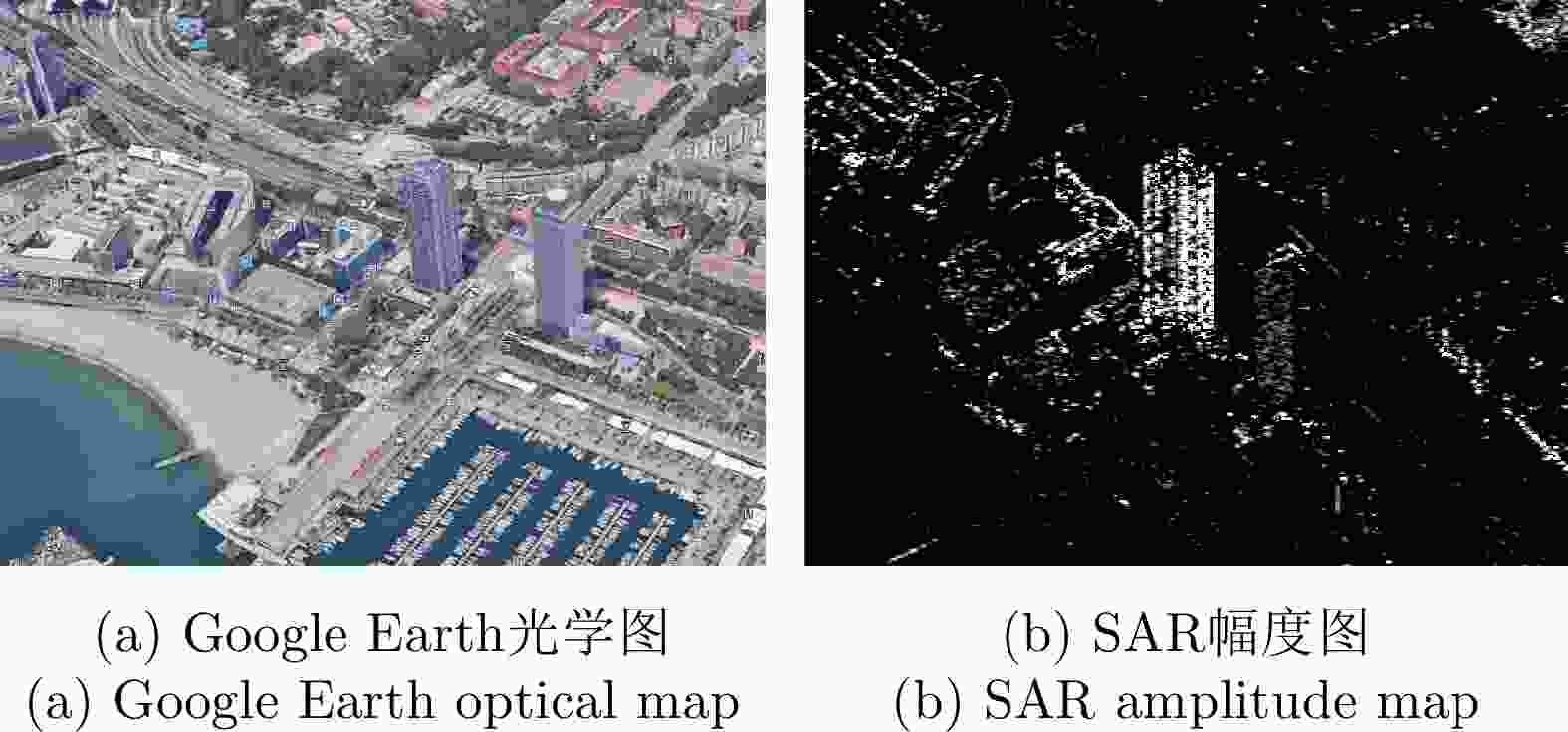
参数	数值
载波频率	9.65 GHz
最小基线间隔	7.98 m
最大基线长度	246.4 m
中心斜距	621.6 km
中心下视角	35.7°
距离向像素尺寸	0.91 m
方位向像素尺寸	1.88 m

下载: 导出CSV

表 6 巴塞罗那数据的平均邻域高度差(m)

Table 6. $\Delta {{\boldsymbol{h}}_{\mathbf{E}}}$ of Barcelona data (m)

未采用自适应高程搜索范围 $\Delta {h_{\text{E}}}$	采用自适应高程搜索范围 $\Delta {h_{\text{E}}}$
22.5561	14.3084

下载: 导出CSV

参考文献(32)

[1]	MUNSON D C, O’BRIEN J D, and JENKINS W K. A tomographic formulation of spotlight-mode synthetic aperture radar[J]. Proceedings of the IEEE, 1983, 71(8): 917–925. doi: 10.1109/PROC.1983.12698
[2]	张斌, 韦立登, 胡庆荣, 等. 基于四阶累积量的机载多基线SAR谱估计解叠掩方法[J]. 雷达学报, 2018, 7(6): 740–749. doi: 10.12000/JR18087 ZHANG Bin, WEI Lideng, HU Qingrong, et al. Solution to layover problemin airborne multi-baseline SAR based on spectrum estimation with fourth-order cumulant[J]. Journal of Radars, 2018, 7(6): 740–749. doi: 10.12000/JR18087
[3]	丁赤飚, 仇晓兰, 徐丰, 等. 合成孔径雷达三维成像——从层析、阵列到微波视觉[J]. 雷达学报, 2019, 8(6): 693–709. doi: 10.12000/JR19090 DING Chibiao, QIU Xiaolan, XU Feng, et al. Synthetic aperture radar three-dimensional imaging—from TomoSAR and array InSAR to microwave vision[J]. Journal of Radars, 2019, 8(6): 693–709. doi: 10.12000/JR19090
[4]	FORNARO G, SERAFINO F, and SOLDOVIERI F. Three-dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507–517. doi: 10.1109/TGRS.2003.809934
[5]	REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873
[6]	FORNARO G, LOMBARDINI F, PAUCIULLO A, et al. Tomographic processing of interferometric SAR data: Developments, applications, and future research perspectives[J]. IEEE Signal Processing Magazine, 2014, 31(4): 41–50. doi: 10.1109/MSP.2014.2312073
[7]	张红, 江凯, 王超, 等. SAR层析技术的研究与应用[J]. 遥感技术与应用, 2010, 25(2): 282–287. doi: 10.11873/j.issn.1004-0323.2010.2.282 ZHANG Hong, JIANG Kai, WANG Chao, et al. The current status of SAR tomography[J]. Remote Sensing Technology and Application, 2010, 25(2): 282–287. doi: 10.11873/j.issn.1004-0323.2010.2.282
[8]	EL MOUSSAWI I, MINH D H T, BAGHDADI N, et al. L-band UAVSAR tomographic imaging in dense forests: Gabon forests[J]. Remote Sensing, 2019, 11(5): 475. doi: 10.3390/rs11050475
[9]	EL MOUSSAWI I, MINH D H T, BAGHDADI N, et al. Monitoring tropical forest structure using SAR tomography at L- and P-band[J]. Remote Sensing, 2019, 11(16): 1934. doi: 10.3390/rs11161934
[10]	PIAU P, BRUNIQUEL J, CAEL J C, et al. Analysis of the resolution of a multitemporal SAR System[C]. IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 1993: 1196–1199.
[11]	ZHU Xiaoxiang and BAMLER R. Tomographic SAR inversion by L₁ norm regularization—the compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. doi: 10.1109/TGRS.2010.2048117
[12]	魏恋欢, 廖明生, BALZ T, 等. 高分辨率SAR层析成像建筑物叠掩散射体提取[J]. 武汉大学学报: 信息科学版, 2014, 39(5): 536–540. doi: 10.13203/j.whugis20120460 WEI Lianhuan, LIAO Mingsheng, BALZ T, et al. Layover building scatterers extraction via high-resolution spaceborne SAR tomography[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 536–540. doi: 10.13203/j.whugis20120460
[13]	毕辉, 金双, 王潇, 等. 基于高分三号SAR数据的城市建筑高分辨率高维成像[J]. 雷达学报, 2022, 11(1): 40–51. doi: 10.12000/JR21113 BI Hui, JIN Shuang, WANG Xiao, et al. High-resolution high-dimensional imaging of urban building based on GaoFen-3 SAR data[J]. Journal of Radars, 2022, 11(1): 40–51. doi: 10.12000/JR21113
[14]	LOMBARDINI F and REIGBER A. Adaptive spectral estimation for multibaseline SAR tomography with airborne L-band data[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003: 2014–2016.
[15]	SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830
[16]	廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 123–129. doi: 10.12000/JR15031 LIAO Mingsheng, WEI Lianhuan, WANG Ziyun, et al. Compressive sensing in high-resolution 3D SAR tomography of urban scenarios[J]. Journal of Radars, 2015, 4(2): 123–129. doi: 10.12000/JR15031
[17]	仇晓兰, 焦泽坤, 彭凌霄, 等. SARMV3D-1.0: SAR微波视觉三维成像数据集[J]. 雷达学报, 2021, 10(4): 485–498. doi: 10.12000/JR21112 QIU Xiaolan, JIAO Zekun, PENG Lingxiao, et al. SARMV3D-1.0: Synthetic aperture radar microwave vision 3D imaging dataset[J]. Journal of Radars, 2021, 10(4): 485–498. doi: 10.12000/JR21112
[18]	ZHU Xiaoxiang and BAMLER R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. doi: 10.1109/TGRS.2011.2160183
[19]	ZHU Xiaoxiang and BAMLER R. Superresolving SAR tomography for multidimensional imaging of urban areas: Compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. doi: 10.1109/MSP.2014.2312098
[20]	ZHANG Bangjie, XU Gang, YU Hangwen, et al. Array 3-D SAR tomography using robust gridless compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5205013. doi: 10.1109/TGRS.2023.3259980
[21]	林赟, 张琳, 韦立登, 等. 无先验模型复杂结构设施SAR全方位三维成像方法研究[J]. 雷达学报, 2022, 11(5): 909–919. doi: 10.12000/JR22148 LIN Yun, ZHANG Lin, WEI Lideng, et al. Research on full-aspect three-dimensional SAR imaging method for complex structural facilities without prior model[J]. Journal of Radars, 2022, 11(5): 909–919. doi: 10.12000/JR22148
[22]	REN Yexian, XIAO Aoran, HU Fengming, et al. Coprime sensing for airborne array interferometric SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5229615. doi: 10.1109/TGRS.2022.3182980
[23]	LI Xiaowan, ZHANG Fubo, LI Yanlei, et al. An elevation ambiguity resolution method based on segmentation and reorganization of TomoSAR point cloud in 3D mountain reconstruction[J]. Remote Sensing, 2021, 13(24): 5118. doi: 10.3390/rs13245118
[24]	仇晓兰, 焦泽坤, 杨振礼, 等. 微波视觉三维SAR关键技术及实验系统初步进展[J]. 雷达学报, 2022, 11(1): 1–19. doi: 10.12000/JR22027 QIU Xiaolan, JIAO Zekun, YANG Zhenli, et al. Key technology and preliminary progress of microwave vision 3D SAR experimental system[J]. Journal of Radars, 2022, 11(1): 1–19. doi: 10.12000/JR22027
[25]	ZHU Xiaoxiang and BAMLER R. Sparse reconstruction techniques for SAR tomography[C]. 17th International Conference on Digital Signal Processing, Corfu, Greece, 2011: 1–8.
[26]	JIAO Zekun, DING Chibiao, QIU Xiaolan, et al. Urban 3D imaging using airborne TomoSAR: Contextual information-based approach in the statistical way[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 170: 127–141. doi: 10.1016/j.isprsjprs.2020.10.013
[27]	WANG Xiao and XU Feng. Tomographic SAR inversion by atomic-norm minimization—the gridless compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5239113. doi: 10.1109/TGRS.2022.3223524
[28]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[29]	CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129–159. doi: 10.1137/S003614450037906X
[30]	王金峰, 皮亦鸣, 曹宗杰. 一种机载SAR层析三维成像算法[J]. 电子与信息学报, 2010, 32(5): 1029–1033. doi: 10.3724/SP.J.1146.2009.00737 WANG Jinfeng, PI Yiming, and CAO Zongjie. An algorithm for airborne SAR tomography 3D imaging[J]. Journal of Electronics &Information Technology, 2010, 32(5): 1029–1033. doi: 10.3724/SP.J.1146.2009.00737
[31]	GUO Rui, WANG Fan, ZANG Bo, et al. High-rise building 3D reconstruction with the wrapped interferometric phase[J]. Sensors, 2019, 19(6): 1439. doi: 10.3390/s19061439
[32]	GUO Rui, GAO Yuxin, ZHANG Zhao, et al. Efficient tomographic inversion based on refined scatterer pre-estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4513305. doi: 10.1109/LGRS.2022.3203037

施引文献

期刊类型引用(7)

1.	付丽梅. 基于选定区域颜色直方图的粒子滤波行人跟踪算法. 软件工程. 2021(07): 31-34 . 百度学术
2.	花文号，陈霄，薛安克. 基于权值选择的多雷达多目标检测前跟踪算法. 杭州电子科技大学学报(自然科学版). 2020(02): 34-39 . 百度学术
3.	冉星浩，杨路，李春波. 基于权值优选的改进二阶中心差分粒子滤波算法. 测控技术. 2020(07): 68-72 . 百度学术
4.	裴家正，黄勇，董云龙，何友，陈小龙. 杂波背景下基于概率假设密度的辅助粒子滤波检测前跟踪改进算法. 雷达学报. 2019(03): 355-365 . 本站查看
5.	裴家正，黄勇，董云龙，何友，陈小龙，陈唯实. 基于PHD的粒子滤波检测前跟踪改进算法. 雷达科学与技术. 2019(03): 263-270+279 . 百度学术
6.	张忠子. 基于改进粒子滤波跟踪算法的运动视频跟踪. 现代电子技术. 2019(15): 59-62 . 百度学术
7.	王经鹤，易伟，孔令讲. 组网雷达多帧检测前跟踪算法研究. 雷达学报. 2019(04): 490-500 . 本站查看

其他类型引用(6)

资源附件(0)

访问统计

图(12) / 表(6)

计量

文章访问数: 788
HTML全文浏览量: 238
PDF下载量: 239
被引次数: 13

1. 引言
2. 系统模型
2.1 目标状态模型
2.2 量测模型
3. 杂波环境下扩展目标的PF-TBD算法
4. 仿真实验
5. 总结

基于自适应高程约束的TomoSAR三维成像

DOI: 10.12000/JR23111 CSTR: 32380.14.JR23111

通讯作者:
郭睿 gr2003@nwpu.edu.cn

计量

Three-dimensional Imaging of Tomographic SAR Based on Adaptive Elevation Constraint

Corresponding author: GUO Rui, gr2003@nwpu.edu.cn

1. 引言

2. 系统模型

2.1 目标状态模型

2.2 量测模型

3. 杂波环境下扩展目标的PF-TBD算法

4. 仿真实验

5. 总结

期刊类型引用(7)

其他类型引用(6)

计量

目录

1. 引言

2. 系统模型

2.1 目标状态模型

2.2 量测模型

3. 杂波环境下扩展目标的PF-TBD算法

4. 仿真实验

5. 总结

期刊介绍

联系我们

基于自适应高程约束的TomoSAR三维成像

DOI: 10.12000/JR23111 CSTR: 32380.14.JR23111

通讯作者: 郭睿 gr2003@nwpu.edu.cn

计量

出版历程

Three-dimensional Imaging of Tomographic SAR Based on Adaptive Elevation Constraint

Corresponding author: GUO Rui, gr2003@nwpu.edu.cn

1. 引言

2. 系统模型

2.1 目标状态模型

2.2 量测模型

3. 杂波环境下扩展目标的PF-TBD算法

4. 仿真实验

5. 总结

期刊类型引用(7)

其他类型引用(6)

计量

出版历程

目录

1. 引言

2. 系统模型

2.1 目标状态模型

2.2 量测模型

3. 杂波环境下扩展目标的PF-TBD算法

4. 仿真实验

5. 总结

期刊介绍

联系我们

通讯作者:
郭睿 gr2003@nwpu.edu.cn